Meteosat Land Surface Temperature Climate Data Record: Achievable Accuracy and Potential Uncertainties
Abstract
:1. Introduction
2. Data and Methods
2.1. Satellite Data
2.2. Generalized Split-Window Model
2.3. Physical Mono-Window Model
2.4. Statistical Mono-Window Model
2.5. Theoretical Uncertainty Characterization
2.6. Ground-Based LST Measurements
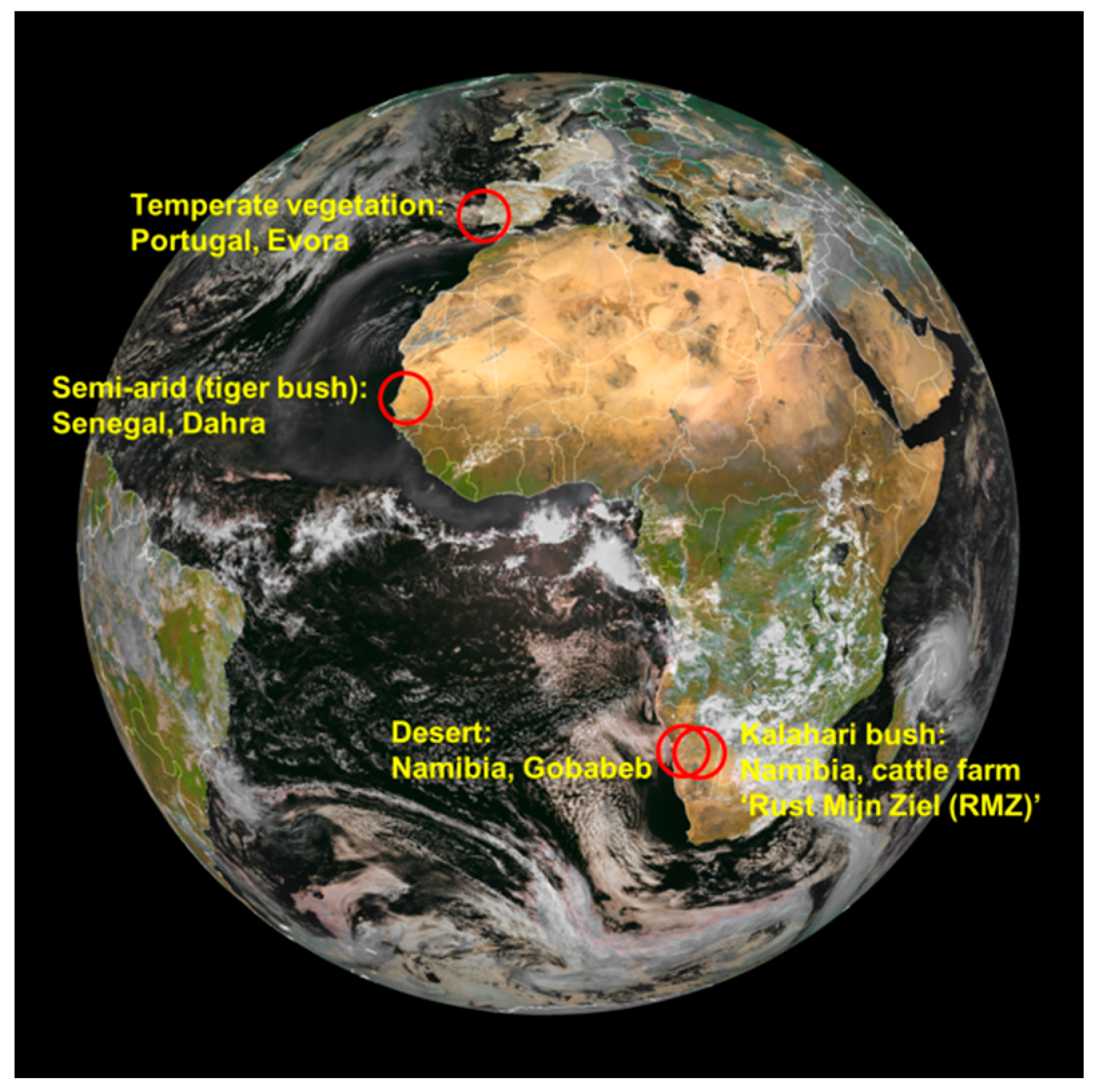
| Dahra | RMZ | Gobabeb | Evora | |
|---|---|---|---|---|
| Location | Senegal | Namibia | Namibia | Portugal |
| Lat.:
15.402336 Lon.: −15.432744 | Lat.:
−23.010532 Lon.:18.352897 | Lat.:
−23.550956 Lon.: 15.05138 | Lat.:
38.540244 Lon.: −8.003368 | |
| Elevation | 90 m | 1450 m | 406 m | 230 m |
| Climate Zone | Tropical Wet-Dry | Steppe | Desert | Mediterranean |
| TCWV 2010 | 17 to 56 mm | 2 to 28 mm | 1 to 38 mm | 2 to 43 mm |
| Vegetation | Grassland; 96% grass,4% tree | Savanna; 85% grass/soil, 15% tree | Baren; 32% tree, 68% grass | Woody savanna with isolated groups of evergreen oak trees |
3. Results and Discussions
3.1. Theoretical Uncertainty Analysis
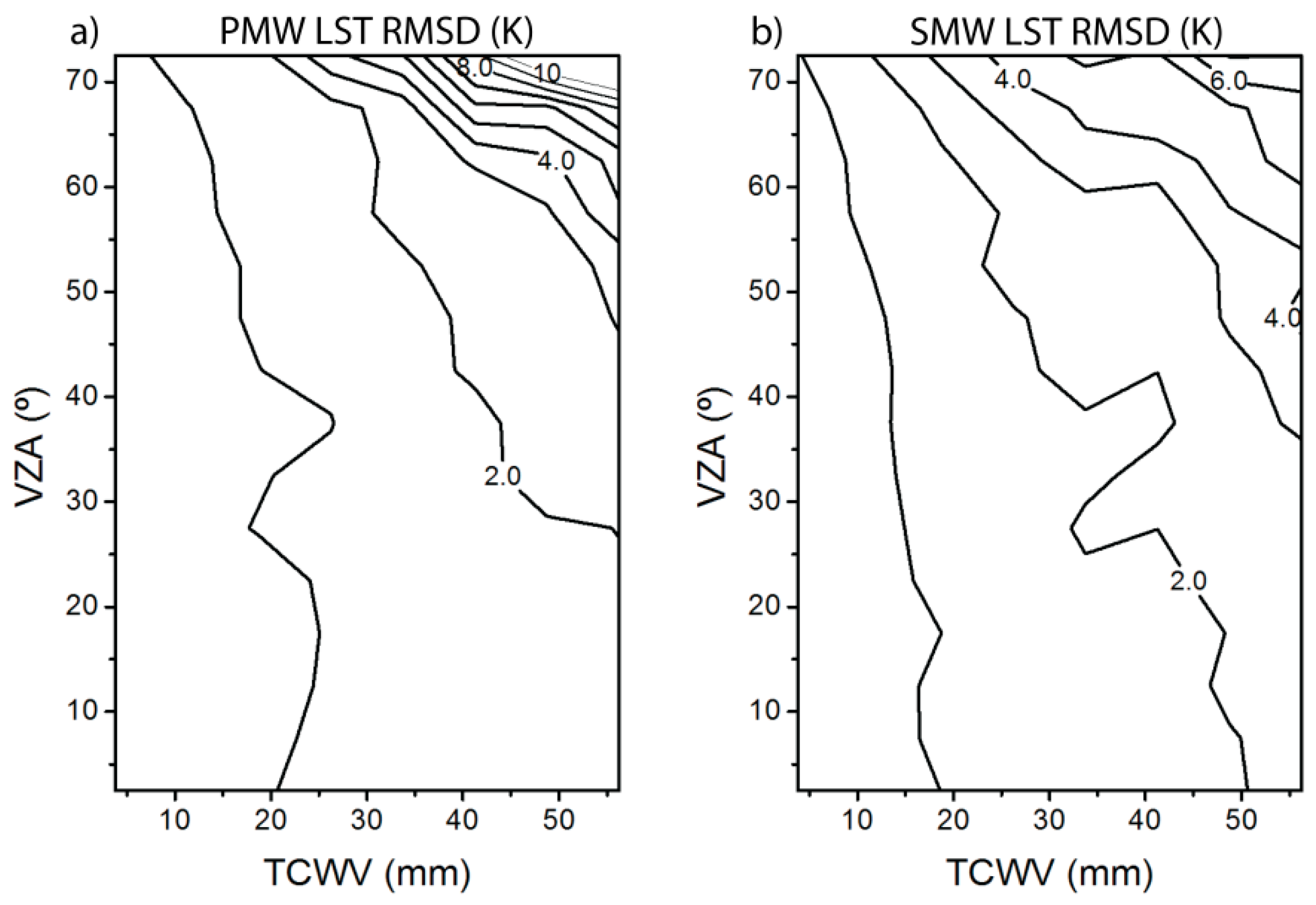
| PMW | SMW | |||
|---|---|---|---|---|
| RMSD (K) | BIAS (K) | RMSD (K) | BIAS (K) | |
| TCWV ≤ 45 mm | 1.6 | −0.2 | 1.6 | −0.1 |
| TCWV > 45 mm | 3.3 | −1.1 | 3.4 | −0.6 |
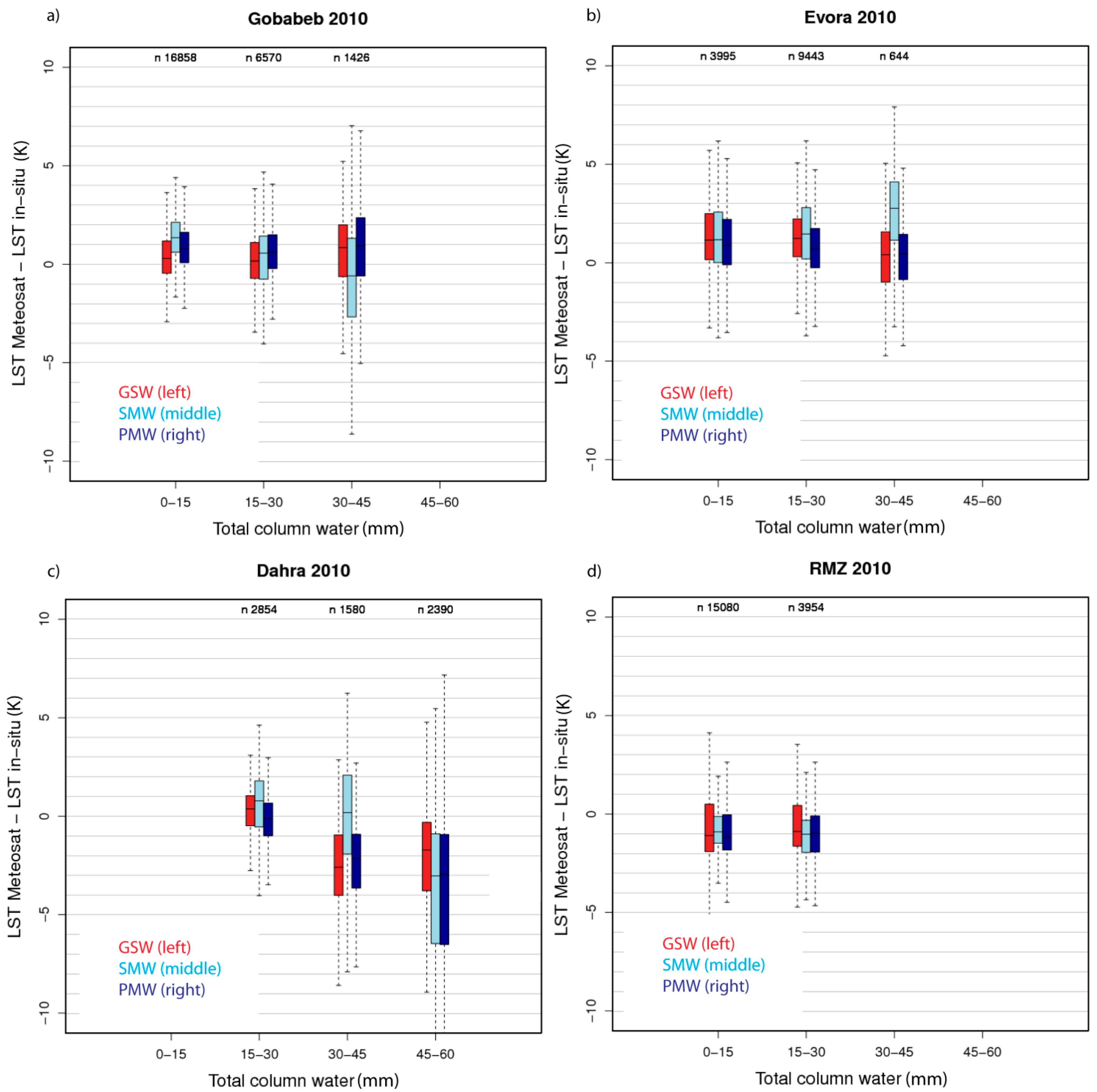
3.2. Ground-Based Validation
| GSW | PMW | SMW | ||||
|---|---|---|---|---|---|---|
| RMSD (K) | BIAS (K) | RMSD (K) | BIAS (K) | RMSD (K) | BIAS (K) | |
| Gobabeb | 1.5 | 0.4 | 1.8 | 0.8 | 2.0 | 0.9 |
| Evora | 2.0 | 1.2 | 1.9 | 0.7 | 2.5 | 1.4 |
| Dahra | 2.3 | −0.8 | 2.6 | −1.2 | 2.4 | 0.4 |
| RMZ | 1.9 | −0.5 | 1.9 | −0.8 | 1.7 | −0.8 |
| GSW | PMW | SMW | ||||
|---|---|---|---|---|---|---|
| RMSD (K) | BIAS (K) | RMSD (K) | BIAS (K) | RMSD (K) | BIAS (K) | |
| Dahra | 3.4 | −2.2 | 6.3 | −4.3 | 5.3 | −3.0 |
3.2.1. Gobabeb Station
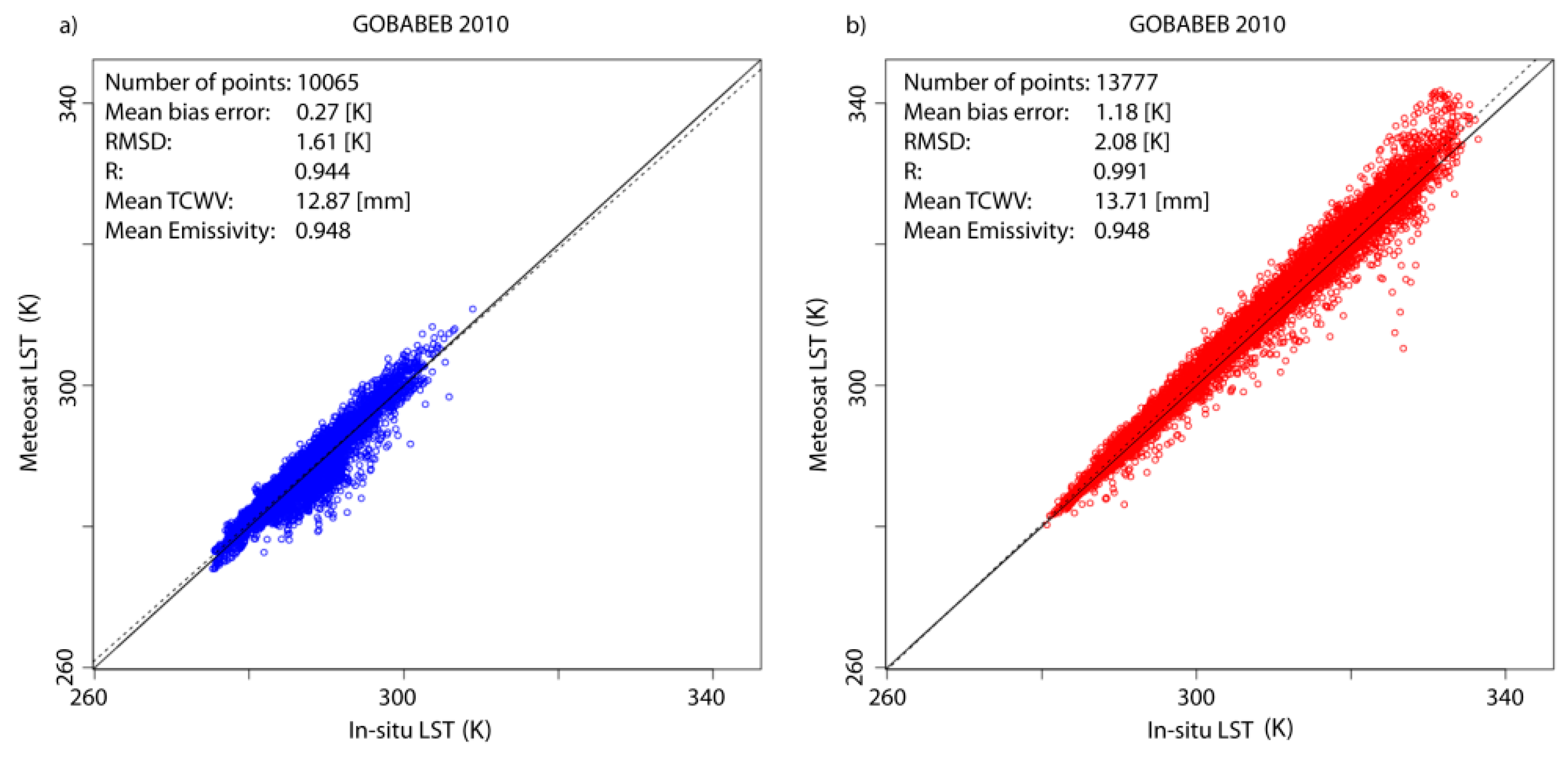
3.2.2. Dahra Station
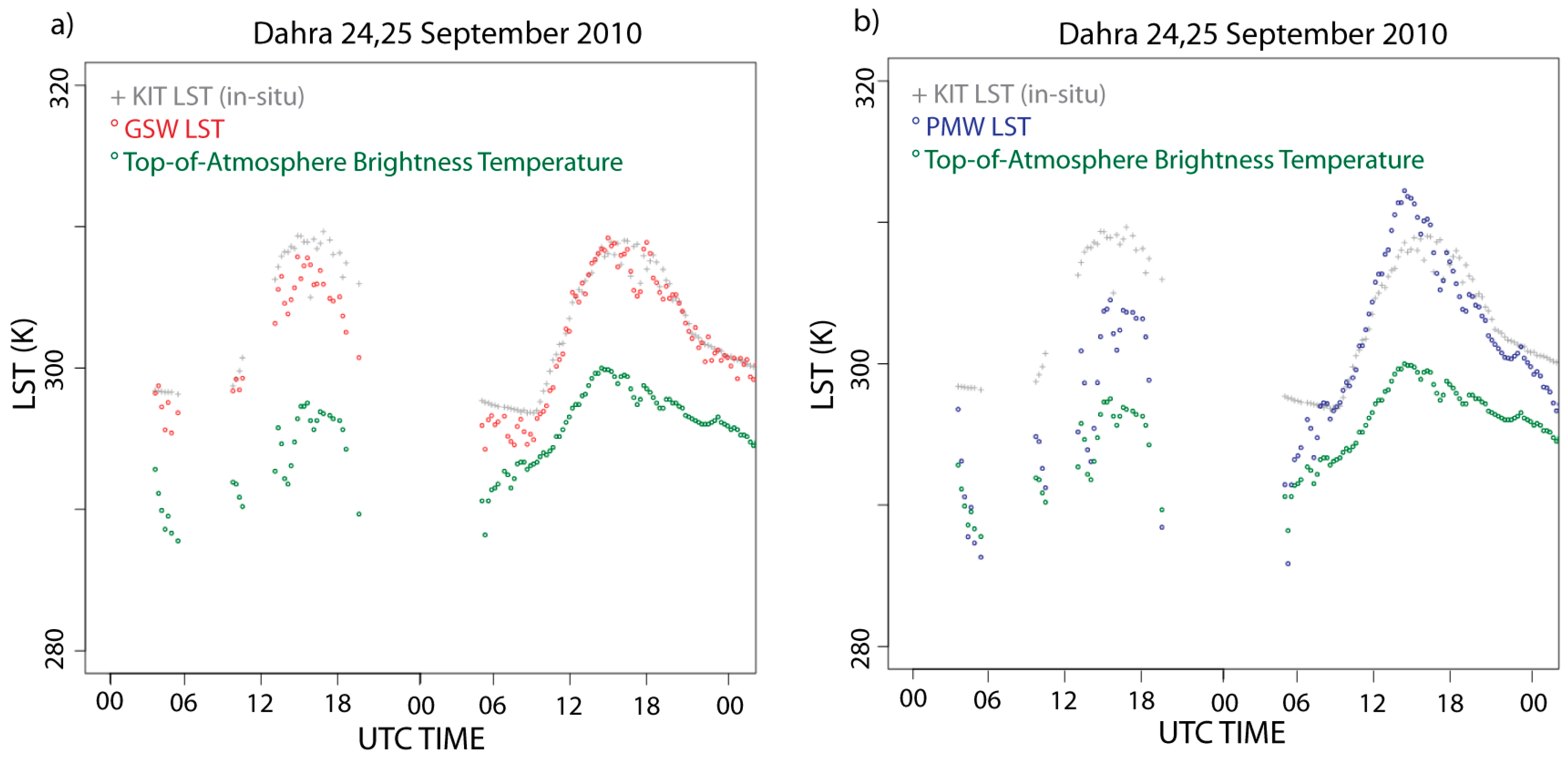
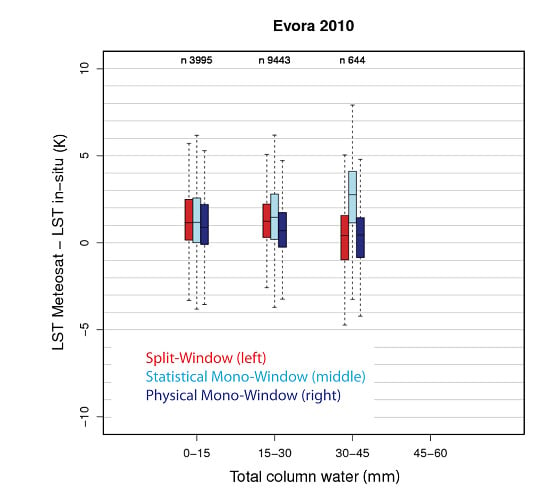
3.2.3. RMZ and Evora Stations
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bodas-Salcedo, A.; Ringer, M.; Jones, A. Evaluation of the surface radiation budget in the atmospheric component of the Hadley Centre Global Environmental Model (HADGEM1). J. Clim. 2008, 21, 4723–4748. [Google Scholar] [CrossRef]
- Wan, Z.; Wang, P.; Li, X. Using MODIS land surface temperature and normalized difference vegetation index products for monitoring drought in the southern Great Plains, USA. Int. J. Remote Sens. 2004, 25, 61–72. [Google Scholar] [CrossRef]
- Kustas, W.; Norman, J. Use of remote sensing for evapotranspiration monitoring over land surfaces. Hydrol. Sci. J. 1996, 41, 495–516. [Google Scholar] [CrossRef]
- Bosilovich, M.; Radakovich, J.; da Silva, A.; Todling, R.; Verter, F. Skin temperature analysis and bias correction in a coupled land-atmosphere data assimilation system. J. Meteorol. Soc. Japan 2007, 85, 205–228. [Google Scholar] [CrossRef]
- Reichle, R.; Kumar, S.; Mahanama, S.; Koster, R.; Liu, Q. Assimilation of satellite-derived skin temperature observations into land surface models. J. Hydrometeorol. 2010, 11, 1103–1122. [Google Scholar] [CrossRef]
- Ghent, D.; Kaduk, J.; Remedios, J.; Ardo, J.; Balzter, H. Assimilation of land surface temperature into the land surface model JULES with an ensemble Kalman filter. J. Geophys. Res.-Atmos. 2010, 115, 19. [Google Scholar] [CrossRef]
- GCOS 2011 Report: Systematic Observation Requirements for Satellite-Based Datasets for Climate 2011 Update. Available online: https://www.wmo.int/pages/prog/gcos/Publications/gcos-154.pdf (accessed on 21 May 2015).
- Heidinger, A.; Laszlo, I.; Molling, C.; Tarpley, D. Using SURFRAD to verify the NOAA single-channel land surface temperature algorithm. J. Atmos. Ocean. Technol. 2013, 30, 2868–2884. [Google Scholar] [CrossRef]
- Garand, L. Toward an integrated land-ocean surface skin temperature analysis from the variational assimilation of infrared radiances. J. Appl. Meteorol. 2003, 42, 570–583. [Google Scholar] [CrossRef]
- Göttsche, F.; Olesen, F. Modelling the effect of optical thickness on diurnal cycles of land surface temperature. Remote Sens. Environ. 2009, 113, 2306–2316. [Google Scholar] [CrossRef]
- Rossow, W.; Schiffer, R. Advances in understanding clouds from ISCCP. Bull. Am. Meteorol. Soc. 1999, 80, 2261–2287. [Google Scholar] [CrossRef]
- Freitas, S.; Trigo, I.; Bioucas-Dias, J.; Göttsche, F. Quantifying the uncertainty of land surface temperature retrievals from Seviri/Meteosat. IEEE Trans. Geos. Remote Sens. 2010, 48, 523–534. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geos. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Trigo, I.; Monteiro, I.; Olesen, F.; Kabsch, E. An assessment of remotely sensed land surface temperature. J. Geophys. Res.-Atmos. 2008, 113, D17. [Google Scholar] [CrossRef]
- Trigo, I.; Freitas, S.C.; Bioucas-Dias, J.; Barroso, C.; Monteiro, I.T.; Viterbo, P. Algorithm Theoretical Basis Document for Land Surface Temperature (LST), LSA-4 (MLST); Land Surface Analysis Satellite Application Facility: Darmstadt, Germany, 2009. [Google Scholar]
- Sun, D.; Pinker, R.; Basara, J. Land surface temperature estimation from the next generation of geostationary operational environmental satellites: GOES M-Q. J. Appl. Meteorol. 2004, 43, 363–372. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.; Sobrino, J. A generalized single-channel method for retrieving land surface temperature from remote sensing data. J. Geophys. Res.-Atmos. 2004, 109, D22. [Google Scholar] [CrossRef]
- Reutter, H.; Olesen, F.; Fischer, H. Distribution of the brightness temperature of land surfaces determined from AVHRR data. Int. J. Remote Sens. 1994, 15, 95–104. [Google Scholar] [CrossRef]
- Scarino, B.; Minnis, P.; Palikonda, R.; Reichle, R.; Morstad, D.; Yost, C.; Shan, B.; Liu, Q. Retrieving clear-sky surface skin temperature for numerical weather prediction applications from geostationary satellite data. Remote Sens. 2013, 5, 342–366. [Google Scholar] [CrossRef]
- Göttsche, F.; Olesen, F.; Bork-Unkelbach, A. Validation of operational land surface temperature products with three years of continuous in-situ measurements. In Proceedings of the EUMETSAT Meteorological Satellite Conference, Oslo, Norway, 5–9 September 2011.
- Yu, X.; Guo, X.; Wu, Z. Land surface temperature retrieval from LANDSAT 8 TIRS-comparison between radiative transfer equation-based method, split window algorithm and single channel method. Remote Sens. 2014, 6, 9829–9852. [Google Scholar] [CrossRef]
- Freitas, S.; Trigo, I.; Macedo, J.; Barroso, C.; Silva, R.; Perdigao, R. Land surface temperature from multiple geostationary satellites. Int. J. Remote Sens. 2013, 34, 3051–3068. [Google Scholar] [CrossRef]
- Göttsche, F.; Olesen, F. Modelling of diurnal cycles of brightness temperature extracted from METEOSAT data. Remote Sens. Environ. 2001, 76, 337–348. [Google Scholar] [CrossRef]
- Peres, L.F.; da Camara, C.C. Emissivity maps to retrieve land-surface temperature from MSG/SEVIRI. IEEE Trans. Geos. Remote Sens. 2005, 43, 1834–1844. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Trigo, I.; Peres, L.; da Carnara, C.; Freitas, S. Thermal land surface emissivity retrieved from SEVIRI/METEOSAT. IEEE Trans. Geos. Remote Sens. 2008, 46, 307–315. [Google Scholar] [CrossRef]
- Saunders, R.; Matricardi, M.; Brunel, P. An improved fast radiative transfer model for assimilation of satellite radiance observations. Q. J. Royal Meteorol. Soc. 1999, 125, 1407–1425. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.; Acharya, P.; Ghetwynd, J.; Bernstein, L.; Shettle, E.; Matthew, M.; Adler-Golden, S. MODTRAN4 User’s Manual; Air Force Research Laboratory: Hanscom, MA, USA, 1999. [Google Scholar]
- Hocking, J.; Rayer, P.J.; Rundle, D.; Saunders, R.W.; Matricardi, M.; Geer, A.; Brunel, P.; Vidot, J. RTTOV v11 Users Guide; Nowcasting Satellite Application Facility (NWC-SAF): Darmstadt, Germany, 2014. [Google Scholar]
- Bento, V. Exploring RTTOV to Retrieve Land Surface Temperature from a Geostationary Satellite Constellation. Master’s Thesis, University Lisbon, Lisbon, Portugal, 2013. [Google Scholar]
- Dee, D.; Uppala, S.; Simmons, A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. Royal Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Borbas, E.E.; Wetzel, S.S.; Huang, H.L.; Li, J. Global profile training database for satellite regression retrievals with estimates of skin temperature and emissivity. In Proceedings of the XIV International ATOVS Study Conference, Beijing, China, 25–31 May 2005; pp. 763–770.
- Hewison, T.J.; König, M. Inter-calibration of Meteosat imagers and IASI. In Proceedings of the EUMETSAT Meteorological Satellite Conference, Darmstadt, Germany, 8–12 September 2008.
- Göttsche, F.; Olesen, F.; Bork-Unkelbach, A. Validation of land surface temperature derived from MSG/SEVIRI with in situ measurements at Gobabeb, Namibia. Int. J. Remote Sens. 2013, 34, 3069–3083. [Google Scholar] [CrossRef]
- Bork-Unkelbach, A. Extrapolation von in-situ Landoberflächentemperaturen auf Satellitenpixel. Ph.D. Thesis, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2012. [Google Scholar]
- Göttsche, F.; Hulley, G. Validation of six satellite-retrieved land surface emissivity products over two land cover types in a hyper-arid region. Remote Sens. Environ. 2012, 124, 149–158. [Google Scholar] [CrossRef]
- Kabsch, E.; Olesen, F.; Prata, F. Initial results of the land surface temperature (LST) validation with the Evora, Portugal ground-truth station measurements. Int. J. Remote Sens. 2008, 29, 5329–5345. [Google Scholar] [CrossRef]
- Theocharous, E.; Usadi, E.; Fox, N.P. CEOS Comparison of IR Brightness Temperature Measurements in Support of Satellite Validation. Part. I: Laboratory and Ocean Surface Temperature Comparison of Radiation Thermometers; National Physical Laboratory: Teddington, UK, 2010. [Google Scholar]
- Kondratyev, K.Y. Radiation in the Atmosphere; Academic Press: New York, NY, USA, 1969. [Google Scholar]
- Guillevic, P.C.; Bork-Unkelbach, A.; Göttsche, F.M.; Hulley, G.; Gastellu-Etchegorry, J.-P.; Olesen, F.S.; Privette, J.L. Directional viewing effects on satellite land surface temperature products over sparse vegetation canopies—A multisensor analysis. IEEE Geos. Remote Sens. Lett. 2013, 10, 1464–1468. [Google Scholar] [CrossRef]
- Peres, L.F.; da Camara, C.C. Land surface temperature and emissivity estimation based on the two-temperature method: Sensitivity analysis using simulated MSG/SEVIRI data. Remote Sens. Environ. 2004, 91, 377–389. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duguay-Tetzlaff, A.; Bento, V.A.; Göttsche, F.M.; Stöckli, R.; Martins, J.P.A.; Trigo, I.; Olesen, F.; Bojanowski, J.S.; Da Camara, C.; Kunz, H. Meteosat Land Surface Temperature Climate Data Record: Achievable Accuracy and Potential Uncertainties. Remote Sens. 2015, 7, 13139-13156. https://doi.org/10.3390/rs71013139
Duguay-Tetzlaff A, Bento VA, Göttsche FM, Stöckli R, Martins JPA, Trigo I, Olesen F, Bojanowski JS, Da Camara C, Kunz H. Meteosat Land Surface Temperature Climate Data Record: Achievable Accuracy and Potential Uncertainties. Remote Sensing. 2015; 7(10):13139-13156. https://doi.org/10.3390/rs71013139
Chicago/Turabian StyleDuguay-Tetzlaff, Anke, Virgílio A. Bento, Frank M. Göttsche, Reto Stöckli, João P. A. Martins, Isabel Trigo, Folke Olesen, Jędrzej S. Bojanowski, Carlos Da Camara, and Heike Kunz. 2015. "Meteosat Land Surface Temperature Climate Data Record: Achievable Accuracy and Potential Uncertainties" Remote Sensing 7, no. 10: 13139-13156. https://doi.org/10.3390/rs71013139
APA StyleDuguay-Tetzlaff, A., Bento, V. A., Göttsche, F. M., Stöckli, R., Martins, J. P. A., Trigo, I., Olesen, F., Bojanowski, J. S., Da Camara, C., & Kunz, H. (2015). Meteosat Land Surface Temperature Climate Data Record: Achievable Accuracy and Potential Uncertainties. Remote Sensing, 7(10), 13139-13156. https://doi.org/10.3390/rs71013139