First Polarimetric GNSS-R Measurements from a Stratospheric Flight over Boreal Forests
Abstract
:1. Introduction
2. Experimental Set-Up and Scenario

3. Results of a Stratospheric Balloon Experiment over Boreal Forests
| GNSS Code | Elevation Angle | PR (dB) (Forests) | PR (dB) (Lakes) |
|---|---|---|---|
| GPS L1 C/A | θe ~ 70° | 4.2 | 8 |
| GPS L2 P(Y) | θe ~ 70° | 14.6 | 20.4 |
| GPS L1 P(Y) | θe ~ 70° | 14.6 | 20.4 |
| GPS L2 C | θe ~ 70° | 8.1 | 12.7 |
| GLONASS L1 C/A | θe ~ 70° | 6.7 | 8.2 |
| GLONASS L2 C/A | θe ~ 70° | 6.3 | - |
| GLONASS L2 P | θe ~ 70° | 6.3 | - |
| Galileo E1 BC | θe ~ 60° | 4.1 | - |
| GNSS Code | SNRr (dB) θe~ 70° | SNRl (dB) θe~ 70° | SNRr (dB) θe~ 60° | SNRl (dB) θe~ 60° | SNRr (dB) θe~ 50° | SNRl (dB) θe~ 50° | SNRr (dB) θe~ 40° | SNRl (dB) θe~ 40° |
|---|---|---|---|---|---|---|---|---|
| GPS L1 C/A | 34 | 13 | 33 | 23 | 32 | 23 | 30 | 23 |
| GPS L2 P(Y) | 19 | - | 16 | - | 13 | - | 10 | - |
| GPS L1 P(Y) | 19 | - | 16 | - | 13 | - | 10 | - |
| GPS L2 C | 28 | 3 | 25 | 3 | 23 | 8 | 21 | 8 |
| GLONASS L1 C/A | 31 | 12 | 31 | 18 | 29 | 25 | 21 | 15 |
| GLONASS L2 C/A | 16 | - | 16 | - | 20 | - | 20 | - |
| GLONASS L2 P | 12 | - | 12 | - | 16 | - | 16 | - |
| Galileo E1 BC | 15 | - | 14 | - | 13 | - | 11 | - |
4. Final Discussions
5. Conclusions
Acknowledgments
Author Contributions
Appendix
Part I: Simulations of the Reflectivity over Boreal Forests
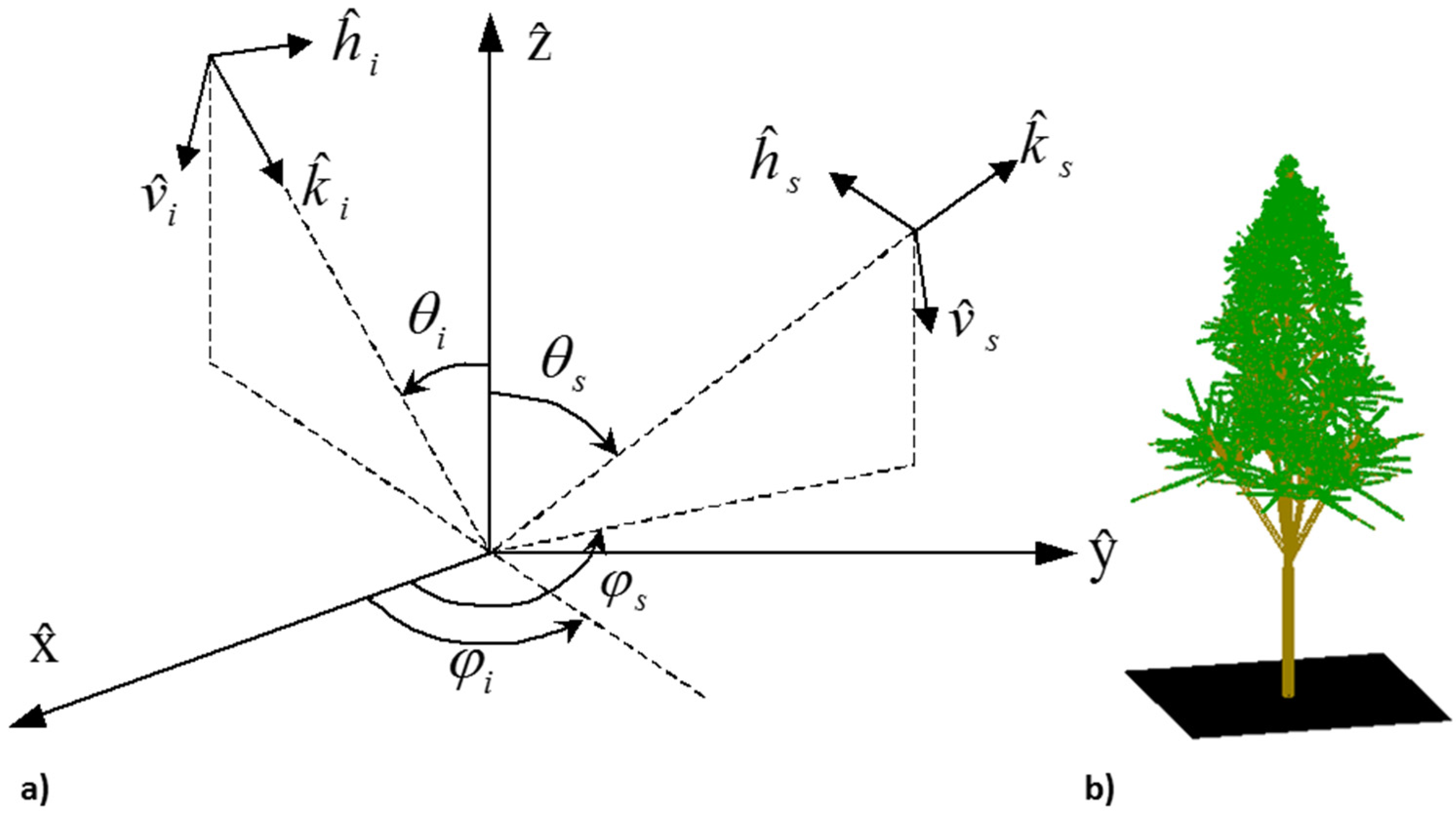
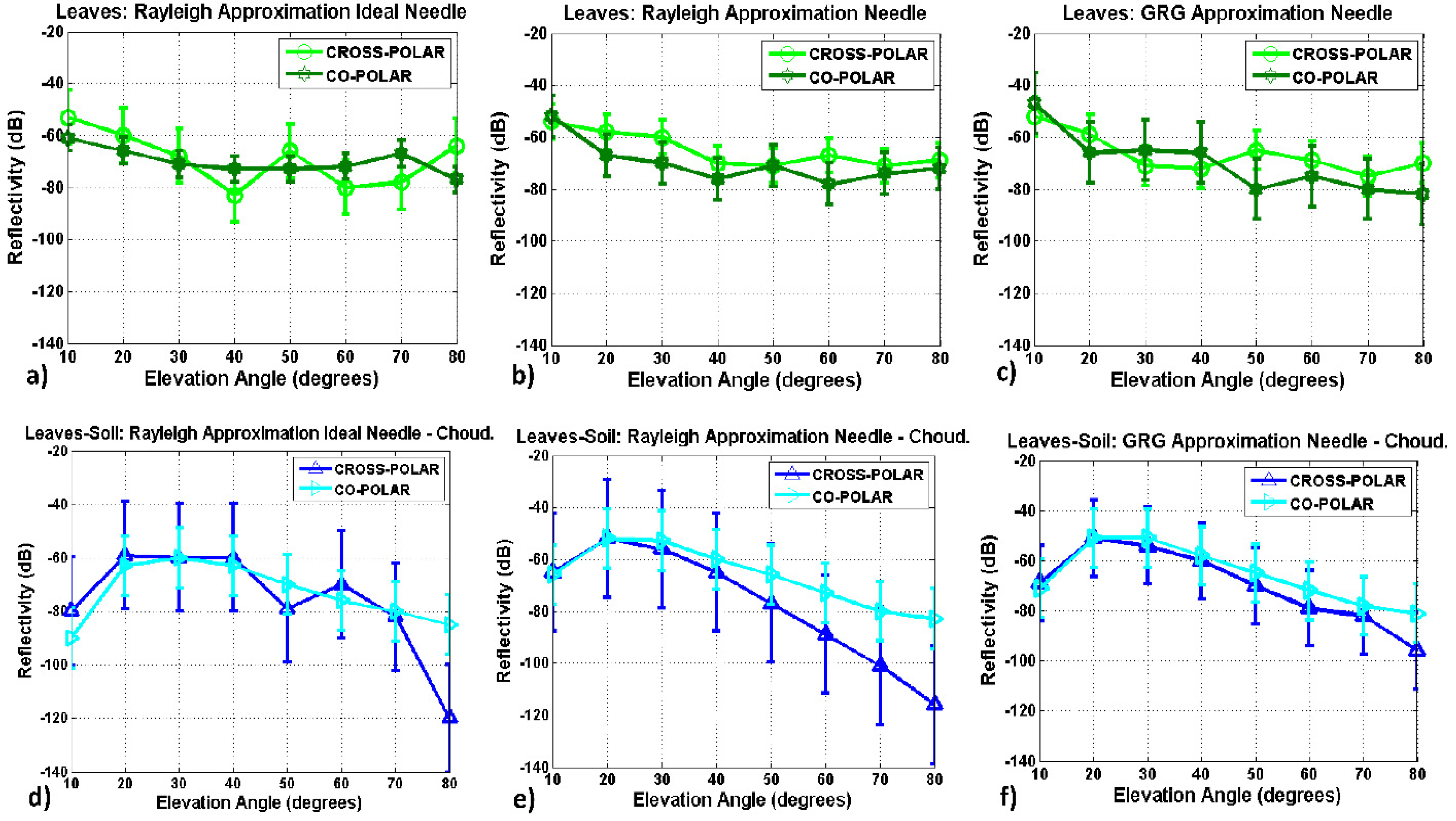
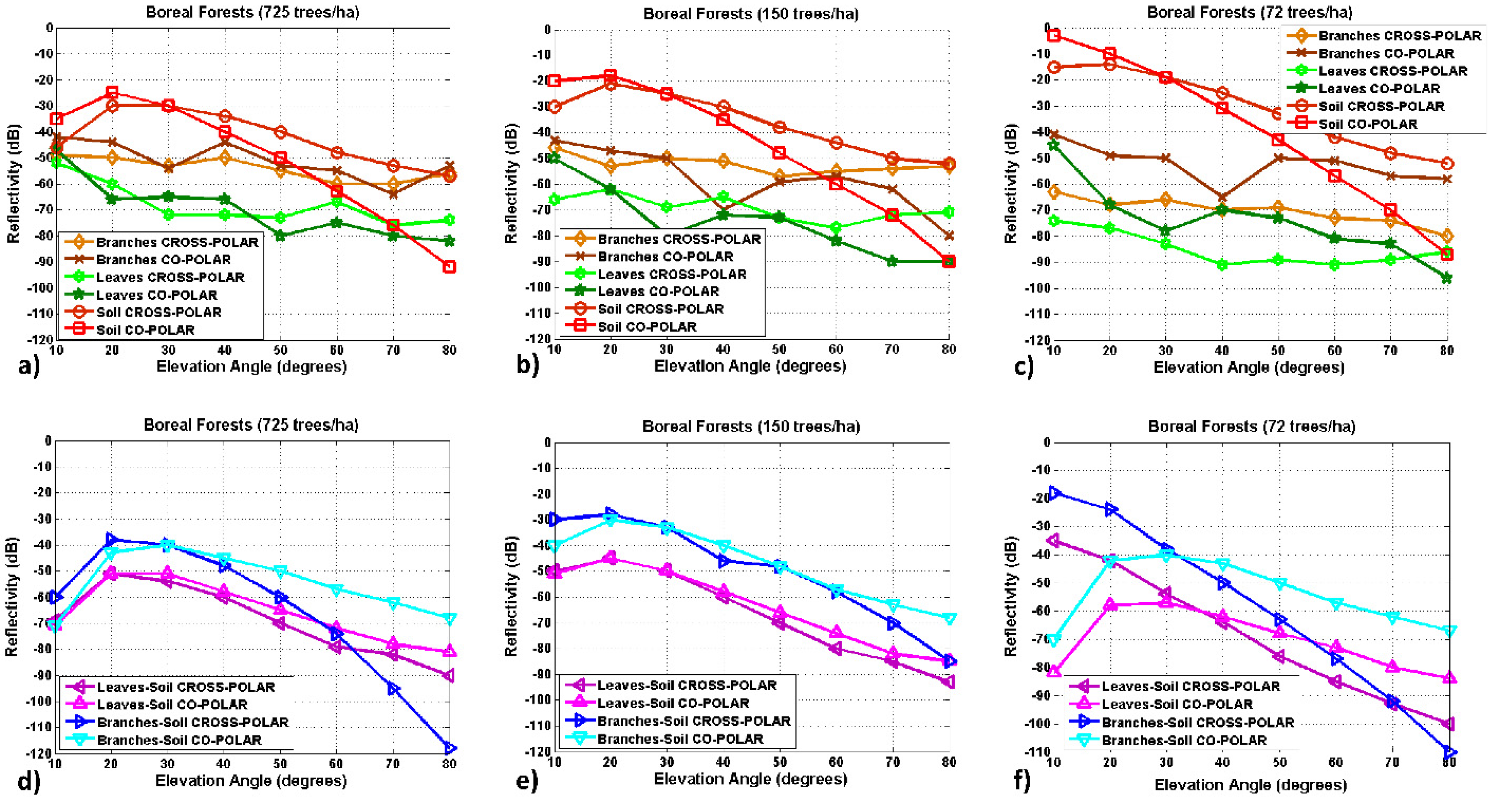
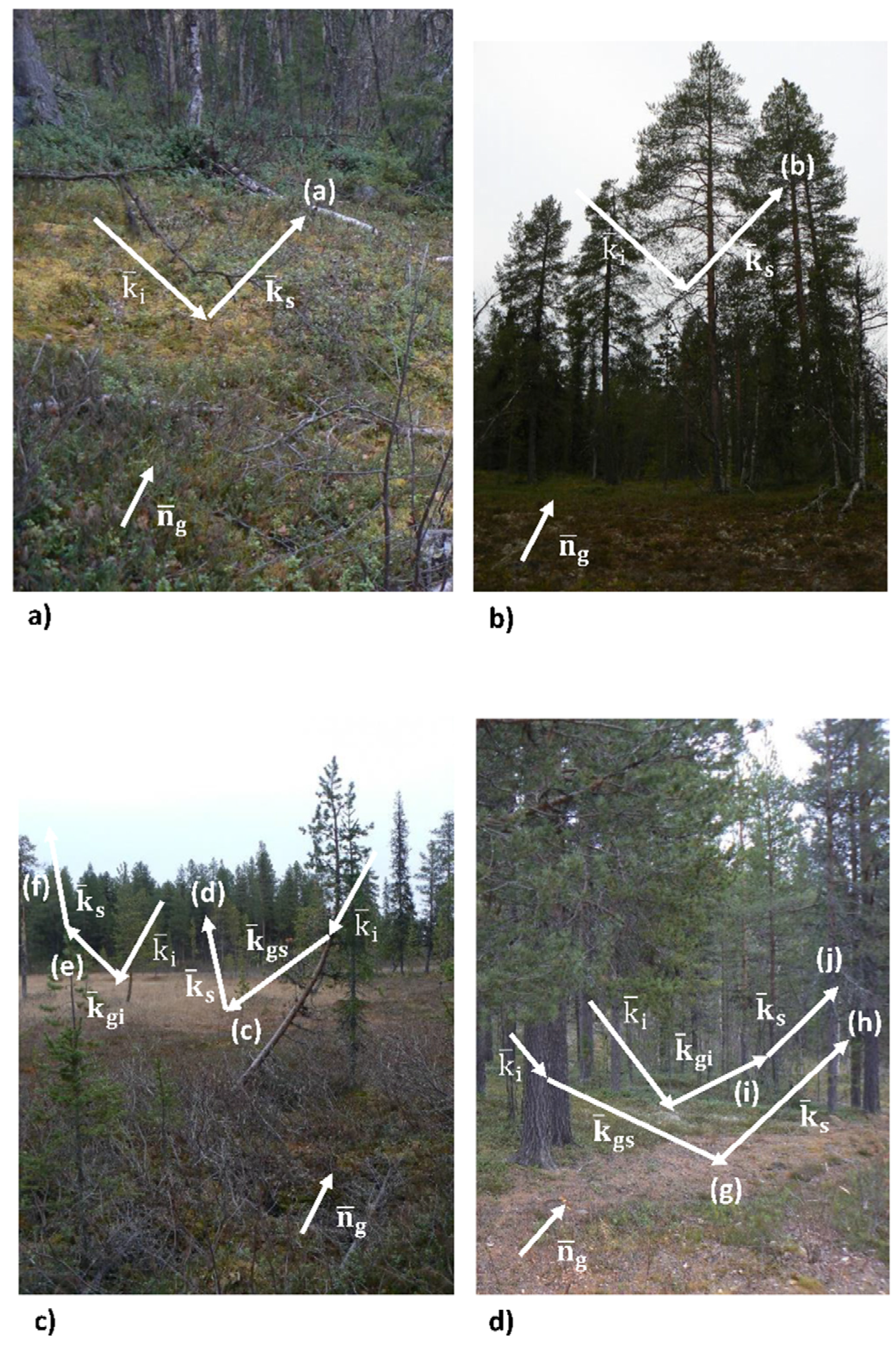
Part II: Theoretical Electromagnetic Model
Conflicts of Interest
References
- Martín-Neira, M. A PAssive Reflectometry and Interferometry System (PARIS): Application to ocean altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Garrison, J.L.; Katzberg, S.J.; Hill, M.I. Effect of sea roughness on bistatically scattered range coded signals from the global positioning system. Geophys. Res. Lett. 1998, 25, 2257–2260. [Google Scholar] [CrossRef]
- Fabra, F. GNSS-R as A Source of Opportunity for Remote Sensing of the Cryosphere. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2014. [Google Scholar]
- Rodriguez-Alvarez, N. Contributions to Earth Observation Using GNSS-R Opportunity Signals. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2011. [Google Scholar]
- Zavorotny, V.U.; Gleason, S.; Cardellach, E.; Camps, A. Tutorial on remote sensing using GNSS bistatic radar of opportunity. IEEE Geosci. Remote Sens. Mag. 2014, 2, 8–45. [Google Scholar] [CrossRef]
- Garrison, J.L.; Komjathy, A.; Zavorotny, V.; Katzberg, S.J. Wind speed measurement using forward scattered GPS signals. IEEE Trans. Geosci. Remote Sens. 2002, 40, 50–65. [Google Scholar] [CrossRef]
- Cardellach, E.; Rius, A.; Martín-Neira, M.; Fabra, F.; Ribó, S.; Kainulainen, J.; Camps, A.; D’Addio, S. Consolidating the precision of interferometric GNSS-R ocean altimetry using airborne experimental data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4992–5004. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Camps, A.; Ramos-Pérez, I.; Rius, A. Experimental evaluation of GNSS-reflectometry altimetric precision using the P (Y) and C/A signals. IEEE Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1493–1500. [Google Scholar] [CrossRef]
- Unwin, M.; Jales, P.; Curiel, A.S.; Brenchley, M.; Sweeting, M.; Gommenginger, C.; Roselló, J. Sea state determination with GNSS reflectometry on TechDemoSat-1. In Proceedings of the 2014 ESA Small Satellites, Systems and Services Symposium, Mallorca, Spain, 26–30 May 2014.
- Unwin, M. TechDemoSat-1 and the GNSS reflectometry experiment. Available online http://www.merrbys.co.uk:8080/CatalogueData/Documents/TDS-1%20SGR-ReSI%20Experiment.pdf (accessed on 5 June 2015).
- Rose, R.; Wells, W.; Rose, D.; Ruf, C.; Ridley, A.; Nave, K. Nanosat technology and managed risk: An update of the CYGNSS microsatellite constellation mission development. In Proceedings of the 28th AIAA/USU Conference on Small Satellites, Logan, UT, USA, 4–7 August 2014; pp. 1–12.
- Wickert, J.; Beyerle, G.; Cardellach, E.; Förste, C.; Gruber, T.; Helm, A.; Hess, M.P.; Hoeg, P.; Jakowski, N.; Kern, M.; et al. GEROS-ISS-GNSS rEflectometry, Radio Occultation and Scatterometry on-board the International Space Station. In Proceedings of 4th International Colloquium Scientific and Fundamental Aspects of the Galileo Programme, Espoo, Finland, 28–31 October 2013.
- Martín-Neira, M.; D’Addio, S.; Buck, C.; Floury, N.; Prieto-Cerdeira, R. The PARIS ocean altimeter in-orbit demonstrator. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2209–2237. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Camps, A.; Jové, R.; Alonso, A.; Olivé, R.; Amèzaga, A.; Vidal, D.; Munoz, J.F. The 3Cat-2 project: GNSS-R In-Orbit demonstrator for earth observation. In Proceedings of the 2014 ESA Small Satellites, Systems and Services Symposium, Mallorca, Spain, 26–30 May 2014.
- Zavorotny, V.U.; Voronovich, A.G. Bistatic GPS signal reflections at various polarizations from rough land surface with moisture content. In Proceedings of the 2000 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, Hawaii, USA, 24–28 July 2000; pp. 2852–2854.
- Ferrazzoli, P.; Guerriero, L.; Pierdicca, N.; Rahmoune, R. Forest biomass monitoring with GNSS-R: Theoretical simulations. Adv. Space Res. 2011, 47, 1823–1832. [Google Scholar] [CrossRef]
- Egido, A.; Paloscia, S.; Motte, E.; Guerriero, L.; Pierdicca, N.; Caparrini, M.; Santi, E.; Fontanelli, G.; Floury, N. Airborne GNSS-R soil moisture and above ground biomass observations. IEEE Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1522–1532. [Google Scholar] [CrossRef]
- Wu, X.R.; Jin, S.G. GPS-Reflectometry: Forest canopies polarization scattering properties and modelling. Adv. Space Res. 2014, 54, 863–870. [Google Scholar] [CrossRef]
- Martínez-Vazquez, A. Emisividad Polarimétrica del Terreno Efecto de la Vegetación. Master’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2001. [Google Scholar]
- Ledesma-Galera, I. Estudio Experimental del Comportamiento Radiométrico de LAS Superfícies naturales. Master’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2002. [Google Scholar]
- Kinnaird, A. BEXUS User Manual. Available online: http://www.rexusbexus.net/index.php?option=com_content&view=article&id=51&Itemid=63 (accessed on 5 December 2014).
- Cardellach, E.; Ribó, S.; Rius, A. Technical Note on Polarimetric Phase Interferometry (POPI). Available online: http://arxiv.org/pdf/physics/0606099.pdf (accessed on 1 March 2015).
- Beckmann, P.; Spizzichino, A. The Scattering of Electromagnetic Waves from Rough Surfaces; Artech House Inc.: Norwood, MA, USA, 1963; p. 125. [Google Scholar]
- Smyrnaios, M.; Schon, S. Multipath Propagation, Characterization and Modelling in GNSS. Available online: http://cdn.intechopen.com/pdfs-wm/43710.pdf (accessed on 9 September 2015).
- Woo, T.K. Optimum semi-codeless carrier phase tracking of L2. In Proceedings the 12th International Technical Meeting of the Satellite Division of the Institute of Navigation, Nashville, TN, USA, 14–17 September 1999; pp. 82–99.
- Yi-Cheng, L.; Sarabandi, K. A Monte Carlo coherent scattering model for forest canopies using fractal-generated trees. IEEE Trans. Geosci. Remote Sens. 1999, 37, 440–451. [Google Scholar] [CrossRef]
- Prusinkiewicz, P.; Lindenmayer, A. The Algorithmic Beauty of Plants; Springer-Verlag: New York, NY, USA, 1990. [Google Scholar]
- Tsang, L.; Kong, J.A.; Shin, R.T. Theory of Microwave Remote Sensing; Wiley Interscience: New York, NY, USA, 1985. [Google Scholar]
- Martínez-Vazquez, I.; Camps, A.; Lopez-Sanchez, J.M.; Vall-llosera, M.; Monerris, A. Numerical simulation of the full-polarimetric emissivity of vines and comparison with experimental data. Remote Sens. 2009, 1, 300–317. [Google Scholar] [CrossRef]
- Caicoya, A.T.; Kugler, F.; Hajnsek, I.; Papathanassiou, K. Boreal forest biomass classification with TANDEM-X. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 3439–3442.
- Global map of forest height produced from NASA’s ICESAT/GLAS, MODIS and TRMM sensors. Available online: http://www.nasa.gov/topics/earth/features/earth20120217map.html (accessed on 1 March 2015).
- Imhoff, M.L. Radar backscattering and biomass saturation: Ramifications for global biomass inventory. IEEE Trans. Geosci. Remote Sens. 1995, 33, 511–518. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Sarabandi, K. Electromagnetic scattering model for a tree trunk above a tilted ground plane. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1063–170. [Google Scholar]
- Karam, M.A.; Fung, A.K.; Antar, Y.M.M. Electromagnetic wave scattering from some vegetation samples. IEEE Trans. Geosci. Remote Sens. 1998, 26, 799–808. [Google Scholar] [CrossRef]
- Choudhury, B.J.; Schmugge, T.J.; Chang, A.; Newton, R.W. Effect of surface roughness on the microwave emission from soils. J. Geophys. Res. 1979, 84, 5699–5706. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Camps, A.; Vall-llosera, M.; Bosch-Lluis, X.; Monerris, A.; Ramos-Pérez, I.; Valencia, E.; Marchán-Hernandez, J.F.; Martinez-Fernandez, J.; Baroncini-Turricchia, G.; et al. Land geophysical parameters retrieval using the interference pattern GNSS-R technique. IEEE Trans. Geosci. Remote Sens. 2011, 49, 71–84. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Radar remote sensing and surface scattering and emission theory. In Microwave Remote Sensing: Active and Passive; Addison-Wesley: Reading, MA, USA, 1982; Volume II, pp. 1540–1541. [Google Scholar]
- Lindermayer, A. Developmental algorithms for multicellular organisms: A survey of L-systems. J. Theor. Bio. 1975, 54, 3–22. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave remote sensing fundamentals and radiometry. In Microwave Remote Sensing: Active and Passive; Addison-Wesley: Reading, MA, USA, 1982; Volume I, pp. 249–251. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carreno-Luengo, H.; Amèzaga, A.; Vidal, D.; Olivé, R.; Munoz, J.F.; Camps, A. First Polarimetric GNSS-R Measurements from a Stratospheric Flight over Boreal Forests. Remote Sens. 2015, 7, 13120-13138. https://doi.org/10.3390/rs71013120
Carreno-Luengo H, Amèzaga A, Vidal D, Olivé R, Munoz JF, Camps A. First Polarimetric GNSS-R Measurements from a Stratospheric Flight over Boreal Forests. Remote Sensing. 2015; 7(10):13120-13138. https://doi.org/10.3390/rs71013120
Chicago/Turabian StyleCarreno-Luengo, Hugo, Adriá Amèzaga, David Vidal, Roger Olivé, Juan Fran Munoz, and Adriano Camps. 2015. "First Polarimetric GNSS-R Measurements from a Stratospheric Flight over Boreal Forests" Remote Sensing 7, no. 10: 13120-13138. https://doi.org/10.3390/rs71013120
APA StyleCarreno-Luengo, H., Amèzaga, A., Vidal, D., Olivé, R., Munoz, J. F., & Camps, A. (2015). First Polarimetric GNSS-R Measurements from a Stratospheric Flight over Boreal Forests. Remote Sensing, 7(10), 13120-13138. https://doi.org/10.3390/rs71013120








