A Practical Split-Window Algorithm for Estimating Land Surface Temperature from Landsat 8 Data
Abstract
:1. Introduction
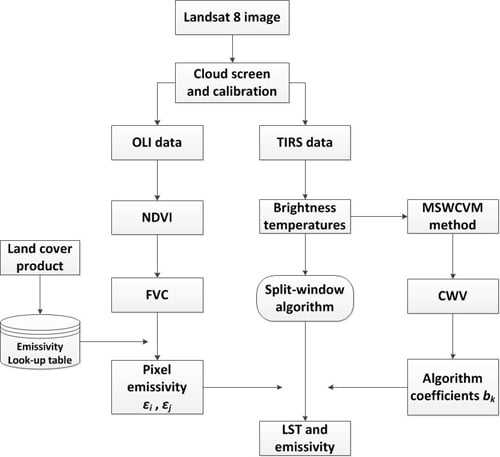
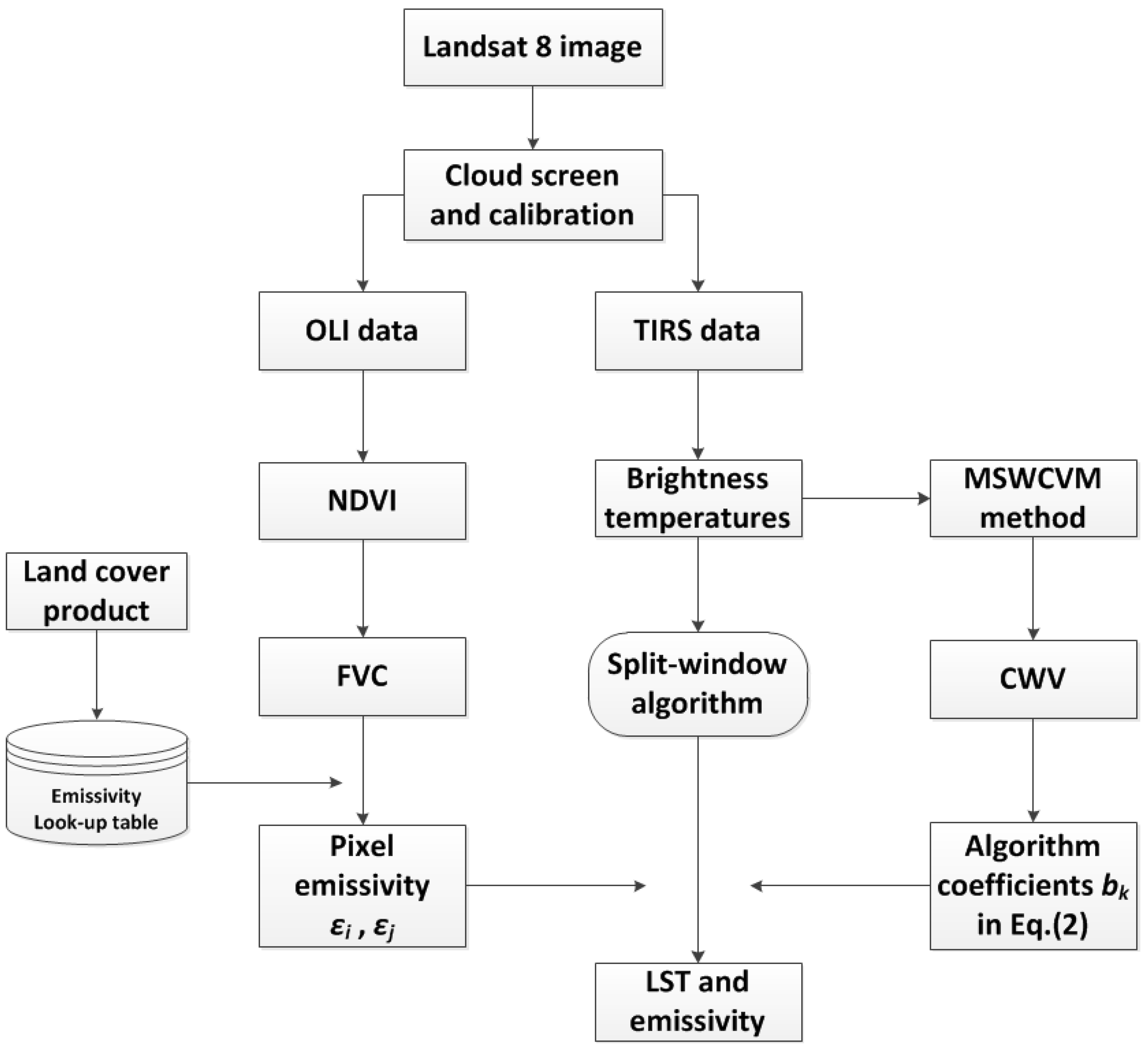
2. Methodology
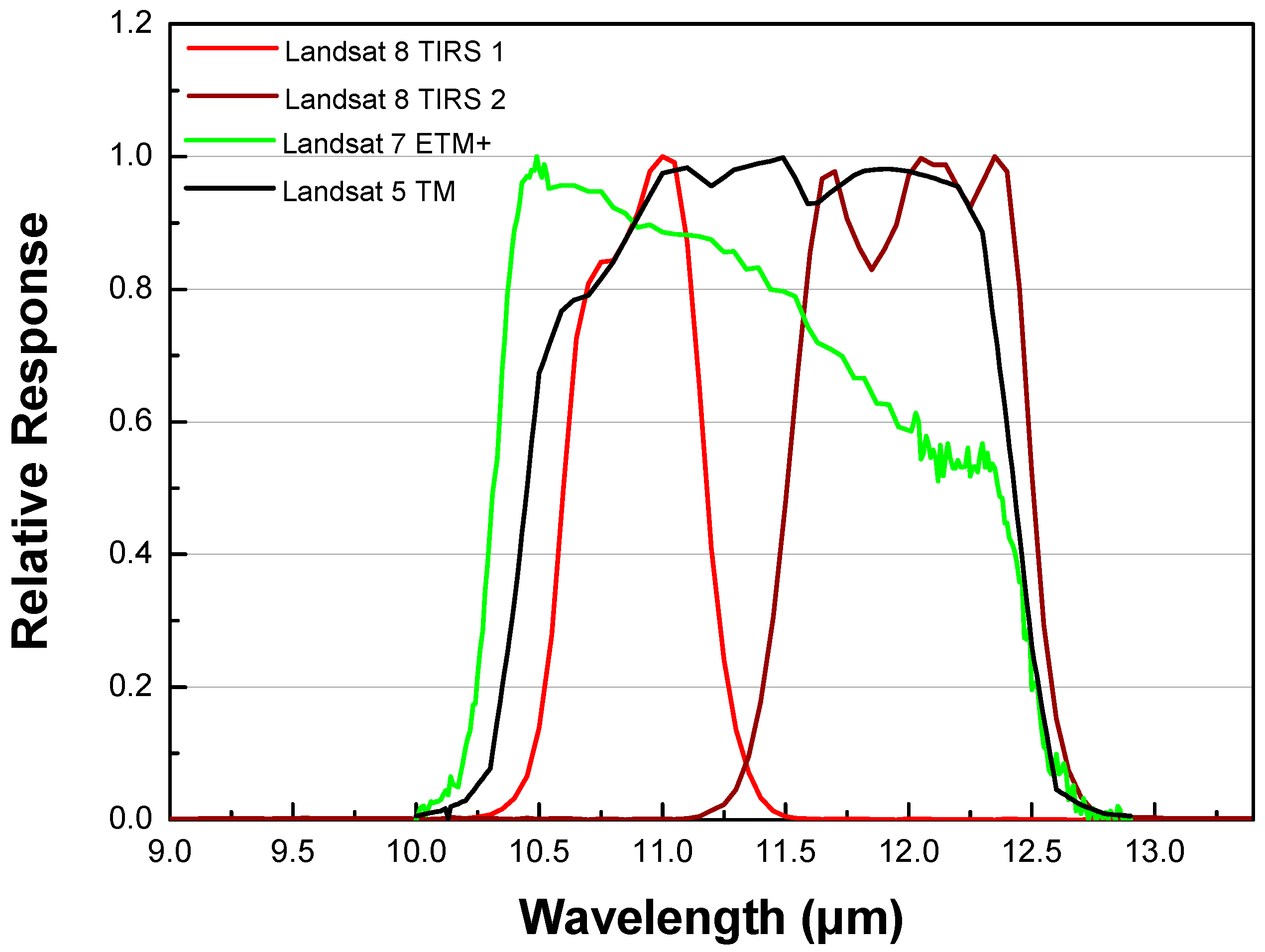
2.1. Split-Window Algorithm Principle
2.2. Algorithm Development for Landsat 8
3. Algorithm Results
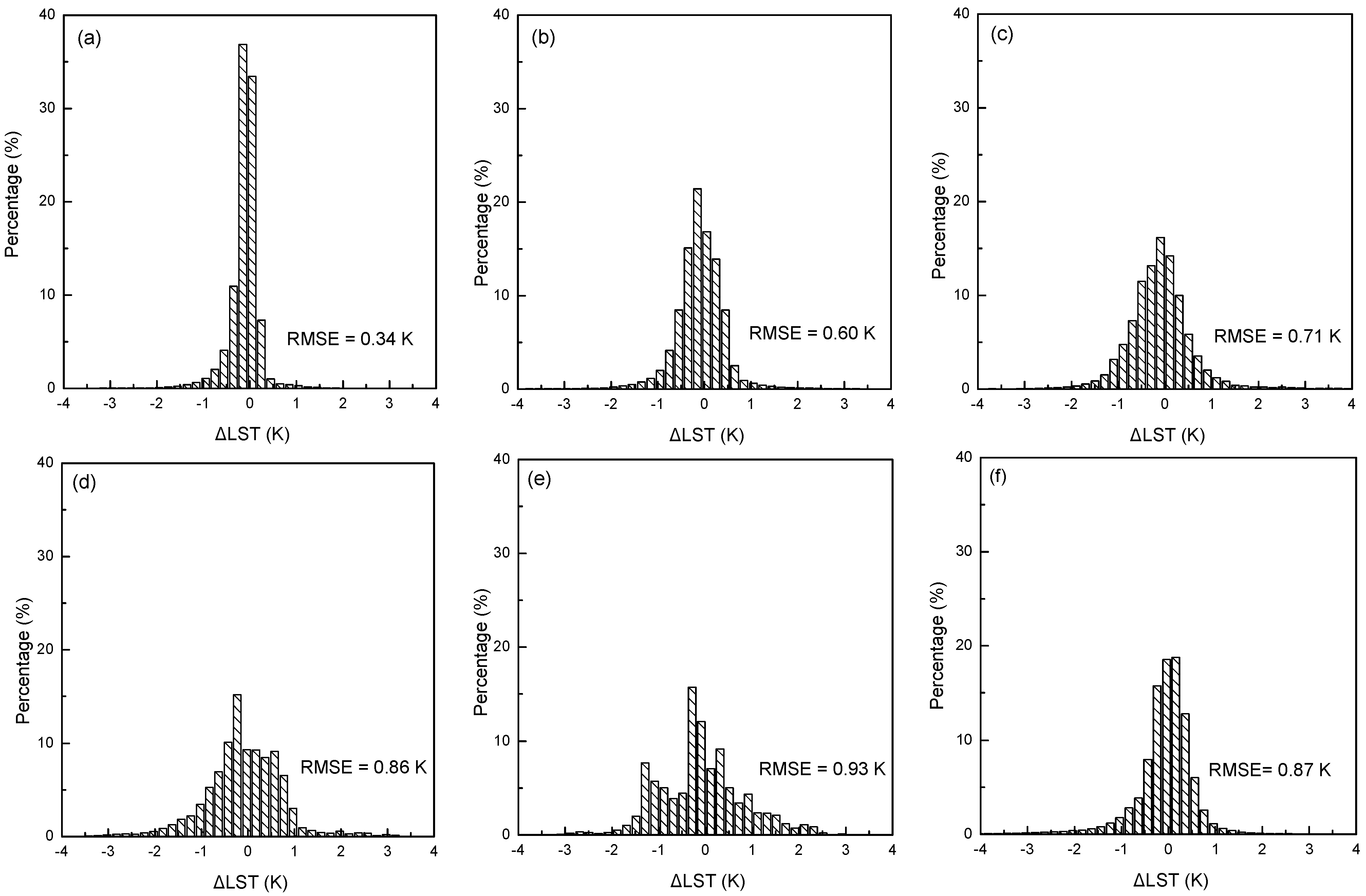
3.1. Algorithm Coefficients
| CWV (g/cm2) | b0 | b1 | b2 | b3 | b4 | b5 | b6 | b7 | RMSE |
|---|---|---|---|---|---|---|---|---|---|
| [0.0, 2.5] | −2.78009 | 1.01408 | 0.15833 | −0.34991 | 4.04487 | 3.55414 | −8.88394 | 0.09152 | 0.34 K |
| [2.0, 3.5] | 11.00824 | 0.95995 | 0.17243 | −0.28852 | 7.11492 | 0.42684 | −6.62025 | −0.06381 | 0.60 K |
| [3.0, 4.5] | 9.62610 | 0.96202 | 0.13834 | −0.17262 | 7.87883 | 5.17910 | −13.26611 | −0.07603 | 0.71 K |
| [4.0, 5.5] | 0.61258 | 0.99124 | 0.10051 | −0.09664 | 7.85758 | 6.86626 | −15.00742 | −0.01185 | 0.86 K |
| [5.0, 6.3] | −0.34808 | 0.98123 | 0.05599 | −0.03518 | 11.96444 | 9.06710 | −14.74085 | −0.20471 | 0.93 K |
| [0.0, 6.3] | −0.41165 | 1.00522 | 0.14543 | −0.27297 | 4.06655 | −6.92512 | −18.27461 | 0.24468 | 0.87 K |
3.2. Determination of LSEs
| Land Cover (Emissivity Class) | Models | Component Description | ||
|---|---|---|---|---|
| Level-1 Type | Level-2 Type | Vegetation Type | Ground Type | |
| Cropland | Rice fields | Vol: bF = 0.0–0.2 | Gr. Veg | Mollisols, Liquid Water |
| Greenhouse farming | Gr. Veg | Mollisols, Liquid Water | ||
| Other croplands | Gr. Veg | Mollisols | ||
| Forest | Broadleaf forests | Vol: bF = 0.7–5.0 | Bdlf | Alfisols, Spodosols |
| Needleleaf forests | Ndle | Alfisols, Spodosols | ||
| Mixed forests | Bdlf , Ndle | Alfisols, Spodosols | ||
| Orchards | Bdlf | Alfisols, Spodosols | ||
| Grasslands | Pastures | Vol: bF = 1.2–5.0 | Gr. Veg | Aridisols, Gr. Veg, Tree and Bush |
| Other grasslands | Gr. Veg | Aridisols, Gr. Veg, Tree and Bush | ||
| Shrublands | - | Vol: bF = 1.2–5.0 | Bdlf, Ndle | Aridisols, Gr. Veg, Tree and Bush |
| Wetlands | Marshland | Spec: σ = 0.2 | - | Alfisols, Gr. Veg and Water |
| Mudflats | - | Alfisols, Gr. Veg and Water | ||
| Waterbodies | Lake | Spec: σ = 0.2 | - | Liquid Water |
| Reservoir/Pond | - | Liquid Water | ||
| River | - | Liquid Water | ||
| Ocean | - | Liquid Water | ||
| Tundra | Shrub and Brush Tundra | Vol: bF = 0.35–0.7 | Bdlf, Ndle | Aridisols, Gr. Veg, Tree and Bush |
| Herbaceous Tundra | Gr. Veg | Aridisols, Gr. Veg, Tree and Bush | ||
| Impervious | Impervious-high albedo | Vol: bF = 0.2–0.5 | Gr. Veg | Paving concrete |
| Impervious-low albedo | Gr. Veg | Paving asphalt | ||
| Barren Land | Dry salt flats | Vol: bF = 0.0–0.2 | Sn.Veg | Salty soil |
| Sandy areas | Sn.Veg | Sand soil | ||
| Bare exposed rock | Sn.Veg | Coarse sandstone | ||
| Bare herbaceous croplands | Sn.Veg | Aridisols, Gr. Veg, Tree and Bush | ||
| Dry lake/river bottom | Sn.Veg | Aridisols, Gr. Veg, Tree and Bush | ||
| Other barren lands | Sn.Veg | Aridisols, Gr. Veg, Tree and Bush | ||
| Snow and ice | Snow | Spec: σ = 0.2 | - | Snow |
| Ice | - | Ice | ||
| Emissivity Class | Mean | |
|---|---|---|
| TIRS-10 | TIRS-11 | |
| Cropland | 0.971 | 0.968 |
| Forest | 0.995 | 0.996 |
| Grasslands | 0.970 | 0.971 |
| Shrublands | 0.969 | 0.970 |
| Wetlands | 0.992 | 0.998 |
| Waterbodies | 0.992 | 0.998 |
| Tundra | 0.980 | 0.984 |
| Impervious | 0.973 | 0.981 |
| Barren Land | 0.969 | 0.978 |
| Snow and ice | 0.992 | 0.998 |
3.3. Determination of Atmospheric CWV
4. Sensitivity Analysis
4.1. Sensitivity Analysis to Instrument Noises
4.2. Sensitivity Analysis to LSEs
| CWV Sub-Ranges (g/cm2) | [0.0, 2.5] | [2.0, 3.5] | [3.0, 4.5] | [4.0, 5.5] | [5.0, 6.3] | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Variables | α | β | α | β | α | β | α | β | α | β |
| Range of Value (K) | [30.70, 61.38] | [−138.62, −66.76] | [45.77, 56.46] | [−112.25, −68.18] | [30.57, 60.88] | [−99.19, −28.91] | [20.94, 54.83] | [−81.41, −10.97] | [12.73, 46.30] | [−58.40, −4.40] |
| Mean (K) | 42.29 | −93.57 | 51.20 | −90.02 | 46.03 | −64.04 | 38.20 | −47.09 | 30.53 | −33.11 |
| Standard deviation (K) | 4.00 | 9.20 | 1.82 | 6.60 | 4.95 | 11.41 | 6.08 | 12.65 | 7.10 | 11.34 |
| LST Error (K) | CWV (g/cm2) | ||||
|---|---|---|---|---|---|
| [0.0, 2.5] | [2.0, 3.5] | [3.0, 4.5] | [4.0, 5.5] | [5.0, 6.3] | |
| Range of Value | [0.73, 1.52] | [0.82,1.25] | [0.42,1.16] | [0.24,0.98] | [0.13,0.75] |
| Mean | 1.02 | 1.04 | 0.79 | 0.61 | 0.45 |
| Standard deviation | 0.10 | 0.06 | 0.12 | 0.13 | 0.13 |
4.3. Sensitivity Analysis to the Atmospheric CWV
| CWV(g/cm2) | [0.0, 2.5] | [2.0, 3.5] | [3.0, 4.5] | [4.0, 5.5] | [5.0, 6.3] |
|---|---|---|---|---|---|
| [0.0, 2.5] | 0.34 K | 1.45 K | - | - | - |
| [2.0, 3.5] | 1.40 K | 0.60 K | 1.40 K | - | - |
| [3.0, 4.5] | - | 1.34 K | 0.71 K | 1.21 K | - |
| [4.0, 5.5] | - | - | 1.29 K | 0.86 K | 2.45 K |
| [5.0, 6.3] | - | - | - | 1.85 K | 0.93 K |
4.4. Comparison amongst Different Split-Window Algorithms
| CWV (g/cm2) | Jiménez-Muñoz | Rozenstein | SW in This Paper | |
|---|---|---|---|---|
| [0.0, 2.5] | 0.46 K | 0.32 K | 0.34 K | 0.46 K |
| [2.0, 3.5] | 0.51 K | 0.56 K | 0.60 K | 1.11 K |
| [3.0, 4.5] | 0.71 K | 0.79 K | 0.71 K | 2.00 K |
| [4.0, 5.5] | 0.87 K | 1.32 K | 0.86 K | 2.33 K |
| [5.0, 6.3] | 0.93 K | 1.26 K | 0.93 K | 3.13 K |
| [0.0, 6.3] | 0.72 K | 1.25 K | 0.87 K | 0.87 K |
5. Application of the Split-Window Algorithm
6. Discussions
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References and Notes
- Price, J.C. The potential of remotely sensed thermal infrared data to infer surface soil-moisture and evaporation. Water Resour. Res. 1980, 16, 787–795. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L.; Tang, B.-H.; Wu, H.; Tang, R.L.; Bi, Y.; Zhou, G. Estimation of diurnal cycle of land surface temperature at high temporal and spatial resolution from clear-sky MODIS data. Remote Sens. 2014, 6, 3247–3262. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L.; Tang, B.-H.; Wu, H.; Tang, R.L. Generation of a time-consistent land surface temperature product from MODIS data. Remote Sens. Environ. 2014, 140, 339–349. [Google Scholar] [CrossRef]
- Becker, F.; Li, Z.-L. Towards a local split window method over land surfaces. Int. J. Remote Sens. 1990, 11, 369–393. [Google Scholar] [CrossRef]
- Becker, F.; Li, Z.-L. Surface temperature and emissivity at various scales: Definition, measurement and related problems. Remote Sens. Rev. 1995, 12, 225–253. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar] [CrossRef]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for advanced spaceborne thermal emission and reflection radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Becker, F.; Li, Z.-L. Temperature-independent spectral indexes in thermal infrared bands. Remote Sens. Environ. 1990, 32, 17–33. [Google Scholar] [CrossRef]
- Watson, K. Two-temperature method for measuring emissivity. Remote Sens. Environ. 1992, 42, 117–121. [Google Scholar] [CrossRef]
- Peres, L.F.; DaCamara, C.C. Land surface temperature and emissivity estimation based on the two-temperature method: Sensitivity analysis using simulated MSG/SEVIRI data. Remote Sens. Environ. 2004, 91, 377–389. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Z.-L. A physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 980–996. [Google Scholar] [CrossRef]
- Ingram, P.M.; Muse, A.H. Sensitivity of iterative spectrally smooth temperature/emissivity separation to algorithmic assumptions and measurement noise. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2158–2167. [Google Scholar] [CrossRef]
- Kealy, P.S.; Hook, S.J. Separating temperature and emissivity in thermal infrared multispectral scanner data - implications for recovering land-surface temperatures. IEEE Trans. Geosci. Remote Sens. 1993, 31, 1155–1164. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Li, Z.-L.; Wu, H.; Wang, N.; Qiu, S.; Sobrino, J.A.; Wan, Z.; Tang, B.-H.; Yan, G. Land surface emissivity retrieval from satellite data. Int. J. Remote Sens. 2013, 34, 3084–3127. [Google Scholar] [CrossRef]
- Gao, C.; Li, Z.-L.; Qiu, S.; Tang, B.; Wu, H.; Jiang, X. An improved algorithm for retrieving land surface emissivity and temperature from MSG-2/SEVIRI data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3175–3191. [Google Scholar] [CrossRef]
- Li, Z.-L.; Petitcolin, F.; Zhang, R.H. A physically based algorithm for land surface emissivity retrieval from combined mid-infrared and thermal infrared data. Sci China Ser. E. 2000, 43, 23–33. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the collection-6 MODIS land-surface temperature/emissivity product. Remote Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Chedin, A.; Scott, N.A.; Wahiche, C.; Moulinier, P. The improved initialization inversion method - a high-resolution physical method for temperature retrievals from satellites of the Tiros-N Series. J. Climate Appl. Meteor. 1985, 24, 128–143. [Google Scholar] [CrossRef]
- Chevallier, F.; Chedin, A.; Cheruy, F.; Morcrette, J.J. TIGR-like atmospheric-profile databases for accurate radiative-flux computation. Quart. J. Roy. Meteorol. Soc. 2000, 126, 777–785. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J. The north American ASTER land surface emissivity database (NAASLED) version 2.0. Remote Sens. Environ. 2009, 113, 1967–1975. [Google Scholar] [CrossRef]
- Tang, B.-H.; Bi, Y.; Li, Z.-L.; Xia, J. Generalized split-window algorithm for estimate of land surface temperature from Chinese geostationary Fengyun meteorological satellite (FY-2C) data. Sensors 2008, 8, 933–951. [Google Scholar] [CrossRef]
- Snyder, W.C.; Wan, Z. BRDF models to predict spectral reflectance and emissivity in the thermal infrared. IEEE Trans. Geosci. Remote Sens. 1998, 36, 214–225. [Google Scholar] [CrossRef]
- Ren, H.; Yan, G.; Chen, L.; Li, Z.-L. Angular effect of MODIS emissivity products and its application to the split-window algorithm. ISPSR J. Photogramm. 2011, 66, 498–507. [Google Scholar] [CrossRef]
- Ren, H.; Liu, R.; Yan, G.; Mu, X.; Li, Z.-L.; Nerry, F.; Liu, Q. Angular normalization of land surface temperature and emissivity using multiangular middle and thermal infrared data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4913–4931. [Google Scholar] [CrossRef]
- Snyder, W.C.; Wan, Z.; Zhang, Y.; Feng, Y.Z. Classification-based emissivity for land surface temperature measurement from space. Int. J. Remote Sens. 1998, 19, 2753–2774. [Google Scholar] [CrossRef]
- Sun, D.; Pinker, R. Implementation of GEOS—based land surface temperature diurnal cycle to avhrr. Int. J. Remote Sens. 2005, 26, 3975–3984. [Google Scholar] [CrossRef]
- Trigo, I.F.; Peres, L.F.; DaCamara, C.C.; Freitas, S.C. Thermal land surface emissivity retrieved from SEVIRI/METEOSAT. IEEE Trans. Geosci. Remote Sens. 2008, 46, 307–315. [Google Scholar] [CrossRef]
- Gong, P.; Wang, J.; Yu, L.; Zhao, Y.; Zhao, Y.; Liang, L.; Niu, Z.; Huang, X.; Fu, H.; Liu, S.; et al. Finer resolution observation and monitoring of global land cover: First mapping results with Landsat TM and ETM+ data. Int. J. Remote Sens. 2013, 34, 2607–2654. [Google Scholar] [CrossRef]
- Belward, A.S.; Estes, J.E.; Kline, K.D. The IGBP-DIS global 1-km land-cover data set discover: A project overview. Photogramm. Eng. Remote Sens. 1999, 65, 1013–1020. [Google Scholar]
- Loveland, T.R.; Reed, B.C.; Brown, J.F.; Ohlen, D.O.; Zhu, Z.; Yang, L.; Merchant, J.W. Development of a global land cover characteristics database and IGBP discover from 1 km AVHRR data. Int. J. Remote Sens. 2000, 21, 1303–1330. [Google Scholar] [CrossRef]
- Wan, Z.; Ng, D.; Dozier, J. Spectral emissivity measurements of land-surface materials and related radiative transfer simulations. Adv. Space Res. 1994, 14, 91–94. [Google Scholar] [CrossRef]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Raissouni, N.; Li, Z.-L. A comparative study of land surface emissivity retrieval from NOAA data. Remote Sens. Environ. 2001, 75, 256–266. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Raissouni, N.; Simarro, J.; Nerry, F.; Petitcolin, F. Atmospheric water vapor content over land surfaces derived from the AVHRR data: Application to the Iberian Peninsula. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1425–1434. [Google Scholar] [CrossRef]
- Li, Z.-L.; Jia, L.; Su, Z.; Wan, Z.; Zhang, R. A new approach for retrieving precipitable water from ATSR2 split-window channel data over land area. Int. J. Remote Sens. 2003, 24, 5095–5117. [Google Scholar] [CrossRef]
- Schroedter-Homscheidt, M.; Drews, A.; Heise, S. Total water vapor column retrieval from MSG-SEVIRI split window measurements exploiting the daily cycle of land surface temperatures. Remote Sens. Environ. 2008, 112, 249–258. [Google Scholar] [CrossRef]
- Wang, N.; Li, Z.-L.; Tang, B.-H.; Zeng, F.N.A.; Li, C.R. Retrieval of atmospheric and land surface parameters from satellite-based thermal infrared hyperspectral data using a neural network technique. Int. J. Remote Sens. 2013, 34, 3485–3502. [Google Scholar] [CrossRef]
- Ren, H.; Du, C.; Qin, Q.; Liu, R.; Meng, J.; Li, J. Atmospheric water vapor retrieval from landsat 8 and its validation. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec, QC, Canada, July 2014; pp. 3045–3048.
- Irons, J.R.; Dwyer, J.L.; Barsi, J.A. The next landsat satellite: The landsat data continuity mission. Remote Sens. Environ. 2012, 122, 11–21. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Li, Z.-L.; Stoll, M.P.; Becker, F. Improvements in the split-window technique for land-surface temperature determination. IEEE Trans. Geosci. Remote Sens. 1994, 32, 243–253. [Google Scholar] [CrossRef]
- Xiong, X.X.; Barnes, W. An overview of MODIS radiometric calibration and characterization. Adv. Atmos Sci. 2006, 23, 69–79. [Google Scholar] [CrossRef]
- Ren, H.; Du, C.; Liu, R.; Qin, Q.; Meng, J.; Li, Z.-L.; Yan, G. Evaluation of radiometric performance for the thermal infrared sensor onboard Landsat 8. Remote Sens. 2014, 6, 12776–12788. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.C.; Sobrino, J.A.; Skokovic, D.; Mattar, C.; Cristobal, J. Land surface temperature retrieval methods from Landsat-8 thermal infrared sensor data. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1840–1843. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Li, Z.-L.; Stoll, M.P.; Becker, F. Multi-channel and multi-angle algorithms for estimating sea and land surface temperature with ATSR data. Int. J. Remote Sens. 1996, 17, 2089–2114. [Google Scholar] [CrossRef]
- Rozenstein, O.; Qin, Z.; Derimian, Y.; Karnieli, A. Derivation of land surface temperature for Landsat-8 TIRS using a split window algorithm. Sensors 2014, 14, 5768–5780. [Google Scholar] [CrossRef] [PubMed]
- Montanaro, M.; Lunsford, A.; Tesfaye, Z.; Wenny, B.; Reuter, D. Radiometric calibration methodology of the Landsat 8 thermal infrared sensor. Remote Sens. 2014, 6, 8803–8821. [Google Scholar] [CrossRef]
- Montanaro, M.; Gerace, A.; Lunsford, A.; Reuter, D. Stray light artifacts in imagery from the Landsat 8 thermal infrared sensor. Remote Sens. 2014, 6, 10435–10456. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, C.; Ren, H.; Qin, Q.; Meng, J.; Zhao, S. A Practical Split-Window Algorithm for Estimating Land Surface Temperature from Landsat 8 Data. Remote Sens. 2015, 7, 647-665. https://doi.org/10.3390/rs70100647
Du C, Ren H, Qin Q, Meng J, Zhao S. A Practical Split-Window Algorithm for Estimating Land Surface Temperature from Landsat 8 Data. Remote Sensing. 2015; 7(1):647-665. https://doi.org/10.3390/rs70100647
Chicago/Turabian StyleDu, Chen, Huazhong Ren, Qiming Qin, Jinjie Meng, and Shaohua Zhao. 2015. "A Practical Split-Window Algorithm for Estimating Land Surface Temperature from Landsat 8 Data" Remote Sensing 7, no. 1: 647-665. https://doi.org/10.3390/rs70100647
APA StyleDu, C., Ren, H., Qin, Q., Meng, J., & Zhao, S. (2015). A Practical Split-Window Algorithm for Estimating Land Surface Temperature from Landsat 8 Data. Remote Sensing, 7(1), 647-665. https://doi.org/10.3390/rs70100647