Radiometric Non-Uniformity Characterization and Correction of Landsat 8 OLI Using Earth Imagery-Based Techniques
Abstract
:1. Introduction
1.1. Relative Radiometric Calibration
1.2. Landsat 8 and the Operational Land Imager (OLI)
| Band Number | Name | Bandwidth (nm) | GSD (m) |
|---|---|---|---|
| 1 | Coastal/Aerosol | 433–453 | 30 |
| 2 | Blue | 450–515 | 30 |
| 3 | Green | 525–600 | 30 |
| 4 | Red | 630–680 | 30 |
| 5 | NIR | 845–885 | 30 |
| 6 | SWIR 1 | 1560–1660 | 30 |
| 7 | SWIR 2 | 2100–2300 | 30 |
| 8 | Panchromatic | 500–680 | 15 |
| 9 | Cirrus | 1360–1390 | 30 |
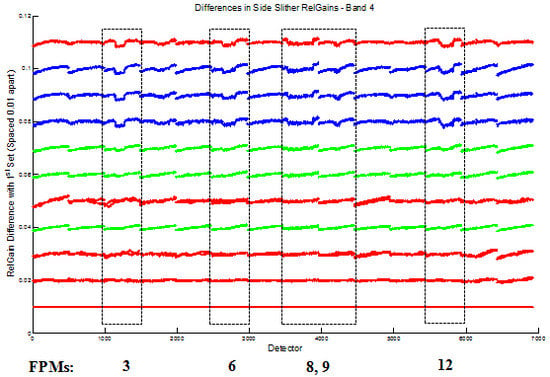
2. Review of Earth Imagery-Based Relative Calibration Methods
2.1. Side-Slither Maneuver
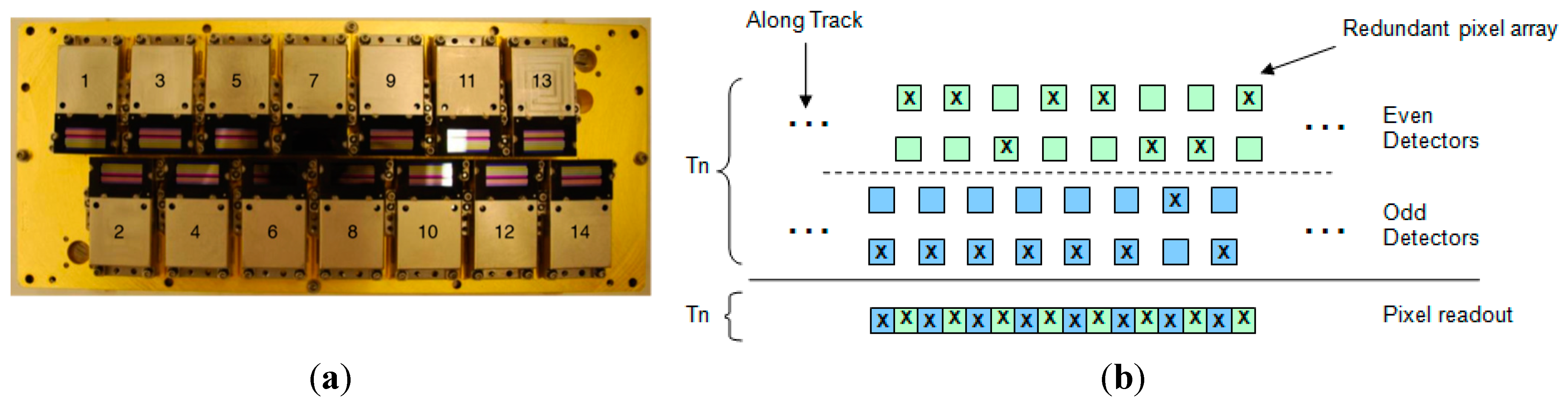
2.2. Lifetime Image Statistics
3. Methodology
3.1. Side-Slither
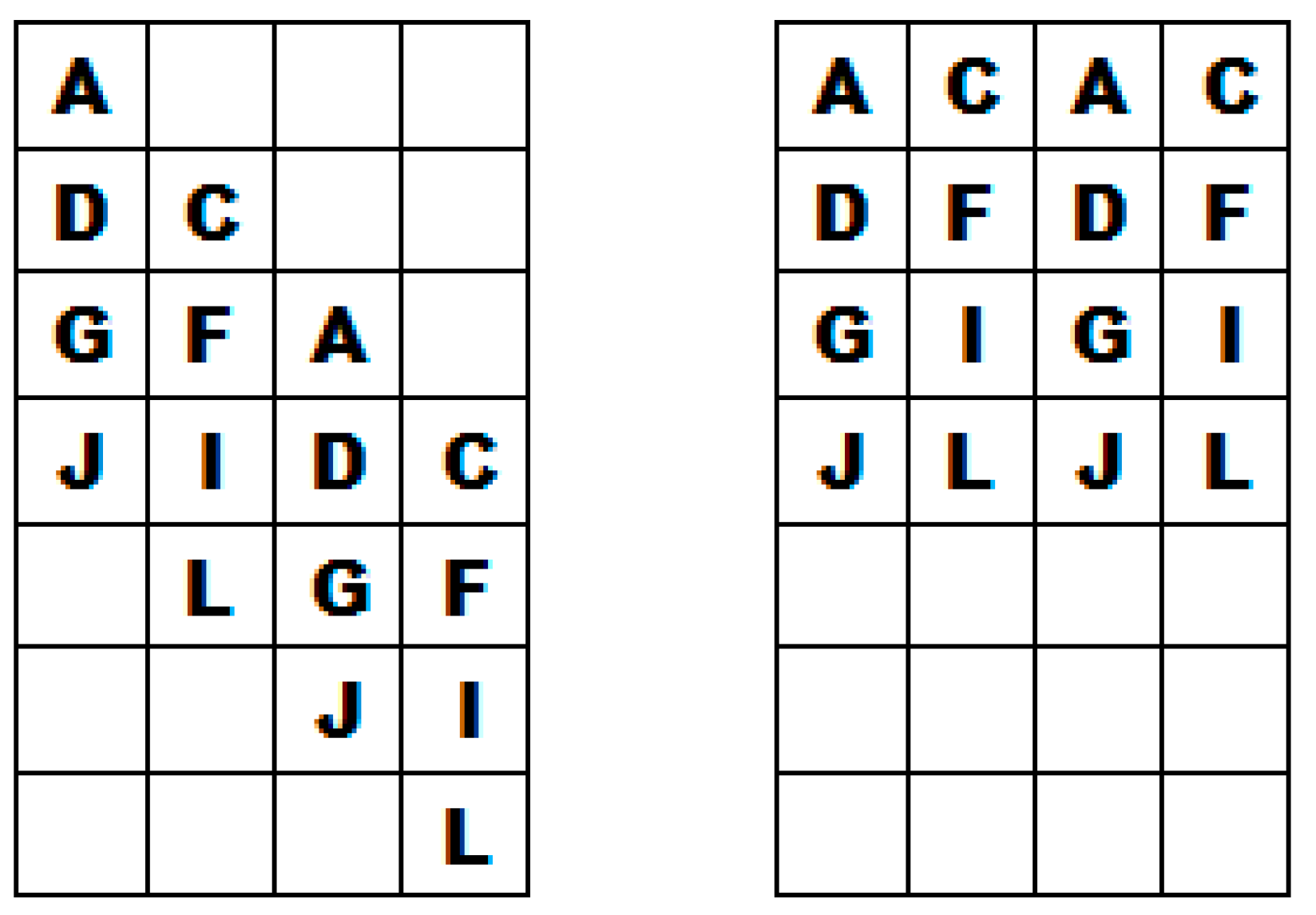
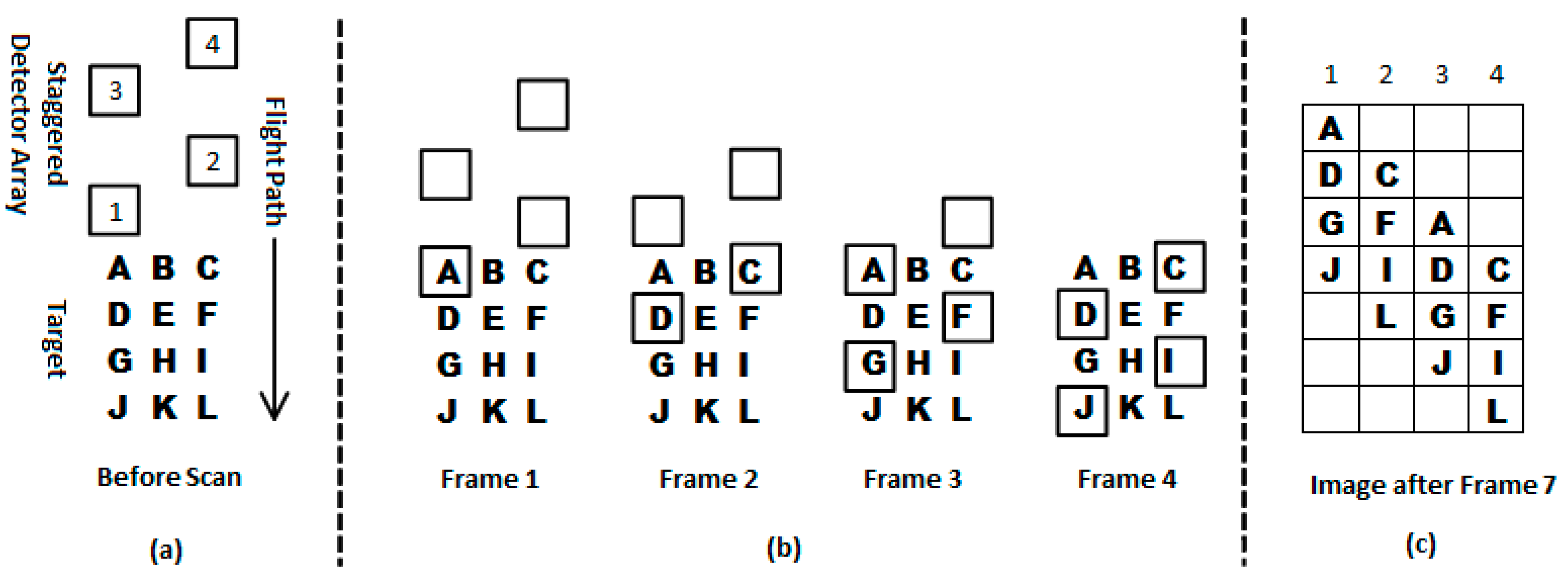
3.1.1. Frame Shift Correction
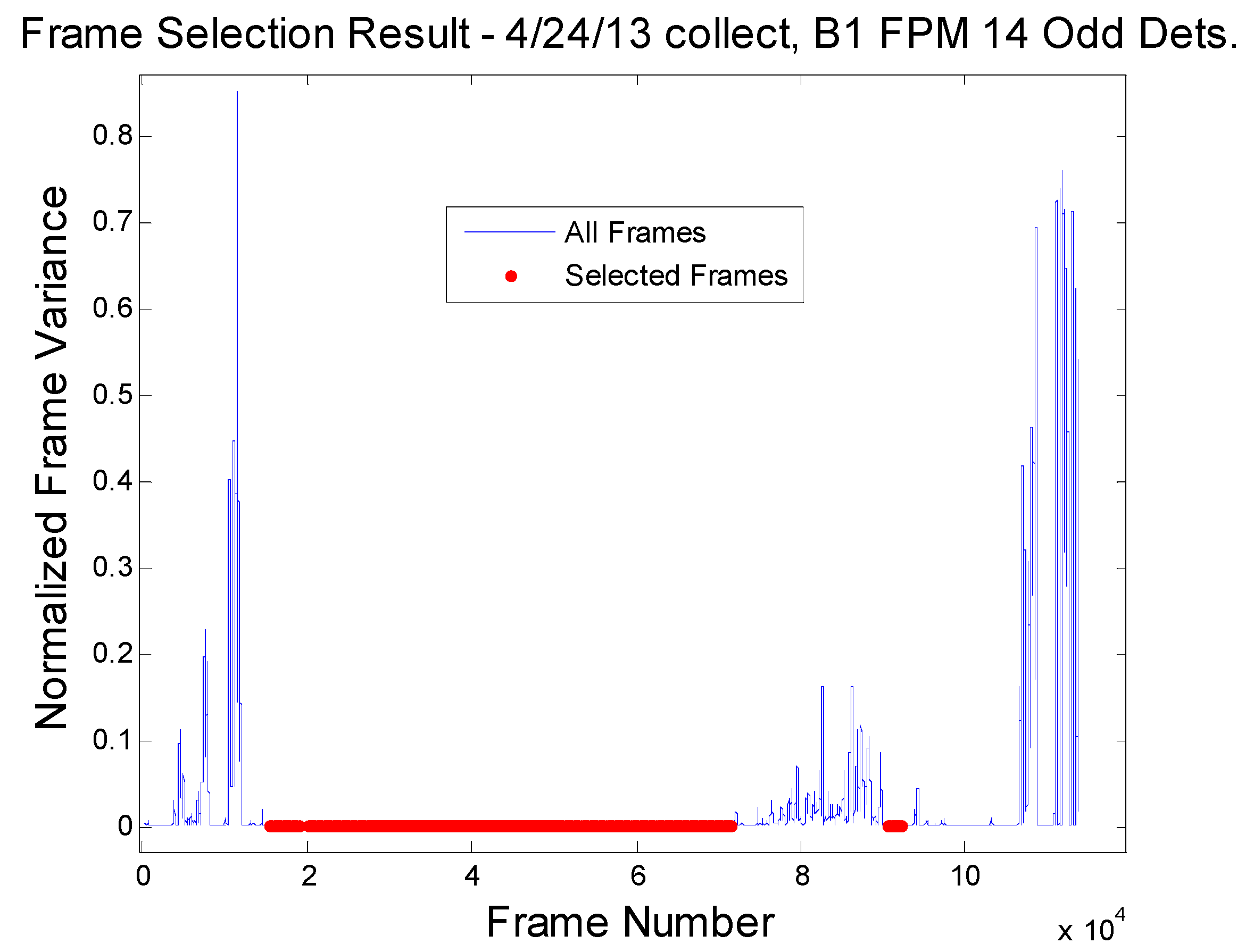
3.1.2. Flat-Field Data Selection
- (1)
- After frame shift correction, the squared coefficient of variation (SCV) is calculated for each frame. This provides a basis for inter-frame comparison.
- (2)
- The SCVs are run through a length-101 maximum filter to put more of a buffer between uniform and non-uniform regions in the base data.
- (3)
- To ensure estimate integrity, the minimum number of contiguous frames for multispectral bands is set to 1000. Slight errors in detector alignment can be compensated for by ensuring that a large region (>10 km) of imagery is obtained, and this is also necessary for even/odd detector normalization. For Band 8, to cover the same ground as the multispectral bands, the minimum is 2000.
- (4)
- First thresholding attempt: Select indices of all continuous regions of at least the minimum length where the absolute difference between SCVs is less than or equal to 0.0001. This value was selected to be an order of magnitude better than the streaking threshold necessary to ensure that no images stripes can be observed visually.
- (5)
- If no regions are selected in the first attempt and the mean absolute difference between SCVs is greater than the first threshold, try Step 4 again using the mean absolute difference between SCVs as the threshold. If no regions are selected after the second threshold (i.e., Step 5), then relative gains are not derived for this band.
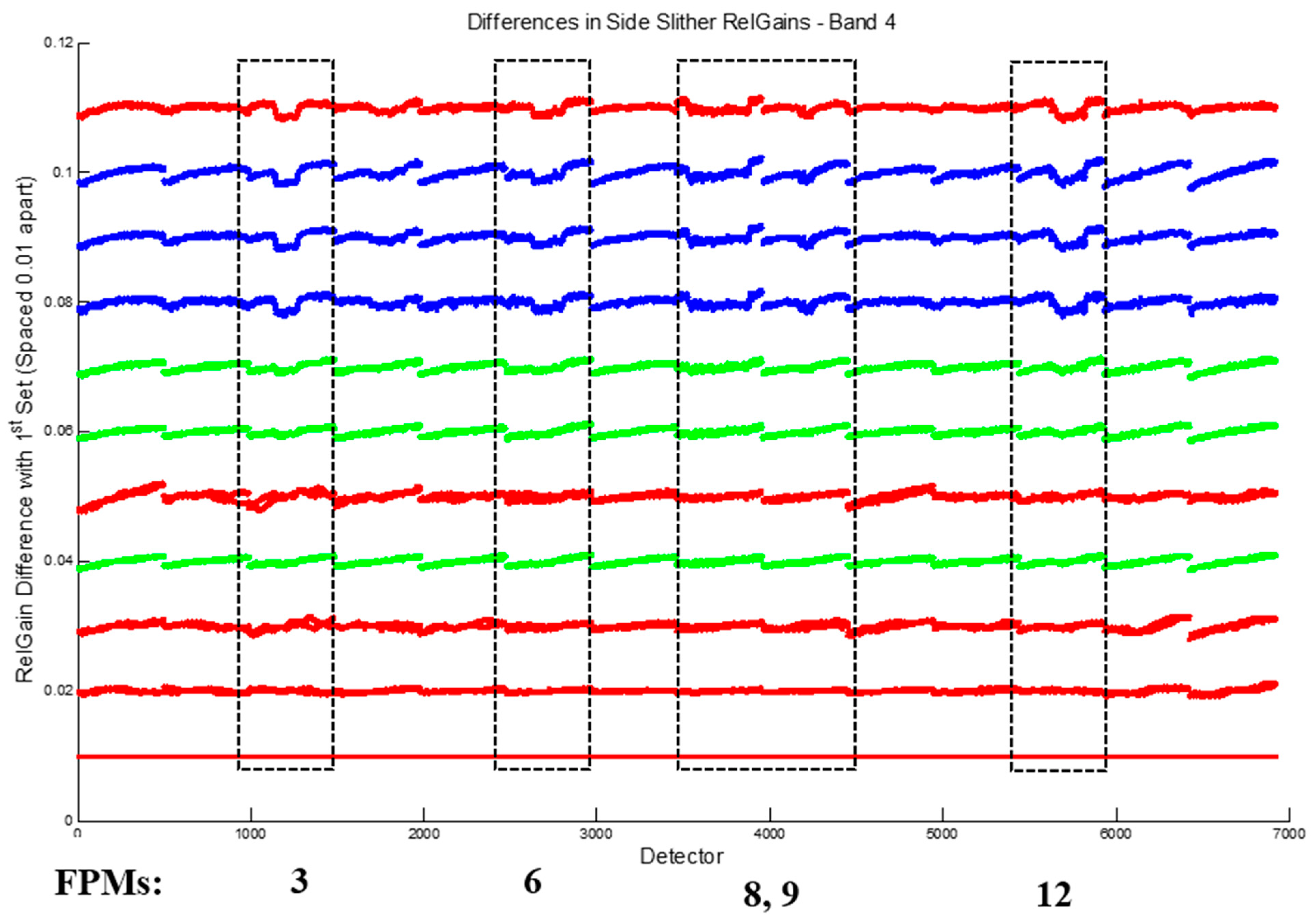
3.1.3. Even/Odd Detector Artifact Removal
- (1)
- Using the output from the flat-field selection algorithm, select common flat-field frames between even/odd sets.
- (2)
- Calculate the frame means for even/odd sets
- (3)
- Normalize each set of means to the overall (even and odd combined) mean. This accounts for differences in radiance due solely to even/odd detector characteristics.
- (4)
- Use a two-sample Kolmogorov–Smirnov test on the two detector mean sets to determine if they are similarly distributed with the following hypotheses at the 95% level:Ho: Even/odd detector sets are sampled from the same population and should be considered together;Ha: Even/odd detectors should not be considered as one set.
3.2. DCC Image Statistics for the Cirrus Band
- (1)
- The scene is between ±30° latitude;
- (2)
- The solar zenith angle for the scene is less than 30°;
- (3)
- In the red band, the scene mean radiance is greater than 220 W/m2/sr/µm;
- (4)
- In the cirrus band, the scene mean radiance is greater than 10 W/m2/sr/µm;
- (5)
- In the first TIRS band (Band 10 in Landsat 8 imagery), the scene mean brightness temperature is less than 220 K.
4. Results and Analysis
4.1. Side-Slither
| Date of Collect | Location | Path | Rows |
|---|---|---|---|
| 3-26-2013 | Niger | 189 | 45–48 |
| 4-5-2013 | Libya/Niger | 187 | 38–49 |
| 4-20-2013 | Egypt | 177 | 36–47 |
| 4-24-2013 | Greenland | 4 | 3–22 |
| 5-6-2013 | Egypt | 177 | 33–47 |
| 5-12-2013 | Greenland | 2 | 4–25 |
| 7-13-2013 | Greenland | 4 | 5–21 |
| 11-30-2013 | Antarctica | 88 | 103–117 |
| 12-16-2013 | Antarctica | 88 | 103–117 |
| 1-1-2014 | Antarctica | 88 | 103–117 |
| 4-11-2014 | Niger | 189 | 44–51 |

| Band | CPF | 3/26/13 (NER) | 4/5/13 (LBY) | 4/20/13 (EGY) | 4/24/13 (GRL) | 5/6/13 (EGY) | 5/12/13 (GRL) | 7/13/13 (GRL) | 11/30/13 (ATA) | 12/16/13 (ATA) | 1/1/14 (ATA) | 4/11/14 (NER) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C/A | 0.027 | 0.039 | 0.032 | 0.028 | 0.021 | 0.027 | 0.017 | 0.009 | 0.051 | 0.027 | 0.030 | 0.035 |
| Blue | 0.022 | 0.023 | 0.026 | 0.022 | 0.012 | 0.018 | 0.016 | 0.010 | 0.051 | 0.022 | 0.022 | 0.023 |
| Green | 0.012 | 0.017 | 0.016 | 0.026 | 0.008 | 0.044 | 0.007 | 0.006 | 0.028 | 0.012 | 0.012 | 0.017 |
| Red | 0.007 | 0.012 | 0.017 | 0.038 | 0.007 | 0.040 | 0.006 | 0.005 | 0.012 | 0.009 | 0.009 | 0.014 |
| NIR | 0.005 | 0.010 | 0.021 | 0.042 | 0.007 | 0.043 | 0.009 | 0.006 | 0.011 | 0.009 | 0.010 | 0.014 |
| PAN | 0.075 | 0.098 | 0.099 | 0.097 | 0.083 | 0.101 | 0.087 | 0.077 | 0.069 | 0.084 | 0.095 | 0.102 |
| Band | CPF | 3/26/13 (NER) | 4/5/13 (LBY) | 4/20/13 (EGY) | 4/24/13 (GRL) | 5/6/13 (EGY) | 5/12/13 (GRL) | 7/13/13 (GRL) | 11/30/13 (ATA) | 12/16/13 (ATA) | 1/1/14 (ATA) | 4/11/14 (NER) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C/A | 0.034 | 0.054 | 0.047 | 0.039 | 0.040 | 0.037 | 0.033 | 0.017 | 0.040 | 0.016 | 0.017 | 0.022 |
| Blue | 0.021 | 0.033 | 0.034 | 0.029 | 0.023 | 0.024 | 0.019 | 0.011 | 0.043 | 0.015 | 0.014 | 0.022 |
| Green | 0.010 | 0.024 | 0.022 | 0.027 | 0.016 | 0.046 | 0.012 | 0.011 | 0.022 | 0.011 | 0.012 | 0.019 |
| Red | 0.009 | 0.015 | 0.018 | 0.038 | 0.012 | 0.041 | 0.010 | 0.010 | 0.012 | 0.011 | 0.012 | 0.014 |
| NIR | 0.008 | 0.013 | 0.023 | 0.042 | 0.011 | 0.043 | 0.013 | 0.010 | 0.013 | 0.012 | 0.013 | 0.017 |
| PAN | 0.015 | 0.028 | 0.029 | 0.039 | 0.018 | 0.036 | 0.019 | 0.016 | 0.023 | 0.018 | 0.018 | 0.033 |
| Band | CPF | 3/26/13 (NER) | 4/5/13 (LBY) | 4/20/13 (EGY) | 4/24/13 (GRL) | 5/6/13 (EGY) | 5/12/13 (GRL) | 7/13/13 (GRL) | 11/30/13 (ATA) | 12/16/13 (ATA) | 1/1/14 (ATA) | 4/11/14 (NER) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C/A | 0.025 | 0.064 | 0.057 | 0.050 | 0.049 | 0.047 | 0.042 | 0.026 | 0.041 | 0.013 | 0.013 | 0.018 |
| Blue | 0.032 | 0.040 | 0.042 | 0.036 | 0.029 | 0.030 | 0.020 | 0.015 | 0.037 | 0.009 | 0.010 | 0.024 |
| Green | 0.017 | 0.025 | 0.025 | 0.030 | 0.018 | 0.049 | 0.013 | 0.011 | 0.020 | 0.007 | 0.007 | 0.015 |
| Red | 0.006 | 0.015 | 0.018 | 0.039 | 0.010 | 0.042 | 0.009 | 0.007 | 0.009 | 0.007 | 0.007 | 0.013 |
| NIR | 0.006 | 0.010 | 0.022 | 0.041 | 0.007 | 0.043 | 0.010 | 0.006 | 0.010 | 0.009 | 0.009 | 0.013 |
| PAN | 0.019 | 0.032 | 0.033 | 0.041 | 0.016 | 0.039 | 0.015 | 0.013 | 0.017 | 0.010 | 0.010 | 0.033 |
| Band | 3/26/13 (NER) | 4/5/13 (LBY) | 4/20/13 (EGY) | 4/24/13 (GRL) | 5/6/13 (EGY) | 5/12/13 (GRL) | 7/13/13 (GRL) | 11/30/13 (ATA) | 12/16/13 (ATA) | 1/1/14 (ATA) | 4/11/14 (NER) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| C/A | - | 0.09 | 0.24 | 0.15 | 0.29 | 0.22 | 0.25 | 0.46 | 0.42 | 0.47 | 0.44 |
| Blue | - | 0.12 | 0.16 | 0.16 | 0.29 | 0.2 | 0.19 | 0.27 | 0.21 | 0.25 | 0.2 |
| Green | - | 0.08 | 0.15 | 0.11 | 0.17 | 0.12 | 0.14 | 0.22 | 0.21 | 0.23 | 0.16 |
| Red | - | 0.12 | 0.14 | 0.12 | 0.21 | 0.14 | 0.13 | 0.18 | 0.19 | 0.23 | 0.15 |
| NIR | - | 0.13 | 0.2 | 0.13 | 0.2 | 0.13 | 0.14 | 0.13 | 0.16 | 0.23 | 0.1 |
| SWIR1 | - | 0.22 | 0.21 | 0.88 | 0.26 | 0.68 | 1.16 | 1.39 | 1.06 | 1.19 | 0.38 |
| SWIR2 | - | 0.24 | 0.22 | 0.72 | 0.25 | 0.68 | 0.75 | 0.63 | 0.68 | 1.24 | 0.24 |
| PAN | - | 0.11 | 0.17 | 0.17 | 0.27 | 0.2 | 0.18 | 0.22 | 0.22 | 0.26 | 0.22 |
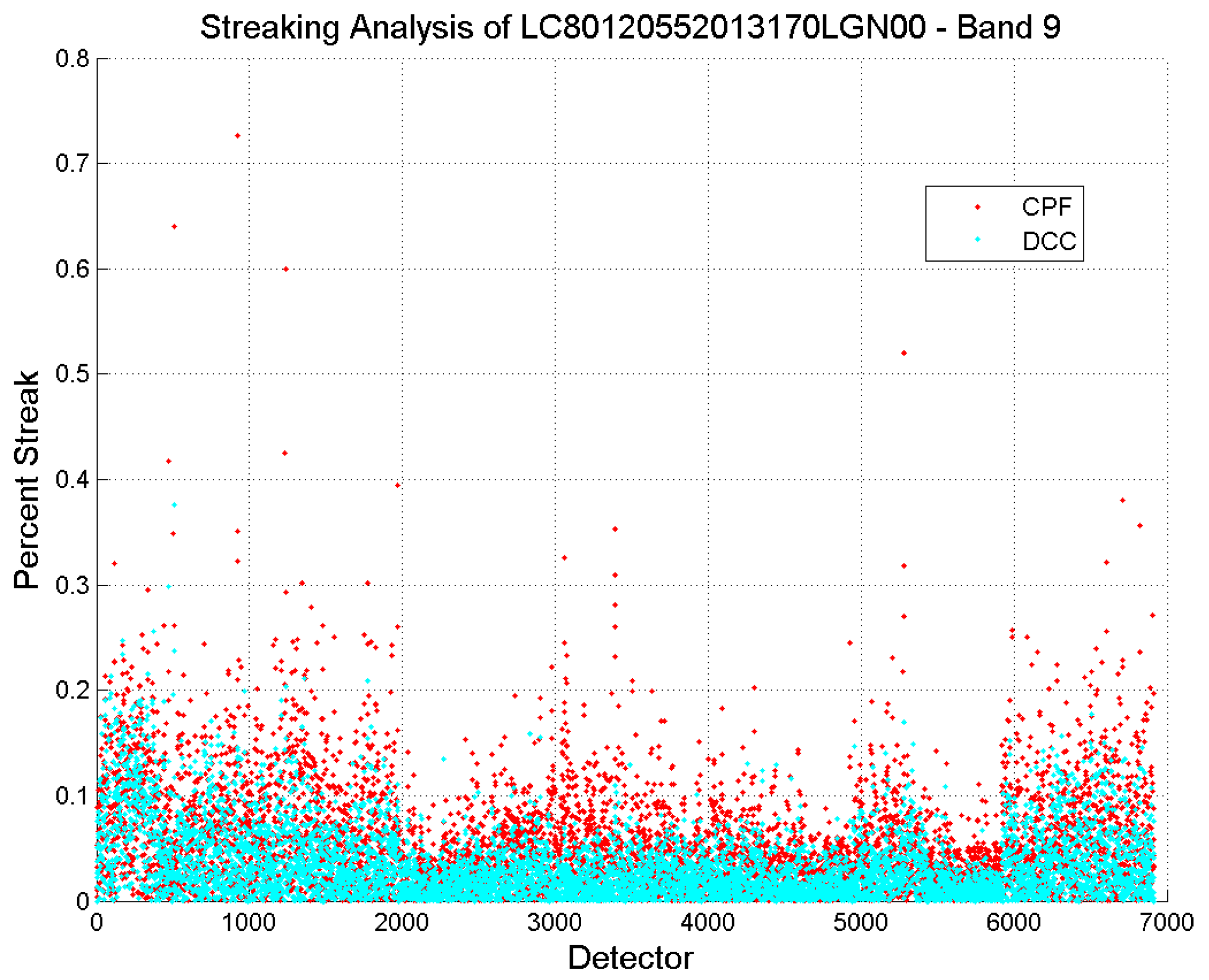
4.2. DCC Image Statistics for Cirrus Band


5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Adriansen, S.; Benhadj, I.; Duhoux, G.; Dierckx, W.; Dries, J.; Heyns, W.; Kleihorst, R.; Livens, S.; Nackaerts, K.; Reusen, I.; et al. Building a calibration and validation system for the PROBA-V satellite mission. In Proceedings of the ISPRS XXXVIII International Calibration and Orientation Workshop, Castelldefels, Spain, 10–12 February 2010.
- Anderson, C.; Naughton, D.; Brunn, A.; Thiele, M. Radiometric correction of RapidEye imagery using the on-orbit side-slither method. Proc. SPIE 2011. [Google Scholar] [CrossRef]
- Operational Land Imager (OLI) Landsat Science. Available online: http://landsat.gsfc.nasa.gov/?p=5447 (accessed on 26 June 2014).
- Landsat 8 Mission Data Format Control Book. Available online: http://landsat.usgs.gov/documents/LDCM-DFCB-004.pdf (accessed on 26 June 2014).
- Markham, B.L.; Barsi, J.A.; Kvaran, G.; Ong, L.; Kaita, E.; Biggar, S.; Czapla-Myers, J.; Mishra, N.; Helder, D.L. Landsat-8 operational land imager radiometric calibration and stability. Remote Sens. 2014, in press. [Google Scholar]
- Knight, E.J.; Kvaran, G. Landsat-8 operational land imager design, characterization, and performance. Remote Sens. 2014, in press. [Google Scholar]
- Henderson, B.G.; Krause, K.S. Relative radiometric correction of QuickBird imagery using the side-slither technique on-orbit. Proc. SPIE 2004. [Google Scholar] [CrossRef]
- Angal, A; Helder, D.L. Advanced land imager relative gain characterization and correction. In Proceedings of Pecora 16—Global Priorities in Land Remote Sensing, Sioux Falls, SD, USA, 25 October 2005.
- Shrestha, A.K. Relative Gain Characterization and Correction for Pushbroom Sensors Based on Lifetime Image Statistics and Wavelet Filtering. Master’s Thesis, South Dakota State University, Brookings, SD, USA, 2010. [Google Scholar]
- Shrestha, A.K.; Helder, D.L.; Anderson, C. Relative gain characterization and correction for pushbroom sensors based on lifetime image statistics. In Proceedings of the Civil Commercial Imagery Evaluation Workshop, Fairfax, VA, USA, 17 March 2010.
- Landsat 8 Cal/Val Algorithm Description Document. Available online: http://landsat.usgs.gov/documents/LDCM_CVT_ADD.pdf (accessed on 26 June 2014).
- Doelling, D.R.; Morstad, D.; Scarino, B.R.; Bhatt, R.; Gopalan, A. The characterization of deep convective clouds as an invariant calibration target and as a visible calibration technique. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1147–1159. [Google Scholar] [CrossRef]
- Doelling, D.R.; Nguyen, L.; Minnis, P. On the use of deep convective clouds to calibrate AVHRR data. Proc. SPIE 2004. [Google Scholar] [CrossRef]
- Morfitt, R.; Markham, B.L.; Micijevic, E.; Scaramuzza, P.; Barsi, J.A.; Levy, R.; Ong, L.; Vanderwerff, K. OLI radiometric performance on-orbit. Remote Sens. 2014, in press. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pesta, F.; Bhatta, S.; Helder, D.; Mishra, N. Radiometric Non-Uniformity Characterization and Correction of Landsat 8 OLI Using Earth Imagery-Based Techniques. Remote Sens. 2015, 7, 430-446. https://doi.org/10.3390/rs70100430
Pesta F, Bhatta S, Helder D, Mishra N. Radiometric Non-Uniformity Characterization and Correction of Landsat 8 OLI Using Earth Imagery-Based Techniques. Remote Sensing. 2015; 7(1):430-446. https://doi.org/10.3390/rs70100430
Chicago/Turabian StylePesta, Frank, Suman Bhatta, Dennis Helder, and Nischal Mishra. 2015. "Radiometric Non-Uniformity Characterization and Correction of Landsat 8 OLI Using Earth Imagery-Based Techniques" Remote Sensing 7, no. 1: 430-446. https://doi.org/10.3390/rs70100430
APA StylePesta, F., Bhatta, S., Helder, D., & Mishra, N. (2015). Radiometric Non-Uniformity Characterization and Correction of Landsat 8 OLI Using Earth Imagery-Based Techniques. Remote Sensing, 7(1), 430-446. https://doi.org/10.3390/rs70100430