Toward a Satellite-Based System of Sugarcane Yield Estimation and Forecasting in Smallholder Farming Conditions: A Case Study on Reunion Island
Abstract
:1. Introduction
2. Materials and Methods
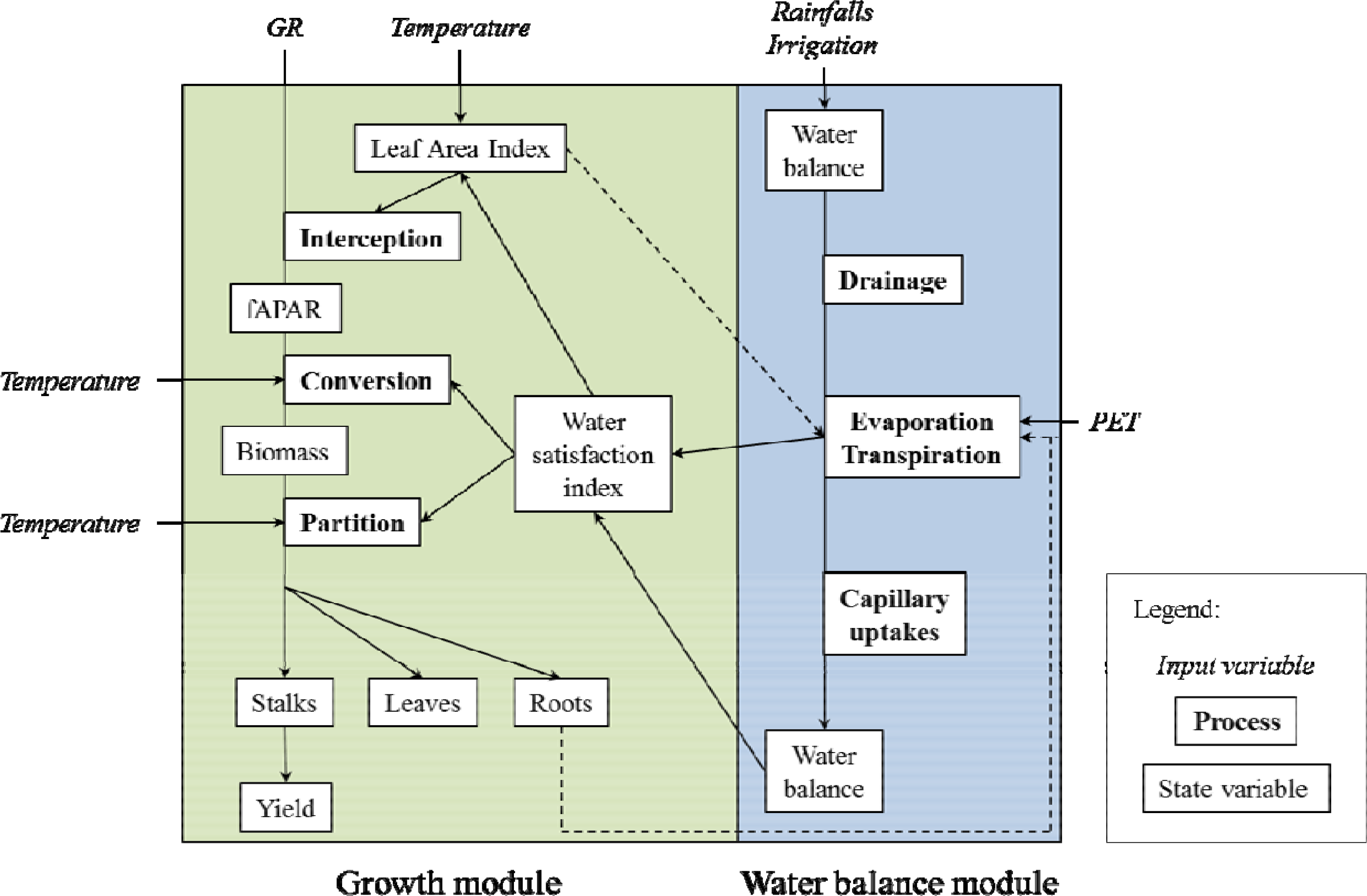
2.1. Coupling a Crop Model with Remote Sensing
2.1.1. The Study Sites
2.1.2. Climatic and Agronomic Data
2.1.3. Remote Sensing Data
2.2. The Remote Sensing-Crop Yield Models
2.2.1. A Prerequisite: The NDVI Interpolation Model
2.2.2. Empirical NDVI Model
2.2.3. Kumar-Monteith Model
2.2.4. MOSICAS Sugarcane Crop Model
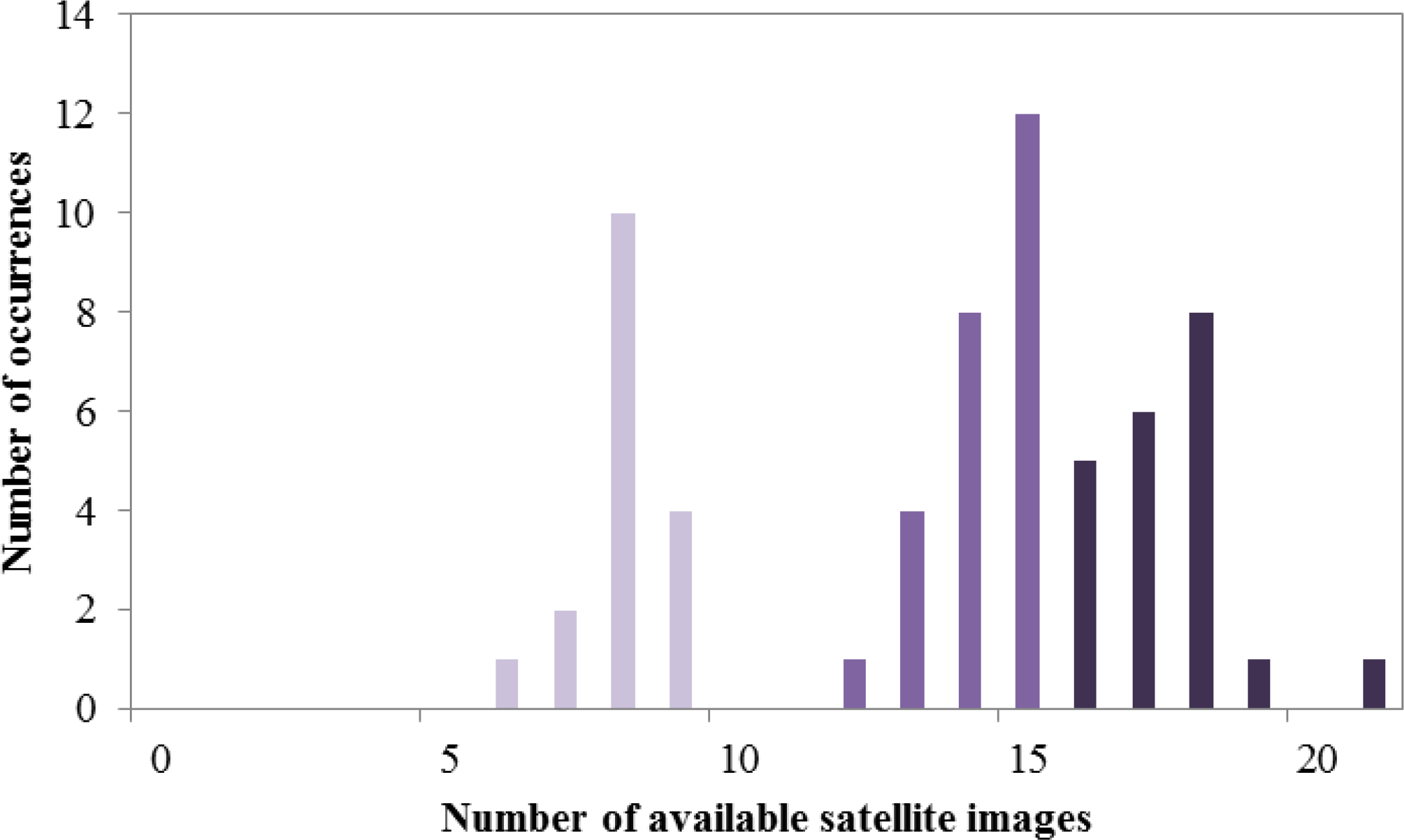
2.2.5. Influence of the Number of Satellite Images
3. Results
3.1. NDVI Temporal Profile
3.2. Comparison of the Methods
3.3. Influence of the Number of Satellite Images
3.4. Early Forecasts
4. Discussion
4.1. Model’s Relevance
4.2. Sources of Errors and Operational Considerations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lobell, D.B.; Asner, G.P.; Ortiz-Monasterio, J.I.; Benning, T.L. Remote sensing of regional crop production in the Yaqui Valley, Mexico: Estimates and uncertainties. Agric. Ecosyst. Environ 2003, 94, 205–220. [Google Scholar]
- Santin-Janin, H.; Garel, M.; Chapuis, J.L.; Pontier, D. Assessing the performance of NDVI as a proxy for plant biomass using non-linear models: A case study on the Kerguelen Archipelago. Polar Biol 2009, 32, 861–871. [Google Scholar]
- Le Maire, G.; Marsden, C.; Nouvellon, Y.; Grinand, C.; Hakamada, R.; Stape, J.-L.; Laclau, J.-P. MODIS NDVI time-series allow the monitoring of eucalyptus plantation biomass. Remote Sens. Environ 2011, 115, 2613–2625. [Google Scholar]
- Houborg, R.; Soegaard, H.; Boegh, E. Combining vegetation index and model inversion methods for the extraction of key vegetation biophysical parameters using terra and aqua modis reflectance data. Remote Sens. Environ 2007, 106, 39–58. [Google Scholar]
- Bartlett, D.S.; Whiting, G.J.; Hartman, J.M. Use of vegetation indices to estimate indices to estimate intercepted solar radiation and net carbon dioxide exchange of a grass canopy. Remote Sens. Environ 1989, 30, 115–128. [Google Scholar]
- Bégué, A. Leaf area index, intercepted photosynthetically active radiation, and spectral vegetation indices: A sensitivity analysis for regular-clumped canopies. Remote Sens. Environ 1993, 46, 45–59. [Google Scholar]
- Kumar, M.; Monteith, J.L. Remote Sensing Crop Growth; Academic Press: Leicester, UK, 1981. [Google Scholar]
- Martiné, J.-F. Analysis and forecasting of the sucrose content of sugarcane crops during the harvest period in Reunion Island. In Proceedings of the 26th Congress of the International Society of Sugar Cane Technologists, Durban, South Africa, 29 July–2 August 2007; pp. 607–612.
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol 2013, 173, 74–84. [Google Scholar]
- Tucker, C.J.; Vanpraet, C.L.; Sharman, M.J.; van Ittersum, G. Satellite remote sensing of total herbaceous biomass production in the Senegalese Sahel: 1980–1984. Remote Sens. Environ 1985, 17, 233–249. [Google Scholar]
- Duveiller, G.; López-Lozano, R.; Baruth, B. Enhanced processing of 1-km spatial resolution fapar time series for sugarcane yield forecasting and monitoring. Remote Sens 2013, 5, 1091–1116. [Google Scholar]
- Mulianga, B.; Bégué, A.; Simoes, M.; Todoroff, P. Forecasting regional sugarcane yield based on time integral and spatial aggregation of MODIS NDVI. Remote Sens 2013, 5, 2184–2199. [Google Scholar]
- Bégué, A.; Lebourgeois, V.; Bappel, E.; Todoroff, P.; Pellegrino, A.; Baillarin, F.; Siegmund, B. Spatio-temporal variability of sugarcane fields and recommendations for yield forecast using NDVI. Int. J. Remote Sens 2010, 31, 5391–5407. [Google Scholar] [Green Version]
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol 1972, 9, 744–766. [Google Scholar]
- Delécolle, R.; Maas, S.J.; Guérif, M.; Baret, F. Remote sensing and crop production models: Present trends. ISPRS J. Photogramm. Remote Sens 1992, 47, 145–161. [Google Scholar]
- Asrar, G.; Kanemasu, E.T.; Jackson, R.D.; Pinter, P.J., Jr. Estimation of total above-ground phytomass production using remotely sensed data. Remote Sens. Environ 1985, 17, 211–220. [Google Scholar]
- Liu, J.; Pattey, E.; Miller, J.R.; McNairn, H.; Smith, A.; Hu, B. Estimating crop stresses, aboveground dry biomass and yield of corn using multi-temporal optical data combined with a radiation use efficiency model. Remote Sens. Environ 2010, 114, 1167–1177. [Google Scholar]
- Dorigo, W.A.; Zurita-Milla, R.; de Wit, A.J.W.; Brazile, J.; Singh, R.; Schaepman, M.E. A review on reflective remote sensing and data assimilation techniques for enhanced agroecosystem modeling. Int. J. Appl. Earth Obs. Geoinf 2007, 9, 165–193. [Google Scholar]
- Atzberger, C. Advances in remote sensing of agriculture: Context description, existing operational monitoring systems and major information needs. Remote Sens 2013, 5, 949–981. [Google Scholar]
- Morel, J.; Martine, J.F.; Begue, A.; Todoroff, P.; Petit, M. A comparison of two coupling methods for improving a sugarcane model yield estimation with a NDVI-derived variable. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XIV of the Conference, Edinburgh, UK, 24–27 September 2012.
- Raunet, M. Le milieu physique et les sols de l’ile de la réunion. In Conséquences pour la Mise en Valeur Agricole; CIRAD: Montpellier, France, 1991; p. 438. [Google Scholar]
- De Boissezon, H.; Rabaute, T.; Marzocchi-Polizzi, S.; Froidefond, J.M.; Dehouck, A.; Pennober, G.; Lafon, V. The Kalideos Databases, Reference Remote Sensing Data Repositories for Coastal Applications—Content and Examples of Applications; OCOSS: Brest, France, 2010; p. 6. [Google Scholar]
- Clevers, J.G.P.W.; Wonder, O.W.; Jongschaap, R.E.E.; Desprats, J.F.; King, C.; Prévot, L.; Bruguier, N. Using spot data for calibrating a wheat growth model under mediterranean conditions. Agronomie 2002, 22, 687–694. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2010. [Google Scholar]
- Lofton, J.; Tubana, B.S.; Kanke, Y.; Teboh, J.; Viator, H.; Dalen, M. Estimating sugarcane yield potential using an in-season determination of normalized difference vegetative index. Sensors 2012, 12, 7529–7547. [Google Scholar]
- Martiné, J.-F. Modélisation de la Production Potentielle de la Canne à Sucre en Zone Tropicale, Sous Conditions Thermiques et Hydriques Contrastées; Institut National Agronomique Paris-Grignon: Paris, France, 2003. [Google Scholar]
- Robertson, M.J.; Wood, A.W.; Muchow, R.C. Growth of sugarcane under high input conditions in tropical Australia. I. Radiation use, biomass accumulation and partitioning. Field Crops Res 1996, 48, 11–25. [Google Scholar]
- Papaioannou, G.; Papanikolaou, N.; Retalis, D. Relationships of photosynthetically active radiation and shortwave irradiance. Theor. Appl. Climatol 1993, 48, 23–27. [Google Scholar]
- Stanhill, G.; Fuchs, M. The relative flux density of photosynthetically active radiation. J. Appl. Ecol 1977, 14, 317–322. [Google Scholar]
- Christensen, S.; Goudriaan, J. Deriving light interception and biomass from spectral reflectance ratio. Remote Sens. Environ 1993, 43, 87–95. [Google Scholar]
- Morel, J.; Bégué, A.; Todoroff, P.; Martine, J.F.; Lebourgeois, V.; Petit, M. Coupling a sugarcane crop model with the remotely sensed time series of fipar to optimise the yield estimation. Eur. J. Agron 2014, in press.. [Google Scholar]
- Lingle, S.E. Sugarcane. In Crop Yield, Physiology and Processes; Smith, D.L., Hamel, C., Eds.; Springer-Verlag: Berlin, Germany, 1999; pp. 287–310. [Google Scholar]
- Gabrielle, B.; Menasseri, S.; Houot, S. Analysis and field evaluation of the ceres models water balance component. Soil Sci. Soc. Am. J 1995, 59, 1403–1412. [Google Scholar]
- Jones, C.A.; Kiniry, J.R.; Dyke, P.T. Ceres-Maize: A Simulation Model of Maize Growth and Development; Texas A&M University Press: Texas, TX, USA, 1986. [Google Scholar]
- Sellers, P.J.; Dickinson, R.E.; Randall, D.A.; Betts, A.K.; Hall, F.G.; Berry, J.A.; Collatz, G.J.; Denning, A.S.; Mooney, H.A.; Nobre, C.A.; et al. Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science 1997, 275, 502–509. [Google Scholar]
- Bappel, E. Apport de la Télédétection Aérospatiale pour l’Aide à la Gestion de la Sole Cannière Réunionnaise; La Réunion: Saint-Denis, France, 2005. [Google Scholar]
- El Hajj, M.; Bégué, A.; Lafrance, B.; Hagolle, O.; Dedieu, G.; Rumeau, M. Relative radiometric normalization and atmospheric correction of a SPOT 5 time series. Sensors 2008, 8, 2774–2791. [Google Scholar]
- Champion, N. Automatic cloud detection from multi-temporal satellite images: Towards the use of pléiades time series. Int. Arc. Photogramm. Remote Sens. Spatial Inf. Sci 2012, 1, 559–564. [Google Scholar]
- El Hajj, M.; Bégué, A.; Guillaume, S.; Martiné, J.-F. Integrating SPOT-5 time series, crop growth modeling and expert knowledge for monitoring agricultural practices—The case of sugarcane harvest on Reunion island. Remote Sens. Environ 2009, 113, 2052–2061. [Google Scholar]
- Baghdadi, N.; Cresson, R.; Todoroff, P.; Moinet, S. Multitemporal observations of sugarcane by TerraSAR-X images. Sensors 2010, 10, 8899–8919. [Google Scholar]



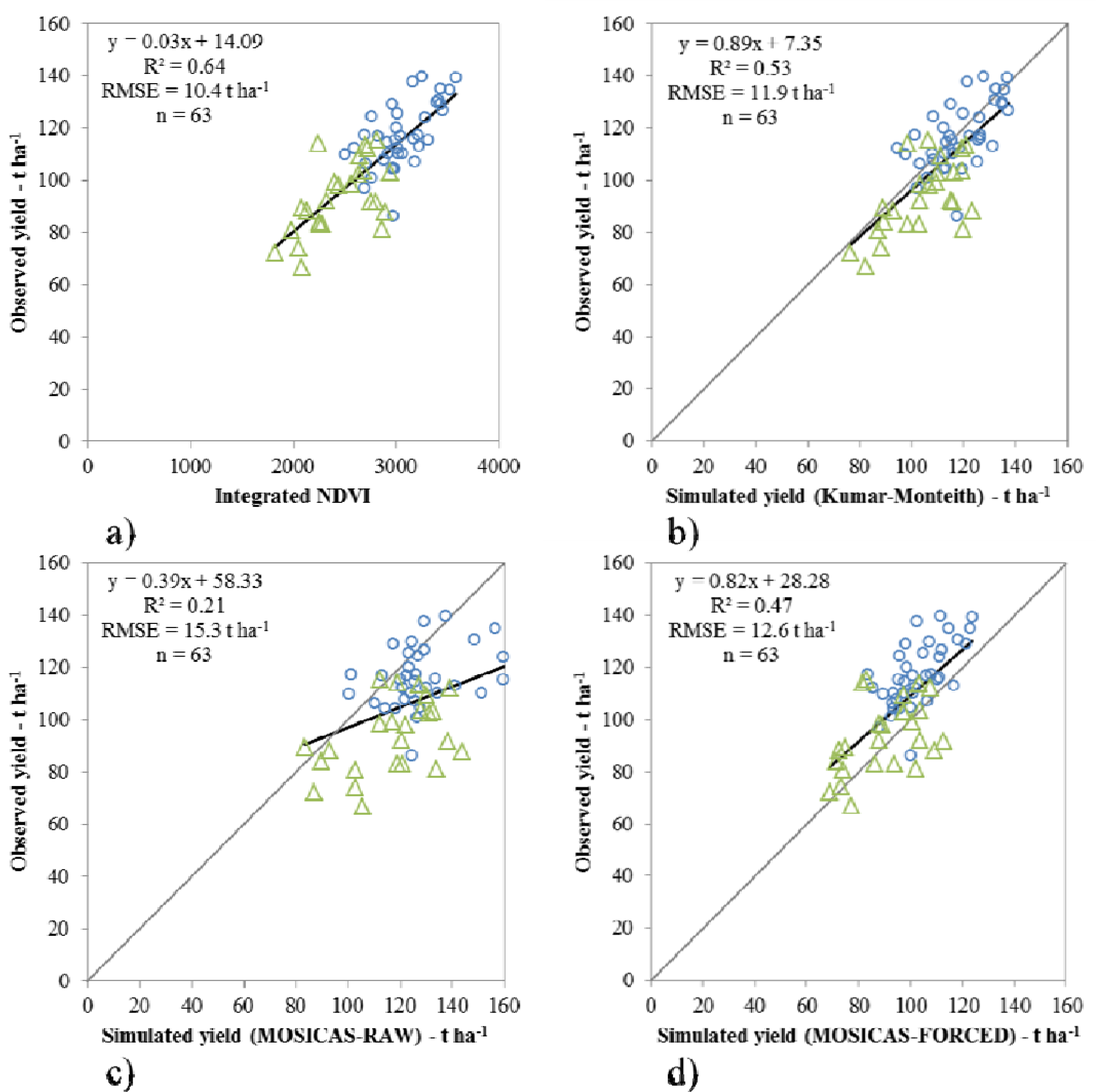

| Model | Integrated NDVI | Kumar-Monteith | MOSICAS-RAW | MOSICAS-FORCED |
|---|---|---|---|---|
| Sugarcane GIS | x | x | x | x |
| Satellite images | ≥5 | ≥5 | 0 | ≥5 |
| Harvest dates | x | x | x | x |
| Daily temperature | x | x | x | x |
| NDVI-degree day model | x | x | x | |
| Global radiation | x | x | x | |
| Rainfall | x | x | ||
| Irrigation | x | x | ||
| Number of inputs | 5 | 6 | 6 | 8 |
| RMSE, in t·ha−1 | 10.4 | 11.9 | 15.3 | 12.6 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Morel, J.; Todoroff, P.; Bégué, A.; Bury, A.; Martiné, J.-F.; Petit, M. Toward a Satellite-Based System of Sugarcane Yield Estimation and Forecasting in Smallholder Farming Conditions: A Case Study on Reunion Island. Remote Sens. 2014, 6, 6620-6635. https://doi.org/10.3390/rs6076620
Morel J, Todoroff P, Bégué A, Bury A, Martiné J-F, Petit M. Toward a Satellite-Based System of Sugarcane Yield Estimation and Forecasting in Smallholder Farming Conditions: A Case Study on Reunion Island. Remote Sensing. 2014; 6(7):6620-6635. https://doi.org/10.3390/rs6076620
Chicago/Turabian StyleMorel, Julien, Pierre Todoroff, Agnès Bégué, Aurore Bury, Jean-François Martiné, and Michel Petit. 2014. "Toward a Satellite-Based System of Sugarcane Yield Estimation and Forecasting in Smallholder Farming Conditions: A Case Study on Reunion Island" Remote Sensing 6, no. 7: 6620-6635. https://doi.org/10.3390/rs6076620
APA StyleMorel, J., Todoroff, P., Bégué, A., Bury, A., Martiné, J.-F., & Petit, M. (2014). Toward a Satellite-Based System of Sugarcane Yield Estimation and Forecasting in Smallholder Farming Conditions: A Case Study on Reunion Island. Remote Sensing, 6(7), 6620-6635. https://doi.org/10.3390/rs6076620





