A Novel Clustering-Based Feature Representation for the Classification of Hyperspectral Imagery
Abstract
:1. Introduction
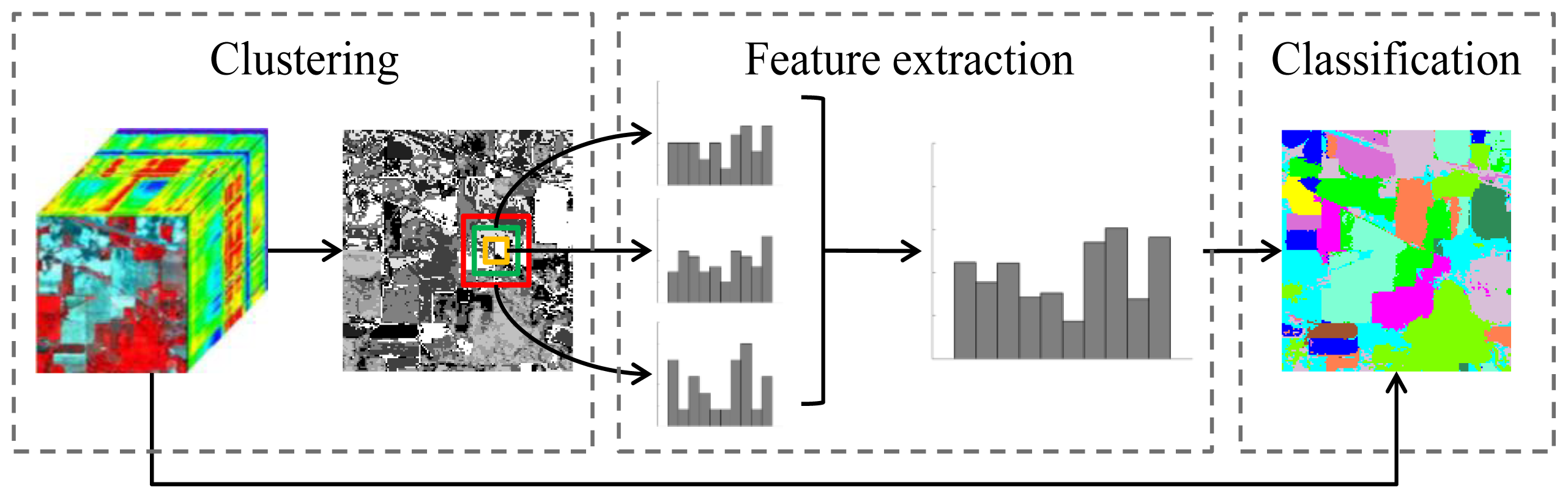
2. Methodology
2.1. Clustering
- (1)
- K-Means: This is a centroid-based clustering method that uses the cluster centers to construct the model for the data grouping. For the sake of minimizing the sum of the distance between points to the centroid vectors, an iterative algorithm is used to modify the model until the desired result is achieved [20]. In the reassignment step, the points are assigned to their nearest cluster centroid:where t represents the t-th iteration, and μi is the mean of the points in cluster ci.
- (2)
- Iterative Self-Organizing Data Analysis Technique Algorithm (ISODATA): The basic idea of ISODATA is similar to k-means in that it minimizes the intra-cluster variability by a reassignment and update process. However, the algorithm improves on k-means by introducing a merging and splitting method during the iteration. Clusters are merged if the distance of their centers is less than a given threshold, or the number of points in a cluster is less than the predefined value. Conversely, a single cluster is divided into two clusters if the standard deviation is higher than a user-specified value, or the number of points exceeds a certain threshold. In this way, the final clustering result is obtained when all the predefined conditions are reached [21].
- (3)
- Fuzzy C-Means (FCM): Differing from the deterministic clustering approaches, the FCM algorithm uses a membership level to describe the relationship between points and clusters [22]. Meanwhile, the centroids of the clusters are related to the coefficients which represent the grades of membership of the clusters, and can be expressed by the weighted mean of all the points:where wpi is the degree of xp belonging to cluster ci, which is defined as:where m donates the level of the cluster fuzziness.In order to obtain the cluster label of each point, the final clusters are obtained by assigning points to the cluster with the maximum membership degree.
- (4)
- Exception Maximization (EM) Algorithm: EM is frequently used for data clustering in machine learning, and works in two alternating steps: (1) the expectation (E) step, which refers to computing the expected value with the previous estimates of the model parameters; and (2) the maximization (M) step, which refers to altering the parameters by maximizing the expectation function [23]. The fundamental principle of the algorithm is to find a maximum likelihood estimate of the parameters through the iterative model. Each feature vector will then be assigned to one cluster on the basis of the maximum posteriori probability.
2.2. Cluster Histogram
2.3. Classification
3. Experimental Section
3.1. Datasets
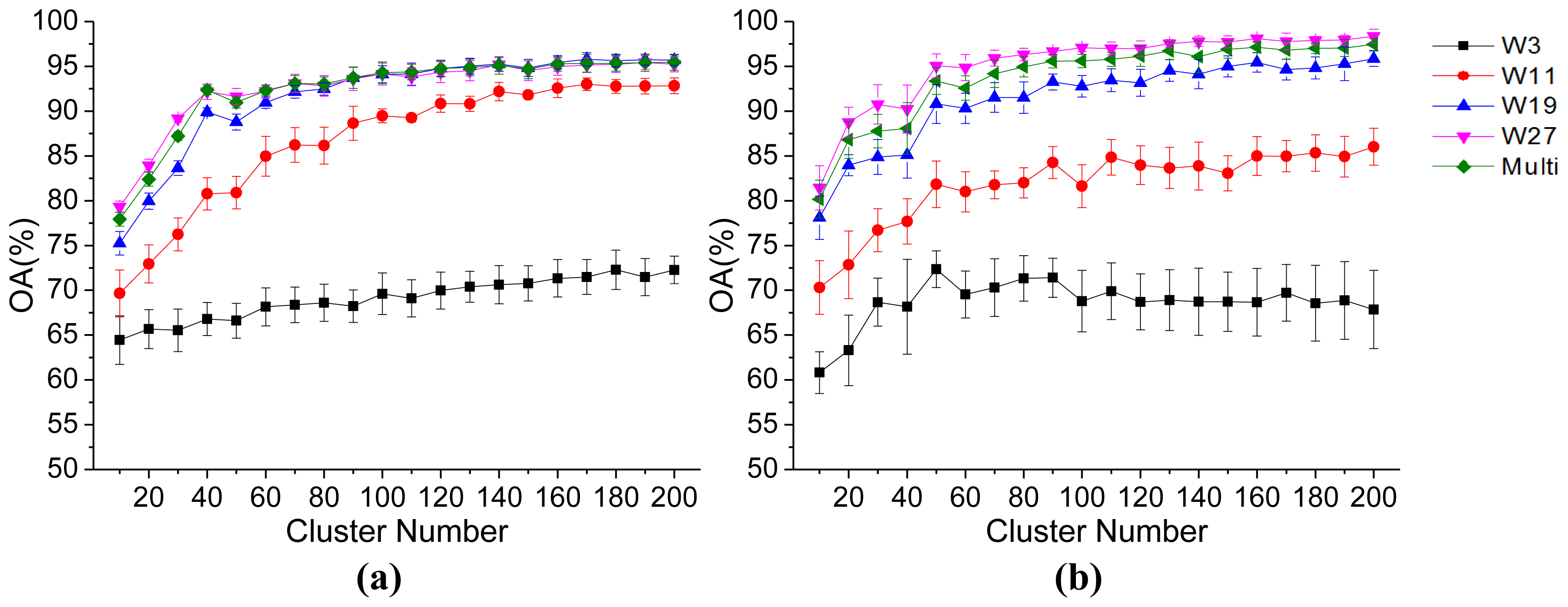
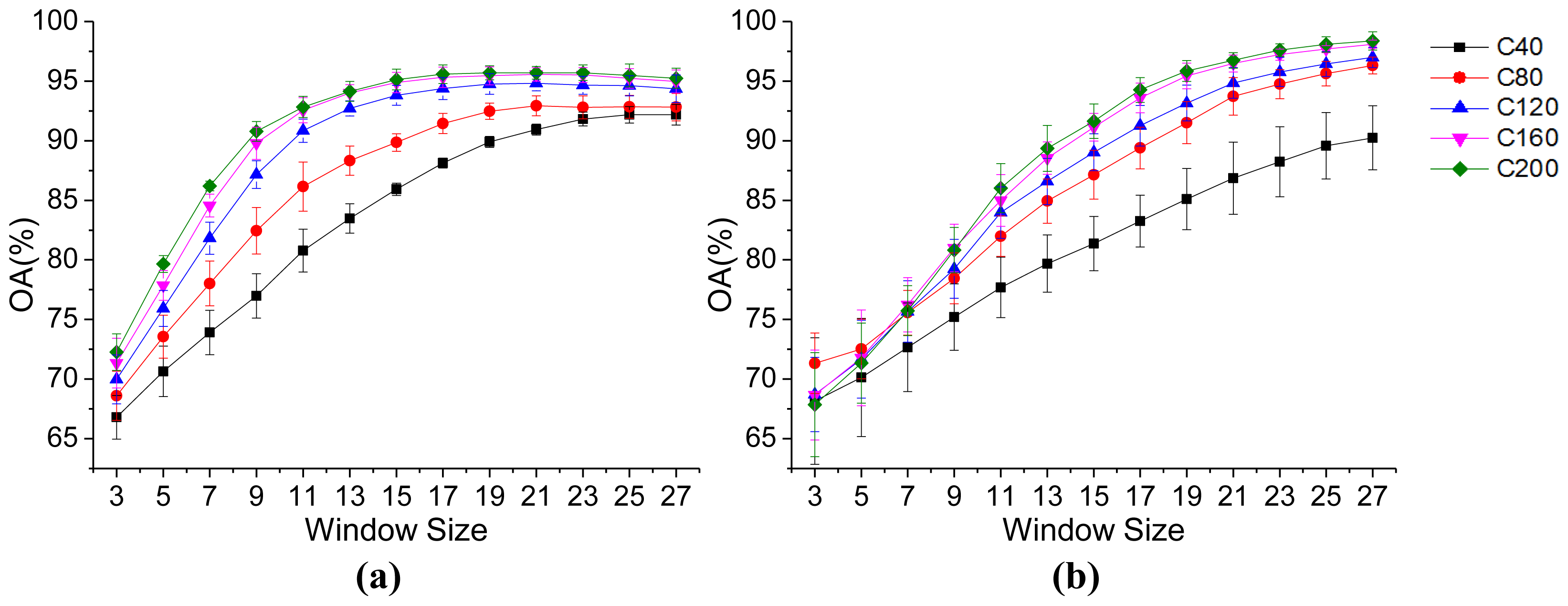
3.2. Parameter Analysis
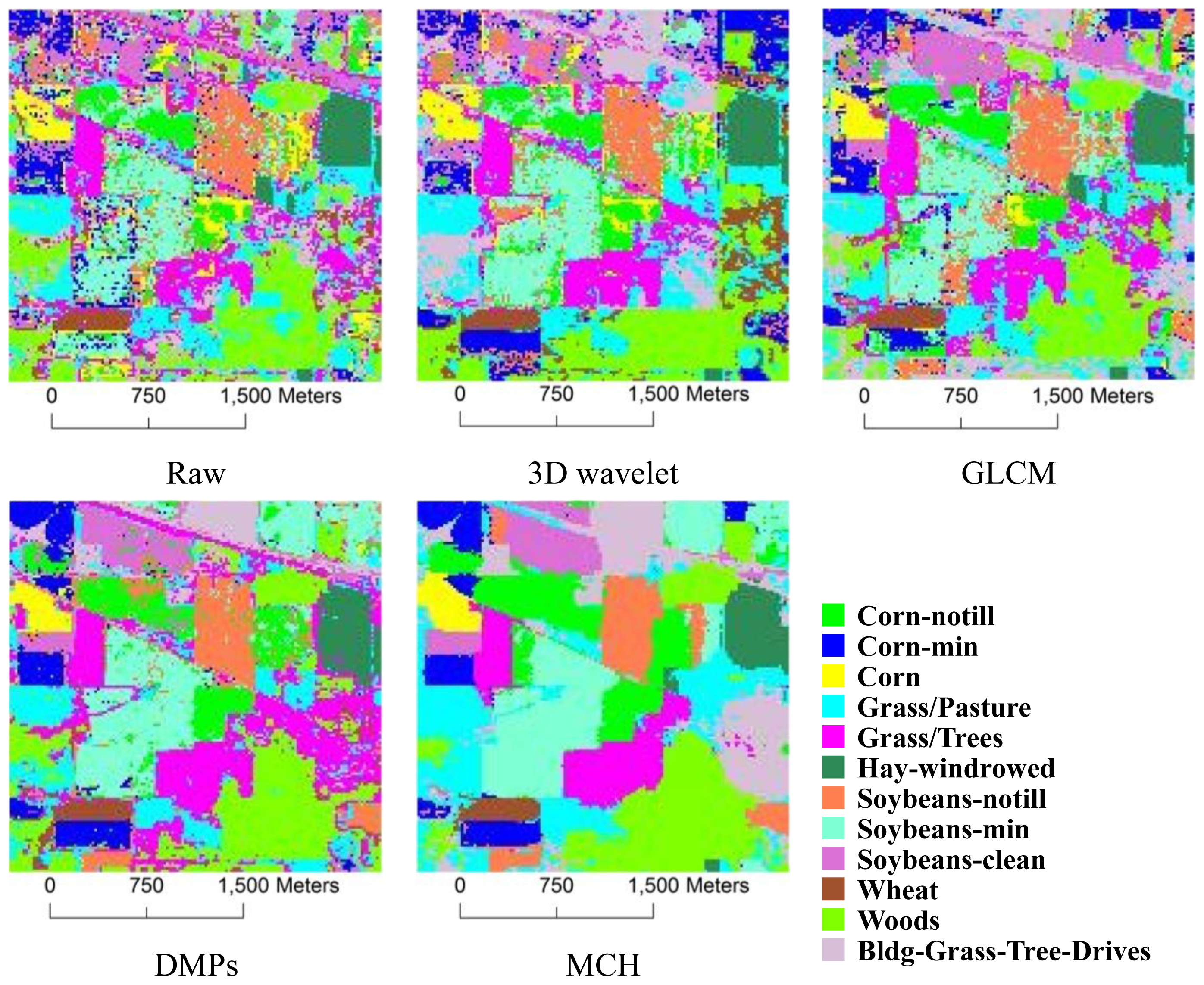
3.3. Results and Comparisons
3.3.1. 3D Wavelet Texture
3.3.2. GLCM
3.3.3. DMPs
3.4. Discussion
- (1)
- Dimensionality of the hyperspectral bands. The Indian Pines image is taken as an example for investigating the effect of the spectral dimensionality for the MCH method. The dimensions of the spectral features used for the clustering are reduced to 10, 30, and 50, according to Equation (4). From Table 9, it can be seen that the spectral dimension of the clustering has little effect on the final classification accuracy. It is therefore sensible to appropriately reduce the spectral dimensionality in order to increase the efficiency of the MCH method, since the computational complexity of clustering is affected by the feature dimensionality.
- (2)
- Initialization of the clustering. To analyze the influence of initialization of the clustering on the classification, the accuracies with different initial clustering centers that are randomly generated are reported in Table 10 for the Indian Pines image. It can be seen that, although the clustering approach gives slightly different clustering results for the different runs, the classification accuracies are stable and the proposed MCH is robust to the clustering initialization.
- (3)
- Comparison with a state-of-the-art spectral-spatial classification technique. In order to further validate the effectiveness of the proposed MCH method, the state-of-the-art spectral-spatial classification approach of Tarabalka et al. [10] is carried out for comparison. In this approach, the pixelwise SVM classification result is refined by majority voting based on a clustering-based segmentation. A post-processing is then performed in order to reduce the classification noise. The comparison results are shown in Table 11, where it can be clearly seen that the MCH method significantly outperforms the state-of-the-art spectral-spatial classification approach of Tarabalka et al. [10].
4. Conclusions
- (1)
- The clustering strategy is able to generate a series of primitive codes which effectively represent the spectral signals in an image.
- (2)
- The cluster histogram in a series of multiscale neighborhoods centered by each pixel is effective in exploiting both the spectral and spatial features. Furthermore, the multi-window strategy assigns large weights to the pixels near the center, which is reasonable due to the complex and multiscale characteristics of the remote sensing data.
- (3)
- The MCH feature extraction and classification method can achieve satisfactory results rapidly and conveniently without defining complicated textural or structural features. It can also be easily carried out in real applications.
Acknowledgments
Conflicts of Interest
- Author ContributionsAll authors made great contributions to the work. Qikai Lu and Xin Huang designed the research and analyzed the results. Qikai Lu wrote the manuscript and performed the experiments. Xin Huang supervised the study and gave insightful suggestions to the manuscript. Liangpei Zhang provided the background knowledge and contributed in the revision of the paper.
References
- Pal, M.; Mather, P.M. An assessment of the effectiveness of decision tree methods for land cover classification. Remote Sens. Environ 2003, 86, 554–565. [Google Scholar]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens 2004, 42, 1778–1790. [Google Scholar]
- Gong, B.; Im, J.; Mountrakis, G. An artificial immune network approach to multi-sensor land use/land cover classification. Remote Sens. Environ 2011, 115, 600–614. [Google Scholar]
- Myint, S.W.; Gober, P.; Brazel, A.; Grossman-Clarke, S.; Weng, Q. Perpixel vs. object-based classification of urban land cover extraction using high spatial resolution imagery. Remote Sens. Environ 2011, 115, 1145–1161. [Google Scholar]
- Huang, X.; Zhang, L. An SVM ensemble approach combining spectral, structural, and semantic features for the classification of high-resolution remotely sensed imagery. IEEE Trans. Geosci. Remote Sens 2013, 51, 257–272. [Google Scholar]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell 2002, 24, 603–619. [Google Scholar]
- Baatz, M.; Schäpe, A. Multiresolution segmentation: An optimization approach for high quality multi-scale image segmentation. Angew. Geogr. Inf 2000, 12, 12–23. [Google Scholar]
- Vincent, L.; Soille, P. Watersheds in digital spaces: An efficient algorithm based on immersion simulations. IEEE Trans. Pattern Anal. Mach. Intell 1991, 13, 583–598. [Google Scholar]
- Meinel, G.; Neubert, M. A comparison of segmentation programs for high resolution remote sensing data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2004, 35, 1097–1105. [Google Scholar]
- Tarabalka, Y.; Benediktsson, J.A.; Chanussot, J. Spectral-spatial classification of hyperspectral imagery based on partitional clustering techniques. IEEE Trans. Geosci. Remote Sens 2009, 47, 2973–2987. [Google Scholar]
- Baraldi, A.; Panniggiani, F. An investigation of the textural characteristics associated with gray level co-occurrence matrix statistical parameters. IEEE Trans. Geosci. Remote Sens 1995, 33, 293–304. [Google Scholar]
- Benediktsson, J.A.; Pesaresi, M.; Arnason, K. Classification and feature extraction for remote sensing images from urban areas based on morphological transformations. IEEE Trans. Geosci. Remote Sens 2003, 41, 1940–1949. [Google Scholar]
- Yoo, H.Y.; Lee, K.; Kwon, B.-D. Quantitative indices based on 3D discrete wavelet transform for urban complexity estimation using remotely sensed imagery. Int. J. Remote Sens 2009, 30, 6219–6239. [Google Scholar]
- Tong, X.; Xie, H.; Weng, Q. Urban land cover classification with airborne hyperspectral data: What features to use? IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens 2013. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, X.; Huang, B.; Li, P. A pixel shape index coupled with spectral information for classification of high spatial resolution remotely sensed imagery. IEEE Trans. Geosci. Remote Sens 2006, 44, 2950–2961. [Google Scholar]
- Pedergnana, M.; Marpu, P.R.; Mura, M.D.; Benediktsson, J.A.; Bruzzone, L. Classification of remote sensing optical and LiDAR data using extended attribute profiles. IEEE J. Sel. Top. Signal Process 2012, 6, 856–865. [Google Scholar]
- Gong, P.; Howarth, P.J. Frequency-based contextual classification and gray-level vector reduction for land-use identification. Photogramm. Eng. Remote Sens 1992, 58, 423–437. [Google Scholar]
- Xu, B.; Gong, P.; Seto, E.; Spear, R. Comparison of gray-level reduction and different texture spectrum encoding methods for land-use classification using a panchromatic IKONOS image. Photogramm. Eng. Remote Sens 2003, 69, 529–536. [Google Scholar]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv 1999, 31, 264–323. [Google Scholar]
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1967; Volume 1, pp. 281–297. [Google Scholar]
- Ball, G.; Hall, D. ISODATA, A Novel Method of Data Analysis and Classification; Technical Report, AD–699616; Stanford University: Stanford, CA, USA, 1965. [Google Scholar]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci 1984, 10, 191–203. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. B 1977, 39, 1–38. [Google Scholar]
- Huang, X.; Lu, Q.; Zhang, L. A multi-index learning approach for classification of high-resolution remotely sensed images over urban areas. ISPRS J. Photogramm. Remote Sens 2014, 90, 36–48. [Google Scholar]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Int. Syst. Technol 2011, 2, 1–27. [Google Scholar]
- MultiSpec. Available online: Https://engineering.purdue.edu/~biehl/MultiSpec/hyperspectral.html (accessed on 20 October 2011).
- Hyperspectral Remote Sensing Scenes. Available online: http://www.ehu.es/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scene (accessed on 12 June 2013).
- Ye, Z.; Prasad, S.; Li, W.; Fowler, J.E.; He, M. Classification based on 3-D DWT and decision fusion for hyperspectral image analysis. IEEE Geosci. Remote Sens. Lett 2014, 11, 173–177. [Google Scholar]
- Pesaresi, M.; Gerhardinger, A.; Kayitakire, F. A robust built-up area presence index by anisotropic rotation-invariant textural measure. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens 2008, 1, 180–192. [Google Scholar]
- Pesaresi, M.; Benediktsson, J.A. A new approach for the morphological segmentation of high-resolution satellite imagery. IEEE Trans. Geosci. Remote Sens 2001, 39, 309–320. [Google Scholar]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ 1991, 37, 35–46. [Google Scholar]
- Powers, D.M.W. Evaluation: From Precision, Recall and F-measure to ROC, Informedness, Markedness & Correlation. J. Mach. Learn. Technol 2011, 2, 37–63. [Google Scholar]
- Van der Meer, F. The effectiveness of spectral similarity measures for the analysis of hyperspectral imagery. Int. J. Appl. Earth Obs. Geoinf 2006, 8, 3–17. [Google Scholar]
- Kaufman, L.; Rousseeuw, P.J. Clustering Large Applications (Program CLARA). In Finding Groups in Data: An Introduction to Cluster Analysis; John Wiley & Sons: New York, NY, USA, 1990. [Google Scholar]

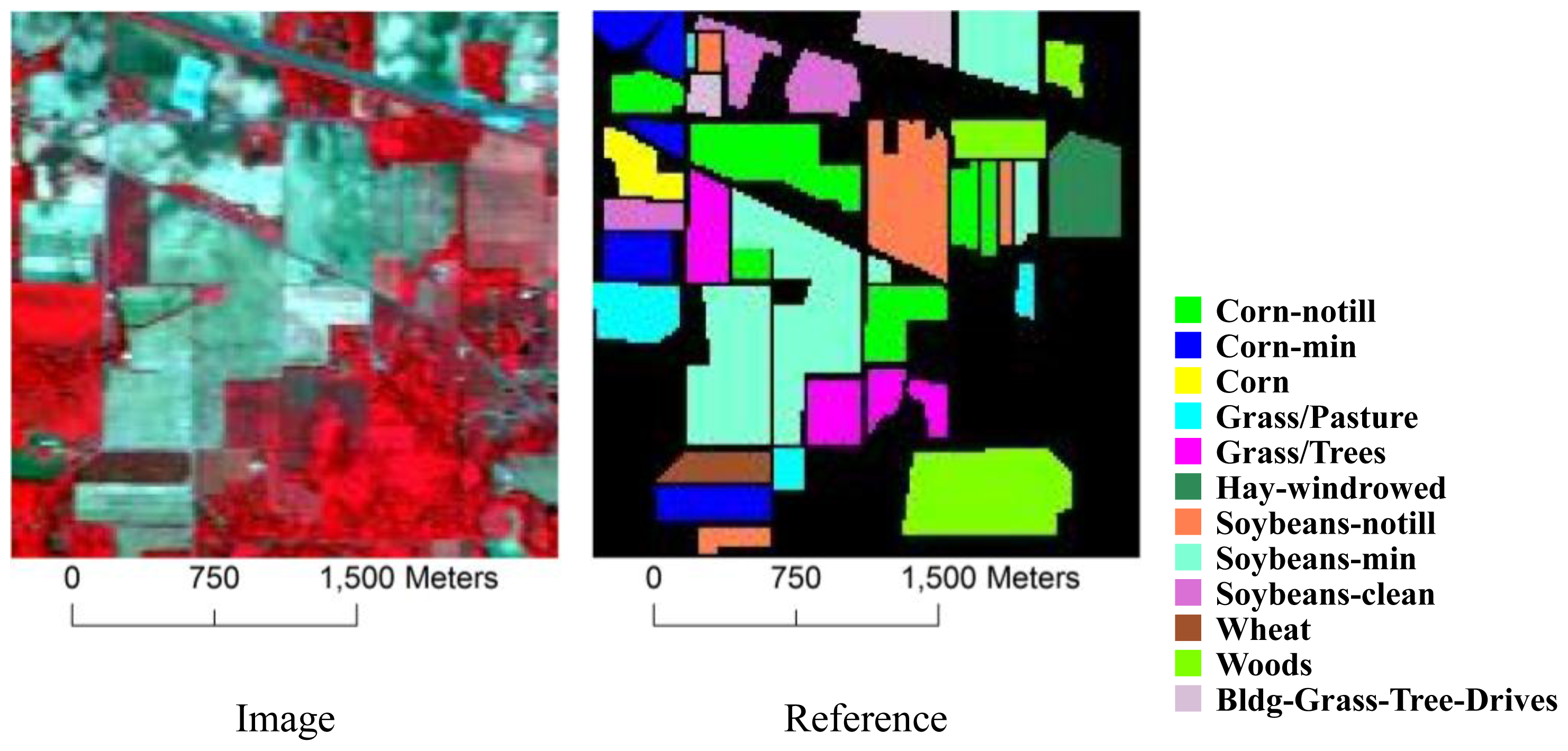

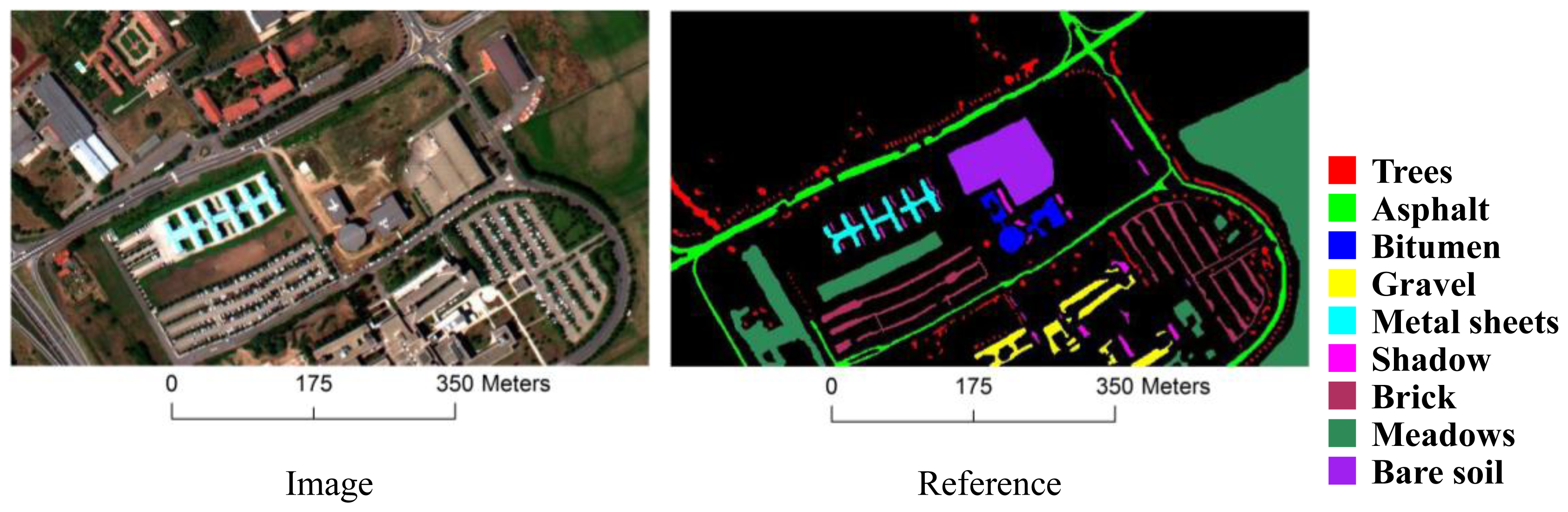


| Class | # Training Samples | # Test Samples |
|---|---|---|
| Corn-notill | 50 | 1434 |
| Corn-mintill | 50 | 834 |
| Corn | 50 | 234 |
| Grass/pasture | 50 | 497 |
| Grass/trees | 50 | 747 |
| Hay-windrowed | 50 | 489 |
| Soybeans-notill | 50 | 968 |
| Soybeans-mintill | 50 | 2468 |
| Soybeans-cleantill | 50 | 614 |
| Wheat | 50 | 212 |
| Woods | 50 | 1294 |
| Bldg-Grass-Tree-Drives | 50 | 380 |
| Total | 600 | 10,171 |
| Class | # Training Samples | # Test Samples |
|---|---|---|
| Roads | 50 | 3299 |
| Grass | 50 | 3075 |
| Water | 50 | 2882 |
| Trails | 50 | 1017 |
| Trees | 50 | 2027 |
| Shadows | 50 | 1093 |
| Roofs | 50 | 5811 |
| Total | 350 | 19,024 |
| Class | # Training Samples | # Test Samples |
|---|---|---|
| Trees | 50 | 3064 |
| Asphalt | 50 | 6631 |
| Bitumen | 50 | 1330 |
| Gravel | 50 | 2099 |
| Metal sheets | 50 | 1345 |
| Shadows | 50 | 947 |
| Bricks | 50 | 3682 |
| Meadows | 50 | 18,649 |
| Bare soil | 50 | 5029 |
| Total | 450 | 42,776 |
| Class | #Training Samples | # Test Samples |
|---|---|---|
| Buildings | 50 | 84,421 |
| Roads | 50 | 18,149 |
| Water | 50 | 38,875 |
| Trees/grass | 50 | 40,630 |
| Shadows | 50 | 12,532 |
| Total | 250 | 194,607 |
| Spectral-Spatial Classification | MCH | |||||||
|---|---|---|---|---|---|---|---|---|
| Raw | 3D Wavelet | GLCM | DMPs | k-Means | ISO | FCM | EM | |
| Corn-notill | 49.51 | 56.33 | 61.33 | 76.93 | 90.15 | 88.12 | 89.09 | 90.39 |
| Corn-mintill | 44.51 | 63.36 | 66.17 | 88.83 | 93.87 | 93.59 | 93.33 | 95.06 |
| Corn | 40.98 | 49.31 | 67.90 | 87.09 | 97.03 | 97.75 | 95.85 | 97.31 |
| Grass/pasture | 70.99 | 86.31 | 76.45 | 90.01 | 96.75 | 97.06 | 97.15 | 96.79 |
| Grass/trees | 82.27 | 90.90 | 91.08 | 94.71 | 99.44 | 99.68 | 99.67 | 99.57 |
| Hay-windrowed | 97.86 | 98.76 | 98.28 | 98.86 | 99.74 | 99.80 | 99.70 | 99.62 |
| Soybeans-notill | 55.51 | 60.28 | 62.15 | 76.17 | 89.89 | 87.98 | 88.86 | 90.14 |
| Soybeans-mintill | 57.17 | 65.02 | 67.28 | 88.32 | 95.08 | 95.05 | 94.98 | 95.15 |
| Soybeans-cleantill | 42.90 | 50.10 | 63.11 | 81.19 | 95.28 | 95.23 | 95.03 | 96.41 |
| Wheat | 87.82 | 96.75 | 98.52 | 99.35 | 99.72 | 99.81 | 99.72 | 99.67 |
| Woods | 86.47 | 93.60 | 91.63 | 98.73 | 99.91 | 99.92 | 99.92 | 99.90 |
| Bldg-Grass-Tree-Drives | 50.34 | 77.26 | 79.91 | 97.56 | 99.37 | 99.66 | 99.03 | 99.63 |
| OA | 61.83 | 70.73 | 73.40 | 88.08 | 95.34 | 94.90 | 95.00 | 95.60 |
| kappa | 0.57 | 0.67 | 0.70 | 0.86 | 0.95 | 0.94 | 0.94 | 0.95 |
| Spectral-Spatial Classification | MCH | |||||||
|---|---|---|---|---|---|---|---|---|
| Raw | 3D Wavelet | GLCM | DMPs | k-Means | ISO | FCM | EM | |
| Roads | 91.70 | 91.79 | 92.04 | 95.37 | 98.98 | 98.87 | 98.81 | 98.84 |
| Grass | 98.85 | 99.32 | 99.22 | 99.72 | 99.86 | 99.84 | 99.86 | 99.76 |
| Water | 86.28 | 88.33 | 96.86 | 96.05 | 98.71 | 100.00 | 99.30 | 99.94 |
| Trails | 66.10 | 90.94 | 90.42 | 97.02 | 99.64 | 99.63 | 99.61 | 99.44 |
| Trees | 98.17 | 98.69 | 98.33 | 99.02 | 99.92 | 99.92 | 99.90 | 99.70 |
| Shadows | 39.93 | 67.70 | 90.53 | 90.17 | 96.86 | 99.63 | 97.77 | 99.50 |
| Roofs | 84.28 | 93.45 | 93.44 | 96.90 | 99.51 | 99.42 | 99.46 | 99.38 |
| OA | 86.61 | 92.28 | 94.80 | 96.75 | 99.24 | 99.55 | 99.34 | 99.48 |
| kappa | 0.84 | 0.91 | 0.94 | 0.96 | 0.99 | 0.99 | 0.99 | 0.99 |
| Spectral-Spatial Classification | MCH | |||||||
|---|---|---|---|---|---|---|---|---|
| Raw | 3D Wavelet | GLCM | DMPs | k-Means | ISO | FCM | EM | |
| Trees | 62.85 | 63.22 | 70.95 | 87.03 | 97.70 | 97.77 | 97.29 | 97.50 |
| Asphalt | 77.94 | 80.60 | 78.81 | 96.16 | 97.99 | 97.90 | 96.86 | 99.59 |
| Bitumen | 49.65 | 56.06 | 59.14 | 99.86 | 99.29 | 99.81 | 96.69 | 100.00 |
| Gravel | 34.48 | 46.42 | 40.04 | 96.00 | 95.94 | 95.51 | 94.67 | 99.73 |
| Metal sheets | 91.00 | 93.99 | 92.72 | 99.71 | 99.93 | 99.88 | 99.83 | 99.93 |
| Shadows | 99.36 | 99.41 | 99.42 | 99.89 | 99.92 | 99.93 | 99.93 | 99.95 |
| Bricks | 59.90 | 66.66 | 69.53 | 92.80 | 97.56 | 98.56 | 96.68 | 99.37 |
| Meadows | 61.98 | 63.90 | 68.12 | 97.07 | 98.25 | 98.75 | 97.78 | 99.60 |
| Bare soil | 31.97 | 33.89 | 39.04 | 99.35 | 95.17 | 96.85 | 94.34 | 99.99 |
| OA | 59.42 | 62.67 | 64.84 | 96.18 | 97.73 | 98.23 | 97.00 | 99.51 |
| kappa | 0.50 | 0.54 | 0.57 | 0.95 | 0.97 | 0.98 | 0.96 | 0.99 |
| Spectral-Spatial Classification | MCH | |||||||
|---|---|---|---|---|---|---|---|---|
| Raw | 3D Wavelet | GLCM | DMPs | k-Means | ISO | FCM | EM | |
| Buildings | 88.47 | 88.79 | 90.82 | 90.07 | 93.27 | 93.58 | 93.54 | 92.75 |
| Roads | 67.41 | 67.92 | 70.92 | 71.95 | 77.69 | 78.63 | 78.38 | 76.42 |
| Water | 99.61 | 98.92 | 98.79 | 99.34 | 99.99 | 99.94 | 99.98 | 99.86 |
| Trees/grass | 97.16 | 97.29 | 98.35 | 96.30 | 99.32 | 99.26 | 99.12 | 99.21 |
| Shadows | 95.43 | 93.82 | 93.12 | 91.34 | 95.95 | 95.30 | 96.03 | 94.71 |
| OA | 90.21 | 90.21 | 91.68 | 91.07 | 94.26 | 94.45 | 94.43 | 93.75 |
| kappa | 0.87 | 0.87 | 0.89 | 0.88 | 0.92 | 0.92 | 0.92 | 0.91 |
| Dim. | k-Means | ISO | FCM | EM | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| 10 | 95.34 | 0.98 | 94.90 | 0.89 | 95.00 | 0.98 | 95.60 | 0.94 |
| 30 | 95.28 | 1.09 | 95.23 | 0.73 | 95.06 | 1.00 | 95.65 | 1.17 |
| 50 | 95.28 | 1.08 | 95.10 | 0.87 | 95.15 | 1.09 | 95.56 | 0.90 |
| All | 95.46 | 0.89 | 95.14 | 0.87 | 94.74 | 0.93 | 95.40 | 0.84 |
| Run | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| k-means | Mean | 95.65 | 95.53 | 94.94 | 95.22 | 95.62 | 95.26 | 95.28 | 95.26 | 94.96 | 95.29 |
| Std. | 0.67 | 0.93 | 1.10 | 0.88 | 0.77 | 1.02 | 0.98 | 0.82 | 0.95 | 0.80 | |
| FCM | Mean | 95.44 | 95.17 | 95.31 | 95.29 | 95.09 | 95.27 | 95.07 | 95.29 | 95.18 | 95.55 |
| Std. | 1.03 | 1.01 | 0.98 | 0.90 | 0.94 | 1.00 | 0.97 | 1.12 | 1.00 | 0.97 | |
| EM | Mean | 95.62 | 95.65 | 95.18 | 95.77 | 95.98 | 95.43 | 95.62 | 95.87 | 95.51 | 95.81 |
| Std. | 0.80 | 0.60 | 1.04 | 0.95 | 0.65 | 1.00 | 0.73 | 0.39 | 0.70 | 0.89 | |
| Datasets | MCH | Tarabalka et al. [10] | ||||
|---|---|---|---|---|---|---|
| k-Means | ISO | FCM | EM | Without PP | With PP | |
| University | 97.73 | 98.23 | 97.00 | 99.51 | 90.57 | 91.20 |
| AVIRIS | 95.34 | 94.90 | 95.00 | 95.60 | 88.53 | 90.64 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lu, Q.; Huang, X.; Zhang, L. A Novel Clustering-Based Feature Representation for the Classification of Hyperspectral Imagery. Remote Sens. 2014, 6, 5732-5753. https://doi.org/10.3390/rs6065732
Lu Q, Huang X, Zhang L. A Novel Clustering-Based Feature Representation for the Classification of Hyperspectral Imagery. Remote Sensing. 2014; 6(6):5732-5753. https://doi.org/10.3390/rs6065732
Chicago/Turabian StyleLu, Qikai, Xin Huang, and Liangpei Zhang. 2014. "A Novel Clustering-Based Feature Representation for the Classification of Hyperspectral Imagery" Remote Sensing 6, no. 6: 5732-5753. https://doi.org/10.3390/rs6065732
APA StyleLu, Q., Huang, X., & Zhang, L. (2014). A Novel Clustering-Based Feature Representation for the Classification of Hyperspectral Imagery. Remote Sensing, 6(6), 5732-5753. https://doi.org/10.3390/rs6065732





