1. Introduction
Understanding patterns of forest disturbances is important for assessing past and future ecosystem structure, function, productivity and diversity [
1,
2]. In recent years, mountain pine beetle (MPB) outbreaks have occurred over extensive areas, from British Columba in Canada to New Mexico in the United States. MPB is endemic to North America; however, the recent outbreaks have reached epidemic levels that have affected millions of hectares of forests [
3]. The effects of MPB infestation range from altered surface fuel and wildfire hazards [
4–
7], changed vegetative composition [
8], converted live carbon sinks to dead and slowly decaying carbon sources [
9–
11], impacted nutrient cycling and water quality [
12,
13], shifted evapotranspiration and albedo, modified local surface energy balance [
14] and changed regional climate [
15]. Those effects are predicted to increase as a consequence of the direct and indirect effects of climatic changes [
16–
18]. However, unlike wildfires that have received intensive mapping efforts at different scales, characterizations of the extent and severity of MPB using multi-temporal data have only begun to emerge [
19–
23].
Remote sensing, both with aerial photography and satellite imagery, has been widely acknowledged as a useful way to map tree mortality over large areas [
24]. Landsat time series stacks (LTSS) are well suited to this type of analysis, because they are freely available, cover a long time period, have a broad spatial extent, are multispectral and have temporal continuity [
20,
25]. Two frequently used disturbance mapping approaches are (1) trajectory-reconstruction and (2) decision trees (DTs). Trajectory-based change detection examples include the Landsat-based detection of trends in disturbance and recovery algorithm (LandTrendr) [
26] and the Vegetation Change Tracker [
27–
29]. Both methods recognize disturbance events by the rate of changes in time series of spectral properties. This makes the first and last years of the trajectory more difficult to judge, because the attribution for a particular year is entirely determined with regard to its spectral deviation from the two adjacent years [
26]. In addition, the event labeling procedure depends on pre-implemented modules in the software and, thus, is not flexible in adjusting to user-defined functions. DT approaches include work by Goodwin
et al. [
30] who utilized the annual changes in normalized difference moisture index and a set of thresholds to classify the presence of MPB infestation over 14 years, resulting in overall accuracies ranging from 71% to 86%. DT-based approaches have the capacity to integrate expert knowledge and flexible classification schemes. However, poor image quality from sensor drift, geometric misregistration and topographic and cloud shadows will introduce distortions to images and affect the accuracy of change detection.
In this study, we describe a forest growth trend analysis method that integrates the robust change detection strengths of the trajectory reconstruction approach and the flexible user-defined advantages of DT approaches to characterize MPB mortality with an 11-year LTSS. We were interested in determining whether or not this proposed method could reach an accuracy target of 85% or greater. Additionally, we compared its accuracy with single-date image classifications, which are still important and commonly used in disturbance mapping, especially in two-date post-classification change detection. We are aware that the accuracy of single-date image classification is not only determined by the input variables and classifiers, but is also heavily dependent on the quality and quantity of training samples [
31], which may have larger impacts than the implemented techniques [
32]. Thus, we also assessed the effect of different sample sizes on the accuracy of single-date image classifications, and we tested how much our proposed method can improve sampling efficiency as compared with the single-date classifiers.
3. Method
3.1. Temporal Segmentation
We developed time series of disturbance maps by combining the temporal trajectory analysis approach of LandTrendr [
26] with a decision tree labeling procedure. Temporal trajectory analysis was used to decompose often noisy time series into a sequence of straight-line segments with distinct features designed to capture the event that happened for the duration of each segment. NBR [
39] was chosen to represent the vegetation condition, because of its sensitivity to disturbance [
26] and its capacity to minimize radiometric differences among images. The general procedure was to use a set of parameters to enhance the signal-to-noise ratio of the NBR time series in order to capture the salient events happening in each period or segment. Details can be found in Kennedy
et al. [
26], and the final effect of temporal segmentation, whether it was under-segmentation (split up into too few parts) or over-segmentation (subdivided into too many parts), was determined by the parameters listed in
Table 3. Optimal LandTrendr parameter settings have been tested in the forests of the Northwest Pacific Region at both Landsat and MODIS scales [
26,
41]. However, because we are not aware of reported parameter results in the literature specific to the Southern Rocky Mountain ecoregion, we tested a range of candidate parameter values (
Table 3).
We ran LandTrendr on all combinations of the candidate parameter values, which resulted in 144 unique combinations in total, and then visually compared their temporal segmentation results with the original NBR time series for the 106 training samples. Thus, the calibration involved 15,264 comparisons. Each individual comparison for a sample was coded in a binary state using two criteria: the overall match in the shape and the timing of vertices. A good match occurred if the disturbance event that happened at that pixel was successfully captured, and the slope and magnitude for each segment deviated little from the central trend. The vertex timing was judged by how well the algorithm captured the onset and ending time of each disturbance event. If both criteria were satisfied, that comparison would be scored as 1, and otherwise, it would be 0. The optimal parameter set was decided based upon the pooled rankings across all training samples. The processing time took about 200 minutes (on 5,376,538 unmasked pixels) for this step, which was run on a workstation with an Intel i7-2600 3.4 GHz quad core CPU and 8 gigabytes of physical memory.
3.2. Decision Tree-Based Spectral Segment Labeling
The outputs of the temporal segmentation included the fitted segments, and a set of vertices connecting individual segments. We employed a DT to attribute disturbance events associated with those vertices and segments, with leaf nodes representing class labels and branches representing decision scenarios. The DT was built with predictors characterizing each segment: the disturbance occurrence onset time, duration and the magnitude of NBR change. We defined the onset time as the starting year of a segment. Magnitude was the absolute change in NBR between the ending year and the onset year, whereas duration was the time elapsed over the length of one segment. Different types of disturbance events were characterized by distinct features. For instance, clearcuts could be recognized by segments with a short duration and large, negative change in NBR, whereas MPB mortality segments tended to have a gradual, but long-duration decline in NBR values.
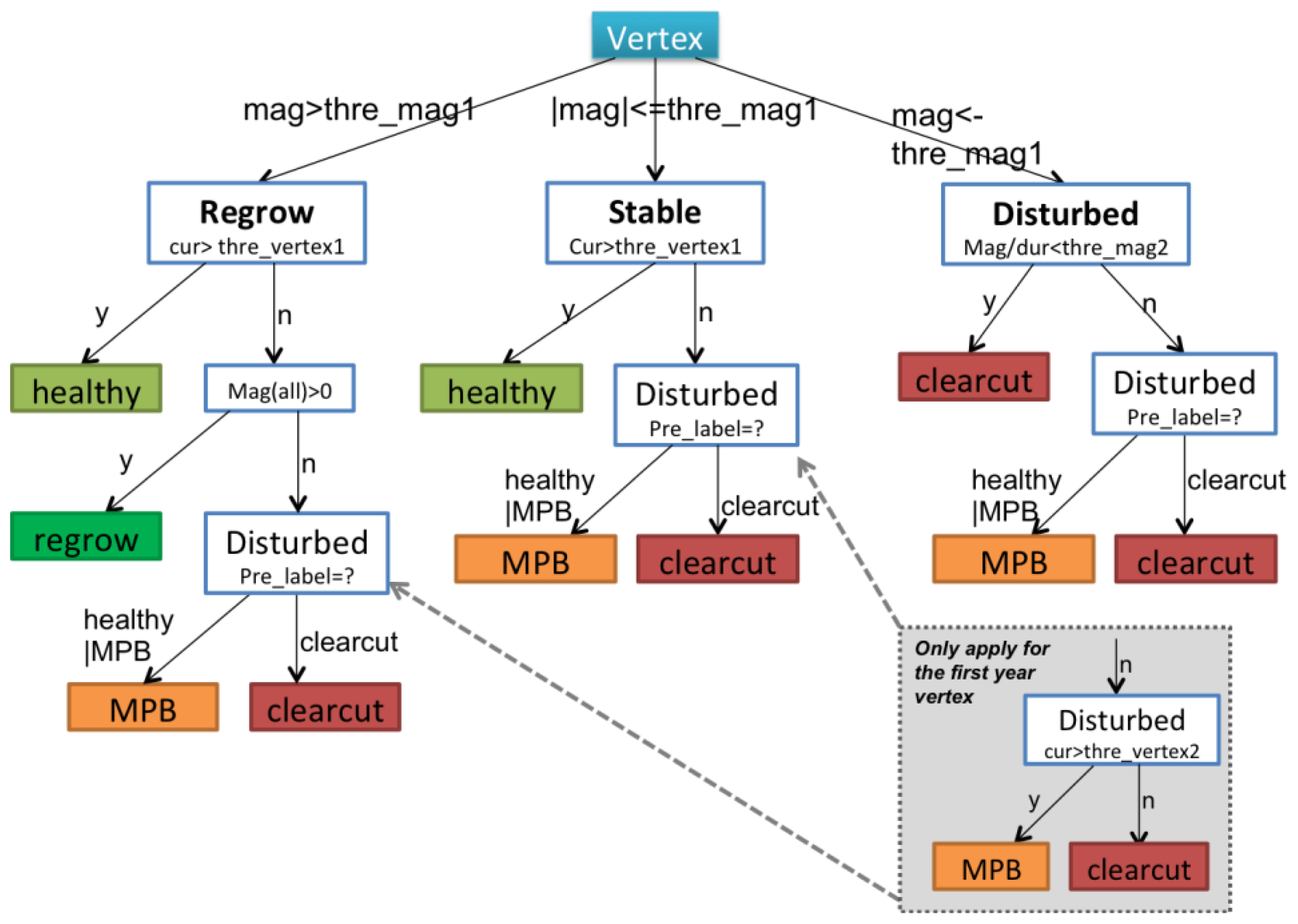
Decision rules were used to identify forest conditions in a top-down sequence (
Figure 3), and the definition of key parameters are explained in
Table 4. These parameters were manually calibrated with the same training samples described in Section 3.1. Specifically:
- (1)
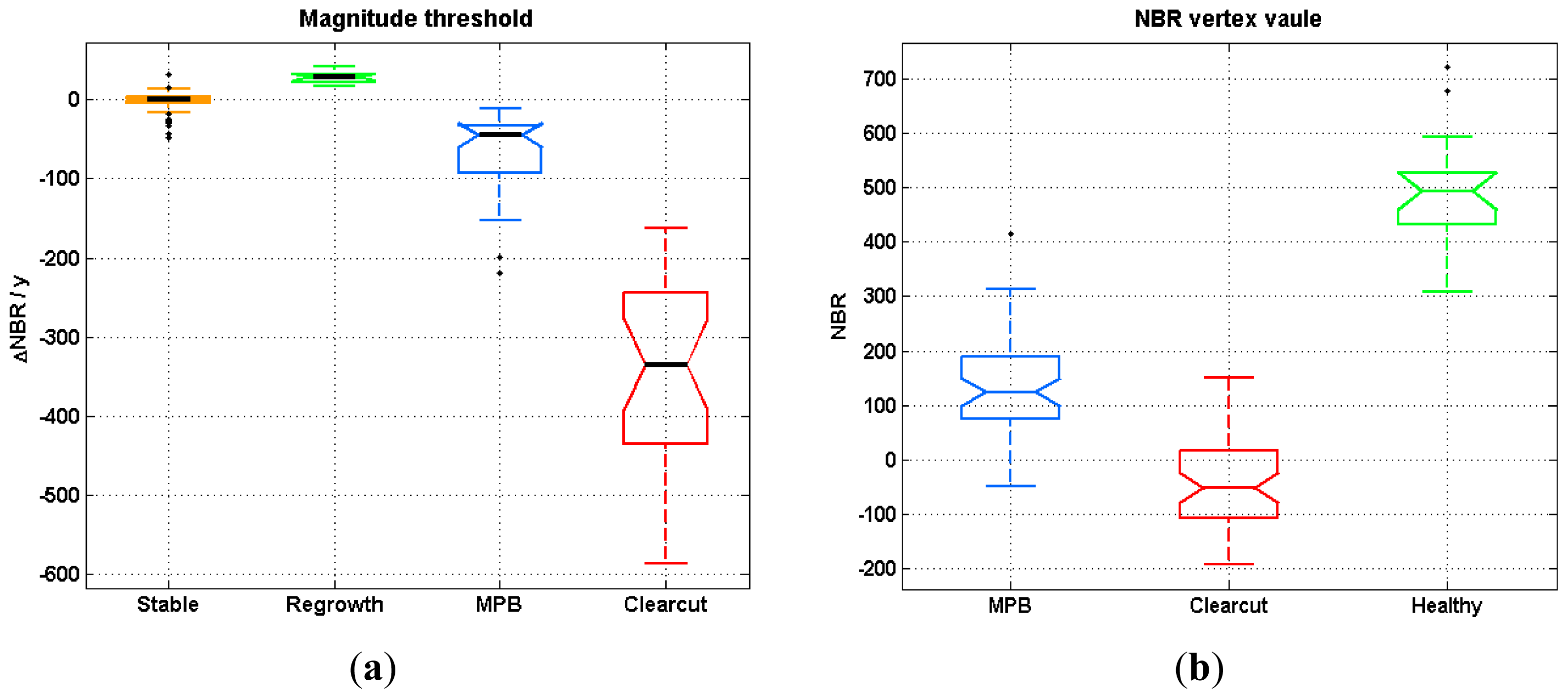
Segments were separated into regrowth, stable or disturbed status according to their magnitude (mag) at the first level of the DT. If the absolute magnitude of one segment was less than the pre-set threshold (<thre_mag1), it was treated as disturbed. If the magnitude was within a threshold range (±thre_mag1), then it was considered to be stable. Otherwise, it was considered to be in a regrowth stage (>thre_mag1).
- (2)
To label a segment as regrowth or stable, healthy vertices were identified based on an NBR threshold (thre_vertex1). Thus, a vertex in either a regrowth or stable period with its NBR value greater than the thre_vertex1 parameter was labeled as healthy.
- (3)
Segments classified as disturbed in Step 2, were labeled as clearcuts if their rate of change in NBR was greater than a second threshold (thre_mag2); otherwise, segments were labeled as MPB mortality. The rate of change was defined as the average NBR change per year, which is a reflection of both magnitude and duration. The thre_mag2 parameter was designed based on the assumption that clearcuts always have more abrupt and rapid decreases in NBR than MPB mortality.
- (4)
In the third level of the DT hierarchy, the label from the previous year (pre_label) was critical in determining the label for the current vertex. This was based on the assumption that events are temporally dependent and forests can only logically transition from certain states to another. For instance, clearcuts often result in abrupt declines in NBR followed by persistent, but slow increases in NBR. Although the magnitude of change in the post-clearcut period is not as sharp as that of the pre-clearcut period, the vertices in the subsequent years will still be assigned as clearcut to ensure that the disturbance class labels have temporal consistency.
- (5)
The final step involved attributing the vertices for the first year of the time series. We separated this step, because there was no vertex information prior to the first year. After MPB mortality, standing tree trunks and branch residuals remain on site, whereas clearcuts usually have a significant amount of bare ground. Thus, NBR values in areas with MPB mortality should generally be higher than they are in clearcut areas. The thre_vertex2 parameter defined the cutoff value for separating clearcuts and MPB mortality in these cases.
3.3. Post-Labeling Process
Both the temporal segmentation and DT were run at the pixel level. Thus, it was possible that two adjacent pixels could simultaneously experience the same event, but were labeled differently due to errors. Since most disturbance events were patchy, the behavior of spatially adjacent pixels could be used to enhance the robustness of the classification. Based on this logic, we filled small holes in a large patch that were undetected or mislabeled. To do this, we first applied a 3 × 3 majority filter to reduce the salt-and-pepper effect and merged pixels into more complete patches, and then, we used a 3-year temporal filter to remove illogical transitions over time. For example, this step would change a pixel classified as MPB mortality in Year 1, healthy in Year 2 and MPB mortality in Year 3, to MPB mortality for all 3 years.
3.4. Single-Date Classification
Single-date mapping strategies were assessed using a traditional maximum likelihood classifier (MLC) and a random forest (RF) algorithm. MLC is a parametric method widely used in forest remote sensing [
44]. In contrast, RF is a machine-learning technique that combines the results of many (thousands) of weak classifiers, such as classification and regression trees [
45]. RF is often praised for its good overall performance, as well as robustness to noise [
46]. We implemented the classifiers on both the raw spectral bands and a combination of raw spectral bands and spectral indices that were sensitive to forest defoliation and canopy water content (
Table 5 [
39,
47–
51]).
3.5. Accuracy Assessment and the Sample Size Effect
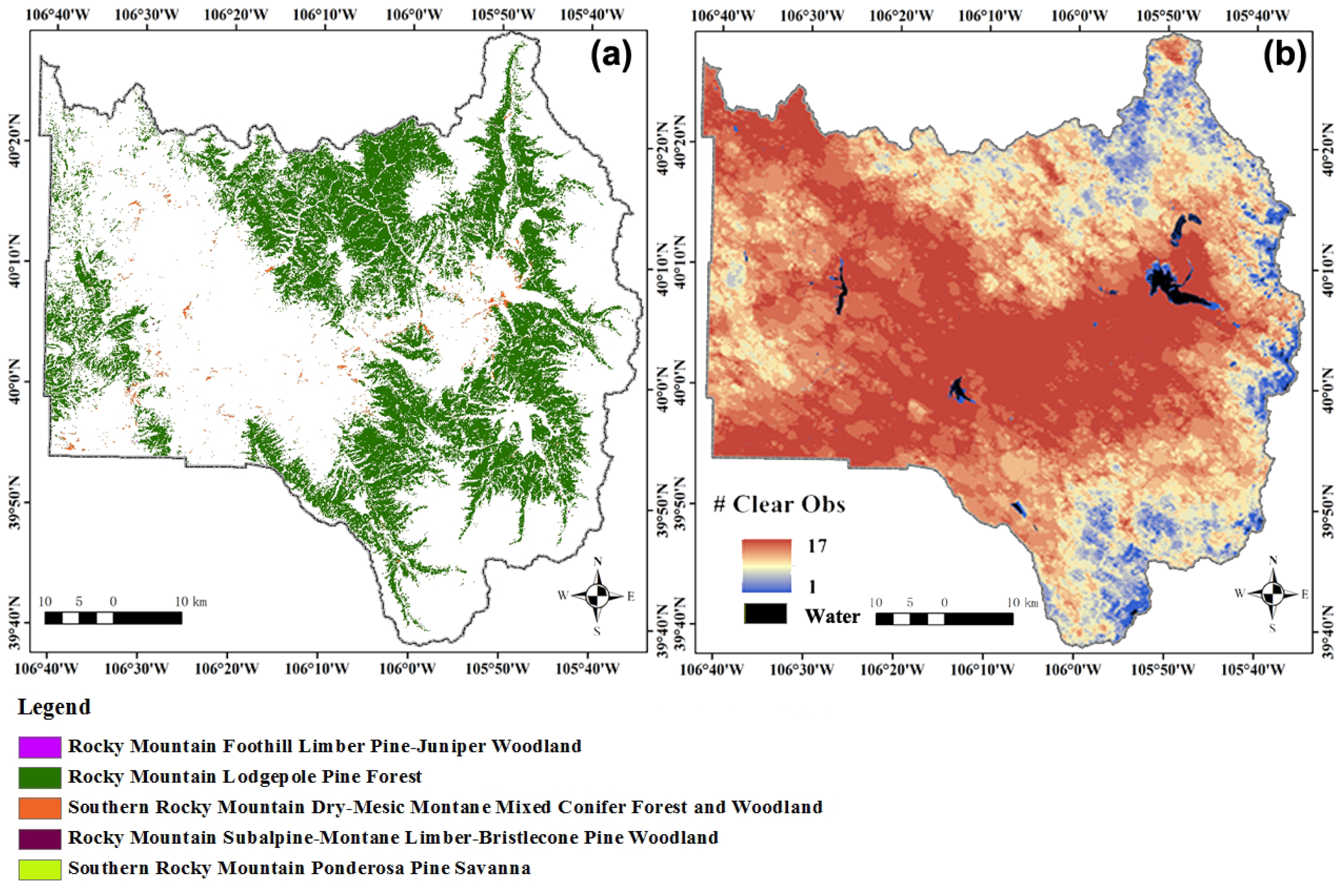
We conducted both qualitative and quantitative accuracy assessments. First, a confusion matrix was created for each individual year, and associated accuracy measures were generated, including the overall accuracy, kappa, producer’s accuracy and user’s accuracy. Second, we also visually evaluated the results by comparing the mapped spatio-temporal pattern of mortality with those observed by the Forest Health Monitoring Aerial Detection Survey (ADS) data [
52]. The ADS data are generated by aerial sketchmapping, a technique for observing and mapping forest damage from an aircraft. Although ADS had been criticized for its imprecision at fine scales due to reasons, such as misregistration and the subjectiveness of the operators [
23], it is reliable when used at coarse scales [
52]. A pilot study initiated in the Rocky Mountain Region demonstrated that all three types of accuracies for the MPB detection in lodgepole pines exceeded 80% when the spatial tolerance was increased to 500 m [
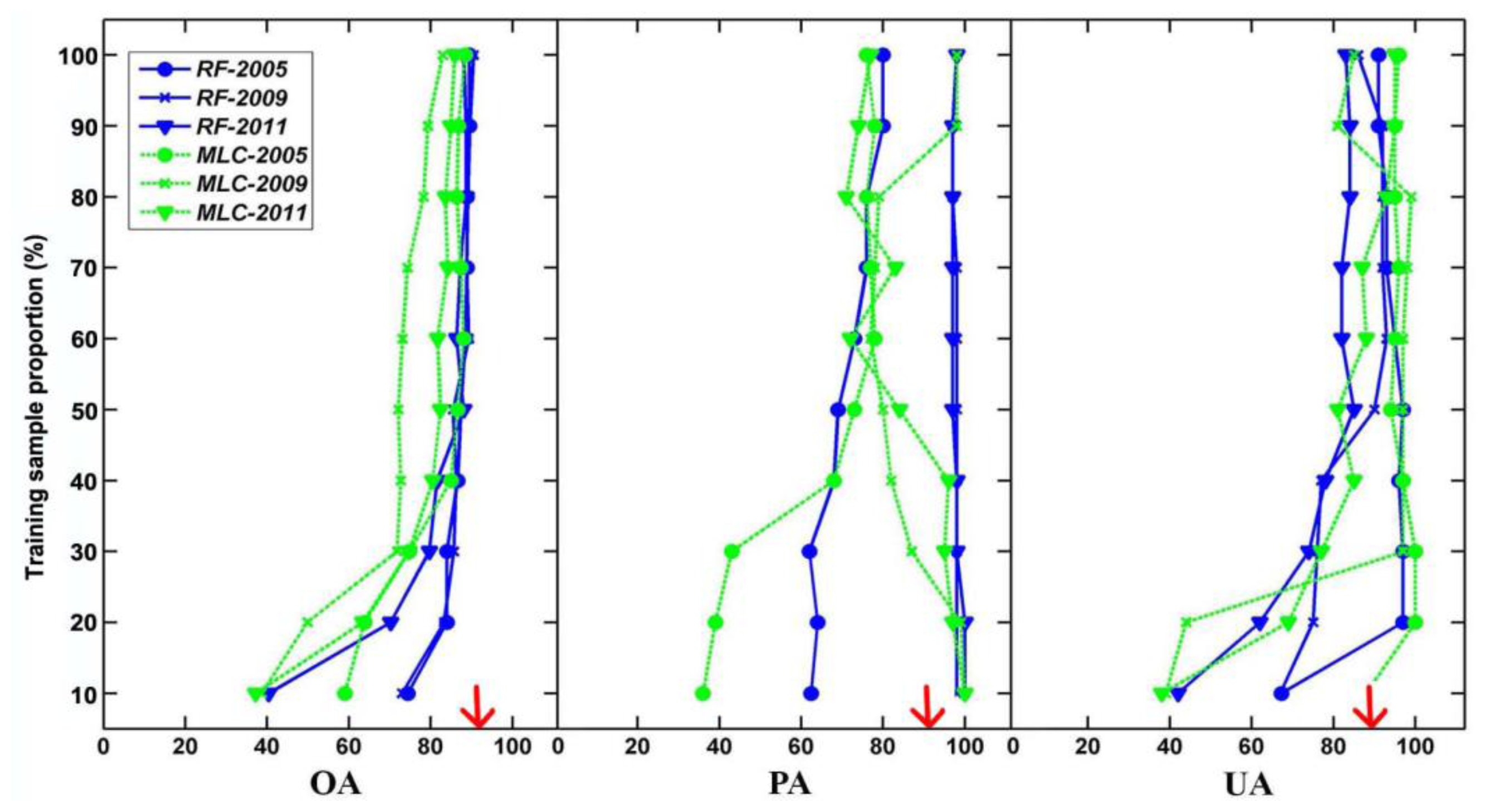
52]. We thus had confidence that the epicenters and patterns of spread derived from ADS polygons could be used as a reference dataset to compare against our results. We also altered the size of the training sample dataset from 106 to 1060 in increments of 10% and tested the effects of sample size on accuracy. This produced 10 corresponding sets of results to test the effect of sample size on accuracy metrics for both the MLC and RF classifications.
5. Discussions
For the single-date classification, we found the following: (1) The RF achieved better overall accuracy than MLC in detecting forest disturbances. MLC relies on assumptions about the data distribution (e.g., normally distributed), whereas the ensemble learning techniques used by RF do not [
53]. Meanwhile, by grouping many individual classifiers, RF combined the strengths and minimized the weaknesses of each [
54]. (2) MLC is less affected by the selection of input layers than RF. RF relies on all outputs produced by each individual tree that is built upon the random selection of input layers, and thus, a larger amount of features could create a higher probability of “irrelevant” features being selected; but, when this occurs, it is usually negated by using the ensemble of results from individual trees. (3) The accuracies of single-date image classifications showed prominent year-to-year variability. The omission error for MPB mortality declined consistently from 2005 to 2011, whereas the omission error for healthy forest increased significantly. During this period, Grand County was in a steady transition from a landscape dominated by healthy forests to a landscape dominated by “grey-stage” forests. Not coincidently, the declining trend in the proportion of healthy forest matches the declining tendency of its omission errors over the years.
From the experiment on the sample size effect, on the one hand, we could determine the optimal sample size in the single-date MPB mortality mapping, which, to our knowledge, has not been discussed before. Both MLC and RF were sensitive to sample size, and several studies are in accordance with our conclusion [
55–
57]. Parametric algorithms are well known for their requirement of representative samples, and this requirement is usually satisfied by having a sufficiently large sample size [
58]. Studies on sample-size effects for non-parametric classifiers are relatively rare. Rodriguez-Galiano
et al. [
59] observed a significant reduction in overall accuracy and the kappa values when the sample size reduced more than 50% of a non-parametric RF applied to Landsat images.
In our case, if we take both accuracy and labor/economic/time costs into consideration, the most optimum sample size for single-date classification is four to five times the original training sample size, which included 106 samples. On the other hand, we could compare the efficiency of single- and multi-date classifications. By using the same 106 training samples, our time series approach substantially outperformed the single-date classification, and their accuracies were similar only after expanding the training sample size to a large number (e.g., 10 times), which matches the finding from another study concluding that either single- or multi-date methods in Landsat-based forest disturbance mapping could result in high classification accuracy [
60], but our results confirm their findings only for large training sample sizes.
Although the forest growth trend analysis method is promising in many ways, several shortcomings exist: (1) Regardless of the high overall accuracy, the commission error for clearcuts and the omission error for beetle mortality were relatively high. The commission errors in clearcuts could be caused by the spectral similarity between post-clearcut pixels dominated by successional vegetation and healthy forest pixels. Errors of commission for MPB mortality usually happened in areas hosting a mixture of grey stage trees and bare land, which could lead to a misclassification to clearcuts. (2) Parameter calibration was the most time-consuming part in the whole procedure and requires the expertise of image analysts. In some sense, the identification of various disturbance types using temporal trajectories is more challenging than the visual interpretation of false-color or true color image composites. Several potential solutions include the use of a tool called TimeSync, which was developed to aid with the temporal segmentation calibration and to verify the output from Landtrendr [
60]. In addition, the Forest Inventory and Analysis (FIA) Program of the U.S. Forest Service consistently collects information on status and trends in forest species, health status, in total tree growth, mortality and removals by harvest. If FIA plots, or similar types of data, and their exact locations are available to users, they could aid the identification of the plots’ disturbance history. In terms of the labeling, although the manmade decision tree, as shown in
Figure 3, can be easily interpreted, a machine learning-based decision tree could be employed to make this step fully automatic.
6. Conclusions
Reconstructed forest disturbance histories are needed for a range of applications, and our paper tested an effective and efficient approach to generating disturbance histories using the Landsat time series stack. Our algorithm was designed to take advantage of differences in the magnitude and direction of changes in spectral indices, which are proxies for the physiological processes following different types of forest disturbances. The site-specific accuracy assessment in the three validation years indicated that the overall accuracy ranged from 86.74% to 94.00%, and the mean value of all types of accuracies was above 85%. Especially, our method outperformed standard classification approaches (maximum likelihood classification and random forest) by 15.8% to 52.3% when small training sample sizes (106 samples per study area) were used, which is a cost-saving advantage. Another strength of our strategy is that most parameters, especially at the attributing stage, are easily interpreted and modified, which will especially benefit users tackling similar problems of labeling change detection results.
In conclusion, our results demonstrate the potential for a forest growth trend analysis to characterize forest disturbance events with an optimal sampling scheme, both in economic and time terms, at a satisfying mapping accuracy level. Some short-term goals for our further studies will include improving the labeling step by replacing it with an automated machine learning technique, linking the magnitude of change with more ecologically meaningful properties, such as vegetation cover, extending the algorithm to the ecoregion scale, building spatio-temporal dynamic outbreak models on the time series maps with projections into the future. In addition to those applications, the spatially explicit information produced by our approach could also serve as raw material to facilitate other research to uncover new patterns of disturbances occurring on the landscape and to investigate the drivers generating the patterns of disturbances.