Next Article in Journal
Human Land-Use Practices Lead to Global Long-Term Increases in Photosynthetic Capacity
Previous Article in Journal
Calibration and Verification of Remote Sensing Instruments and Observations
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 6
Issue 6
10.3390/rs6065696
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Mapping Mountain Pine Beetle Mortality through Growth Trend Analysis of Time-Series Landsat Data

by
Lu Liang
1,
Yanlei Chen
1,
Todd J. Hawbaker
2,
Zhiliang Zhu
3 and
Peng Gong
1,4,5,*
1
Department of Environmental Science, Policy and Management, University of California, Berkeley, CA 94720, USA
2
Geological Survey, P.O. Box 25046, DFC, MS 980, Denver, CO 80225, USA
3
Geological Survey, 12201 Sunrise Valley Drive, Reston, VA 20192, USA
4
Ministry of Education Key Laboratory for Earth System Modeling, Center for Earth System Science, Tsinghua University, Beijing 100084, China
5
Joint Center for Global Change Studies, Beijing 100875, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2014, 6(6), 5696-5716; https://doi.org/10.3390/rs6065696
Submission received: 14 March 2014 / Revised: 9 June 2014 / Accepted: 9 June 2014 / Published: 18 June 2014
Browse Figures
Versions Notes

Abstract

:
Disturbances are key processes in the carbon cycle of forests and other ecosystems. In recent decades, mountain pine beetle (MPB; Dendroctonus ponderosae) outbreaks have become more frequent and extensive in western North America. Remote sensing has the ability to fill the data gaps of long-term infestation monitoring, but the elimination of observational noise and attributing changes quantitatively are two main challenges in its effective application. Here, we present a forest growth trend analysis method that integrates Landsat temporal trajectories and decision tree techniques to derive annual forest disturbance maps over an 11-year period. The temporal trajectory component successfully captures the disturbance events as represented by spectral segments, whereas decision tree modeling efficiently recognizes and attributes events based upon the characteristics of the segments. Validated against a point set sampled across a gradient of MPB mortality, 86.74% to 94.00% overall accuracy was achieved with small variability in accuracy among years. In contrast, the overall accuracies of single-date classifications ranged from 37.20% to 75.20% and only become comparable with our approach when the training sample size was increased at least four-fold. This demonstrates that the advantages of this time series work flow exist in its small training sample size requirement. The easily understandable, interpretable and modifiable characteristics of our approach suggest that it could be applicable to other ecoregions.

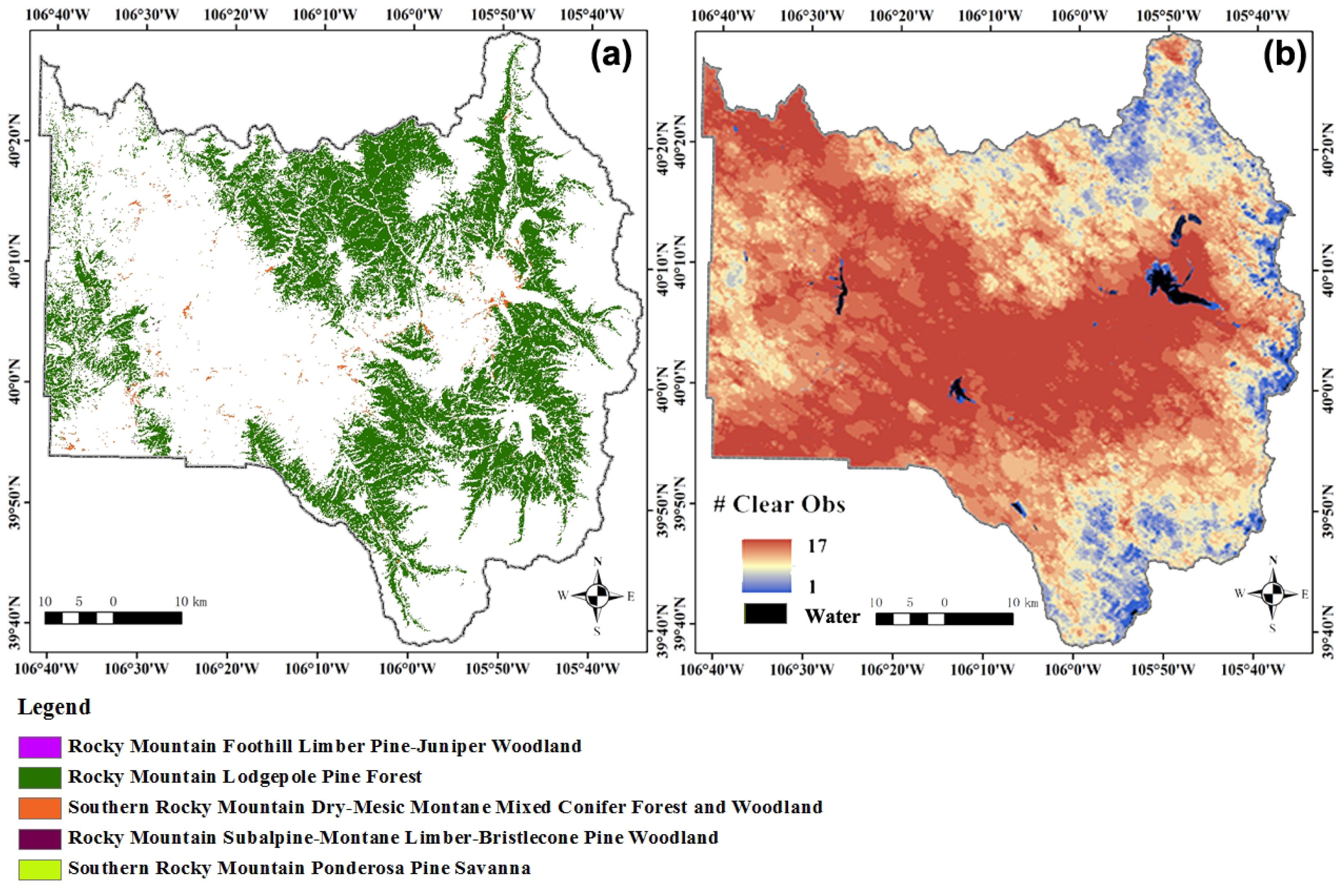
1. Introduction

Understanding patterns of forest disturbances is important for assessing past and future ecosystem structure, function, productivity and diversity [1,2]. In recent years, mountain pine beetle (MPB) outbreaks have occurred over extensive areas, from British Columba in Canada to New Mexico in the United States. MPB is endemic to North America; however, the recent outbreaks have reached epidemic levels that have affected millions of hectares of forests [3]. The effects of MPB infestation range from altered surface fuel and wildfire hazards [4–7], changed vegetative composition [8], converted live carbon sinks to dead and slowly decaying carbon sources [9–11], impacted nutrient cycling and water quality [12,13], shifted evapotranspiration and albedo, modified local surface energy balance [14] and changed regional climate [15]. Those effects are predicted to increase as a consequence of the direct and indirect effects of climatic changes [16–18]. However, unlike wildfires that have received intensive mapping efforts at different scales, characterizations of the extent and severity of MPB using multi-temporal data have only begun to emerge [19–23].
Remote sensing, both with aerial photography and satellite imagery, has been widely acknowledged as a useful way to map tree mortality over large areas [24]. Landsat time series stacks (LTSS) are well suited to this type of analysis, because they are freely available, cover a long time period, have a broad spatial extent, are multispectral and have temporal continuity [20,25]. Two frequently used disturbance mapping approaches are (1) trajectory-reconstruction and (2) decision trees (DTs). Trajectory-based change detection examples include the Landsat-based detection of trends in disturbance and recovery algorithm (LandTrendr) [26] and the Vegetation Change Tracker [27–29]. Both methods recognize disturbance events by the rate of changes in time series of spectral properties. This makes the first and last years of the trajectory more difficult to judge, because the attribution for a particular year is entirely determined with regard to its spectral deviation from the two adjacent years [26]. In addition, the event labeling procedure depends on pre-implemented modules in the software and, thus, is not flexible in adjusting to user-defined functions. DT approaches include work by Goodwin et al. [30] who utilized the annual changes in normalized difference moisture index and a set of thresholds to classify the presence of MPB infestation over 14 years, resulting in overall accuracies ranging from 71% to 86%. DT-based approaches have the capacity to integrate expert knowledge and flexible classification schemes. However, poor image quality from sensor drift, geometric misregistration and topographic and cloud shadows will introduce distortions to images and affect the accuracy of change detection.
In this study, we describe a forest growth trend analysis method that integrates the robust change detection strengths of the trajectory reconstruction approach and the flexible user-defined advantages of DT approaches to characterize MPB mortality with an 11-year LTSS. We were interested in determining whether or not this proposed method could reach an accuracy target of 85% or greater. Additionally, we compared its accuracy with single-date image classifications, which are still important and commonly used in disturbance mapping, especially in two-date post-classification change detection. We are aware that the accuracy of single-date image classification is not only determined by the input variables and classifiers, but is also heavily dependent on the quality and quantity of training samples [31], which may have larger impacts than the implemented techniques [32]. Thus, we also assessed the effect of different sample sizes on the accuracy of single-date image classifications, and we tested how much our proposed method can improve sampling efficiency as compared with the single-date classifiers.

2. Study Area and Data

2.1. Study Area

Our study area was located in Grand County, in north-central Colorado (Figure 1), with a total land area of 4783 km2. This landscape is dominated by evergreen forests mainly composed of lodgepole pine (Pinus contorta), along with other tree species, as well as shrub and grass cover types. Summer in Grand County is typically hot and dry, which is suitable for MPB development. The average precipitation per year is approximately 400 mm, whereas the U.S. average is 930 mm. This county has one of the highest concentrations of lodgepole pines and has been heavily affected by the MPB outbreak that started around 2002 and reached the peak of tree mortality between 2005 and 2008 [33].

2.2. Landsat Time Series Stack

Grand County lies entirely within Landsat path 34 row 32. We restricted the image acquisition season from June to September, because this snow-free period is the recommended time window to detect MPB mortality [20]. For each year, one cloud-free or mildly contaminated image was selected to build the LTSS, and if no such image existed, several partly cloudy images with a similar phenology were used as replacements (Table 1). All data were processed to Level 1T (terrain corrected). Radiometric calibration and atmospheric correction for cloud and aerosol effects were performed using the Landsat Ecosystem Disturbance Adaptive Processing System [34]. Clouds and their shadows were automatically screened using the Function of mask (FMASK) algorithm [35]. Cloud removal effects were judged satisfactory via visual checking, though the extent of cloud cover was slightly overestimated. We accepted this false positive error, because commission errors were more desirable than omission errors in cloud filling. The number of clear observations in the LTSS over the period of 2000 to 2011 is shown in Figure 2, and 98% of the study region contained more than 10 cloud-free observations.
Since MPBs attack a limited number of tree species, we confined our analysis to the extent of their host species in the LANDFIRE Refresh 2001 Existing Vegetation Type data layer (EVT), which was developed using circa 2001 (1999–2003) Landsat imagery [36]. The spatial resolution of the LANDFIRE data matches the LTSS, and the time period of the imagery from which the EVT data were derived depicts the pre-disturbance distribution of vegetation in Grand County. Currently, MPB mortality is concentrated in lodgepole and ponderosa pine (Pinus ponderosa) forests, but other pine species, like limber pine (Pinus flexilis) and bristlecone pine (Pinus aristata), have also been found to be suitable hosts [37]. We included all EVT pixels that contain any of those species (Table S1), and smoothed the image with a 3 × 3 majority filter, which was designed to reduce observed salt-and-pepper effects and to minimize omission errors that are much higher than commission errors for the selected classes [38].

2.3. Reference Sample Selection

We randomly placed training samples over forested areas and reconstructed their disturbance history with the aid of normalized burn ratio (NBR) time series from the LTSS and the 1-m resolution U.S. Department of Agriculture (USDA) National Agricultural Imagery Program (NAIP) imagery (obtained from the USDA Geospatial Data Gateway), which were available for years 2005, 2009 and 2011 in Grand County. The NBR time series were calculated using bands 4 and 7 from the Landsat imagery [39] and then multiplied by 100, so they could be represented as integer values instead of floating point values. For each training location, we identified the disturbance event type, duration and onset time (Table 2). Disturbance event types included: healthy, MPB mortality or clearcuts. Fire was not included, because large fires did not occur in our study area during the time period of this study (2000 to 2011), as indicated by the U.S. Geological Survey Monitoring Trends in Burn Severity database [40]. In total, we collected 106 training samples, among which, 53 were sites with MPB mortality, 37 were clearcuts and 16 were healthy. We selected the relatively small number of training samples, because many studies suggested that trajectory-based methods perform well when trained with a relatively small sample size [23,26,41]. Statistical classifiers require more training data to fully represent each class in the feature space [42]. Thus, we expanded the original training sample size by 10 times to a total of 1060 training samples. For those newly added samples, we only identified their disturbance types in the three years for which NAIP imagery were available instead of the whole NBR trajectory from the LTSS.
For validation purposes, we randomly sampled points in strata that were formed in the complete temporal-spectral space as a representation of the gradient of MPB mortality. In this manner, our test samples were able to cover a complete spectrum of disturbance events and a range of mortality. Considering the large data volume of the 11-year LTSS, for which the dimension was 2964 (rows) × 2901 (columns) × 102 (bands), we employed an efficient unsupervised classification tool, Clustering Based on Eigenspace Transformation, to improve the speed of clustering over conventional K-means without losing accuracy [43]. Fifty strata were developed, and we proportionately allocated a total of 100 points to each stratum. In the absence of sufficient ground and ancillary information, we visually interpreted the status for each point at each individual year. By checking the proportion of points in the three classes, we found that they are almost equally distributed without severe over- or under-representation; the mean number of validation samples in each disturbance type each year was 39 (healthy), 38 (MPB mortality) and 23 (clearcuts; Table S2).

3. Method

3.1. Temporal Segmentation

We developed time series of disturbance maps by combining the temporal trajectory analysis approach of LandTrendr [26] with a decision tree labeling procedure. Temporal trajectory analysis was used to decompose often noisy time series into a sequence of straight-line segments with distinct features designed to capture the event that happened for the duration of each segment. NBR [39] was chosen to represent the vegetation condition, because of its sensitivity to disturbance [26] and its capacity to minimize radiometric differences among images. The general procedure was to use a set of parameters to enhance the signal-to-noise ratio of the NBR time series in order to capture the salient events happening in each period or segment. Details can be found in Kennedy et al. [26], and the final effect of temporal segmentation, whether it was under-segmentation (split up into too few parts) or over-segmentation (subdivided into too many parts), was determined by the parameters listed in Table 3. Optimal LandTrendr parameter settings have been tested in the forests of the Northwest Pacific Region at both Landsat and MODIS scales [26,41]. However, because we are not aware of reported parameter results in the literature specific to the Southern Rocky Mountain ecoregion, we tested a range of candidate parameter values (Table 3).
We ran LandTrendr on all combinations of the candidate parameter values, which resulted in 144 unique combinations in total, and then visually compared their temporal segmentation results with the original NBR time series for the 106 training samples. Thus, the calibration involved 15,264 comparisons. Each individual comparison for a sample was coded in a binary state using two criteria: the overall match in the shape and the timing of vertices. A good match occurred if the disturbance event that happened at that pixel was successfully captured, and the slope and magnitude for each segment deviated little from the central trend. The vertex timing was judged by how well the algorithm captured the onset and ending time of each disturbance event. If both criteria were satisfied, that comparison would be scored as 1, and otherwise, it would be 0. The optimal parameter set was decided based upon the pooled rankings across all training samples. The processing time took about 200 minutes (on 5,376,538 unmasked pixels) for this step, which was run on a workstation with an Intel i7-2600 3.4 GHz quad core CPU and 8 gigabytes of physical memory.

3.2. Decision Tree-Based Spectral Segment Labeling

The outputs of the temporal segmentation included the fitted segments, and a set of vertices connecting individual segments. We employed a DT to attribute disturbance events associated with those vertices and segments, with leaf nodes representing class labels and branches representing decision scenarios. The DT was built with predictors characterizing each segment: the disturbance occurrence onset time, duration and the magnitude of NBR change. We defined the onset time as the starting year of a segment. Magnitude was the absolute change in NBR between the ending year and the onset year, whereas duration was the time elapsed over the length of one segment. Different types of disturbance events were characterized by distinct features. For instance, clearcuts could be recognized by segments with a short duration and large, negative change in NBR, whereas MPB mortality segments tended to have a gradual, but long-duration decline in NBR values.
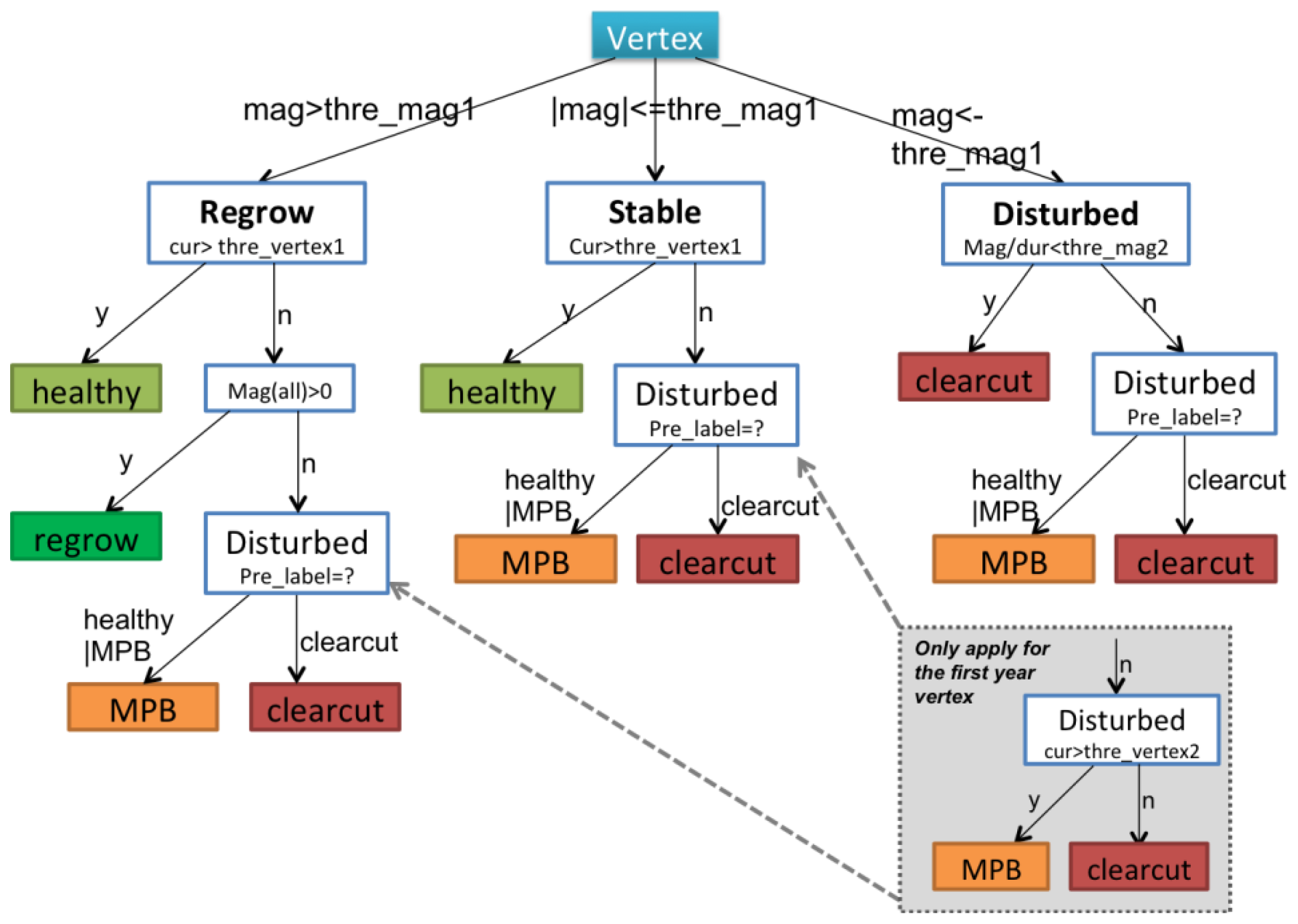
Decision rules were used to identify forest conditions in a top-down sequence (Figure 3), and the definition of key parameters are explained in Table 4. These parameters were manually calibrated with the same training samples described in Section 3.1. Specifically:
(1)
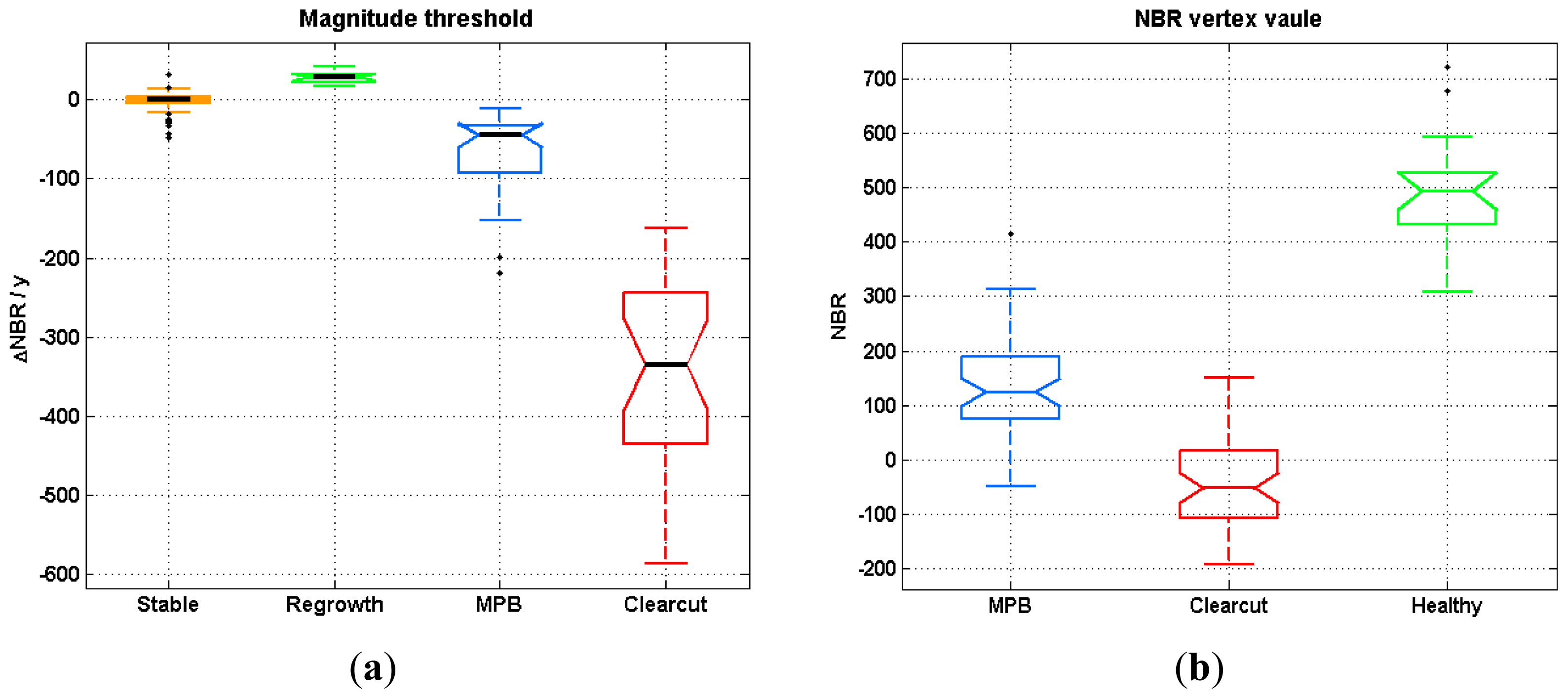
Segments were separated into regrowth, stable or disturbed status according to their magnitude (mag) at the first level of the DT. If the absolute magnitude of one segment was less than the pre-set threshold (<thre_mag1), it was treated as disturbed. If the magnitude was within a threshold range (±thre_mag1), then it was considered to be stable. Otherwise, it was considered to be in a regrowth stage (>thre_mag1).
(2)
To label a segment as regrowth or stable, healthy vertices were identified based on an NBR threshold (thre_vertex1). Thus, a vertex in either a regrowth or stable period with its NBR value greater than the thre_vertex1 parameter was labeled as healthy.
(3)
Segments classified as disturbed in Step 2, were labeled as clearcuts if their rate of change in NBR was greater than a second threshold (thre_mag2); otherwise, segments were labeled as MPB mortality. The rate of change was defined as the average NBR change per year, which is a reflection of both magnitude and duration. The thre_mag2 parameter was designed based on the assumption that clearcuts always have more abrupt and rapid decreases in NBR than MPB mortality.
(4)
In the third level of the DT hierarchy, the label from the previous year (pre_label) was critical in determining the label for the current vertex. This was based on the assumption that events are temporally dependent and forests can only logically transition from certain states to another. For instance, clearcuts often result in abrupt declines in NBR followed by persistent, but slow increases in NBR. Although the magnitude of change in the post-clearcut period is not as sharp as that of the pre-clearcut period, the vertices in the subsequent years will still be assigned as clearcut to ensure that the disturbance class labels have temporal consistency.
(5)
The final step involved attributing the vertices for the first year of the time series. We separated this step, because there was no vertex information prior to the first year. After MPB mortality, standing tree trunks and branch residuals remain on site, whereas clearcuts usually have a significant amount of bare ground. Thus, NBR values in areas with MPB mortality should generally be higher than they are in clearcut areas. The thre_vertex2 parameter defined the cutoff value for separating clearcuts and MPB mortality in these cases.

3.3. Post-Labeling Process

Both the temporal segmentation and DT were run at the pixel level. Thus, it was possible that two adjacent pixels could simultaneously experience the same event, but were labeled differently due to errors. Since most disturbance events were patchy, the behavior of spatially adjacent pixels could be used to enhance the robustness of the classification. Based on this logic, we filled small holes in a large patch that were undetected or mislabeled. To do this, we first applied a 3 × 3 majority filter to reduce the salt-and-pepper effect and merged pixels into more complete patches, and then, we used a 3-year temporal filter to remove illogical transitions over time. For example, this step would change a pixel classified as MPB mortality in Year 1, healthy in Year 2 and MPB mortality in Year 3, to MPB mortality for all 3 years.

3.4. Single-Date Classification

Single-date mapping strategies were assessed using a traditional maximum likelihood classifier (MLC) and a random forest (RF) algorithm. MLC is a parametric method widely used in forest remote sensing [44]. In contrast, RF is a machine-learning technique that combines the results of many (thousands) of weak classifiers, such as classification and regression trees [45]. RF is often praised for its good overall performance, as well as robustness to noise [46]. We implemented the classifiers on both the raw spectral bands and a combination of raw spectral bands and spectral indices that were sensitive to forest defoliation and canopy water content (Table 5 [39,47–51]).

3.5. Accuracy Assessment and the Sample Size Effect

We conducted both qualitative and quantitative accuracy assessments. First, a confusion matrix was created for each individual year, and associated accuracy measures were generated, including the overall accuracy, kappa, producer’s accuracy and user’s accuracy. Second, we also visually evaluated the results by comparing the mapped spatio-temporal pattern of mortality with those observed by the Forest Health Monitoring Aerial Detection Survey (ADS) data [52]. The ADS data are generated by aerial sketchmapping, a technique for observing and mapping forest damage from an aircraft. Although ADS had been criticized for its imprecision at fine scales due to reasons, such as misregistration and the subjectiveness of the operators [23], it is reliable when used at coarse scales [52]. 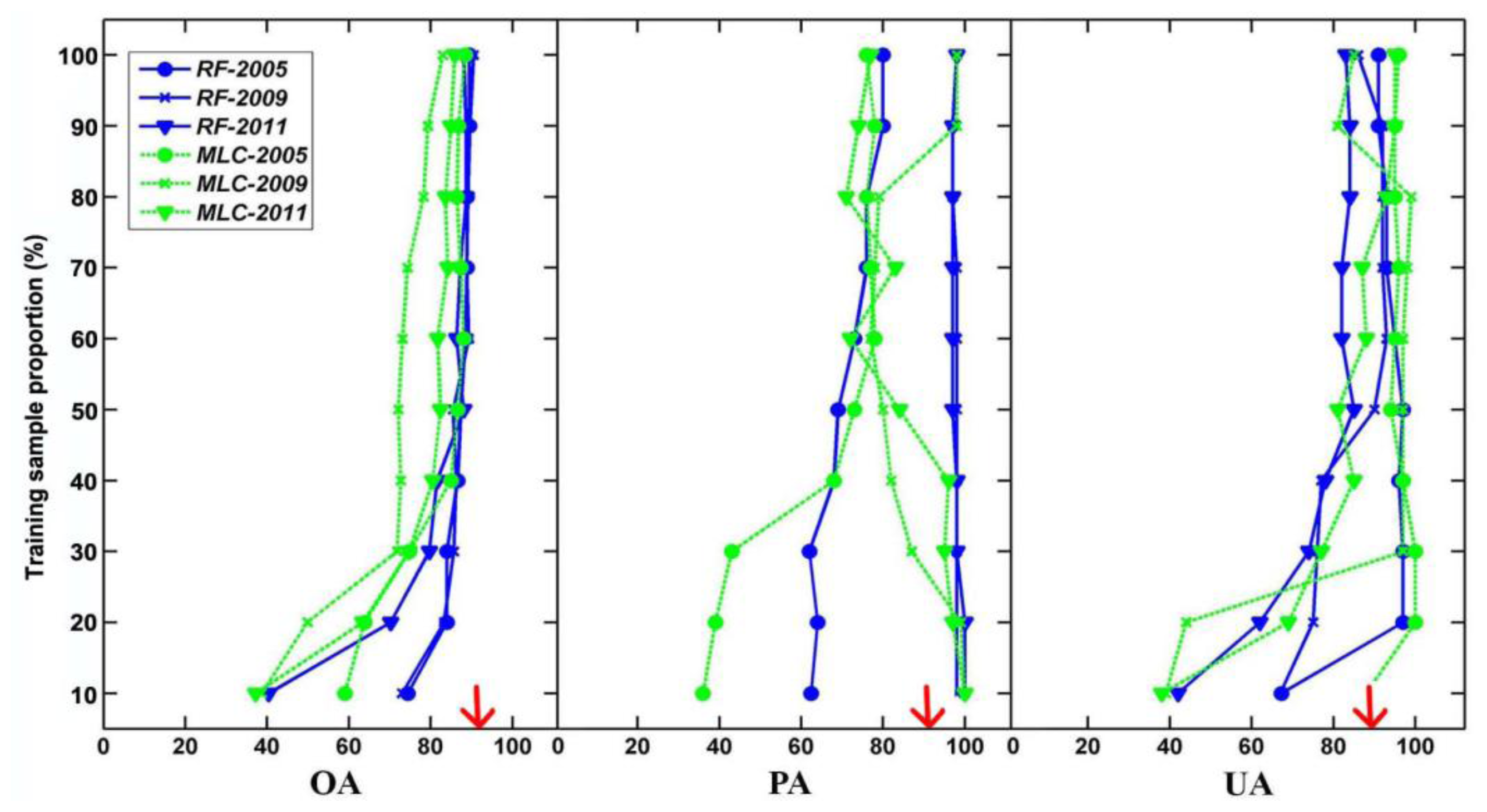A pilot study initiated in the Rocky Mountain Region demonstrated that all three types of accuracies for the MPB detection in lodgepole pines exceeded 80% when the spatial tolerance was increased to 500 m [52]. We thus had confidence that the epicenters and patterns of spread derived from ADS polygons could be used as a reference dataset to compare against our results. We also altered the size of the training sample dataset from 106 to 1060 in increments of 10% and tested the effects of sample size on accuracy. This produced 10 corresponding sets of results to test the effect of sample size on accuracy metrics for both the MLC and RF classifications.

4. Results

4.1. Parameter Calibration for Temporal Segmentation and Decision Tree Labeling

Parameter calibration in the forest growth trend analysis involved two parts. At the temporal segmentation stage, the set of parameters producing the highest score from all 144 combinations was chosen (Table 3). By using the same set of training samples, we also determined the four threshold values in the DT. We set the allowed variability in NBR for stable segments (thre_mag1) to be 20 (the unit for all thresholds was NBR × 100) as reflected from Figure 4. The cut-off NBR value of vertices (thre_vertex1) to distinguish healthy forest from disturbances was 350. Threshold Thre_mag2, used to separate clearcuts from MPB mortality, was set at −150. A higher degree of overlap was observed between the post-clearcut and MPB mortality NBR values, and thus, we set thre_vertex2 to the third quantile of NBR values in clearcuts, which was 50.

4.2. The Performance of Forest Growth Trend Analysis

The forest growth trend analysis achieved an overall annual accuracy ranging from 86.74% to 94.00%, and the average was 90.31% (Table 6). Except for the user’s accuracy for MPB mortality (84.81%) and the producer’s accuracy for clearcuts (77.30%), the mean value for all types of accuracies was above 85%. Larger standard deviations of accuracies among different years were found in the producer’s accuracy for healthy forest and the producer’s accuracy for clearcuts. As indicated from the confusion matrix (Table S2) and Figure 5, healthy pixels were well distinguished from the two disturbance types in the first few years and became less separable from MPB mortality after 2005. Pixels with MPB mortality were confused with either healthy or clearcut classes, but the proportion was not high. Confusion between clearcuts and healthy classes occurred in the first few years of our study and then between clearcuts and MPB mortality in later years. Visual examination showed that the shifting of MPB outbreak epicenters and the expansion of the outbreak boundaries was congruent between the two independent datasets (ADS and validation points). Maps of the onset year of MPB mortality revealed that the MPB outbreak in Grand County was initiated at multiple locations and spread outward from those locations over time to affect nearly all habitats with suitable hosts (Figure 6).

4.3. Comparison with Single-Date Classification and Sample Size Effects

The accuracy achieved by the single-date classification ranged between 37.20% and 75.20% and was lower than the time series classification, running on either the raw or combined spectral bands trained by the same set of samples (Table 7). We also observed that the time-series classification accuracies were relatively stable over time. In contrast, the single-date image classifications had high year-to-year variability in accuracy, which was shown by a distinct, increasing trend of the producer’s accuracy for MPB mortality from 2005 to 2011. The producer’s accuracy for healthy forest decreased substantially over the same time period. Table 7 also listed the accuracies generated from RF and MLC with only the raw spectral bands and the combined use of raw spectral bands and spectral indices. The accuracy of the RF classification improved when the spectral indices were included as predictors, and this effect was not evident with the MLC. Between the two single-date classification methods, RF had better overall performance than MLC.
By varying the number of training samples used to train the MLC and RF classifiers in 10% increments to a maximum of 1060 training samples, we obtained 10 sets of results for the single-date classifications. Figure 7 shows the relationships between accuracy and sample size, for overall accuracy generated from the MLC and RF classifiers, as well as the producer’s accuracy and the user’s accuracy for the MPB mortality class. Despite some small fluctuations, all accuracies increased with the training sample size, and the changes were especially pronounced for the initial increases in sample size. The highest overall accuracies were achieved when 100%, 100% and 90% of the training samples were used by RF (89.43%, 90.48%, 88.66%) and 100% of the training samples were used by MLC (88.41%, 82.93%, 85.90%). This improvement was substantial compared to the results based on the original set of 106 training samples. The overall accuracy for RF increased by 30% on average from the smallest to the highest training sample size, 8% for the producer’s accuracy and 33% for the user’s accuracy. For MLC, the average increase was 40% in overall accuracy, 31% in the producer’s accuracy and 43% in the user’s accuracy between the smallest and largest training sample sizes. We also noticed that after a certain training sample size, the accuracy stopped increasing or even slightly decreased, and the saturation position was around the 40% sample size (or 424 points) for all accuracy metrics and both classifiers. Accuracies after the saturation point were comparable to the time series classification results.

5. Discussions

For the single-date classification, we found the following: (1) The RF achieved better overall accuracy than MLC in detecting forest disturbances. MLC relies on assumptions about the data distribution (e.g., normally distributed), whereas the ensemble learning techniques used by RF do not [53]. Meanwhile, by grouping many individual classifiers, RF combined the strengths and minimized the weaknesses of each [54]. (2) MLC is less affected by the selection of input layers than RF. RF relies on all outputs produced by each individual tree that is built upon the random selection of input layers, and thus, a larger amount of features could create a higher probability of “irrelevant” features being selected; but, when this occurs, it is usually negated by using the ensemble of results from individual trees. (3) The accuracies of single-date image classifications showed prominent year-to-year variability. The omission error for MPB mortality declined consistently from 2005 to 2011, whereas the omission error for healthy forest increased significantly. During this period, Grand County was in a steady transition from a landscape dominated by healthy forests to a landscape dominated by “grey-stage” forests. Not coincidently, the declining trend in the proportion of healthy forest matches the declining tendency of its omission errors over the years.
From the experiment on the sample size effect, on the one hand, we could determine the optimal sample size in the single-date MPB mortality mapping, which, to our knowledge, has not been discussed before. Both MLC and RF were sensitive to sample size, and several studies are in accordance with our conclusion [55–57]. Parametric algorithms are well known for their requirement of representative samples, and this requirement is usually satisfied by having a sufficiently large sample size [58]. Studies on sample-size effects for non-parametric classifiers are relatively rare. Rodriguez-Galiano et al. [59] observed a significant reduction in overall accuracy and the kappa values when the sample size reduced more than 50% of a non-parametric RF applied to Landsat images.
In our case, if we take both accuracy and labor/economic/time costs into consideration, the most optimum sample size for single-date classification is four to five times the original training sample size, which included 106 samples. On the other hand, we could compare the efficiency of single- and multi-date classifications. By using the same 106 training samples, our time series approach substantially outperformed the single-date classification, and their accuracies were similar only after expanding the training sample size to a large number (e.g., 10 times), which matches the finding from another study concluding that either single- or multi-date methods in Landsat-based forest disturbance mapping could result in high classification accuracy [60], but our results confirm their findings only for large training sample sizes.
Although the forest growth trend analysis method is promising in many ways, several shortcomings exist: (1) Regardless of the high overall accuracy, the commission error for clearcuts and the omission error for beetle mortality were relatively high. The commission errors in clearcuts could be caused by the spectral similarity between post-clearcut pixels dominated by successional vegetation and healthy forest pixels. Errors of commission for MPB mortality usually happened in areas hosting a mixture of grey stage trees and bare land, which could lead to a misclassification to clearcuts. (2) Parameter calibration was the most time-consuming part in the whole procedure and requires the expertise of image analysts. In some sense, the identification of various disturbance types using temporal trajectories is more challenging than the visual interpretation of false-color or true color image composites. Several potential solutions include the use of a tool called TimeSync, which was developed to aid with the temporal segmentation calibration and to verify the output from Landtrendr [60]. In addition, the Forest Inventory and Analysis (FIA) Program of the U.S. Forest Service consistently collects information on status and trends in forest species, health status, in total tree growth, mortality and removals by harvest. If FIA plots, or similar types of data, and their exact locations are available to users, they could aid the identification of the plots’ disturbance history. In terms of the labeling, although the manmade decision tree, as shown in Figure 3, can be easily interpreted, a machine learning-based decision tree could be employed to make this step fully automatic.

6. Conclusions

Reconstructed forest disturbance histories are needed for a range of applications, and our paper tested an effective and efficient approach to generating disturbance histories using the Landsat time series stack. Our algorithm was designed to take advantage of differences in the magnitude and direction of changes in spectral indices, which are proxies for the physiological processes following different types of forest disturbances. The site-specific accuracy assessment in the three validation years indicated that the overall accuracy ranged from 86.74% to 94.00%, and the mean value of all types of accuracies was above 85%. Especially, our method outperformed standard classification approaches (maximum likelihood classification and random forest) by 15.8% to 52.3% when small training sample sizes (106 samples per study area) were used, which is a cost-saving advantage. Another strength of our strategy is that most parameters, especially at the attributing stage, are easily interpreted and modified, which will especially benefit users tackling similar problems of labeling change detection results.
In conclusion, our results demonstrate the potential for a forest growth trend analysis to characterize forest disturbance events with an optimal sampling scheme, both in economic and time terms, at a satisfying mapping accuracy level. Some short-term goals for our further studies will include improving the labeling step by replacing it with an automated machine learning technique, linking the magnitude of change with more ecologically meaningful properties, such as vegetation cover, extending the algorithm to the ecoregion scale, building spatio-temporal dynamic outbreak models on the time series maps with projections into the future. In addition to those applications, the spatially explicit information produced by our approach could also serve as raw material to facilitate other research to uncover new patterns of disturbances occurring on the landscape and to investigate the drivers generating the patterns of disturbances.

Supplementary Information

remotesensing-06-05696-s001.pdf

Acknowledgments

We are grateful to the U.S. Geological Survey, Climate and Land Use Mission Area Land Remote Sensing Program, which provided funding to support this research (Grant Number G12AC20085). Three anonymous reviewers and Bruce Wylie, Diane Stephens and Janet Slate provided insightful comments on a previous draft of this manuscript, and their comments helped greatly to improve the completeness and clarity of the manuscript. Any use of trade, firm or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.

Conflicts of Interest

The authors declare no conflict of interest.
  • Author ContributionsAll authors have made significant contributions to the manuscript. Zhiliang Zhu and Peng Gong had the original idea, supervised the study, and contributed in manuscript revision. Lu Liang is the main author who wrote the manuscript. Lu Liang and Todd J. Hawbaker developed the algorithm. Lu Liang and Yanlei Chen conducted pre-processing of the images and the accuracy assessment. Todd J. Hawbaker contributed in the language editing.

References

  1. Turner, M.G. Disturbance and landscape dynamics in a changing world. Ecology 2010, 91, 2833–2849. [Google Scholar]
  2. Wang, W.; Peng, C.; Kneeshaw, D.D.; Larocque, G.R.; Luo, Z. Drought-induced tree mortality: Ecological consequences, causes, and modeling. Environ. Rev 2012, 20, 109–121. [Google Scholar]
  3. Hicke, J.A.; Meddens, A.J.; Allen, C.D.; Kolden, C.A. Carbon stocks of trees killed by bark beetles and wildfire in the western United States. Environ. Res. Lett 2013, 8, 035032. [Google Scholar]
  4. Parker, T.J.; Clancy, K.M.; Mathiasen, R.L. Interactions among fire, insects and pathogens in coniferous forests of the interior western United States and Canada. Agric. For. Entomol 2006, 8, 167–189. [Google Scholar]
  5. Jenkins, M.J.; Hebertson, E.; Page, W.; Jorgensen, C.A. Bark beetles, fuels, fires and implications for forest management in the Intermountain West. For. Ecol. Manag 2008, 254, 16–34. [Google Scholar]
  6. Hicke, J.A.; Johnson, M.C.; Hayes, J.L.; Preisler, H.K. Effects of bark beetle-caused tree mortality on wildfire. For. Ecol. Manag 2012, 271, 81–90. [Google Scholar]
  7. Schoennagel, T.; Veblen, T.T.; Negron, J.F.; Smith, J.M. Effects of mountain pine beetle on fuels and expected fire behavior in lodgepole pine forests, Colorado, USA. PLoS One 2012, 7, e30002. [Google Scholar]
  8. Collins, B.J.; Rhoades, C.C.; Hubbard, R.M.; Battaglia, M.A. Tree regeneration and future stand development after bark beetle infestation and harvesting in Colorado lodgepole pine stands. For. Ecol. Manag 2011, 261, 2168–2175. [Google Scholar]
  9. Kurz, W.A.; Dymond, C.; Stinson, G.; Rampley, G.; Neilson, E.; Carroll, A.; Ebata, T.; Safranyik, L. Mountain pine beetle and forest carbon feedback to climate change. Nature 2008, 452, 987–990. [Google Scholar]
  10. Running, S.W. Ecosystem disturbance, carbon, and climate. Science 2008, 321, 652–653. [Google Scholar]
  11. Caldwell, M.; Hawbaker, T.; Briggs, J.; Cigan, P.; Stitt, S. Simulated impacts of mountain pine beetle and wildfire disturbances on forest vegetation composition and carbon stocks in the Southern Rocky Mountains. Biogeosciences 2013, 10, 12919–12965. [Google Scholar]
  12. Edburg, S.L.; Hicke, J.A.; Brooks, P.D.; Pendall, E.G.; Ewers, B.E.; Norton, U.; Gochis, D.; Gutmann, E.D.; Meddens, A.J. Cascading impacts of bark beetle-caused tree mortality on coupled biogeophysical and biogeochemical processes. Front. Ecol. Environ 2012, 10, 416–424. [Google Scholar]
  13. Mikkelson, K.M.; Bearup, L.A.; Maxwell, R.M.; Stednick, J.D.; McCray, J.E.; Sharp, J.O. Bark beetle infestation impacts on nutrient cycling, water quality and interdependent hydrological effects. Biogeochemistry 2013, 115, 1–21. [Google Scholar]
  14. Boon, S. Snow ablation energy balance in a dead forest stand. Hydrol. Process 2009, 23, 2600–2610. [Google Scholar]
  15. Maness, H.; Kushner, P.; Fung, I. Summertime climate response to mountain pine beetle disturbance in British Columbia. Nat. Geosci 2013, 6, 65–70. [Google Scholar]
  16. Raffa, K.F.; Aukema, B.H.; Bentz, B.J.; Carroll, A.L.; Hicke, J.A.; Turner, M.G.; Romme, W.H. Cross-scale drivers of natural disturbances prone to anthropogenic amplification: The dynamics of bark beetle eruptions. Bioscience 2008, 58, 501–517. [Google Scholar]
  17. Bentz, B.J.; Régnière, J.; Fettig, C.J.; Hansen, E.M.; Hayes, J.L.; Hicke, J.A.; Kelsey, R.G.; Negrón, J.F.; Seybold, S.J. Climate change and bark beetles of the western United States and Canada: Direct and indirect effects. BioScience 2010, 60, 602–613. [Google Scholar]
  18. Williams, A.P.; Allen, C.D.; Millar, C.I.; Swetnam, T.W.; Michaelsen, J.; Still, C.J.; Leavitt, S.W. Forest responses to increasing aridity and warmth in the southwestern United States. Proc. Natl. Acad. Sci 2010, 107, 21289–21294. [Google Scholar]
  19. Coops, N.C.; Wulder, M.A.; White, J.C. Integrating remotely sensed and ancillary data sources to characterize a mountain pine beetle infestation. Remote Sens. Environ 2006, 105, 83–97. [Google Scholar]
  20. Wulder, M.A.; Dymond, C.C.; White, J.C.; Leckie, D.G.; Carroll, A.L. Surveying mountain pine beetle damage of forests: A review of remote sensing opportunities. For. Ecol. Manag 2006, 221, 27–41. [Google Scholar]
  21. Goodwin, N.R.; Magnussen, S.; Coops, N.C.; Wulder, M.A. Curve fitting of time-series Landsat imagery for characterizing a mountain pine beetle infestation. Int. J. Remote Sens 2010, 31, 3263–3271. [Google Scholar]
  22. Meddens, A.J.; Hicke, J.A.; Vierling, L.A. Evaluating the potential of multispectral imagery to map multiple stages of tree mortality. Remote Sens. Environ 2011, 115, 1632–1642. [Google Scholar]
  23. Meigs, G.W.; Kennedy, R.E.; Cohen, W.B. A Landsat time series approach to characterize bark beetle and defoliator impacts on tree mortality and surface fuels in conifer forests. Remote Sens. Environ 2011, 115, 3707–3718. [Google Scholar]
  24. Hansen, M.C.; Loveland, T.R. A review of large area monitoring of land cover change using Landsat data. Remote Sens. Environ 2012, 122, 66–74. [Google Scholar]
  25. Franklin, S.; Wulder, M.; Skakun, R.; Carroll, A. Mountain pine beetle red-attack forest damage classification using stratified Landsat TM data in British Columbia, Canada. Photogramm. Eng. Remote Sens 2003, 69, 283–288. [Google Scholar]
  26. Kennedy, R.E.; Yang, Z.; Cohen, W.B. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. Landtrendr—Temporal segmentation algorithms. Remote Sens. Environ 2010, 114, 2897–2910. [Google Scholar]
  27. Huang, C.; Goward, S.N.; Masek, J.G.; Thomas, N.; Zhu, Z.; Vogelmann, J.E. An automated approach for reconstructing recent forest disturbance history using dense Landsat time series stacks. Remote Sens. Environ 2010, 114, 183–198. [Google Scholar]
  28. Vogelmann, J.E.; Kost, J.R.; Tolk, B.; Howard, S.; Short, K.; Chen, X.; Huang, C.; Pabst, K.; Rollins, M.G. Monitoring landscape change for landfire using multi-temporal satellite imagery and ancillary data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2011, 4, 252–264. [Google Scholar]
  29. Masek, J.G.; Goward, S.N.; Kennedy, R.E.; Cohen, W.B.; Moisen, G.G.; Schleweiss, K.; Huang, C. United States forest disturbance trends observed with Landsat time series. Ecosystems 2013, 16, 1087–1104. [Google Scholar]
  30. Goodwin, N.R.; Coops, N.C.; Wulder, M.A.; Gillanders, S.; Schroeder, T.A.; Nelson, T. Estimation of insect infestation dynamics using a temporal sequence of Landsat data. Remote Sens. Environ 2008, 112, 3680–3689. [Google Scholar]
  31. Gong, P.; Wang, J.; Yu, L.; Zhao, Y.; Zhao, Y.; Liang, L.; Niu, Z.; Huang, X.; Fu, H.; Liu, S.; et al. Finer resolution observation and monitoring of global land cover: First mapping results with Landsat TM and ETM+ data. Int. J. Remote Sens 2013, 34, 2607–2654. [Google Scholar]
  32. Campbell, J.B. Introduction to Remote Sensing; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
  33. Klutsch, J.G.; Negron, J.F.; Costello, S.L.; Rhoades, C.C.; West, D.R.; Popp, J.; Caissie, R. Stand characteristics and downed woody debris accumulations associated with a mountain pine beetle (dendroctonus ponderosae hopkins) outbreak in Colorado. For. Ecol. Manag 2009, 258, 641–649. [Google Scholar]
  34. Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, K.F.; Gao, F.; Kutler, J.; Lim, T.-K. A Landsat surface reflectance dataset for North America, 1990–2000. IEEE Geosci. Remote Sens. Lett 2006, 3, 68–72. [Google Scholar]
  35. Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ 2012, 118, 83–94. [Google Scholar]
  36. Nelson, K.J.; Connot, J.; Peterson, B.; Martin, C. The landfire refresh strategy: Updating the national dataset. Fire Ecol 2013, 9, 80–101. [Google Scholar]
  37. Gibson, K.E.; Skov, K.; Kegley, S.; Jorgensen, C.; Smith, S.; Witcosky, J. Mountain Pine Beetle Impacts in High-Elevation Five-Needle Pines: Current Trends and Challenges; U.S. Department of Agriculture, Forest Service, Forest Health Protection: Washington, DC, USA, 2008. [Google Scholar]
  38. National c2001 Assessment. Available online: http://www.landfire.gov/dp_quality_assessment.php (accessed on 12 June 2014).
  39. Key, C.H.; Benson, N.C. Landscape Assessment: Remote Sensing of Severity, the Normalized Burn Ratio and Ground Measure of Severity, the Composite Burn Index; General Technical Report RMRS-GTR-164-CD: LA1-LA51; U.S. Department of Agriculture, Rocky Mountain Research Station: Ogden, UT, USA, 2005. [Google Scholar]
  40. Eidenshink, J.; Schwind, B.; Brewer, K.; Zhu, Z.L.; Quayle, B.; Howard, S. A project for monitoring trends in burn severity. Fire Ecol 2007, 3, 3–20. [Google Scholar]
  41. Sulla-Menashe, D.; Kennedy, R.E.; Yang, Z.; Braaten, J.; Krankina, O.N.; Friedl, M.A. Detecting forest disturbance in the Pacific Northwest from MODIS time series using temporal segmentation. Remote Sens. Environ 2013. [Google Scholar] [CrossRef]
  42. Mathur, A.; Foody, G.M. Crop classification by support vector machine with intelligently selected training data for an operational application. Int. J. Remote Sens 2008, 29, 2227–2240. [Google Scholar]
  43. Chen, Y.; Gong, P. Clustering based on eigenspace transformation—CBEST for efficient classification. ISPRS J. Photogramm. Remote Sens 2013, 83, 64–80. [Google Scholar]
  44. Jensen, J.R. Introductory Digital Image Processing: A Remote Sensing Perspective; Prentice-Hall Inc: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
  45. Breiman, L. Random forests. Mach. Learn 2001, 45, 5–32. [Google Scholar]
  46. Dietterich, T.G. An experimental comparison of three methods for constructing ensembles of decision trees: Bagging, boosting, and randomization. Mach. Learn 2000, 40, 139–157. [Google Scholar]
  47. Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ 1979, 8, 127–150. [Google Scholar]
  48. Wilson, E.H.; Sader, S.A. Detection of forest harvest type using multiple dates of Landsat TM imagery. Remote Sens. Environ 2002, 80, 385–396. [Google Scholar]
  49. Rock, B.; Vogelmann, J.; Williams, D.; Vogelmann, A.; Hoshizaki, T. Remote detection of forest damage. BioSci.-Am. Inst. Biol. Sci 1986, 36, 439–445. [Google Scholar]
  50. Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ 1996, 58, 257–266. [Google Scholar]
  51. Crist, E.P.; Cicone, R.C. A physically-based transformation of Thematic Mapper data—The TM tasseled cap. IEEE Trans. Geosci. Remote Sens 1984. [Google Scholar] [CrossRef]
  52. Johnson, E.W.; Ross, J. USDA Forest Service Rocky Mountain Region Forest Health Aerial Survey Accuracy Assessment 2005 Report; Technical Report R2-06-08; USDA Forest Service: Lakewood, CO, USA, 2005. [Google Scholar]
  53. Friedl, M.A.; Brodley, C.E. Decision tree classification of land cover from remotely sensed data. Remote Sens. Environ 1997, 61, 399–409. [Google Scholar]
  54. Ghimire, B.; Rogan, J.; Miller, J. Contextual land-cover classification: Incorporating spatial dependence in land-cover classification models using random forests and the getis statistic. Remote Sens. Lett 2010, 1, 45–54. [Google Scholar]
  55. Pal, M.; Mather, P.M. An assessment of the effectiveness of decision tree methods for land cover classification. Remote Sens. Environ 2003, 86, 554–565. [Google Scholar]
  56. Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens 2005, 26, 217–222. [Google Scholar]
  57. Foody, G.M. Sample size determination for image classification accuracy assessment and comparison. Int. J. Remote Sens 2009, 30, 5273–5291. [Google Scholar]
  58. Li, C.C.; Wang, J.; Wang, L.; Hu, L.Y.; Gong, P. Comparison of classification algorithms and training sample sizes in urban land classification with Landsat Thematic Mapper imagery. Remote Sens 2013. [Google Scholar] [CrossRef]
  59. Rodriguez-Galiano, V.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens 2012, 67, 93–104. [Google Scholar]
  60. Meddens, A.J.; Hicke, J.A.; Vierling, L.A.; Hudak, A.T. Evaluating methods to detect bark beetle-caused tree mortality using single-date and multi-date Landsat imagery. Remote Sens. Environ 2013, 132, 49–58. [Google Scholar]
  61. Cohen, W.B.; Yang, Z.; Kennedy, R. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 2. Timesync—Tools for calibration and validation. Remote Sens. Environ 2010, 114, 2911–2924. [Google Scholar]
Remotesensing 06 05696f1 1024
Figure 1. The study area used for our analyses. The Southern Rocky Mountain ecoregion is shown in blue, and Grand County, Colorado, USA, is shown in red. The imagery is a false-color composite of one Landsat image acquired on 21 August 2009.
Figure 1. The study area used for our analyses. The Southern Rocky Mountain ecoregion is shown in blue, and Grand County, Colorado, USA, is shown in red. The imagery is a false-color composite of one Landsat image acquired on 21 August 2009.
Remotesensing 06 05696f1
Remotesensing 06 05696f2 1024
Figure 2. Forest type map for Grand County, from (a) the LANDFIRE existing vegetation type data and (b) the number of clear Landsat observations over the period of 2000 to 2011.
Figure 2. Forest type map for Grand County, from (a) the LANDFIRE existing vegetation type data and (b) the number of clear Landsat observations over the period of 2000 to 2011.
Remotesensing 06 05696f2
Remotesensing 06 05696f3 1024
Figure 3. The decision tree used to attribute temporal segments into the different disturbance classes.
Figure 3. The decision tree used to attribute temporal segments into the different disturbance classes.
Remotesensing 06 05696f3
Remotesensing 06 05696f4 1024
Figure 4. Tukey boxplot for (a) the averaged annual normalized burn ratio (NBR, multiplied by 100) changes of stable, regrowth, MPB mortality and clearcut plots; (b) current vertex values of post-MPB mortality, post-clearcut events and healthy plots. The bottom and top of the box are the first and third quartiles, and the band inside the box is the median. The whiskers represent the 1.5 interquartile range of the lower and upper quartile.
Figure 4. Tukey boxplot for (a) the averaged annual normalized burn ratio (NBR, multiplied by 100) changes of stable, regrowth, MPB mortality and clearcut plots; (b) current vertex values of post-MPB mortality, post-clearcut events and healthy plots. The bottom and top of the box are the first and third quartiles, and the band inside the box is the median. The whiskers represent the 1.5 interquartile range of the lower and upper quartile.
Remotesensing 06 05696f4
Remotesensing 06 05696f5 1024
Figure 5. The proportion of validation samples that were erroneously labeled in other classes.Notes: H, healthy; M, MPB mortality; C, clearcut; H2M is explained as “healthy samples classified to MPB mortality”.
Figure 5. The proportion of validation samples that were erroneously labeled in other classes.Notes: H, healthy; M, MPB mortality; C, clearcut; H2M is explained as “healthy samples classified to MPB mortality”.
Remotesensing 06 05696f5
Remotesensing 06 05696f6 1024
Figure 6. (a) Classification results of the forest growth trend analysis in the years 2000, 2005 and 2011; (b) maps of the onset year, duration and magnitude of mountain pine beetle (MPB) mortality.
Figure 6. (a) Classification results of the forest growth trend analysis in the years 2000, 2005 and 2011; (b) maps of the onset year, duration and magnitude of mountain pine beetle (MPB) mortality.
Remotesensing 06 05696f6
Remotesensing 06 05696f7 1024
Figure 7. Relationships between accuracy and sample size for the maximum likelihood classifier (MLC) and random forests (RF) using multiple training sets. Graphs arranged from left to right display the trends of overall accuracy, the producer’s accuracy and the user’s accuracy for the mountain pine beetle (MPB) mortality class as the training sample proportion increases from 0.1 to one. Blue and solid lines represent RF results, whereas green and dashed lines represent MLC results. Red arrows indicate the mean accuracies produced by the forest growth trend analysis in the years 2005, 2009 and 2011.
Figure 7. Relationships between accuracy and sample size for the maximum likelihood classifier (MLC) and random forests (RF) using multiple training sets. Graphs arranged from left to right display the trends of overall accuracy, the producer’s accuracy and the user’s accuracy for the mountain pine beetle (MPB) mortality class as the training sample proportion increases from 0.1 to one. Blue and solid lines represent RF results, whereas green and dashed lines represent MLC results. Red arrows indicate the mean accuracies produced by the forest growth trend analysis in the years 2005, 2009 and 2011.
Remotesensing 06 05696f7
Table
Table 1. Characteristics of the Landsat images used in this analysis.
Table 1. Characteristics of the Landsat images used in this analysis.
YearMonth and DayJulian DayCloud Cover (%)Cloud Cover over MPB Host Area (%) *
12000July 1319342.351.09
22000July 212014.74
32001June 2817918.874.24
42001July 2220317.05
52002July 11821.920.15
62003July 41855.480.49
72004July 818810.497.94
82005September 112542.080.25
92006July 282092.301.26
102007July 3121220.394.22
112007August 1622813.19
122008August 2023128.919.79
132008September 524736.83
142009August 212332.040.00
152010September 252683.370.89
162011August 1122322.132.67
172011August 2723916.45
Notes: MPB, mountain pine beetle;
*the final cloud cover in a particular year in MPB host forest areas is after using clean pixels in one image to fill cloudy areas in another image that is in the same phenological state.
Table
Table 2. Examples of normalized burn ratio (NBR) trajectories, National Agricultural Imagery Program (NAIP) data and in situ photos for healthy forest, MPB mortality and clearcut classes.
Table 2. Examples of normalized burn ratio (NBR) trajectories, National Agricultural Imagery Program (NAIP) data and in situ photos for healthy forest, MPB mortality and clearcut classes.
ClassLandsatNAIPPhoto
Healthy conifer forestRemotesensing 06 05696f8Remotesensing 06 05696f9Remotesensing 06 05696f10
MPB mortalityRemotesensing 06 05696f11Remotesensing 06 05696f12Remotesensing 06 05696f13
ClearcutRemotesensing 06 05696f14Remotesensing 06 05696f15Remotesensing 06 05696f16
Table
Table 3. LandTrendr parameters, descriptions, suggested values from Kennedy et al. (2010) [26] and the values tested for this study and ultimately selected for this study to reduce the raw normalized burn ratio (NBR) time series values to a number of linear segments.
Table 3. LandTrendr parameters, descriptions, suggested values from Kennedy et al. (2010) [26] and the values tested for this study and ultimately selected for this study to reduce the raw normalized burn ratio (NBR) time series values to a number of linear segments.
ParameterDescription and UnitsKennedy et al. (2010) [26]Values TestedValue Selected
DespikeAn outlier will be removed if the proportional difference in NBR values between two adjacent points is less than this parameter.0.900.75; 0.9; 10.90
Max_segThe maximum number of segments allowed in fitting.43; 4; 54
VertexOvershootThe first round regression detected vertices can overshoot (max_seg + 1) vertices by this value.30; 30
pvalA pixel will be considered as no change if its p-value of the F-statistic for the entire trajectory is above this threshold.0.050.05; 0.10.1
Recovery_thresholdIf the slope of a segment positively spans the whole spectral range within 1/recovery_threshold years, it will be rejected.0.250.25; 10.25
BestModelProportionA simpler model will be chosen if its F-statistic exceeds this proportion of the best fitting model.0.750.75; 10.75
Table
Table 4. Abbreviations and control parameters used in the decision tree.
Table 4. Abbreviations and control parameters used in the decision tree.
ParameterDescription
magMagnitude of change in NBR between the current vertex and the following vertex: NBRnext year-NBRcurrent year.
curThe NBR value for current vertex.
pre_labelThe vertex label in the previous year.
thre_mag1The magnitude threshold that distinguished stable from either disturbance or recovery.
thre_mag2The magnitude threshold that separated MPB mortality from clearcut.
thre_vertex1If the current vertex NBR value was above this threshold, it was treated as healthy, otherwise, it was further analyzed into disturbance types.
thre_vertex2If first year’s vertex value was below this threshold, it was treated as a clearcut pixel and MPB mortality otherwise.
Notes: MPB, mountain pine beetle; NBR, normalized burn ratio.
Table
Table 5. Spectral indices used in the single-date classifications, including formulas and references.
Table 5. Spectral indices used in the single-date classifications, including formulas and references.
Spectral IndicesFormulaReference
Normalized Difference Vegetation Index(b4 − b3)/(b4 + b3)[47]
Normalized Difference Moisture Index(b4 − b5)/(b4 + b5)[48]
Moisture Stress Indexb5/b4[49]
Normalized Difference Wetness Index(b2 − b4)/(b2 + b4)[50]
Normalized Burn Ratio(b4 − b7)/(b4 + b7)[39]
Tasseled Cap Brightness0.3037 × b1 + 0.2793 × b2 + 0.4743 × b3 + 0.5585×b4 + 0.5082 × b5 + 0.1863 × b7[51]
Tasseled Cap Greenness−0.2848 × b1 − 0.2435 × b2 − 0.5436 × b3 + 0.7243 × b4 + 0.084 × b5 − 0.18 × b7[51]
Tasseled Cap Wetness0.1509 × b1 + 0.1973 × b2 + 0.3279 × b3 + 0.3406 × b4 − 0.7112 × b5 − 0.4572 × b7[51]
Note: band numbers in the formulas refer to the Landsat 5 band order.
Table
Table 6. Accuracy assessment results for individual years of the time series classification.
Table 6. Accuracy assessment results for individual years of the time series classification.
YearHealthyMPB MortalityClearcut
OAKappaPAUAPAUAPAUA
200089.0082.21100.0083.0288.8994.1265.00100.00
200190.0084.23100.0095.74100.0079.4958.33100.00
200289.0082.88100.0095.5693.7578.9564.0094.12
200393.0088.92100.0093.1894.8792.5075.0093.75
200492.0087.41100.00100.0089.7489.7478.9578.95
200591.0085.5191.4997.7397.1480.9577.78100.00
200686.7478.9972.9796.4395.2478.4394.7494.74
200794.0090.4992.11100.0097.6789.3689.4794.44
200891.0086.2082.3596.5597.5084.7892.3196.00
200991.0085.8187.1096.43100.0084.6280.00100.00
201090.0084.5697.1497.1495.0084.4472.0090.00
201187.0079.6481.2592.8695.3580.3980.0095.24
mean90.3184.7492.0395.3995.4384.8177.3094.77
SD2.183.459.254.463.475.4711.355.92
Notes: OA, overall accuracy; PA, producer’s accuracy; UA, user’s accuracy; SD, standard deviation.
Table
Table 7. Accuracy comparison among the time series classification, random forests (RF) and maximum likelihood classifier (MLC) with the same set of 2005, 2009 and 2011 validation samples. Only the mountain pine beetle (MPB) mortality class is included here.
Table 7. Accuracy comparison among the time series classification, random forests (RF) and maximum likelihood classifier (MLC) with the same set of 2005, 2009 and 2011 validation samples. Only the mountain pine beetle (MPB) mortality class is included here.
YearTime-Series Trend AnalysisRFMLC
rawcombinedrawcombined
2005UA80.9568.0067.3071.9688.00
PA97.1418.7862.4085.0865.90
OA91.0063.8274.4075.2073.50
2009UA84.6246.15100.0039.630.00
PA100.0035.4348.70100.00100.00
OA91.0053.4772.9040.9438.70
2011UA80.3978.4777.8037.9222.20
PA95.3583.0610.80100.00100.00
OA87.0066.6240.4038.1537.20
Notes: “raw” denotes classification with solely spectral data, and “combined” denotes classification with the combined use of spectral and index data; PA, producer’s accuracy; UA, user’s accuracy; OA, overall accuracy.

Share and Cite

MDPI and ACS Style

Liang, L.; Chen, Y.; Hawbaker, T.J.; Zhu, Z.; Gong, P. Mapping Mountain Pine Beetle Mortality through Growth Trend Analysis of Time-Series Landsat Data. Remote Sens. 2014, 6, 5696-5716. https://doi.org/10.3390/rs6065696

AMA Style

Liang L, Chen Y, Hawbaker TJ, Zhu Z, Gong P. Mapping Mountain Pine Beetle Mortality through Growth Trend Analysis of Time-Series Landsat Data. Remote Sensing. 2014; 6(6):5696-5716. https://doi.org/10.3390/rs6065696

Chicago/Turabian Style

Liang, Lu, Yanlei Chen, Todd J. Hawbaker, Zhiliang Zhu, and Peng Gong. 2014. "Mapping Mountain Pine Beetle Mortality through Growth Trend Analysis of Time-Series Landsat Data" Remote Sensing 6, no. 6: 5696-5716. https://doi.org/10.3390/rs6065696

Article Metrics

Back to TopTop