A Bayesian Based Method to Generate a Synergetic Land-Cover Map from Existing Land-Cover Products
Abstract
:1. Introduction
2. Materials
2.1. Land-Cover Datasets
2.2. Validation Data
3. Method
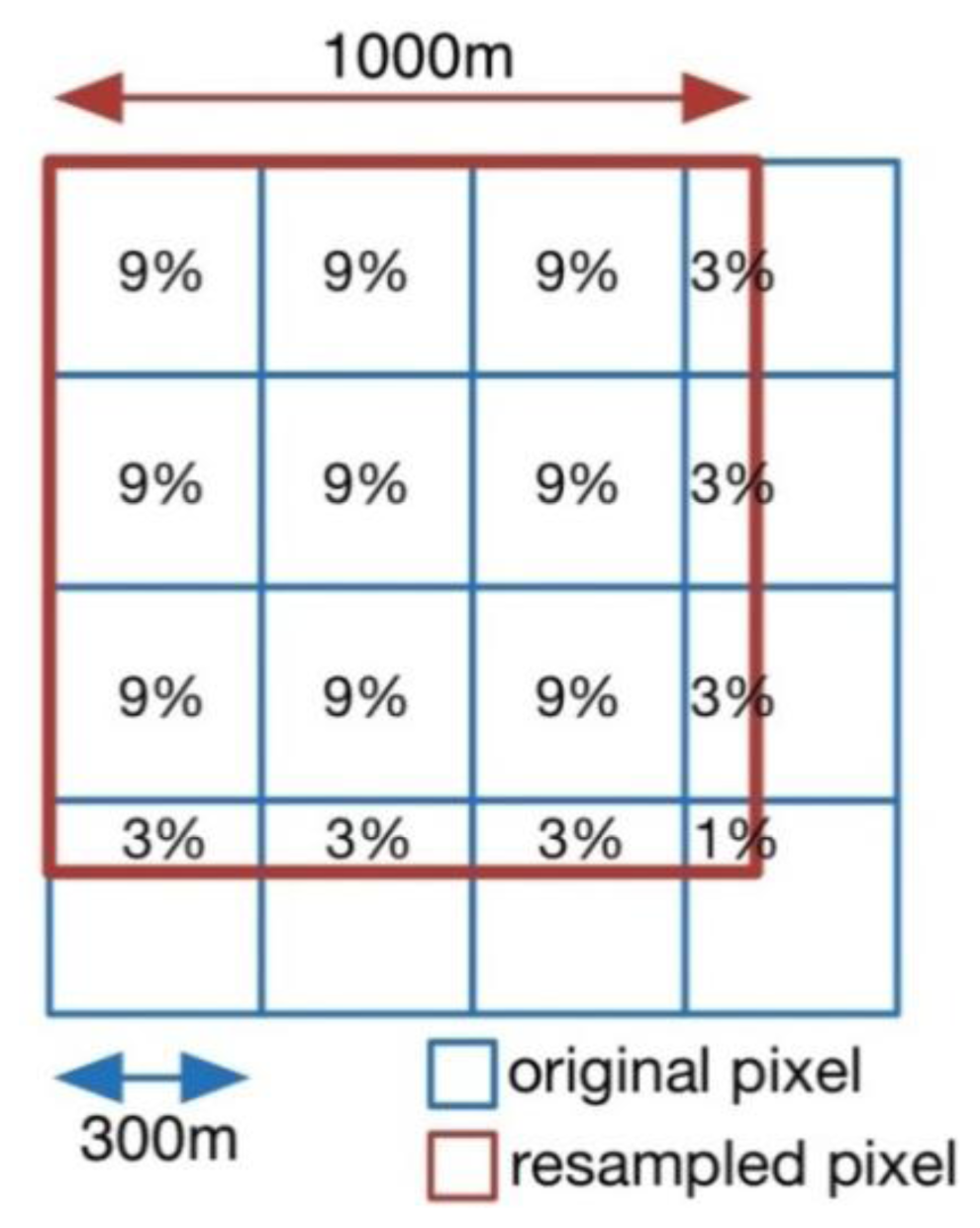
3.1. Reclassification and Resampling
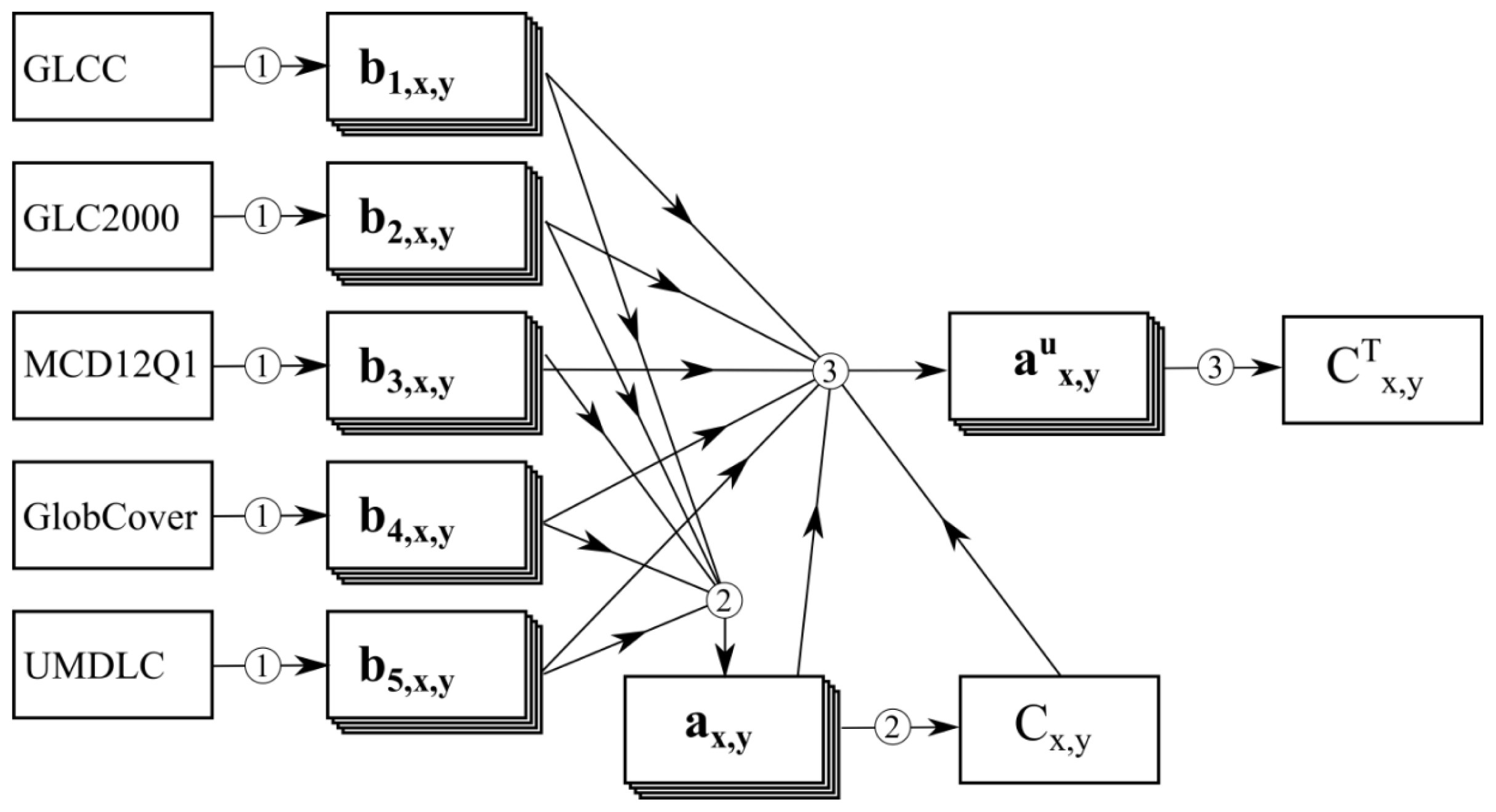
3.2. Generate Prior Global Land Cover Map
3.3. Update State Vector of Each Pixel
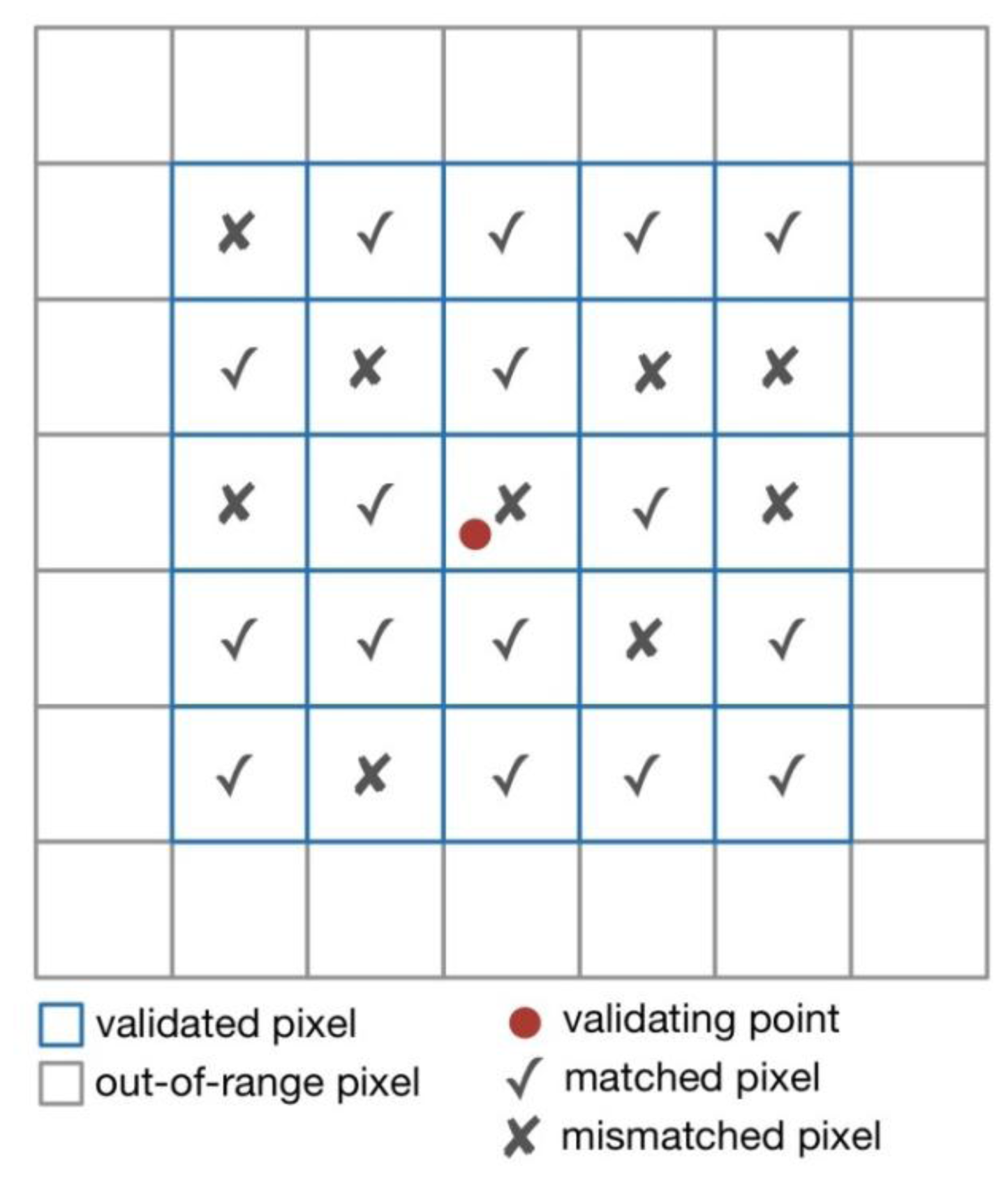
3.4. Validation
4. Result
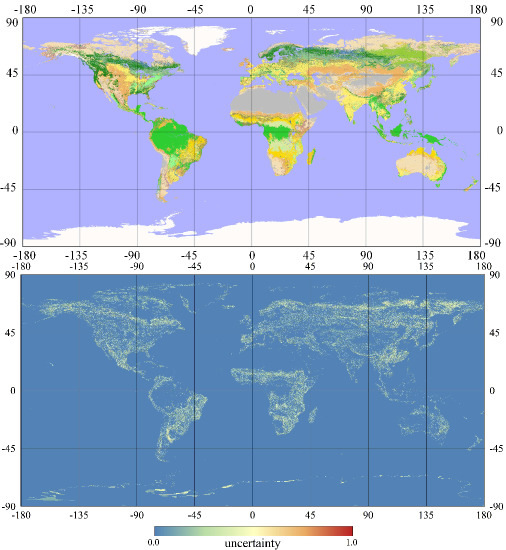
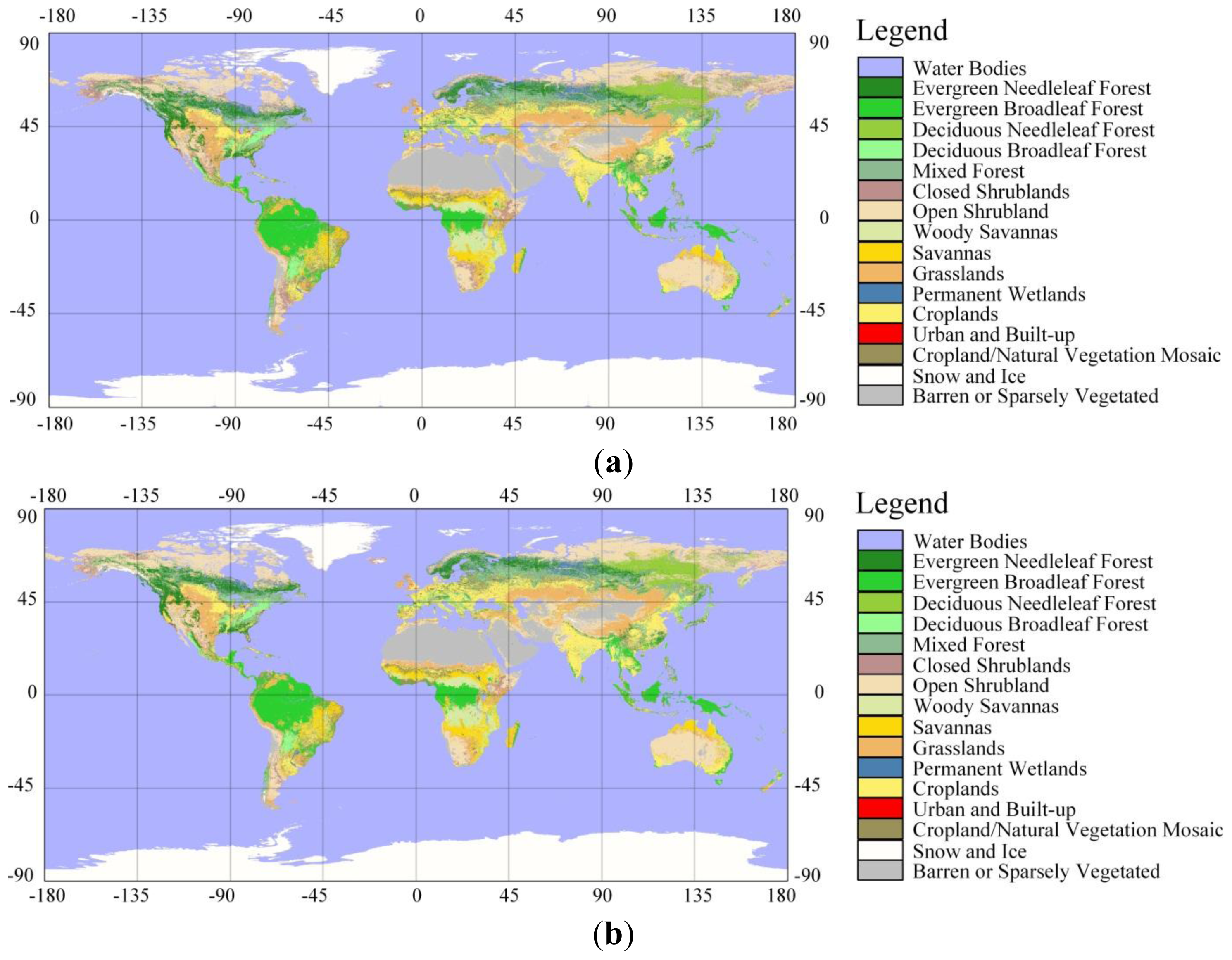
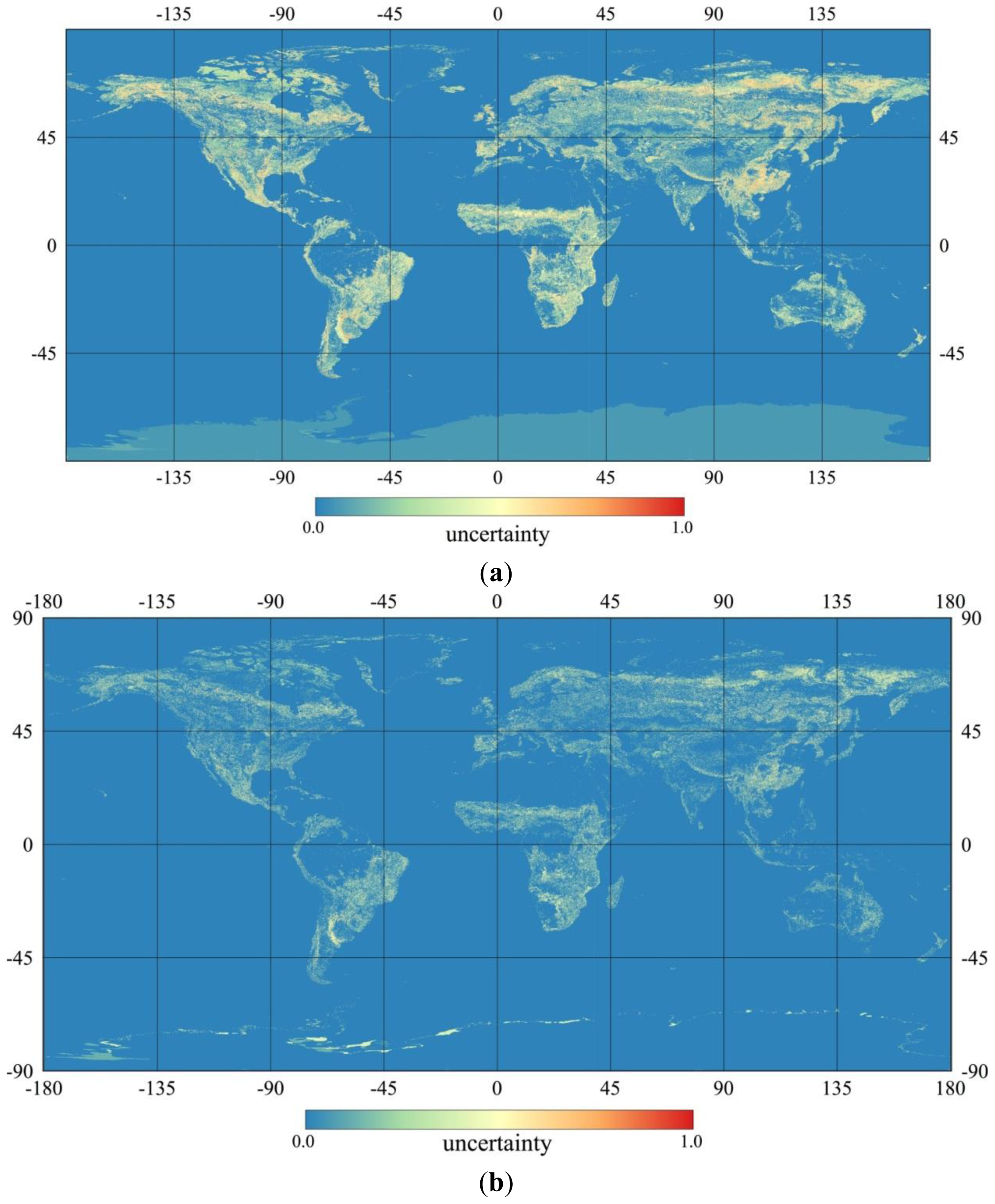
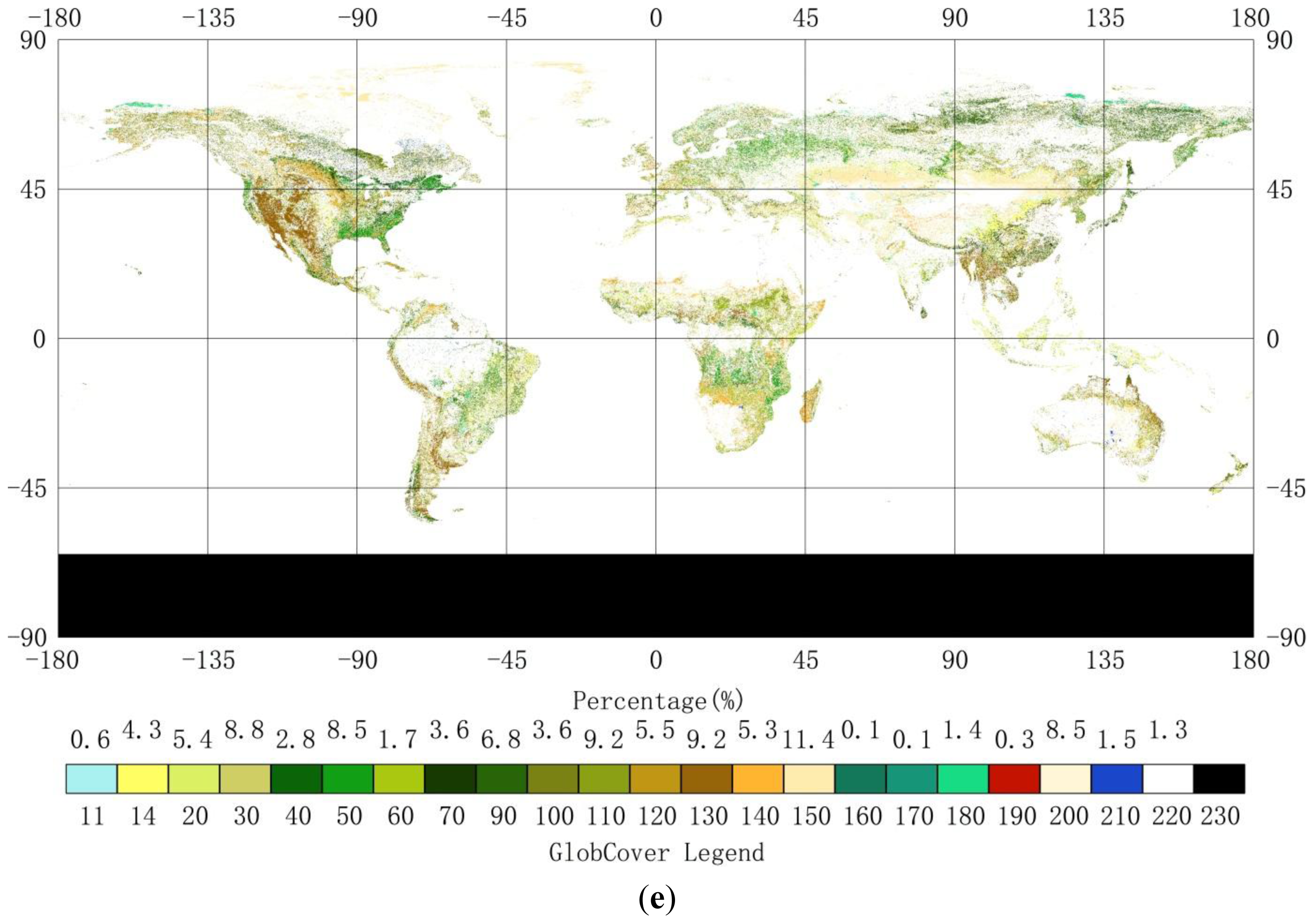
4.1. Posterior Global Land Cover Map and its Uncertainty
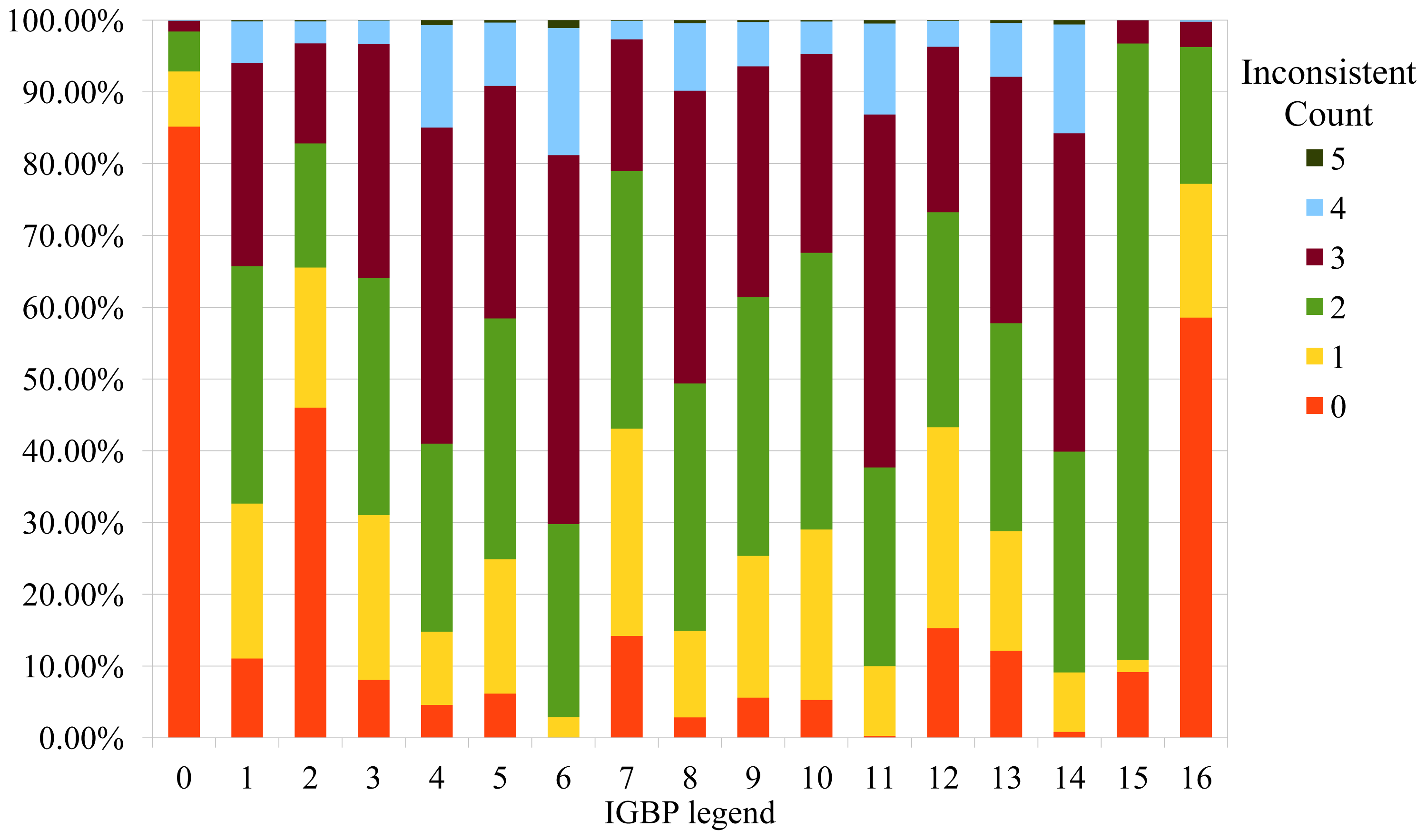
4.2. Validation
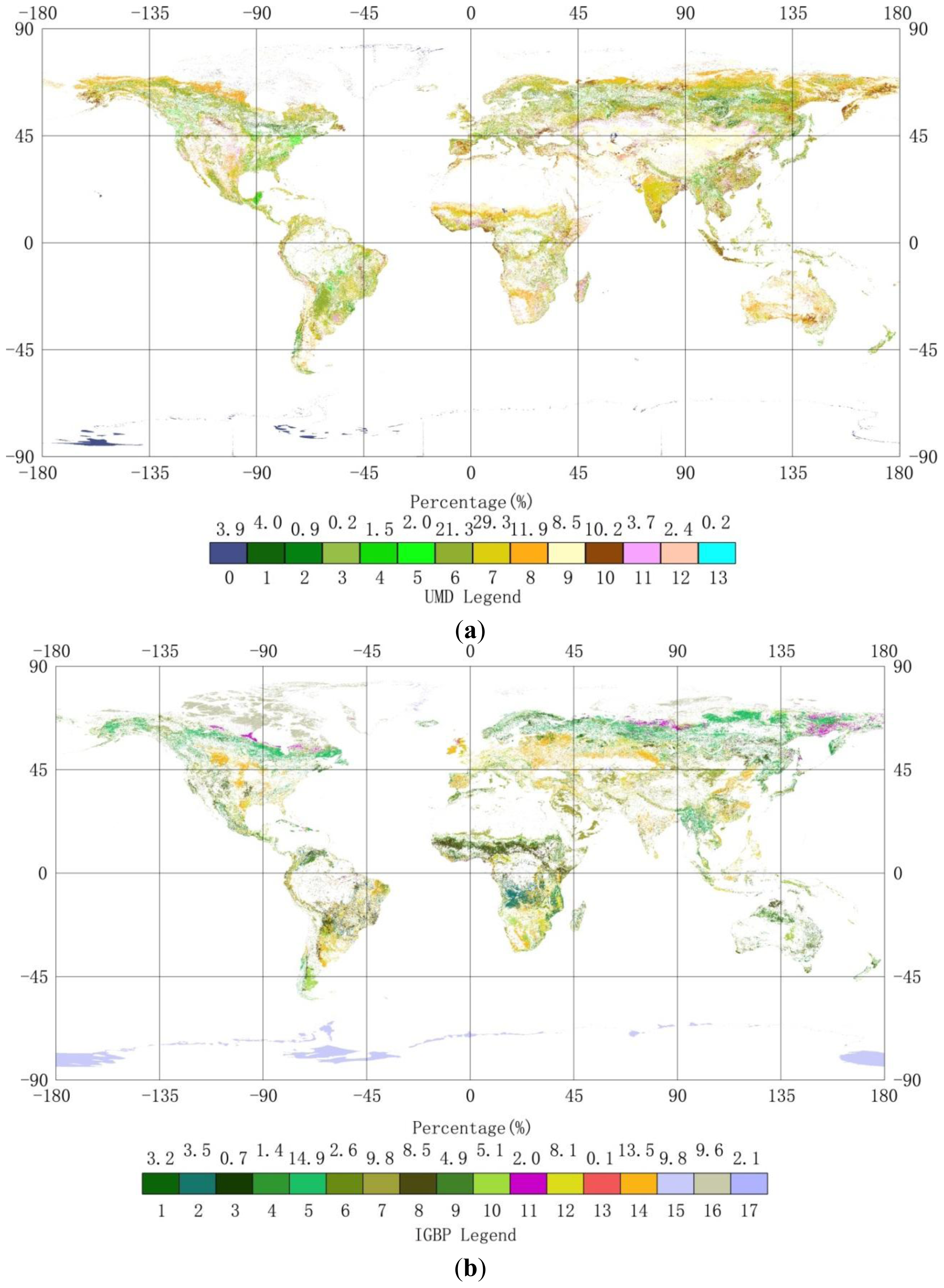
4.3. Compare synGLC with the Existing Global Land Cover Maps
5. Discussion
5.1. Assumptions and Limitations
- (1)
- Each land cover map can make a mistake with 50% probability;
- (2)
- Classification of each land cover map is independent;
- (3)
- Classification with high agreement is true.
5.2. Legends Translation
5.3. Effects of Land Cover Changes
5.4. Strength of Our Method
6. Conclusions
Acknowledgment
Conflicts of Interest
- Author ContributionsAll authors contributed extensively to the work presented in this paper. Baozhang Chen and Hairong Zhang proposed the research idea. Guang Xu and Baozhang Chen designed the algorithm. Guang Xu, Huifang Zhang and Jianwu Yan analyzed the data. Guang Xu and Baozhang Chen interpreted the results and wrote the paper. Jing Chen, Xianming Dou, Mingliang Che and Xiaofeng Lin aided with the results interpretation, discussion and editing the paper.
References
- Bonan, G.B.; Oleson, K.W.; Vertenstein, M.; Levis, S.; Zeng, X.; Dai, Y.; Dickinson, R.E.; Yang, Z.-L. The land surface climatology of the community land model coupled to the NCAR community climate model. J. Clim 2002, 15, 3123–3149. [Google Scholar]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar]
- Zhang, K.; Kimball, J.S.; Mu, Q.; Jones, L.A.; Goetz, S.J.; Running, S.W. Satellite based analysis of northern ET trends and associated changes in the regional water balance from 1983 to 2005. J. Hydrol 2009, 379, 92–110. [Google Scholar]
- Foley, J.A.; DeFries, R.; Asner, G.P.; Barford, C.; Bonan, G.; Carpenter, S.R.; Chapin, F.S.; Coe, M.T.; Daily, G.C.; Gibbs, H.K. Global consequences of land use. Science 2005, 309, 570–574. [Google Scholar]
- Chen, B.; Chen, J.M.; Ju, W. Remote sensing-based ecosystem-atmosphere simulation scheme (EASS)—Model formulation and test with multiple-year data. Ecol. Modell 2007, 209, 277–300. [Google Scholar]
- Dai, Y.; Zeng, X.; Dickinson, R.E.; Baker, I.; Bonan, G.B.; Bosilovich, M.G.; Denning, A.S.; Dirmeyer, P.A.; Houser, P.R.; Niu, G. The common land model. Bull. Am. Meteorol. Soc 2003, 84, 1013–1023. [Google Scholar]
- Perez-Hoyos, A.; Garcia-Haro, F.J.; San-Miguel-Ayanz, J. A methodology to generate a synergetic land-cover map by fusion of different land-cover products. Int. J. Appl. Earth Observ. Geoinf 2012, 19, 72–87. [Google Scholar]
- Hansen, M.C.; Defries, R.S.; Townshend, J.R.G.; Sohlberg, R. Global land cover classification at 1 km spatial resolution using a classification tree approach. Int. J. Remote Sens 2000, 21, 1331–1364. [Google Scholar]
- GLCF: AVHRR Global Land Cover Classification. Available online: http://glcf.umd.edu/data/landcover/ (accessed on 3 April 2014).
- Loveland, T.R.; Reed, B.C.; Brown, J.F.; Ohlen, D.O.; Zhu, Z.; Yang, L.; Merchant, J.W. Development of a global land cover characteristics database and IGBP discover from 1 km AVHRR data. Int. J. Remote Sens 2000, 21, 1303–1330. [Google Scholar]
- Global Land Cover Characterization. Available online: http://edc2.usgs.gov/glcc/globe_int.php (accessed on 3 April 2014).
- Bartholome, E.; Belward, A.S. GLC2000: A new approach to global land cover mapping from earth observation data. Int. J. Remote Sens 2005, 26, 1959–1977. [Google Scholar]
- Global Environment Monitoring (GEM). Available online: http://bioval.jrc.ec.europa.eu/products/glc2000/products.php (accessed on 3 April 2014).
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X.M. MODIS collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ 2010, 114, 168–182. [Google Scholar]
- Friedl, M.A.; McIver, D.K.; Hodges, J.C.F.; Zhang, X.Y.; Muchoney, D.; Strahler, A.H.; Woodcock, C.E.; Gopal, S.; Schneider, A.; Cooper, A.; et al. Global land cover mapping from MODIS: Algorithms and early results. Remote Sens. Environ 2002, 83, 287–302. [Google Scholar]
- MCD12Q1|LP DAAC: NASA Land Data Products and Services. Available online: https://lpdaac.usgs.gov/products/modis_products_table/mcd12q1 (accessed on 3 April 2014).
- Bontemps, S.; Defourny, P.; Bogaert, E.V.; Arino, O.; Kalogirou, V.; Perez, J.R. Globcover 2009—Products Description and Validation Report; European Spatial Agency and Université Catholique de Louvain: Frascati, Italy, 2011. Available online: http://due.esrin.esa.int/globcover/LandCover2009/GLOBCOVER2009_Validation_Report_2.2.pdf (accessed on 3 July 2013).
- ESA-Data User Element. Available online: http://due.esrin.esa.int/globcover/ (accessed on 3 April 2014).
- Fritz, S.; Lee, L. Comparison of land cover maps using fuzzy agreement. Int. J. Geogr. Inf. Sci 2005, 19, 787–807. [Google Scholar]
- Giri, C.; Zhu, Z.L.; Reed, B. A comparative analysis of the global land cover 2000 and MODIS land cover data sets. Remote Sens. Environ 2005, 94, 123–132. [Google Scholar]
- Hansen, M.C.; Reed, B. A comparison of the IGBP discover and University of Maryland 1 km global land cover products. Int. J. Remote Sens 2000, 21, 1365–1373. [Google Scholar]
- Latifovic, R.; Olthof, I. Accuracy assessment using sub-pixel fractional error matrices of global land cover products derived from satellite data. Remote Sens. Environ 2004, 90, 153–165. [Google Scholar]
- Jung, M.; Henkel, K.; Herold, M.; Churkina, G. Exploiting synergies of global land cover products for carbon cycle modeling. Remote Sens. Environ 2006, 101, 534–553. [Google Scholar]
- See, L.M.; Fritz, S. A method to compare and improve land cover datasets: Application to the GLC-2000 and MODIS land cover products. IEEE Trans. Geosci. Remote Sens 2006, 44, 1740–1746. [Google Scholar]
- Fritz, S.; You, L.; Bun, A.; See, L.; McCallum, I.; Schill, C.; Perger, C.; Liu, J.; Hansen, M.; Obersteiner, M. Cropland for Sub-Saharan Africa: A synergistic approach using five land cover data sets. Geophys. Res. Lett 2011, 38, L04404. [Google Scholar]
- Defourny, P.; Schouten, L.; Bartalev, S.; Bontemps, S.; Cacetta, P.; Wit, A.D.; Bella, C.D.; Gérard, B.; Giri, C.; Gond, V.; et al. Accuracy Assessment of a 300 m Global Land Cover Map: The GlobCover Experience. Proceedings of the 33rd International Symposium on Remote Sensing of Environment, Stresa, Italy, 4–8 May 2009.
- Defourny, P.; Mayaux, P.; Herold, M.; Bontemps, S. Global Land Cover Map Validation Experiences: Toward the Characterization of Quantitative Uncertainty. In Remote Sensing of Land Use and Land Cover: Principles and Applications; Remote Sensing Applications Series; Giri, C.P., Ed.; CPC Press-Taylor & Francis: Boca Raton, FL, USA, 2012; Volume Chapter 14, pp. 207–222. [Google Scholar]
- Friedl, M.A.; Muchoney, D.; McIver, D.; Gao, F.; Hodges, J.C.F.; Strahler, A.H. Characterization of North American land cover from NOAA-AVHRR data using the EOS MODIS land cover classification algorithm. Geophys. Res. Lett 2000, 27, 977–980. [Google Scholar]
- Muchoney, D.; Borak, J.; Chi, H.; Friedl, M.; Gopal, S.; Hodges, J.; Morrow, N.; Strahler, A. Application of the MODIS global supervised classification model to vegetation and land cover mapping of Central America. Int. J. Remote Sens 2000, 21, 1115–1138. [Google Scholar]
- Schneider, A.; Friedl, M.A.; Potere, D. A new map of global urban extent from MODIS satellite data. Environ. Res. Lett 2009, 4, 044003. [Google Scholar]
- Schneider, A.; Friedl, M.A.; Potere, D. Mapping global urban areas using MODIS 500-m data: New methods and datasets based on “urban ecoregions”. Remote Sens. Environ 2010, 114, 1733–1746. [Google Scholar]
- Sulla-Menashe, D.; Friedl, M.A.; Krankina, O.N.; Baccini, A.; Woodcock, C.E.; Sibley, A.; Sun, G.Q.; Kharuk, V.; Elsakov, V. Hierarchical mapping of northern Eurasian land cover using MODIS data. Remote Sens. Environ 2011, 115, 392–403. [Google Scholar]
- Olofsson, P.; Stehman, S.V.; Woodcock, C.E.; Sulla-Menashe, D.; Sibley, A.M.; Newell, J.D.; Friedl, M.A.; Herold, M. A global land-cover validation data set, part I: Fundamental design principles. Int. J. Remote Sens 2012, 33, 5768–5788. [Google Scholar]
- Stehman, S.V.; Olofsson, P.; Woodcock, C.E.; Herold, M.; Friedl, M.A. A global land-cover validation data set, II: Augmenting a stratified sampling design to estimate accuracy by region and land-cover class. Int. J. Remote Sens 2012, 33, 6975–6993. [Google Scholar]
- Running, S.W.; Loveland, T.R.; Pierce, L.L. A vegetation classification logic-based on remote-sensing for use in global biogeochemical models. AMBIO 1994, 23, 77–81. [Google Scholar]
- Pflugmacher, D.; Krankina, O.N.; Cohen, W.B.; Friedl, M.A.; Sulla-Menashe, D.; Kennedy, R.E.; Nelson, P.; Loboda, T.V.; Kuemmerle, T.; Dyukarev, E.; et al. Comparison and assessment of coarse resolution land cover maps for northern Eurasia. Remote Sens. Environ 2011, 115, 3539–3553. [Google Scholar]
- McCallum, I.; Obersteiner, M.; Nilsson, S.; Shvidenko, A. A spatial comparison of four satellite derived 1 km global land cover datasets. Int. J. Appl. Earth Observ. Geoinf 2006, 8, 246–255. [Google Scholar]
- Herold, M.; Woodcock, C.E.; di Gregorio, A.; Mayaux, P.; Belward, A.S.; Latham, J.; Schmullius, C.C. A joint initiative for harmonization and validation of land cover datasets. IEEE Trans. Geosci. Remote Sens 2006, 44, 1719–1727. [Google Scholar]
- Clemen, R.T.; Winkler, R.L. Combining probability distributions from experts in risk analysis. Risk Anal 1999, 19, 187–203. [Google Scholar]
- Sleeter, B.M.; Sohl, T.L.; Loveland, T.R.; Auch, R.F.; Acevedo, W.; Drummond, M.A.; Sayler, K.L.; Stehman, S.V. Land-cover change in the conterminous United States from 1973 to 2000. Glob. Environ. Chang 2013, 23, 733–748. [Google Scholar]


| Dataset | Coverage Year | Spatial Resolution | Legend | Website |
|---|---|---|---|---|
| UMDLC | 1981–1994 | 1 km | 14 classes | [9] |
| GLCC | 1992–1993 | 1 km | IGBP | [11] |
| GLC2000 | 2000 | 1/112 degree | FAO LCCS | [13] |
| MCD12Q1 | 2005 | 500 m | IGBP | [16] |
| GlobCover | 2009 | 1/360 degree | UN LCCS | [18] |
| Validation Data | Legend | Sample Size |
|---|---|---|
| GLC2000ref | FAO LCCS | 1253 |
| GlobCover2005ref | UN LCCS | 4258 |
| STEP | IGBP | 1780 |
| VIIRS | IGBP | 3667 |
| IGBP No. | Description |
|---|---|
| 0 | Water |
| 1 | Evergreen Needleleaf Forest |
| 2 | Evergreen Broadleaf Forest |
| 3 | Deciduous Needleleaf Forest |
| 4 | Deciduous Broadleaf Forest |
| 5 | Mixed Forests |
| 6 | Closed Shrublands |
| 7 | Open Shrublands |
| 8 | Woody Savannas |
| 9 | Savannas |
| 10 | Grasslands |
| 11 | Permanent Wetlands |
| 12 | Croplands |
| 13 | Urban and Built-Up |
| 14 | Cropland/Natural Vegetation mosaic |
| 15 | Snow and Ice |
| 16 | Barren or Sparsely Vegetated |
| Value | UMD Land Cover Name | IGBP Class Value | State Probability Vector Of IGPB Class (Zero before Decimal Point Omitted) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |||
| 0 | Water | 0 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 1 | Evergreen Needleleaf Forest | 1 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 2 | Evergreen Broadleaf Forest | 2 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 3 | Deciduous Needleleaf Forest | 3 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 4 | Deciduous Broadleaf Forest | 4 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 5 | Mixed Forests | 5 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 6 | Woodland | 8,11 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 |
| 7 | Wooded Grassland | 9,11 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.033 | 0.250 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 |
| 8 | Closed Shrubland | 6 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 9 | Open Shrubland | 7 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 10 | Grassland | 10 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 11 | Cropland | 12,14 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.033 | 0.250 | 0.033 | 0.033 |
| 12 | Bare ground | 15,16 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.250 |
| 13 | Urban and Built-up | 13 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 |
| 255 | No data | - | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 |
| Value | GLC2000-Class | IGBP-Value | State Probability Vector of IGPB Class (Zero before Decimal Point Omitted) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |||
| 1 | Tree Cover, broadleaved, evergreen | 2 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 2 | Tree Cover, broadleaved, deciduous, closed | 4 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 3 | Tree Cover, broadleaved, deciduous, open | 8,9 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.250 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 |
| 4 | Tree Cover, needle-leaved, evergreen | 1 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 5 | Tree Cover, needle-leaved, deciduous | 3 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 6 | Tree Cover, mixed leaf type | 5 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 7 | Tree Cover, regularly flooded, fresh | 2,11 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 |
| 8 | Tree Cover, regularly flooded, saline, (daily variation) | 2,11,0 | 0.167 | 0.036 | 0.167 | 0.036 | 0.036 | 0.036 | 0.036 | 0.036 | 0.036 | 0.036 | 0.036 | .167 | 0.036 | 0.036 | 0.036 | 0.036 | 0.036 |
| 9 | Mosaic: Tree cover/Other natural vegetation | 6,7 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.250 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 |
| 10 | Tree Cover, burnt | 3,5,7 | 0.036 | 0.036 | 0.036 | 0.167 | 0.036 | 0.167 | 0.036 | 0.167 | 0.036 | 0.036 | 0.036 | 0.036 | 0.036 | 0.036 | 0.036 | 0.036 | 0.036 |
| 11 | Shrub Cover, closed-open, evergreen (with or without sparse tree layer) | 7,8 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.250 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 |
| 12 | Shrub Cover, closed-open, deciduous (with or without sparse tree layer) | 6,7,9 | 0.036 | 0.036 | 0.036 | 0.036 | 0.036 | 0.036 | 0.167 | 0.167 | 0.036 | 0.167 | 0.036 | 0.036 | 0.036 | 0.036 | 0.036 | 0.036 | 0.036 |
| 13 | Herbaceous Cover, closed-open | 6,10 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 |
| 14 | Sparse Herbaceous or sparse shrub cover | 7,10 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 |
| 15 | Regularly flooded shrub and/or herbaceous cover | 7,11 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 |
| 16 | Cultivated and managed areas | 12 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 |
| 17 | Mosaic: Cropland/Tree Cover/Other Natural Vegetation | 14 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 |
| 18 | Mosaic: Cropland/Shrub and/or Herbaceous cover | 14 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 |
| 19 | Bare Areas | 16 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 |
| 20 | Water Bodies (natural & artificial) | 0 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 21 | Snow and Ice (natural & artificial) | 15 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 |
| 22 | Artificial surfaces and associated areas | 13 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 |
| 23 | No data | - | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 |
| Value | GlobCover-Label | IGBP Value | State Probability Vector of IGPB Class (Zero before Decimal Point Omitted) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |||
| 11 | Post-flooding or irrigated croplands (or aquatic) | 12 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 |
| 14 | Rainfed croplands | 12 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 |
| 20 | Mosaic cropland (50%–70%)/vegetation (grassland/shrubland/forest) (20%–50%) | 12,14 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.033 | 0.250 | 0.033 | 0.033 |
| 30 | Mosaic vegetation (grassland/shrubland/forest) (50%–70%)/cropland (20%–50%) | 10,14 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 |
| 40 | Closed to open (>15%) broadleaved evergreen or semi-deciduous forest (>5 m) | 2 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 50 | Closed (>40%) broadleaved deciduous forest (>5 m) | 4 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 60 | Open (15%–40%) broadleaved deciduous forest/woodland (>5 m) | 8 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 70 | Closed (>40%) needleleaved evergreen forest (>5 m) | 1,6 | 0.033 | 0.250 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 |
| 90 | Open (15%–40%) needleleaved deciduous or evergreen forest (>5 m) | 1,3,5,8 | 0.038 | 0.125 | 0.038 | 0.125 | 0.038 | 0.125 | 0.038 | 0.038 | 0.125 | 0.038 | 0.038 | 0.038 | 0.038 | 0.038 | 0.038 | 0.038 | 0.038 |
| 100 | Closed to open (>15%) mixed broadleaved and needleleaved forest (>5 m) | 5 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 110 | Mosaic forest or shrubland (50%–70%)/grassland (20%–50%) | 6 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 120 | Mosaic grassland (50%–70%)/forest or shrubland (20%–50%) | 7 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 130 | Closed to open (>15%) (broadleaved or needleleaved, evergreen or deciduous) shrubland (<5 m) | 6,9 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 |
| 140 | Closed to open (>15%) herbaceous vegetation (grassland, savannas or lichens/mosses) | 7,10 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 |
| 150 | Sparse (<15%) vegetation | 7,16 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 |
| 160 | Closed to open (>15%) broadleaved forest regularly flooded (semi-permanently or temporarily)-Fresh or brackish water | 2 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 170 | Closed (>40%) broadleaved forest or shrubland permanently flooded-Saline or brackish water | 11 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 180 | Closed to open (>15%) grassland or woody vegetation on regularly flooded or waterlogged soil-Fresh, brackish or saline water | 11 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 |
| 190 | Artificial surfaces and associated areas (Urban areas >50%) | 13 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 | 0.031 | 0.031 |
| 200 | Bare areas | 16 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 |
| 210 | Water bodies | 0,15 | 0.250 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.250 | 0.033 |
| 220 | Permanent snow and ice | 15 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.031 | 0.500 | 0.031 |
| 230 | No data (burnt areas, clouds, …) | - | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 |
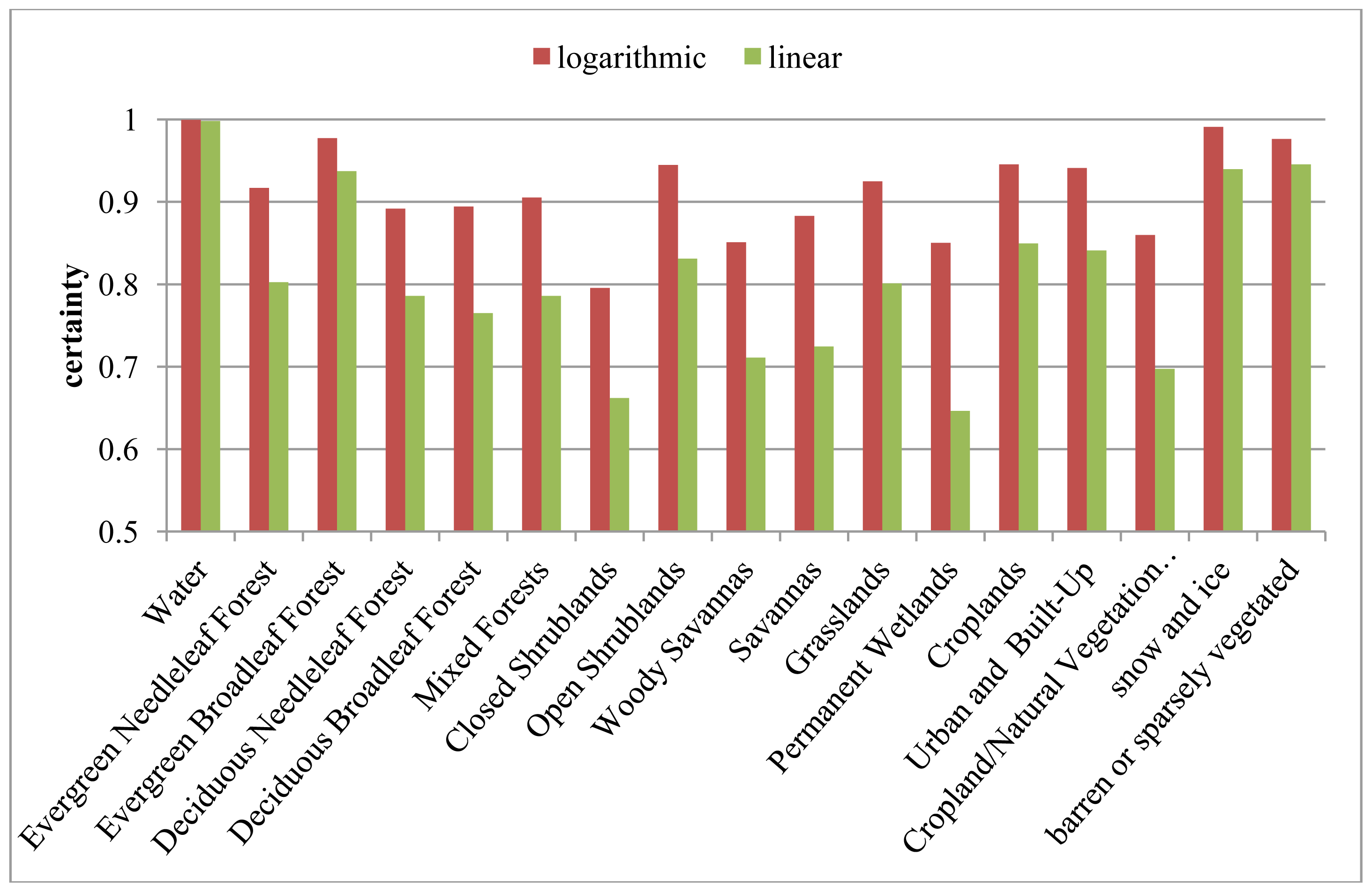
| IGBP | Description | Linear | Logarithmic | Relative Difference |
|---|---|---|---|---|
| 0 | Water | 67.83% | 67.35% | −0.71% |
| 1 | Evergreen Needleleaf Forest | 1.33% | 1.30% | −2.24% |
| 2 | Evergreen Broadleaf Forest | 1.82% | 1.86% | 2.11% |
| 3 | Deciduous Needleleaf Forest | 0.67% | 0.66% | −1.92% |
| 4 | Deciduous Broadleaf Forest | 0.58% | 0.56% | −4.07% |
| 5 | Mixed Forests | 1.18% | 1.26% | 6.63% |
| 6 | Closed Shrublands | 1.22% | 0.66% | −46.09% |
| 7 | Open Shrublands | 4.00% | 4.42% | 10.65% |
| 8 | Woody Savannas | 1.04% | 1.05% | 0.96% |
| 9 | Savannas | 0.98% | 1.02% | 4.32% |
| 10 | Grasslands | 1.98% | 2.06% | 4.05% |
| 11 | Permanent Wetlands | 0.37% | 0.32% | −11.59% |
| 12 | Croplands | 2.27% | 2.45% | 7.98% |
| 13 | Urban and Built-Up | 0.06% | 0.06% | 0.30% |
| 14 | Cropland/Natural Vegetation mosaic | 1.32% | 1.14% | −13.41% |
| 15 | Snow and Ice | 10.58% | 10.89% | 2.92% |
| 16 | Barren or Sparsely Vegetated | 2.79% | 2.95% | 5.81% |
| Reference Data | GlobCover2005ref | GLC2000ref | STEP | VIIRS | Average |
|---|---|---|---|---|---|
| Land Cover Maps | |||||
| synGLC-linear | 66.56%/4 | 57.04%/3 | 60.88%/3 | 40.27%/4 | 56.19%/3.5 |
| synGLC-log | 66.8%/3 | 57.18%/2 | 62.68%/2 | 40.89%/3 | 56.89%/2.5 |
| GLC2000 | 68.13%/2 | 61.24%/1 | 52.74%/4 | 38.48%/5 | 55.14%/3.0 |
| GLCC | 57.19%/7 | 49.46%/5 | 41.42%/7 | 33.11%/7 | 45.3%/6.5 |
| GlobCover | 70.43%/1 | 56.55%/4 | 50.7%/5 | 41.13%/2 | 54.7%/3.0 |
| MCD12Q1 | 63%/5 | 49.41%/6 | 85.34%/1 | 46.28%/1 | 61.01%/3.25 |
| UMDLC | 59.54%/6 | 43.03%/7 | 46%/6 | 36.64%/6 | 46.3%/6.25 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Xu, G.; Zhang, H.; Chen, B.; Zhang, H.; Yan, J.; Chen, J.; Che, M.; Lin, X.; Dou, X. A Bayesian Based Method to Generate a Synergetic Land-Cover Map from Existing Land-Cover Products. Remote Sens. 2014, 6, 5589-5613. https://doi.org/10.3390/rs6065589
Xu G, Zhang H, Chen B, Zhang H, Yan J, Chen J, Che M, Lin X, Dou X. A Bayesian Based Method to Generate a Synergetic Land-Cover Map from Existing Land-Cover Products. Remote Sensing. 2014; 6(6):5589-5613. https://doi.org/10.3390/rs6065589
Chicago/Turabian StyleXu, Guang, Hairong Zhang, Baozhang Chen, Huifang Zhang, Jianwu Yan, Jing Chen, Mingliang Che, Xiaofeng Lin, and Xianming Dou. 2014. "A Bayesian Based Method to Generate a Synergetic Land-Cover Map from Existing Land-Cover Products" Remote Sensing 6, no. 6: 5589-5613. https://doi.org/10.3390/rs6065589
APA StyleXu, G., Zhang, H., Chen, B., Zhang, H., Yan, J., Chen, J., Che, M., Lin, X., & Dou, X. (2014). A Bayesian Based Method to Generate a Synergetic Land-Cover Map from Existing Land-Cover Products. Remote Sensing, 6(6), 5589-5613. https://doi.org/10.3390/rs6065589