2.1. Study Area and Datasets
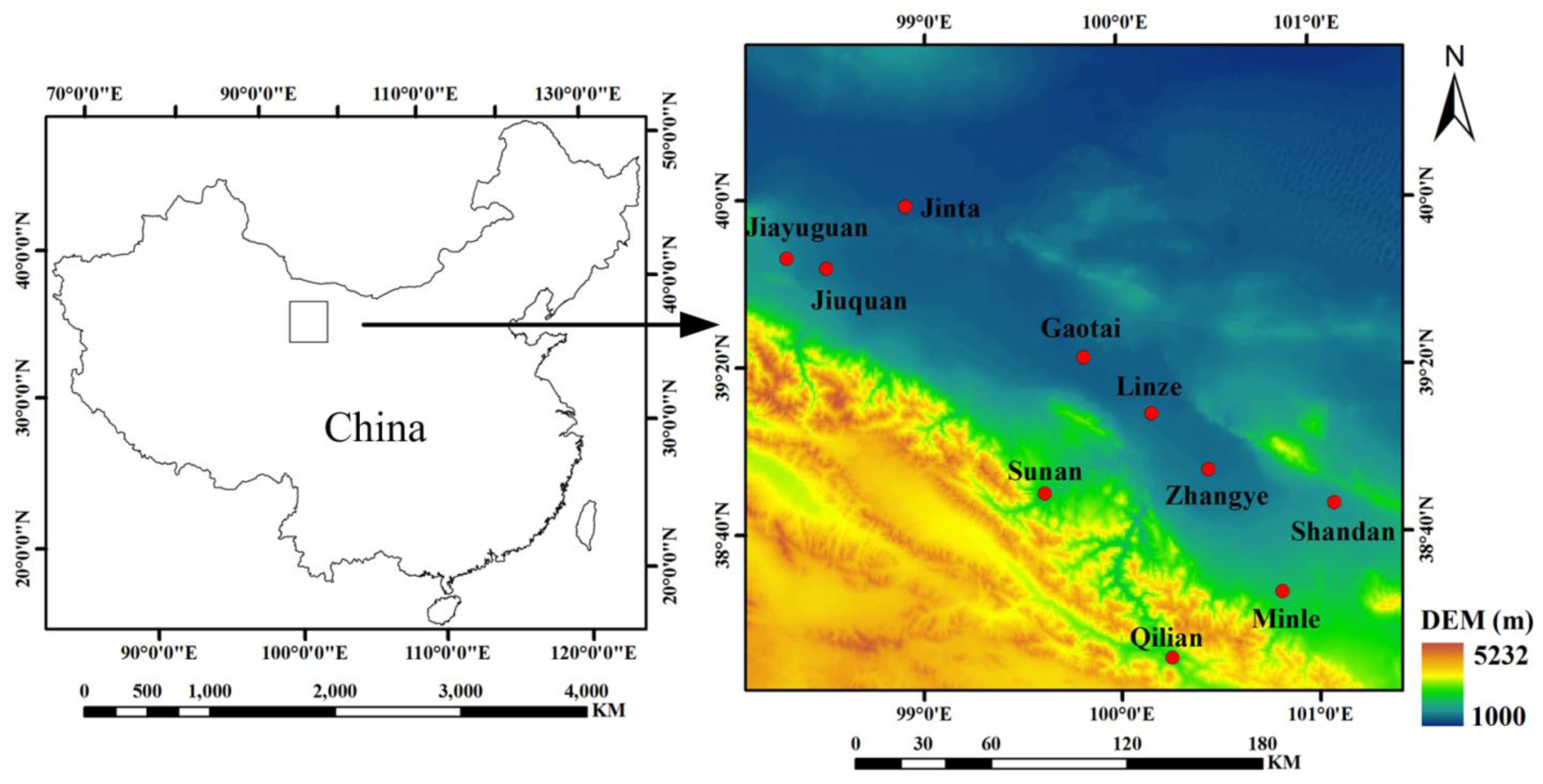
The study area, the Heihe River basin, is located in northwestern China (
Figure 1). The Heihe River is the most important inland river in northwestern China. The Heihe River basin has an elevation higher than 1000 m and an arid climate with low atmospheric water vapor content [
34]. It is one of the most arid regions in China. The land surface processes in the study area are important components of many field experiments, such as the HEIhe basin Field Experiment (HEIFE) [
35]. The Watershed Allied Telemetry Experimental Research (WATER), which was a simultaneous remote sensing and ground-based experiment, was conducted in the study area from March to July of 2008. The overall objectives of this field experiment were to improve the understanding of hydrological and related ecological processes on a catchment scale, to accumulate a comprehensive dataset for the development of watershed science, and to promote the applicability of quantitative remote sensing in watershed science studies [
36].
Atmospheric profiles are necessary to investigate the radiative transfer between the Sun-target-sensor paths. Eighteen radiosonde profiles under clear-sky conditions were collected in the study area during the field experiment from March to July of 2008. These radiosonde profiles covered elevations ranging from 1360 m to 3414 m and atmospheric water vapor contents ranging from 0.098 g·cm
−2 to 1.706 g·cm
−2. The March radiosonde profiles represented dry and cold weather, whereas those acquired in July represented relatively humid and warm weather. Outputs of the Global Data Assimilation System (GDAS) were also collected for examining the atmospheric parameters in the study area. GDAS is one of the operational systems of the National Weather Service’s National Center for Environmental Prediction (NCEP). It is run four times per day (at 00, 06, 12, and 18 UTC), and the outputs include geopotential height, atmospheric temperature at 26 fixed pressure levels and relative humidity at 21 levels. The output is in GRIB (GRIdded Binary) format and extends from (0W, 90°S) to (1°W, 90°N), with 1° × 1° spatial resolution. Publications have reported that GDAS outputs yield advantages for applications such as atmospheric correction of thermal infrared remote sensing images [
37], at-sensor signal simulation with radiative transfer models [
38], and calibration of thermal remote sensors [
39]. Four grids located in the study area, including (100°E, 38°N), (100°E, 39°N), (98°E, 40°N), and (99°E, 40°N), were selected to extract the atmospheric profiles. The temporal coverage of the extracted GDAS atmospheric profiles spans January to December 2008. Finally, 422 GDAS atmospheric profiles under clear-sky conditions were extracted to establish the prior knowledge database of the atmospheric state in the study area.
In situ LST measurements were collected near the Biandukou site (location: 100.97°E, 38.27°N; elevation: 2690 m). The land surface at the this site was homogenous during the field experiment, and the dominating land cover type was bare cropland covered by soil and sparse barley straws, as well as some meadows with dry grasses. Simultaneous filed measurements were conducted on 14 March 2008, for comparing the measured LSTs with the LSTs provided by the Terra and Aqua MODIS. Two key areas were selected to collect the ground truths of the LSTs. The locations of these two key areas were (100.98°E, 38.22°N) and (100.97°E, 38.26°N). Both of these two key areas were homogenous with bare soil. The key areas and their surrounding areas were homogenous. The size of each key area was set at 120 by 120 m, and each key area was divided into 16 sub-areas with 30 by 30 m sizes.
During the daytime on 14 March 2008, the overpassing times of the Terra and Aqua satellites were 04:30 and 06:10 (UTC). While the satellites were overpassing, the radiative temperature at the center of each sub-area was measured using Testo handheld infrared thermometers (IRT). The wavelength range of this instrument is 8 μm to 14 μm. The temperature range is −35.0 °C to 950.0 °C, and the precision is ±0.75 °C in the temperature range of −35.0 °C to 75.0 °C. Next, the radiative temperatures within a key area were averaged to denote the radiative temperature of the key area. The measured surface radiative temperatures with IRT were converted to the surface temperatures after correcting the broadband emissivity and atmospheric influences. Due to the lack of instruments for measuring the surface emissivities, the broadband emissivity of bare soil was assumed to be 0.950. Details about the conversion of radiative temperatures to surface temperatures can be found in [
40].
2.2. Regression Models for Atmospheric Parameters
The construction of this method involves three stages. In the first stage, the radiative transfer equations of MODIS channels 31 and 32 are simplified. In the second stage, the GDAS atmospheric profiles are used to simulate channel-integrated atmospheric parameters in MODIS channels 31 and 32 based on the MODTRAN4 code [
41]. Regression models that describe the relationships between these parameters are developed. In the third stage, new radiative transfer equations are established by substituting the regression models into the simplified radiative transfer equations. The LST is calculated with the genetic algorithm through iteration and optimization processes.
The radiative transfer equation (RTE) in the thermal infrared range is based on the following assumptions [
3,
42]: (1) the atmosphere is at local thermodynamic equilibrium; (2) no scattering occurs, and thus only cloud-free and non-hazy conditions are considered; and (3) the target is a Lambertian surface. Assuming that the land is a Lambertian surface in the thermal infrared range, the radiative transfer process from the ground to the remote sensor can be described as
Equation (1) [
43]:
where λ is the wavelength; Lλ is the TOA radiance; ɛλ is the surface emissivity; τλ is the total transmittance of the atmosphere; B(λ, Ts) is the radiance emitted by a blackbody at temperature Ts; and
and
are the atmospheric downwelling and upwelling radiance, respectively.
B(
λ,
Ts) can be calculated using Planck’s function, but deriving an operative expression of the temperature is complex, and the function should be simplified. Applying Taylor’s approximation of radiance around a certain temperature value or linearization is a commonly used method [
20,
44]. We calculated the channel-integrated radiances of MODIS channels 31 and 32 in the temperature range of 250.0 K to 340.0 K, with a temperature increment of 0.5 K, according to the variability of LST in the study area. Then, the relationships between temperature and radiance in these two thermal channels were investigated. A significant linear relationship was found between the radiance and the temperature. Six linear functions are proposed to replace Planck’s functions of MODIS channels 31 and 32 in three temperature ranges. These linear functions follow the general form:
where
i = 31, 32;
Bi is the radiance in channel
i; T is temperature; and
ai and
bi are coefficients. The values
ai,
bi, and the parameters of regression analysis are listed in
Table 2.
Equation (2) can also be extended to other areas because the radiance only depends on the temperature and the effective wavelength of the thermal channel.
In
Equation (1), the atmospheric upwelling radiance
is usually computed as [
45]:
where
Z is the altitude of the remote sensor;
Tz is the atmospheric temperature at altitude
z; and
τλ(
θ,
z,
Z) is the upwelling atmospheric transmittance from altitude
z to the sensor height
Z. After employing the mean value theorem to express the upwelling radiance,
can be expressed as [
46]:
where Ta is the effective mean atmospheric temperature.
With a similar simplification,
can be calculated as:
where
is the average temperature of the atmospheric downwelling radiance. Qin
et al. (2001) concluded that using
Ta to replace
in
Equation (5) does not have much influence on the accuracy of the retrieved LST [
46]. Therefore, it is reasonable to use
replace
. Consequently, the channel-integrated thermal radiances acquired by MODIS channels 31 and 32 at TOA can be described as follows:
The parameters in
Equation (6) have the same meanings as those in
Equation (1), and the subscript
i means that the parameters are for MODIS channels 31 or 32. According to the correlations between atmospheric radiations in adjacent thermal channels of a sensor, it is reasonable to assume that the atmospheric parameters, including
τ31,
,
τ32, and
, can be expressed as functions of a single parameter. Therefore, radiative transfer simulations are conducted to analyze the relationships between these atmospheric parameters. The extracted atmospheric profiles from the described GDAS datasets are put into the MODTRAN4 code to simulate the TOA radiances and other atmospheric parameters. It should be noted that the altitude, pressure, air temperature, and humidity at each layer of each atmospheric profile are used here. The radiative transfer simulations follow these conditions: (1) the MODTRAN4 code is executed in the thermal radiance mode; (2) the sensor view zenith angles in MODTRAN4 are set to range from 0° to 60° in 5° increments to cover the view angles of MODIS; and (3) the sky is clear, and the visibility is 23 km. The water vapor content along the atmospheric path can be extracted from MODTRAN4 outputs. The simulated parameters are converted to the channel-integrated values following [
47]:
where <x> is the channel-integrated value of the parameter x; λmin and λmax are the lower and upper wavelengths of the corresponding channels; x(λ) is the value of parameter x at wavelength λ; and f(λ) is the spectral response function.
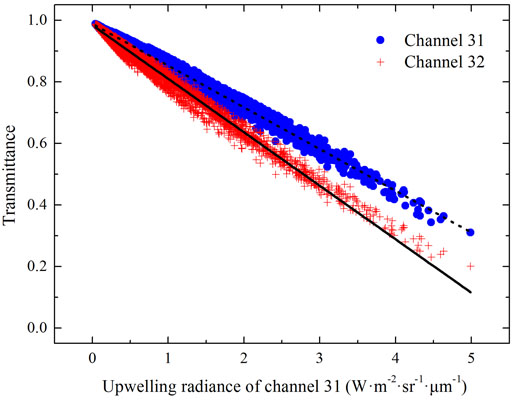
In total, 5486 samples covering 13 zenith angles for all GDAS atmospheric profiles are used to analyze the relationships between
τ31,
τ32,
and
. The scatter plots between
and the other three parameters are displayed in
Figure 2. Regression analysis reveals that
τ31 and
τ32 can be linearly parameterized by
with sufficient accuracy, and
can be estimated by
with a quadric function. The adjusted
R2 values used to establish the regressions between
τ31,
τ32,
and
are 0.990, 0.988, and 1.0, respectively. All the correlations are significant at the 0.001 probability level. The formula is listed below:
We use the eighteen radiosonde profiles collected during the field experiment to quantify the uncertainties of
Equation (8). The simulated
of all the radiosonde profiles based on the MODTRAN4 code are used to calculate
τ31,
τ32 and
following
Equation (8). Statistics on the errors of the calculated values, including the error ranges, standard deviations of the error and absolute error, mean absolute errors (MAEs), and root-mean-square errors (RMSEs), are presented in
Table 3. Based on
Table 3, it can be concluded that the regression models are highly accurate.
Table 3 also demonstrates that the calculated
τ32 has a slightly larger error than
τ31 does because MODIS channel 32 suffers stronger significant atmospheric influences than channel 31 does.
2.3. Determination of LST with a Genetic Algorithm
The genetic algorithm (GA) is a technique for searching and optimizing based on selection and natural genetics [
48]. The basic principle of the GA is similar to natural selection and inheritance during biological evolution. It begins with a population that contains potential solutions. Then, an objective function is used to assess each potential solution. The solutions with good abilities are selected and inherited by the next generation. The other solutions are changed by mutation or crossover. The new potential solutions are assessed again with the objective function. The iteration process stops when the objective function reaches the defined threshold or the iteration time exceeds a pre-defined value. Compared with other optimization algorithms, the GA has a good ability for global optimization and does not trend to a local solution. The GA has a high probability of finding the global optimal solution even when the objective function has noise [
49].
The GA can resolve ill-posed problems where there are more unknowns than equations. These ill-posed problems are common when retrieving parameters from remote sensing data. Xu
et al. (2001) and Zhuang
et al. (2001) reported instances where the GA was used to retrieve the component temperature from multi-angular thermal remote sensing images, and they concluded that the GA is a robust tool for estimating the component temperature [
50,
51]. Song and Zhao (2007) applied the GA to retrieve component temperature from MODIS data based on a linear spectral mixing model [
52]. The GA appears to be a good method for retrieving the LST from thermal remote sensing images.
In the case where LSEs in MODIS channels 31 and 32 have been obtained, there are two unknowns left after substituting the regression models into the two RTEs. The unknown parameters are LST and
. It is straightforward to obtain their analytical solutions. If the LST is calculated directly from the two RTEs, the errors and noises of the parameters (e.g., LSEs) and regression models may lead to an unacceptable error in the LST. To obtain physically meaningful estimations, the variation ranges of LST and
should be determined first to constrain the equation solutions. The GA is able to generate stable results and is not sensitive to the parameter errors or noises with the objective function [
49,
50]. Furthermore, the GA does not tend to generate local solutions for non-linear inversion problems. Although a disadvantage of using the GA for solving multi-dimensional problems is that it is time-consuming, the present problem that must be solved is positive definite, and the GA is efficient. Therefore, the GA algorithm in the Global Optimization Toolbox provided by the Matlab software is used here.
After replacing
τ31,
τ32, and
in the RTEs of MODIS channels 31 and 32 with
Equation (8), two new RTEs are obtained, as follows:
The configuration of GA for calculating LST from
Equations (9) and
(10) contains the following four steps:
- (1)
Defining the ranges of
and Ts: The ranges of
and Ts are defined as 0.01 W·m−2·sr−1·μm−1 to 3.0 W·m−2·sr−1·μm−1 and 250.0 K to 340.0 K, respectively. The previous two ranges are set according to the conditions of the study area and our investigations of the radiosonde profiles, GDAS profiles, and MODIS LST/emissivity products. On the one hand, the maximum value of
calculated based on all the in situ atmospheric radiosondes is 1.8821 W·m−2·sr−1·μm−1, appearing in the region with low elevation in summer. For all the GDAS profiles, over 98% of the simulated samples have
lower than 3.0 W·m−2·sr−1·μm−1, and the GDAS profiles are found to overestimate the water vapor contents. On the other hand, a range of 250.0 K to 340.0 K covers most possible conditions in the study area, according to our finding based on MODIS LST products of the study area.
- (2)
Defining the initial values of
Ts and
: Considering that the atmospheric effects in MODIS channel 32 are more significant than those in channel 31, the at-sensor brightness temperature of channel 31,
Tb31, is used as the initial value of
Ts. It is difficult to determine the initial value of
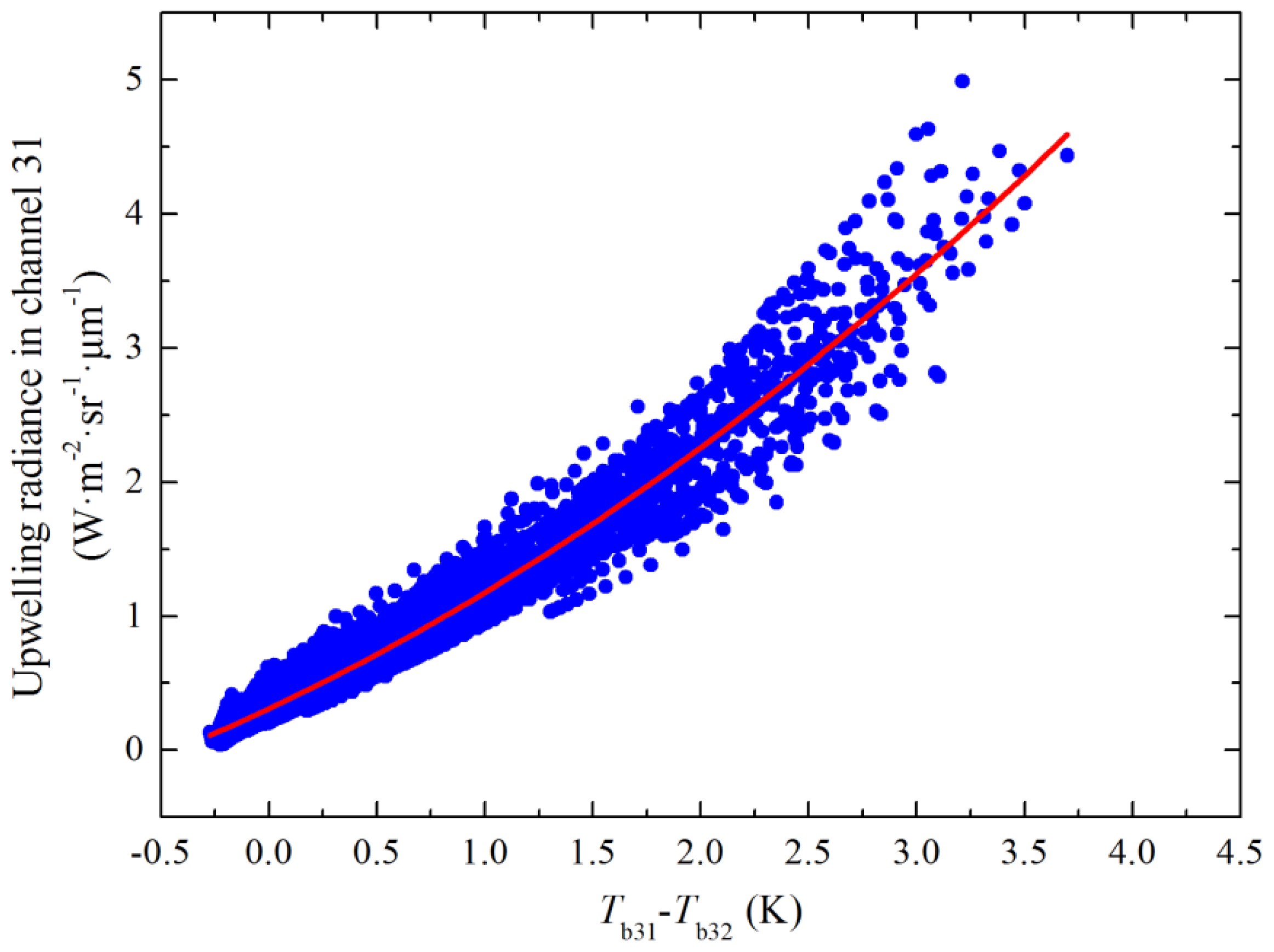
because there is no knowledge about the atmospheric condition. However, we find that there is a significant correlation between
and
Tb31–
Tb32 (see
Figure 3). Their relationship can be written as:
In total, 5486 samples are used to infer
Equation (11). The adjusted
R2 value of the regression is 0.964, and the correlation is significant at the 0.001 probability level, demonstrating that
Equation (11) is sufficiently accurate to calculate the initial value of
. Because of the searching and optimizing processes, the results generated by the GA are not significantly influenced by the initial values of the unknowns.
- (3)
Designing the objective function of GA: The estimated Ts and
should balance the radiative transfer equations. Therefore, the following function is used as the objective function to select appropriate individuals during iteration:
where the objective value, F, should be close to 0.
- (4)
Specifying the population size (Popsize), maximum number of generations (Maxgen), crossover fraction (Pc) and mutation fraction (Pm): These parameters may significantly influence the optimization of GA [
50–
52]. Determining these parameters is a repetitive process. A group of parameters derived from the simulation of a radiosonde profile, which were acquired at the Biandukou site on 5 July 2008, is used for an experiment. These parameters are an LST of 300.9 K, TOA spectral radiances of 9.3994 W·m
−2·sr
−1·μm
−1 and 8.7839 W·m
−2·sr
−1·μm
−1 for channels 31 and 32, respectively.
First, Popsize is set to range from 10 to 90, and the Maxgen is set to range from 20 to 180. These two ranges are set by following the trial and error process. The GA is run five times for each Popsize and Maxgen pair, and the MAE of the retrieved LSTs is calculated (
Table 4).
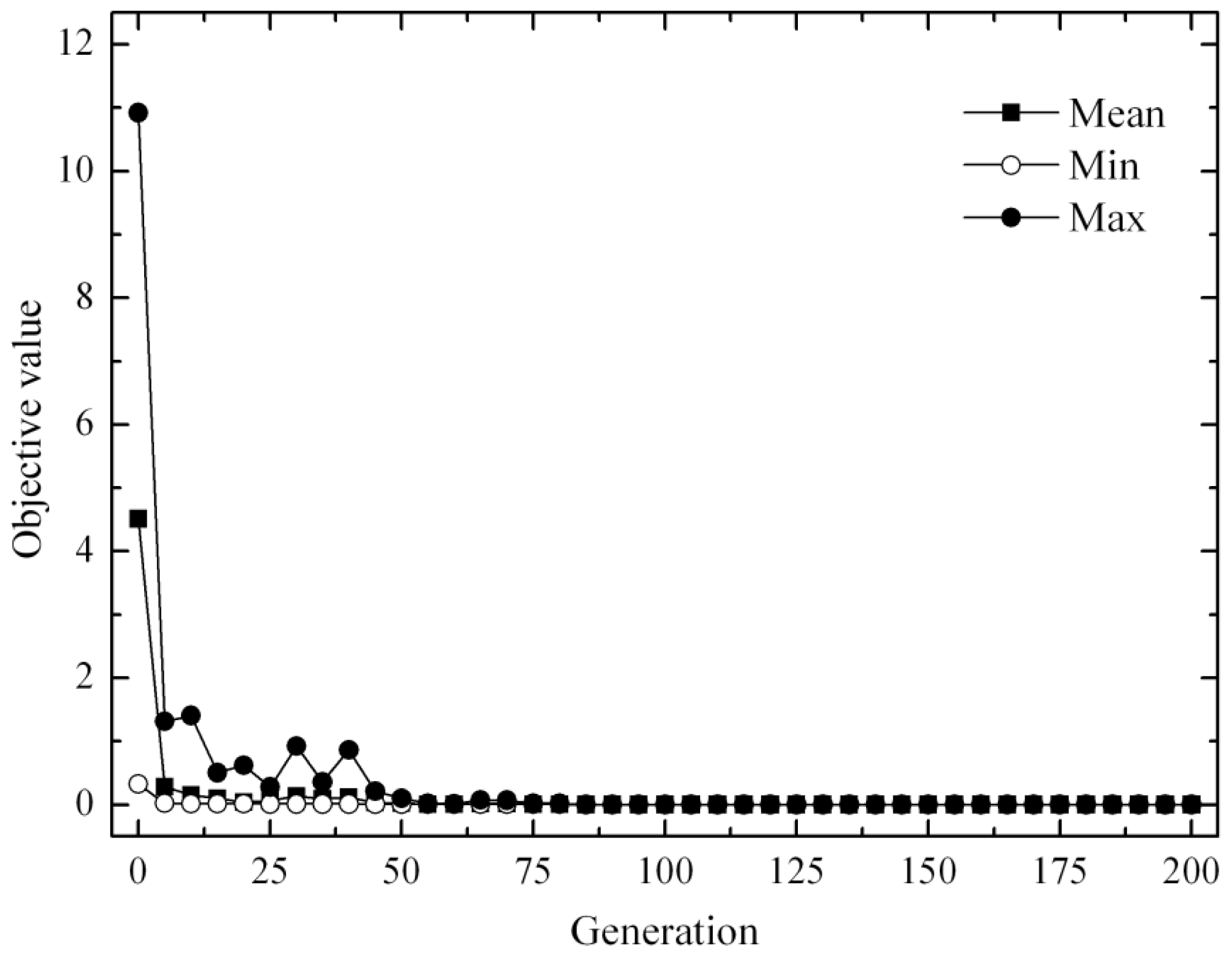
Figure 4 shows example minimum, mean, and maximum objective values of all individuals in each generation during the iteration process. The LST error decreases when Popsize increases. Setting Maxgen as 100 and Popsize as 50 is a good timesaving choice. The convergence becomes very stable after the maximum number of generations reaches 100.
Second, we examine the determination of the mutation fraction and crossover fraction (Pc) of the GA. The GA uses the mutation and crossover functions to produce new individuals at each generation. In this research, Pm is set as “adaptive feasible” for constrained minimization, which randomly generates adaptive directions with respect to the last successful or unsuccessful generation. Pc is commonly set at 0.4 to 0.9. A smaller value of Pc will limit the ability for an individual to mutate and find the global optimum, but a greater value will cause an unstable solution of the GA [
52]. We chose values for Pc ranging from 0.4 to 0.9 with an increment of 0.1 and tested the GA five times for each Pc value. The errors of the calculated LSTs are listed in
Table 5.
Table 5 shows that the LST errors are 0.3 when the Pc is 0.4 to 0.8. The LST error increases when Pc is 0.9. This phenomenon suggests that premature convergence occurs. The GA requires a relatively long time to converge when Pc is set to a smaller value. Pc is set to 0.8 in this research.