Daily Evaporative Fraction Parameterization Scheme Driven by Day–Night Differences in Surface Parameters: Improvement and Validation
Abstract
: In a previous study, a daily evaporative fraction (EF) parameterization scheme was derived based on day–night differences in surface temperature, air temperature, and net radiation. Considering the advantage that incoming solar radiation can be readily retrieved from remotely sensed data in comparison with surface net radiation, this study simplified the daily EF parameterization scheme using incoming solar radiation as an input. Daily EF estimates from the simplified scheme were nearly equivalent to the results from the original scheme. In situ measurements from six Ameriflux sites with different land covers were used to validate the new simplified EF parameterization scheme. Results showed that daily EF estimates for clear skies were consistent with the in situ EF corrected by the residual energy method, showing a coefficient of determination of 0.586 and a root mean square error of 0.152. Similar results were also obtained for partly clear sky conditions. The non-closure of the measured energy and heat fluxes and the uncertainty in determining fractional vegetation cover were likely to cause discrepancies in estimated daily EF and measured counterparts. The daily EF estimates of different land covers indicate that the constant coefficients in the simplified EF parameterization scheme are not strongly site-specific.1. Introduction
Studies on surface energy and water budgets require accurate evapotranspiration (ET) information at large spatial scales [1,2]. Satellite-based data can be used for the ET estimation [3,4]. Physical ET models based on remotely sensed data (e.g., one-source models and two-source models [5–11]) require ground-based measurements. This hinders the application of these models particularly to ungauged areas with few ground-based measurements. Therefore, it is advantageous to develop ET models that completely depend on surface parameters/variables retrieved from remote sensing. Surface parameters/variables that can be extracted from remotely sensed data mainly include surface temperature, surface emissivity, albedo, vegetation indices, leaf area index, soil moisture, net radiation, solar radiation, and air temperature [12–22]. Some simple methods can estimate surface energy fluxes by directly using these remotely sensed surface parameters/variables (e.g., empirical equations and the triangle feature space [23–28]). However, the dependence of site and spatial domain is the main disadvantage of these methods [29,30]. In addition, these methods are mainly driven by remotely sensed surface variables from a one-time observation.
The temporal variation in remotely sensed parameters/variables contains important information on surface fluxes, and it has been shown to be insensitive to retrieval error from remote sensing [31–37]. Based on surface energy balance, the bulk heat transfer equation for sensible heat flux, and the assumption of fairly invariant evaporative fraction (EF) during the daytime, Lu et al. (2013) [38] derived a new parameterization scheme of directly estimating daily EF, which is parameterized as a function of temporal variations in surface temperature, air temperature, and net radiation. The input requirements can be easily met by remotely sensed data from the MODIS sensor and sensors onboard geostationary meteorological satellites. The parameterization scheme was applied to the Yucheng station in North China and encouraging results were obtained. Considering the relatively easy estimation of incoming solar radiation from remotely sensed data, this study will simplify the daily EF parameterization scheme using incoming solar radiation as an input. Details about the simplification will be presented in Section 2. To further clarify the potential ability of the simplified EF parameterization scheme and examine whether it is site-specific, ground-based measurements from Ameriflux sites with different vegetation types will be used to validate the EF estimates. Data and processing will be described in Section 3. Results and the uncertainties for EF estimates are analyzed in Section 4, and summaries and conclusions will be provided in Section 5.
2. Method
On the basis of the surface energy balance equation, surface latent heat flux (LE) at any time t in a day is expressed as follows:
The derivative of Equation (1) with respect to t is written as follows:
H is theoretically determined by aerodynamic temperature (Taero). Because Taero is not easily measured, surface radiative temperature (Ts) is frequently used to replace Taero for H estimates. By defining radiometric heat conductance (Prad) corresponding to Ts [39,40], H is expressed as follows:
Combining Equations (2) and (4), the following equation is derived:
From a study by Carlson et al. (1995) [23], Prad almost linearly varies with fractional vegetation coverage (fc). G is frequently assumed to be proportional to Rn, depending on fc [5]. On the basis of the assumptions of relatively invariant EF during the daytime and low evaporation at night [41,42], daily average EF can be substituted by an instantaneous EF during the daytime. As a result, daily EF is parameterized as [38]:
The variable dt in above equations is not required for a long period. It is generally universal that Ts, Ta, and Rn on cloud-free days vary linearly with time during the morning [31,33]. Therefore, the slope of the linear relationship can be used in Equation (6). Additionally, the day–night differences in Ts, Ta, and Rn can be also applied because the day–night differences in surface parameters are almost positively proportioned to their variations during the morning, i.e.,
Incoming solar radiation (Rg) is the main driving source of surface energy [43]. Figure 1 shows the relationships between Rn and Rg based on ALEX-simulated data and in situ measurements. It can be inferred that Rn is generally positively proportional to Rg with a coefficient of determination (R2) larger than 0.98. Therefore, ΔRn in Equation (7) can be further replaced by ΔRg but with different coefficients.
Using ΔRg as an input variable of Equation (7) can obviate the calculation for longwave radiation. Furthermore, estimating Rg from remotely sensed data is easier than estimating Rn. Another purpose for using ΔRg is that there is no incoming solar radiation at night, and only a one-time measurement of Rg in a day can meet the input requirements of Equation (7). Constant coefficients A, B, and C in Equation (7) corresponding to the input variable ΔRg are obtained using the ALEX-simulated data under different surface and atmospheric conditions. Daily EF is consequently expressed as follows:
3. Data and Processing
3.1. Study Sites
The input variables of Equation (8) can be obtained from remotely sensed data. Because there are numerous uncertainties in the processes of retrieving surface parameters/variables [44,45], the ground-based measurements from six Ameriflux sites with different land covers are used to validate the performance of the EF parameterization scheme of Equation (8). Among these stations, five stations (US-Ne2, US-Seg, US-SRC, US-Me6, and US-UMB) are located in the United States, and one (BR-Sa3) is located in Brazil. Land use and land cover at the stations include croplands (CRO), grasslands (GRA), open shrublands (OSH), evergreen needleleaf forests (ENF), deciduous broadleaf forests (DBF), and evergreen broadleaf forests (EBF), respectively (see Figure 3). The surface elevation varies from 234 to 1622 m, and the soil textures include deep silty clay loams, loamy sand, sandy loam, sandy lake deposits, and yellow dystrophic latosol. Basic information about these stations is listed in Table 1.
3.2. In situ Measurements
In situ measurements (meteorological variables, radiation data, and fluxes data from the eddy covariance (EC)) are collected from the Ameriflux network website [46] for the US-Ne2 station in 2011, the US-Seg station in 2010, the US-SRC station in 2011, the US-Me6 station in 2012, the US-UMB station in 2012, and the BR-Sa3 station in 2003. Collected Ta and Rg are directly used to drive the EF parameterization scheme of Equation (8). Rn, H, LE, and G are used to calculate the EC-measured daily EF and then to evaluate the EF estimates. The daily EF is calculated as the ratio of daily averaged LE to daily averaged Rn, neglecting the effect of G on EF at the daily scale. Ts is not directly measured at these sites. Incoming and outgoing longwave radiation (Ld and Lu) was used to calculate Ts by the equation of Ts = ((Lu − (1 − ɛ)Ld)/σɛ)1/4 with an assumption of 0.98 of surface emissivity (ɛ) in this study (σ is the Stefan–Boltzmann constant).
Averaged values of the main meteorological variables of precipitation, air temperature, and relative humidity in one year were calculated based on the collected data (see Table 2). Annual precipitation at six sites varied from 182 to 1461 mm, annual mean air temperature ranged from 8 to 25 °C, and annual mean relative humidity ranged from 33% to 79%. There were missing measurements because of sensor malfunction, power outages, unfavorable weather, and other unknown reasons. Gaps in the missing data at the US-Ne2, US-Seg, and US-Me6 stations were filled by adopting the approach that combines measurement, interpolation, and empirical data synthesis [47], whereas the missing flux data at the US-SRC, US-UMB, and BR-Sa3 stations were not filled. Days with missing flux data were not considered in this study. Data at the US-Seg, US-SRC, US-Me6, and BR-Sa3 stations were averaged at a 30-min interval, whereas data at the Us-Ne2 and US-UMB stations were within 1 h.
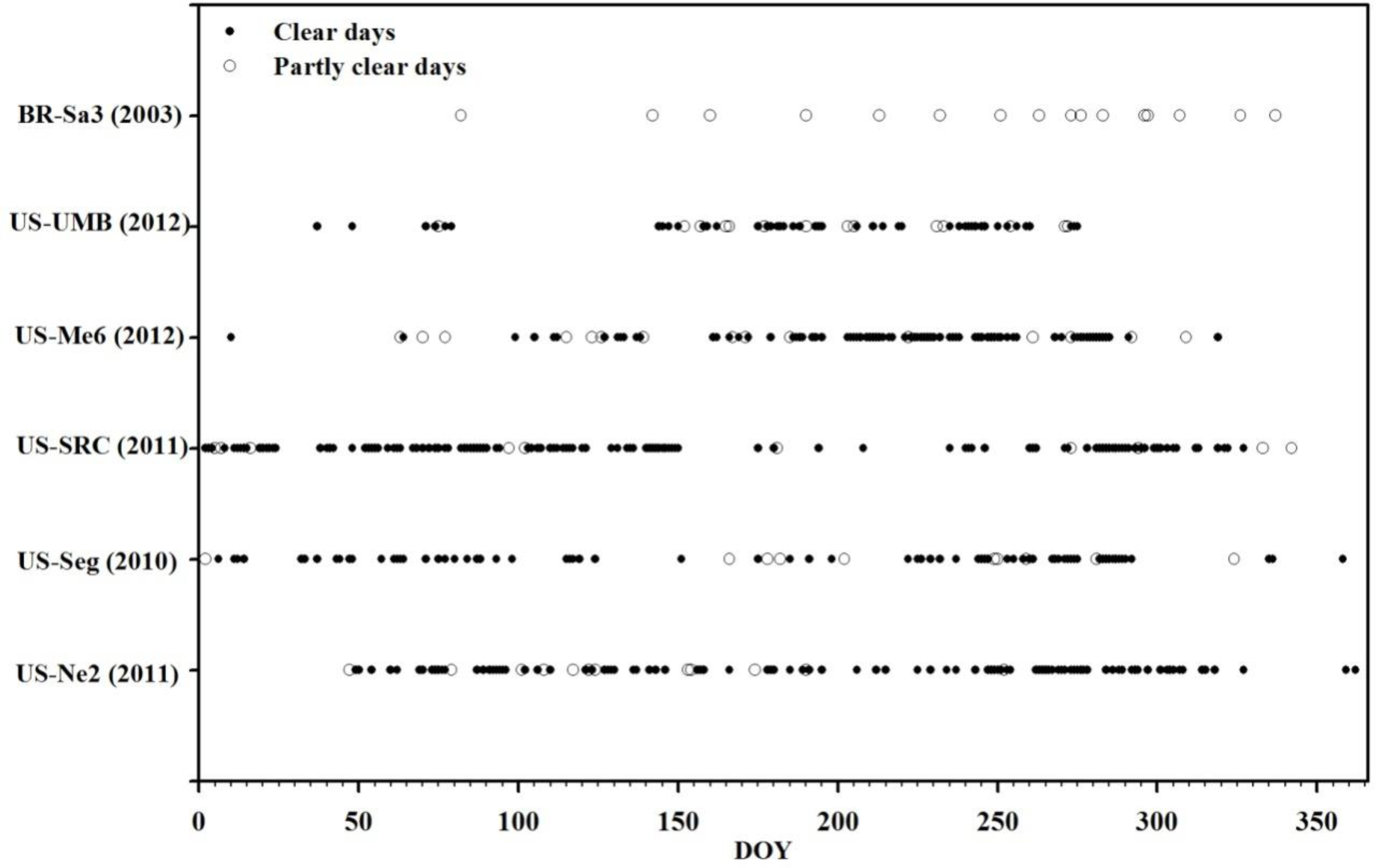
The EF parameterization scheme in Section 2 was derived under the assumption that EF was relatively invariant during the daytime, which most frequently occurs on cloud-free days with high radiation and humidity [41]. An automatic procedure based on Tang et al. (2013) [48] was developed to select available data for days in which EF was relatively invariant. Automated techniques were designed considering that (1) the maximum of Rg in a day occurs in the midday between 11:00 and 13:00; (2) Rg increases monotonically from sunrise to midday and decreases monotonically from midday to sunset; (3) days with daily (24 h) averaged Rg < 100 W/m2 because of low solar radiation, which may occur in winter or be caused by full cloud cover during a day, are excluded; (4) days with daily mean Ta < 0 due to low solar radiation and with ΔTs and ΔTa less than 0 that were probably influenced by nighttime cloud are excluded. Days having a measured daily EF < 0 and > 1 were also not utilized. A total of 408 cloud-free days were selected at these stations including 95 days in 2011 at the US-Ne2 station, 71 days in 2010 at the US-Seg station, 118 days in 2011 at the US-SRC station, 79 days in 2012 at the US-Me6 station, and 45 days in 2012 at the US-UMB station (see filled circles in Figure 4). Cloud-free days were not observed at the BR-Sa3 station in 2003 because of strong convective weather in the tropical region.
Because remote sensing observations represent a snapshot in time, it is not easy to judge whether an entire day is clear using remotely sensed data. Therefore, the performance of EF parameterization for partly clear days, i.e., no cloud cover during the afternoon here, will also be discussed in this study. For the selection of partly clear days, the automatic procedure for judging clear days is equally applicable but not to regard the monotonic increase from sunrise to midday. A total of 77 partly clear days (marked by open circles in Figure 4) were selected including 12, 10, 10, 15, 14, 16 partly clear days at the US-Ne2 station, at the US-Seg station, at the US-SRC station, at the US-Me6 station, at the US-UMB station, and at the BR-Sa3 station, respectively.
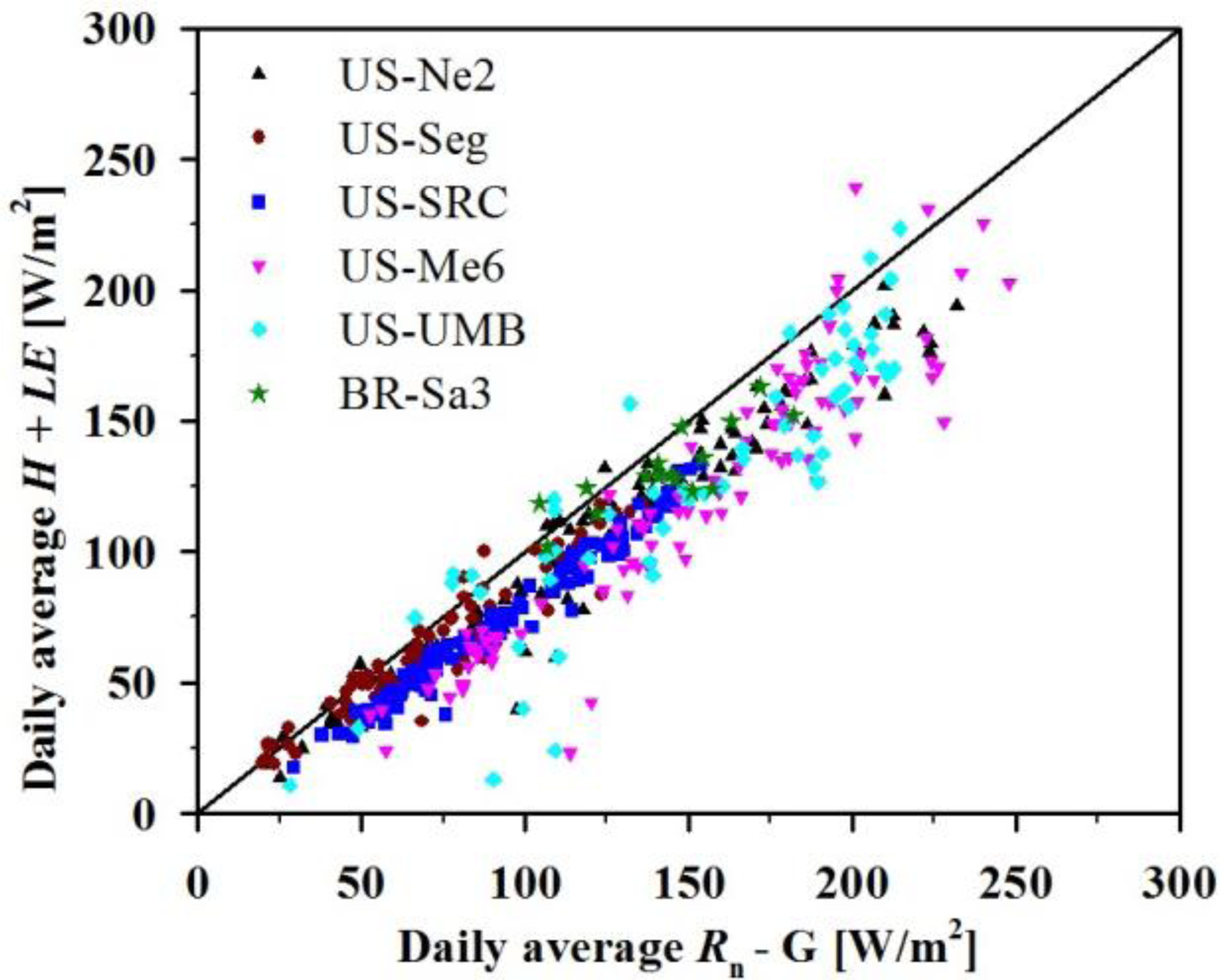
The energy balance non-closure in EC-based measurements was frequently reported in many previous studies [49]. As shown in Figure 5, daily average H + LE are all less than daily average Rn − G for clear and partly clear skies at the six sites. The mean energy balance ratio (EBR) is ∼0.83, and the RMSE is ∼25 W/m2. For each site, the daily-scale statistics of energy balance closure of EC-based measurements including EBR, R2, RMSE, and BIAS are listed in Table 3. The most serious energy balance non-closure in EC-based measurements occurs at the US-Me6 station with a mean EBR of 0.78, and the RMSE between H + LE and Rn − G is 35.2 W/m2. At the BR-Sa3 station, the EC-measured daily average H + LE is closer to Rn − G with an EBR of 0.93. In general, the inconsistent source areas between radiation flux (Rn − G) and turbulent flux (H + LE), and neglecting some terms in surface energy balance equation such as storage heat in forest vegetation, the energy due to photosynthesis and advection, may be the main reasons for non-closure in the energy balance from EC-based measurements.
3.3. Fractional Vegetation Cover fc
Apart from the variables ΔTs, ΔTa, and ΔRg, fc is also required as an input for the EF parameterization scheme presented as Equation (8). Because of the lack of in situ measurements for vegetation cover, MOD13Q1 and MYD13Q1 products in the spatial resolution of 250 m, which provide the normalized difference vegetation index (NDVI) every 16 days, are combined to calculate fc every 8 days by linear mixture modeling [50], and computed using Equation (9):
4. Results and Discussions
4.1. Daily EF Estimates for Clear Skies and Partly Clear Skies
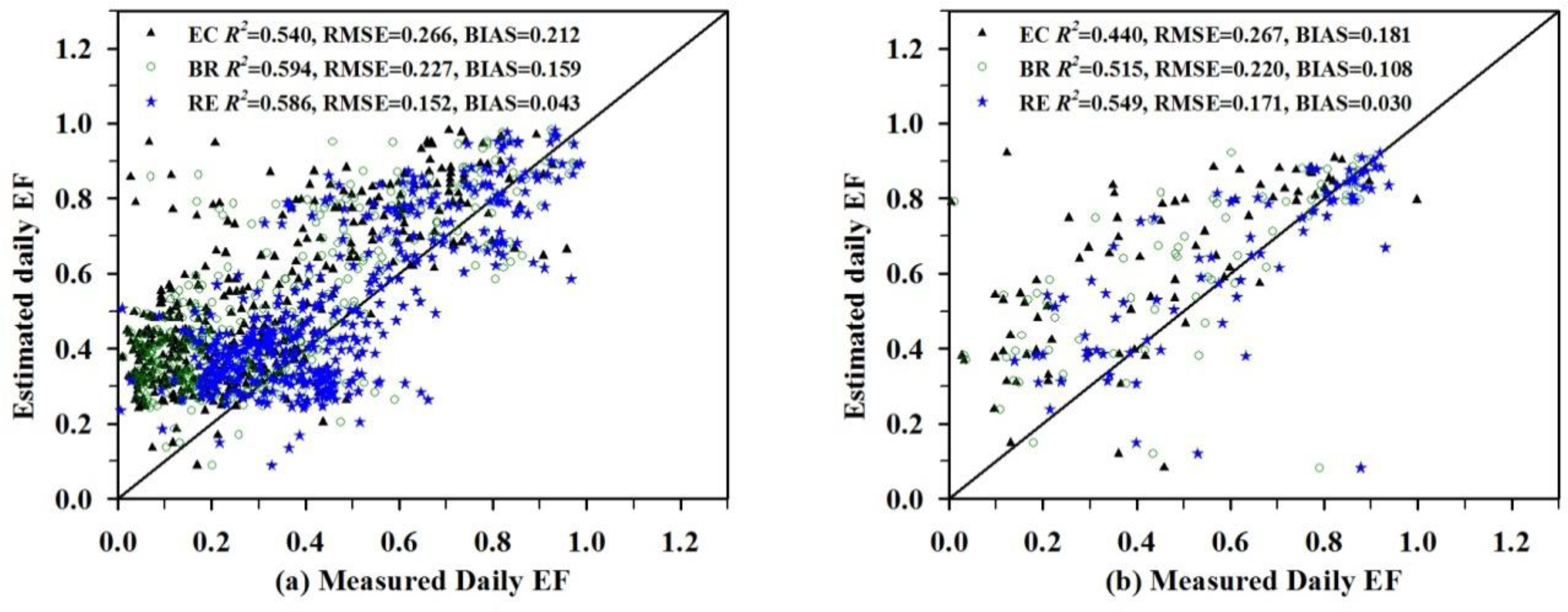
For 408 cloud-free days, with known ΔTs, ΔTa, and ΔRg from in situ measurements and fc from remotely sensed data, daily EF was estimated using Equation (8). Compared with EC-based measurements, daily EF was overestimated by 0.212 (see black triangles in Figure 6a). The overestimation was mainly caused by the underestimation of LE from EC measurements. Two methods were frequently used to correct EC-measured LE, i.e., the residual energy (RE) method and the Bowen ratio (BR) method [49]. The LE corrected by the RE method is equal to Rn − G − H with the assumption of relatively accurate measurements for H. The BR method is to assume that the non-closure of energy balance is not only caused by EC-measured LE but also by EC-measured H. The imbalance of energy is partitioned into H and LE according to the Bowen ratio, i.e., H_BR = H × (Rn − G) /(H + LE) and LE_BR = LE × (Rn − G)/(H + LE). The corrected LE is then used to calculate EC-measured daily EF. When the estimated EF from Equation (8) is compared with the BR/RE-corrected EF, the overestimation in EF is reduced (see green circles and blue symbols in Figure 6a, respectively). Daily EF estimates are closer to the RE-corrected EF, showing an RMSE of 0.152 and an R2 of 0.586. For selected 77 partly clear days, daily EF estimates from Equation (8) are also closer to the RE-corrected daily EF with an R2 of 0.549 and an RMSE of 0.171 (see Figure 6b). The result indicates that the EF parameterization scheme of Equation (8) can also be applied to estimate daily EF for partly clear skies, which mainly occur during the afternoon.
4.2. Uncertainty in EF Estimates Caused by fc
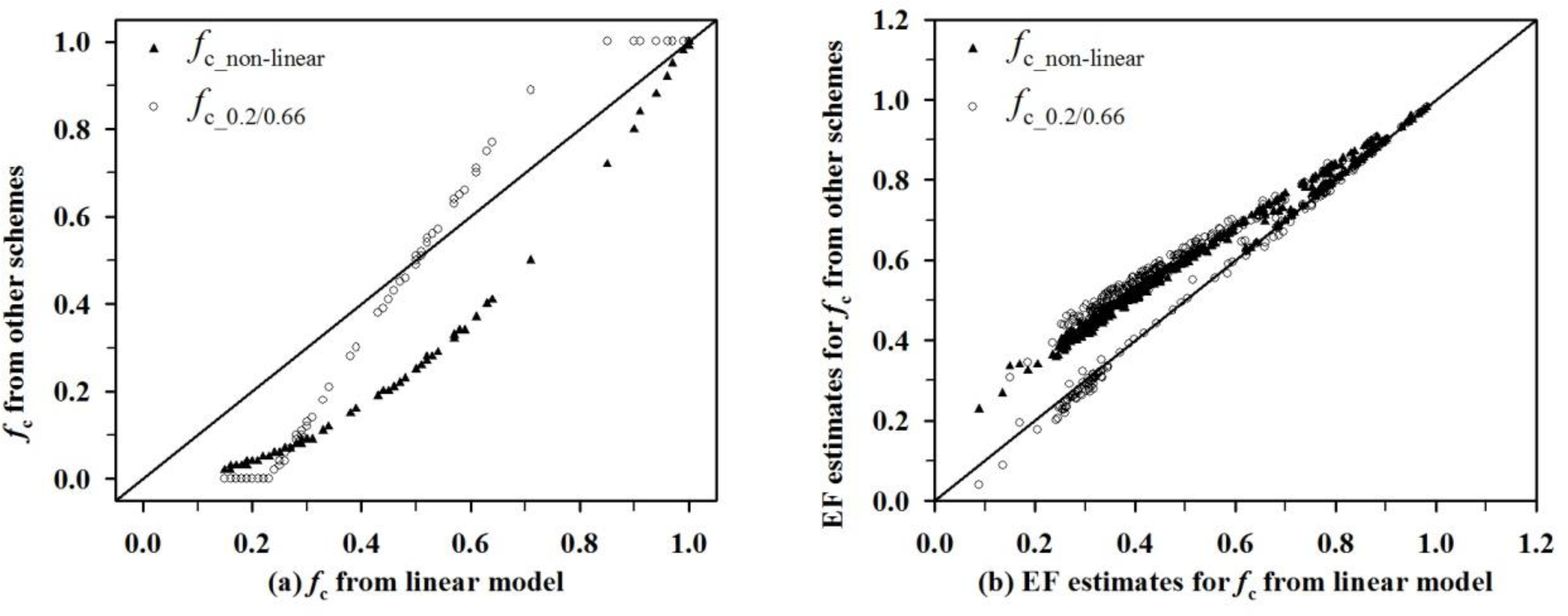
Uncertainty in determining input variable fc is also a source of error for daily EF estimates. Because fc is from the 16-day MODIS NDVI products at spatial resolution of 250 m, the different temporal and spatial scales between in situ measurements and the MODIS sensor could result in discrepancies between estimated daily EF and measured values. Sensitivity and error analysis for fc made by [38] concluded that 0.2 variations in fc can lead to approximately 0.1 mean variations in daily EF estimates. Different schemes for calculating fc and the assignments for NDVImax and NDVImin can produce different daily EF estimates (see Figure 7 and Table 4). fc from a non-linear model relating to NDVI [53], i.e., the square of equation (6), is less than that from the linear model with an RMSE of 0.183 (see filled triangles in Figure 7a). The underestimation in fc will cause the overestimation of daily EF according to the mathematical formulation of equation (8). Therefore, when fc from the non-linear model is used as an input for equation (8), daily EF estimates are greater than the results from the linear model with an RMSE of ∼0.1 (see filled triangles in Figure 7b). The larger bias is on the lower range of EF values, most of which are related to the condition of low fc. When the NDVImax and NDVImin in the linear model of Equation (6) are given as 0.66 and 0.2, respectively [51,53], fc is less than the values calculated by 0 and 0.86 as inputs for low fc. The opposite is true for high fc (see open circles in Figure 7a). For daily EF estimates, the RMSE caused by different assignments for NDVImax and NDVImin is also ∼0.1 (see open circles in Figure 7b). Those open circles deviating from the 1:1 line in Figure 7b correspond to low fc conditions, which are attributed to underestimation of fc. The larger bias also occurs at the lower EF condition. Therefore, daily EF estimation from Equation (8) is more sensitive to low fc, particularly for a low ET surface. The implicit assumption in Equation (8) that EF is relatively invariant during the daytime may be valid at this situation. Sensitivity of EF estimates to low ET surfaces is similar to the findings of Long et al. (2014) [54], where uncertainties among the ET products increased with aridity. A low ET surface is generally related to low soil water content. Further study is required to determine if soil water content can be used as an input parameter for Equation (8), and to find the best approach for parameterizing the EF equation.
4.3. Performance of EF Parameterization Scheme for Different Land Covers
The six stations used in this study correspond to six different land covers. Daily EF estimates for clear days and partly clear days were both considered in this section. The estimated EF for each station is compared with the RE-corrected EF, which is shown in Figure 8. Most of the absolute biases of daily EF estimates from Equation (8) for different vegetation types are less than 0.1, and the RMSEs are not more than 0.2. The estimated daily EF for CRO and OSH surfaces are correlated more strongly to the RE-corrected EF with the R2 of 0.640 and 0.650, respectively. For those surfaces covered by GRA, ENF, DBF, and EBF vegetation types, most results appear to be consistent with the RE-corrected EF, but some scatter points and relatively concentrated distribution of daily EF lead to the low R2. It seems that surface elevation and soil texture have no obvious contribution to the errors of EF estimates, i.e., the errors of EF estimates do not strongly depend on surface elevation and soil texture. Errors of daily EF estimates, daily averaged Rg, daily total precipitation, fc, and ΔTs − ΔTa of six stations are displayed in Figures 9 and 14 to further evaluate the reason for discrepancies.
- (1)
For the surface covered by CRO vegetation types, which is at the US-Ne2 station, a majority of the EF estimates are satisfied (see Figure 8a), and the errors vary from −0.2 to 0.2 (see Figure 9). Several large errors (>0.3) for EF estimates occur on DOY 75, 79, 128, 129, 293, 294, 359, and 362 (marked by red circles in Figure 9). The overestimation on DOY 75 may be mainly caused by the small value of ΔTs − ΔTa, which is mostly from measurement errors or is influenced by high wind speed (wind speed in the afternoon at approximately 13:30 on DOY 75 is ∼9 m/s). The error on DOY 79 could be attributed to the effect of clouds, and obvious low averaged Rg was observed on the day. The overestimation on DOY 128, 129, 293, and 294 may be due to the underestimation in fc. On DOY 359 and 362, low Rg that occurred in winter may be the main reason leading to the negative biases of EF estimates. This is because under the condition of low solar radiation, the implicit assumption of relatively invariant EF in Equation (8) is not well met. In general, under the condition of strong solar radiation, sufficient soil water content, dense vegetation cover, and low ΔTs − ΔTa, errors in EF estimates are relatively small.
- (2)
At the US-Seg station covered by GRA vegetation type, the climate is semi-arid, and the annual precipitation of the region is ∼230 mm, with a major portion (>50%) occurring in a summer rainy season, July to September [55]. In 2010, the total precipitation was only 182 mm (see Table 2). Therefore, EF from measurements at the US-Seg station was generally low, even less than 0.6 (see Figure 8b). Most of the EF estimates from Equation (8) generally fall into this range but with a slight overestimation. According to Equation (8), the underestimation in fc would lead to an overestimation in EF. Therefore, low fc of ∼0.2 in 2010 (may be underestimated) results in the overestimation of EF at the US-Seg station. On DOY 6, 336, and 358, larger errors may be caused by low solar radiation in winter (see Figure 10). The relatively concentrated distribution of daily EF at the US-Seg station in 2010, approximately from 0.2 to 0.6, may lead to the low R2 of 0.148 in Figure 8b.
- (3)
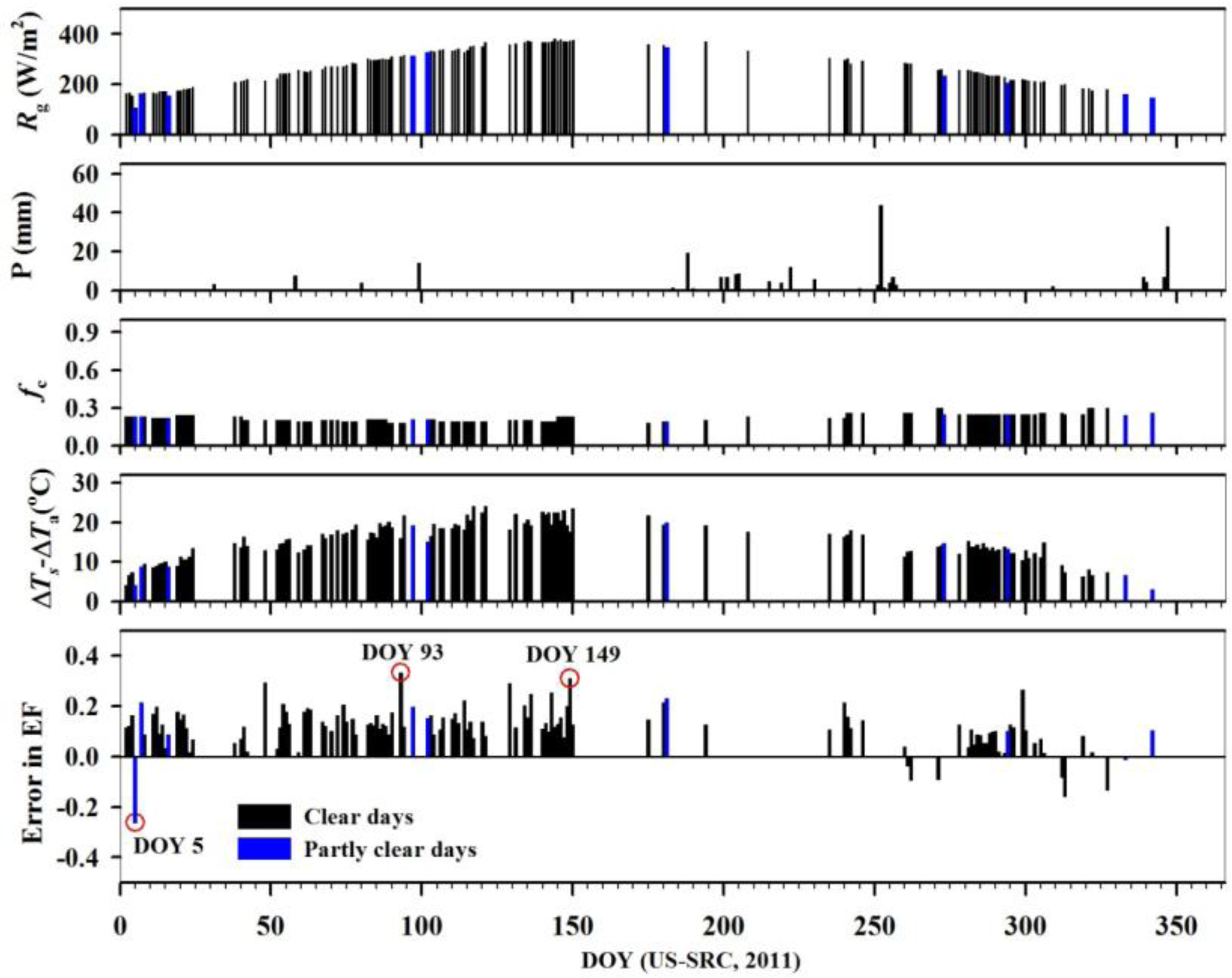
At the US-SRC station, most of daily EF values lie in the range of 0.1 to 0.6 (see Figure 8c). This may be related to low precipitation of ∼229 mm and low vegetation cover of ∼0.3 in 2011 (see Table 2 and Figure 11, respectively). Although the R2 between the estimated EF and measured values is high, there is an overestimation when measured EF is low (See Figure 8c). As analyzed in Section 4.2, Equation (8) is more sensitive to low fc for daily EF estimates, particularly for a low ET surface. It is difficult to accurately determine fc particularly at the sparse vegetation surface covered by OSH types. Therefore, the potential underestimation in fc may lead to the overestimation of daily EF at the US-SRC station. The obvious underestimation on DOY 5 was primarily because of the effect of clouds. The positive biases on DOY 93 and DOY 149 were from the relative low values of ΔTs − ΔTa probably due to high wind speed (wind speeds at approximately 13:30 on DOY 93 and DOY 149 were ∼6 m/s and 8 m/s, respectively). The energy balance non-closure in EC-based measurements at this station with the EBR of 0.79 (see Table 3) may have led to discrepancies between the estimated EF and measured values.
- (4)
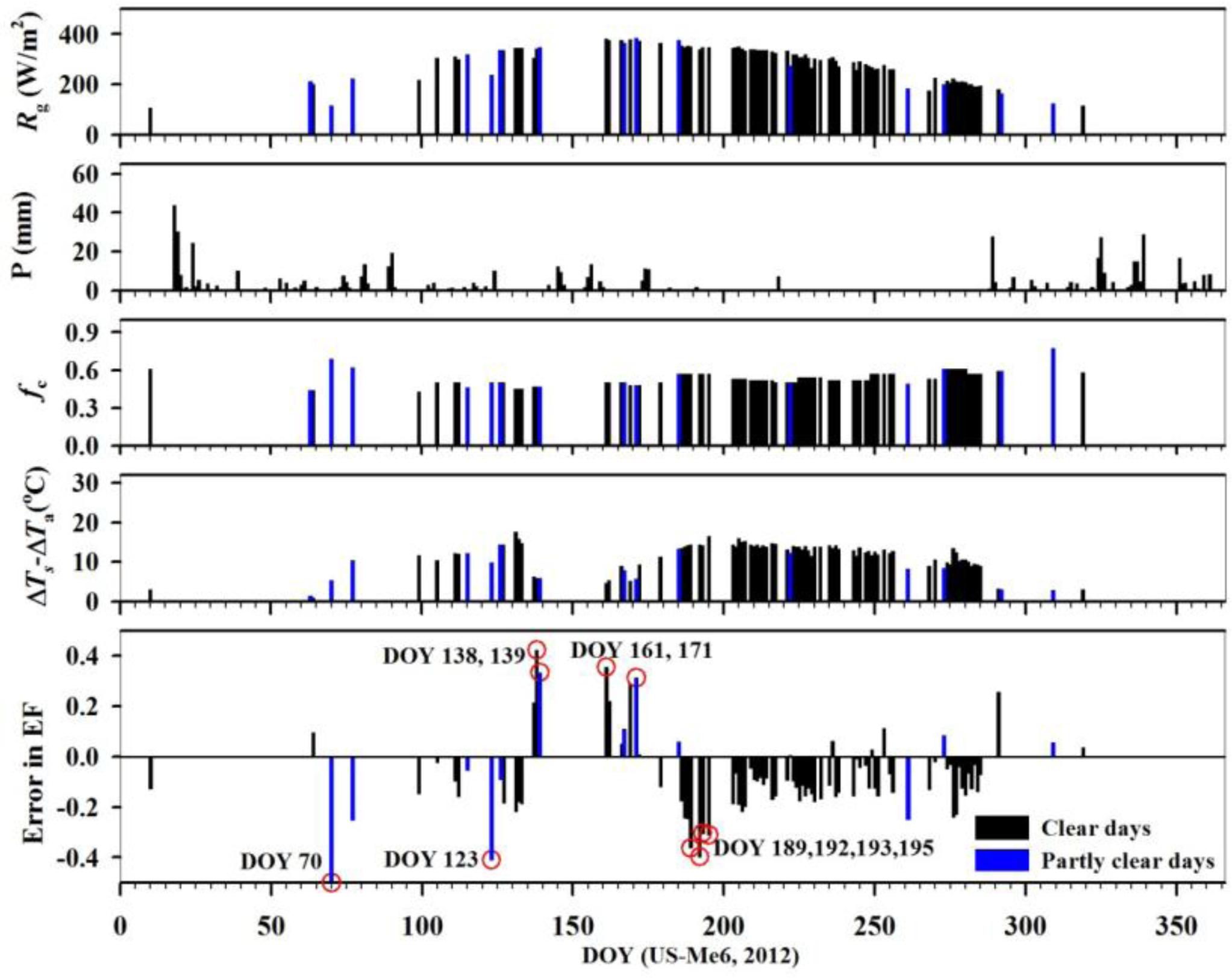
At the US-Me6 station covered by evergreen needleleaf forest, the simplified EF parameterization scheme gave the worst results with an RMSE of 0.192 (see Figure 8d), and most of the EF was underestimated (see Figure 12). This may be related to the local climate having warm dry summers and cool wet winters. Most precipitation (∼97% of annual rainfall) falls between October and June. The climatic condition of the warm dry summer and cool wet winter may not easily meet the assumption of Equation (8) because EF during the daytime is relatively invariant when there is high radiation and humidity. The underestimation of EF on DOY 70 and 123 and the overestimation on DOY 139 and 171 may result from clouds, whereas the overestimation on DOY 138 and 161 was evidently from low values of ΔTs − ΔTa due to high wind speed of ∼6 m/s. There was no precipitation on DOY 189, 192, 193, and 195, i.e., there was insufficient water in the soil, resulting in less ET on these days. The low EF from Equation (8) seems more reasonable; therefore, large negative biases on DOY 189, 192, 193, and 195 were attributed to the uncertainty in measurements or the errors from the RE correction method. As shown in Table 3, energy balance non-closure is most noticeable for EC-based measurements that occurred at this station.
- (5)
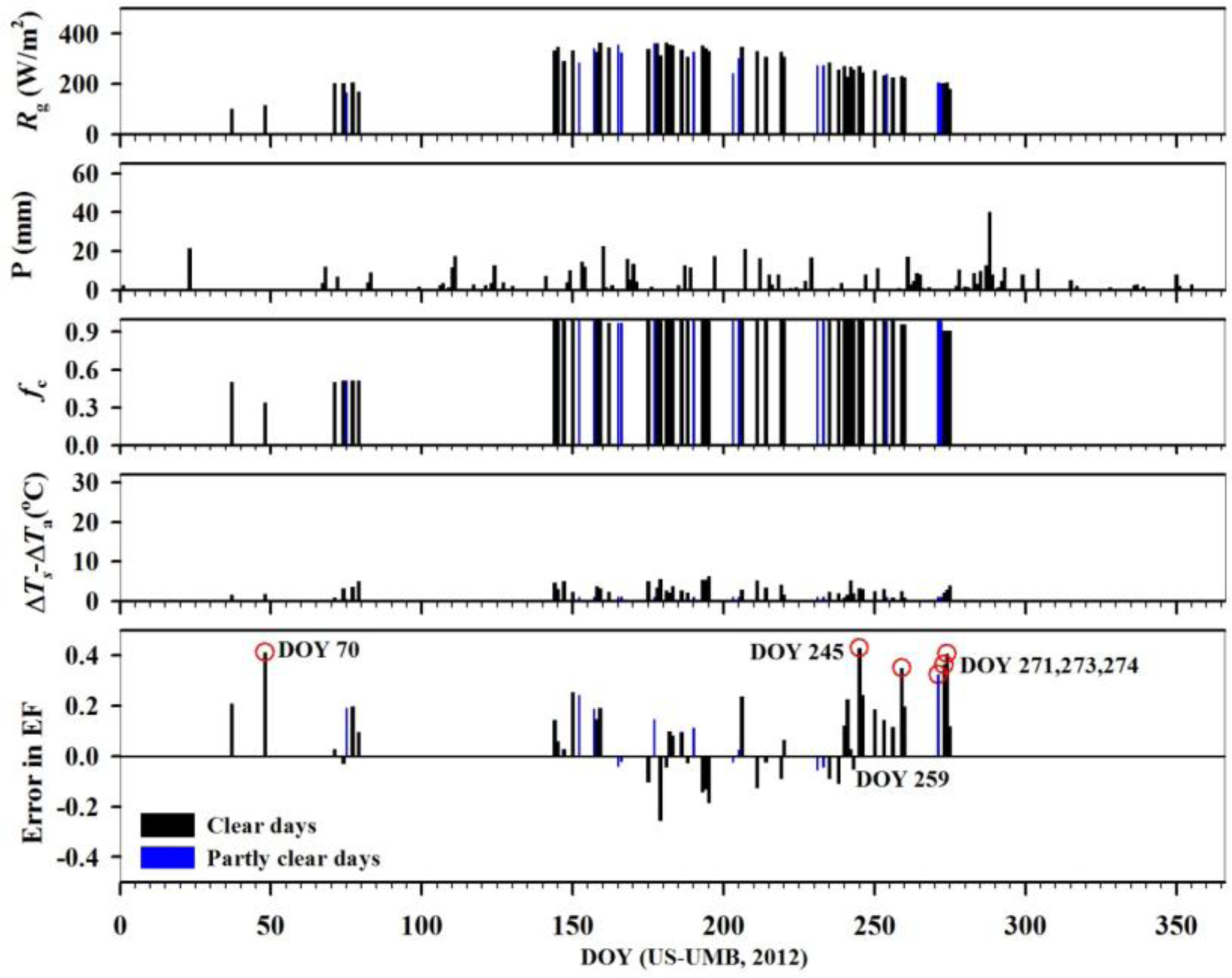
For the surface covered with deciduous broadleaf forest, daily EF mainly varies from 0.5 to 1 (see Figure 8e). This is related to the temperature and humidity climate at the US-UMB station with a mean temperature of 9 °C and total precipitation of 609 mm in 2012 (see Table 2). The overestimation on DOY 70 may be caused by low solar radiation and underestimation in fc (see Figure 13). During the summer days from June to September, the surface is completely covered by broadleaf vegetation, and soil moisture is ample. Under this condition, high ET value is more reasonable. Therefore, the large overestimation of EF on DOY 245, 259, 271, 273, and 274 may be from the uncertainty in measurements or errors for energy imbalance correction.
- (6)
The rainy tropical climate results in high EF of ∼0.8 at the BR-Sa3 station covered by evergreen broadleaf forest (EBF) during one year (see Figure 8f), being coincident with the estimated values close to 0.8. The concentrated distribution of EF during one year leads to low R2. Although the data displayed in Figure 14 occurred on partly clear days, there is not an obvious large bias for daily EF estimates at this station. The abundant rainfall and dense vegetation led to the low values of ΔTs − ΔTa and reduced the effects of clouds on EF estimates.
5. Conclusions
Lu et al. (2013) [38] developed a method for estimating daily evaporative fraction (EF) derived by day–night differences in surface temperature (Ts), air temperature (Ta), and net radiation (Rn). Because incoming solar radiation (Rg) can be readily estimated from remotely sensed data and there is a strong relationship between Rg and Rn, this study simplified the equation for estimating daily EF using Rg. The accuracy of the simplified EF parameterization scheme with ΔRg as an input is nearly equivalent to that with ΔRn as an input.
When in situ measurements from Ameriflux sites are used to drive the simplified parameterization scheme, daily EF estimates for clear days are closer to the RE-corrected daily EF with a coefficient of determination of 0.586 and a root mean square error of 0.152. It is not an easy thing to judge the sky condition using several remote sensing observations. However, the developed method can be used to estimate daily EF for partly clear days with the accuracy similar to that for clear sky condition. Errors from the correction for energy imbalance in EC-based measurements and the uncertainty in calculating fractional vegetation cover (fc) are the primary factors that lead to discrepancies between estimated and measured daily EF. Daily EF estimates from the simplified parameterization scheme are more sensitive to low fc conditions with low ET surfaces. Analyses of daily EF estimates at six vegetation surfaces indicate that the constant coefficients in the simplified EF parameterization scheme are not strongly site-specific, and could be applied to different land covers with reasonable accuracy if surface vegetation cover can be accurately determined. EF estimates are more accurate for regions that are characteristically warm and humid with strong solar radiation and adequate soil water content.
The input requirements of relatively few variables that can be easily obtained from remotely sensed data, i.e., the day–night difference in surface and air temperatures, can reduce uncertainties in EF estimates due to retrieval error from remote sensing. Only by using the parameters/variables of fc, ΔTs, ΔTa, and ΔRg, can Equation (8) estimate daily EF, which can be further used to partition the surface available energy into sensible and latent heat fluxes. Although the accuracy of the EF parameterization scheme is acceptable, there is still room for improving the model, particularly for low ET surfaces with low fc. Further study should be directed toward improving daily EF estimates by introducing other retrieval variables from remote sensing, such as soil moisture.
Acknowledgments
We thank the AmeriFlux Principal Investigators who provided data for our project through the Ameriflux network website ( http://ameriflux.ornl.gov/). We greatly thank Di Long from the Bureau of Economic Geology, Jackson School of Geosciences, The University of Texas at Austin, who provided many excellent suggestions for improving this study. This work was supported by the National Natural Science Foundation of China under Grant 41201366 and 41101332. The authors would like to thank Enago ( www.enago.cn) for the English language review.
Author Contributions
Jing Lu mainly wrote the manuscript and was responsible for the research design, data preparation and analysis. Ronglin Tang, Huajun Tang, and Zhao-Liang Li assisted in methodology development and research design, and also participated in manuscript writing and revision. Yuyun Bi and Kun Shao participated in data collection and processing. Guoqing Zhou and Jelila Labed performed the data validation analysis, and helped polish the language of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References and Notes
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar]
- Trenberth, K.E.; Fasullo, J.T.; Kiehl, J. Earth’s global energy budget. Bull. Amer. Meteor. Soc 2009, 90, 311–323. [Google Scholar]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys 2008, 29, 421–469. [Google Scholar]
- Li, Z.-L.; Tang, R.L.; Wan, Z.M.; Bi, Y.Y.; Zhou, C.H.; Tang, B.H.; Yan, G.J.; Zhang, X.Y. A review of current methodologies for regional evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci 2002, 6, 85–99. [Google Scholar]
- Bastiaanssen, W.; Menenti, M.; Feddes, R.; Holtslag, A. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol 1998, 212, 198–212. [Google Scholar]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface-temperature. Agric. For. Meteorol 1995, 77, 263–293. [Google Scholar]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)—Model. J. Irrig. Drain. E. ASCE 2007, 133, 380–394. [Google Scholar]
- Mu, Q.Z.; Zhao, M.S.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ 2011, 115, 1781–1800. [Google Scholar]
- Long, D.; Singh, V.P. A two-source trapezoid model for evapotranspiration (TTME) from satellite imagery. Remote Sens. Environ 2012, 121, 370–388. [Google Scholar]
- Tang, R.L.; Li, Z.-L.; Jia, Y.Y.; Li, C.R.; Sun, X.M.; Kustas, W.P.; Anderson, M.C. An intercomparison of three remote sensing-based energy balance models using Large Aperture Scintillometer measurements over a wheat–corn production region. Remote Sens. Environ 2011, 115, 3187–3202. [Google Scholar]
- Li, Z.-L.; Wu, H.; Wang, N.; Qiu, S.; Sobrino, J.A.; Wan, Z.M.; Tang, B.H.; Yan, G.J. Land surface emissivity retrieval from satellite data. Int. J. Remote Sens 2013, 34, 3084–3127. [Google Scholar]
- Wittich, K.; Hansing, O. Area-averaged vegetative cover fraction estimated from satellite data. Int. J. Biometeorol 1995, 38, 209–215. [Google Scholar]
- Bisht, G.; Venturini, V.; Islam, S.; Jiang, L. Estimation of the net radiation using MODIS (Moderate Resolution Imaging Spectroradiometer) data for clear sky days. Remote Sens. Environ 2005, 97, 52–67. [Google Scholar]
- Tang, B.H.; Li, Z.-L.; Zhang, R.H. A direct method for estimating net surface shortwave radiation from MODIS data. Remote Sens. Environ 2006, 103, 115–126. [Google Scholar]
- Zhao, X.; Liang, S.L.; Liu, S.H.; Yuan, W.P.; Xiao, Z.Q.; Liu, Q.; Cheng, J.; Zhang, X.T.; Tang, H.R.; Zhang, X.; et al. The global land surface satellite (GLASS) remote sensing data processing system and products. Remote Sens 2013, 5, 2436–2450. [Google Scholar]
- Stisen, S.; Sandholt, I.; Norgaard, A.; Fensholt, R.; Eklundh, L. Estimation of diurnal air temperature using MSG SEVIRI data in West Africa. Remote Sens. Environ 2007, 110, 262–274. [Google Scholar]
- Tang, B.H.; Li, Z.-L. Estimation of instantaneous net surface longwave radiation from MODIS cloud-free data. Remote Sens. Environ 2008, 112, 3482–3492. [Google Scholar]
- Jacome, A.; Bernier, M.; Chokmani, K.; Gauthier, Y.; Poulin, J.; De Seve, D. Monitoring volumetric surface soil moisture content at the La Grande basin boreal wetland by radar multi polarization data. Remote Sens 2013, 5, 4919–4941. [Google Scholar]
- Wan, Z.M.; Li, Z.-L. Radiance-based validation of the V5 MODIS land-surface temperature product. Int. J. Remote Sens 2008, 29, 5373–5395. [Google Scholar]
- Jiang, G.M.; Li, Z.-L. Split-window algorithm for land surface temperature estimation from MSG1-SEVIRI data. Int. J. Remote Sens 2008, 29, 6067–6074. [Google Scholar]
- Wang, N.; Wu, H.; Nerry, F.; Li, C.R.; Li, Z.-L. Temperature and emissivity retrievals from hyperspectral thermal infrared data using linear spectral emissivity constraint. IEEE Trans. Geosci. Remote Sens 2011, 49, 1291–1303. [Google Scholar]
- Carlson, T.N.; Capehart, W.J.; Gillies, R.R. A new look at the simplified method for remote sensing of daily evapotranspiration. Remote Sens. Environ 1995, 54, 161–167. [Google Scholar]
- Jackson, R.; Hatfield, J.; Reginato, R.; Idso, S.; Pinter, P., Jr. Estimation of daily evapotranspiration from one time-of-day measurements. Agr. Water Manage 1983, 7, 351–362. [Google Scholar]
- Jiang, L.; Islam, S. A methodology for estimation of surface evapotranspiration over large areas using remote sensing observations. Geophys. Res. Lett 1999, 26, 2773–2776. [Google Scholar]
- Carlson, T. An overview of the “triangle method” for estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors 2007, 7, 1612–1629. [Google Scholar]
- Tang, R.L.; Li, Z.-L.; Tang, B.H. An application of the Ts-VI triangle method with enhanced edges determination for evapotranspiration estimation from MODIS data in arid and semi-arid regions: Implementation and validation. Remote Sens. Environ 2010, 114, 540–551. [Google Scholar]
- Wang, K.C.; Liang, S.L. An improved method for estimating global evapotranspiration based on satellite determination of surface net radiation, vegetation index, temperature, and soil moisture. J. Hydrometeorol 2008, 9, 712–727. [Google Scholar]
- Long, D.; Singh, V.P.; Scanlon, B.R. Deriving theoretical boundaries to address scale dependencies of triangle models for evapotranspiration estimation. J. Geophys. Res 2012, 117. [Google Scholar] [CrossRef]
- Tang, R.L.; Li, Z.-L.; Chen, K.-S.; Jia, Y.Y.; Li, C.R.; Sun, X.M. Spatial-scale effect on the SEBAL model for evapotranspiration estimation using remote sensing data. Agric. For. Meteorol 2013, 174, 28–42. [Google Scholar]
- Stisen, S.; Sandholt, I.; Norgaard, A.; Fensholt, R.; Jensen, K.H. Combining the triangle method with thermal inertia to estimate regional evapotranspiration—Applied to MSG-SEVIRI data in the Senegal River basin. Remote Sens. Environ 2008, 112, 1242–1255. [Google Scholar]
- Wang, K.C.; Li, Z.Q.; Cribb, M. Estimation of evaporative fraction from a combination of day and night land surface temperatures and NDVI: A new method to determine the Priestley-Taylor parameter. Remote Sens. Environ 2006, 102, 293–305. [Google Scholar]
- Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Mecikalski, J.R. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sens. Environ 1997, 60, 195–216. [Google Scholar]
- Norman, J.M.; Kustas, W.P.; Prueger, J.H.; Diak, G.R. Surface flux estimation using radiometric temperature: A dual temperature-difference method to minimize measurement errors. Water Resour. Res 2000, 36, 2263–2274. [Google Scholar]
- Zhao, W.; Li, Z.-L.; Wu, H.; Tang, B.H.; Zhang, X.Y.; Song, X.N.; Zhou, G.Q. Determination of bare surface soil moisture from combined temporal evolution of land surface temperature and net surface shortwave radiation. Hydrol. Process 2013, 27, 2825–2833. [Google Scholar]
- Zhao, W.; Li, Z.-L. Sensitivity study of soil moisture on the temporal evolution of surface temperature over bare surfaces. Int. J. Remote Sens 2013, 34, 3314–3331. [Google Scholar]
- Lu, J.; Tang, R.L.; Tang, H.J.; Li, Z.-L. A new parameterization scheme for estimating surface energy fluxes with continuous surface temperature, air temperature, and surface net radiation measurements. Water Resour. Res 2014, 50, 1245–1259. [Google Scholar]
- Lu, J.; Tang, R.L.; Tang, H.J.; Li, Z.-L. Derivation of daily evaporative fraction based on temporal variations in surface temperature, air temperature, and net radiation. Remote Sens 2013, 5, 5369–5396. [Google Scholar]
- Chehbouni, A.; Lo Seen, D.; Njoku, E.; Monteny, B. Examination of the difference between radiative and aerodynamic surface temperatures over sparsely vegetated surfaces. Remote Sens. Environ 1996, 58, 177–186. [Google Scholar]
- Lhomme, J.; Chehbouni, A.; Monteny, B. Sensible heat flux-radiometric surface temperature relationship over sparse vegetation: Parameterizing B−1. Bound. Lay. Meteorol 2000, 97, 431–457. [Google Scholar]
- Gentine, P.; Entekhabi, D.; Polcher, J. The diurnal behavior of evaporative fraction in the soil-vegetation-atmospheric boundary layer continuum. J. Hydrometeorol 2011, 12, 1530–1546. [Google Scholar]
- Crago, R.D. Conservation and variability of the evaporative fraction during the daytime. J. Hydrol 1996, 180, 173–194. [Google Scholar]
- Trenberth, K.E.; Fasullo, J.T. Tracking earth’s energy. Science 2010, 328, 316–317. [Google Scholar]
- Li, Z.-L.; Tang, B.H.; Wu, H.; Ren, H.Z.; Yan, G.J.; Wan, Z.M. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ 2013, 131, 14–37. [Google Scholar]
- Li, Z.-L.; Zhang, R.; Sun, X.; Su, H.; Tang, X.; Zhu, Z.; Sobrino, J. Experimental system for the study of the directional thermal emission of natural surfaces. Int. J. Remote Sens 2004, 25, 195–204. [Google Scholar]
- AmeriFlux Site and Data Exploration System. Available online: http://ameriflux.ornl.gov/ (accessed on 13 October 2013).
- Suyker, A.E.; Verma, S.B. Interannual water vapor and energy exchange in an irrigated maize-based agroecosystem. Agric. For. Meteorol 2008, 148, 417–427. [Google Scholar]
- Tang, R.L.; Li, Z.-L.; Sun, X.M. Temporal upscaling of instantaneous evapotranspiration: An intercomparison of four methods using eddy covariance measurements and MODIS data. Remote Sens. Environ 2013, 138, 102–118. [Google Scholar]
- Twine, T.; Kustas, W.; Norman, J.; Cook, D.; Houser, P.; Meyers, T.; Prueger, J.; Starks, P.; Wesely, M. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol 2000, 103, 279–300. [Google Scholar]
- Quarmby, N.; Townshend, J.; Settle, J.; White, K.; Milnes, M.; Hindle, T.; Silleos, N. Linear mixture modelling applied to AVHRR data for crop area estimation. Int. J. Remote Sens 1992, 13, 415–425. [Google Scholar]
- Carlson, T.N.; Perry, E.M.; Schmugge, T.J. Remote estimation of soil moisture availability and fractional vegetation cover for agricultural fields. Agric. For. Meteorol 1990, 52, 45–69. [Google Scholar]
- Prihodko, L.; Goward, S.N. Estimation of air temperature from remotely sensed surface observations. Remote Sens. Environ 1997, 60, 335–346. [Google Scholar]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ 1997, 62, 241–252. [Google Scholar]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in evapotranspiration from land surface modeling, remote sensing, and GRACE satellites. Water Resour. Res 2014, 50, 1131–1151. [Google Scholar]
- Kurc, S.A.; Small, E.E. Soil moisture variations and ecosystem-scale fluxes of water and carbon in semiarid grassland and shrubland. Water Resour. Res 2007, 43. [Google Scholar] [CrossRef]







| Site ID | Site Name | Latitude | Longitude | Elevation (m) | Land Cover | Climate | Soil Texture |
|---|---|---|---|---|---|---|---|
| US-Ne2 | Mead Irrigated Rotation | 41.1649°N | 96.4701°W | 362 | CRO | Temperate | Deep silty clay loams |
| US-Seg | Sevilleta Desert Grassland | 34.3623°N | 106.7019°W | 1622 | GRA | Semi-arid | Loamy sand |
| US-SRC | Santa Rita Creosote | 31.9083°N | 110.8395°W | 991 | OSH | Subtropical | Sandy loam |
| US-Me6 | Metolius Young Pine Burn | 44.3232°N | 121.6043°W | 996 | ENF | Warm dry summers and cool wet winters | Sandy loam |
| US-UMB | UMBS | 45.5598°N | 84.7138°W | 234 | DBF | Temperate northern | Sandy lake deposits |
| BR-Sa3 | LBA Tapajos KM83 Logged Forest | 3.018°S | 54.971°W | 100 | EBF | Tropical | Yellow dystrophic latosol |
| Site ID | Year | Precipitation (mm) | (°C) | (%) | Filled | Temporal Resolution |
|---|---|---|---|---|---|---|
| US-Ne2 | 2011 | 805 | 10 | 75 | Yes | Hourly |
| US-Seg | 2010 | 182 | 14 | 41 | Yes | Half-hourly |
| US-SRC | 2011 | 229 | 20 | 33 | No | Half-hourly |
| US-Me6 | 2012 | 596 | 8 | 65 | Yes | Half-hourly |
| US-UMB | 2012 | 603 | 9 | 71 | No | Hourly |
| BR-Sa3 | 2003 | 1461 | 25 | 79 | No | Half-hourly |
| Site ID | Year | EBR | R2 | RMSE (W/m2) | BIAS (W/m2) |
|---|---|---|---|---|---|
| US-Ne2 | 2011 | 0.86 | 0.951 | 20.7 | −16.6 |
| US-Seg | 2010 | 0.90 | 0.906 | 12.9 | −8.6 |
| US-SRC | 2011 | 0.79 | 0.975 | 20.1 | −19.3 |
| US-Me6 | 2012 | 0.78 | 0.872 | 35.2 | −30.1 |
| US-UMB | 2012 | 0.84 | 0.791 | 33.1 | −23.5 |
| BR-Sa3 | 2003 | 0.93 | 0.678 | 16.7 | −11.5 |
| fc_non-linear | EF_non-linear | fc_0.2/0.66 | EF_0.2/0.66 | |
|---|---|---|---|---|
| R2 | 0.964 | 0.990 | 0.966 | 0.879 |
| RMSE | 0.183 | 0.100 | 0.155 | 0.101 |
| BIAS | −0.167 | 0.088 | −0.099 | 0.070 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lu, J.; Tang, R.; Tang, H.; Li, Z.-L.; Zhou, G.; Shao, K.; Bi, Y.; Labed, J. Daily Evaporative Fraction Parameterization Scheme Driven by Day–Night Differences in Surface Parameters: Improvement and Validation. Remote Sens. 2014, 6, 4369-4390. https://doi.org/10.3390/rs6054369
Lu J, Tang R, Tang H, Li Z-L, Zhou G, Shao K, Bi Y, Labed J. Daily Evaporative Fraction Parameterization Scheme Driven by Day–Night Differences in Surface Parameters: Improvement and Validation. Remote Sensing. 2014; 6(5):4369-4390. https://doi.org/10.3390/rs6054369
Chicago/Turabian StyleLu, Jing, Ronglin Tang, Huajun Tang, Zhao-Liang Li, Guoqing Zhou, Kun Shao, Yuyun Bi, and Jelila Labed. 2014. "Daily Evaporative Fraction Parameterization Scheme Driven by Day–Night Differences in Surface Parameters: Improvement and Validation" Remote Sensing 6, no. 5: 4369-4390. https://doi.org/10.3390/rs6054369
APA StyleLu, J., Tang, R., Tang, H., Li, Z.-L., Zhou, G., Shao, K., Bi, Y., & Labed, J. (2014). Daily Evaporative Fraction Parameterization Scheme Driven by Day–Night Differences in Surface Parameters: Improvement and Validation. Remote Sensing, 6(5), 4369-4390. https://doi.org/10.3390/rs6054369






