1. Introduction
Plant functional types (PFTs) are groups of plants defined according to several factors, including their functions at organismic level, their responses to environmental factors, and/or their effects on ecosystems [
1]. This is particularly relevant for monitoring present state and possible changes in mountainous areas, which “support many different ecosystems and have among the highest species richness globally”. Furthermore, in semi arid and arid regions of the Tibetan Plateau, PFTs play a significant role in biospheric carbon storage and carbon sequestration. Thus it is not surprising that these areas are expected to experience most severe ecological impacts and, therefore, are counted as highly vulnerable [
2].
Therefore, reliable information about the geographic distribution of major PFTs in these regions is necessary. Traditional land classifications are biome-based and arbitrary products of the classifying scheme rather than existing natural units [
3]. The key distinction between biome
versus PFT classification is that the latter attempts to unmix mixed pixels. That is, a biome class such as “savanna” needs to be decomposed into proportions of component plant types, grass, broad leaf trees,
etc. However, representing vegetation by patches of PFTs reduces species diversity in ecological function to a few key plant types whose leaf physiology and carbon allocation are known. Thus analyses of composition and function of ecosystems in a changing environment are possible. This PFT concept has gained favor also amongst modelers, who are trying to predict how vegetation will respond to the effects of climate change.
At present there are three PFT classifications available: (i) Global PFT data sets are obtained from satellite based products; they are produced by the Moderate Resolution Imaging Spectroradiometer (MODIS) Land Team [
4]. (ii) PFTs are also extracted from already existing land cover data sets [
3,
5–
8] and, finally (iii) PFTs are derived from Regional Scale Multisource Evidential Reasoning [
9], using remote sensing techniques to map higher accuracy regional PFTs. For application to the complex structures of mountainous areas like the Tibetan Plateau these mappings have limitations, as specified below.
PFT products are generated as one of the five MODIS Land Cover products, for which the decision trees classification method is used. Several studies have demonstrated the utility and advantage of decision trees in land cover classification from regional to global scales [
10,
11]. Moreover, Strahler, Muchoney, Borak, Friedl, Gopal, Lambin and Moody [
4] note that the International Geosphere-Biosphere Program (IGBP) classes can be re-labeled or “cross-walked” to provide compatibility with current and future land cover classification systems. However,
Sun et al. (2008) indicate that the error characteristics (such as magnitudes, spatial and temporal variation) of the MODIS PFT products have not been fully characterized. In addition, detailed information on how to “cross-walk” to the PFT classes are not released [
12]. Finally, investigators extracting PFT information from preexisting land cover maps pioneered the development of PFT data sets over broad areas, and still use this method in recent research. However, this PFT information from preexisting land cover maps is predominantly used in global scale analyses using relatively coarse resolution, and investigators are frequently forced to make assumptions about missing information [
7,
12]. When several land cover maps are required for producing PFT, compatibility among those maps will be an issue. Moreover, updating such PFT data sets could not be independent from updating land cover maps. (iii)
Sun et al. (2008) present a method of multisource mapping of PFTs using a suite of MODIS products which improve the overall accuracy and kappa statistic [
9]. However, they also note that evidence reasoning could not solve the issue of incorporating regional variations in the spectral and morphological characteristics of PFTs. That is, the method could not obtain a classification procedure for mapping over larger geographic areas (like continents).
Representative information on the time evolution of remote sensing and vegetation data sets can be employed to characterize vegetation types and thereby avoid climate induced phenological shifts. These temporal trajectory analyses are conveniently grouped into four categories [
13]: (i) quantifying differences in time series values, (ii) accounting for temporal correlation and non-stationarity, (iii) measuring temporal correlation and, finally (iv) implementing a natural set of harmonic modes. This Fourier mode decomposition is advantageous in areas where human activity is limited, where strong periodicities exist. Thus it could be used to filter non-systematic noise and to separate spatial variations from temporal variability as demonstrated in applications to spectral satellite images or derived vegetation indices and biophysical products (especially Normalized Difference Vegetation Index, see [
14–
19]).
PFTs in mountainous areas which, to our knowledge, have not been subjected to this analysis technique, is the focus of this study. That is, comprising hierarchical and soft classifications, including digital elevation information, and applying suitable measures of similarity (between candidate pixels and reference types) lead to a novel combinatorial approach to map PFTs in mountainous regions. The methodology, data used and processing procedure is presented in Section 2, followed by an application to the Eastern Tibetan Plateau (Section 3), and a discussion concludes the analysis (Section 4).
2. Methods of Analysis
Datasets and the strategy of improving the PFT classification are introduced in the following. The scheme used in this study is similar as the one used in the standard MODIS PFTs product: evergreen needle leaf trees (ENT), evergreen broad leaf trees (EBT), deciduous needle leaf trees (DNT), deciduous broad leaf trees (DBT), shrub, grass, Cereal crop and broadleaf crop are combined to crop (CC), barren or sparse vegetation (BSV) but without snow and ice (SI), urban and built up types, which are out of scope of the PFTs distribution. For simplicity, the types used will be referred to by their initials.
Three data sets are used as inputs which include five year of half-month data of MODIS NDVI (MOD13A1, 2006 to 2010), five year of annual data of MODIS PFT (MCD12Q1, 2006 to 2010), and the Shuttle Radar Topography Mission (SRTM) elevation data: (i) MOD13A1 data is provided every 16 days at 500-m spatial resolution as a gridded level-3 product in the sinusoidal projection. These are global MODIS vegetation indices, designed to provide consistent spatial and temporal comparisons of vegetation conditions. They are closely related to percent green cover, the fraction of Photosynthetically Active Radiation (fPAR) absorbed by vegetation and, therefore, to gross primary productivity as demonstrated by satellite-based analyses of land surface vegetation [
20–
22]. (ii) MCD12Q1, the MODIS Terra plus Aqua 500m resolution Land Cover Type product, incorporates five different land cover classification schemes, derived through a supervised decision-trees classification method. PFT product is generated as one of the five MODIS Land Cover products. The PFT product is used for comparability and training of soft classification determined from temporally stable pixels in the MCD12Q1 time series (temporal resolution of one year). (iii) SRTM is a global digital elevation model (DEM) spearheaded by the National Geospatial-Intelligence Agency (NGA), NASA, the Italian Space Agency (ASI) and the German Aerospace Center (DLR) with 90 meter resolutions for the world [
23].
The SRTM dataset in this study is resized according to the spatial resolution of MODIS product by nearest neighbor resampling in ENVI software. Some geostatistical approach would probably generate more accurate outcomes for relief data than nearest neighbor resampling [
24]. But considering both efficiency and specific study regions, we choose, instead of geostatistical approach, nearest neighbor resampling. Previous records support that the hierarchical approach, even coupled with coarse DEM information, is effective in increasing the accuracy of vegetation classification over very rugged terrain [
25].
The validation datasets are provided by the Vegetation Map of the People’s Republic of China (1:1,000,000, field survey, and for simplicity referred to as China Vegetation Map in the following) and by Makehe Forest Region vegetation map (1:50,000, field survey completed in late 2009, see Section 3). The China Vegetation Map [
26], completed in late 2007, describes vegetation distributions, including 11 vegetation type groups (such as broadleaf forest), 55 vegetation types (such as temperate deciduous broad leaf trees) and 960 vegetation species (such as pine, spruce, oak and so on), which are usually used as testing data (see, for example, [
27,
28]).
Fourier transform: The first step of the hierarchical soft classification methodology is to transform the original image time series into frequency domain using fast Fourier transform (FFT, see
Equation (1)). Each pixel location in the original image contains a time series, which is a periodic signal. The FFT decomposes the periodic signal into a set of scaled sine and cosine waves that can be summed to reconstruct the original signal and can be used to transform any equidistant discrete time series ft. The Fourier transformed components of NDVI time series to segment remote sensing hard vegetation types are successfully reported in the previous research (see introduction) and is given by:
where
t is an index representing NDVI layer number;
ft is the
tth time series value;
k is the number of Fourier component (or harmonic) and
N is the total number of layers in the time series. According to Euler’s formula
eiθ = cos
θ +
i sin θ,
Equation (1) can be decomposed into a set of cosine (real part) and sine (imaginary part) waves
. The cosine and sine parts,
and
provide amplitude
and phase
of each harmonic.
Classification: The classification procedure follows a stepwise hierarchy from broad spatial partitioning to a detailed soft diagnostics, which requires a metric to estimate the similarity between reference and candidate pixels. Similar to a top-down hierarchical classification, we consider a multiple stage process in which broad categories are separated first and finer categories within broad categories are further classified afterwards.
By setting a threshold value for the amplitude
A0 we define broad categories (threshold values are set according to the mean, standard deviation, and especially standard error of the five-year NDVI average, details in Section 3).
A0 represents the amplitude of the average NDVI, which is closely related to the biomass information of land surface vegetation [
29]. Similar amplitude
A0 types are separated first as broad categories and detailed PFTs within broad categories could be further separated by different phenological and elevation information.
The soft classification satisfies characteristics of PFTs which (compared with hard classes, such as “savanna”) are proportions of component of plant types, grass, broad leaf trees,
etc. Transforming input time series into partitioning frequency regions is a critical step for combining similar integrated NDVI and phenological information. Due to its generality, the theory of transforming and partitioning does not specify how to compute similarity measures of PFTs by preserving their soft attributes. Therefore, soft classification is introduced in this study to enable a better mapping behavior of land surface PFTs, particularly regarding points that are challenging because they lie on transition or mixed zones [
30]. In summary, soft PFT similarity measures are implemented following the three subsequent steps.
Step-1: Extraction of persistent PFT pixels: Traditional reference selection requires ground truth or visual interpretation, but which are untypical for the 500 m resolution MODIS products. Our reference selection considers pixels (from 2006 to 2010 MODIS PFTs products) which consistently belong to the same PFT over the 5-year period to be representative. The persistent pixels of each PFT selected in this step are used as a mask to generate mean reference vectors of each PFT in the next step.
Step-2: Reference vectors for individual PFTs: In this paper, each pixel is referred to as a candidate pixel, containing the same number of values as number of layers. A vector is introduced for each candidate pixel to record those values. Thus, the dimension of a vector equals to the number of layers. Among candidate pixels, those for reference are persistent pixels selected from Step-1. A reference vector is a mean vector including a set of mean values, each of which represents a mean of a particular PFT in a input layer, such as amplitude AK, phase PHIK and elevation. The mean value for each layer is computed by first summing all data value of the pixels corresponding to a PFT, and then dividing the sum by the number of pixels in that mask. For example, suppose we select the first 15 amplitudes AK and phases PHIK, include digital elevation data and the amplitude A0, we obtain 32 layers; that is, the dimension of a mean vector for each PFT yields 32.
Step-3: Similarity measure: The distance from each candidate vector to this mean vector of each PFT class (
i) for each layer is calculated as:
where
PVx,y,layer is the pixel value at location (
x,
y) on a particular layer;
MEANi,layer is the mean value in a PFT mask on the same particular layer. In this way, each PFT is defined by a mean reference vector. The distance metric is a scale insensitive metric which will not be over dominated by large range layers, such as
A0 and the digital elevation model, due to subtracting a mean PFT vector in associated spatial portioning regions. The measure of similarities between a mean reference vectors and candidate vectors are based on normalized distances (
Equation (3)):
where
di is the distance of a candidate pixel from the mean vector of a PFT class
i; normalized (Xi) is an index describing the candidate pixel belonging to class
i by converting distance
i to scale 0∼1. If the vectors are identical (the
di in
Equation (2) is 0), in this case, in such a case the normalization of
Equation (3) is assumed to return 1.
3. Application of the Hierarchical Soft Classification: Results for Eastern Tibet
The eastern Tibetan Plateau (
Figure 1) covers a large part of the Eurasian continent (25°N to 38°N, 88°E to 105°E); it comprises topographically, biologically and climatically complex areas. The elevation ranges from 120 m to more than 7200 m and the average altitude is about 3900 m. Several major rivers originate there, including the Yanu Zangbo River, Lancang River, Nu River, Yellow River, Yangtze River, Dadu River, Min River and Jialing River. Biologically, due to the integrated influence from latitudinal, longitudinal and altitudinal zonality, land cover types show a rich diversity (
Figure 1). However, the Tibetan Plateau not only has unique climatic conditions and physical environment, but is also sensitive to global change, which makes a very fragile environment for vegetation growth. Climatically, high altitudes are associated with relatively low temperatures and very strong gradients [
31]. It contains five provinces of China, including the whole Qinghai province, part of Xizang (Tibet), Sichuan, Gansu and Yunnan provinces.
Suitably employing the tools introduced in the previous section provides a two level hierarchical classification scheme to stratify eastern Tibetan Plateau into smaller mapping categories and to describe detailed variation of PFTs within smaller mapping categories.
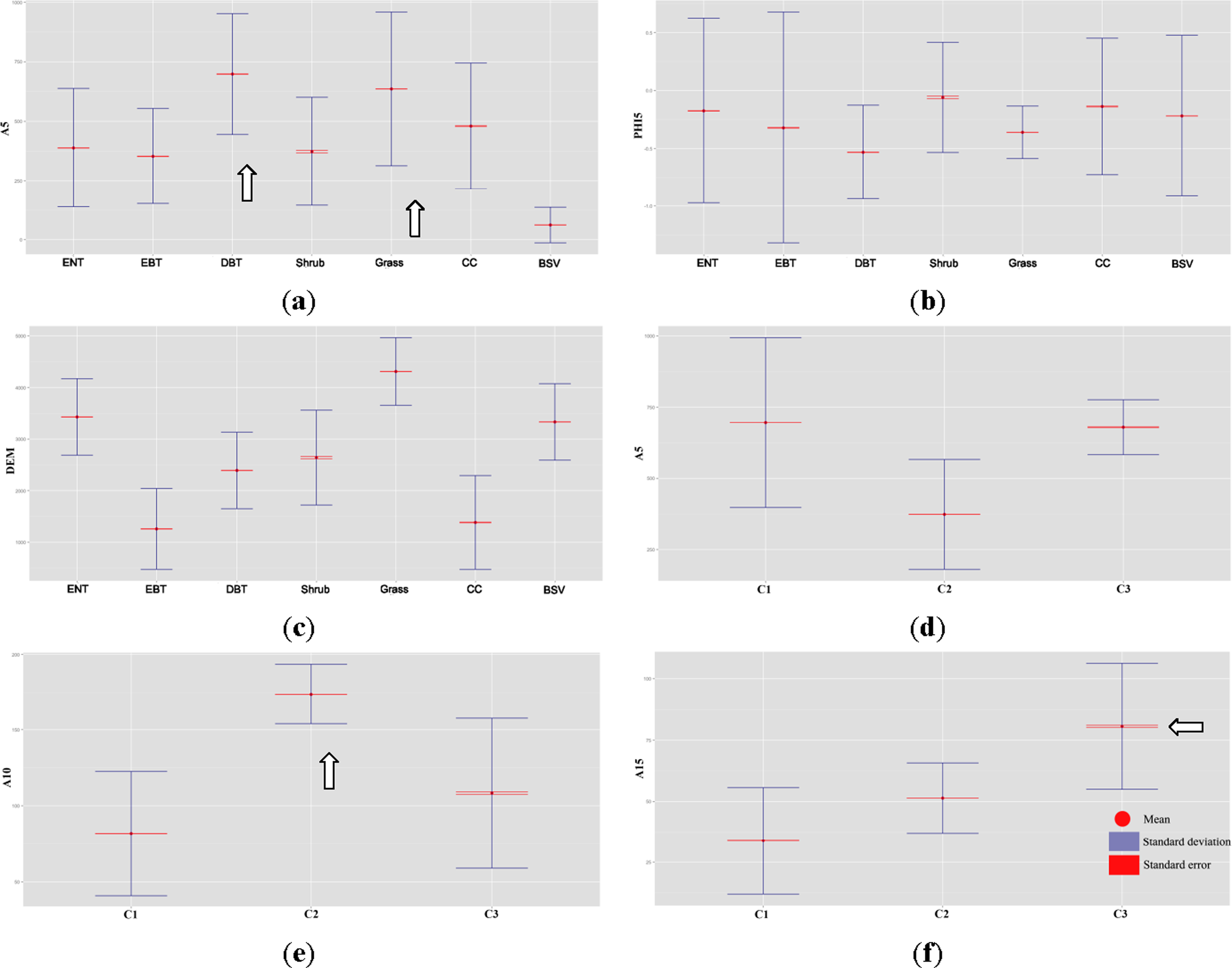
First level classification (Fourier transform and spatial partitioning): After Fourier based decomposition, we define four broad categories (as first level) by setting thresholds for the amplitude
A0 according to the mean, standard deviation, and especially standard error of each PFT: Water or snow and ice (category1,
A0 < 0), these type are is should to show no vegetation, that is, the average
NDVI ∼
A0 is supposed to be below 0; barren or sparse vegetation (category2, 0 <
A0 < 1000); grass and part of shrub (category3, 1000 <
A0 < 4000); the rest (category4,
A0 > 4000) with five types (see
Figure 2a). Generally, standard deviation is a measure of dispersion within a data set whereas standard error is considered to be the level of error (dispersion) of the data from a population mean. Therefore, standard error in
Figure 2a indicates that each PFT sample is representative for a population. Besides standard error,
Table 1 presents accuracy assessment using random points for the four categories. The producer’s and the user’s accuracies for the four categories are used to support the selected threshold.
Figure 2b–f shows the spatial partitioning results according to the setting of threshold values, which are generated to keep the detailed PFTs mapping from being dominated by large range layers such as
A0.
Second level classification: The following second level of hierarchical classification employs data from the Eastern Tibetan Plateau on the step-by-step basis introduced above.
(
i)
Selection of reference (persistent) samples for supervised classification is commonly accomplished in three ways by (1) ground truth observation, (2) visual interpretation of the observed image and (3) using higher spatial resolution satellite images. Reference samples from ground truth of complex topography (like the eastern Tibetan Plateau, lat × long ≈ 13 × 17 degrees) are untypical. Likewise, visual interpretation of NDVI time series (including the digital elevation information) is uncommon, if only the inputs of this study are used; finally, reference samples selected from higher spatial resolution satellite images often require a too sophisticated data fusion process. Therefore, a novel procedure is introduced to obtain reference samples for complex mountainous regions, which is flexible, robust and easy to apply: Assume that the accuracy of those pixels persistently belonging to the same PFT in five years is sufficiently high to represent the unique pattern of a distinct PFT. Then data fusion is not necessary because both of the two products (MODIS PFT and MODIS NDVI) share the same spatial resolution, coordinate system, and even satellite. In addition, smoothing by spatial averaging (Section 2) enhances the ability for reference samples to provide a distinct and representative PFT. It appears that, among the selected pixels, none of them belongs to Deciduous Needle leaf trees. Therefore, it will not be considered in the detailed PFTs mapping process in the following case study. The remaining five or seven PFTs are taken as examples, which are represented in terms of their most relevant Fourier harmonics and by their living elevation situation (
Figure 3).
The following points are noted: (i) Harmonic mode represents complete cycles over the five-year time series. That is, the annual cycle shows large amplitude
A5 (
Figure 3a). (ii) Vegetation elevation attributes (
Figure 3c) the altitude living order for PFTs from high to low levels: evergreen needle leaf > deciduous broadleaf tree > evergreen broad leaf tree. (iii) Annual, semi-annual and one-third annual crop modes are represented by the 5th amplitude component, the 10th amplitude component and in the 15th amplitude component, separately (
Figure 3g–i). (iv) The phase information shows a large variability for each PFT, representing the large inter-annual fluctuation in the phenological profile of a specific PFT (due to different climatic condition in different parts of the study area).
(
ii)
Reference mean vectors (and representative layers) are selected according to their ability to discriminate different PFTs. First, integrated NDVI, amplitude
A0, contains information about the time mean characteristics of different PFTs. For example, in long time series the integrated NDVI of evergreen broadleaf tree (Category4 in
Figure 2a) is greater than of deciduous broadleaf tree. Next, the amplitudes of the annual, semi-annual and one-third annual modes provide support for discrimination of PFTs (see standard error, the level of dispersion, in
Figure 3); for this study area, the semi-annual vegetation mode appears to be sufficient. Finally, the digital elevation model can also improve the accuracy of PFTs mapping, because each PFT may show a distinct upper and lower limit of plant growth. Now, a reference spatial average for each PFT is determined from all representative layers; the phase information is not considered due to the large spatial and/or inter-annual variability of each PFT.
(
iii)
The similarity measure is based on the differences of integrated NDVI, phenological and altitudinal behavior between a reference mean vector of each PFT compared with the candidate vectors using the normalized distance (
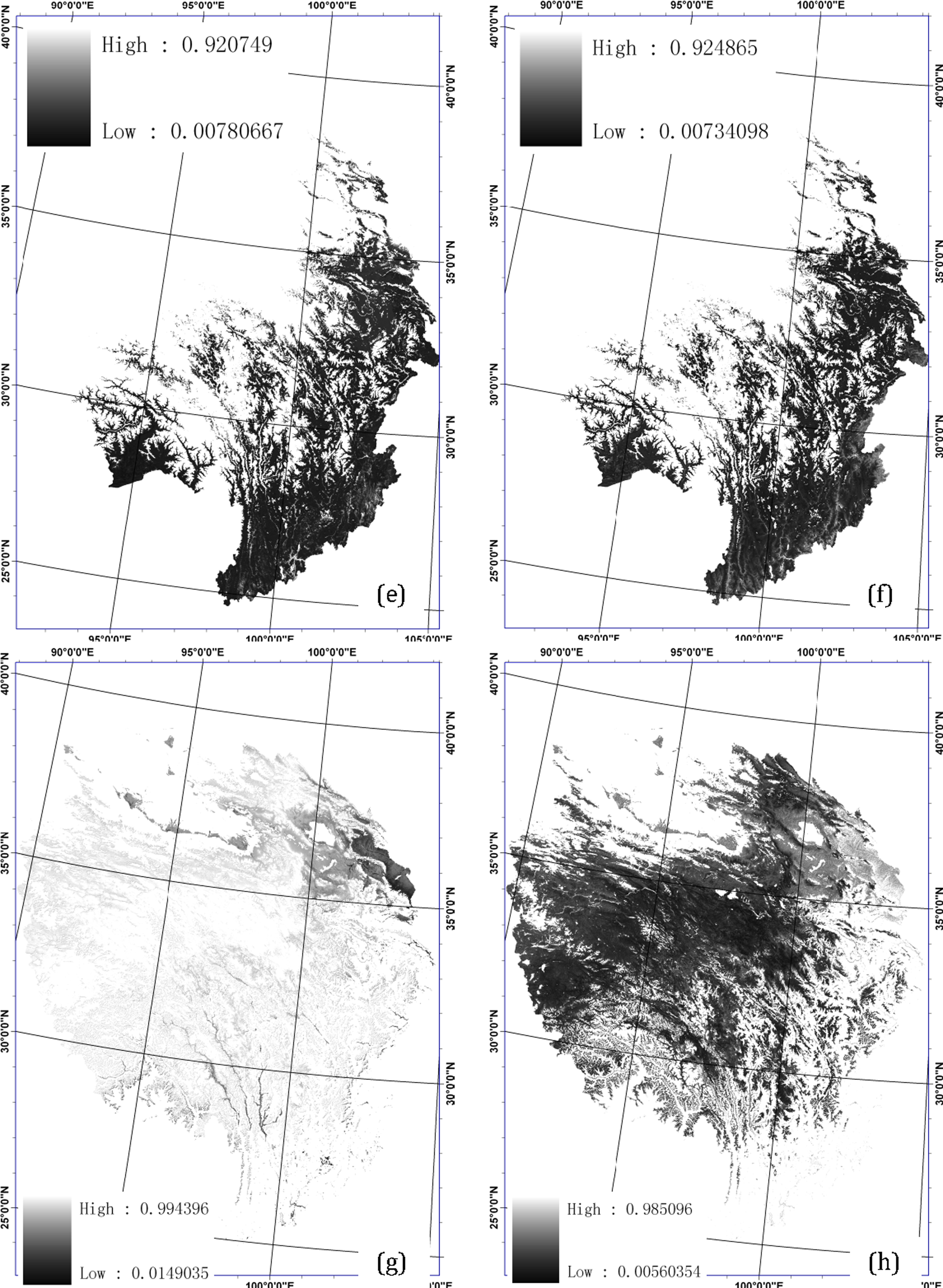
Equation (3)). Two vectors of better match in all layers have a greater normalized distance value. It is worth noting that the study area is divided into four categories where potential vegetation type is different as demonstrated by the normalized distance of PFTs (
Figure 4, note that Category2 is assigned into a single Type, Category1 is out of the scope of vegetation classification, thus, both of them are not shown).
Assessment and visualization: The similarity measure calculates soft PFT results, which are proportional components of plant types. Accuracy assessment requires additional interpretation to pass from these soft PFT results to a hard classification map. Thus we assign a pixel with the greatest normalized distance to the PFT (hereafter refer to hardened classifications) just in the interest of showing the spatial distribution of dominant PFTs and a better comparability between the MODIS product and this PFT results.
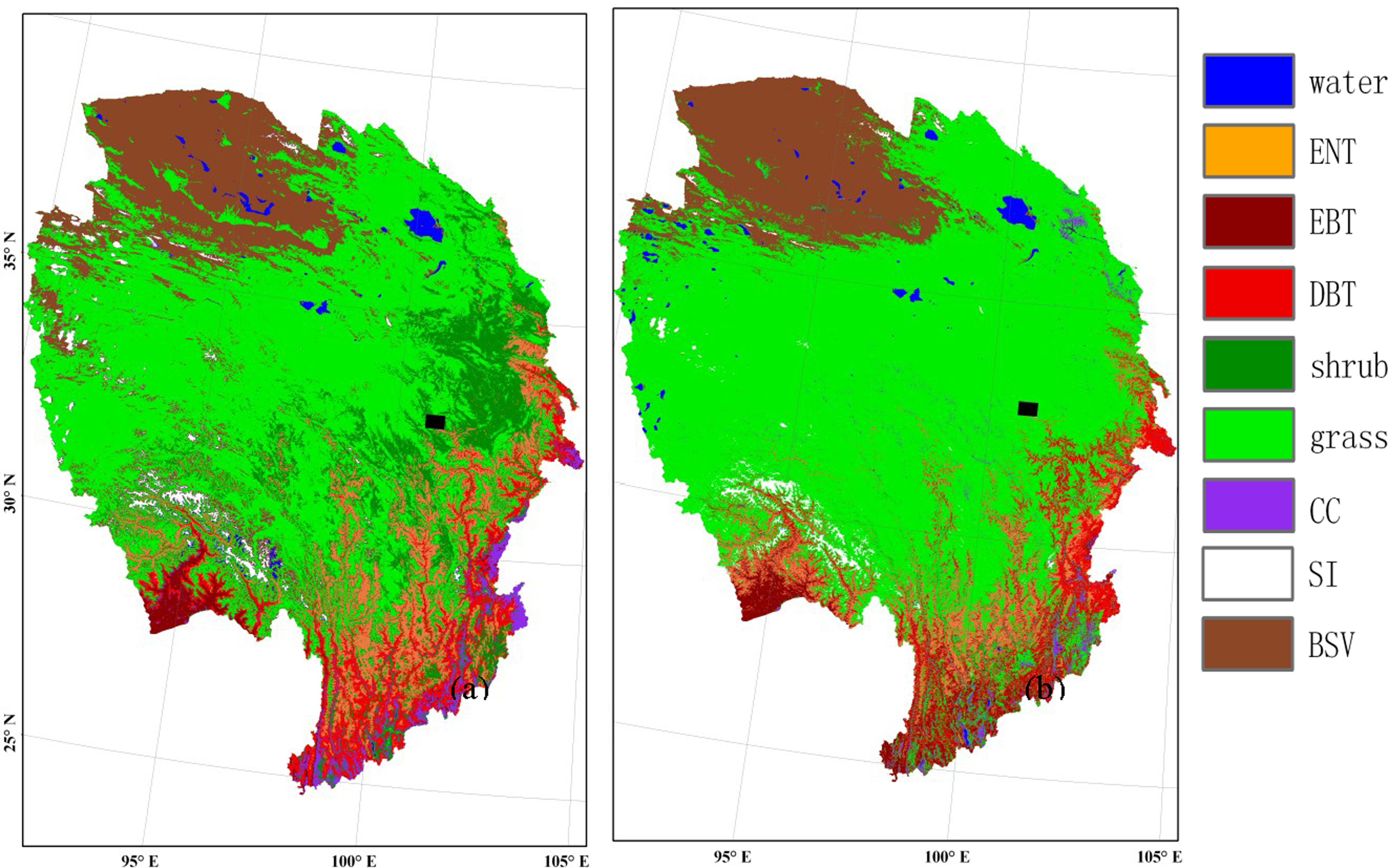
Figure 5a shows hardened classifications and
Figure 5b shows the MODIS 2007 PFT product.
Figure 6 is a highlight comparison of vegetation distribution from Makehe Forest Region located in Sanjiangyuan Nature Reserve. To be comparable, closed/open forest and closed/open shrub of the 1:50,000 field survey are combined to forest (green), shrub (yellow) and others (white), as well as results from hierarchical soft time-space classification and MODIS (see
Figure 6). Besides a visual comparison of vegetation maps, a statistical approach is also applied to compare classification to field data in order to evaluate accuracy.
Tables 1 and
2 summarize the hierarchical classification result and the MODIS 2007 PFT products compared with reference points from the China Vegetation Map. A total of 13,081 reference points were selected from the China Vegetation Map using the proportionate stratified random method with a minimum sample size of 100. Classification accuracies include producer’s and user’s accuracy and kappa statistics. Furthermore, we employ a spatial pixel-by-pixel comparison between MODIS PFT products and our hierarchical soft time-space classification scheme (
Table 3).
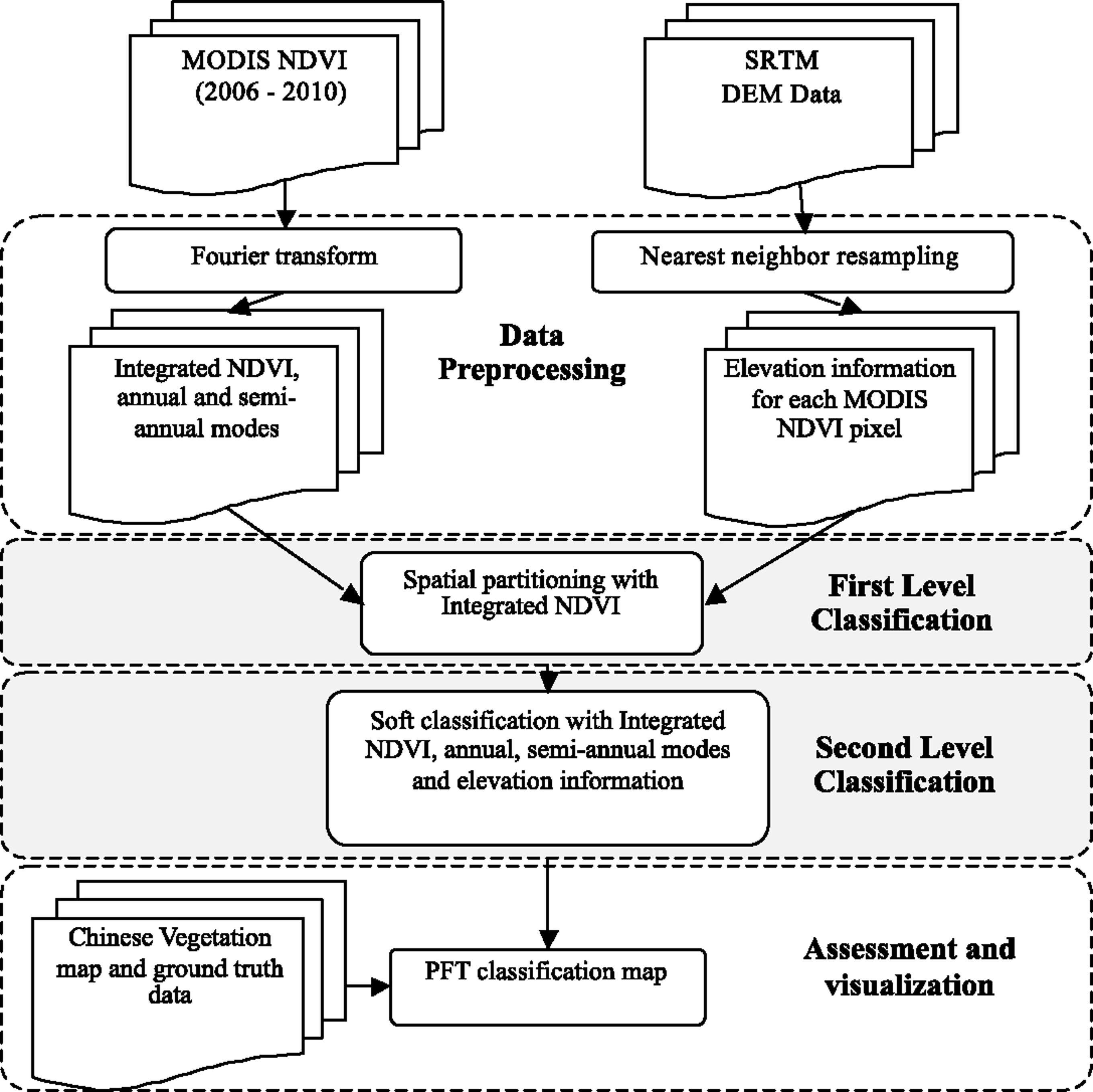
To make the overall approach better validated and more comprehensible, a flowchart (
Figure 7) and statistics of vegetation coverage in Makehe Forest Region are provided (
Table 4).
Comparison and discussion: Our hierarchical soft classification scheme is applied to map PFTs in a complex terrain environment (spanning a height of more than seven kilometers) and compared with the classical MODIS PFT product. The following results are achieved.
(
i)
Hierarchical soft classification scheme: The confusion matrix (
Table 1) shows the accuracy of both the first level coarse categories and the detailed PFTs results (based on 13,081 reference points selected from China Vegetation Map). The producer’s (user’s) accuracies of the coarse categories are 63.06%, 92.84%, 64.60%, 69.61% (69.14%, 59.27%, 83.61%, 59.15%), respectively. The accuracy of detailed PFTs results could have been improved by improving the accuracy of the coarse categories. However, we set threshold values according to the mean and standard deviation of the five-year average
NDVI ∼
A0 to keep the scheme generally applicable.
Detailed classification, which employs the soft similarity measure by combing Fourier components and elevation model, groups the pixels in proportional relation to the vegetation types and thus provide a higher accuracy than MODIS PFT products (see from
Tables 1 and
2). For almost all vegetation types this yields a close relation to the China Vegetation Map (field survey), especially for PFTs in high integrated NDVI regions (
A0 > 4000). For example, the producer’s accuracy increases (in absolute terms) by 3.27%, 20.60%, 17.77%, and 27.6% for evergreen needle leaf trees, evergreen broad leaf trees, deciduous broad leaf trees, and shrub, respectively. For user’s accuracies, the maximum improvement occurs for the evergreen broad leaf trees increasing from 42.77% (MODIS 2007 PFT products) to 81.16% (our hierarchical soft classification). The overall accuracy achieved increases from 57.68% (MODIS 2007 PFT products) to 64.42% (research result), with the Kappa Coefficient improving by 0.1. Note that Water and Snow are not included as a PFT and therefore not considered for comparison with MODIS.
(
ii)
MODIS PFT scheme: A pixel-to-pixel comparison between the hierarchical soft classification result and the MODIS 2007 PFT product is also calculated (
Table 3). Confusion matrix shows how vegetation types are transferred from MODIS product to this hierarchical classification by adopting the classification procedure in Section 2; that is, 60.80% of the MODIS 2007 PFT product matches the hierarchical classification result. Grass and sparse vegetation types show high consistency. Geographical comparison between the hierarchical soft classification result and the MODIS 2007 PFT product is shown in
Figure 5. More spatial details achieved by using the hierarchical classification compared to the MODIS 2007 PFT product, such as regions around latitude 30°∼35°and regions near the boundaries of lakes and permanent glaciers. The barren or sparse vegetated type appears in regions near the boundaries of lakes and permanent glacier, which may be attributed to the seasonal change of the lake area or level and to the melting of non-permanent snow and ice.
(
iii)
Field survey evaluation: The total area of Makehe forest region is 101,602 hm
2. The forest area itself comprises 23 385 hm
2 [
32]. Therefore, the forested area (non-forest area) accounts for 23.02% (76.98%) of the total area. Statistics of vegetation coverage as well as related comparisons among the hierarchical soft time-space classification result, MODIS 2007 product and field survey records applied in Makehe Forest Region are provided (
Table 4). It is noted that, in the aspect of forest coverage percentage, the hierarchical soft time-space classification improves PFTs mapping accuracy in high mountains regions compared to MODIS product.
Generally, the overall idea of spatial partitioning is to reduce the variability of the average NDVI ∼
A0 so that similarity measure is not dominated by large range layers. Phase information is neglected to assure this procedure to be robust enough for bypassing inter-annual phenological variations within a specific PFT due to regions dependent climatic condition. Neglecting phase information is also the solution for the problem mentioned by
Sun et al. (2008) that evidence reasoning could not solve the issue of incorporating regional variations in the spectral and morphological characteristics of PFTs [
9]. Spatial averages of persistent pixels selected from five year MODIS PFT product are representative to show the unique pattern of each distinct PFT. A soft similarity measure between a candidate vector and an average vector is suitable for the mixed pixel problem, which lies at the heart of the PFT philosophy.
These statistics reveal that the hierarchical soft time-space classification improves the accuracy for most of PFTs, especially in types with higher NDVI values (e.g., Category4, see pixel-to-pixel comparison). That is, for complex mountainous terrain the hierarchical soft classification scheme (based on freely downloadable data) provides PFT maps of higher accuracy (compared to MODIS products) and can be applied to larger areas (compared to the multisource evidence reasoning scheme). In addition, the barren or sparse vegetated type appears in regions near the boundaries of lakes and permanent glaciers. This suggests that the hierarchical soft classification may provide a tool to monitor lake areas or levels changes and the depiction of snow lines. It should also be noted that the PFT maps presented in this paper are generated at the regional level, whereas the MODIS PFT is a global product.
There are limitations and, therefore, scope for future research: (i) Fourier based techniques are advantageous when strong periodicity exists in the temporal series and for filtering non-systematic noise [
9]. However, Fourier decomposition may be less appropriate and perhaps alternatives methods (e.g., wavelets) need to be explored, if abrupt changes occur. Piao
et al. [
33] use a Morlet Wavelet Function to detect vegetation change in the same region, but it shows less abrupt changes occurring in our study region which supports Fourier based techniques to be used in this study region using a 5-years time series. Further research will compare both Fourier and wavelet techniques to provide a map in areas where the Yak-Pica-pasture degradation problem persistently arises and in areas where these deleterious dynamics arise in non-persistent regions. (ii) Data and method: Initial studies have used integrated NDVI values to estimate biomass production through the fAPAR [
29]. But the relationship between NDVI and biomass can be problematic in some cases, and some other vegetation index could be superior to NDVI, especially at high fAPAR values [
34] which requires further analysis in future research. EVI has been developed with exactly this limitation in mind and thus would be an arguably more appropriate index over large and diverse regions. In this study, we use a primary integrated NDVI segmentation and assisting phenology and elevation information to avoid the NDVI saturation problem. For further improvement detailed classification may be necessary, enhancing the accuracy of spatial partitioning and including other appropriate input data sets (for example, adding Leaf Area Index (LAI) data and/or biomass map). However, due to the accuracy and the spatial resolution (1000 m) of MODIS LAI data, we have not used it in this study. Three distance measures have been applied to Fourier based techniques, which combine amplitudes and phases in one equation [
13]. Besides that, three other similarity measures are mentioned and compared for detailed vegetation classification, see [
35,
36]. The simple and effective Euclidean distance employed in this study makes the combination of amplitude and phase information more flexible, even elimination of phase information. A further comparison between NDVI and EVI time series and between different distance measures may be required. (iii) Accuracy statistics: The accuracy statistic provided in this study relates to dominant classes only but soft classifications can, by definition, be more accurate than hard classifications [
37]. For example, large (sub-pixel) areas of bare ground in the Tibetan grasslands might be completely undetected in biome (hard) classifications.