Segmentation of Sloped Roofs from Airborne LiDAR Point Clouds Using Ridge-Based Hierarchical Decomposition
Abstract
:1. Introduction
2. Methodology
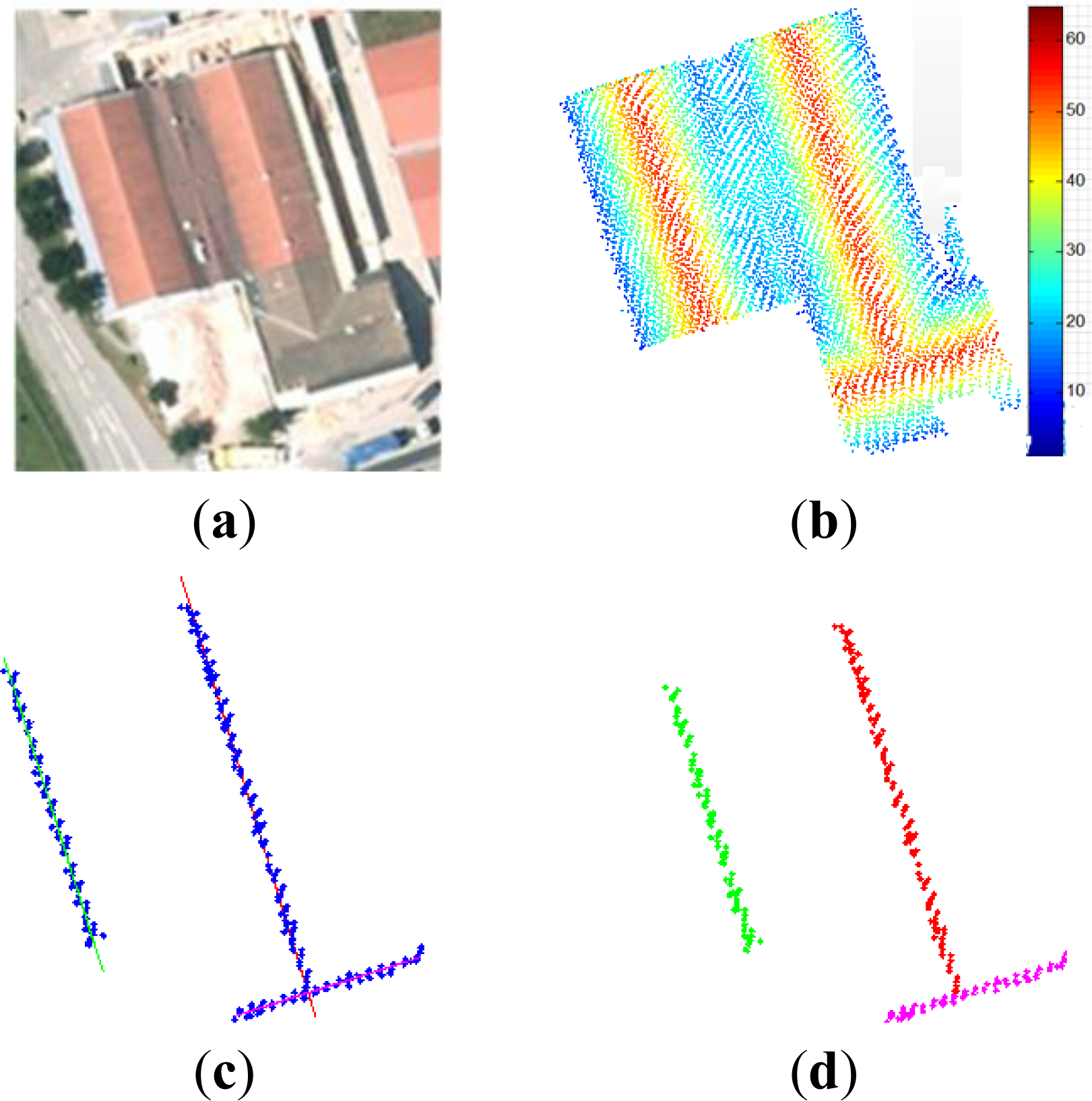
2.1. Detection of Roof Ridges
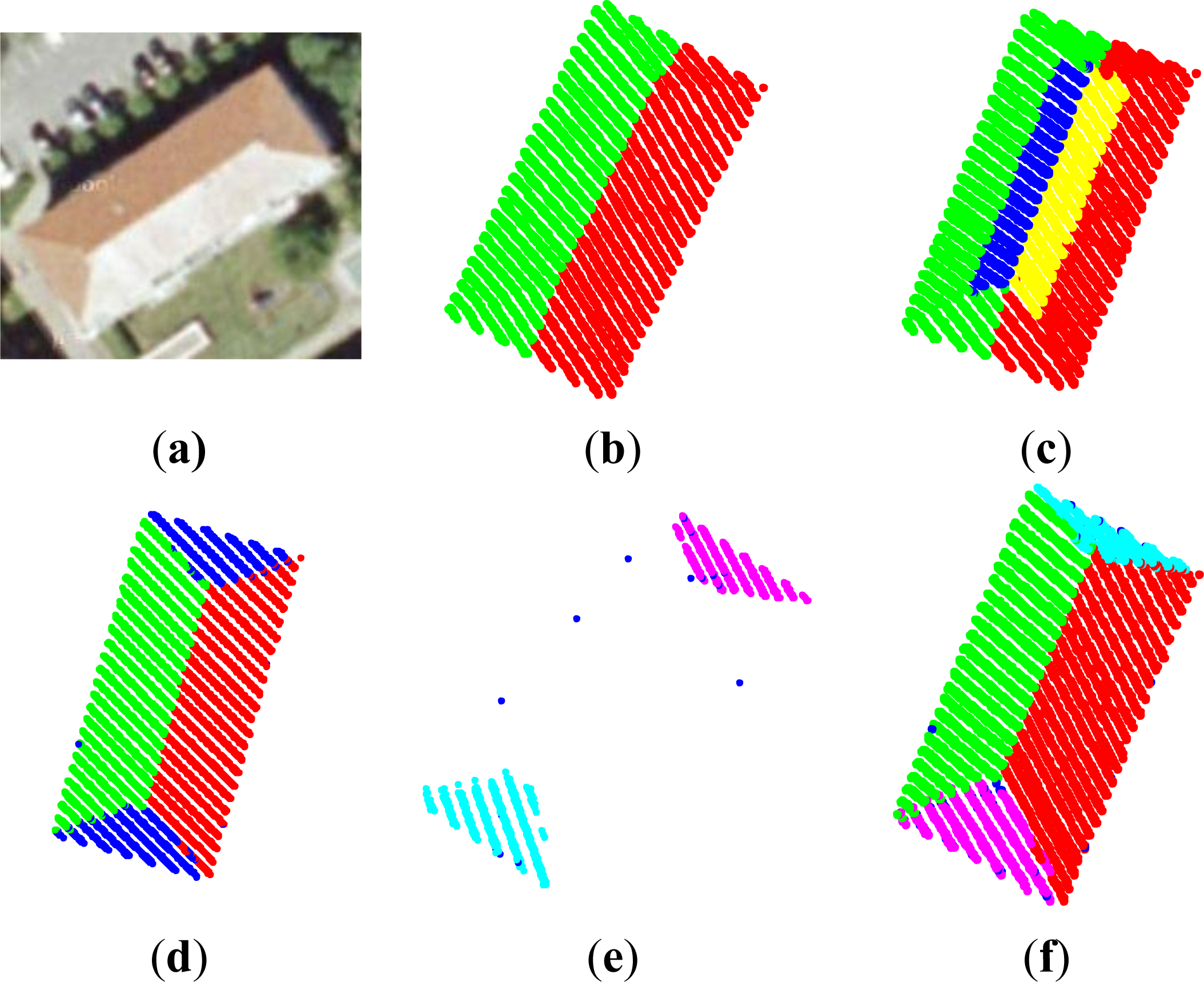
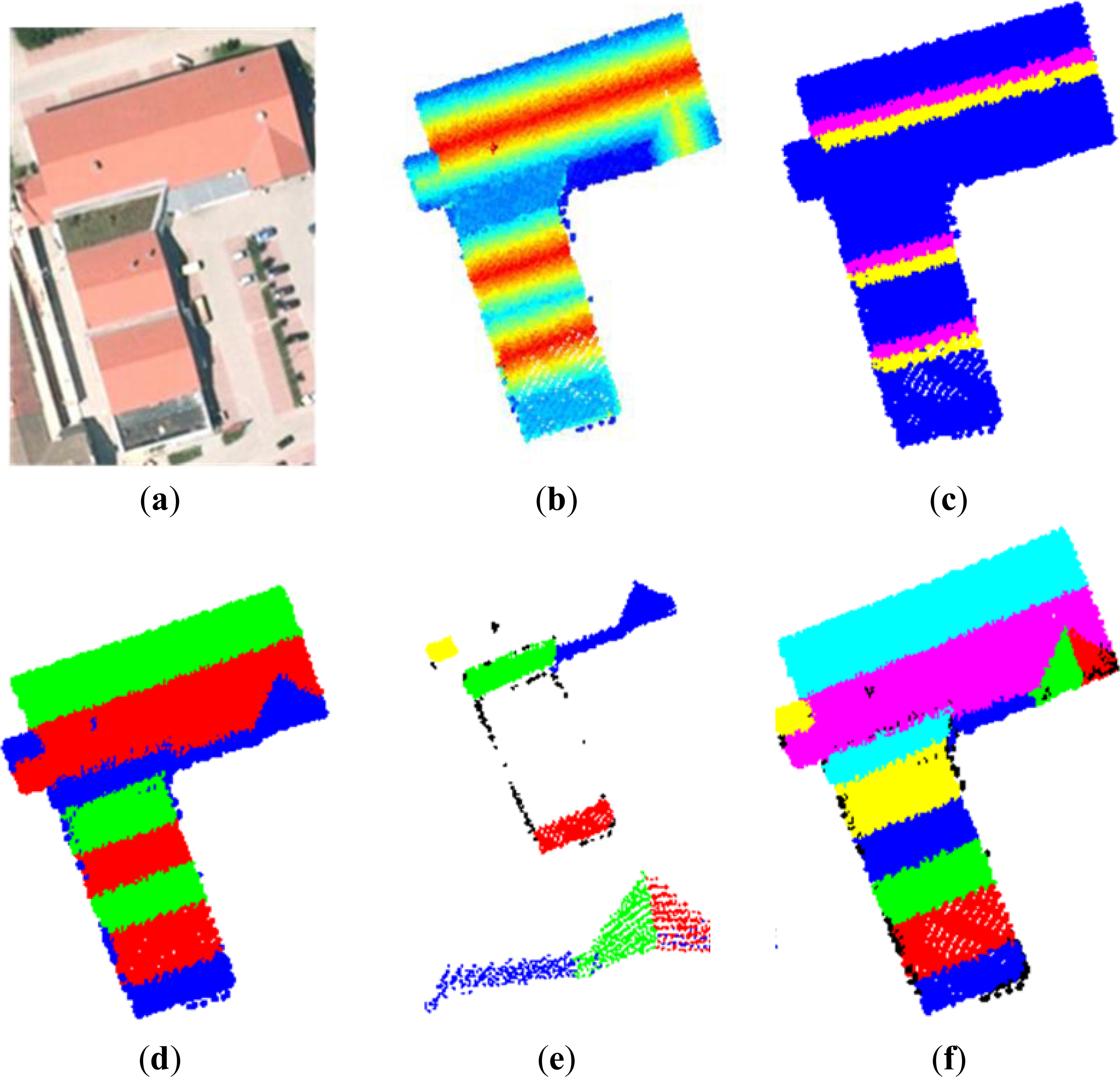
2.2. Segmentation of Points along Hierarchical Decomposition of Roof Structure
3. Dataset and Pre-Processing
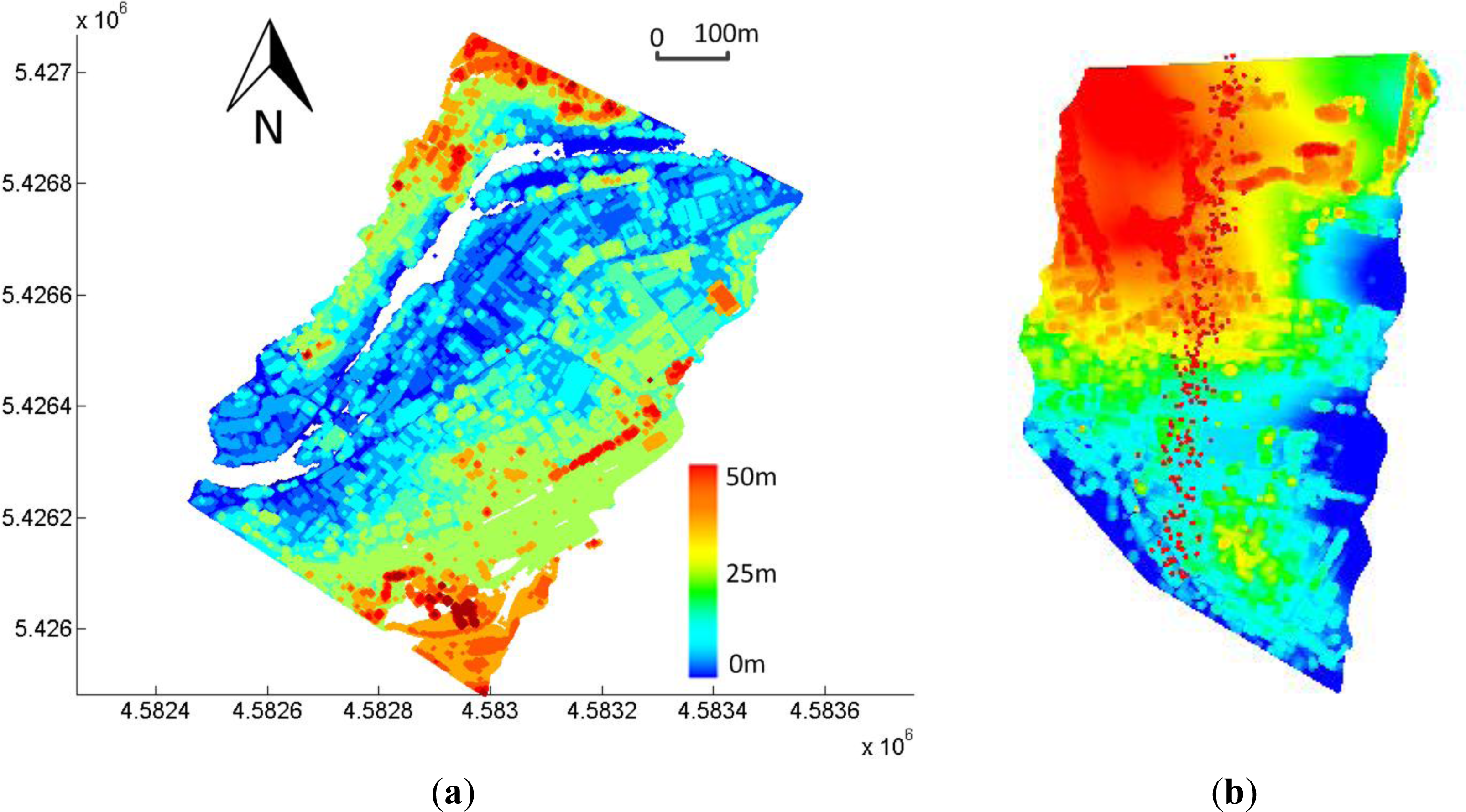
3.1. Experimental Data
3.2. OSM Aided Extraction of Building Roofs
4. Experimental Analysis
4.1. Evaluation of Segmented Roofs
4.2. Computational Performance
5. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Roux, M.; McKeown, D.M. Feature Matching for Building Extraction from Multiple Views. Proceedings of the 1994 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Menterey, CA, USA, 21–23 June 1994; pp. 331–339.
- Wu, J.-W.; Sun, J.; Yao, W.; Stilla, U. Building Boundary Improvement for True Orthophoto Generation by Fusing Airborne LiDAR Data. Proceedings of the IEEE and ISPRS Joint Event on Urban Remote Sensing (JURSE2011), Munich, Germany, 11–13 April 2011; pp. 1–4.
- Chen, L.C.; Teo, T.A.; Shao, Y.C.; Lai, Y.C.; Rau, J.Y. Fusion of LIDAR data and optical imagery for building modelling. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2004, 35, 586–591. [Google Scholar]
- Tarantino, E.; Figorito, B. Extracting buildings from true color stereo aerial images using a decision making strategy. Remote Sens 2011, 3, 1553–1567. [Google Scholar]
- Lin, C.; Huertas, A.; Nevatia, R. Detection of Buildings Using Perceptual Grouping and Shadows. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 21–23 June 1994; pp. 62–69.
- Jaynes, C.; Marengoni, M.; Hanson, A.; Riseman, E.; Schultz, H. Knowledge-Directed Reconstruction from Multiple Aerial Images. Proceedings of the ARPA Image Understanding Workshop, New Orleans, LA, USA, May 1997; Volume II,. pp. 971–976.
- Noronha, S.; Nevatia, R. Detection and modeling of buildings from multiple aerial images. IEEE Trans. Pattern Anal. Mach. Intell 2011, 23, 501–518. [Google Scholar]
- Shi, F.; Xi, Y.; Li, X.; Duan, Y. An automation system of rooftop detection and 3D building modeling from aerial images. J. Intell. Robot. Syst 2011, 62, 383–396. [Google Scholar]
- Fischer, A.; Kolbe, T.H.; Lang, F.; Cremers, A.B.; Förstner, W.; Plümer, L.; Steinhage, V. Extracting buildings from aerial images using hierarchical aggregation in 2D and 3D. Comput. Vis. Image Underst 1998, 72, 185–203. [Google Scholar]
- Suveg, I.; Vosselman, G. Automatic 3D building reconstruction. Proc. SPIE 2002. [Google Scholar] [CrossRef]
- Hammoudi, K.; Dornaika, F.A. Featureless approach to 3D polyhedral building modeling from aerial images. Sensors 2011, 11, 228–259. [Google Scholar]
- Brunn, A.; Weidner, U. Extracting buildings from digital surface models. Int. Arch. Photogramm. Remote Sens 1997, 32, 17–19. [Google Scholar]
- Galvanin, E.A.S.; Poz, A.P.D. Extraction of building roof contours from lidar data using a Markov random field based approach. IEEE Trans. Geosci. Remote Sens 2012, 50, 981–987. [Google Scholar]
- Sirmacek, B.; Taubenbock, H.; Reinartz, P.; Ehlers, M. Performance evaluation for 3-D city model generation of six different DSMs from air and spaceborne sensors. IEEE J. Sel. Top. Appl 2012, 5, 59–70. [Google Scholar]
- Brenner, C. Building reconstruction from images and laser scanning. Int. J. Appl. Earth Obs. Geoinf 2005, 6, 187–198. [Google Scholar]
- Vosselman, G. Building reconstruction using planar faces in very high density height data. Int. Arch. Photogramm. Remote Sens 1999, 32, 87–92. [Google Scholar]
- Haala, N.; Kada, M. An update on automatic 3D building reconstruction. ISPRS J. Photogramm. Remote Sens 2010, 65, 570–580. [Google Scholar]
- Brenner, C. Interactive Modelling Tools for 3D Building Reconstruction. In Photogrammetric Week 99’; Fritsch, D., Spiller, R., Eds.; Wichmann Verlag: Berlin, Germany, 1999; pp. 23–34. [Google Scholar]
- Vosselman, G.; Dijkman, S. 3D building model reconstruction from point clouds and ground plans. Int. Arch. Photogramm. Remote Sens. Spat. Infor. Sci 2001, 34, 37–44. [Google Scholar]
- Alharthy, A.; Bethel, J. Heuristic Filtering and 3D Feature Extraction from Lidar Data. Proceedings of the ISPRS Commission III, Graz, Austria, 9–13 September 2002.
- You, S.; Hu, J.; Neumann, U.; Fox, P. Urban Site Modeling from Lidar. Proceedings of the Computational Science and Its Applications—ICCSA 2003, Montreal, QC, Canada, 18–21 May 2003; pp. 579–588.
- Rottensteiner, F.; Briese, C. Automatic Generation of Building Models from LiDAR Data and the Integration of Aerial Images. Proceedings of the ISPRS Working Group III/3 Workshop on 3-D Reconstruction from Airborne Laserscanner and InSAR Data, Dresden, Germany, 8–10 October 2003; Volume XXXIV. pp. 174–180.
- Hu, J.; You, S.; Neumann, U. Approaches to large-scale urban modeling. IEEE Comput. Graph. Appl 2003, 23, 62–69. [Google Scholar]
- Tack, F.; Buyuksalih, G.; Goossens, R. 3D building reconstruction based on given ground plan information and surface models extracted from spaceborne imagery. ISPRS J. Photogramm. Remote Sens 2012, 67, 52–64. [Google Scholar]
- Rottensteiner, R. Automatic generation of high-quality building models from LiDAR data. IEEE Comput. Graph. Appl 2003, 23, 42–50. [Google Scholar]
- Dorninger, P.; Pfeifer, N. A comprehensive automated 3D approach for building extraction, reconstruction, and regularization from airborne laser scanning point clouds. Sensors 2008, 8, 7323–7343. [Google Scholar]
- Maas, H.-G.; Vosselman, G. Two algorithms for extracting building models from raw laser altimetry data. ISPRS J. Photogramm. Remote Sens 1999, 54, 153–163. [Google Scholar]
- Tarsha-Kurdi, F.; Landes, T.; Grussenmeyer, P. Extended RANSAC algorithm for automatic detection of building roof planes from LiDAR data. Photogramm. J. Finl 2008, 21, 97–109. [Google Scholar]
- Hebel, M.; Stilla, U. Simultaneous calibration of ALS systems and alignment of multiview LiDAR scans of urban areas. IEEE Trans. Geosci. Remote Sens 2012, 50, 2364–2379. [Google Scholar]
- Susaki, J. Knowledge-based modeling of buildings in dense urban areas by combining airborne LiDAR data and aerial images. Remote Sens 2013, 5, 5944–5968. [Google Scholar]
- Huang, H.; Brenner, C.; Sester, M. A generative statistical approach to automatic 3D building roof reconstruction from laser scanning data. ISPRS J. Photogramm. Remote Sens 2013, 79, 29–43. [Google Scholar]
- Kada, M. Scale-Dependent Simplification of 3D Building Models Based on Cell Decomposition and Primitive Instancing. Proceedings of the 8th International Conference On Spatial Information Theory (COSIT’07), Melbourne, Australiia, 19–23 September 2007; Springer-Verlag: Berlin/Heidelberg, Germany; pp. 222–237.
- Haala, N.; Becker, S.; Kada, M. Cell Decomposition for the Generation of Building Models at Multiple Scales. Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences (PCV06), Bonn, Germany, 20–22 September 2006.
- Henn, A.; Gröger, G.; Stroh, V.; Plümer, L. Model driven reconstruction of roofs from sparse LiDAR point clouds. ISPRS J. Photogramm. Remote Sens 2013, 76, 17–29. [Google Scholar]
- Oude Elberink, S.; Vosselman, G. Building reconstruction by target based graph matching on incomplete laser data: Analysis and limitations. Sensors 2009, 9, 6101–6118. [Google Scholar]
- Verma, V.; Kumar, R.; Hsu, S. 3D Building Detection and Modeling from Aerial LiDAR Data. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), New York, NY, USA, 2006; Volume 2,. pp. 2213–2220.
- Kim, K.; Shan, J. Building roof modelling from airborne laser scanning data based on level set approach. ISPRS J. Photogramm. Remote Sens 2011, 66, 484–497. [Google Scholar]
- Sampath, A.; Shan, J. Segmentation and reconstruction of polyhedral building roofs from aerial LiDAR point clouds. IEEE Trans. Geosci. Remote Sens 2010, 48, 1554–1567. [Google Scholar]
- Zhou, Q.-Y.; Neumann, U. 2.5D Building Modeling by Discovering Global Regularities. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 326–333.
- Rottensteiner, F.; Trinder, J.; Clode, S.; Kubik, K. Automated delineation of roof planes in LiDAR data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2008, 36, 221–226. [Google Scholar]
- Fischer, M.A.; Bolles, R. Random sample consensus: A paradigm for modelling fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar]
- Jain, A.K.; Murty, M.N.P.; Flynn, J. Data clustering: A review. ACM Comput. Surv 1999, 31, 264–323. [Google Scholar]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Unsupervised Learning and Clustering. In Pattern Classification, 2nd ed; Wiley: Hoboken, NJ, USA, 2001; pp. 519–598. [Google Scholar]
- Berkhin, P. A Survey of Clustering Data Mining Techniques. In Grouping Multidimensional Data: Recent Advances in Clustering; Kogan, J., Nicholas, C., Teboulle, M., Eds.; Springer-Verlag: New York, NY, USA, 2006; pp. 25–71. [Google Scholar]
- Fan, H.; Zipf, A.; Fu, Q.; Neis, P. Quality assessment of building footprints data on OpenStreetMap. Int. J. Geogr. Inf. Sci 2013, 28, 700–719. [Google Scholar]
- Rottensteiner, F.; Sohn, G.; Gerke, M.; Wegner, J.D.; Breitkopf, U.; Jung, J. Results of the ISPRS benchmark on urban object detection and 3D building reconstruction. ISPRS J. Photogramm. Remote Sens 2014, in press.. [Google Scholar]



| Location | Equipment | Date of Acquisition | Average Point Density | Scan Angle |
|---|---|---|---|---|
| Regen | Riegl LMS-Q560 | 2007 May | 6 | +30° |
| Kirchdorf | Riegl LMS-Q560 | 2007 May | 9 | +30° |
| Figure # | #Building | # Segmented Roof Facets | # Roof Facets in Data | Completeness (%) | Geometric Accuracy (RMSd−m) |
|---|---|---|---|---|---|
| 3 | 1 | 12 | 13 | 92.3 | 0.17 |
| 1 | 4 | 4 | 100 | 0.24 | |
| 2 | 6 | 6 | 100 | 0.31 | |
| 3 | 5 | 5 | 100 | 0.37 | |
| 6 | 4 | 8 | 8 | 100 | 1.09 |
| 5 | 9.7 | 11 | 88.2 | 0.35 | |
| 6 | 8 | 8 | 100 | 0.46 | |
| 7 | 28 | 34 | 82.4 | 0.45 | |
| Mean | 95.4 | 0.43 | |||
| Figure # | Building # | Number of Points | # Average Iterations of Plane Fitting | Computation Time (s) |
|---|---|---|---|---|
| 4 | 1 | 13,362 | 7.3 | 8.49 |
| 1 | 5952 | 3.8 | 1.89 | |
| 2 | 4697 | 4.0 | 1.21 | |
| 3 | 4554 | 4.0 | 1.05 | |
| 5 | 4 | 1551 | 5.9 | 0.66 |
| 5 | 17,788 | 5.3 | 9.51 | |
| 6 | 8522 | 7.4 | 7.91 | |
| 7 | 15,426 | 10.3 | 17.44 | |
| Mean | 6.02 | |||
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fan, H.; Yao, W.; Fu, Q. Segmentation of Sloped Roofs from Airborne LiDAR Point Clouds Using Ridge-Based Hierarchical Decomposition. Remote Sens. 2014, 6, 3284-3301. https://doi.org/10.3390/rs6043284
Fan H, Yao W, Fu Q. Segmentation of Sloped Roofs from Airborne LiDAR Point Clouds Using Ridge-Based Hierarchical Decomposition. Remote Sensing. 2014; 6(4):3284-3301. https://doi.org/10.3390/rs6043284
Chicago/Turabian StyleFan, Hongchao, Wei Yao, and Qing Fu. 2014. "Segmentation of Sloped Roofs from Airborne LiDAR Point Clouds Using Ridge-Based Hierarchical Decomposition" Remote Sensing 6, no. 4: 3284-3301. https://doi.org/10.3390/rs6043284
APA StyleFan, H., Yao, W., & Fu, Q. (2014). Segmentation of Sloped Roofs from Airborne LiDAR Point Clouds Using Ridge-Based Hierarchical Decomposition. Remote Sensing, 6(4), 3284-3301. https://doi.org/10.3390/rs6043284




