Estimation of Diurnal Cycle of Land Surface Temperature at High Temporal and Spatial Resolution from Clear-Sky MODIS Data
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. MSG-SEVIRI Data
2.3. MODIS Data
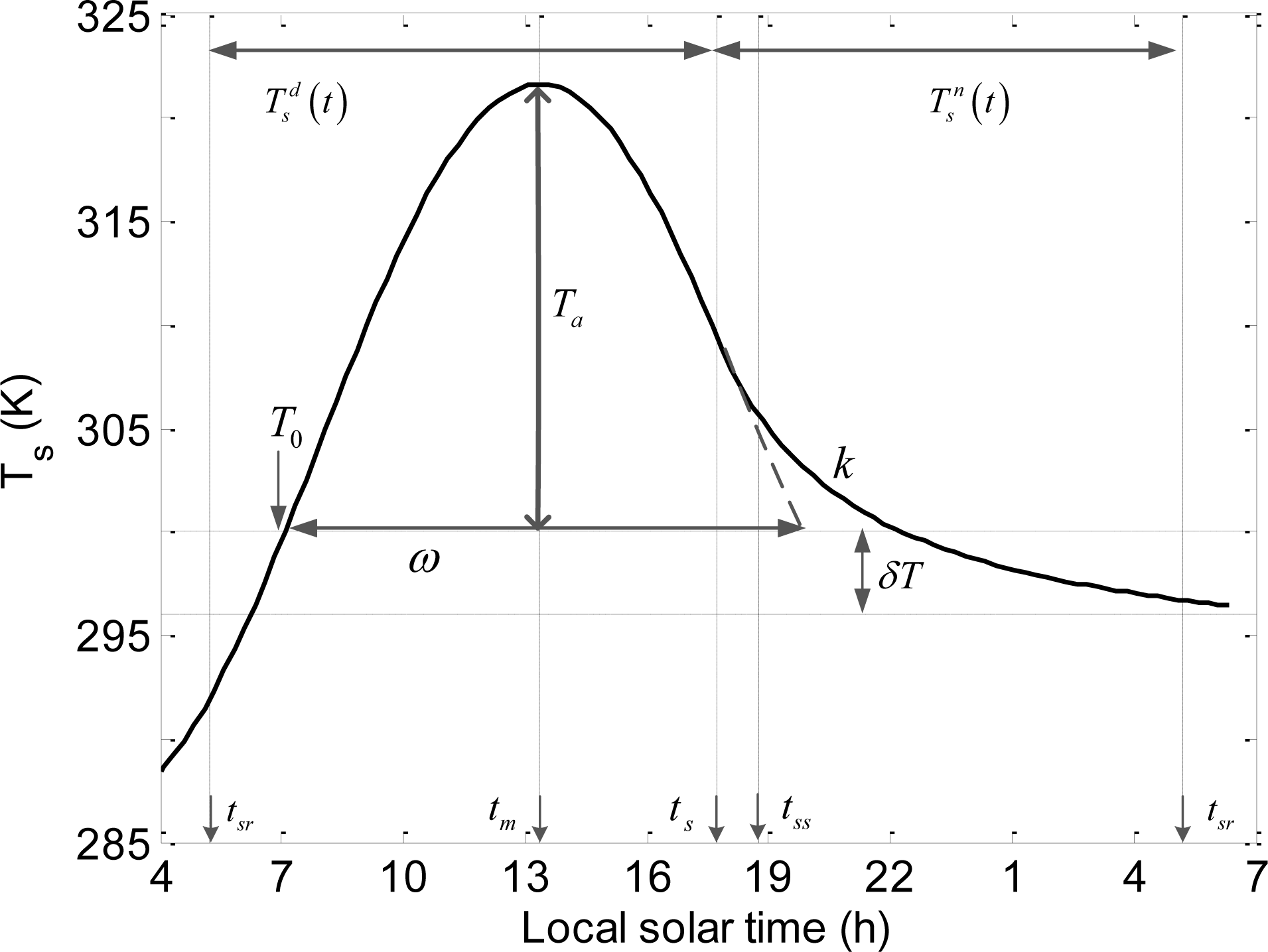
3. Methodology
4. Results and Discussion
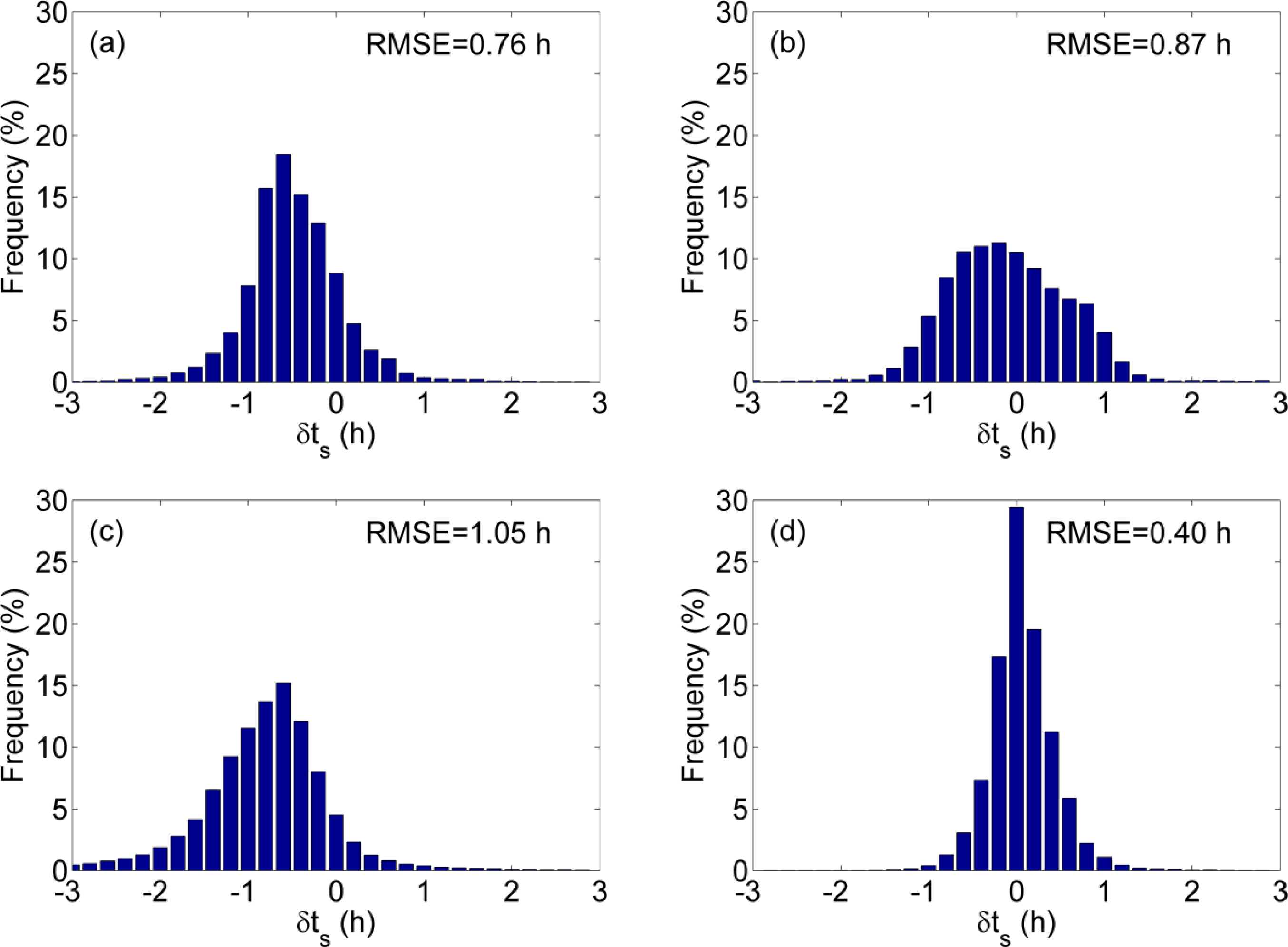
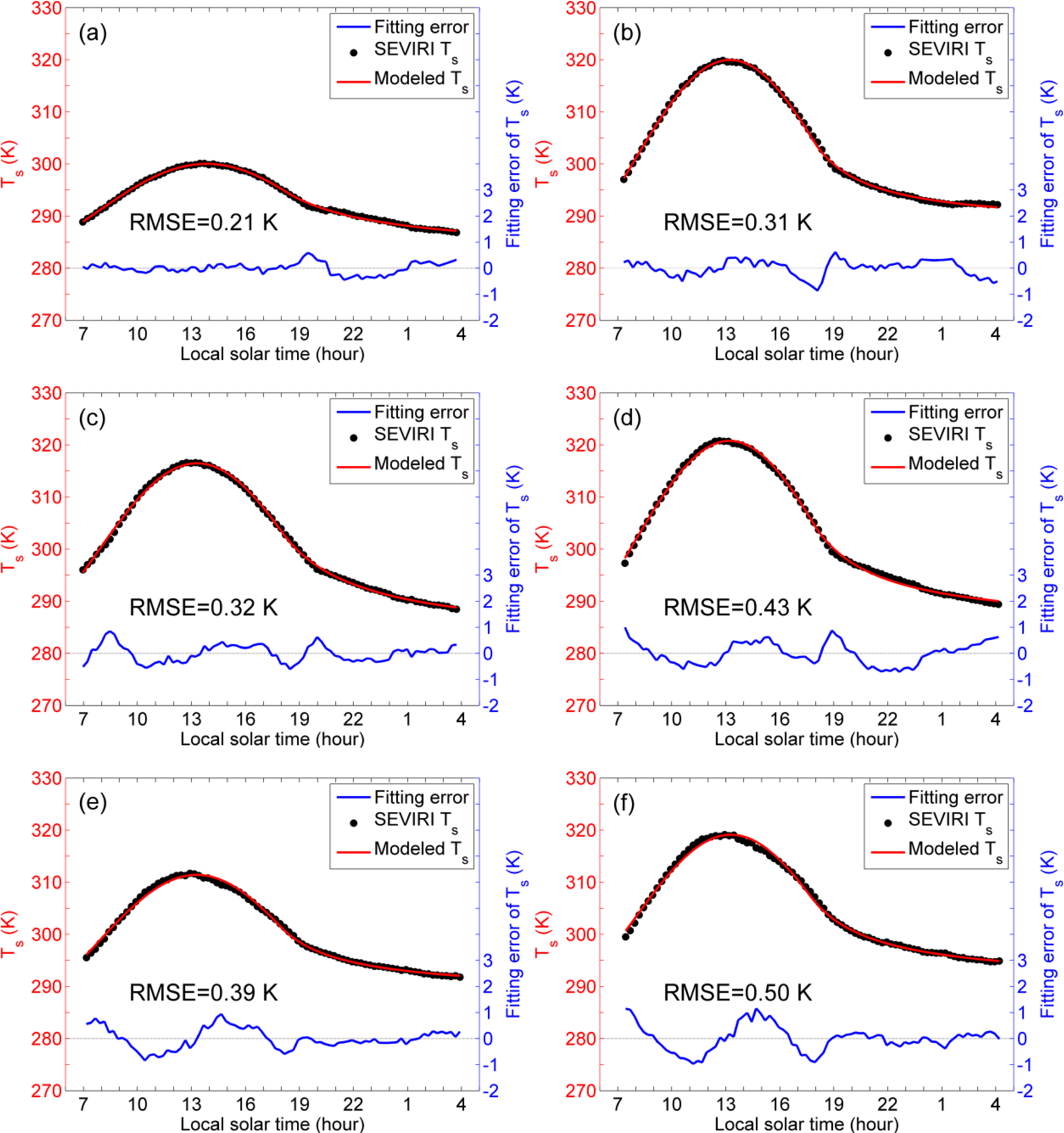
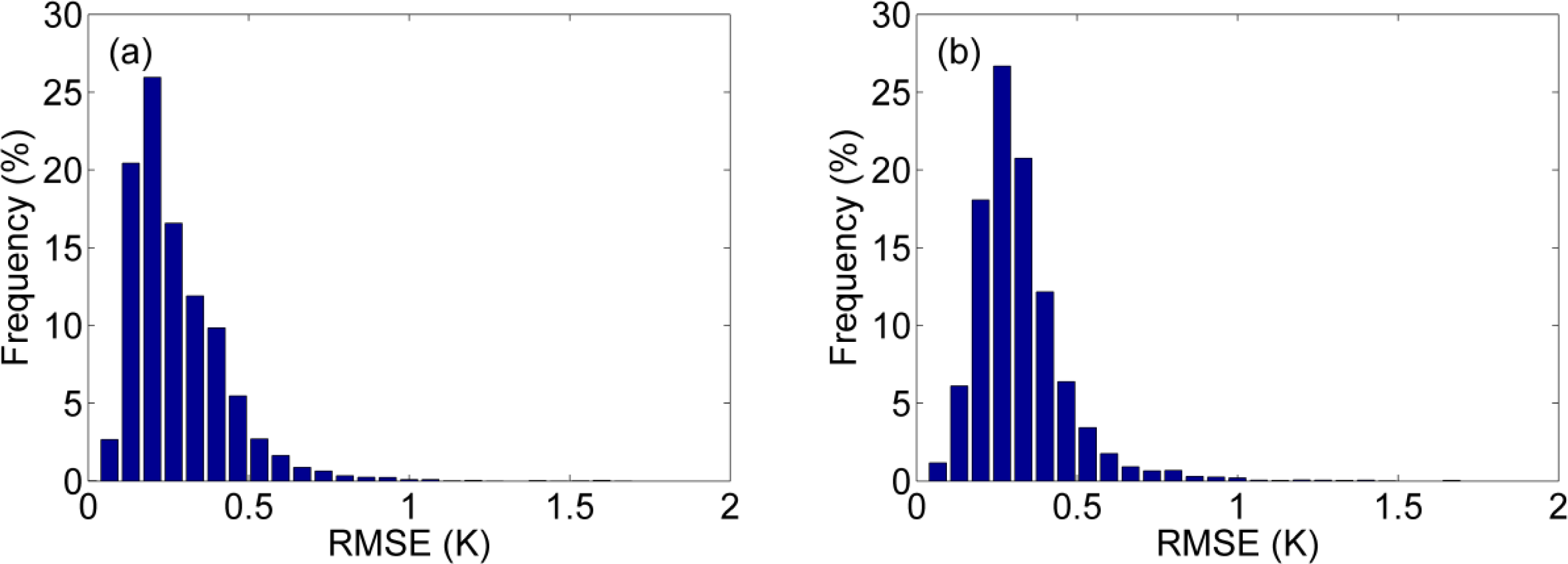
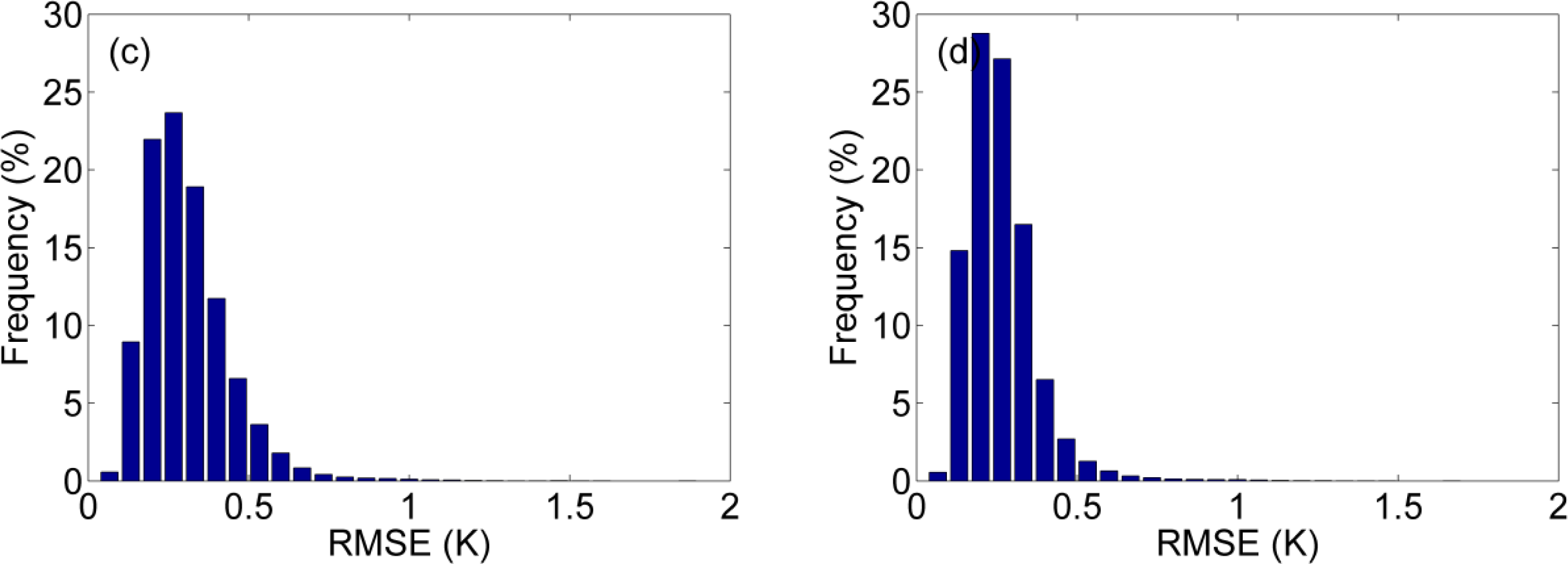
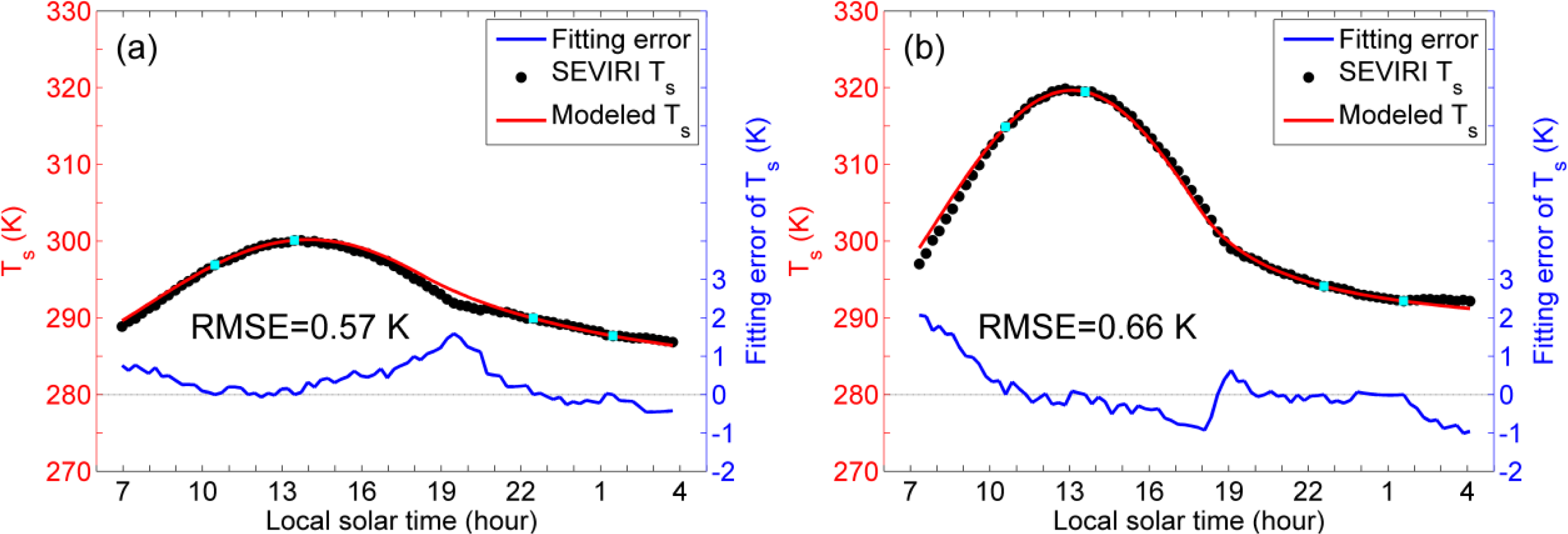
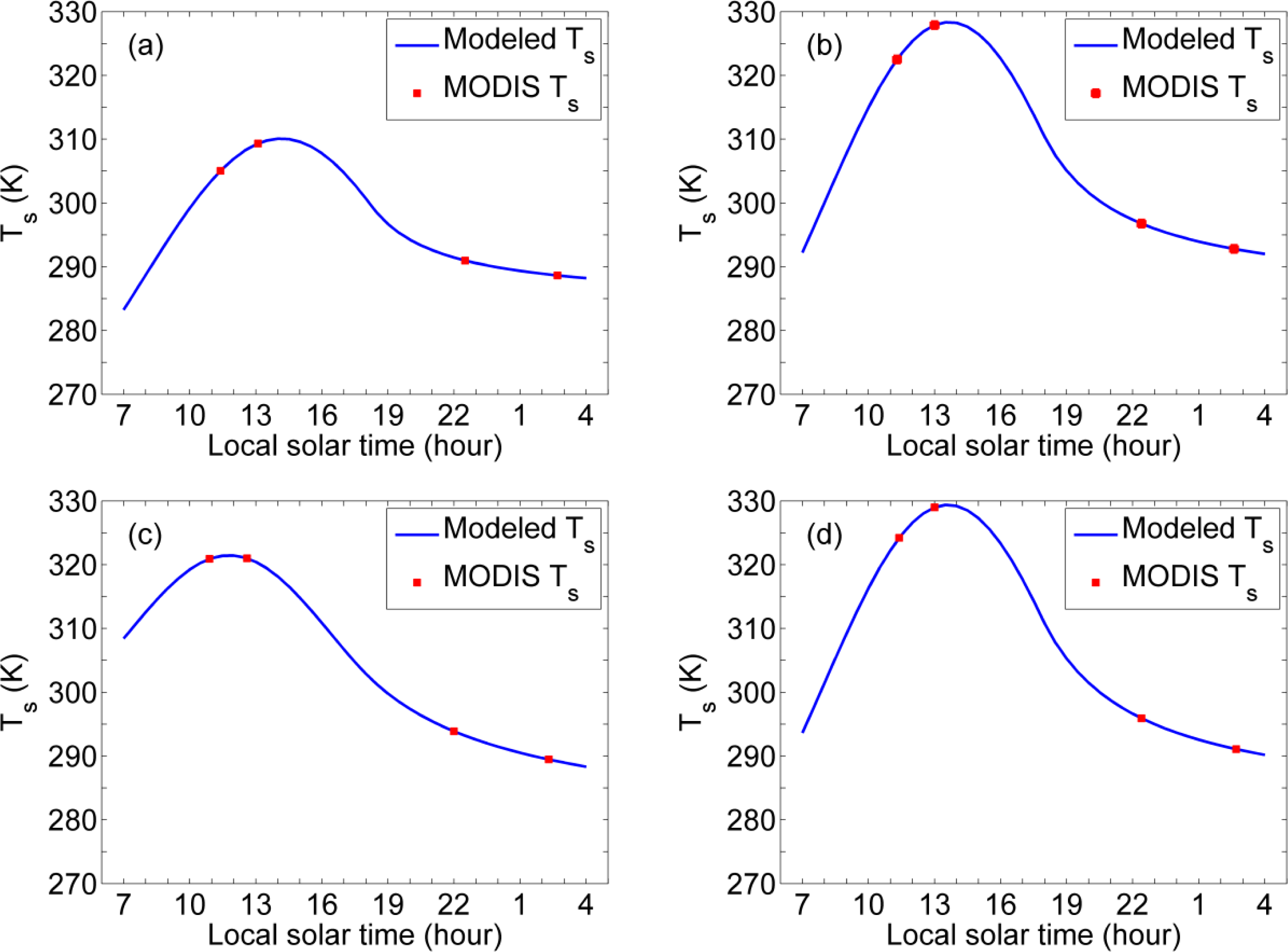
4.1. Evaluation of the 4-parameter DTC Model
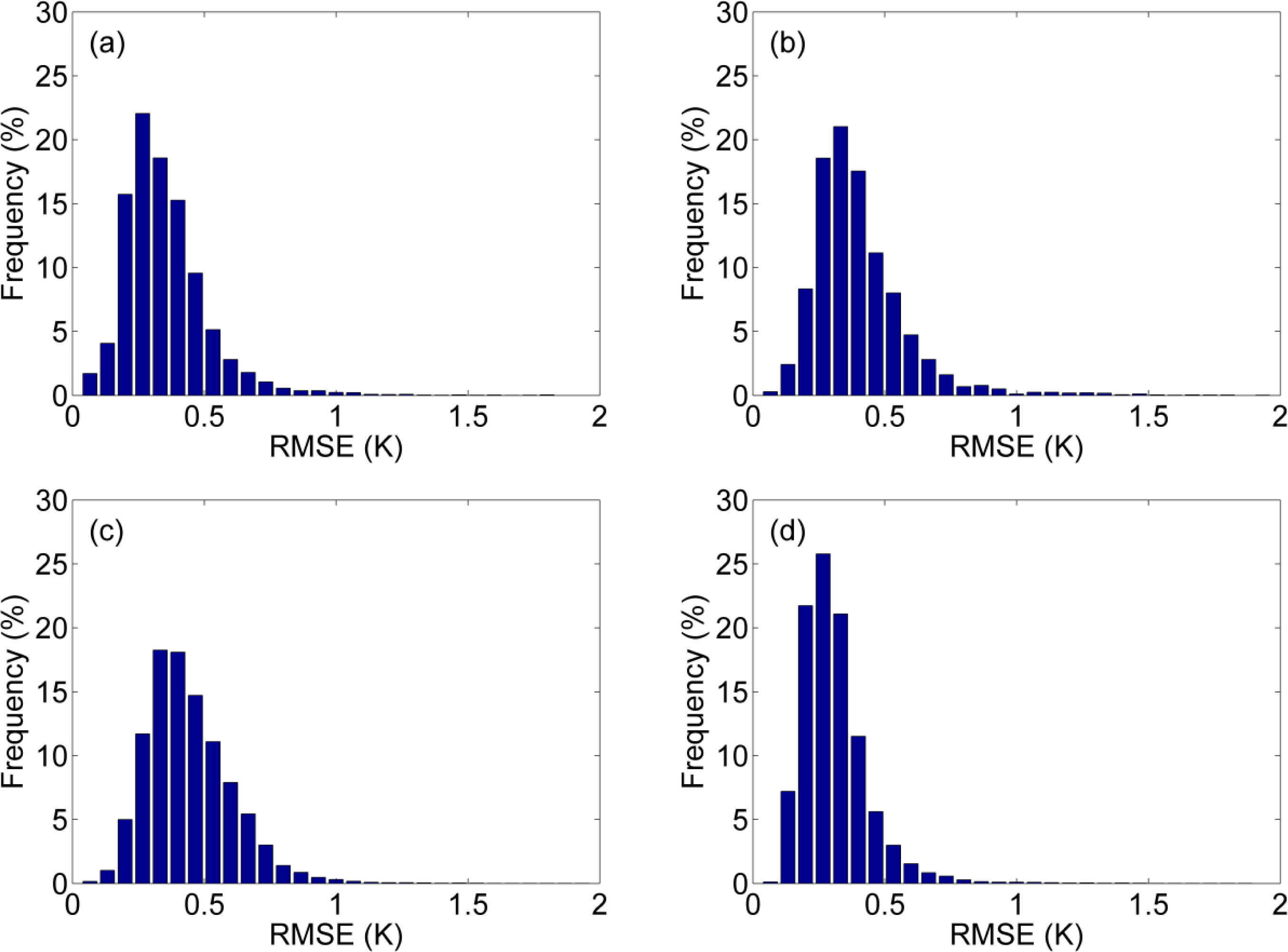
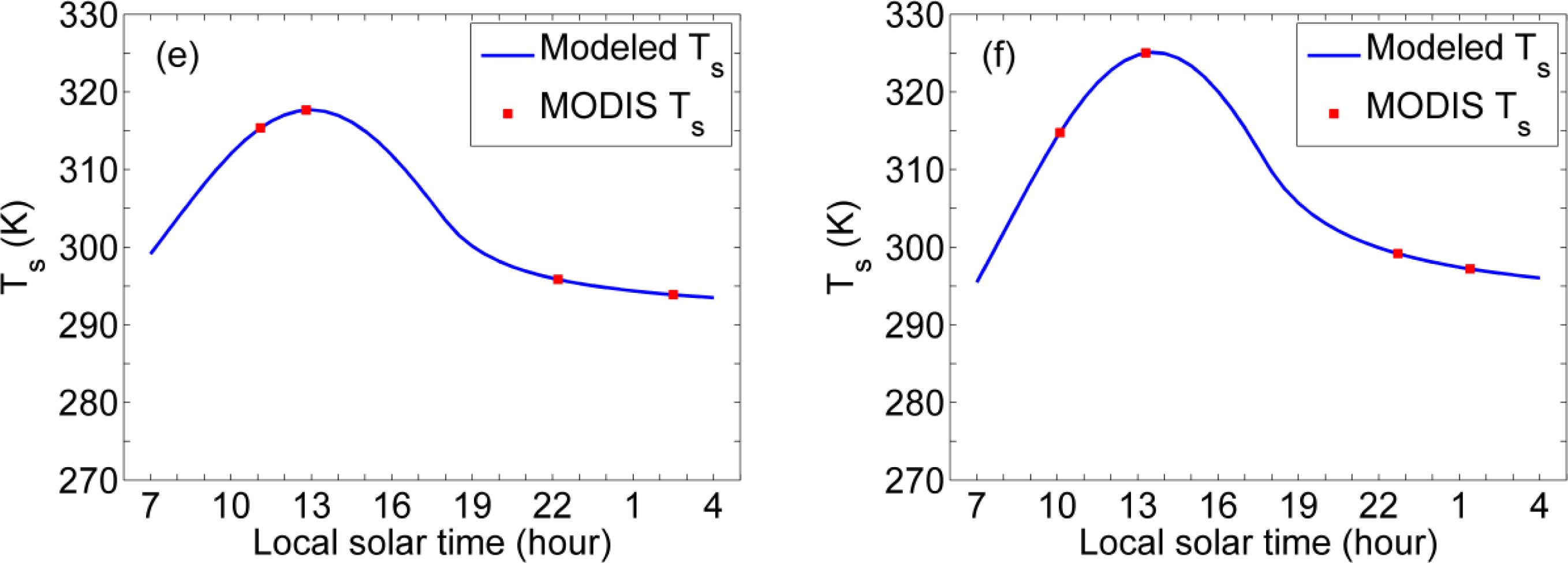
4.2. Fitting the 4-Parameter DTC Model to Four Observations
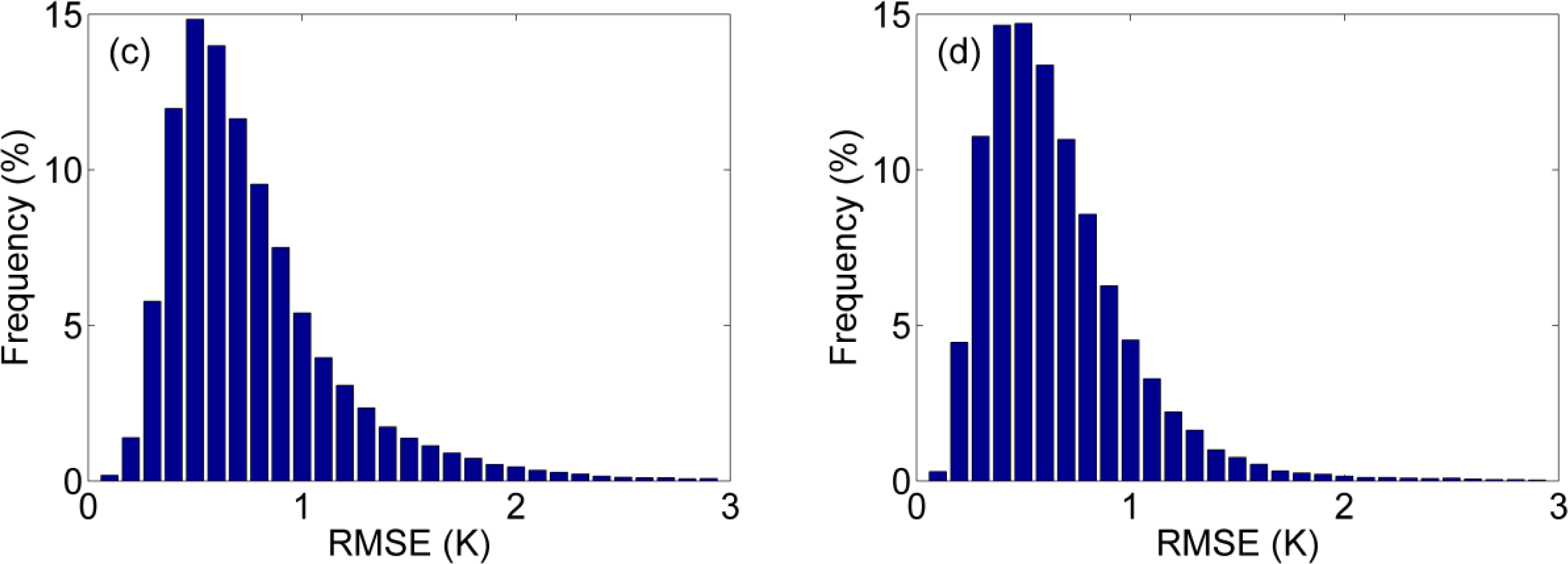
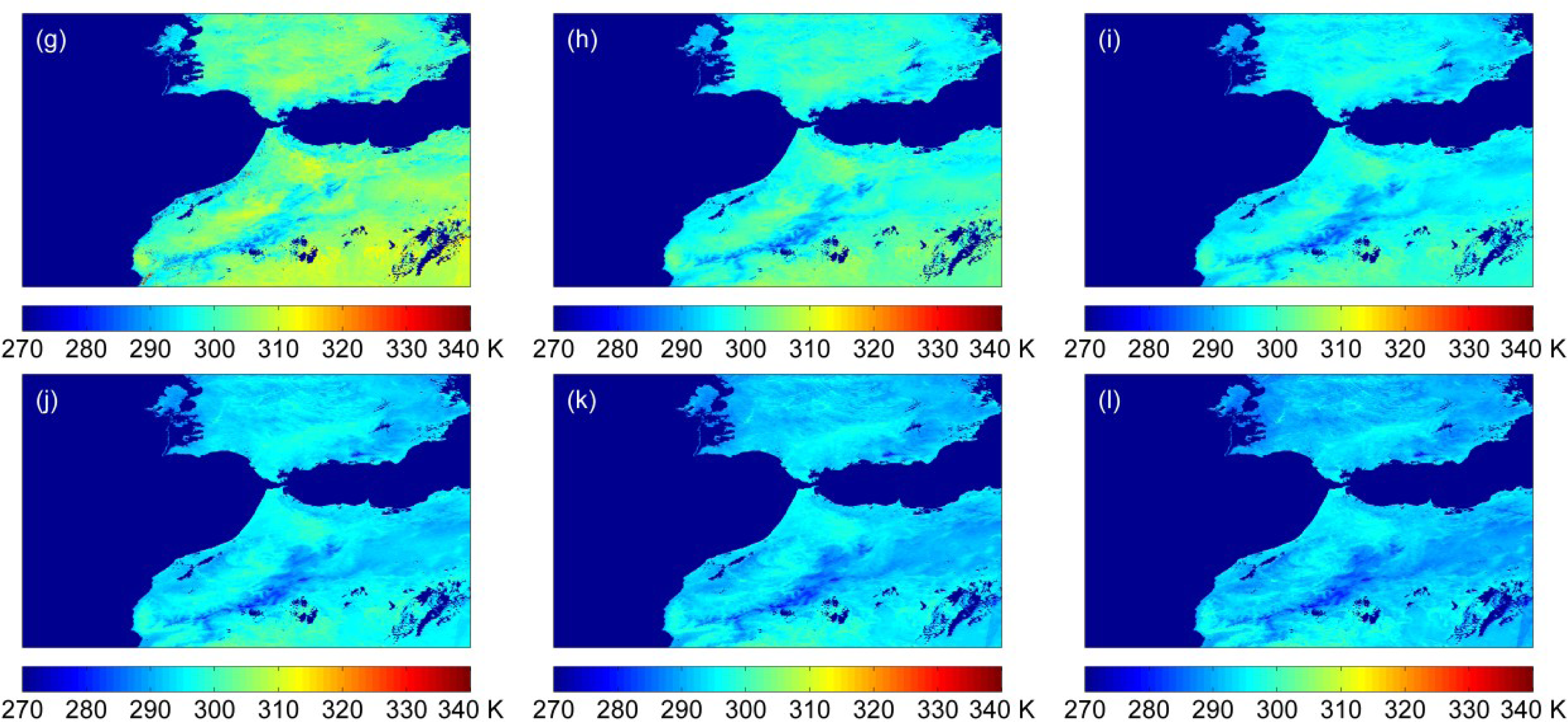
4.3. Application to MODIS Data
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References and Notes
- Scarino, B.; Minnis, P.; Palikonda, R.; Reichle, R.H.; Morstad, D.; Yost, C.; Shan, B.; Liu, Q. Retrieving clear-sky surface skin temperature for numerical weather prediction application from geostationary satellite data. Remote Sens 2013, 5, 342–366. [Google Scholar]
- Wan, Z.; Li, Z.-L. A physics-based algorithm for retrieving land surface emissivity and temperature from EOS/MODIS data. IEEE Trans. Geosci. Remote Sens 1997, 35, 980–996. [Google Scholar]
- Li, Z.-L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A review of current methodologies for regional evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ 2013, 131, 14–37. [Google Scholar]
- Cho, A.-R.; Suh, M.-S. Evaluation of land surface temperature operationally retrieved from Korean geostationary satellite (COMS) data. Remote Sens 2013, 5, 3951–3970. [Google Scholar]
- Li, Z.-L.; Wu, H.; Wang, N.; Qiu, S.; Sobrino, J.A.; Wan, Z.; Tang, B.-H.; Yan, G. Land surface emissivity retrieval from satellite data. Int. J. Remote Sens 2013, 34, 3084–3127. [Google Scholar]
- Ignatov, A.; Gutman, G. Monthly mean diurnal cycles in surface temperatures over land for global climate studies. J. Climate 1999, 12, 1900–1910. [Google Scholar]
- Aires, F.; Prigent, C.; Rossow, W. Temporal interpolation of global surface skin temperature diurnal cycle over land under clear and cloudy conditions. J. Geophys. Res 2004, 109, 1–18. [Google Scholar]
- Duan, S.-B.; Li, Z.-L.; Wang, N.; Wu, H.; Tang, B.-H. Evaluation of six land-surface diurnal temperature cycle models using clear-sky in situ and satellite data. Remote Sens. Environ 2012, 124, 15–25. [Google Scholar]
- Duan, S.-B.; Li, Z.-L.; Tang, B.-H.; Wu, H.; Tang, R. Direct estimation of land-surface diurnal temperature cycle model parameters from MSG-SEVIRI brightness temperatures under clear sky conditions. Remote Sens. Environ 2014, in press.. [Google Scholar]
- Keramitsoglou, I.; Kiranoudis, C.T.; Weng, Q. Downscaling geostationary land surface temperature imagery for urban analysis. IEEE Geosci. Remote Sens. Lett 2013, 10, 1253–1257. [Google Scholar]
- Zhan, W.; Chen, Y.; Voogt, J.; Zhou, J.; Wang, J.; Liu, W.; Ma, W. Interpolating diurnal surface temperatures of an urban facet using sporadic thermal observations. Build. Environ 2012, 57, 239–252. [Google Scholar]
- Bechtel, B.; Zakšek, K.; Hoshyaripour, G. Downscaling land surface temperature in an urban area: A case study for Hamburg, Germany. Remote Sens 2012, 4, 3184–3200. [Google Scholar]
- Zhou, J.; Chen, Y.; Zhang, X.; Zhan, W. Modelling the diurnal variations of urban heat islands with multi-source satellite data. Int. J. Remote Sens 2013, 34, 7568–7588. [Google Scholar]
- Duan, S.-B.; Li, Z.-L.; Tang, B.-H.; Wu, H.; Tang, R. Generation of a time-consistent land surface temperature product from MODIS data. Remote Sens. Environ 2014, 140, 339–349. [Google Scholar]
- Jiang, G. Retrieval of Land Surface Emissivity and Land Surface Temperature from MSG1-SEVIRI Data. Ph.D. Dissertation, University of Strasbourg, Strasbourg, France. 2007. [Google Scholar]
- Jin, M.; Treadon, R.E. Correcting the orbit drift effect on AVHRR land surface skin temperature measurements. Int. J. Remote Sens 2003, 24, 4543–4558. [Google Scholar]
- Schroedter-Homscheidt, M.; Drews, A.; Heise, S. Total water vapour column retrieval from MSG-SEVIRI split window measurements exploiting the daily cycle of land surface temperature. Remote Sens. Environ 2008, 112, 249–258. [Google Scholar]
- Jin, M.; Dickinson, R.E. Interpolation of surface radiative temperature measured from polar orbiting satellites to a diurnal cycle 1. Without clouds. J. Geophys. Res 1999, 104, 2105–2116. [Google Scholar]
- Sun, D.; Pinker, R. Implementation of GOES-based land surface temperature diurnal cycle to AVHRR. Int. J. Remote Sens 2005, 26, 3975–3984. [Google Scholar]
- Inamdar, A.K.; French, A.; Hook, S.; Vaughan, G.; Luckett, W. Land surface temperature retrieval at high spatial and temporal resolutions over the southwestern United States. J. Geophys. Res 2008, 113, D07107. [Google Scholar] [CrossRef]
- Jiang, G.; Li, Z.-L. Split-window algorithm for land surface temperature estimation from MSG1-SEVIRI data. Int. J. Remote Sens 2008, 29, 6067–6074. [Google Scholar]
- Jiang, G.; Li, Z.-L.; Nerry, F. Land surface emissivity retrieval from combined mid-infrared and thermal infrared data of MSG-SEVIRI. Remote Sens. Environ 2006, 105, 326–340. [Google Scholar]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens 1996, 34, 892–905. [Google Scholar]
- Duan, S.-B.; Li, Z.-L.; Wu, H.; Tang, B.-H.; Jiang, X.; Zhou, G. Modeling of day-to-day temporal progression of clear-sky land surface temperature. IEEE Geosci. Remote Sens. Lett 2013, 10, 1050–1054. [Google Scholar]
- Göttsche, F.-M.; Olesen, F.-S. Modelling of diurnal cycles of brightness temperature extracted from METEOSAT data. Remote Sens. Environ 2001, 76, 337–348. [Google Scholar]
- Göttsche, F.-M.; Olesen, F.-S. Modelling the effect of optical thickness on diurnal cycles of land surface temperature. Remote Sens. Environ 2009, 113, 2306–2316. [Google Scholar]
- Frey, C.M.; Kuenzer, C.; Dech, S. Quantitative comparison of the operational NOAA-AVHRR LST product of DLR and the MODIS LST product V005. Int. J. Remote Sens 2012, 33, 7165–7183. [Google Scholar]
- Pinheiro, A.C.T.; Privette, J.L.; Guillevic, P. Modeling the observed angular anisotropy of land surface temperature in a savanna. IEEE Trans. Geosci. Remote Sens 2006, 44, 1036–1047. [Google Scholar]
- Pinheiro, A.C.T.; Privette, J.L.; Mahoney, R.; Tucker, C.J. Directional effects in a daily AVHRR land surface temperature dataset over Africa. IEEE Trans. Geosci. Remote Sens 2004, 42, 1941–1954. [Google Scholar]
- Rasmussen, M.O.; Göttsche, F.-M.; Olesen, F.-S.; Sandholt, I. Directional effects on land surface temperature estimation from Meteosat Second Generation for savanna landscapes. IEEE Trans. Geosci. Remote Sens 2011, 49, 4458–4468. [Google Scholar]
- Rasmussen, M.O.; Pinheiro, A.C.T.; Proud, S.R.; Sandholt, I. Modeling angular dependences in land surface temperature from the SEVIRI instrument onboard the Geostationary Meteosat Second Generation satellites. IEEE Trans. Geosci. Remote Sens 2010, 48, 3123–3133. [Google Scholar]
- Neteler, M. Estimating daily land surface temperature in mountainous environment by reconstructed MODIS LST data. Remote Sens 2010, 2, 333–351. [Google Scholar]
- Ke, L.; Ding, X.; Song, C. Reconstruction of time-series MODIS LST in central Qinghai-Tibet Plateau using geostatistical approach. IEEE Geosci. Remote Sens. Lett 2013, 10, 1602–1606. [Google Scholar]
- Hengl, T.; Heuvelink, G.B.M.; Perčec Tadić, M.; Pebesma, E.J. Spatio-temporal prediction of daily temperatures using time-series of MODIS LST images. Theor. Appl. Climatol 2012, 107, 265–277. [Google Scholar]




| Site | Latitude | Longitude | Elevation | Land Cover Type |
|---|---|---|---|---|
| A | 43.909°N | 0.235°E | 153.1 m | Forest |
| B | 34.161°N | 1.677°W | 1134.2 m | Shrubland |
| C | 40.030°N | 7.166°W | 381.7 m | Woodland |
| D | 33.941°N | 0.769°W | 1080.4 m | Grassland |
| E | 37.405°N | 4.326°W | 746.2 m | Cropland |
| F | 30.642°N | 3.564°E | 347.6 m | Unvegetated |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Duan, S.-B.; Li, Z.-L.; Tang, B.-H.; Wu, H.; Tang, R.; Bi, Y.; Zhou, G. Estimation of Diurnal Cycle of Land Surface Temperature at High Temporal and Spatial Resolution from Clear-Sky MODIS Data. Remote Sens. 2014, 6, 3247-3262. https://doi.org/10.3390/rs6043247
Duan S-B, Li Z-L, Tang B-H, Wu H, Tang R, Bi Y, Zhou G. Estimation of Diurnal Cycle of Land Surface Temperature at High Temporal and Spatial Resolution from Clear-Sky MODIS Data. Remote Sensing. 2014; 6(4):3247-3262. https://doi.org/10.3390/rs6043247
Chicago/Turabian StyleDuan, Si-Bo, Zhao-Liang Li, Bo-Hui Tang, Hua Wu, Ronglin Tang, Yuyun Bi, and Guoqing Zhou. 2014. "Estimation of Diurnal Cycle of Land Surface Temperature at High Temporal and Spatial Resolution from Clear-Sky MODIS Data" Remote Sensing 6, no. 4: 3247-3262. https://doi.org/10.3390/rs6043247
APA StyleDuan, S.-B., Li, Z.-L., Tang, B.-H., Wu, H., Tang, R., Bi, Y., & Zhou, G. (2014). Estimation of Diurnal Cycle of Land Surface Temperature at High Temporal and Spatial Resolution from Clear-Sky MODIS Data. Remote Sensing, 6(4), 3247-3262. https://doi.org/10.3390/rs6043247









