GIS-Based Roughness Derivation for Flood Simulations: A Comparison of Orthophotos, LiDAR and Crowdsourced Geodata
Abstract
:1. Introduction
2. Related Work
2.1. Flood Simulation
2.2. Hydraulic Roughness Coefficient
2.3. Risk Estimation
3. Study Area and Datasets
3.1. Study Area
3.2. Datasets
4. Methods
4.1. Roughness Parameterization
4.2. Hydrodynamic-Numerical Modeling
4.3. Risk Estimation
5. Results and Discussion
5.1. Roughness Maps
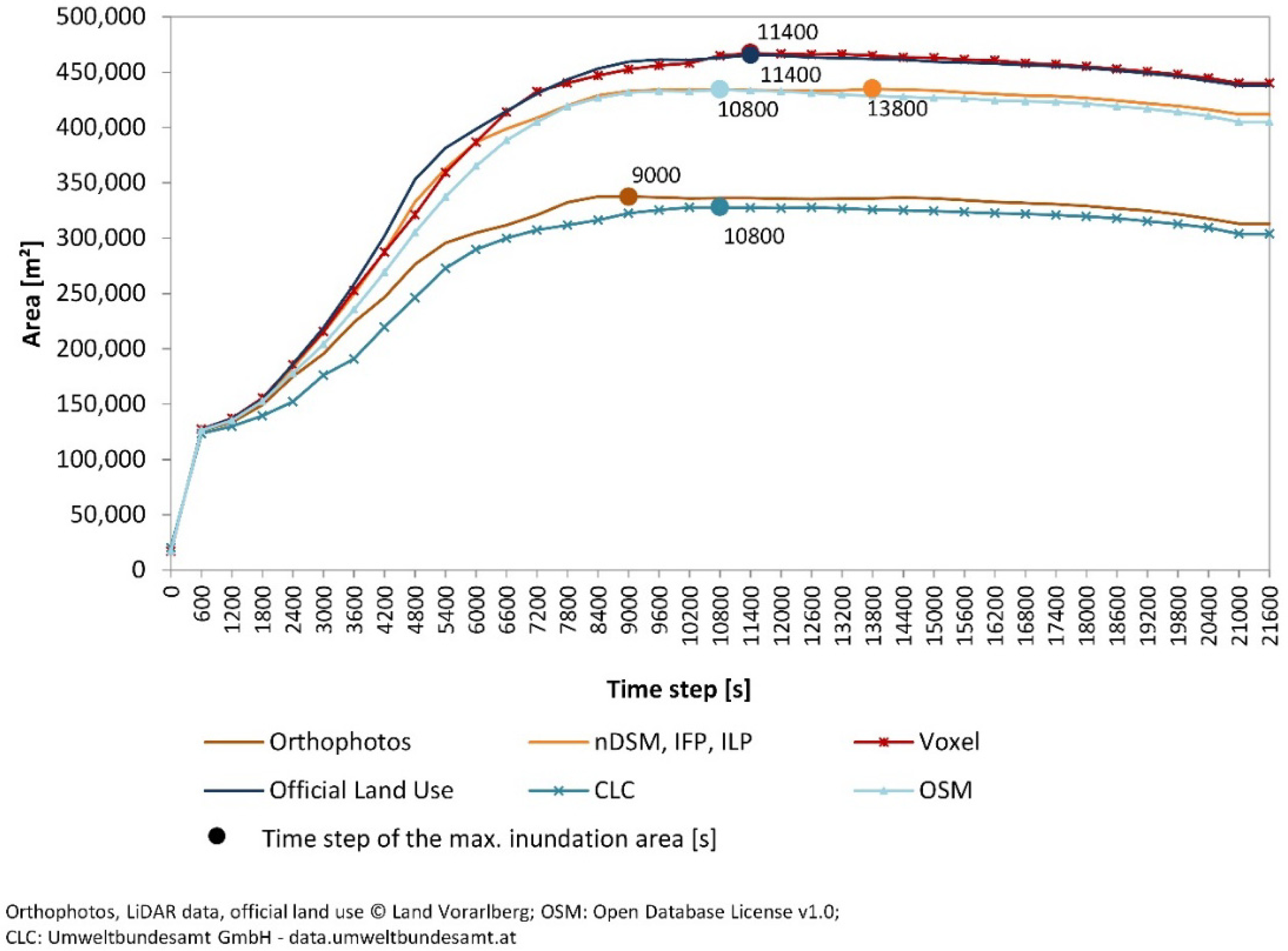
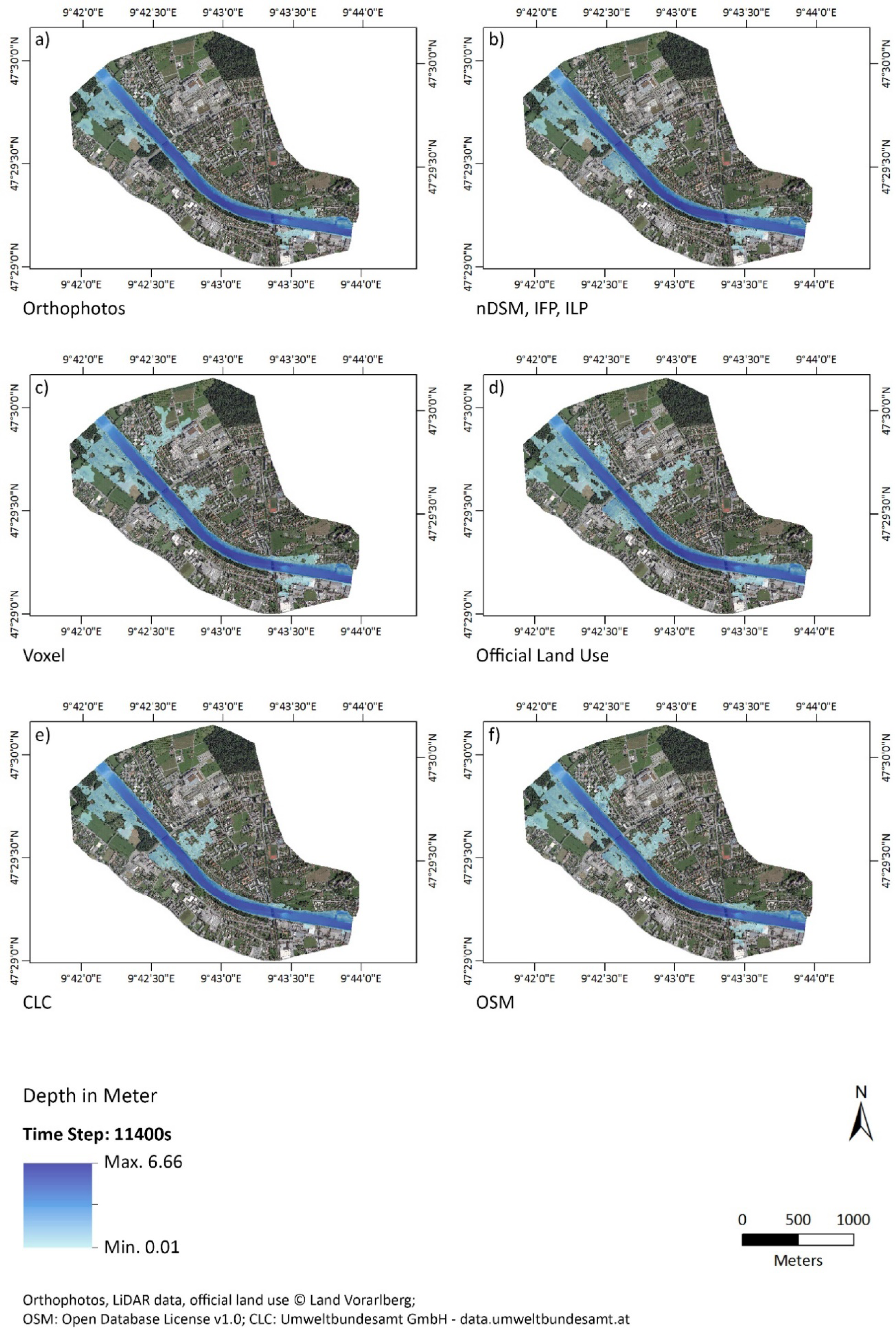
5.1. Water Depth and Flood Intensity
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- CRED EM-DAT. The International Disaster Database: Natural Disaster Trends. Available online: http://www.emdat.be/natural-disasters-trends (accessed on 30 September 2013).
- Pasche, E. The New EU-Flood Policy and Its Consequences for Urban Flood Management. In Special Aspects of Urban Flood Management: Proceedings of Cost Session Aquaterra Conference 2007; Pasche, E., Ed.; COST Office: Hamburg, Germany, 2008; pp. 137–160. [Google Scholar]
- Berchtold, M. Lebensader Bregenzerach—von Schoppernau nach Egg: Phase I Bestandsaufnahme. Available online: http://www.vorarlberg.at/pdf/bregenzerach__bestandserh.pdf (accessed on 30 September 2013).
- Amt der Vlbg. Landesreg. Das Starkregen- und Hochwasserereignis des August 2005 in Vorarlberg: Ein Bericht des Amtes der Vorarlberger Landesregierung. Available online: http://www.vorarlberg.at/pdf/naturereignisdokumentatio.pdf (accessed on 1 May 2013).
- Straatsma, M.W.; Baptist, M.J. Floodplain roughness parameterization using airborne laser scanning and spectral remote sensing. Remote Sens. Environ 2008, 112, 1062–1080. [Google Scholar]
- Straatsma, M.; Huthoff, F. Uncertainty in 2D hydrodynamic models from errors in roughness parameterization based on aerial images. Phys. Chem. Earth Parts A/B/C 2011, 36, 324–334. [Google Scholar]
- Wagner, W.; Vetter, M.; Bartsch, A. Novel Microwave- and Lidar Remote Sensing Techniques for Monitoring of In-Land Water Resources. In Acatech Materialien Nr. 7; Munich, Germany, 2011; pp. 1–42. [Google Scholar]
- Mandlburger, G.; Hauer, C.; Höfle, B.; Habersack, H.; Pfeifer, N. Optimisation of LiDAR derived terrain models for river flow modelling. Hydrol. Earth Syst. Sci 2009, 13, 1453–1466. [Google Scholar]
- Vetter, M.; Höfle, B.; Hollaus, M.; Gschöpf, C.; Mandlburger, G.; Pfeifer, N.; Wagner, W. Vertical vegetation structure analysis and hydraulic roughness determination using dense ALS point cloud data—A voxel based approach. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2011, 38, Part 5/W 12. 265–270. [Google Scholar]
- Merkel, U.; Kron, A.; Oberle, P. Combined 1- and 2-Dimensional Numerical Modelling Techniques for Operational Flood Simulation in Complex River Systems: Case Study “Middle Elbe”. In Special Aspects of Urban Flood Management, Proceedings of Cost Session Aquaterra Conference; Pasche, E., Ed.; COST Office: Hamburg, Germany, 2008; pp. 241–264. [Google Scholar]
- Oberle, P. Integrales Hochwassersimulationssystem Neckar: Verfahren, Werkzeuge, Anwendungen und Übertragung; Universität Fridericiana zu Karlsruhe (TH): Karlsruhe, Germany, 2004. [Google Scholar]
- Vetsch, D.; Rousselot, P.; Fäh, R. Flussgebietsmodellierung mit der Simulationssoftware BASEMENT. Wasser Energie Luft 2011, 103, 313–319. [Google Scholar]
- Lane, S.N.; Bradbrook, K.F.; Richards, K.S.; Biron, P.A.; Roy, A.G. The application of computational fluid dynamics to natural river channels: Three-dimensional versus two-dimensional approaches. Geomorphology 1999, 29, 1–20. [Google Scholar]
- Chow, V.T. Open-Channel Hydraulics; Reprint, 1959; Blackburn Press: Caldwell, NJ, USA, 2009. [Google Scholar]
- Medeiros, S.C.; Hagen, S.C.; Weishampel, J.F. Comparison of floodplain surface roughness parameters derived from land cover data and field measurements. J. Hydrol 2012, 452–453, 139–149. [Google Scholar]
- Doncker, L.; Troch, P.; Verhoeven, R.; Bal, K.; Meire, P.; Quintelier, J. Determination of the manning roughness coefficient influenced by vegetation in the river Aa and Biebrza river. Environ. Fluid Mech 2009, 9, 549–567. [Google Scholar]
- Lumbroso, D.; Gaume, E. Reducing the uncertainty in indirect estimates of extreme flash flood discharges. J. Hydrol 2012, 414–415, 16–30. [Google Scholar]
- Arcement, G.J.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains; US Government Printing Office: Washington, DC, USA, 1989. [Google Scholar]
- Mandlburger, G. Topographische Modelle für Anwendungen in Hydraulik und Hydrologie. Technische Universität Wien, Vienna, October 2006. [Google Scholar]
- Bates, P.D.; Horritt, M.S.; Smith, C.N.; Mason, D. Integrating remote sensing observations of flood hydrology and hydraulic modelling. Hydrol. Process 1997, 11, 1777–1795. [Google Scholar]
- Mason, D.C.; Cobby, D.M.; Horritt, M.S.; Bates, P.D. Floodplain friction parameterization in two-dimensional river flood models using vegetation heights derived from airborne scanning laser altimetry. Hydrol. Process 2003, 17, 1711–1732. [Google Scholar]
- Thieken, A.H.; Kreibich, H.; Müller, M.; Merz, B. Coping with floods: Preparedness, response and recovery of flood-affected residents in Germany in 2002. Hydrol. Sci. J 2007, 52, 1016–1037. [Google Scholar]
- Büchele, B.; Kreibich, H.; Kron, A.; Thieken, A.; Ihringer, J.; Oberle, P.; Merz, B.; Nestmann, F. Flood-risk mapping: Contributions towards an enhanced assessment of extreme events and associated risks. Nat. Hazards Earth Syst. Sci 2006, 6, 485–503. [Google Scholar]
- Thieken, A.H. Hochwasserschutz in Deutschland: Neue modelle zur abschätzung von hochwasserschäden. Ökologisches Wirtschaften 2008, 3, 30–34. [Google Scholar]
- Thieken, A.H.; Ackermann, V.; Elmer, F.; Kreibich, H.; Kuhlmann, B.; Kunert, U.; Maiwald, H.; Merz, B.; Müller, M.; Piroth, K.; et al. Methods for the Evaluation of Direct and Indirect Flood Losses. Proceedings of the 4th International Symposium on Flood Defence: Managing Flood Risk, Reliability and Vulnerability, Toronto, ON, Canada, 6–8 May 2008.
- Egli, T.E. Hochwasserschutz und Raumplanung: Schutz vor Naturgefahren mit Instrumenten der Raumplanung, dargestellt am Beispiel von Hochwasser und Murgängen; Vdf, Hochsch.-Verl. an der ETH: Zürich, Switzerland, 1996; Volume 100. [Google Scholar]
- Schwarz, J.; Maiwald, H.; Gerstberger, A. Quantifizierung der Schäden infolge Hochwassereinwirkung: Fallstudie Eilenburg. Bautechnik 2005, 82, 845–856. [Google Scholar]
- Maiwald, H.; Schwarz, J. Ermittlung von Hochwasserschäden unter Berücksichtigung der Bauwerksverletzbarkeit: EDAC-Hochwasserschadensmodell.; Zentrum für die Ingenieuranalyse von Erdbebenschäden: Scientific technical reports 01; Verlag der Bauhaus-Universität Weimar: Weimar, Germany, 2011. [Google Scholar]
- Bundesamt für Umwelt Schweiz. Hilfe-Assistent zum Excel-Tool Methode BWG für die Abschätzung des Schadenpotentials: Überschwemmung und Übermurung. Available online: http://www.bafu.admin.ch/dokumentation/03393/03517/index.html?lang=de (accessed on 12 March 2013).
- Godina, R.; Holzmann, H.; Lehmann, T.; Formayer, H.; Haas, P; Floodrisk, II. Vertiefung und Vernetzung zukunftsweisender Umsetzungsstrategien zum integrierten Hochwasserschutz. Available online: https://imp.boku.ac.at/klima/literatur/FRII_Endbericht_final.pdf (accessed on 13 March 2013).
- Land Vorarlberg. Abflussmessstationen in Vorarlberg: Messstation Kennelbach. Available online: http://www.vorarlberg.at/abfluss/ (accessed on 13 March 2013).
- Amt der Vlbg. Landesreg. Abt. Wasserwirtschaft. Nationaler Gewässerbewirtschaftungsplan 2009: Bregenzerach: Maßnahmenkonzept. 2010. Available online: http://www.vorarlberg.at/pdf/ngp_bregenzerach.pdf (accessed on 19 March 2013).
- Landesvermessungsamt Feldkirch. Orthofotomosaik Vorarlberg 2009; 2010.
- TopScan GmbH, Projektbericht bezüglich der Laserscannermessung Unterland und Vorderwald im Auftrag des Landesvermessungsamtes Feldkirch; TopScan GmbH: Rheine, German, 2006.
- Höfle, B.; Pfeifer, N. Correction of laser scanning intensity data: Data and model-driven approaches. ISPRS J. Photogramm. Remote Sens 2007, 62, 415–433. [Google Scholar]
- Jäger, F. Landnutzungsklassifizierung aus hochauflösenden Orthofotos Land Vorarlberg 2001/02: Technischer Bericht; GeoVille Informationssysteme:Innsbruck: Austria, 2007. [Google Scholar]
- Umweltbundesamt GmbH. CORINE Land Cover. Available online: http://www.umweltbundesamt.at/umwelt/raumordnung/flaechennutzung/corine/ (accessed on 5 March 2013).
- Resch, B. People as Sensors and Collective Sensing-Contextual Observations Complementing Geo-Sensor Network Measurements. In Progress in Location-Based Services; Krisp, J.M., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 391–406. [Google Scholar]
- Lechner, M. Nutzungspotentiale Crowdsource-Erhobener Geodaten auf Verschiedenen Skalen. Albert-Ludwigs-Universität, Freiburg im Breisgau, Germany, September 2011. [Google Scholar]
- Vetter, M.; Höfle, B.; Mandlburger, G.; Rutzinger, M. Estimating changes of riverine landscapes and riverbeds by using airborne LiDAR data and river cross-sections. Zeitschrift für Geomorphologie 2011, 55, 51–65. [Google Scholar]
- Visual Learning Systems, Feature Analyst 4.2 for ArcGIS: Reference Manual; Visual Learning Systems, Inc.: Missoula, MT, USA, 2001–2008.
- Heipke, C.; Mayer, H.; Wiedemann, C.; Jamet, O. Evaluation of automatic road extraction. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 1997, 32, Part 3–2W2. 47–56. [Google Scholar]
- Arie, B.-D. Comparison of classification accuracy using Cohen’s Weighted Kappa. Expert Syst. Appl 2008, 34, 825–832. [Google Scholar]
- Lowry, R. VasserStats: Kappa. Available online: http://vassarstats.net/kappa.html (accessed on 16 March 2013).
- Bechteler, W.; Nujić, M.; Patt, H.; Vogel, G. Hydraulische und Wasserbauliche Grundlagen. In Hochwasser-Handbuch: Auswirkungen und Schutz; Patt, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 59–168. [Google Scholar]
- Volz, C.; Rousselot, P.; Vetsch, D.; Müller, R.; Fäh, R. Dual-Mesh Ansatz zur Numerischen Simulation von Sedimenttransport auf Unstrukturierten Berechnungsgittern. In Wasserbau in Bewegung... von der Statik zur Dynamik: Beiträge zum 15. Gemeinschafts-Symposium der Wasserbau-Institute TU München, TU Graz und ETH Zürich: Vom 1. bis 3. Juli 2010 in Wallgau, Oberbayem; Rutschmann, P., Ed.; Technische Universität München: Munich, Germany, 2010; pp. 203–212. [Google Scholar]
- Fäh, R.; Mueller, R.; Rousselot, P.; Vetsch, D.; Volz, C.; Vonwiller, L.; Veprek, R.; Farshi, D. System Manuals of BASEMENT: Version 2.2; Labratory of Hydraulics, Glaciology and Hydrology (VAW), ETH Zürich: Zurich, Switzerland, 2011. [Google Scholar]
- Syme, W.J. Flooding In Urban Areas—2D Modelling Approaches for Buildings and Fences. Proceedings of the Engineers Australia, 9th National Conference on Hydraulics in Water Engineering, Darwin, NT, Australia, 23–26 September 2008.
- Wang, J.; Zeng, C.; Lehrbass, B. Building Extraction from LiDAR and Aerial Images and Its Accuracy Evaluation. Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 64–67.
- Vetter, M. Airborne Laser Scanning Terrain and Land Cover Models as Basis for Hydrological and Hydraulic Studies; Centre for Water Resource Systems, Technische Universität Wien: Vienna, Austria, 2013. [Google Scholar]
- Neis, P.; Zielstra, D.; Zipf, A. Comparison of volunteered geographic information data contributions and community development for selected world regions. Future Internet 2013, 5, 282–300. [Google Scholar]

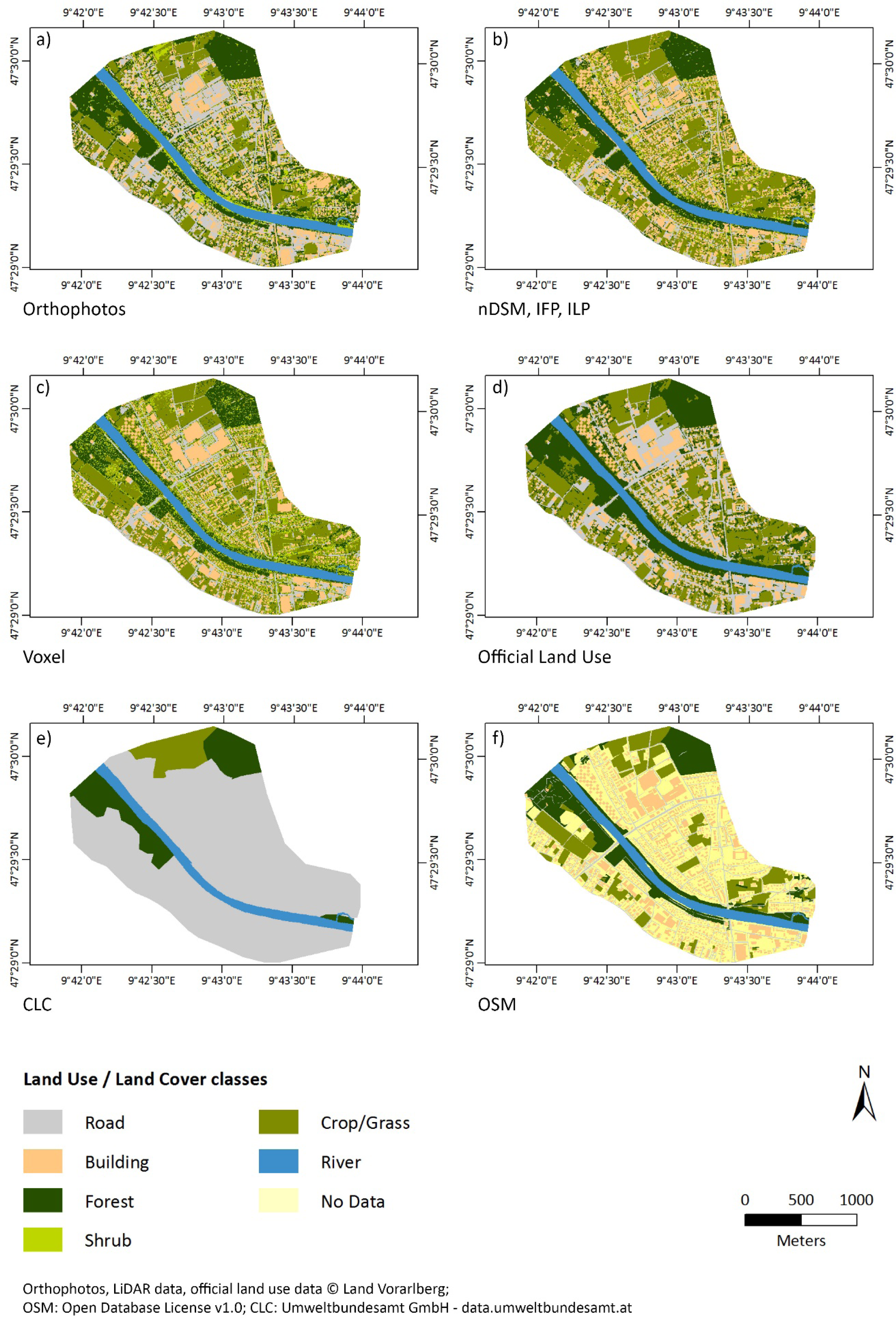

| Data Source | Provider | Date | Dataset |
|---|---|---|---|
| Orthophotos | Federal State of Vorarlberg | 2009 | TC and CIR image |
| LiDAR data | Federal State of Vorarlberg | 2003 | Point cloud, nDSM, signal intensity |
| Official land use data | Federal State of Vorarlberg | 2001/2002 | Vector polygons |
| OpenStreetMap data (OSM) | OpenStreetMap contributors | 2013 | Vector polygons and polylines |
| CORINE Land Cover (CLC) | Environment Agency Austria | 2006 | Vector polygons |
| Class | Max. Height (Con. no. 1) | Threshold on pCon/pCell |
|---|---|---|
| Crop/Grass | ≤0.25 m | |
| Shrub | >0.25 m and <5 m | ≤0.75 |
| Forest | ≥5 m | ≥0.75 |
| LULC Class | Manning’s n Values | LULC ID |
|---|---|---|
| Building | 0.4 | 1 |
| Forest | 0.15 | 3 |
| Shrub | 0.1 | 2 |
| River | 0.05 | 5 |
| Road | 0.016 | 4 |
| Crop/grass | 0.035 | 7 |
| No data | 0.03 | 6 |
| Flood Intensity | Water Depth h (m) |
|---|---|
| I (weak) | <0.5 |
| II (moderate) | 0.5 ≤ h ≤ 2.0 |
| III (high) | >2.0 |
| LiDAR Data | Orthophotos | |||
|---|---|---|---|---|
| Correctness | Completeness | Correctness | Completeness | |
| River | 100.00% | 99.34% | 100.00% | 100.00% |
| Crop/Grass | 94.22% | 88.89% | 96.15% | 70.64% |
| Forest | 90.22% | 86.94% | 89.29% | 88.24% |
| Shrub | 50.44% | 75.67% | 70.08% | 87.91% |
| Building | 77.33% | 60.95% | 79.37% | 76.40% |
| Road | 83.78% | 87.27% | 71.81% | 89.17% |
| Overall accuracy | 82.67% | 83.17% | ||
| Average accuracy | 83.99% | 85.39% | ||
| Quality | 70.45% | 72.40% | ||
| Kappa | 0.9253 | 0.9124 | ||
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dorn, H.; Vetter, M.; Höfle, B. GIS-Based Roughness Derivation for Flood Simulations: A Comparison of Orthophotos, LiDAR and Crowdsourced Geodata. Remote Sens. 2014, 6, 1739-1759. https://doi.org/10.3390/rs6021739
Dorn H, Vetter M, Höfle B. GIS-Based Roughness Derivation for Flood Simulations: A Comparison of Orthophotos, LiDAR and Crowdsourced Geodata. Remote Sensing. 2014; 6(2):1739-1759. https://doi.org/10.3390/rs6021739
Chicago/Turabian StyleDorn, Helen, Michael Vetter, and Bernhard Höfle. 2014. "GIS-Based Roughness Derivation for Flood Simulations: A Comparison of Orthophotos, LiDAR and Crowdsourced Geodata" Remote Sensing 6, no. 2: 1739-1759. https://doi.org/10.3390/rs6021739
APA StyleDorn, H., Vetter, M., & Höfle, B. (2014). GIS-Based Roughness Derivation for Flood Simulations: A Comparison of Orthophotos, LiDAR and Crowdsourced Geodata. Remote Sensing, 6(2), 1739-1759. https://doi.org/10.3390/rs6021739





