Land Surface Temperature Retrieval Using Airborne Hyperspectral Scanner Daytime Mid-Infrared Data
Abstract
:1. Introduction
2. Methodology and Data Simulation
2.1. Basic Theory
2.2. Data
2.3. LST Retrieval Method from Two AHS MIR Channels
2.3.1. Estimation of Direct Solar Radiance
Relationship between Direct Solar Radiance and WVC
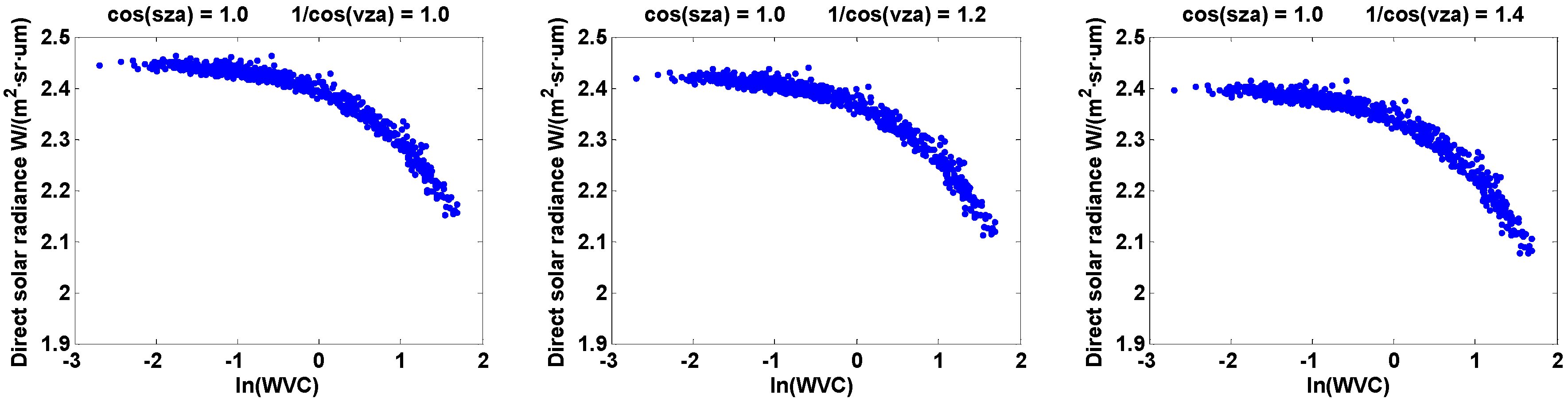
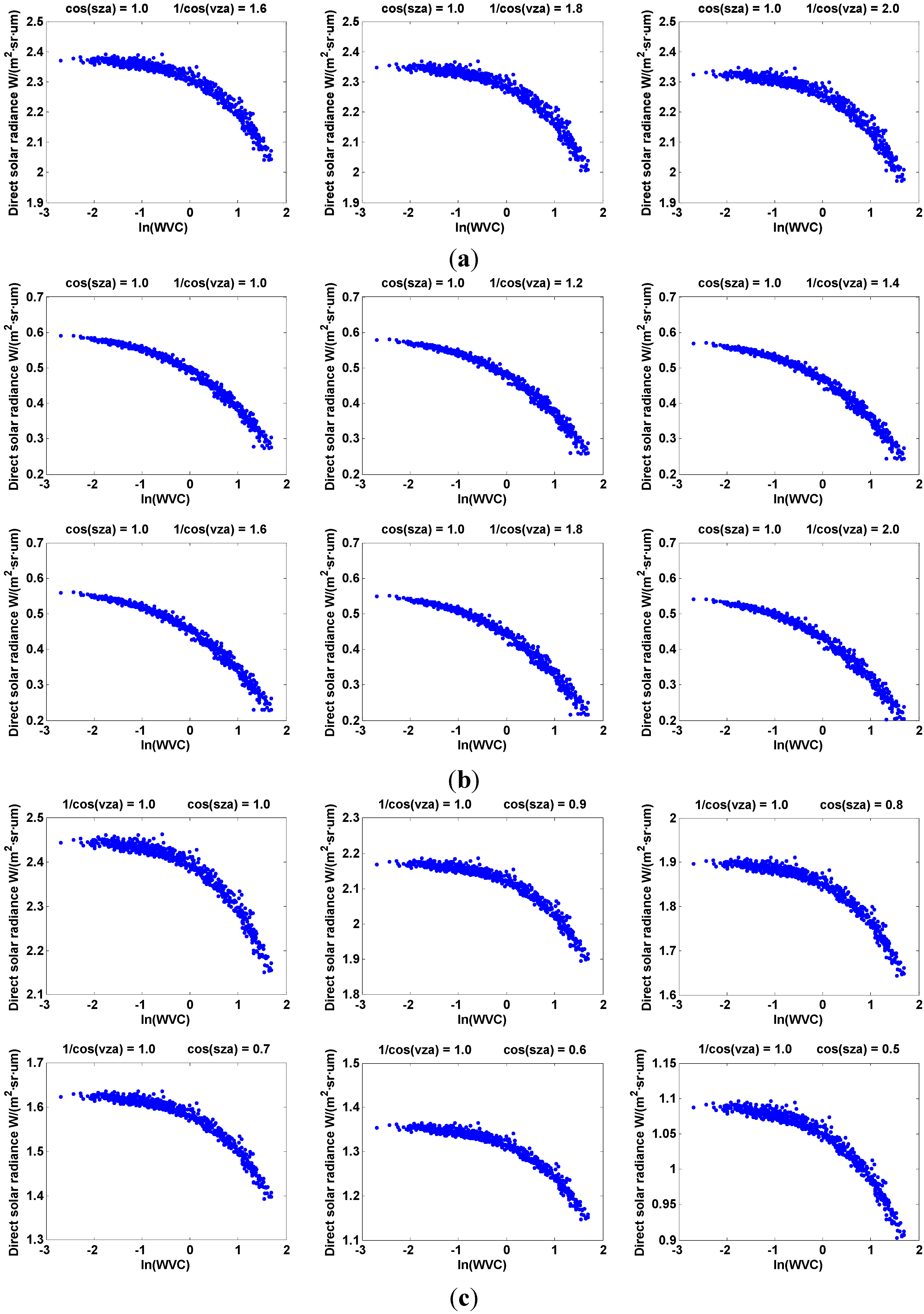
Direct Solar Radiance at Different VZAs
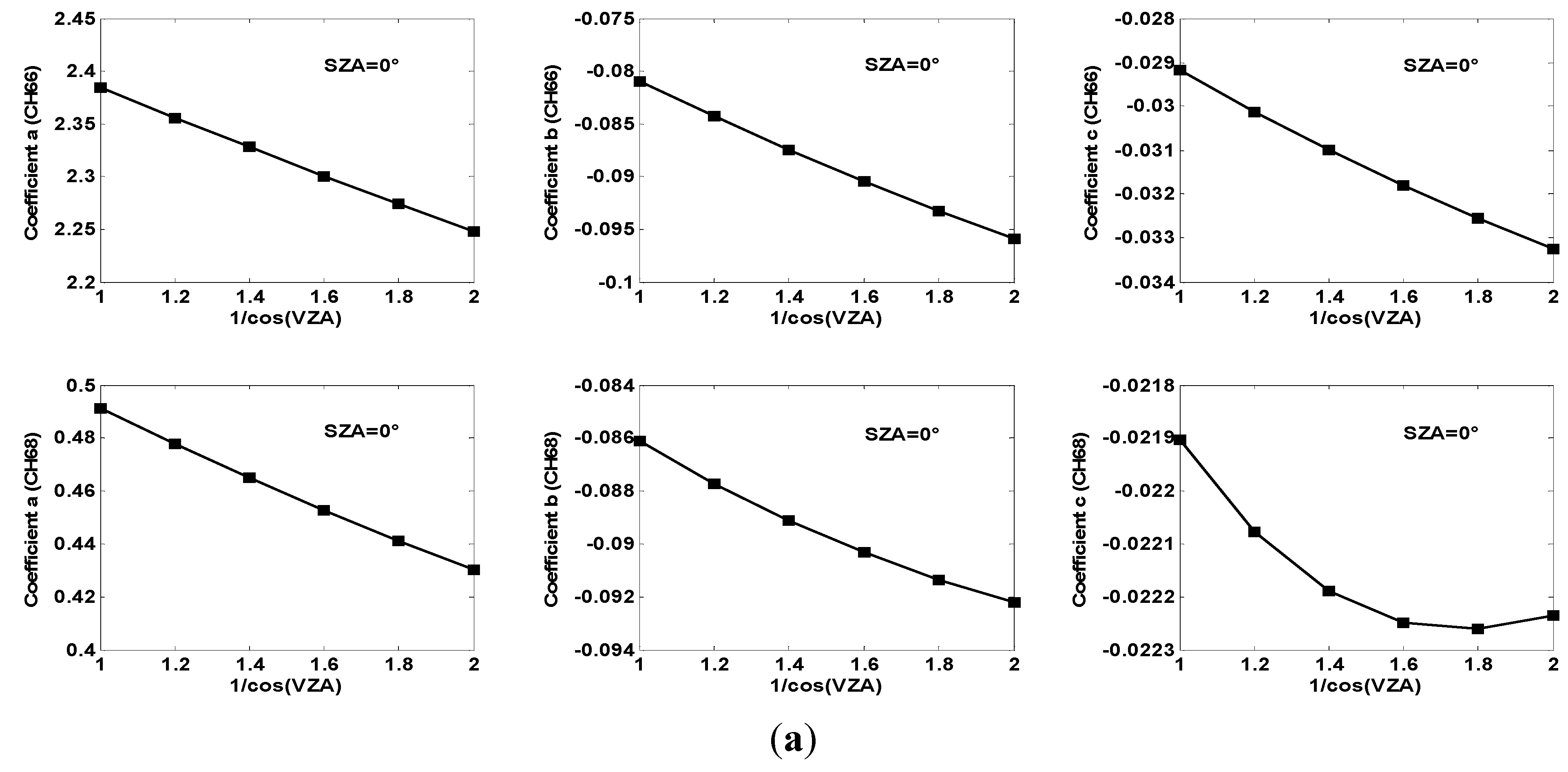
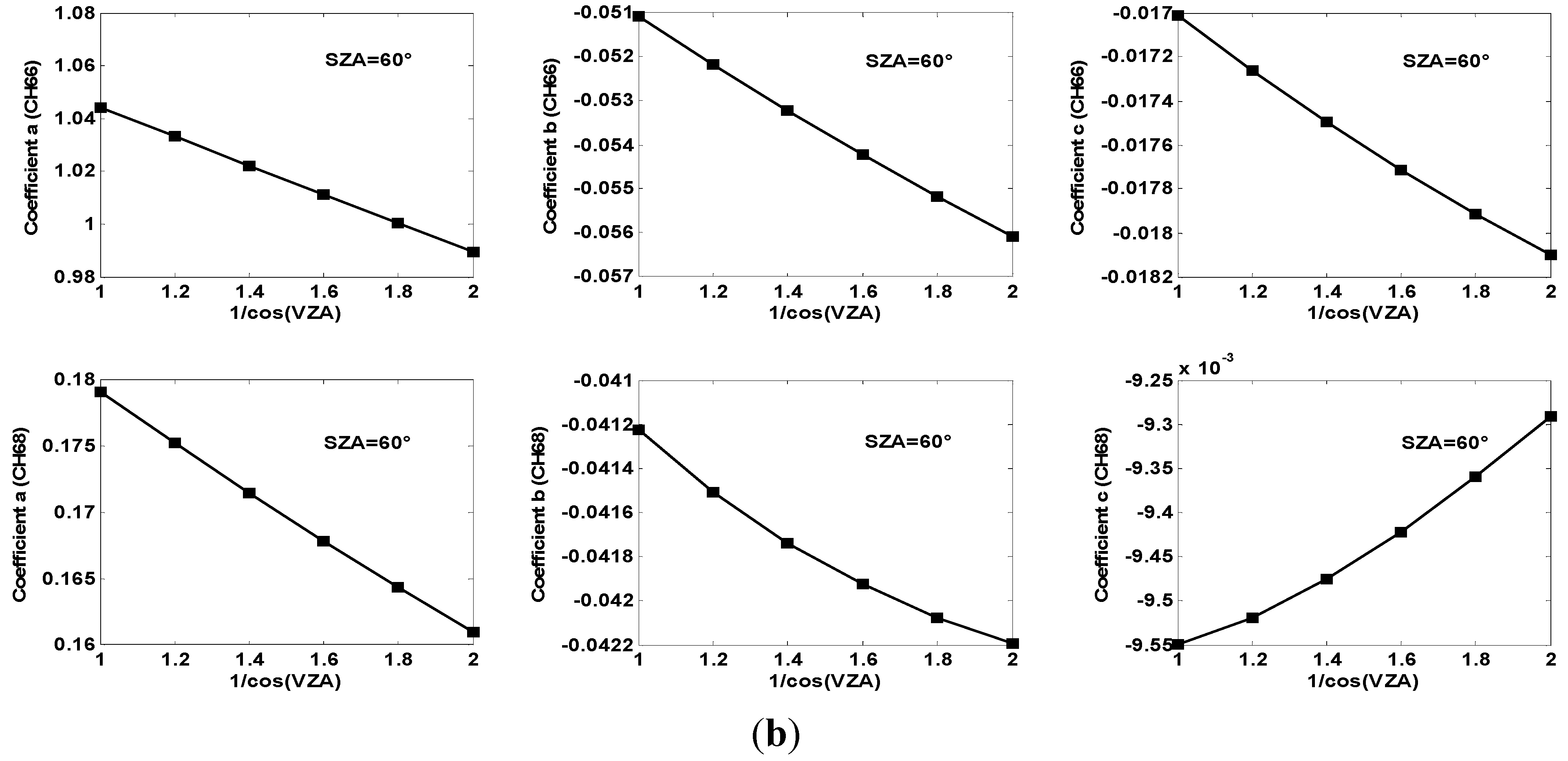
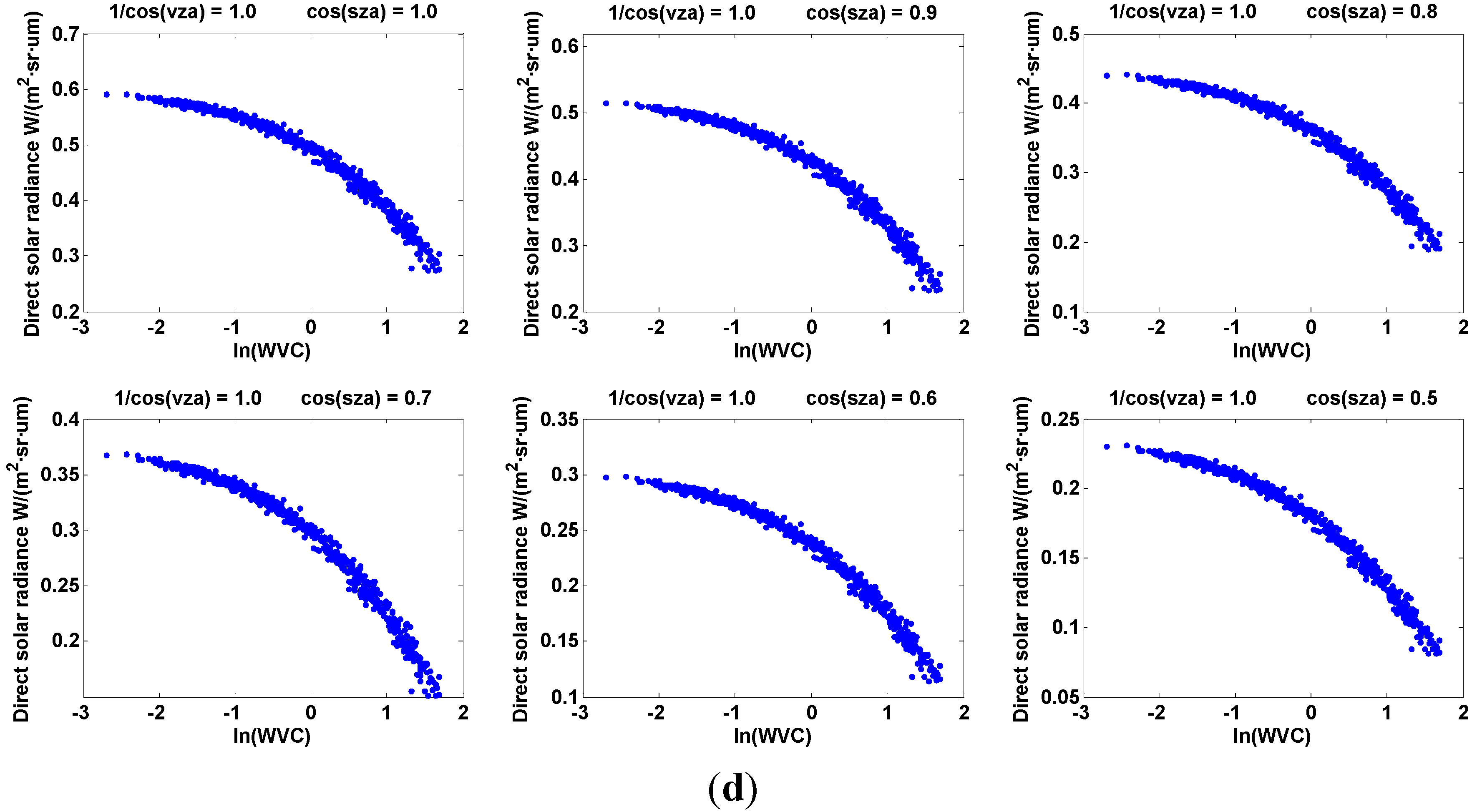
Direct Solar Radiance at Different SZAs
2.3.2. Estimation of LST
3. Results and Analysis
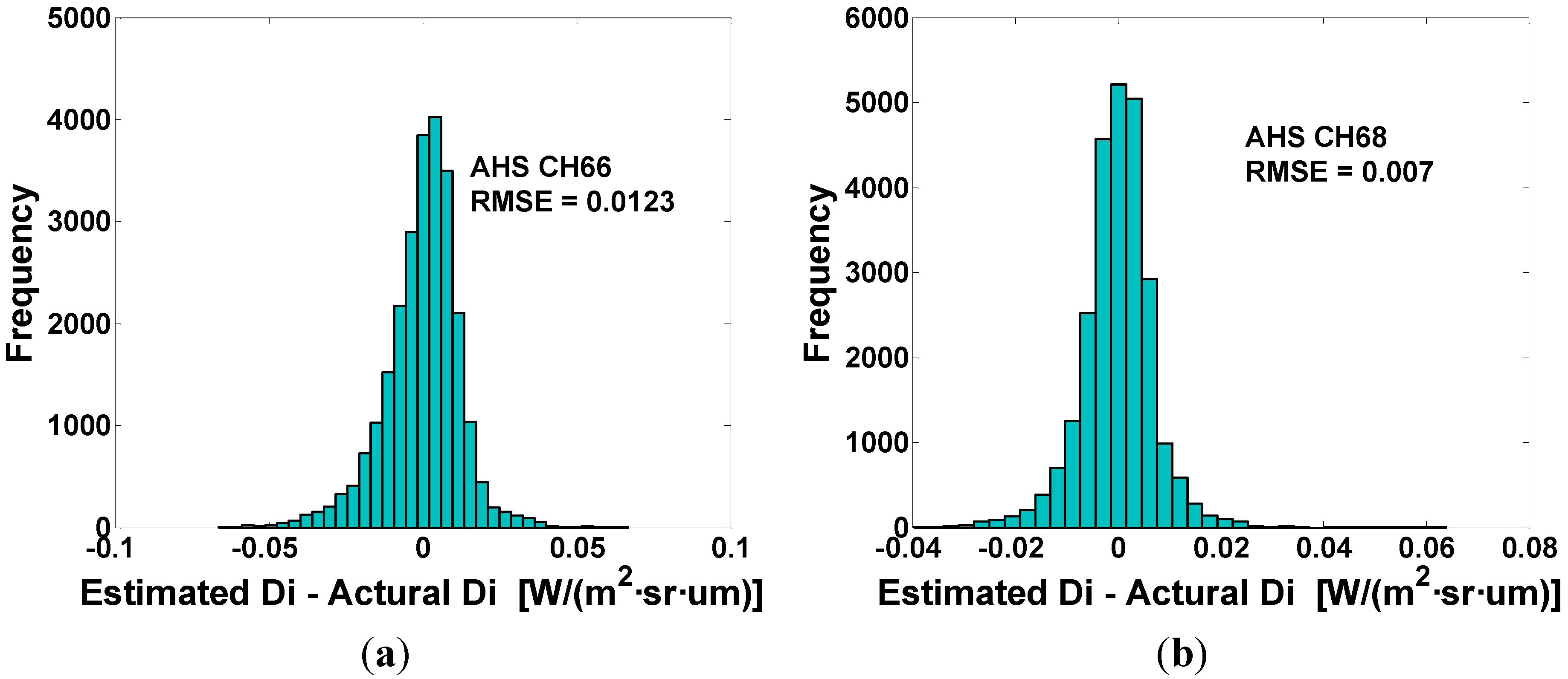
3.1. Estimated Result of Direct Solar Radiance
| Channel Coefficient | a11 | a10 | a21 | a20 | b11 | b10 | b21 | b20 | c11 | c10 | c21 | c20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AHS CH66 | 2.849 | −0.325 | −0.162 | 0.028 | −0.037 | −0.026 | −0.020 | 0.005 | −0.018 | −0.007 | −0.006 | 0.002 |
| AHS CH68 | 0.709 | −0.163 | −0.086 | 0.026 | −0.080 | −0.001 | −0.010 | 0.004 | −0.024 | 0.002 | −0.001 | 0.001 |
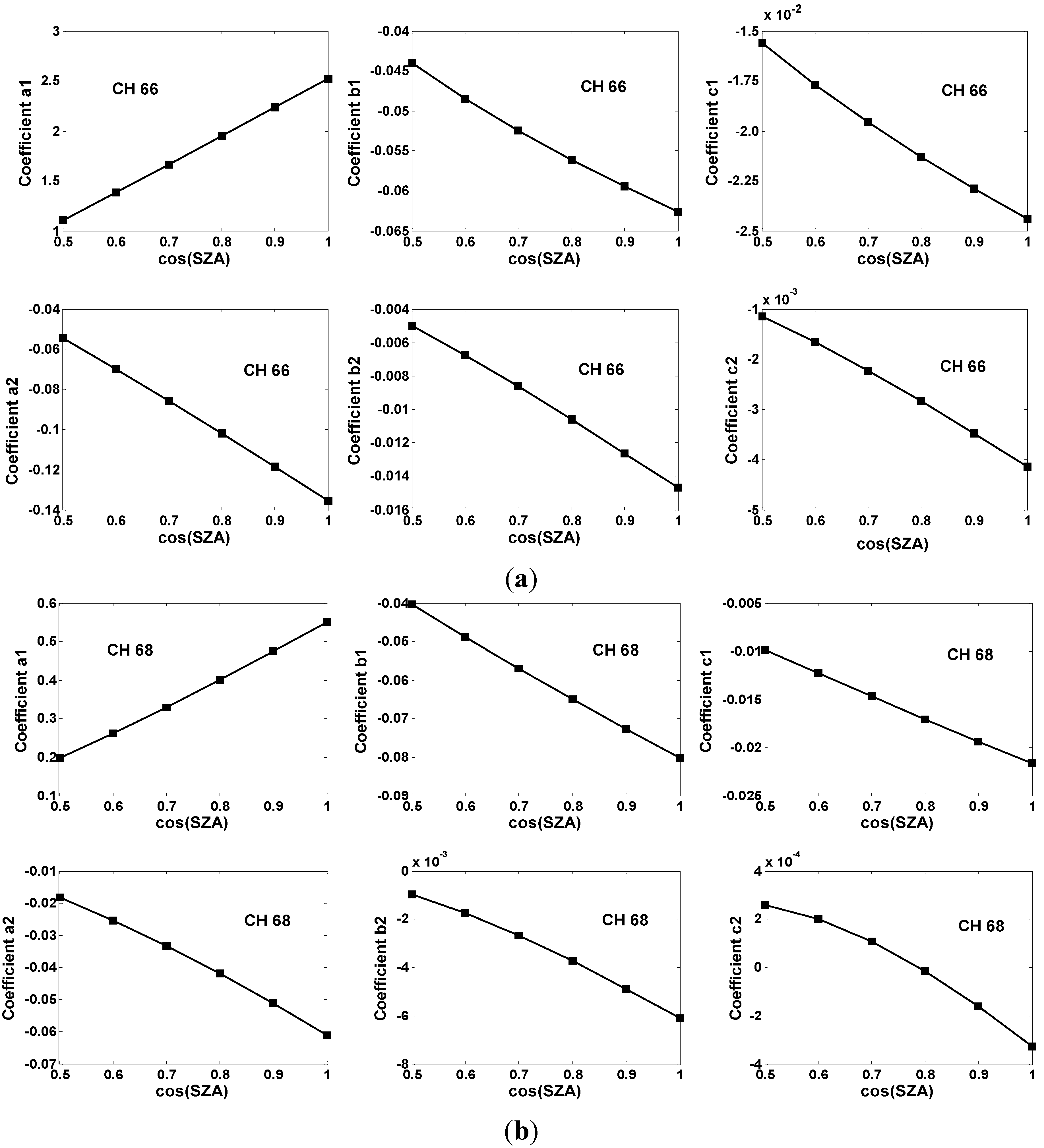
3.2. Coefficients of LST Retrieval Method
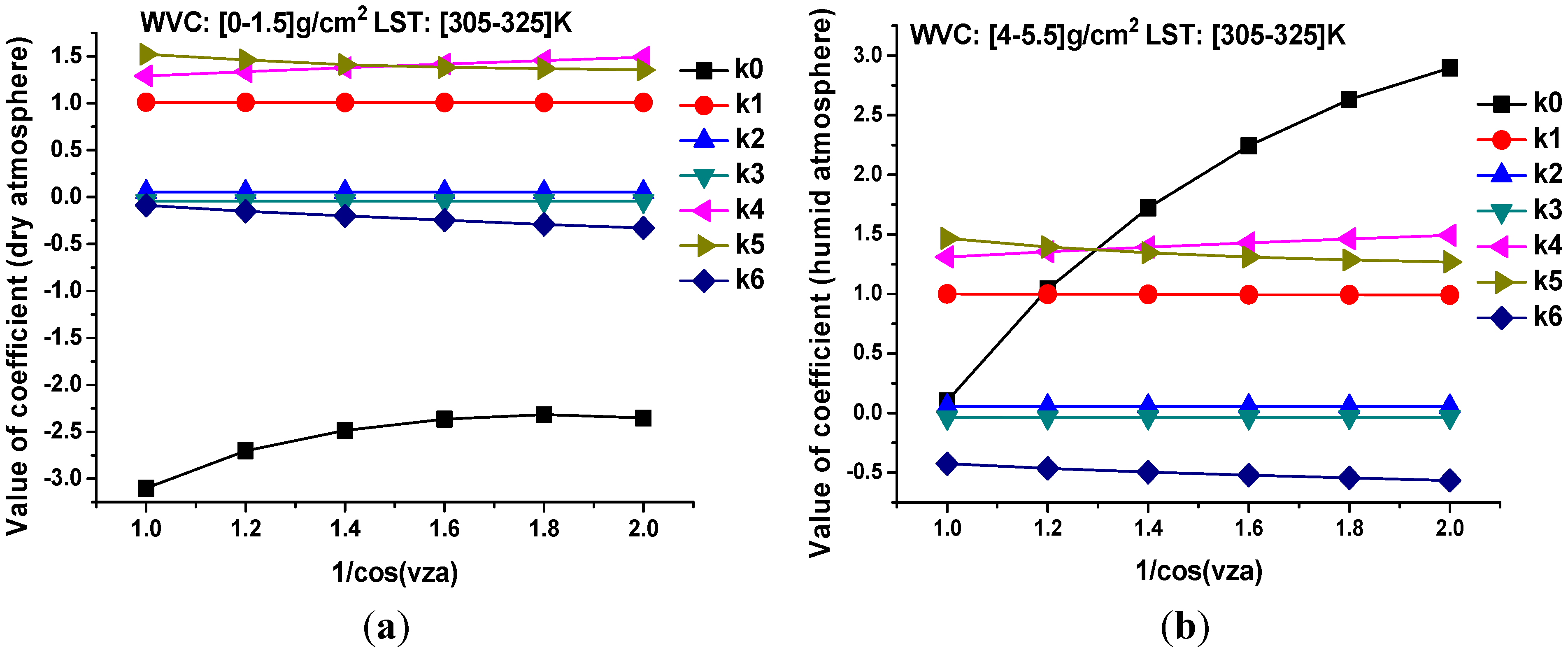
3.3. Result of LST Retrieval

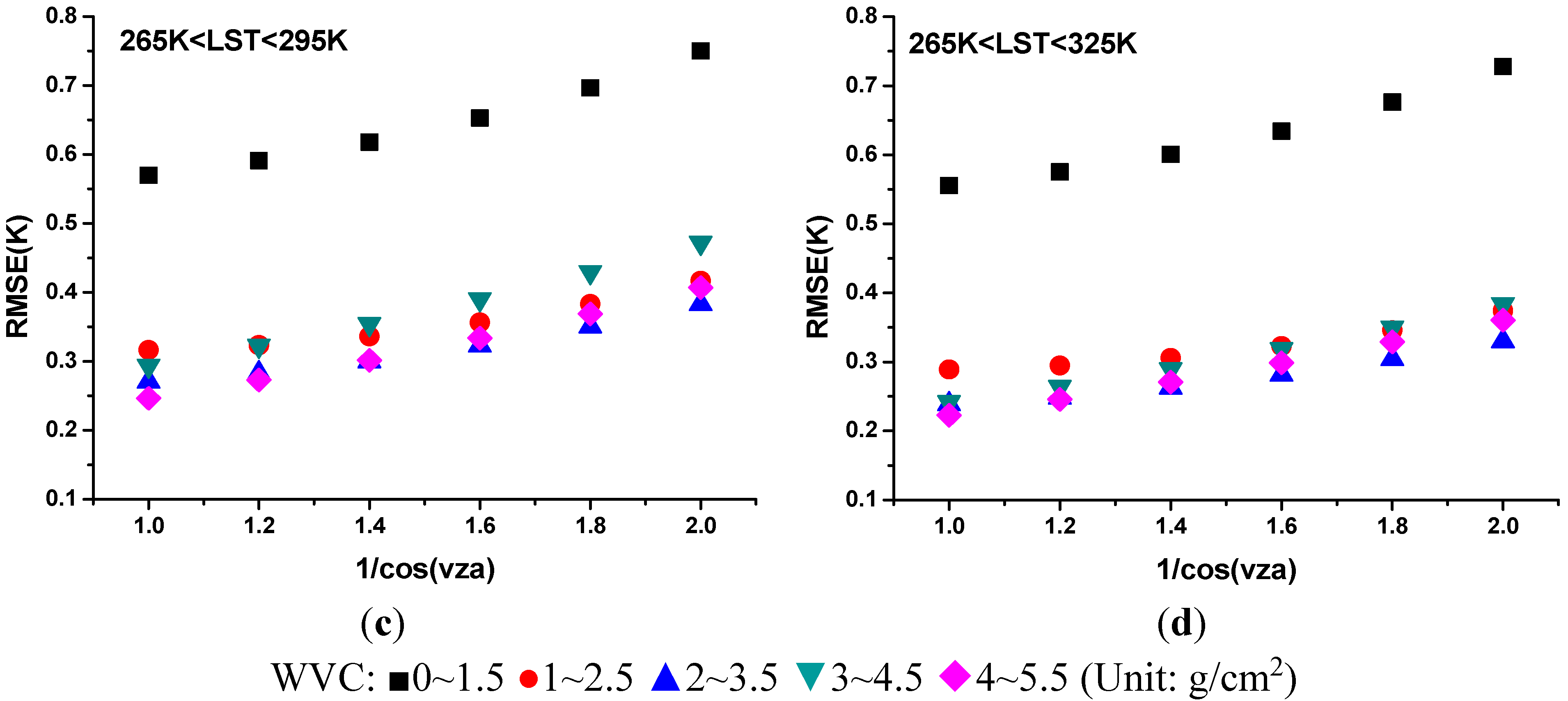
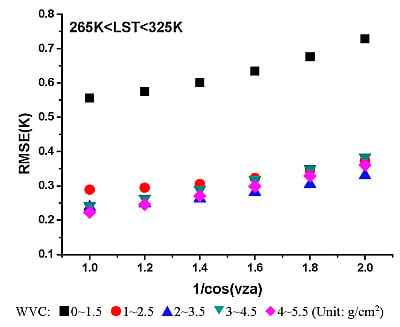
4. Sensitivity Analysis
4.1. Sensitivity Analysis to Instrumental Noises
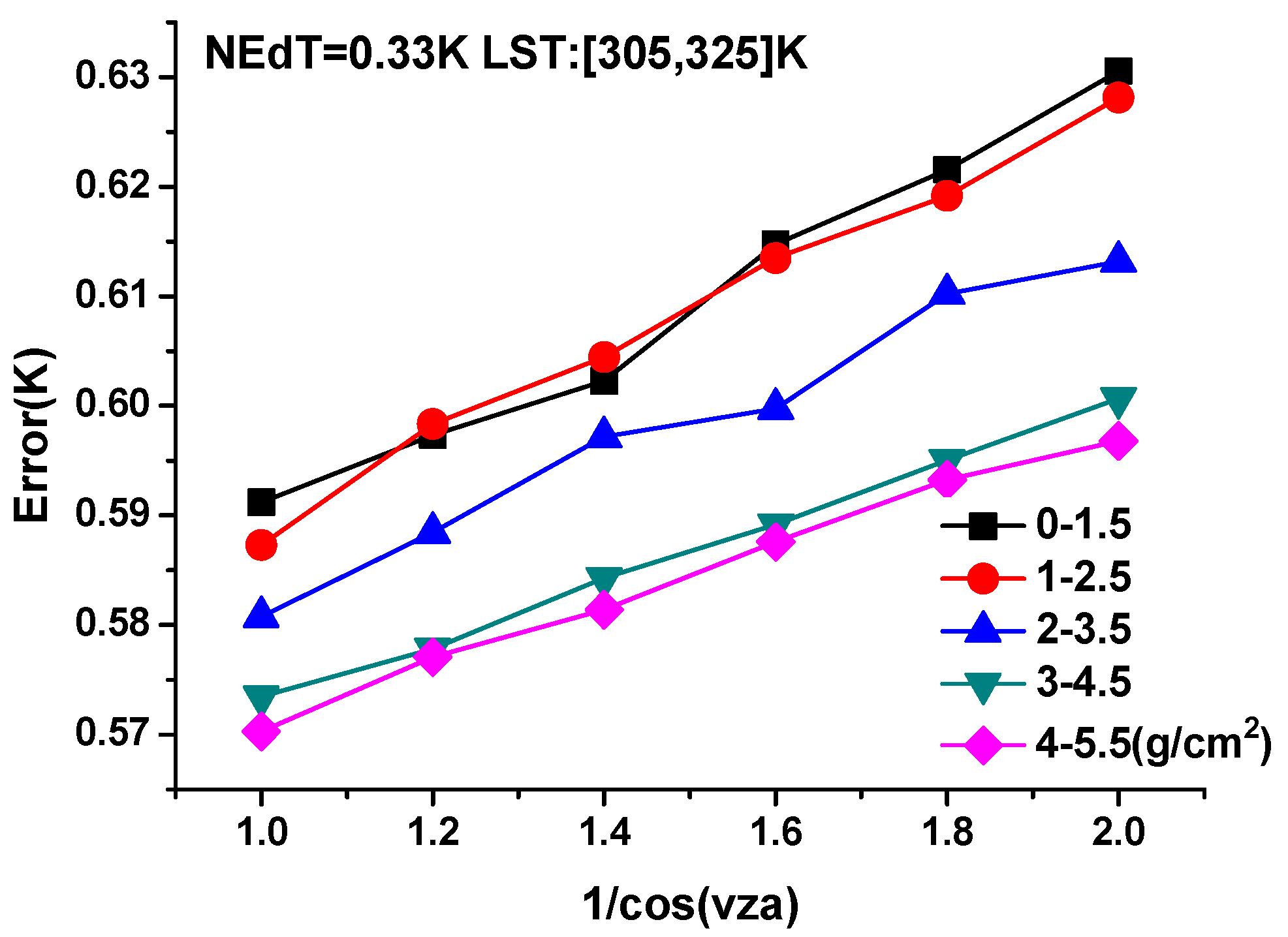
4.2. Sensitivity Analysis to LSEs
| WVC (g/cm2) | 305~325 (K) Error | 290~310 (K) Error | 265~295 (K) Error | 265~325 (K) Error |
|---|---|---|---|---|
| 0~1.5 | 0.50 | 1.04 | 2.83 | 2.71 |
| 1~2.5 | 0.49 | 0.94 | 1.68 | 1.31 |
| 2~3.5 | 0.44 | 0.84 | 1.37 | 0.92 |
| 3~4.5 | 0.40 | 0.76 | 1.40 | 0.81 |
| 4~5.5 | 0.40 | 0.74 | 1.26 | 0.73 |
4.3. Sensitivity Analysis to WVC
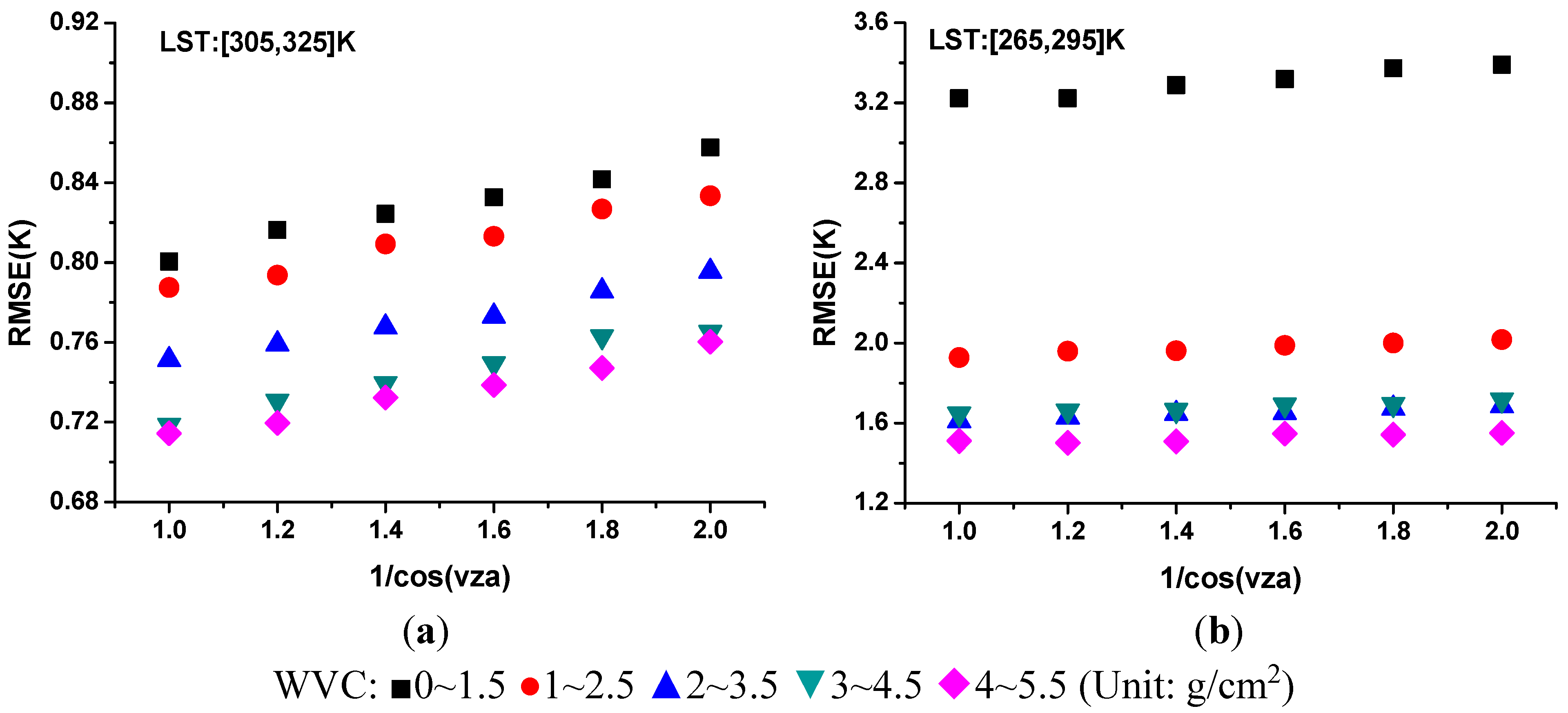
5. Preliminary Application to AHS data
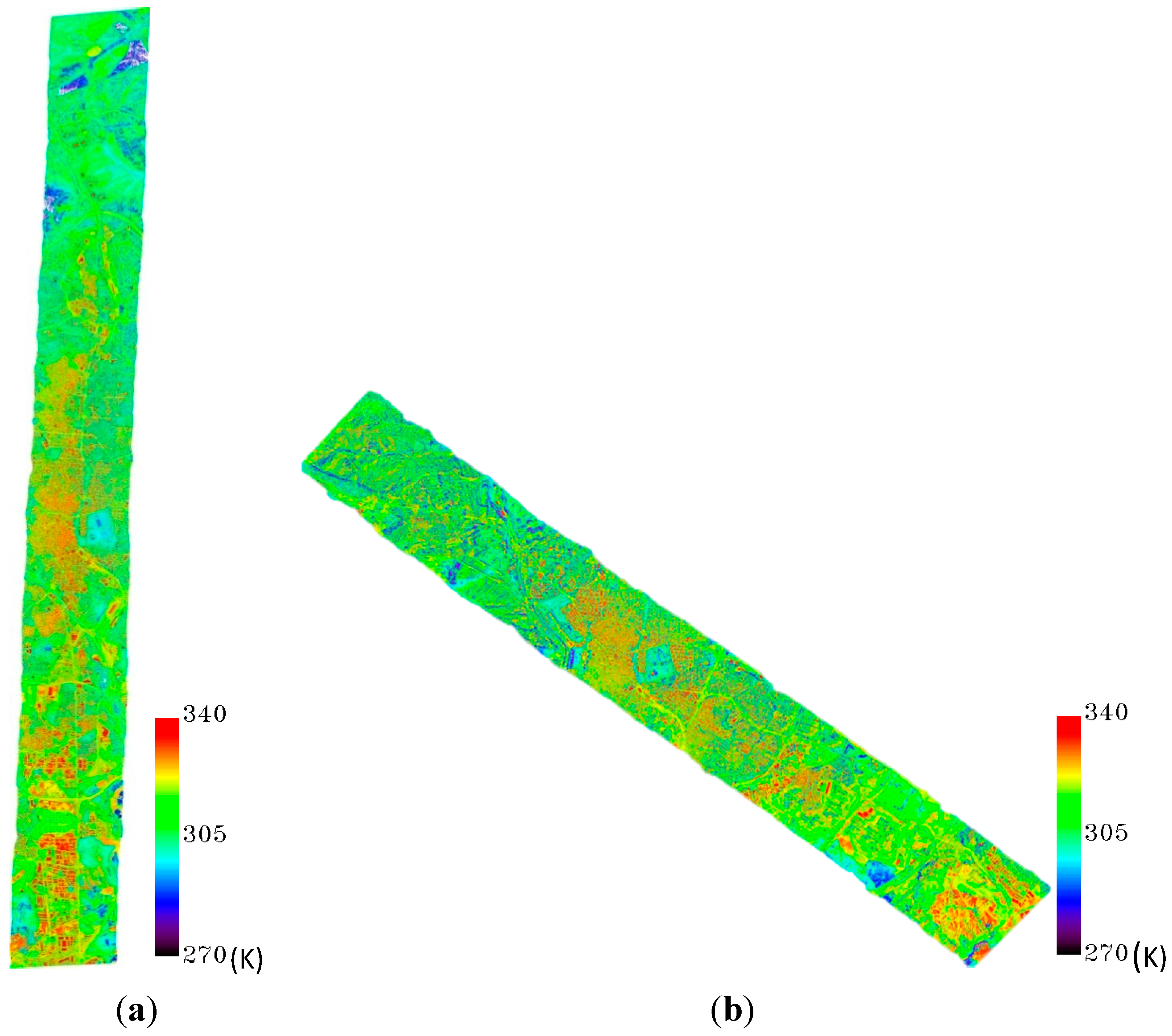
5.1. Data Processing
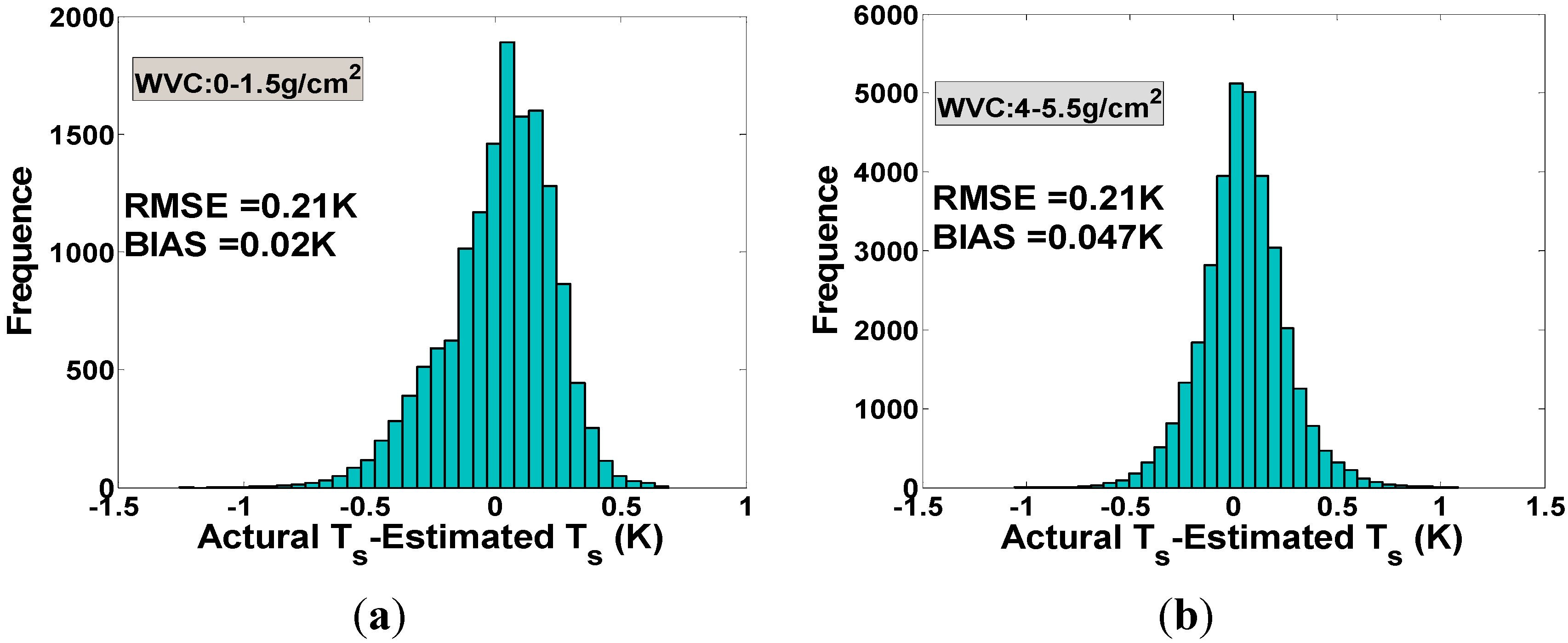
5.2. Results and Validation
| Instrument | Spectral Range (um) | Temperature Range (°C) | Accuracy (K) | Resolution | FOV |
|---|---|---|---|---|---|
| Cimel CE312-1 | 8~13 | −80 to 50 | 0.1 | 8 mK | 10° |
| 11.5~12.5 | 50 mK | ||||
| 10.5~11.5 | 50 mK | ||||
| 8.2~9.2 | 50 mK | ||||
| Cimel CE312-2 | 8~13 | −80 to 60 | 0.1 | 8 mK | 10° |
| 11~11.7 | 50 mK | ||||
| 10.3~11 | 50 mK | ||||
| 8.9~9.3 | 50 mK | ||||
| 8.5~8.9 | 50 mK | ||||
| 8.1~8.5 | 50 mK | ||||
| Heitronics KT19 | 9.6~11.5 | −50 to 200 | 0.1 | 0.05 K | 2° |
| NEC TH9100 | 8~14 | −40 to 120 | 2 | 0.1 K (320 × 240) | 22° × 16° |

| Coordinate | Surface Type | LSE | Retrieved LST | In situ Measurement | In situ Bias | |
|---|---|---|---|---|---|---|
| ε66 | ε68 | |||||
| 40°25′1.65″N, 3°41′2.65″W | Water | 0.976 | 0.979 | 297.6K | 298.3K | 0.3K |
| 40°32′52.44″N, 3°41′48.45″W | Bare soil | 0.769 | 0.799 | 314.8K | 313.9K | 0.6K |
| 40°32′51.71″N, 3°41′54.33″W | Grass | 0.984 | 0.987 | 306.3K | 304.0K | 2K |

6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References and Notes
- Hansen, J.; Ruedy, R.; Sato, M.; Lo, K. Global surface temperature change. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Bastiaanssen, W.; Menenti, M.; Feddes, R.; Holtslag, A. A remote sensing surface energy balance algorithm for land (SEBAL) 1. Formulation. J. Hydrol. 1998, 212, 198–212. [Google Scholar]
- Anderson, M.; Norman, J.; Kustas, W.; Houborg, R.; Starks, P.; Agam, N. A thermal-based remote sensing technique for routine mapping of land-surface carbon, water and energy fluxes from field to regional scales. Remote Sens. Environ. 2008, 112, 4227–4241. [Google Scholar] [CrossRef]
- Karnieli, A.; Agam, N.; Pinker, R.T.; Anderson, M.; Imhoff, M.L.; Gutman, G.G.; Panov, N.; Goldberg, A. Use of NDVI and land surface temperature for drought assessment: Merits and limitations. J. Climate 2010, 23, 618–633. [Google Scholar] [CrossRef]
- Kustas, W.; Anderson, M. Advances in thermal infrared remote sensing for land surface modeling. Agric. Forest Meteorol. 2009, 149, 2071–2081. [Google Scholar] [CrossRef]
- Zhang, R.; Tian, J.; Su, H.; Sun, X.; Chen, S.; Xia, J. Two improvements of an operational two-layer model for terrestrial surface heat flux retrieval. Sensors 2008, 8, 6165–6187. [Google Scholar] [CrossRef]
- Cho, A.-R.; Suh, M.-S. Evaluation of land surface temperature operationally retrieved from Korean geostationary satellite (COMS) data. Remote Sens. 2013, 5, 3951–3970. [Google Scholar] [CrossRef]
- Bechtel, B.; Zakšek, K.; Hoshyaripour, G. Downscaling land surface temperature in an urban area: A case study for hamburg, germany. Remote Sens. 2012, 4, 3184–3200. [Google Scholar] [CrossRef]
- Weng, Q. Thermal infrared remote sensing for urban climate and environmental studies: Methods, applications, and trends. ISPRS J. Photogramm. Remote Sens. 2009, 64, 335–344. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Sur. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Arnfield, A.J. Two decades of urban climate research: A review of turbulence, exchanges of energy and water, and the urban heat island. Int. J. Climatol. 2003, 23, 1–26. [Google Scholar] [CrossRef]
- Su, Z. The surface energy balance system (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Kogan, F.N. Operational space technology for global vegetation assessment. Bull. Am. Meteorol. Soc. 2001, 82, 1949–1964. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Sobrino, J.; El Kharraz, J.; Li, Z.-L. Surface temperature and water vapour retrieval from MODIS data. Int. J. Remote Sens. 2003, 24, 5161–5182. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Sobrino, J.A. A generalized single-channel method for retrieving land surface temperature from remote sensing data. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Qin, Z.H.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from landsat tm data and its application to the Israel-Egypt border region. Int. J. Remote Sens. 2001, 22, 3719–3746. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Tran. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar] [CrossRef]
- Becker, F.; Li, Z.-L. Towards a local split window method over land surfaces. Int. J. Remote Sens. 1990, 11, 369–393. [Google Scholar] [CrossRef]
- Li, Z.-L.; Wu, H.; Wang, N.; Qiu, S.; Sobrino, J.A.; Wan, Z.; Tang, B.-H.; Yan, G. Land surface emissivity retrieval from satellite data. Int. J. Remote Sens. 2013, 34, 3084–3127. [Google Scholar] [CrossRef]
- Mushkin, A.; Balick, L.K.; Gillespie, A.R. Extending surface temperature and emissivity retrieval to the mid-infrared (3–5 μm) using the multispectral thermal imager (MTI). Remote Sens. Environ. 2005, 98, 141–151. [Google Scholar] [CrossRef]
- Salisbury, J.W.; D’Aria, D.M. Emissivity of terrestrial materials in the 3–5 μm atmospheric window. Remote Sens. Environ. 1994, 47, 345–361. [Google Scholar] [CrossRef]
- Sun, D.; Pinker, R.T. Estimation of land surface temperature from a geostationary operational environmental satellite (GOES-8). J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Baker, N. Polar Satellite System (JPSS) VIIRS Land Surface Temperature Algorithm Theoretical Basis Document (ATBD) GSFC JPSS. Available online: http://npp.gsfc.nasa.gov/sciencedocuments/ATBD_122011/474-00051_LandSurfTemp_Rev-_20110422.pdf (accessed on 05 December 2011).
- Li, Z.-L.; Petitcolin, F.; Zhang, R. A physically based algorithm for land surface emissivity retrieval from combined mid-infrared and thermal infrared data. Sci. China Series E: Tech. Sci. 2000, 43, 23–33. [Google Scholar]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Zarco-Tejada, P.J.; Sepulcre-Cantó, G.; de Miguel, E. Land surface temperature derived from airborne hyperspectral scanner thermal infrared data. Remote Sens. Environ. 2006, 102, 99–115. [Google Scholar] [CrossRef]
- Chevallier, F.; Chéruy, F.; Scott, N.; Chédin, A. A neural network approach for a fast and accurate computation of a longwave radiative budget. J. Appl. Meteorol. 1998, 37, 1385–1397. [Google Scholar] [CrossRef]
- Chedin, A.; Scott, N.A.; Wahiche, C.; Moulinier, P. The improved initialization inversion method: A high resolution physical method for temperature retrievals from satellites of the TIROS-N series. J. Climate appl. Meteorol. 1985, 24, 128–143. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; El-Kharraz, J.; Gómez, M.; Romaguera, M.; Sòria, G. Single-channel and two-channel methods for land surface temperature retrieval from DAIS data and its application to the Barrax site. Int. J. Remote Sens. 2004, 25, 215–230. [Google Scholar] [CrossRef]
- Jiang, G.M.; Zhou, W.; Liu, R. Development of split-window algorithm for land surface temperature estimation from the VIRR/FY-3A measurements. IEEE Geosci. Remote Sens. Lett. 2013, 10, 952–956. [Google Scholar] [CrossRef]
- Jim#xE9;nez-Muñoz, J.C.; Gómez, J.A.; Fernández-Renau, A.; Holguín, J.A.; de Miguel, E.; de la Cámara, O.G.; Prado, E. Comportamiento geométrico y radiométrico del sensor ahs durante la campaña multitemporal cefles2 geometric and radiometric performance of the ahs sensor along cefles2. Revista de Teledetección 2010, 34, 16–21. [Google Scholar]
- Sobrino, J.A. Dual-Use European Security IR Experiment 2008 (DESIREX 2008) Final Report. Available online: https://earth.esa.int/c/document_library/get_file?folderId=21020&name=DLFE-905.pdf (accessed on 24 March 2009).
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhao, E.; Qian, Y.; Gao, C.; Huo, H.; Jiang, X.; Kong, X. Land Surface Temperature Retrieval Using Airborne Hyperspectral Scanner Daytime Mid-Infrared Data. Remote Sens. 2014, 6, 12667-12685. https://doi.org/10.3390/rs61212667
Zhao E, Qian Y, Gao C, Huo H, Jiang X, Kong X. Land Surface Temperature Retrieval Using Airborne Hyperspectral Scanner Daytime Mid-Infrared Data. Remote Sensing. 2014; 6(12):12667-12685. https://doi.org/10.3390/rs61212667
Chicago/Turabian StyleZhao, Enyu, Yonggang Qian, Caixia Gao, Hongyuan Huo, Xiaoguang Jiang, and Xiangsheng Kong. 2014. "Land Surface Temperature Retrieval Using Airborne Hyperspectral Scanner Daytime Mid-Infrared Data" Remote Sensing 6, no. 12: 12667-12685. https://doi.org/10.3390/rs61212667
APA StyleZhao, E., Qian, Y., Gao, C., Huo, H., Jiang, X., & Kong, X. (2014). Land Surface Temperature Retrieval Using Airborne Hyperspectral Scanner Daytime Mid-Infrared Data. Remote Sensing, 6(12), 12667-12685. https://doi.org/10.3390/rs61212667