Parameterization of the Satellite-Based Model (METRIC) for the Estimation of Instantaneous Surface Energy Balance Components over a Drip-Irrigated Vineyard
Abstract
:1. Introduction
Theoretical Basis
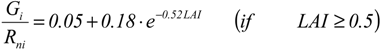
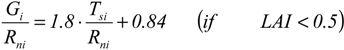
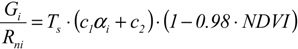
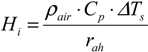
2. Materials and Methods

2.1. Vine Surface Energy Balance Measurements
| Sensor | Manufacturer, Model | Quantity | Heigt (m) | Origin |
|---|---|---|---|---|
| Four-component Net Radiometer | Kipp & Zonen, CNR1 | 1 | 4.7 | Delft, The Netherlands |
| Net Radiometer | REBS, Q7.1 | 1 | 4.7 | Washington, USA |
| Soil heat flux plates | Campbell Scientific, HTF3 | 8 | −0.08 | Utah, USA |
| Soil averaged temperature | Campbell Scientific, TCAV | 4 | −0.06 and −0.04 | Utah, USA |
| Fast response open path Infrared Gas Analyzer | LI-COR Inc., LI-7500 | 1 | 4.7 | Nebraska, USA |
| 3D Sonic anemometer | Campbell Scientific, CSAT3 | 1 | 4.7 | Utah, USA |
| Wind speed and direction | Young, 03101-5 | 1 | 4.7 | Florida, USA |
| Air temperature and relative humidity | Vaisala, HMP45C | 1 | 4.7 | Massachusetts, USA |
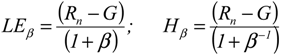
2.2. Reference Evapotranspiration
2.3. Ground Measurements of Vineyard Reflectance
2.4. Landsat Satellite Datasets and Image Processing
| Growing Season | Date (mm-dd-yy) | DOY * | Satellite | Overpass Time (Local Time) |
|---|---|---|---|---|
| 2006–2007 | 12-29-2006 | 363 | Landsat 7 ETM+ | 11:24:41 |
| 01-12-2007 | 14 | Landsat 7 ETM+ | 11:24:41 | |
| 2007–2008 | 11-30-2007 | 334 | Landsat 7 ETM+ | 11:24:47 |
| 12-16-2007 | 350 | Landsat 7 ETM+ | 11:24:47 | |
| 01-01-2008 | 1 | Landsat 7 ETM+ | 11:24:49 | |
| 01-17-2008 | 17 | Landsat 7 ETM+ | 11:24:49 | |
| 01-25-2008 | 25 | Landsat 5 TM | 11:25:33 | |
| 02-02-2008 | 33 | Landsat 7 ETM+ | 11:24:47 | |
| 02-18-2008 | 49 | Landsat 7 ETM+ | 11:24:44 | |
| 2008–2009 | 10-23-2008 | 297 | Landsat 5 TM | 11:18:16 |
| 11-16-2008 | 321 | Landsat 7 ETM+ | 11:23:38 | |
| 12-02-2008 | 337 | Landsat 7 ETM+ | 11:23:50 | |
| 01-03-2009 | 3 | Landsat 7 ETM+ | 11:24:06 | |
| 02-20-2009 | 51 | Landsat 7 ETM+ | 11:24:26 | |
| 03-08-2009 | 67 | Landsat 7 ETM+ | 11:24:34 |
2.5. Calibration of LAI, zom and G functions
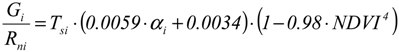
2.6. Statistical Comparison between Measured and Estimated Values
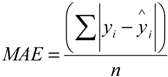
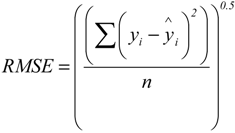
3. Results and Discussion
| Season | DOY | Cf | Rni/Rsin_i | β | Hβi/Rni | LEβi/Rni | Gi/Rni |
|---|---|---|---|---|---|---|---|
| 2006–2007 | 363 | 1.09 | 0.68 | 0.91 | 0.37 | 0.41 | 0.22 |
| 14 | 0.80 | 0.67 | 1.24 | 0.44 | 0.36 | 0.22 | |
| 2007–2008 | 334 | 0.84 | 0.56 | 1.90 | 0.52 | 0.27 | 0.21 |
| 350 | 0.61 | 0.63 | 1.25 | 0.43 | 0.35 | 0.22 | |
| 1 | 0.88 | 0.58 | 1.09 | 0.41 | 0.38 | 0.21 | |
| 17 | 0.96 | 0.65 | 1.16 | 0.43 | 0.37 | 0.20 | |
| 25 | 0.78 | 0.68 | 1.49 | 0.48 | 0.32 | 0.20 | |
| 33 | 0.68 | 0.68 | 0.99 | 0.39 | 0.39 | 0.21 | |
| 49 | 1.01 | 0.76 | 1.18 | 0.41 | 0.35 | 0.24 | |
| 2008–2009 | 297 | 0.76 | 0.66 | 3.17 | 0.63 | 0.20 | 0.17 |
| 321 | 1.11 | 0.68 | 1.47 | 0.37 | 0.25 | 0.38 | |
| 337 | 0.66 | 0.74 | 1.48 | 0.5 | 0.34 | 0.16 | |
| 3 | 0.85 | 0.73 | 0.68 | 0.3 | 0.44 | 0.25 | |
| 51 | 1.08 | 0.71 | 1.89 | 0.48 | 0.25 | 0.27 | |
| 67 | 0.76 | 0.7 | 1.66 | 0.47 | 0.29 | 0.24 | |
| Average | 0.86 | 0.67 | 1.44 | 0.44 | 0.33 | 0.23 | |
| St. Dev. | 0.16 | 0.05 | 0.59 | 0.08 | 0.07 | 0.05 |

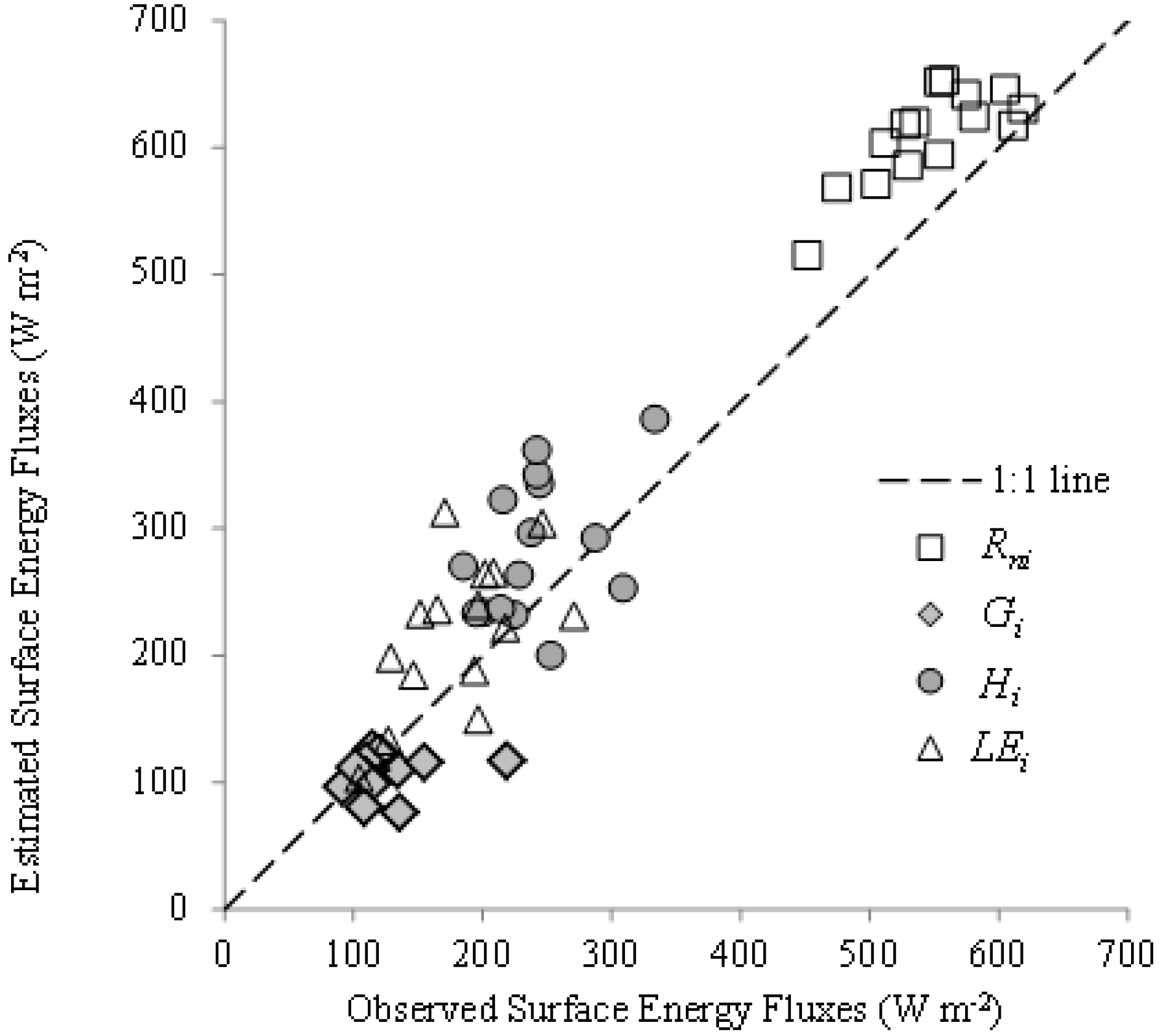
Comparison between Measured and Estimated Variables
| (a) Comparisons Using the Calibrated Function of LAI, zom and G | |||||
| Variable | RMSE | MAE | b | d | t-Test |
| LAI vs. LAI_M | 0.3 (m2∙m−2) | 0.2 (m2∙m−2) | 1.04 | 0.30 | T |
| zomi vs. zom_M | 0.01 (m) | 0.01 (m) | 0.98 | 0.64 | T |
| Rni vs. Rn_M | 69 (W∙m−2) | 63 (W∙m−2) | 1.11 | 0.60 | F |
| Gi vs. G_M | 34 (W∙m−2) | 21 (W∙m−2) | 0.83 | 0.39 | F |
| Hβi vs. H_M | 67 (W∙m−2) | 57 (W∙m−2) | 1.16 | 0.52 | F |
| LEβi vs. LE_M | 60 (W∙m−2) | 48 (W∙m−2) | 1.17 | 0.67 | F |
| (b) Comparisons Using Original Function of LAI, zom and G [27] | |||||
| Variable | RMSE | MAE | b | d | t-Test |
| LAI vs. LAI_M | 0.6 (m2∙m−2) | 0.6 (m2∙m−2) | 0.42 | 0.30 | F |
| zomi vs. zom_M | 0.08 (m) | 0.08 (m) | 0.19 | 0.50 | F |
| αi vs. α_M | 0.04 | 0.04 | 0.79 | 0.28 | F |
| Rni vs. Rn_M | 70 (W∙m−2) | 64 (W∙m−2) | 1.11 | 0.60 | F |
| Gi vs. G_M | 33 (W∙m−2) | 26.3 (W∙m−2) | 0.95 | 0.30 | T |
| Hβi vs. H_M | 51 (W∙m−2) | 43 (W∙m−2) | 1.13 | 0.68 | F |
| LEβi vs. LE_M | 43 (W∙m−2) | 35 (W∙m−2) | 1.15 | 0.81 | F |
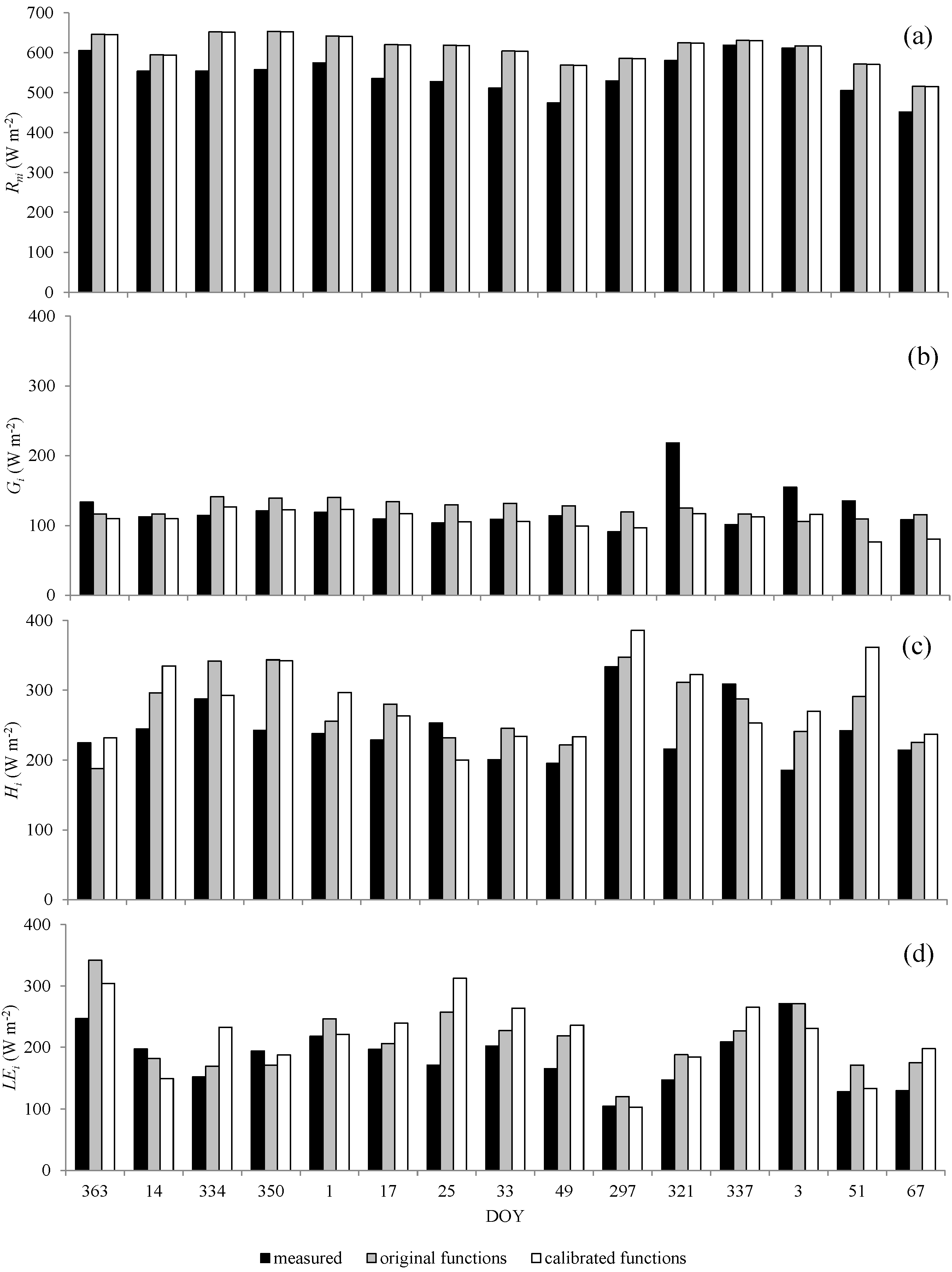
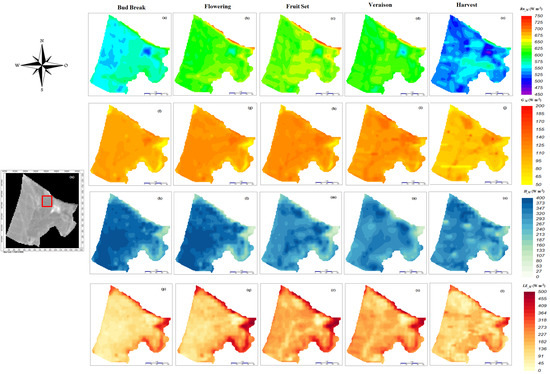
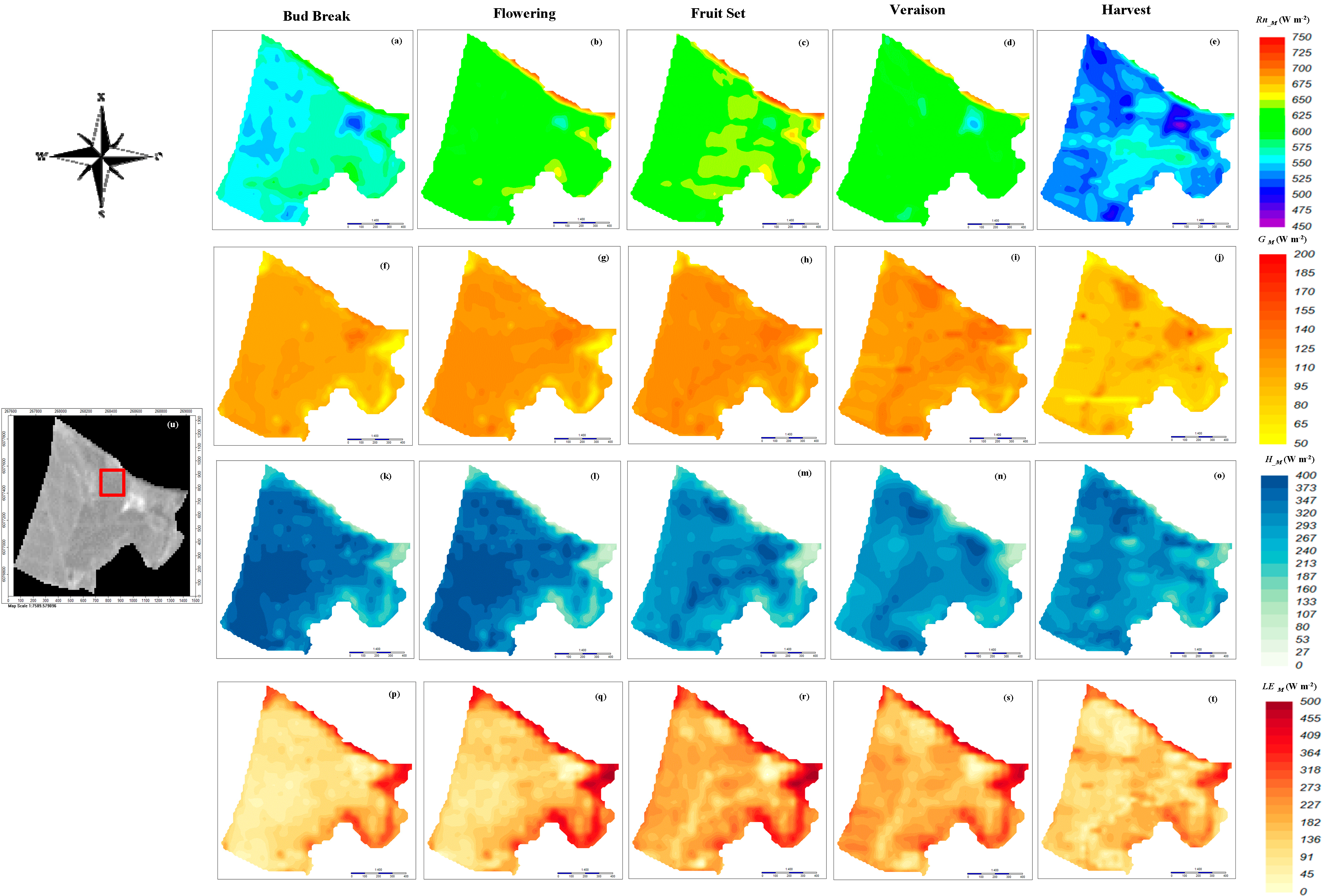
Spatial Variability of the Estimated Surface Energy Balance Components for the Complete Vineyard
4. Conclusions
Appendix: Definition of Variables
| Symbol | Definition |
| Cf | Ratio of turbulent fluxes to available energy or energy balance closure (= (H + LE)/(Rn − G)) (dimensionless) |
| Cp | Specific heat capacity of air (1004 J kg−1∙K−1) |
| d | Zero plane displacement for heigth (m) |
| ETa | Actual evapotranspiration (mm∙d−1) |
| ETa_M | ETa computed for METRIC for each pixel (mm∙d−1) |
| ETi | ETa at the instant of satellite overpass (mm∙h−1) |
| ETi_M | Instantaneous ETa calculated for METRIC for each pixel (mm∙h−1) |
| ETo | Penman-Montetith reference evapotranspiration computed for grass (mm∙d−1) |
| ETo_i | Hourly reference evapotranspiration at the time of satellite overpass (mm∙h−1) |
| ETr | Reference evapotranspiration (for alfalfa) (mm∙d−1) |
| fc | Fractional cover (fraction) |
| Fi_M | Reference evapotranspiration fraction computed by METRIC at the time of satellite Overpass (= ETi_M/EToh) (dimensionless) |
| G | Soil heat flux (W∙m−2) |
| G_M | Soil heat flux estimated by METRIC at the time of satellite overpass (W∙m−2) |
| Gi | Soil heat flux at the instant of satellite overpass (W∙m−2) |
| H | Sensible heat flux (W∙m−2) |
| H_M | Sensible heat flux estimated by METRIC at the time of satellite overpass (W∙m−2) |
| hc | Canopy heigth (m) |
| Hcold | Sensible heat flux at the instant of at the time of satellite overpass for the cold Pixel (W∙m−2) |
| Hi | Sensible heat flux at the instant of satellite overpass (W∙m−2) |
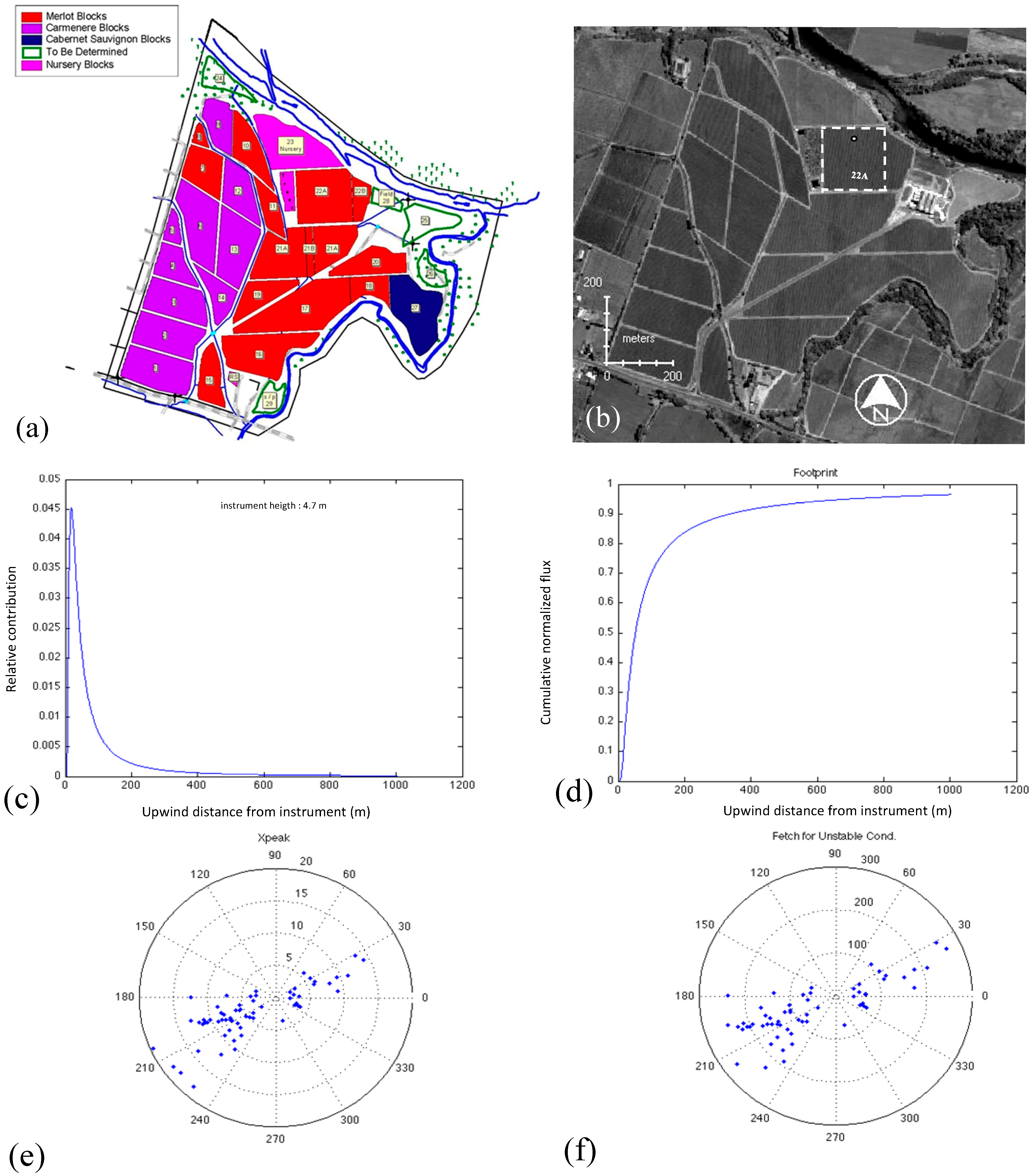
| Hβ | Sensible heat flux forced to close the energy balance using the Bowen ratio (W∙m−2) |
| LAI | Leaf Area Index (m2∙m−2) |
| LAI_M | Leaf Area Index estimated by satellite scene at each pixel (m2∙m−2) |
| LE | Sensible heat flux (W∙m−2) |
| LE_M | Latent heat flux estimated by METRIC at the time of satellite overpass (W∙m−2) |
| LEi | Sensible heat flux at the instant of at the time of satellite overpass (W∙m−2) |
| LEβ | Latent heat flux forced to close the energy balance using the Bowen ratio (W∙m−2) |
| NDVI | Normalized Difference Vegetation Index (dimensionless) |
| q' | Humidity (kg∙kg−1) |
| rah | Aerodynamic resistance to heat transport (s∙m−1) |
| RHa_o | Relative humidity for a short reference surface (fescue grass) (%) |
| RL↑ | Outgoing longwave radiation (W∙m−2) |
| RL↓ | Incoming longwave radiation (W∙m−2) |
| Rn_M | Net radiation estimated by METRIC at the time of satellite overpas (W∙m−2) |
| Rncold | Net radiation flux at the instant of at the time of satellite overpass for the cold pixel (W∙m−2) |
| Rni | Net radiation at the instant of satellite overpass (W∙m−2) |
| rs | Row spacing (m) |
| Rs↓ | Incoming shortwave radiation (W∙m−2) |
| Rsin | Measured incoming solar radiation radiation (W∙m−2) |
| Rsin_o | Incoming solar radiation in reference conditions (fescue grass) (W m−2∙h−1) |
| Rso | Measured outgoing solar radiation radiation (W∙m−2) |
| SAVI | Soil Adjusted Vegetation Index (dimensionless) |
| T | Instantaneous sonic temperature (°K) |
| Ta | Air temperature over the vineyard (fescue grass) (°C) |
| Ta_o | Air temperature for short reference surface (fescue grass) (°C) |
| Taz1 and Taz2 | Near surface air temperature (°K) |
| Ts | Surface radiometric temperature (°C or °K) |
| Tsi | Instantaneous surface radiometric temperature calculated for each pixel (°C or °K) |
| u2 | Mean wind speed at 2-m height in reference conditions (fescue grass) (m∙s−1) |
| VPD | Vapor pressure deficit (kPa) |
| w' | Wind speed (m∙s−1) |
| wbd | Weighting coefficient of the Landsat bands for calculating broad-band surface Albedo (dimensionless) |
| zom | Aerodynamic roughness length for momentum transfer (m) |
| zom_M | Aerodynamic roughness length for momentum transfer computed by METRIC (m) |
| α | Surface albedo (dimensionless) |
| α_M | Broadband surface albedo at the time of satellite overpass computed by METRIC (dimensionless) |
| αi | Surface albedo at the instant of satellite overpass (dimensionless) |
| β | Bowen ratio (= H/LE) (dimensionless) |
| ΔTs | Near-surface air temperature gradient (ΔTs = Taz1 − Taz2) above each pixel, where Taz1 and Taz2 are near surface air temperature at heights z1 and z2 (m), respectively (°K) |
| ε0 | Surface emissivity (dimensionless) |
| θFC | Volumetric soil water content at field capacity (m3∙m−3) |
| θi | Measured volumetric soil water content (m3∙m−3) |
| θWP | Volumetric soil water content at wilting point (m3∙m−3) |
| λ | Latent heat of vaporization (J∙kg−1) |
| ρair | Air density (kg∙m−3) |
| ρs,bd | At-surface “s” reflectance for each “bd” band (dimensionless) |
| Ψx | Midday stem water potential (MPa) |
Acknowledgments
Author Contributions
Conflict of Interest
References
- Costa, J.M.; Ortuno, M.F.; Chaves, M.M. Deficit irrigation as a strategy to save water: Physiology and potential application to horticulture. J. Integr. Plant Biol. 2007, 49, 1421–1434. [Google Scholar] [CrossRef]
- Chaves, M.M.; Santos, T.P.; Souza, C.R.; Ortuño, M.F.; Rodrigues, M.L.; Lopes, C.M.; Maroco, J.P.; Pereira, J.S. Deficit irrigation in grapevine improves water-use efficiency while controlling vigour and production quality. Ann. Appl. Biol. 2007, 150, 237–252. [Google Scholar] [CrossRef]
- Fereres, E.; Soriano, M.A. Deficit irrigation for reducing agricultural water use. J. Exp. Bot. 2007, 58, 147–159. [Google Scholar] [CrossRef] [PubMed]
- Williams, L.E.; Matthews, M.A. Grapevine. In Irrigation of Agricultural Crops–Agronomy Monograph; Stewart, B.A., Nielson, D.R., Eds.; ASA-CSSA-SSSA: Madison, WI, USA, 1990; Volume 30; pp. 1019–1059. [Google Scholar]
- Poblete-Echeverria, C.; Ortega-Farias, S. Estimation of actual evapotranspiration for a drip-irrigated Merlot vineyard using a three-source model. Irrig. Sci. 2009, 28, 65–78. [Google Scholar] [CrossRef]
- Ferreyra, R.; Selles, V.; Peralta, J.; Burgos, L.; Valenzuela, J. Efectos de la restricción del riego en distintos períodos de desarrollo de la vid cv. Cabernet sauvignon sobre producción y calidad del vino. Agric. Tec. 2002, 62, 406–417. [Google Scholar]
- Trambouze, W.; Bertuzzi, P.; Voltz, M. Comparison of methods for estimating actual evapotranspiration in a row-cropped vineyard. Agric. For. Meteorol. 1998, 91, 193–208. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 1. Model formulation. J. Geophys. Res. Atmos. 2007, 112, D10117. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL)—1. Formulation. J. Hydrol. 1998, 213, 198–212. [Google Scholar] [CrossRef]
- Verstraeten, W.W.; Veroustraete, F.; Feyen, J. Assessment of evapotranspiration and soil moisture content across different scales of observation. Sensors 2008, 8, 70–117. [Google Scholar] [CrossRef]
- Steiner, J.L.; Hatfield, J.L. Winds of change: A century of agroclimate research. Agron. J. 2008, 100, S132–S152. [Google Scholar] [CrossRef]
- Ortega-Farias, S.; Carrasco, M.; Olioso, A.; Acevedo, C.; Poblete, C. Latent heat flux over Cabernet Sauvignon vineyard using the Shuttleworth and Wallace model. Irrig. Sci. 2007, 25, 161–170. [Google Scholar] [CrossRef]
- Balbontin-Nesvara, C.; Calera-Belmonte, A.; Gonzalez-Piqueras, J.; Campos-Rodriguez, I.; Lopez-Gonzalez, M.L.; Torres-Prieto, E. Vineyard evapotranspiration measuraments in a semiarid environment: Eddy covariance and bowen ratio comparison. Agrociencia 2010, 45, 87–103. [Google Scholar]
- Oliver, H.R.; Sene, K.J. Energy and water balances of developing vines. Agric. For. Meteorol. 1992, 61, 167–185. [Google Scholar] [CrossRef]
- Heilman, J.L.; McInnes, K.J.; Savage, M.J.; Gesch, R.W.; Lascano, R.J. Soil and canopy energy balances in a west Texas vineyard. Agric. For. Meteorol. 1994, 71, 99–114. [Google Scholar] [CrossRef]
- Kordova-Biezuner, L.; Mahrer, I.; Schwartz, C. Estimation of actual evapotranspiration from vineyard by utilizing eddy correlation method. Acta Hortic. 2000, 537, 167–175. [Google Scholar]
- Campos, I.; Neale, C.M.U.; Calera, A.; Balbontín, C.; González-Piqueras, J. Assessing satellite-based basal crop coefficients for irrigated grapes (Vitis vinifera L.). Agric. Water Manag. 2010, 98, 45–54. [Google Scholar] [CrossRef]
- Kleissl, J.; Hong, S.H.; Hendrickx, J.M.H. New Mexico scintillometer network supporting remote sensing and hydrologic and meteorological models. Bull. Am. Meteorol. Soc. 2009, 90. [Google Scholar] [CrossRef]
- Gowda, P.H.; Chávez, J.L.; Colaizzi, P.D.; Evett, S.R.; Howell, T.A.; Tolk, J.A. Remote sensing based energy balance algorithms for mapping ET: Current status and future challenges. Trans. ASABE 2007, 50, 1639–1644. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef]
- Courault, D.; Seguin, B.; Olioso, A. Review on estimation of evapotranspiration from remote sensing data: From empirical to numerical modeling approaches. Irrig. Drain. Syst. 2005, 19, 223–249. [Google Scholar] [CrossRef]
- Kalma, J.; McVicar, T.; McCabe, M. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Santos, C.; Lorite, I.J.; Tasumi, M.; Allen, R.G.; Fereres, E. Performance assessment of an irrigation scheme using indicators determined with remote sensing techniques. Irrig. Sci. 2010, 28, 461–477. [Google Scholar] [CrossRef]
- Gowda, P.; Chavez, J.; Colaizzi, P.; Evett, S.; Howell, T.; Tolk, J. ET mapping for agricultural water management: Present status and challenges. Irrig. Sci. 2008, 26, 223–237. [Google Scholar] [CrossRef]
- Seguin, B.; Courault, D.; Guérif, M. Surface temperature and evapotranspiration: Application of local scale methods to regional scales using satellite data. Remote Sens. Environ. 1994, 49, 287–295. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC) applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R.; Kjaersgaard, J.H. METRIC—Mapping Evapotranspiration at High Resolution, Application Manual. Available online: http://www.kimberly.uidaho.edu/water/metric/index.html (accessed on 30 May 2014).
- Singh, R.K.; Irmak, A.; Irmak, S.; Martin, D.L. Application of SEBAL model for mapping evapotranspiration and estimating surface energy fluxes in South-Central Nebraska. J. Irrig. Drain. Eng. 2008, 134, 273–285. [Google Scholar] [CrossRef]
- ASCE-EWRI. The ASCE standarized reference evapotranspiration equation. In Report of the ASCE-EWRI Task Committee on Standarization of Reference Evapotranspiration; ASCE-EWRI: Kimberly, ID, USA, 2005; p. 147. [Google Scholar]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC) Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Chávez, J.; Neale, C.; Prueger, J.; Kustas, W. Daily evapotranspiration estimates from extrapolating instantaneous airborne remote sensing ET values. Irrig. Sci. 2008, 27, 67–81. [Google Scholar] [CrossRef]
- Carrasco-Benavides, M.; Ortega-Farías, S.; Lagos, L.O.; Kleissl, J.; Morales, L.; Poblete-Echeverría, C.; Allen, R. Crop coefficients and actual evapotranspiration of a drip-irrigated Merlot vineyard using multispectral satellite images. Irrig. Sci. 2012, 1–13. [Google Scholar]
- Allen, R.; Irmak, A.; Trezza, R.; Hendrickx, J.M.H.; Bastiaanssen, W.; Kjaersgaard, J. Satellite-based ET estimation in agriculture using SEBAL and METRIC. Hydrol. Proc. 2011, 25, 4011–4027. [Google Scholar] [CrossRef]
- Tasumi, M.; Allen, R.G.; Trezza, R.; Wright, J.L. Satellite-based energy balance to assess within-population variance of crop coefficient curves. J. Irrig. Drain. Eng. 2005, 131, 94–109. [Google Scholar] [CrossRef]
- Galleguillos, M.; Jacob, F.; Prévot, L.; French, A.; Lagacherie, P. Comparison of two temperature differencing methods to estimate daily evapotranspiration over a Mediterranean vineyard watershed from ASTER data. Remote Sens. Environ. 2011, 115, 1326–1340. [Google Scholar] [CrossRef]
- Galleguillos, M.; Jacob, F.; Prevot, L.; Lagacherie, P.; Liang, S.L. Mapping daily evapotranspiration over a mediterranean vineyard watershed. IEEE Geosci. Remote Sens. Lett. 2011, 8, 168–172. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Pelgrum, H.; Soppe, R.W.O.; Allen, R.G.; Thoreson, B.P.; Teixeira, A.H. Thermal-infrared technology for local and regional scale irrigation analyses in horticultural systems. Acta Hortic. 2008, 793, 33–46. [Google Scholar]
- Santos, C.; Lorite, I.J.; Allen, R.G.; Tasumi, M. Aerodynamic parameterization of the satellite-based energy balance (METRIC) model for ET estimation in rainfed olive orchards of Andalusia, Spain. Water Resour. Manag. 2012, 26, 3267–3283. [Google Scholar] [CrossRef]
- Teixeira, A.H.; Bastiaanssen, W.G.M.; Ahmad, M.D.; Bos, M.G. Reviewing SEBAL input parameters for assessing evapotranspiration and water productivity for the Low-Middle Sao Francisco River basin, Brazil Part B: Application to the regional scale. Agric. For. Meteorol. 2009, 149, 477–490. [Google Scholar] [CrossRef]
- Ortega-Farias, S.; Poblete-Echeverría, C.; Brisson, N. Parameterization of a two-layer model for estimating vineyard evapotranspiration using meteorological measurements. Agric. For. Meteorol. 2010, 150, 276–286. [Google Scholar] [CrossRef]
- Tasumi, M.; Allen, R.G.; Trezza, R. At-surface reflectance and albedo from satellite for operational calculation of land surface energy balance. J. Hydrol. Eng. 2008, 13, 51–63. [Google Scholar] [CrossRef]
- Tasumi, M. Progress in Operational Estimation of Regional Evapotranspiration Using Satellite Imagery. Ph.D. Thesis, University of Idaho, Moscow, ID, USA, 2003. [Google Scholar]
- Basso, B.; Cammarano, D.; DeVita, P. Remotely sensed vegetation indices: Theory and applications for crop management. Riv. Ital. Agrometeorol. 2004, 1, 36–53. [Google Scholar]
- Kjaersgaard, J.H.; Allen, R.G.; Garcia, M.; Kramber, W.; Trezza, R. Automated selection of anchor pixels for landsat based evapotranspiration estimation. In World Environmental and Water Resources Congress 2009 Great Rivers; ASCE, Ed.; ASCE: Kansas City, MO, USA, 2009; pp. 4400–4410. [Google Scholar]
- Coombe, B.G. Growth Stages of the Grapevine: Adoption of a system for identifying grapevine growth stages. Aust. J. Grape Wine Res. 1995, 1, 104–110. [Google Scholar] [CrossRef]
- Li, S.; Tong, L.; Li, F.; Zhang, L.; Zhang, B.; Kang, S. Variability in energy partitioning and resistance parameters for a vineyard in northwest China. Agric. Water Manag. 2009, 96, 955–962. [Google Scholar] [CrossRef]
- Webb, E.; Pearman, G.; Leuning, R. Correction of flux measurements for density effects due to heat and water vapour transfer. Q. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Schotanus, P.; Nieuwstadt, F.T.M.; de Bruin, H.A.R. Temperature measurement with a sonic anemometer and its application to heat and moisture fluctuations. Bound. Layer Meteorol. 1983, 26, 81–93. [Google Scholar] [CrossRef]
- Wilczak, J.; Oncley, S.; Stage, S. Sonic anemometer tilt correction algorithms. Bound. Layer Meteorol. 2001, 99, 127–150. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- Chávez, J.; Howell, T.; Copeland, K. Evaluating eddy covariance cotton ET measurements in an advective environment with large weighing lysimeters. Irrig. Sci. 2009, 28, 35–50. [Google Scholar] [CrossRef]
- Poblete-Echeverría, C.; Ortega-Farias, S. Calibration and validation of a remote sensing algorithm to estimate energy balance components and daily actual evapotranspiration over a drip-irrigated Merlot vineyard. Irrig. Sci. 2012, 30, 537–553. [Google Scholar] [CrossRef]
- Earth Resources Observation and Science Center (EROS). USGS Global Visualization Viewer. Available online: http://glovis.usgs.gov/ (accessed on 1 September 2010).
- Earth Resources Observation and Science Center (EROS). Landsat Processing Details. Available online: http://landsat.usgs.gov/Landsat_Processing_Details.php (accessed on 22 July 2014).
- Cuenca, R.; Ciotti, S.; Hagimoto, Y. Application of landsat to evaluate effects of irrigation forbearance. Remote Sens. 2013, 5, 3776–3802. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. FAO irrigation and drainage paper No. 56. In Crop Evapotranspiration Guidelines for Computing Crop Water Requirements; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; p. 298. [Google Scholar]
- Folhes, M.T.; Renno, C.D.; Soares, J.V. Remote sensing for irrigation water management in the semi-arid Northeast of Brazil. Agric. Water Manag. 2009, 96, 1398–1408. [Google Scholar] [CrossRef]
- Fuentes, S.; Poblete-Echeverría, C.; Ortega-Farias, S.; Tyerman, S.; de Bei, R. Automated estimation of leaf area index from grapevine canopies using cover photography, video and computational analysis methods. Aust. J. Grape Wine Res. 2014, 20, 465–473. [Google Scholar] [CrossRef]
- Yang, R.C.; Kozak, A.; Smith, J.H.G. The potential of Weibull-type functions as flexible growth curves. Can. J. For. Res. 1978, 8, 424–431. [Google Scholar]
- Sene, K.J. Parameterisations for energy transfers from a sparse vine crop. Agric. For. Meteorol. 1994, 71, 1–18. [Google Scholar] [CrossRef]
- Singh, R.K.; Irmak, A. Estimation of crop coefficients using satellite remote sensing. J. Irrig. Drain. Eng. ASCE 2009, 135, 597–608. [Google Scholar] [CrossRef]
- Mayer, D.G.; Butler, D.G. Statistical validation. Ecol. Model. 1993, 68, 21–32. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O’donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. 1985, 90, 8995–9005. [Google Scholar] [CrossRef]
- Williams, L.E.; Trout, T.J. Relationships among vine- and soil-based measures of water status in a thompson seedless vineyard in response to high-frequency drip irrigation. Am. J. Enol. Vitic. 2005, 56, 357–366. [Google Scholar]
- Choné, X.; Van Leeuwen, C.; Dubourdieu, D.; Gaudillère, J.P. Stem water potential is a sensitive indicator of Grapevine water status. Ann. Bot. 2001, 87, 477–483. [Google Scholar] [CrossRef]
- Ferreyra, R.; Selles, G.; Peralta, J.; Burgos, L.; Valenzuela, J. Efectos de la Restricción del Riego En Distintos Períodos de Desarrollo de la Vid cv. Cabernet Sauvignon Sobre Producción y Calidad del Vino. Agric. Tec. 2002, 62, 406–417. [Google Scholar]
- Pieri, P.; Gaudillere, J.P. Sensitivity to training system parameters and soil surface albedo of solar radiation intercepted by vine rows. Vitis 2003, 42, 77–82. [Google Scholar]
- Yunusa, I.A.M.; Walker, R.R.; Lu, P. Evapotranspiration components from energy balance, sapflow and microlysimetry techniques for an irrigated vineyard in inland Australia. Agric. For. Meteorol. 2004, 127, 93–107. [Google Scholar] [CrossRef]
- Macedo Pezzopane, J.R.; Pedro Júnior, M.J. Balanço de energia em vinhedo de “Niagara Rosada”. Bragantia 2003, 62, 155–161. [Google Scholar]
- Teixeira, A.H.D.C.; Bastiaanssen, W.G.M.; Bassoi, L.H. Crop water parameters of irrigated wine and table grapes to support water productivity analysis in the São Francisco river basin, Brazil. Agric. Water Manag. 2007, 94, 31–42. [Google Scholar] [CrossRef]
- Carrasco, M.; Ortega-Farias, S. Evaluation of a model to simulate net radiation over a vineyard cv. Cabernet Sauvignon. Chil. J. Agric. Res. 2008, 68, 156–165. [Google Scholar] [CrossRef]
- Green, A.; Green, S.; Caspari, H. Latent heat flux from a vineyard using scintillometry. Terr. Atmos. Ocean. Sci. 2000, 2, 525–542. [Google Scholar]
- Heilman, J.L.; McInnes, K.J.; Gesch, R.W.; Lascano, R.J.; Savage, M.J. Effects of trellising on the energy balance of a vineyard. Agric. For. Meteorol. 1996, 81, 79–93. [Google Scholar] [CrossRef]
- Cammalleri, C.; Ciraolo, G.; La Loggia, G.; Maltese, A. Daily evapotranspiration assessment by means of residual surface energy balance modeling: A critical analysis under a wide range of water availability. J. Hydrol. 2012, 452–453, 119–129. [Google Scholar] [CrossRef]
- Johnson, L.F.; Roczen, D.E.; Youkhana, S.K.; Nemani, R.R.; Bosch, D.F. Mapping vineyard leaf area with multispectral satellite imagery. Comput. Electron. Agric. 2003, 38, 33–44. [Google Scholar] [CrossRef]
- Hall, A.; Louis, J.P.; Lamb, D.W. Low-resolution remotely sensed images of winegrape vineyards map spatial variability in planimetric canopy area instead of leaf area index. Aust. J. Grape Wine Res. 2008, 14, 9–17. [Google Scholar] [CrossRef]
- Liu, S.; Lu, L.; Mao, D.; Jia, L. Evaluating parameterizations of aerodynamic resistance to heat transfer using field measurements. Hydrol. Earth Syst. Sci. 2007, 11, 769–783. [Google Scholar] [CrossRef]
- Chávez, J.; Gowda, P.; Howell, T.; Neale, C.; Copeland, K. Estimating hourly crop ET using a two-source energy balance model and multispectral airborne imagery. Irrig. Sci. 2009, 28, 79–91. [Google Scholar] [CrossRef]
- Choi, M.; Kustas, W.P.; Anderson, M.C.; Allen, R.G.; Li, F.; Kjaersgaard, J.H. An intercomparison of three remote sensing-based surface energy balance algorithms over a corn and soybean production region (Iowa, U.S.) during SMACEX. Agric. For. Meteorol. 2009, 149, 2082–2097. [Google Scholar] [CrossRef]
- Shaomin, L.; Guang, H.; Li, L.; Defa, M. Estimation of regional evapotranspiration by TM/ETM+ data over heterogeneous surfaces. Am. Soc. Photogramm. Remote Sens. 2007, 73, 1169–1178. [Google Scholar] [CrossRef]
- Wang, J.; Sammis, T.W.; Gutschick, V.P.; Gebremichael, M.; Miller, D.R. Sensitivity analysis of the surface energy balance algorithm for land (SEBAL). Trans. ASABE 2009, 52, 801–811. [Google Scholar] [CrossRef]
- González-Dugo, M.P.; González-Piqueras, J.; Campos, I.; Andréu, A.; Balbontín, C.; Calera, A. Evapotranspiration monitoring in a vineyard using satellite-based thermal remote sensing. Proc. SPIE 2012, 8531. [Google Scholar] [CrossRef]
- Lu, J.; Tang, R.; Tang, H.; Li, Z.-L. Derivation of daily evaporative fraction based on temporal variations in surface temperature, air temperature, and net radiation. Remote Sens. 2013, 5, 5369–5396. [Google Scholar] [CrossRef]
- Mokhtari, M.H.; Ahmad, B.; Hoveidi, H.; Busu, I. Sensitivity anaysis of METRIC-based evapotranspiration algorithm. Int. J. Environ. Res. 2013, 72, 407–422. [Google Scholar]
- Wang, X.-G.; Wang, W.; Huang, D.; Yong, B.; Chen, X. Modifying SEBAL model based on the trapezoidal relationship between land surface temperature and vegetation index for actual evapotranspiration estimation. Remote Sens. 2014, 6, 5909–5937. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P. A modified surface energy balance algorithm for land (M-SEBAL) based on a trapezoidal framework. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P. Assessing the impact of end-member selection on the accuracy of satellite-based spatial variability models for actual evapotranspiration estimation. Water Resour. Res. 2013, 49, 2601–2618. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P. Integration of the GG model with SEBAL to produce time series of evapotranspiration of high spatial resolution at watershed scales. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Singh, R.K.; Irmak, A. Treatment of anchor pixels in the METRIC model for improved estimation of sensible and latent heat fluxes. Hydrol. Sci. J. 2011, 56, 895–906. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrasco-Benavides, M.; Ortega-Farías, S.; Lagos, L.O.; Kleissl, J.; Morales-Salinas, L.; Kilic, A. Parameterization of the Satellite-Based Model (METRIC) for the Estimation of Instantaneous Surface Energy Balance Components over a Drip-Irrigated Vineyard. Remote Sens. 2014, 6, 11342-11371. https://doi.org/10.3390/rs61111342
Carrasco-Benavides M, Ortega-Farías S, Lagos LO, Kleissl J, Morales-Salinas L, Kilic A. Parameterization of the Satellite-Based Model (METRIC) for the Estimation of Instantaneous Surface Energy Balance Components over a Drip-Irrigated Vineyard. Remote Sensing. 2014; 6(11):11342-11371. https://doi.org/10.3390/rs61111342
Chicago/Turabian StyleCarrasco-Benavides, Marcos, Samuel Ortega-Farías, Luis Octavio Lagos, Jan Kleissl, Luis Morales-Salinas, and Ayse Kilic. 2014. "Parameterization of the Satellite-Based Model (METRIC) for the Estimation of Instantaneous Surface Energy Balance Components over a Drip-Irrigated Vineyard" Remote Sensing 6, no. 11: 11342-11371. https://doi.org/10.3390/rs61111342
APA StyleCarrasco-Benavides, M., Ortega-Farías, S., Lagos, L. O., Kleissl, J., Morales-Salinas, L., & Kilic, A. (2014). Parameterization of the Satellite-Based Model (METRIC) for the Estimation of Instantaneous Surface Energy Balance Components over a Drip-Irrigated Vineyard. Remote Sensing, 6(11), 11342-11371. https://doi.org/10.3390/rs61111342