This section will address the methodology associated with using the NOAA buoys to calibrate the Landsat thermal bands. The same method is used for all the Landsat instruments with only the instrument specific relative spectral response (RSR) functions changing.
2.1. Sub Surface to Skin Temperature Adjustment
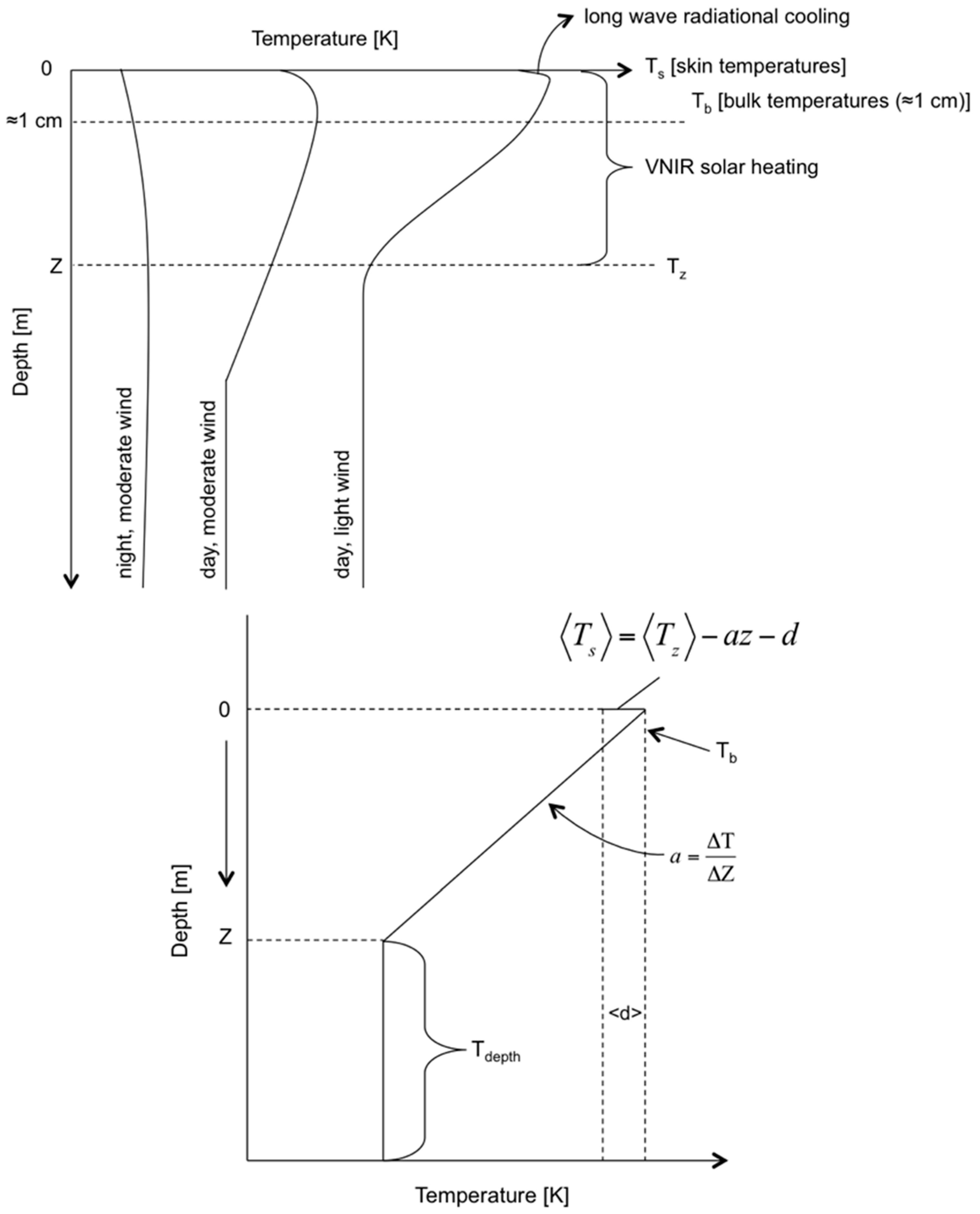
The NOAA buoys measure the water temperature between 0.6 m and 1.5 m below the surface depending on the buoy type. The Landsat sensors “see” the surface radiance being emitted from the top microns of the water surface. Therefore, in order to use the buoy temperatures measured at some depth for calibration, this subsurface temperature must first be corrected to surface or bulk temperature (
i.e., temperature change due to mixing from the depth of the temperature measurement to a few millimeters below the surface) and then to the skin temperature (
i.e., temperature change due to cooling by radiation from the top microns) that the satellites see. The near surface water temperature varies on a diurnal cycle driven predominately by insolation. This roughly sinusoidal cycle is dampened as a function of depth and wind speed. In addition, there is a temporal lag in the phase that increases with depth and decreases with wind speed. Zeng
et al. (1999) [
12] did an extensive study of this phenomenon including the development of coefficients characterizing the dependency of the diurnal damping and phase delay with depth and wind speed. Using the diurnal temperature and wind speed history from the buoy data for the 24 h preceding the satellite overpass, the subsurface temperatures can be converted to surface temperatures using the coefficients derived by Zeng
et al. (1999) [
12]. Note that this process breaks down for low wind speeds where there is little mixing between the subsurface and near surface water resulting in poor correlation of any type between the temperatures. As a result, data for conditions with wind speeds below 0.2 m/s are rejected from the analysis. At high wind speeds (above 8 m/s) the surface waters are well mixed and no subsurface to surface correction is applied (see
Figure 1). However, for all conditions, a skin temperature correction is applied. This is a small correction needed to account for the radiative cooling of the top microns of the water which are constantly trying to achieve radiative equilibrium with the “cold” sky (note that during the clear sky conditions used for calibration the sky is always considered “cold”). The process consists of three steps.
The first step is to find the average skin temperature over a 24-h period from
where
z is the depth of the temperature measurement for the buoy (m),
is the average temperature from the buoy measurement at this depth z over a 24 h period in Kelvin (K),
is the average skin temperature over a 24 h period (K), and d is the surface cool skin effect (K). Donlon
et al. (2002) [
13] showed that for a range of clear sky conditions the surface to skin correction (d) could be approximated with a constant value of 0.17 K (
i.e., the skin is 0.17 K cooler than the surface) and this value is used for this study. Finally,
a is the thermal gradient represented by
where
μm is the 24 h average wind speed at a height of 10 m above sea level (m/s) (available from sensors on the buoy).
The second step in the process acknowledges that the surface temperature will vary with time (diurnal variation), and can be solved empirically using
where
T(
z, t) is the buoy temperature at depth
z and time
t, cz is a phase term, and e
−bz accounts for dampening of the amplitude with depth. This second step is accomplished by solving for
f(
t) through the interpolation of
f(
t −
cz) around the specific time of interest (
t). The phase constant (hr/m) was empirically derived by Zeng
et al. (1999) [
12] to be:
and the damping constant with depth (m) to be:
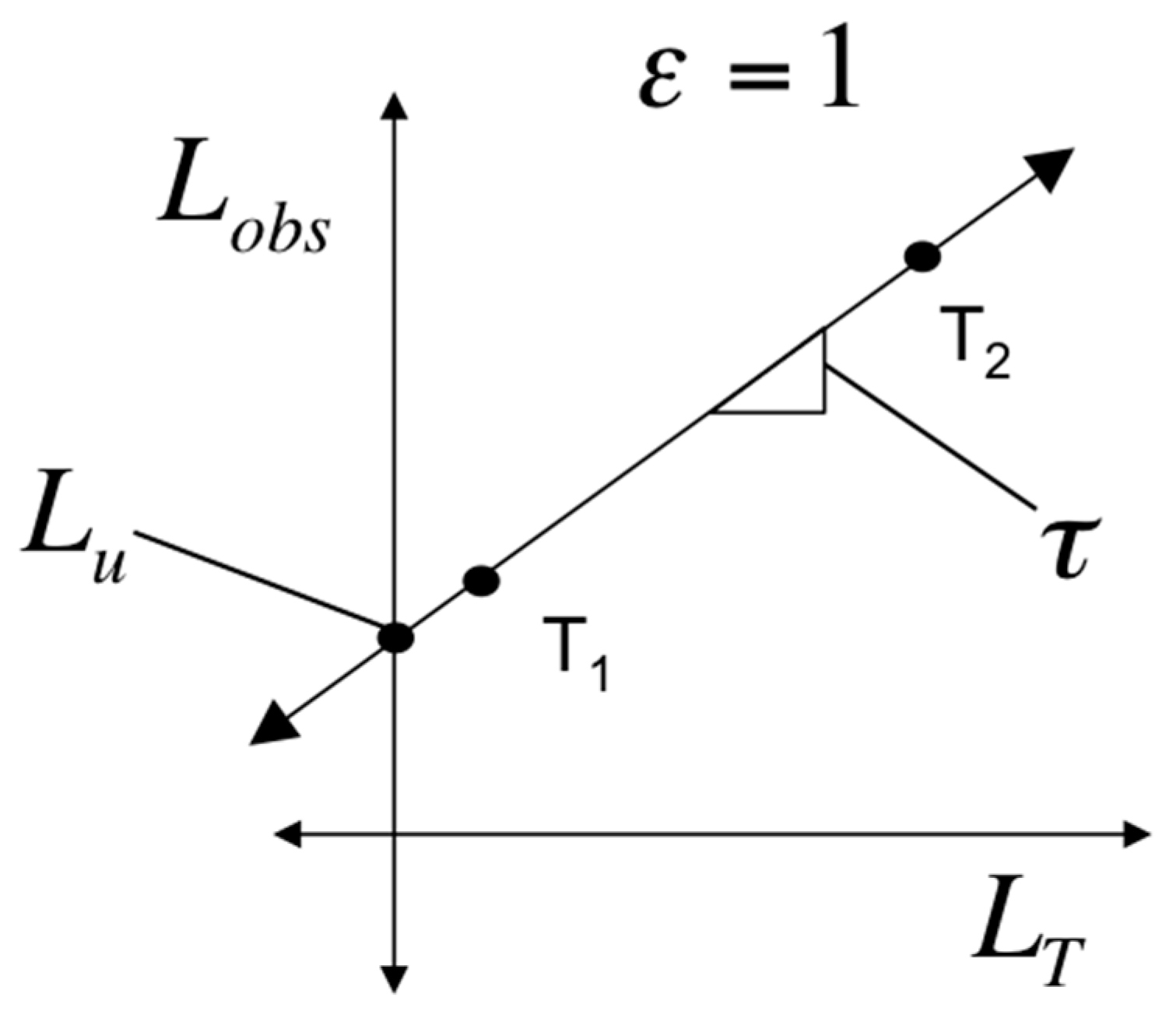
Graphically this step can be seen in
Figure 2. This can be viewed as first correcting the diurnal temperature variation for the dampening effect of depth and then correcting for the temporal phase shift between the peak temperature at the surface and the peak temperature at depth.
Figure 1.
Illustration of parameters used in Equations (1) and (2).
Figure 1.
Illustration of parameters used in Equations (1) and (2).
Figure 2.
Graphic representation of the unknown diurnal surface temperature at time t (left), and the Zeng empirical correction method (right).
Figure 2.
Graphic representation of the unknown diurnal surface temperature at time t (left), and the Zeng empirical correction method (right).
The final step in estimating the skin temperature is completed using the 24 h average skin temperature and f(t) solved for in steps 1 and 2 respectively to yield
T(0, t) represents the skin temperature at the time of interest, or in other words the skin temperature at the time of the spacecraft collection. Padula
et al. (2011) [
3] applied this approach to a small set of buoys with large fetch (open water upwind from the buoy site) and clear sky conditions (
i.e., Landsat calibration conditions) and demonstrated its applicability to a wider range of conditions than the South Pacific where Zeng
et al. (1999) [
12] gathered the data used to develop the coefficients. Note that this entire process when applied to a wide range of buoys typically amounts to corrections of only a few tenths Kelvin (large corrections would only be needed at low wind speeds and are rejected as untrusted); however, because we are attempting to achieve an overall calibration with a residual error of that same order, this level of correction is necessary.
2.2. Use of Radiative Transfer Models to Estimate Top of Atmosphere (ToA) Radiance from Skin Temperature
The next step in the calibration process is to estimate a top of atmosphere (ToA) radiance from the skin temperature to directly compare to the radiance observed by the Landsat thermal instruments. This is accomplished using the MODTRAN radiative transfer code [
8] with careful characterization of the atmospheric inputs to the model. The ToA or effective in band sensor reaching spectral radiance can be expressed as [
14]
L
Tλ is the Planckian spectral radiance (W∙m
−2∙sr
−1∙μm
−1) emitted from the surface due to the skin temperature (T) solved for in
Section 2.1, τ(λ) is the wavelength (λ) dependent transmission, L
dλ is the downwelled spectral radiance which will be reflected (1 − ε(λ)) from the water, and L
uλ is the path radiance along the sensor to ground line of sight. RSR (λ) is the known relative spectral response of the particular thermal band of the Landsat instrument under calibration and ε (λ) is a lab measured spectral emissivity of water.
MODTRAN is used to solve for the unknowns τ, L
u, and L
d in Equation (7) based on estimates of the atmospheric profile between the sensor and the ground (the temperature and water vapor profiles are particularly critical in the Landsat bands). MODTRAN radiative transfer code has been used in conjunction with ground truth data to support all Landsat calibration and it has been shown that errors in the process are dominated by lack of knowledge of atmospheric variables rather than the radiative transfer code itself. The residual error in the process is on the order of a few tenths Kelvin [
3].
The inputs to MODTRAN come from the nearest radiosonde which typically has measured the temperature, pressure and relative humidity up to 20–30 km. A standard atmosphere is appended to the radiosonde data to characterize the more stable atmosphere up to space. Because the radiosonde may be tens of kilometers (or even up to 100 km) from the buoy and have sampled the atmosphere hours before the satellite over pass, the lowest and most critical atmospheric layers (surface to 1–2 km) are updated using local surface air temperature and relative humidity data (e.g., from the buoy) interpolated from the surface to the thermal inversion layer, or to 1 km if no inversion layer exists [
15].
The ToA spectral radiance obtained from the MODTRAN model can be directly compared to the observed radiance (Lobs) obtained by converting the sampled Landsat digital number (DN) to spectral radiance using the metadata in the Landsat header. Any difference is described as the error in the calibration. By taking many samples over a range of temperatures a sound estimate of the calibration state of the instrument can be made.
2.3. Data Sources and Web Access to Data Needed for Operational Calibration
The process described in
Section 2.1 and
Section 2.2 for calibrating the Landsat thermal bands is relatively straight forward for an expert with the appropriate software tools and a day to gather and combine the data to yield one calibration point. The effort to operationalize (or semi automate) the process did not involve any major changes to the analytical process. Rather, it involved a major effort to define a database of necessary inputs for each buoy as a function of time (the buoys can move from year to year) and tools to automatically obtain, sample, organize, format, and filter the data from the internet for input to the existing analytical tools.
The operational buoy calibration approach leverages several existing IDL analytical tools for the core radiometric calibration by linking them with automated input retrievals in one cohesive Python workflow. The entire workflow initiates with the selection of a specific date to be processed as it was initially designed to continuously run, checking daily for any new Landsat scenes with buoy data for that current day. However, a simple batch process can be used to process many dates in cases of historic investigations or when the Landsat archive has been reprocessed with updated calibration. Given a specific date and which instrument to evaluate (Landsat 4, 5, 7, or 8), the workflow identifies a list of all possible paths imaged on that day. This is possible because, once each satellite achieves its final orbit each path is on a predictable 16 day repeat. The Python workflow steps through all possible paths for that given day and all buoys within each path.
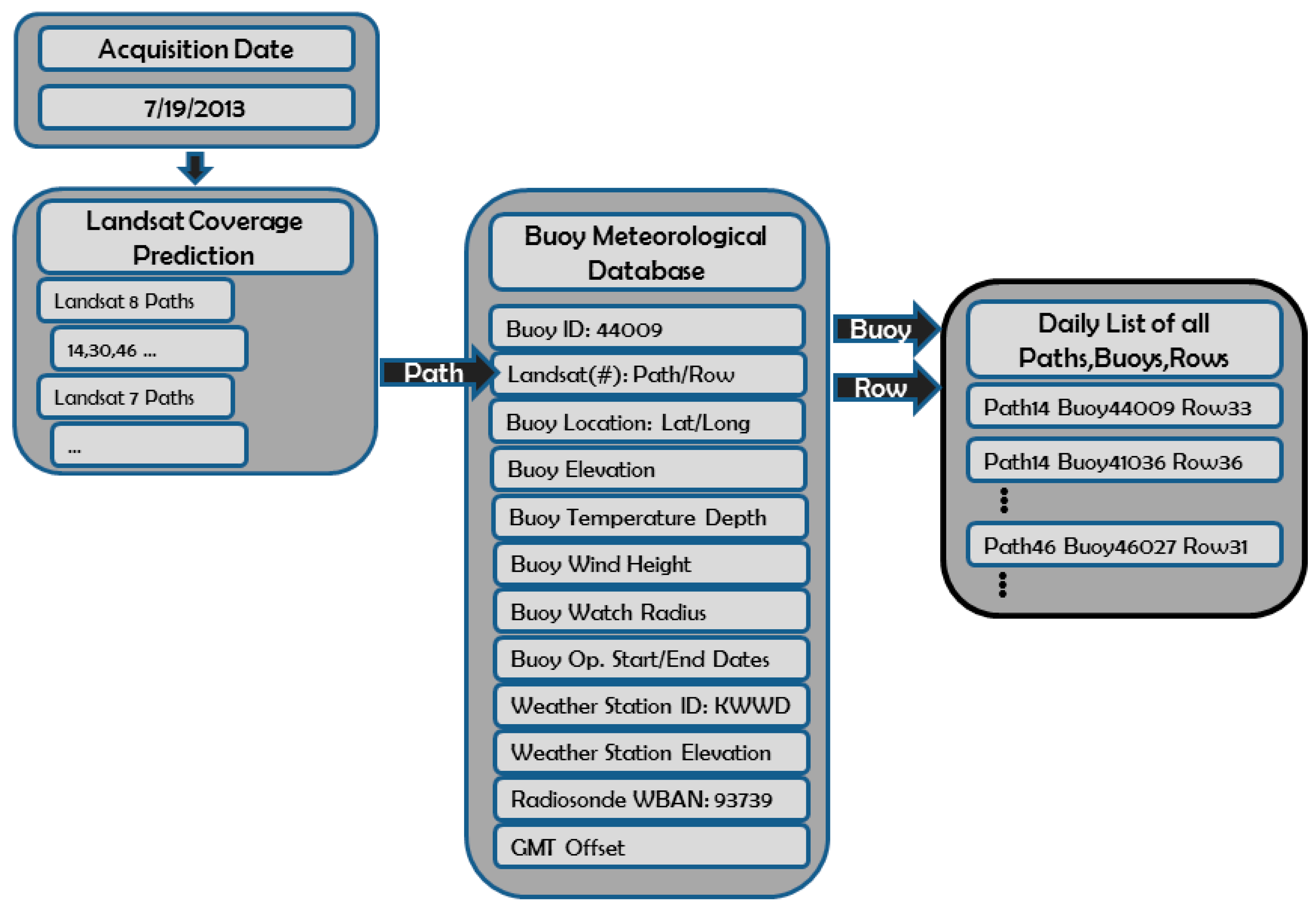
This brings us to the real driving force behind the process, the buoy meteorological database that describes all the necessary inputs for each specific buoy, such as, operational start and stop date, location, watch radius, depth of temperature measurement and height of wind measurement. The watch radius of the buoy is the distance a buoy can drift on the anchor chain from the nominal anchor location; this will be important in screening buoys later in the process. The corresponding radiosonde and weather station identification codes and the Landsat scene’s WRS-2 path and row are also stored within this database. It is also necessary for the database to maintain a temporal record of the buoy locations over the years as the deployment position may change slightly. Given a specific path, the workflow queries this database to generate a list of all the possible buoys to be processed within that path. For example,
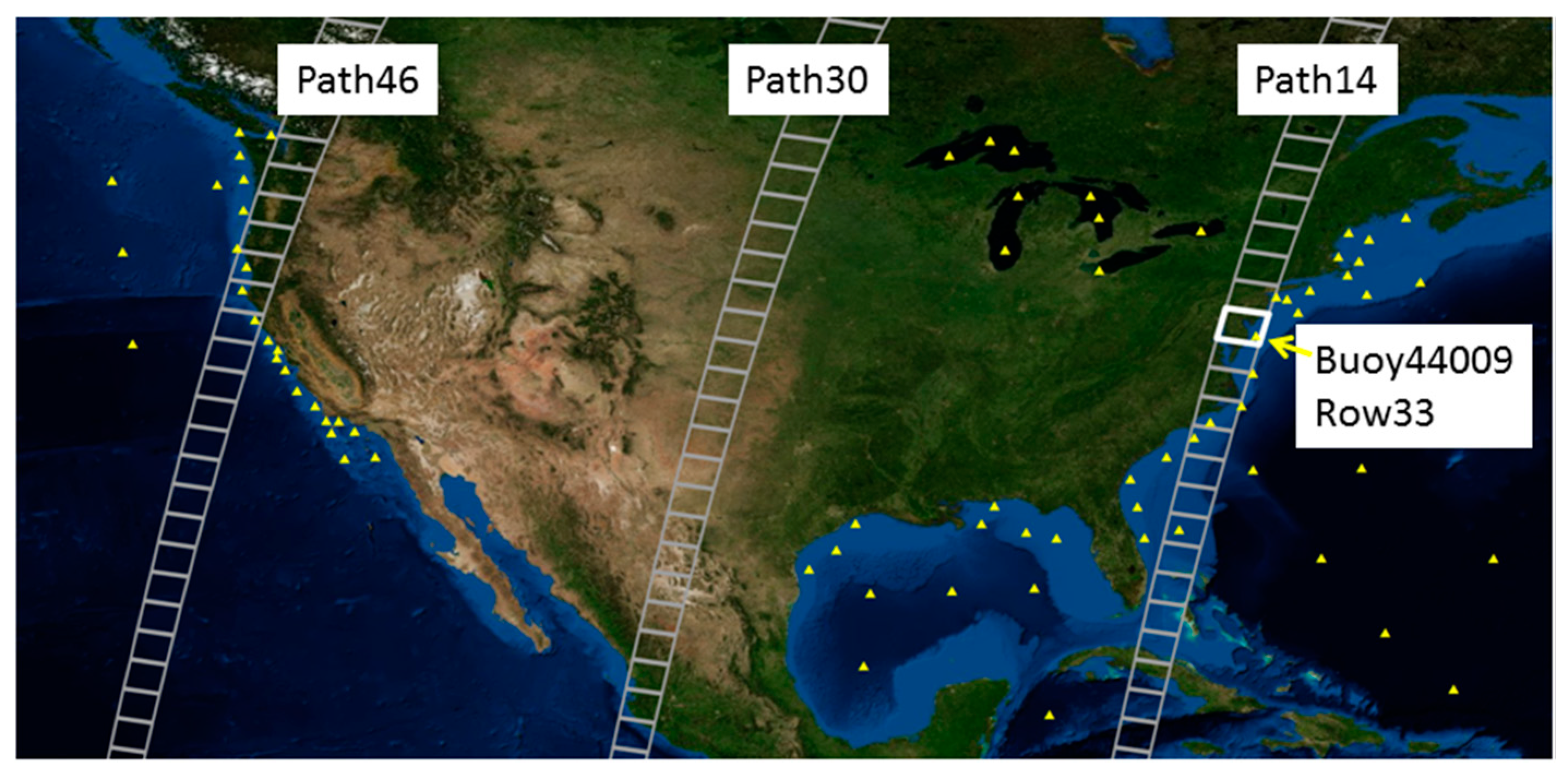
Figure 3 illustrates the possible paths for Landsat 8 for a specific date.
Once a specific path and buoy has been identified, the row is selected for that buoy location, which identifies the specific scene to automatically download directly from the USGS Earth Explorer [
16] using a customized wget retrieval. Next all the necessary inputs are identified from the buoy meteorological database and automatically downloaded from diverse web servers.
Figure 3.
Example of possible Landsat 8 paths, buoys, and specific scene rows for 19 July 2013; triangles indicate buoy location.
Figure 3.
Example of possible Landsat 8 paths, buoys, and specific scene rows for 19 July 2013; triangles indicate buoy location.
- ○
The atmospheric profile data is obtained through a PhP script call to NOAA’s ESRL Radiosonde Database [
17].
- ○
The surface weather data is extracted from Weather Underground [
18].
- ○
The buoy data is downloaded from NOAA’s National Data Buoy Center [
7].
Figure 4.
Selection of specific Landsat scenes and corresponding buoys for a given date using the buoy meteorological database.
Figure 4.
Selection of specific Landsat scenes and corresponding buoys for a given date using the buoy meteorological database.
Though invaluable, the buoy data presents its own set of challenges since the data format, missing data flags, and download location changes depending on length of time since the buoy measurement. There are at least three different formats: data measured in the past 45 days, data more than a year old, data taken within the current year but more than 45 days old. In the operational scenario this workflow would be constantly running on the past 45 day product. However, historic studies or cases when the entire Landsat archive has been reprocessed require that the workflow handles all buoy format nuances. Buoy data availability requires further verification as many buoys are retrieved for the winter months or may be offline due to instrument maintenance.
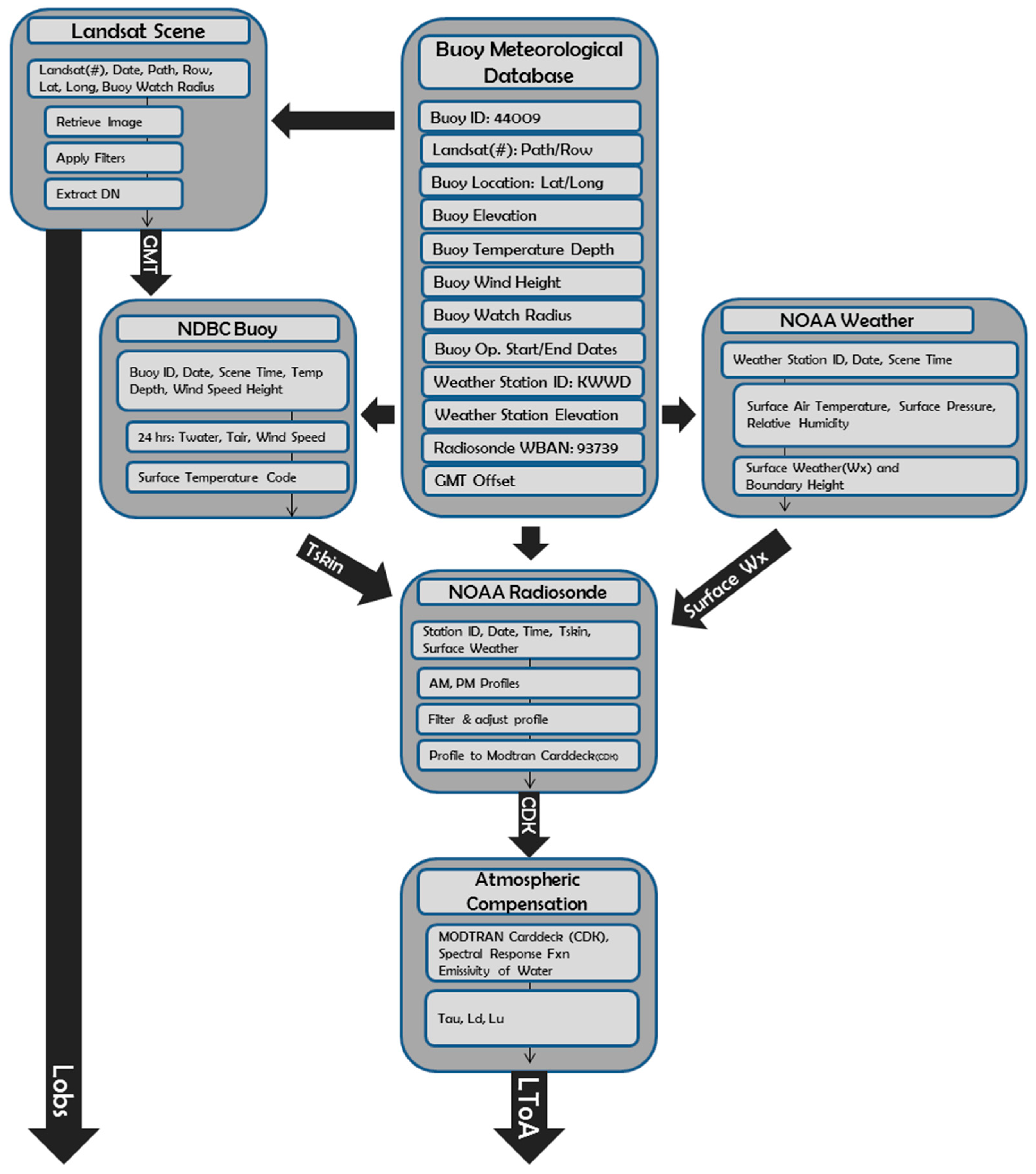
Once all the input data are acquired, they are screened for missing values and formatted for acceptance into the sub surface to skin temperature adjustment and atmospheric compensation as described previously in
Section 2.1 and
Section 2.2. This portion of the workflow is illustrated in
Figure 5.
Figure 5.
Workflow illustrating: assembling the necessary inputs, Landsat scene filtering, buoy to surface temperature adjustment, and atmospheric compensation.
Figure 5.
Workflow illustrating: assembling the necessary inputs, Landsat scene filtering, buoy to surface temperature adjustment, and atmospheric compensation.
2.4. Automated Screening of Landsat Data
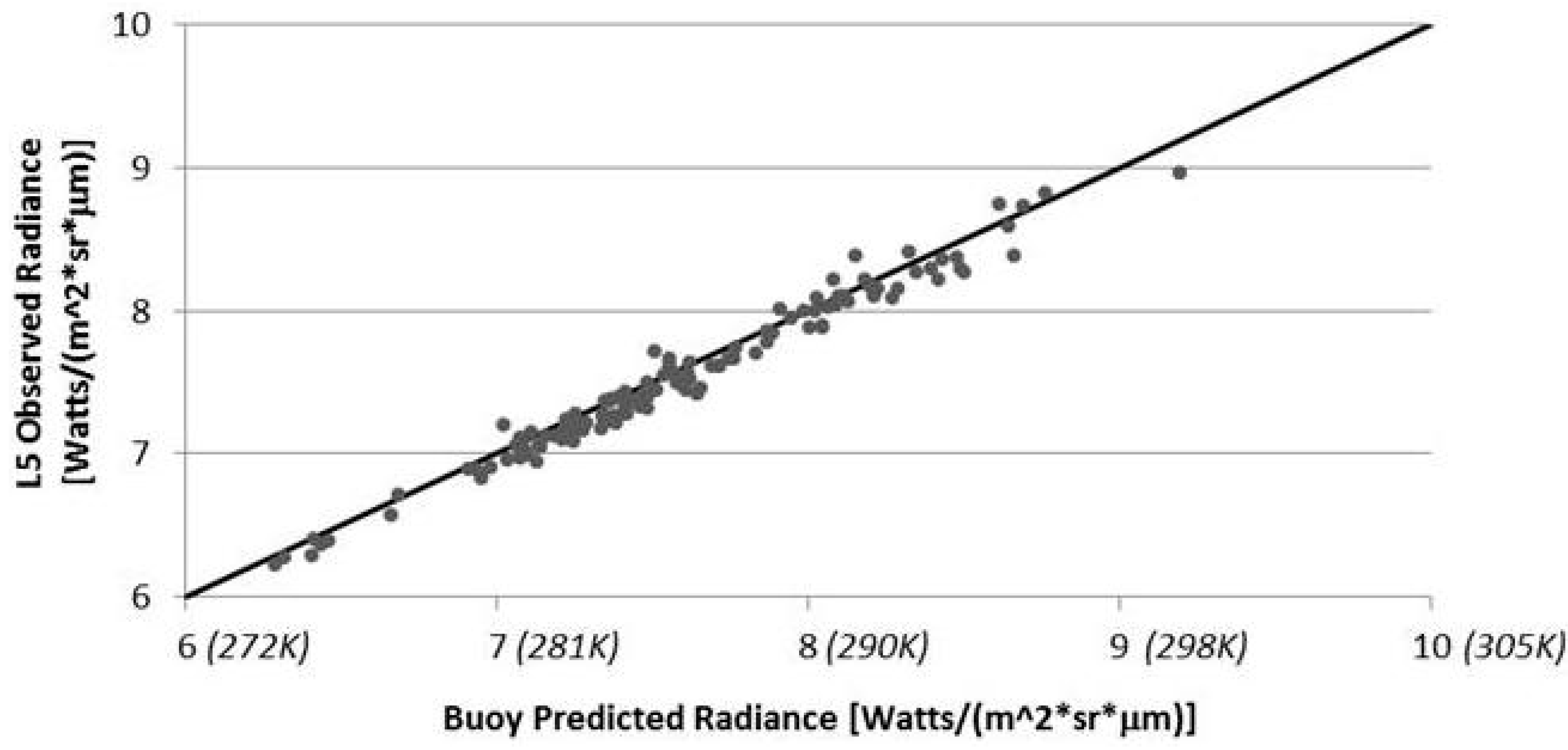
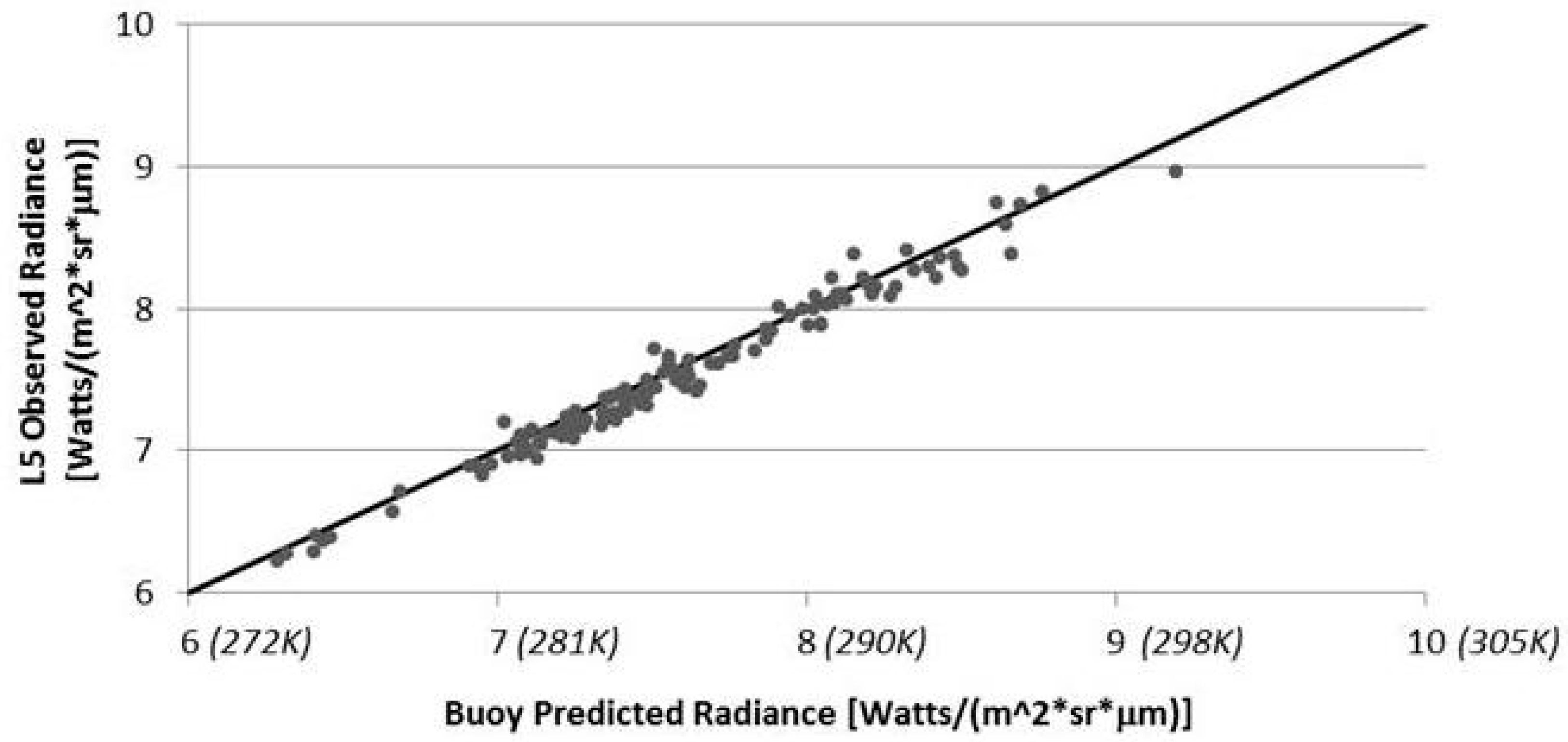
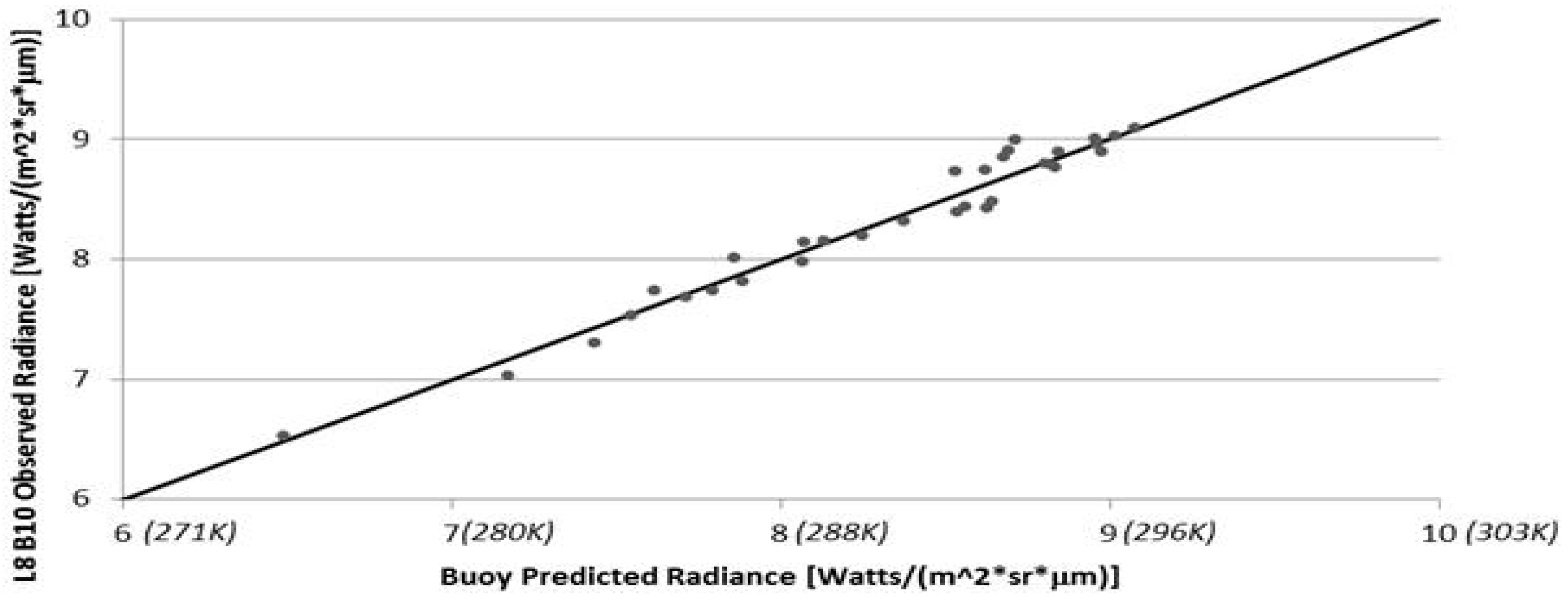
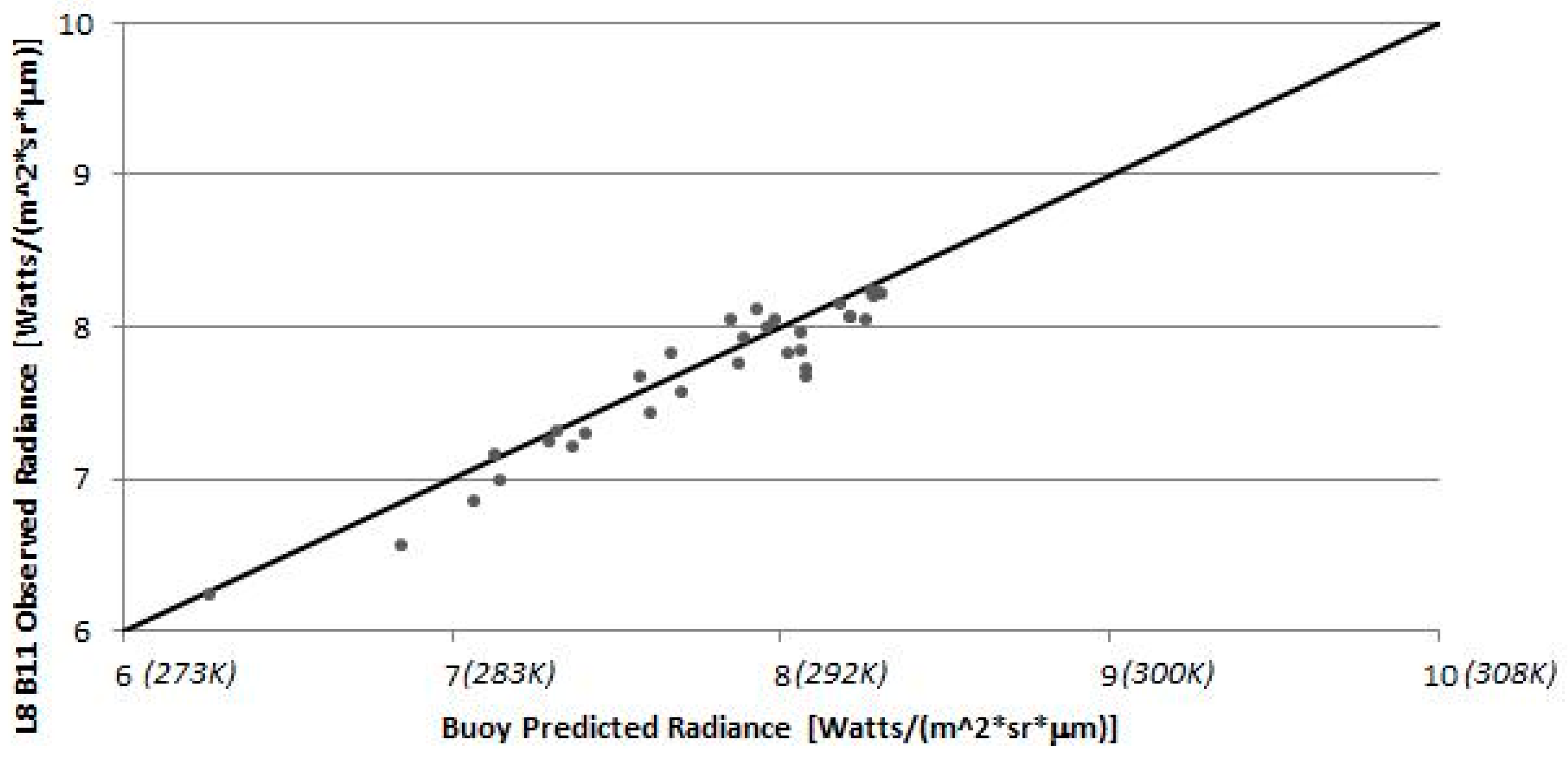
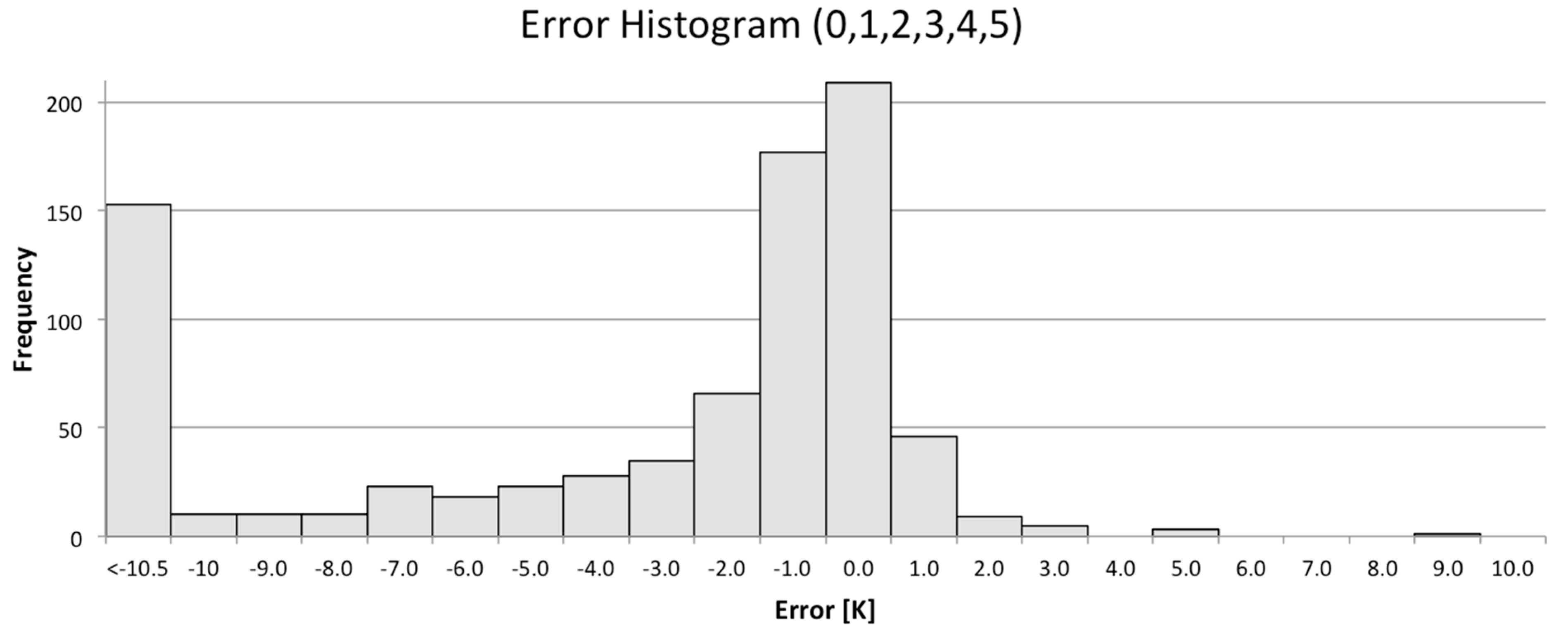
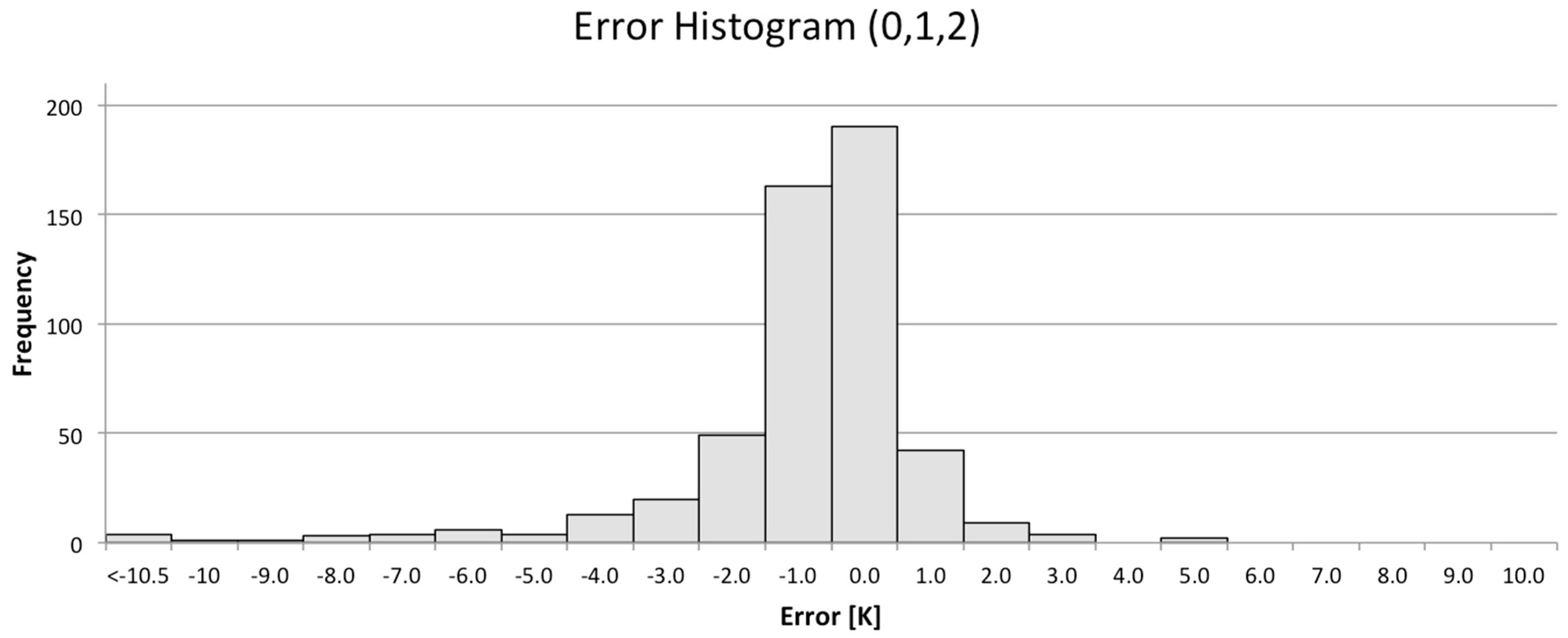
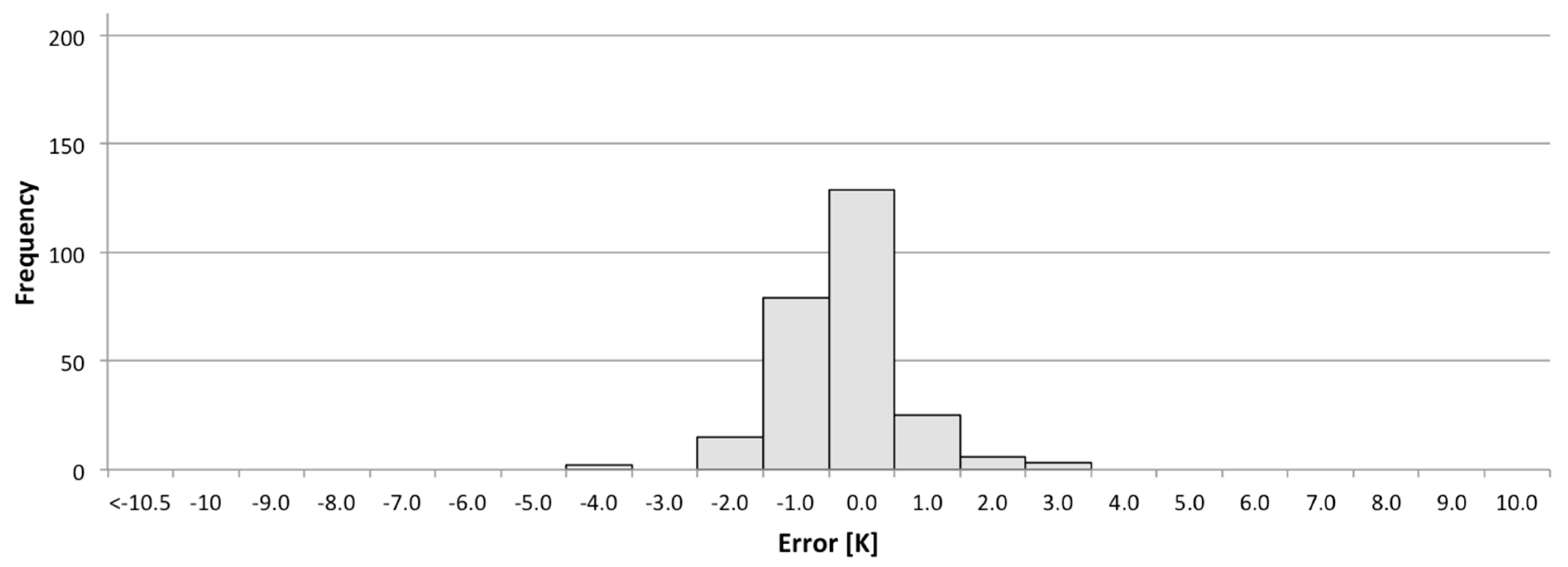
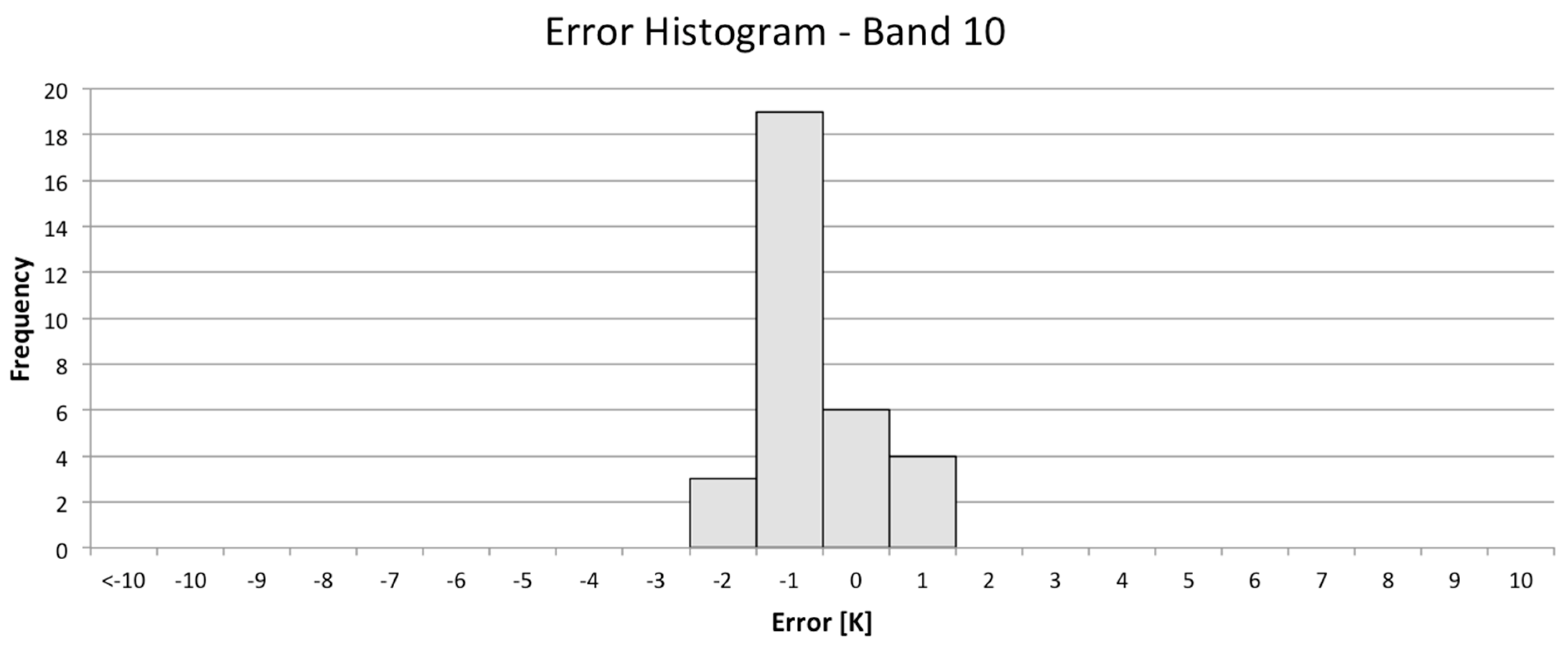
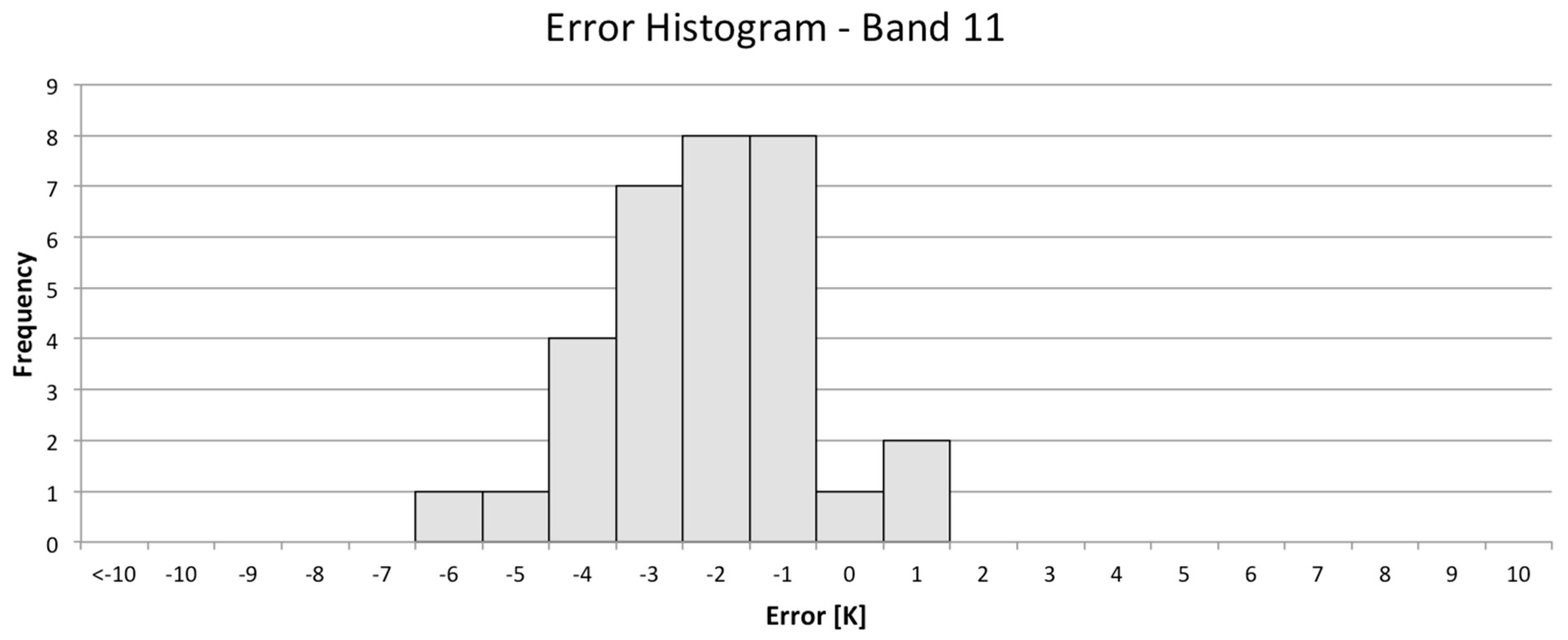
Every time a Landsat satellite passes over a NOAA buoy a potential calibration point is generated. However, most of these points are not appropriate for use in generating high quality calibration data. In order to isolate only high quality data in which we have high confidence, a number of data filters were developed to exclude inappropriate or questionable points. This starts at the data ingest process where missing data or ill formatted data will cause buoy, radiosonde or local weather data to be rejected. Any of these errors will cause the calibration point to be rejected. In addition, certain buoys consistently yield untrustworthy results; for example, they may have excessively large watch radii (i.e., for example, at deep water sites, the watch radius could be as large as a kilometer, so we do not have confidence in where the buoy is within a Landsat scene). These buoys are culled from the database to avoid unnecessary processing. Once the data passes the basic data integrity test, the Landsat image can be downloaded and additional filtering to isolate calibration quality data begins. At this point, the majority of the data are filtered by a series of image based tests that involve thresholds on the data variability around the nominal buoy location. The standard deviation of all points within the watch radius and within 0.22 km of the nominal buoy location is calculated. The local window is used to estimate the observed spectral radiance for comparison to the buoy predicted radiance. This window has a small threshold (0.039 W∙m−2∙sr−1∙μm−1) because variation within that window would suggest local variation in water temperature or local cloud contamination, either of which should cause the point to be rejected. A slightly larger threshold (0.044 W∙m−2∙sr−1∙μm−1) is used for the larger window; this allows for some small variation in the water temperature but screens for any variation that might be introduced by clouds in the surround. To screen for uniform clouds between the buoy and the sensor, a threshold is used to reject points where the difference between the surface air temperature and the sensor observed apparent temperature is too large (cloud apparent temperatures are typically much colder than surface air temperature). Additional checks include filters for excessive water vapor in the air column (as calculated by MODTRAN), too many moist layers (as estimated by low dew point depression) and low lapse rates (temperature decrease per 100 meters of altitude increase). Failure to pass through any filter will result in rejection of a point. As a result of this screening process, only about 20% of the points that pass the initial data contamination test get through the image based and atmospheric condition calibration data quality filters.
At this point, the satellite spectral radiance averaged over the region encompassed by the watch circle is compared to (differenced from) the spectral radiance propagated from the buoy skin temperature to ToA using the MODTRAN radiative transfer process to produce a single point in the calibration assessment. To test this methodology, hundreds of points were produced for the well calibrated Landsat 5 and Landsat 7 instruments [
3,
5] to confirm that the results agreed with the traditional calibration. Only then, if appropriate—
i.e., a successful comparison—would the method be applied to the Landsat 8 calibration for which it was designed. The results of these successful comparisons are discussed in the following section.