Hybrid Ensemble Classification of Tree Genera Using Airborne LiDAR Data
Abstract
:1. Introduction
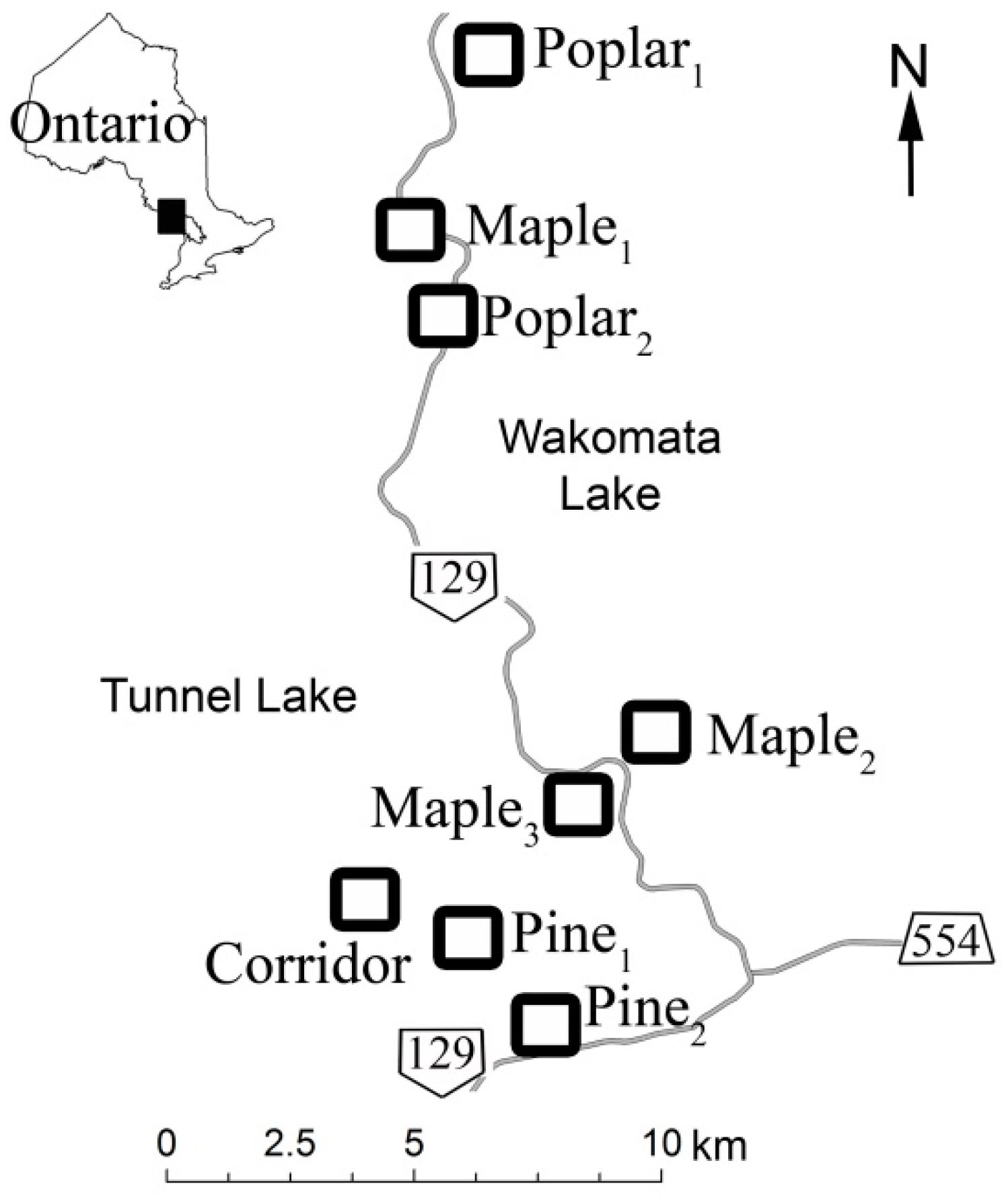
2. Study Area and Data

3. Methods
3.1. Overview of the Methodology
3.2. Random Forests
3.3. Feature Reduction
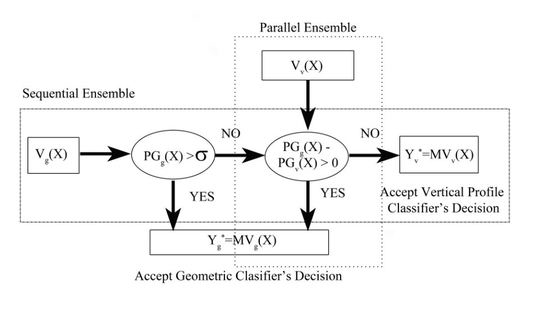
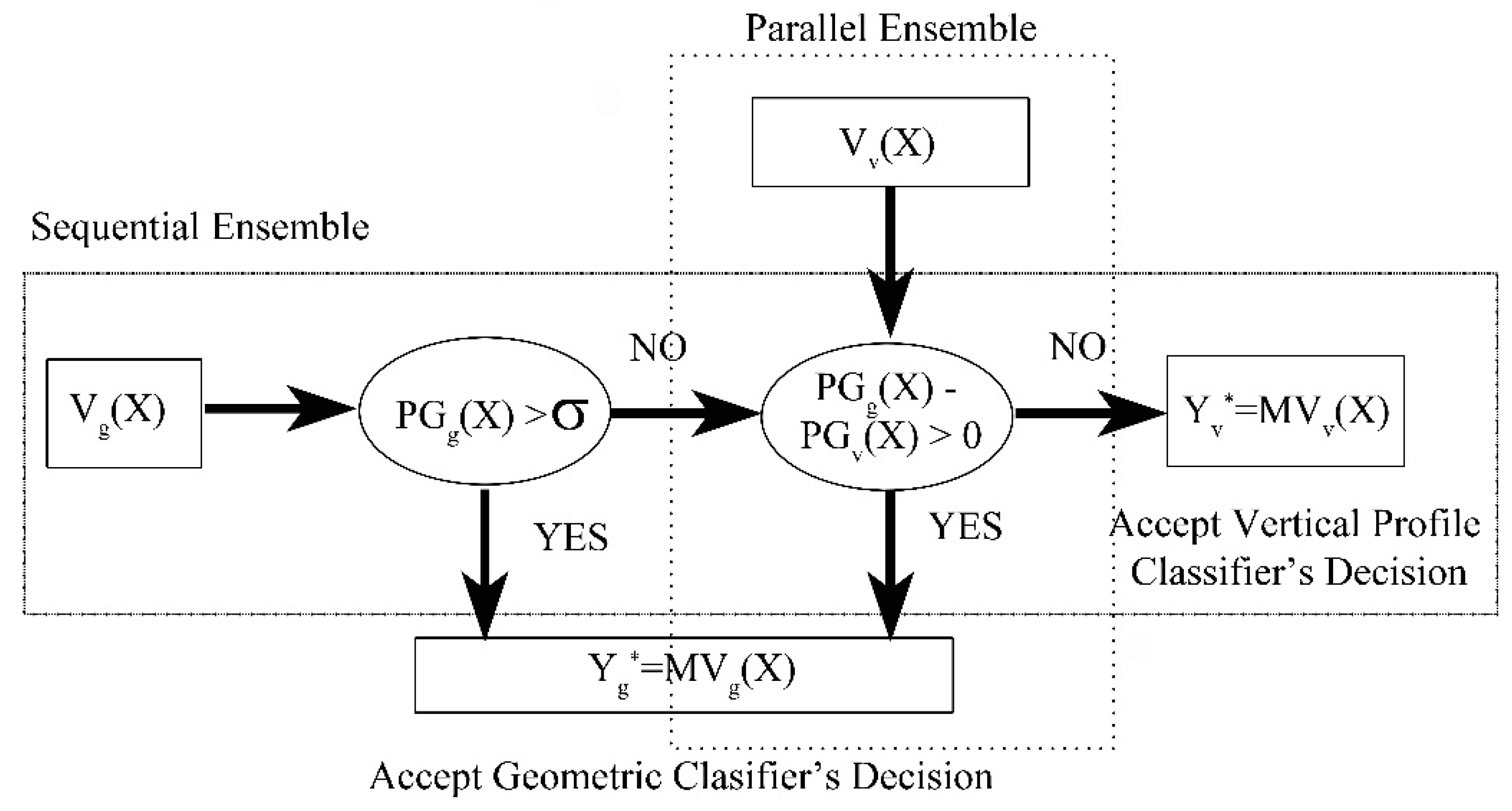
3.4. Geometric Classifier, Vertical Profile Classifier and Ensemble Methods
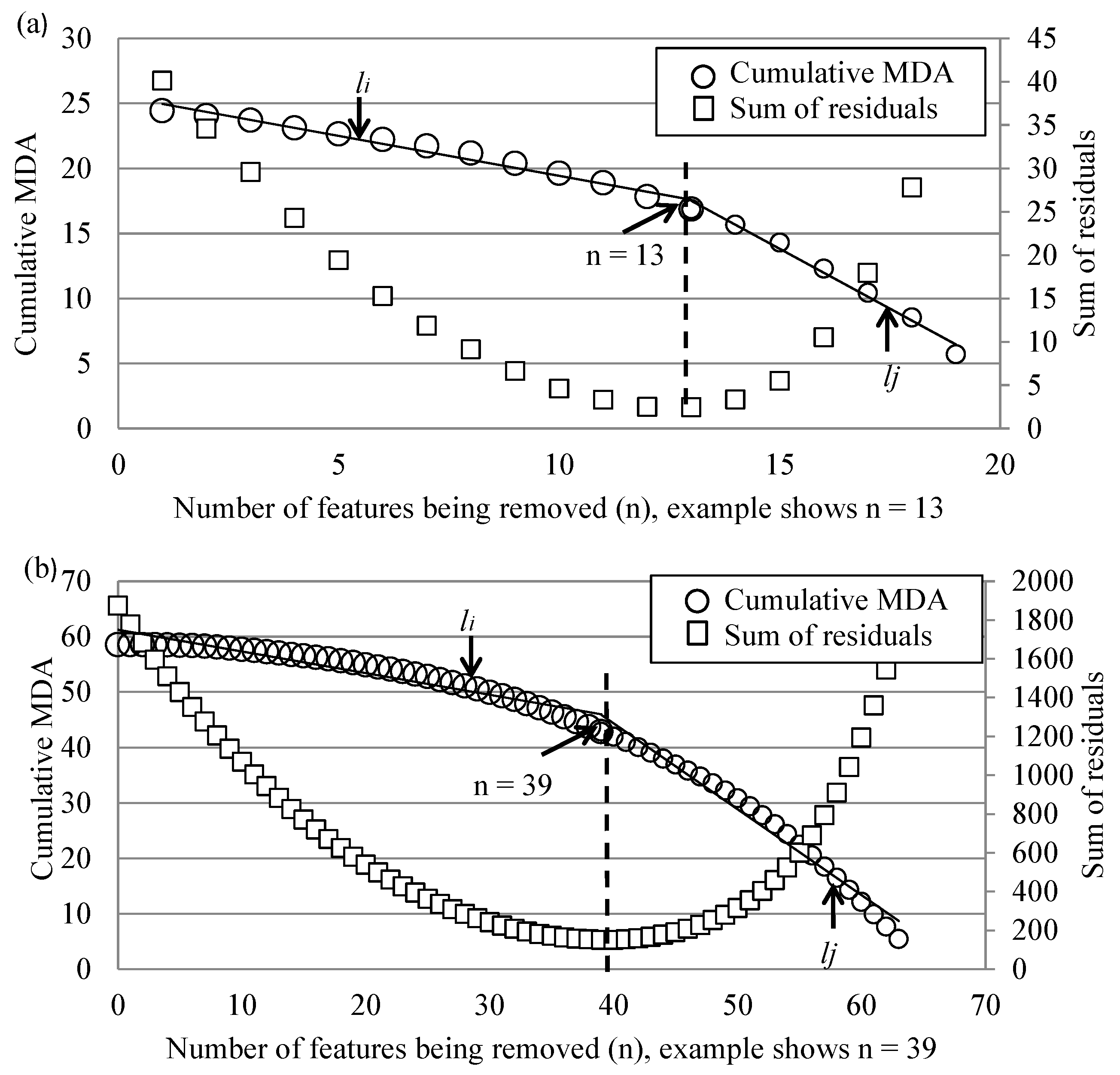
3.5. Parameter σ Estimation
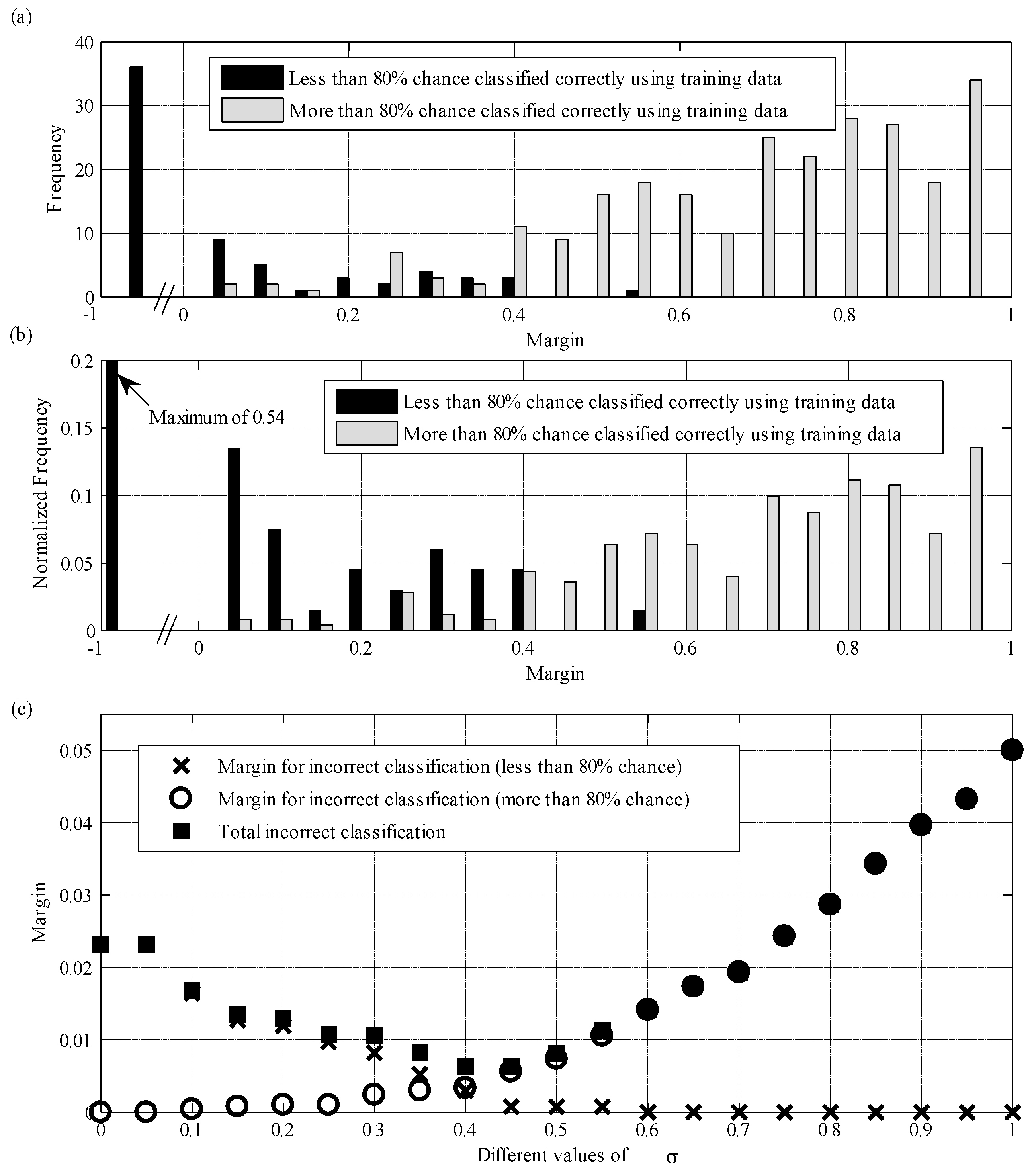
4. Results and Discussion
4.1. Selected Feature Tables
| No. | Description |
|---|---|
| F1 | Average derived best bit line segment lengths divided by tree height |
| F2 | Average line segment lengths multiplied by the ratio between tree crown height and tree height |
| F3 | Volume of the tree crown convex hull divided by the number of points in the crown |
| F4 | Average distance from each point to the closest facet of the convex hull |
| F5 | Buffer each LiDAR point outward at a radius of 2% of the tree height, calculate the overlapped volume of the spheres divided by the number of points in the tree crown |
| F6 | Tree crown height divided by the tree height |
| 10th Percentile | 50th Percentile | 90th Percentile |
|---|---|---|
| % of canopy return (V1S, V2L) | ||
| % return count (V3F, V4S, V5L) | % return count(V6F, V7S, V8L) | |
| Mean height of canopy return (V9F, V10L) | ||
| SD of height (V11F, V12S) | ||
| SD height for canopy return (V13F, V14L) | ||
| CV height for canopy return (V15F, V16S) | ||
| Kurtosis of variation height for canopy return (V17S, V18L) | ||
| Skewness of variation height for canopy return (V19S, V20L) | ||
| Mean intensity (V21L) | Mean intensity (V22F, V23S) | |
| SD of intensity (V24F) | ||
| CV intensity of canopy return (V25L) | ||
| Skewness of variation intensity of canopy return (V26S) | ||
4.2. Classification Performance
| Geometric | Vertical | Ensemble | |
|---|---|---|---|
| Random Forests | 88.0 | 88.8 | 91.2 |
| LDA | 85.6 | 78.0 | 89.4 |
| kNN | 85.3 | 70.9 | 85.6 |
| SVM | 79.1 | 80.4 | 88.7 |
| Expected | User’s Accuracy (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Pine | Poplar | Maple | |||||||
| Predicted | Pine | 856 | 906 | 115 | 132 | 19 | 12 | 86.5 | 86.3 |
| Poplar | 123 | 87 | 771 | 736 | 2 | 7 | 86.0 | 88.7 | |
| Maple | 27 | 13 | 1 | 19 | 486 | 488 | 94.6 | 93.8 | |
| Producer’s Accuracy (%) | 85.1 | 90.1 | 86.9 | 83.0 | 95.9 | 96.3 | |||
| Expected | User’s Accuracy (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Pine | Poplar | Maple | |||||||
| Predicted | Pine | 903 | 908 | 94 | 109 | 5 | 21 | 90.1 | 87.5 |
| Poplar | 86 | 80 | 786 | 777 | 3 | 5 | 89.8 | 90.1 | |
| Maple | 17 | 18 | 7 | 1 | 499 | 481 | 95.4 | 96.2 | |
| Producer’s Accuracy (%) | 89.8 | 90.3 | 88.6 | 87.6 | 98.4 | 94.9 | |||
4.3. Results from Point Density Analysis
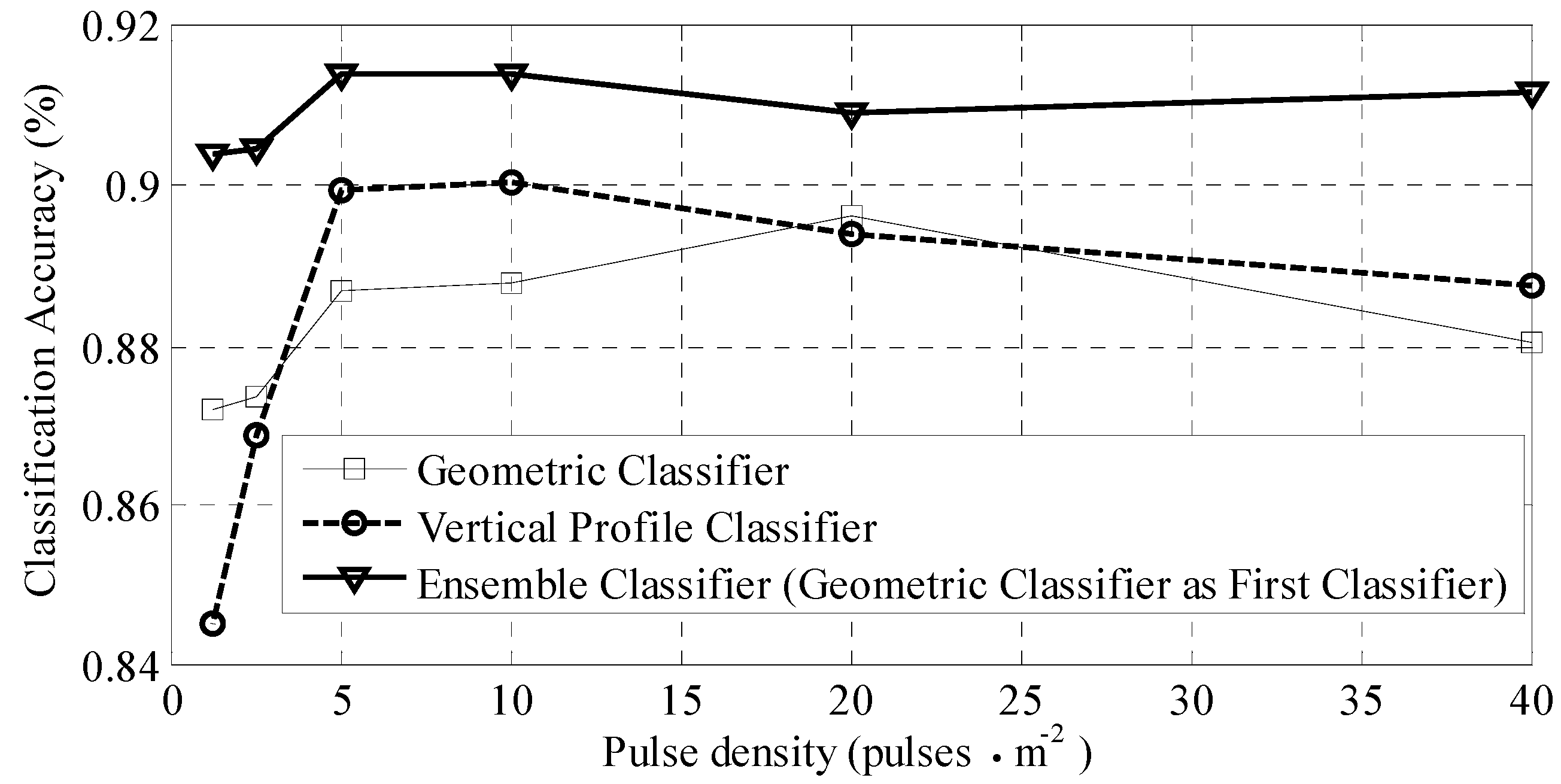
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Clark, M.L.; Roberts, D.A.; Clark, D.B. Hyperspectral discrimination of tropical rain forest tree species at leaf to crown scales. Remote Sens. Environ. 2005, 96, 375–398. [Google Scholar] [CrossRef]
- Cochrane, M.A. Using vegetation reflectance variability for species level classification of hyperspectral data. Int. J. Remote Sens. 2000, 21, 2075–2087. [Google Scholar] [CrossRef]
- Holmgren, J.; Persson, A. Identifying species of individual trees using airborne laser scanning. Remote Sens. Environ. 2004, 90, 415–423. [Google Scholar] [CrossRef]
- Barilotti, A.; Crosilla, F.; Sepic, F. Curvature Analysis of LiDAR Data for Single Tree Species Classification in Alpine Latitude Forests. Available online: http://www.isprs.org/proceedings/xxxviii/3-w8/papers/129_laserscanning09.pdf (accessed on 12 September 2009).
- Brandtberg, T. Classifying individual tree species under leaf-off and leaf-on conditions using airborne LIDAR. ISPRS J. Photogramm. Remote Sens. 2007, 61, 325–340. [Google Scholar] [CrossRef]
- Kato, A.; Moskal, L.M.; Schiess, P.; Swanson, M.E.; Calhoun, D.; Stuetzle, W. Capturing tree crown formation through implicit surface reconstruction using airborne LIDAR data. Remote Sens. Environ. 2009, 113, 1148–1162. [Google Scholar] [CrossRef]
- Mellor, A.; Haywood, A.; Stone, C.; Jones, S. The performance of random forests in an operational setting for large area sclerophyll forest classification. Remote Sens. 2013, 5, 2838–2856. [Google Scholar] [CrossRef]
- Ørka, H.O.; Næsset, E.; Bollandsås, O.M. Utilizing Airborne Laser Intensity for Tree Species Classification. Available online: http://www.isprs.org/proceedings/XXXVI/3-W52/final_papers/Oerka_2007.pdf (accessed on 14 September 2007).
- Korpela, I.; Ørka, H.O.; Maltamo, M.; Tokola, T. Tree species classification using airborne LiDAR—Effects of stand and tree parameters, downsizing of training set, intensity normalization and sensor type. Silva Fenn. 2010, 44, 319–339. [Google Scholar] [CrossRef]
- Kim, S.; Hinckley, T.; Briggs, D. Classifying individual tree genera using stepwise cluster analysis based on height and intensity metrics derived from airborne laser scanner data. Remote Sens. Environ. 2011, 115, 3329–3342. [Google Scholar] [CrossRef]
- Samadzadegan, F.; Bigdeli, B.; Ramzi, P. A multiple classifier system for classification of LIDAR remote sensing data using multi-class SVM. Multi. Classif. Syst. 2010, 5997, 254–263. [Google Scholar]
- Ruta, D.; Gabrys, B. An overview of classifier fusion methods. Comp. Inf. Sys. 2000, 7, 1–10. [Google Scholar]
- Zhou, Z.H. Ensemble Methods: Foundations and Algorithms (Chapman & Hall/CRC Machine Learning & Pattern Recognition); CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Briem, G.J.; Benediktsson, J.A.; Sveinsson, J.R. Multiple classifiers applied to multisource remote sensing data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2291–2299. [Google Scholar] [CrossRef]
- Palmason, J.A.; Benediktsson, J.A.; Sveinsson, J.R.; Chanussot, J. Fusion of Morphological and Spectral Information for Classification of Hyperspectral Urban Remote Sensing Data. Available online: http://www.gipsa-lab.grenoble-inp.fr/~jocelyn.chanussot/publis/ieee_igarss_06_palmason_fusionhyper.pdf (accessed on 4 September 2014).
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar]
- Dietterich, T.G. An experimental comparison of three methods for constructing ensembles of decision trees: Bagging, boosting and randomization. Mach. Learn. 2000, 40, 139–158. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. System Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar]
- Ghimire, B.; Rogan, J.; Rodriguez-Galiano, V.F.; Panday, P.; Neeti, N. An evaluation of bagging, boosting, and random forests for land-cover classification in Cape Cod, Massachusetts, USA. GISci. Remote Sens. 2012, 49, 623–643. [Google Scholar] [CrossRef]
- Dettling, M. Bagboosting for tumor classification with gene expression data. Bioinformatics 2004, 20, 3583–3593. [Google Scholar] [CrossRef] [PubMed]
- Ali, K.M.; Pazzani, M.J. Error reduction through learning multiple descriptions. Mach. Learn. 1996, 24, 173–202. [Google Scholar]
- Breiman, L. Arcing classifiers. Ann. Stat. 1998, 26, 801–824. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Colkesen, I. An assessment of the effectiveness of a rotation forest ensemble for land-use and land-cover mapping. Int. J. Remote Sens. 2013, 34, 4224–4241. [Google Scholar] [CrossRef]
- Engler, R.; Waser, L.T.; Zimmermann, N.E.; Schaub, M.; Berdos, S.; Ginzler, C; Psomas, A. Combining ensemble modeling and remote sensing for mapping individual tree species at high spatial resolution. Forest Ecol. Manag. 2013, 310, 64–73. [Google Scholar] [CrossRef]
- Li, M; Im, J.; Beier, C. Machine learning approaches for forest classification and change analysis using multi-temporal Landsat TM images over Hungtington Wildlife Forest. GISci. Remote Sens. 2013, 50, 361–384. [Google Scholar]
- Kumar, S.; Ghosh, J.; Crawford, M.M. Hierarchical fusion of multiple classifiers for hyperspectral data analysis. Pattern Anal. Appl. 2002, 5, 210–220. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, Z.; Selch, D. Fusing LIDAR and digital aerial photography for object-based forest mapping in the Florida Everglades. GISci. Remote Sens. 2013, 50, 562–573. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by random Forest. R. News. 2002, 2, 18–22. [Google Scholar]
- Vauhkonen, J.; Korpela, I.; Maltamo, M.; Tokola, T. Imputation of single-tree attributes using airborne laser scanning-based height, intensity, and alpha shape metrics. Remote Sens. Environ. 2010, 114, 1263–1276. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Tokola, T.; Maltamo, M.; Packalen, P. Effects of pulse density on predicting characteristics of individual trees of Scandinavian commercial species using alpha shape metrics based on ALS data. Can. J. Remote Sens. 2008, 34, S441–S459. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Tokola, T.; Packalen, P.; Maltamo, M. Identification of Scandinavian commercial species of individual trees from airborne laser scanning data using alpha shape metrics. Forest Sci. 2009, 55, 37–47. [Google Scholar]
- Ørka, H.O.; Næsset, E.; Bollandsås, O.M. Classifying species of individual trees by intensity and structure features derived from airborne laser scanner data. Remote Sens. Environ. 2009, 113, 1163–1174. [Google Scholar] [CrossRef]
- Ko, C.; Sohn, G.; Remmel, T.K. Tree genera classification with geometric features from high-density airborne LiDAR. Can. J. Remote Sens. 2013, 39, S73–S85. [Google Scholar] [CrossRef]
- Ko, C.; Sohn, G.; Remmel, T.K. A comparative study using geometric and vertical profile features derived from airborne LiDAR for classifying tree genera. Available online: http://www.isprs-ann-photogramm-remote-sens-spatial-inf-sci.net/I-3/129/2012/isprsannals-I-3-129-2012.pdf (accessed on 5 August–1 September 2012).
- Magnusson, M.; Fransson, J.E.S.; Holmgren, J. Effects on estimation accuracy of forest variables using different pulse density of laser data. Forest Sci. 2007, 53, 619–626. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing. Available online: http://www.R-project.org/ (accessed on 5 September 2014).
- Alexander, C.; Bøchera, P.K.; Arge, L.; Svenning, J.C. Regional-scale mapping of tree cover, height and main phenological tree types using airborne laser scanning data. Remote Sens. Environ. 2014, 147, 156–172. [Google Scholar] [CrossRef]
- Long, J.A.; Lawrence, R.L; Greenwood, M.C.; Marshall, L.; Miller, P.R. Object-oriented crop classification using multitemporal ETM+ SLC-off imagery. GISci. Remote Sens. 2013, 50, 418–436. [Google Scholar]
- Ghosh, A.; Fassnacht, F.E.; Joshi, P.K.; Koch, B. A framework for mapping tree species combining hyperspectral and LiDAR data: Role of selected classifiers and sensor across three spatial scales. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 49–63. [Google Scholar] [CrossRef]
- Schwing, A.; Zach, C.; Zheng, Y.; Pollefeys, M. Adaptive Random Forest—How Many “Experts” to Ask before Making a Decision. Available online: http://alexander-schwing.de/papers/SchwingEtAl_CVPR2011b.pdf (accessed on 5 September 2014).
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Tong, S.; Koller, D. Support vector machine active learning with applications to text classification. J. Mach. Learn. Res. 2002, 2, 45–66. [Google Scholar]
- Rokach, L. Ensemble-based classifiers. Artif. Intell. Rev. 2010, 33, 1–39. [Google Scholar] [CrossRef]
- Jain, A.; Zongker, D. Feature selection: Evaluation, application, and small sample performance. IEEE Trans. Pattern Anal. 1997, 19, 153–158. [Google Scholar] [CrossRef]
- Serpico, S.B.; D’Inca, M.; Melgani, F.; Moser, G. A Comparison of Feature Reduction Techniques for Classification of Hyperspectral Remote Sensing Data. Available online: http://www.researchgate.net/publication/253371695_Comparison_of_feature_reduction_techniques_for_classification_of_hyperspectral_remote_sensing_data (accessed on 5 September 2014).
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, C.; Sohn, G.; Remmel, T.K.; Miller, J. Hybrid Ensemble Classification of Tree Genera Using Airborne LiDAR Data. Remote Sens. 2014, 6, 11225-11243. https://doi.org/10.3390/rs61111225
Ko C, Sohn G, Remmel TK, Miller J. Hybrid Ensemble Classification of Tree Genera Using Airborne LiDAR Data. Remote Sensing. 2014; 6(11):11225-11243. https://doi.org/10.3390/rs61111225
Chicago/Turabian StyleKo, Connie, Gunho Sohn, Tarmo K. Remmel, and John Miller. 2014. "Hybrid Ensemble Classification of Tree Genera Using Airborne LiDAR Data" Remote Sensing 6, no. 11: 11225-11243. https://doi.org/10.3390/rs61111225
APA StyleKo, C., Sohn, G., Remmel, T. K., & Miller, J. (2014). Hybrid Ensemble Classification of Tree Genera Using Airborne LiDAR Data. Remote Sensing, 6(11), 11225-11243. https://doi.org/10.3390/rs61111225