Reduction of Uncorrelated Striping Noise—Applications for Hyperspectral Pushbroom Acquisitions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials

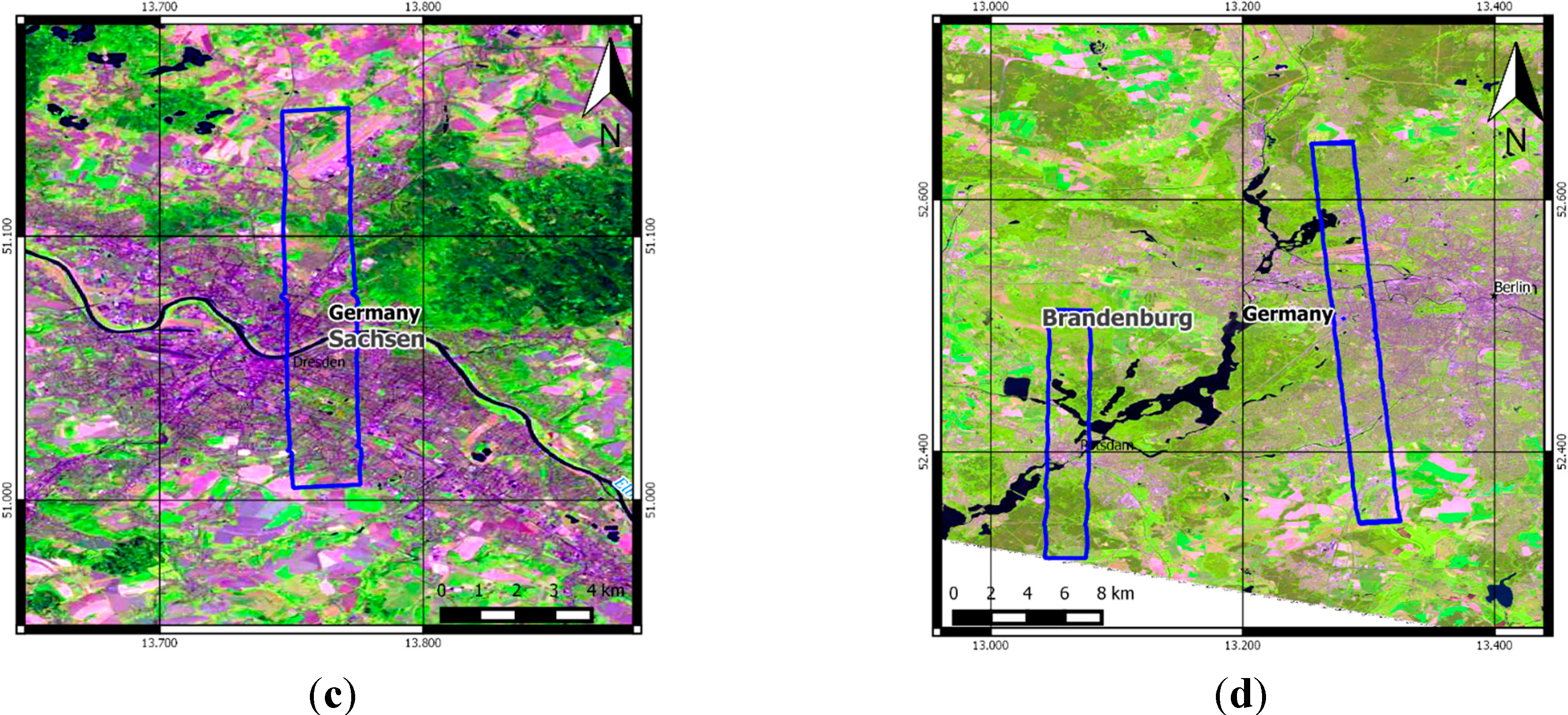


2.2. Methods
2.2.1. Selected Current Approaches
2.2.2. Proposed Approach
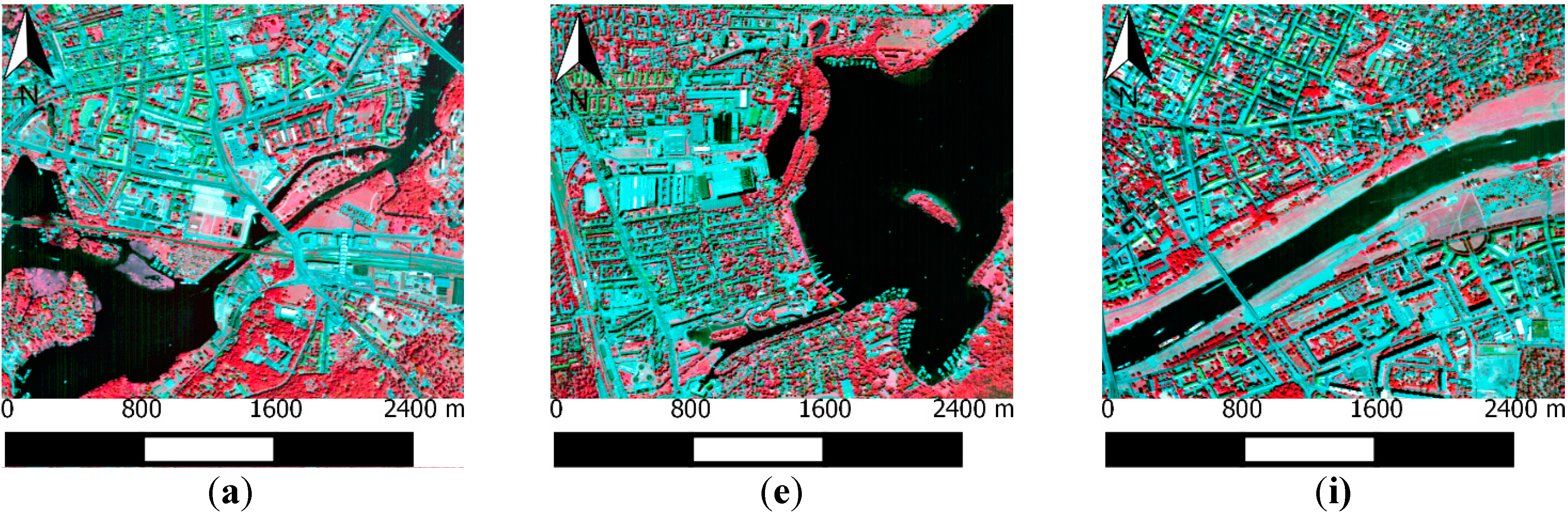
2.3. Evaluation Metrics
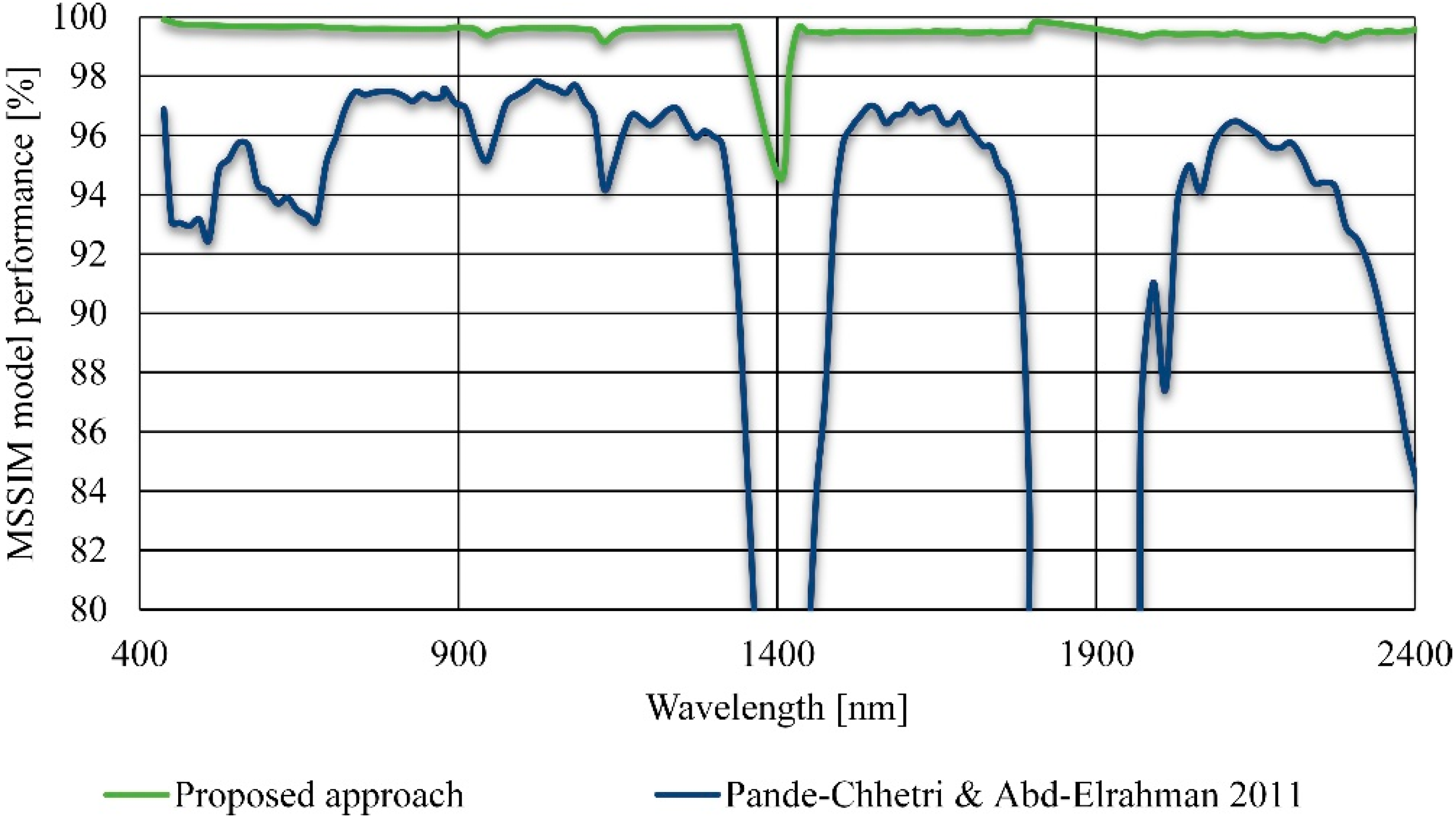
2.3.1. For Artificially Degraded Images (HyMAP)
2.3.2. For Striped Real Images (Hyperion/AISA Dual)
3. Results and Discussion
3.1. For Artificially Degraded Images (HyMAP)
| Approach/Indicator | M1 | M2 | M3 | M4 | M5 | M6 |
|---|---|---|---|---|---|---|
| Average PSNR [%] | 99.92 | 97.09 | 97.20 | 83.50 | 99.81 | 85.87 |
| (3σ) | (0.30) | (11.22) | (14.45) | (19.97) | (4.56) | (27.54) |
| Average MSSIM [%] | 99.58 | 93.40 | 93.43 | 80.57 | 95.68 | 65.94 |
| (3σ) | (1.43) | (29.99) | (29.92) | (46.47) | (22.79) | (24.07) |
| Average Column Correlation[%] | 99.96 | 91.34 | 86.19 | 78.65 | 93.77 | 95.77 |
| (3σ) | (0.4) | (11.54) | (8.70) | (15.73) | (6.72) | (7.23) |
| Average Spectral Correlation [%] | 99.93 | 91.35 | 86.03 | 76.39 | 91.97 | 94.37 |
| (3σ) | (3.32) | (49.06) | (47.76) | (62.19) | (27.51) | (55.55) |
| Average [%] | 99.85 | 93.29 | 90.71 | 79.78 | 95.31 | 85.49 |
| (3σ) | (1.36) | (25.45) | (25.21) | (36.09) | (15.40) | (28.60) |
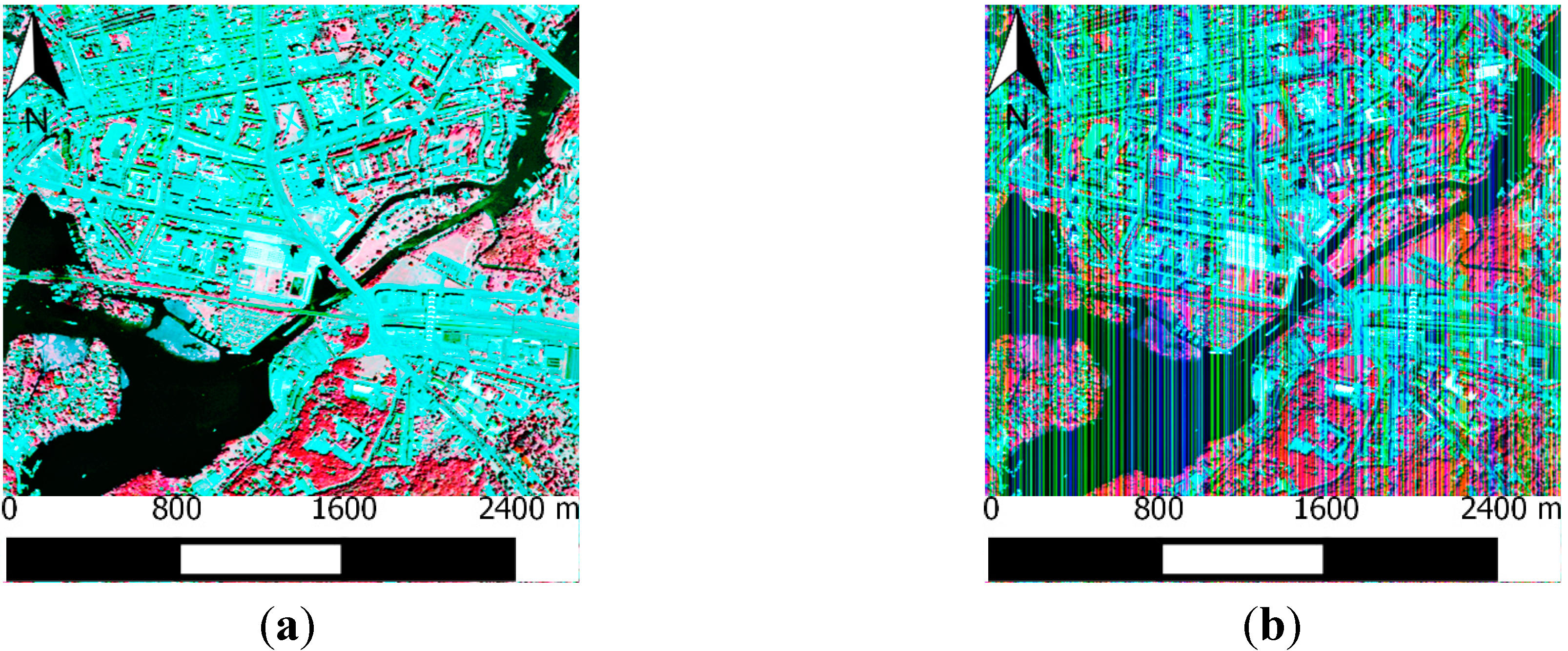
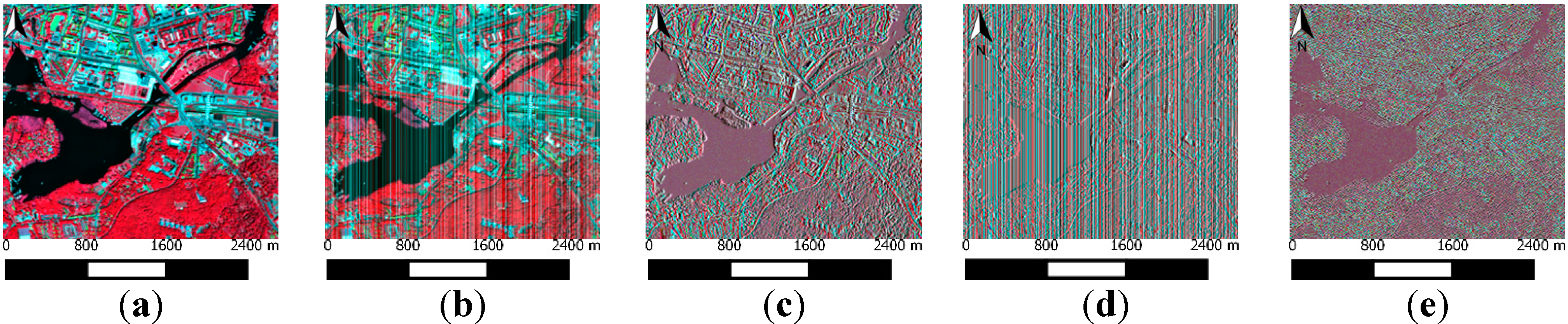
3.2. For Real Images (Hyperion/AISA Dual)
| Approach/Indicator | M1 | M2 | M3 | M4 | M5 | M6 |
|---|---|---|---|---|---|---|
| Median AAHPD/Hyperion [#] | 0.00004 | 0.00028 | 0.00034 | 0.00084 | 0.00060 | 0.00166 |
| (3σ) | (0.0029) | (0.0021) | (5.5623) | (0.3825) | (0.0031) | (0.0136) |
| Median AAHPD/AISA [#] | 0.02311 | 0.0634 | 0.18276 | 0.05955 | 0.06011 | 0.09223 |
| (3σ) | (1.3208) | (1.3666) | (157.7) | (1.3317) | (1.4045) | (1.8410) |
| Average AAHPD [#] | 0.00962 | 0.03144 | 0.04128 | 0.02516 | 0.02733 | 0.031 |
| (3σ) | (0.6476) | (0.6557) | (59.052) | (0.9894) | (0.6759) | (0.7650) |
| Median CIAG/Hyperion [#] | 1.0 | 1.0 | 0.88 | 0.97 | 0.51 | 0.38 |
| (3σ) | (0.21) | (0.66) | (0.71) | (0.84) | (0.93) | (0.81) |
| Median CIAG/AISA [#] | 1.0 | 1.0 | 0.06 | 0.24 | 1.0 | 0.19 |
| (3σ) | (0.25) | (0.1) | (0.68) | (0.63) | (0.03) | (0.34) |
| Average CIAG [#] | 1.0 | 1.0 | 0.47 | 0.6 | 0.76 | 0.28 |
| (3σ) | (0.23) | (0.38) | (0.70) | (0.74) | (0.48) | (0.57) |
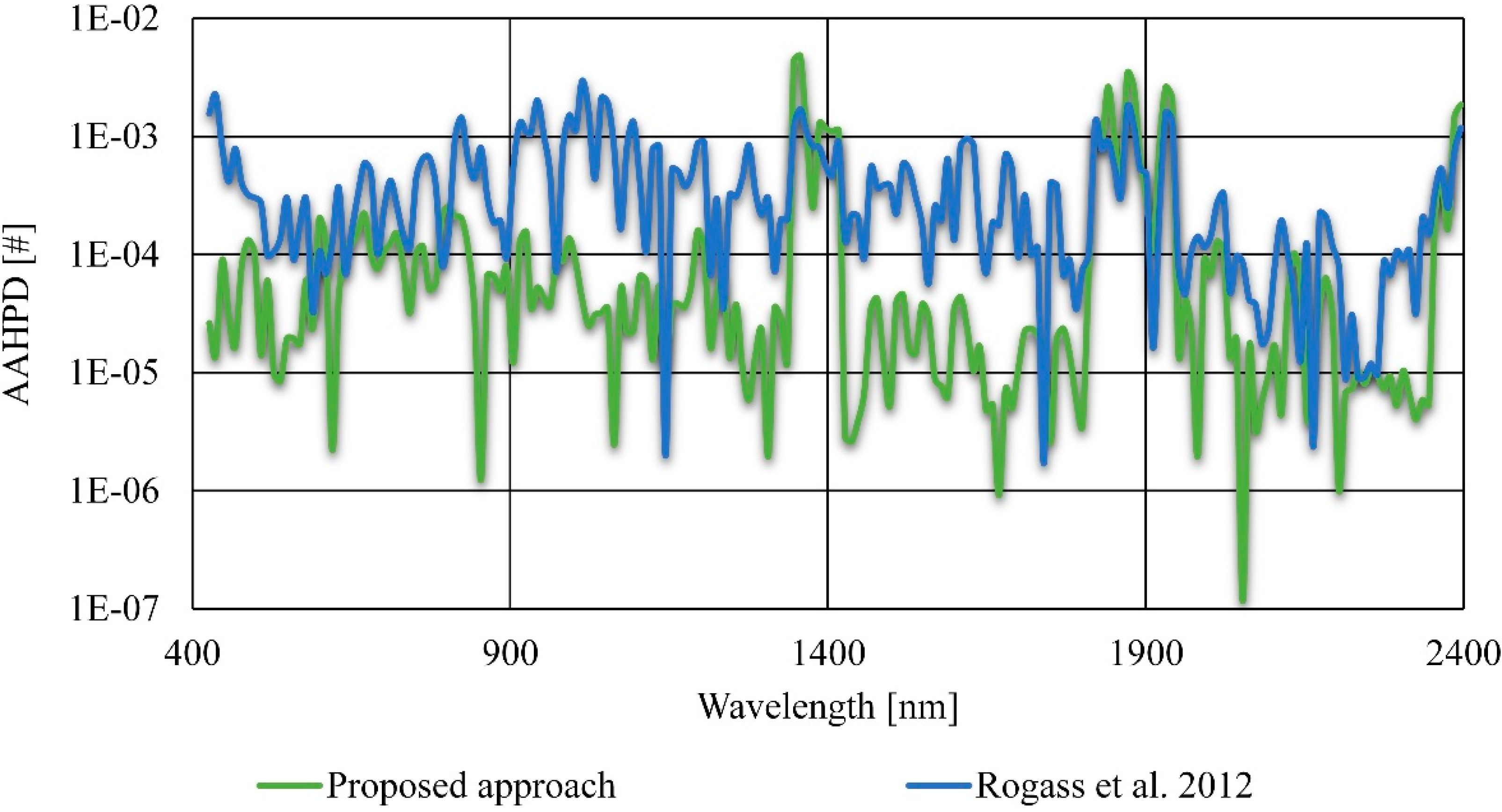



3.3. For Artificially Degraded and Real Images
| Approach/Indicator | M1 | M2 | M3 | M4 | M5 | M6 |
|---|---|---|---|---|---|---|
| PSNR [#] | 1 | 4 | 3 | 6 | 2 | 5 |
| SSIM [#] | 1 | 4 | 3 | 5 | 2 | 6 |
| Column Correlation [#] | 1 | 4 | 5 | 6 | 3 | 2 |
| Overall Correlation [#] | 1 | 4 | 5 | 6 | 3 | 2 |
| Visual comparison HyMAP [#] | 1 | 3 | 2 | 6 | 4 | 5 |
| Median AAHPD/Hyperion [#] | 1 | 2 | 3 | 5 | 4 | 6 |
| Median AAHPD/AISA [#] | 1 | 4 | 6 | 2 | 3 | 5 |
| Median CIAG/Hyperion [#] | 1 | 2 | 4 | 3 | 5 | 6 |
| Median CIAG/AISA [#] | 3 | 2 | 6 | 4 | 1 | 5 |
| Visual comparison Hyperion [#] | 1 | 3 | 1 | 5 | 2 | 4 |
| Visual comparison AISA [#] | 1 | 5 | 1 | 3 | 4 | 2 |
| Average [#] | 1 (1) | 3 (2) | 4 (4) | 6 (5) | 2 (3) | 5 (5) |
| (Ʃ all, Ʃ objectively only) | (13, 10) | (37, 18) | (39, 35) | (51, 37) | (33, 23) | (48, 37) |
4. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cocks, T.; Jenssen, R.; Stewart, A.; Wilson, I.; Shields, T. The HyMapTM Airborne Hyperspectral Sensor: The System, Calibration and Performance. Available online: http://www.neodc.rl.ac.uk/docs/Hymap_specs.pdf (accessed on 5 September 2014).
- Pearlman, J.; Carman, S.; Segal, C.; Jarecke, P.; Clancy, P.; Browne, W. Overview of the Hyperion Imaging Spectrometer for the NASA EO-1 mission. In Proceedings of IEEE 2001 International Geoscience and Remote Sensing Symposium, Sydney, Australia, 9–13 July 2001; pp. 3036–3038.
- Specim. Available online: http://www.specim.fi/index.php/products/airborne/aisadual (accessed on 17 February 2014).
- Rogass, C.; Spengler, D.; Bochow, M.; Segl, K.; Lausch, A.; Doktor, D.; Roessner, S.; Behling, R.; Wetzel, H.U.; Kaufmann, H. Reduction of radiometric miscalibration—Applications to pushbroom sensors. Sensors 2011, 11, 6370–6395. [Google Scholar] [CrossRef] [PubMed]
- Oppelt, N.; Mauser, W. The airborne visible/infrared imaging spectrometer AVIS: Design, characterization and calibration. Sensors 2007, 7, 1934–1953. [Google Scholar] [CrossRef]
- Janesick, J.R. DN to [lambda]; SPIE Press: Bellingham, WA, USA, 2007. [Google Scholar]
- Tian, H. Noise Analysis in CMOS Image Sensors. Available online: http://www-isl.stanford.edu/~abbas/group/papers_and_pub/hui_thesis.pdf (accessed on 5 September 2014).
- Holst, G.C. CCD Arrays, Cameras and Displays; JCD Publishing: Winter Park, FL, USA, 1996. [Google Scholar]
- Rogass, C.; Spengler, D.; Bochow, M.; Segl, K.; Lausch, A.; Doktor, D.; Roessner, S.; Behling, R.; Wetzel, H.U.; Urata, K.; Hueni, A.; Kaufmann, H. A Contribution to the Reduction of Radiometric Miscalibration of Pushbroom Sensors; INTECH Open Access Publisher: Rijeka, Croatia, 2012. [Google Scholar]
- Goodenough, D.G.; Dyk, A.; Niemann, K.O.; Pearlman, J.S.; Chen, H.; Han, T.; Murdoch, M.; West, C. Processing Hyperion and ALI for forest classification. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1321–1331. [Google Scholar] [CrossRef]
- Datt, B.; McVicar, T.R.; Van Niel, T.G.; Jupp, D.L.B.; Pearlman, J.S. Preprocessing EO-1 Hyperion hyperspectral data to support the application of agricultural indexes. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1246–1259. [Google Scholar] [CrossRef]
- Staenz, K.; Neville, R.A.; Clavette, S.; Landry, R.; White, H.P.; Hitchcock, R. Retrieval of Surface Reflectance from Hyperion Radiance Data. Available online: http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=1026135&url=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Fabs_all.jsp%3Farnumber%3D1026135 (accessed on 5 September 2014).
- Pande-Chhetri, R.; Abd-Elrahman, A. De-striping hyperspectral imagery using wavelet transform and adaptive frequency domain filtering. ISPRS J. Photogramm. Remote Sens. 2011, 66, 620–636. [Google Scholar] [CrossRef]
- Pande-Chhetri, R.; Abd-Elrahman, A. Filtering high-resolution hyperspectral imagery in a maximum noise fraction transform domain using wavelet-based de-striping. Int. J. Remote Sens. 2013, 34, 2216–2235. [Google Scholar] [CrossRef]
- Scheffler, D.; Karrasch, P. Destriping of hyperspectral image data: An evaluation of different algorithms using EO-1 Hyperion data. J. Appl. Remote Sens. 2014, 8. [Google Scholar] [CrossRef]
- Oliveira, P.; Gomes, L. Interpolation of signals with missing data using Principal Component Analysis. Multidimens. Syst. Signal. Process. 2010, 21, 25–43. [Google Scholar] [CrossRef]
- Tsai, F.; Chen, W.W. Striping noise detection and correction of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 4122–4131. [Google Scholar] [CrossRef]
- Cavalli, R.M.; Fusilli, L.; Pascucci, S.; Pignatti, S.; Santini, F. Hyperspectral sensor data capability for retrieving complex urban land cover in comparison with multispectral data: Venice city case study (Italy). Sensors 2008, 8, 3299–3320. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, L.; Zhang, X.; Zhang, B.; Tong, Q. Simulation of EO-1 Hyperion data from ALI multispectral data based on the spectral reconstruction approach. Sensors 2009, 9, 3090–3108. [Google Scholar] [CrossRef] [PubMed]
- Garcia, J.; Moreno, J. Removal of Noises in CHRIS/Proba Images: Application to the SPARC Campaign Data. Available online: http://earth.esa.int/workshops/chris_proba_04/papers/9_GARCIA.pdf (accessed on 5 September 2014).
- Shen, H.F.; Ai, T.H.; Li, P.X. Destriping and Inpainting of Remote Sensing Images Using Maximum A-Posteriori Method. Available online: http://www.isprs.org/proceedings/XXXVII/congress/1_pdf/11.pdf (accessed on 5 September 2014).
- Simpson, J.J.; Gobat, J.I.; Frouin, R. Improved destriping of GOES images using finite impulse response filters. Remote Sens. Environ. 1995, 52, 15–35. [Google Scholar] [CrossRef]
- Simpson, J.J.; Stitt, J.R.; Leath, D.M. Improved finite impulse response filters for enhanced destriping of geostationary satellite data. Remote Sens. Environ. 1998, 66, 235–249. [Google Scholar] [CrossRef]
- Bouali, M.; Ladjal, S. Toward optimal destriping of MODIS data using a unidirectional variational model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2924–2935. [Google Scholar] [CrossRef]
- Carfantan, H.; Idier, J. Statistical linear destriping of satellite-based pushbroom-type images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1860–1871. [Google Scholar] [CrossRef]
- Gomez-Chova, L.; Alonso, L.; Guanter, L.; Camps-Valls, G.; Calpe, J.; Moreno, J. Correction of systematic spatial noise in push-broom hyperspectral sensors: Application to CHRIS/PROBA images. Appl. Opt. 2008, 47, F46–F60. [Google Scholar] [CrossRef] [PubMed]
- Tendero, Y.; Gilles, J. ADMIRE: A locally adaptive single-image, non-uniformity correction and denoising algorithm: Application to uncooled IR camera. Proc. SPIE 2012, 8353. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, L. A map-based algorithm for destriping and inpainting of remotely sensed images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1492–1502. [Google Scholar] [CrossRef]
- Shen, H.; Liu, Y.; Ai, T.; Wang, Y.; Wu, B. Universal reconstruction method for radiometric quality improvement of remote sensing images. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 278–286. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, L.; Shen, H. Hyperspectral image denoising employing a spectral-spatial adaptive total variation model. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3660–3677. [Google Scholar] [CrossRef]
- Bouali, M. A simple and robust destriping algorithm for imaging spectrometers: Application to MODIS data. In Proceedings of ASPRS 2010 Annual Conference, San Diego, CA, USA, 26–30 April 2010; pp. 84–93.
- Shen, H.; Jiang, W.; Zhang, H.; Zhang, L. A piece-wise approach to removing the nonlinear and irregular stripes in MODIS data. Int. J. Remote Sens. 2013, 35, 44–53. [Google Scholar] [CrossRef]
- Chen, J.; Shao, Y.; Guo, H.; Wang, W.; Zhu, B. Destriping CMODIS data by power filtering. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2119–2124. [Google Scholar] [CrossRef]
- Corsini, G.; Diani, M.; Walzel, T. Striping removal in MOS-B data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1439–1446. [Google Scholar] [CrossRef]
- Di Bisceglie, M.; Episcopo, R.; Galdi, C.; Ullo, S.L. Destriping MODIS data using overlapping field-of-view method. IEEE Trans. Geosci. Remote Sens. 2009, 47, 637–651. [Google Scholar] [CrossRef]
- Rakwatin, P.; Takeuchi, W.; Yasuoka, Y. Stripe noise reduction in MODIS data by combining histogram matching with facet filter. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1844–1856. [Google Scholar] [CrossRef]
- Sang, B.; Schubert, J.; Kaiser, S.; Mogulsky, V.; Neumann, C.; Forster, K.; Hofer, S.; Stuffler, T.; Kaufmann, H.; Muller, A. The EnMAP hyperspectral imaging spectrometer: Instrument concept, calibration and technologies. Imaging Spectrom. 2008, 13, 708605–708615. [Google Scholar]
- Hofer, S.; Kaufmann, H.; Stuffler, T.; Penné, B.; Schreier, G.; Müller, A.; Eckardt, A.; Bach, H.; Benz, U.; Haydn, R. EnMAP hyperspectral imager: An advanced optical payload for future applications in Earth observation programs. Proc. SPIE 2006, 6366. [Google Scholar] [CrossRef]
- Richter, R.; Schlapfer, D. Geo-atmospheric processing of airborne imaging spectrometry data. Part II: Atmospheric/topographic correction. Int. J. Remote Sens. 2002, 23, 2631–2649. [Google Scholar] [CrossRef]
- Pearlman, J.S.; Barry, P.S.; Segal, C.C.; Shepanski, J.; Beiso, D.; Carman, S.L. Hyperion, a space-based imaging spectrometer. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1160–1173. [Google Scholar] [CrossRef]
- Box, G.; Muller, M.E. A note on the generation of random normal deviates. Ann. Math. Stat. 1958, 29, 610–611. [Google Scholar] [CrossRef]
- Green, A.A.; Berman, M.; Switzer, P.; Craig, M.D. A transformation for ordering multispectral data in terms of image quality with implications for noise removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef]
- Bovik, A.C. Handbook of Image and Video Processing; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Arce, G.R. Nonlinear Signal Processing: A Statistical Approach; Wiley-Interscience: Hoboken, NJ, USA, 2004. [Google Scholar]
- Wang, Z.; Bovik, A.C. Mean squared error: Love it or leave it? A new look at signal fidelity measures. IEEE Signal. Process. Mag. 2009, 26, 98–117. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rogass, C.; Mielke, C.; Scheffler, D.; Boesche, N.K.; Lausch, A.; Lubitz, C.; Brell, M.; Spengler, D.; Eisele, A.; Segl, K.; et al. Reduction of Uncorrelated Striping Noise—Applications for Hyperspectral Pushbroom Acquisitions. Remote Sens. 2014, 6, 11082-11106. https://doi.org/10.3390/rs61111082
Rogass C, Mielke C, Scheffler D, Boesche NK, Lausch A, Lubitz C, Brell M, Spengler D, Eisele A, Segl K, et al. Reduction of Uncorrelated Striping Noise—Applications for Hyperspectral Pushbroom Acquisitions. Remote Sensing. 2014; 6(11):11082-11106. https://doi.org/10.3390/rs61111082
Chicago/Turabian StyleRogass, Christian, Christian Mielke, Daniel Scheffler, Nina K. Boesche, Angela Lausch, Christin Lubitz, Maximilian Brell, Daniel Spengler, Andreas Eisele, Karl Segl, and et al. 2014. "Reduction of Uncorrelated Striping Noise—Applications for Hyperspectral Pushbroom Acquisitions" Remote Sensing 6, no. 11: 11082-11106. https://doi.org/10.3390/rs61111082
APA StyleRogass, C., Mielke, C., Scheffler, D., Boesche, N. K., Lausch, A., Lubitz, C., Brell, M., Spengler, D., Eisele, A., Segl, K., & Guanter, L. (2014). Reduction of Uncorrelated Striping Noise—Applications for Hyperspectral Pushbroom Acquisitions. Remote Sensing, 6(11), 11082-11106. https://doi.org/10.3390/rs61111082






