A Synergistic Methodology for Soil Moisture Estimation in an Alpine Prairie Using Radar and Optical Satellite Data
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area and Ground Data
2.2. Optical Remote Sensing Data
| HJ-1A CCD1 | α | ||
|---|---|---|---|
| Band 1 | 0.7696 | 7.3250 | 1914.324 |
| Band 2 | 0.7815 | 6.0737 | 1825.419 |
| Band 3 | 1.0914 | 3.6123 | 1542.664 |
| Band 4 | 1.0281 | 1.9028 | 1073.826 |
2.3. Radarsat-2 Data
3. Methods
3.1. Bare Soil Scattering
3.2. Effect of Vegetation
3.2.1. Vegetation Backscattering Model
3.2.2. Modification of the Vegetation Backscattering Model
3.3. Inversion of Soil Moisture
4. Results and Discussion
4.1. Backscattering Simulations
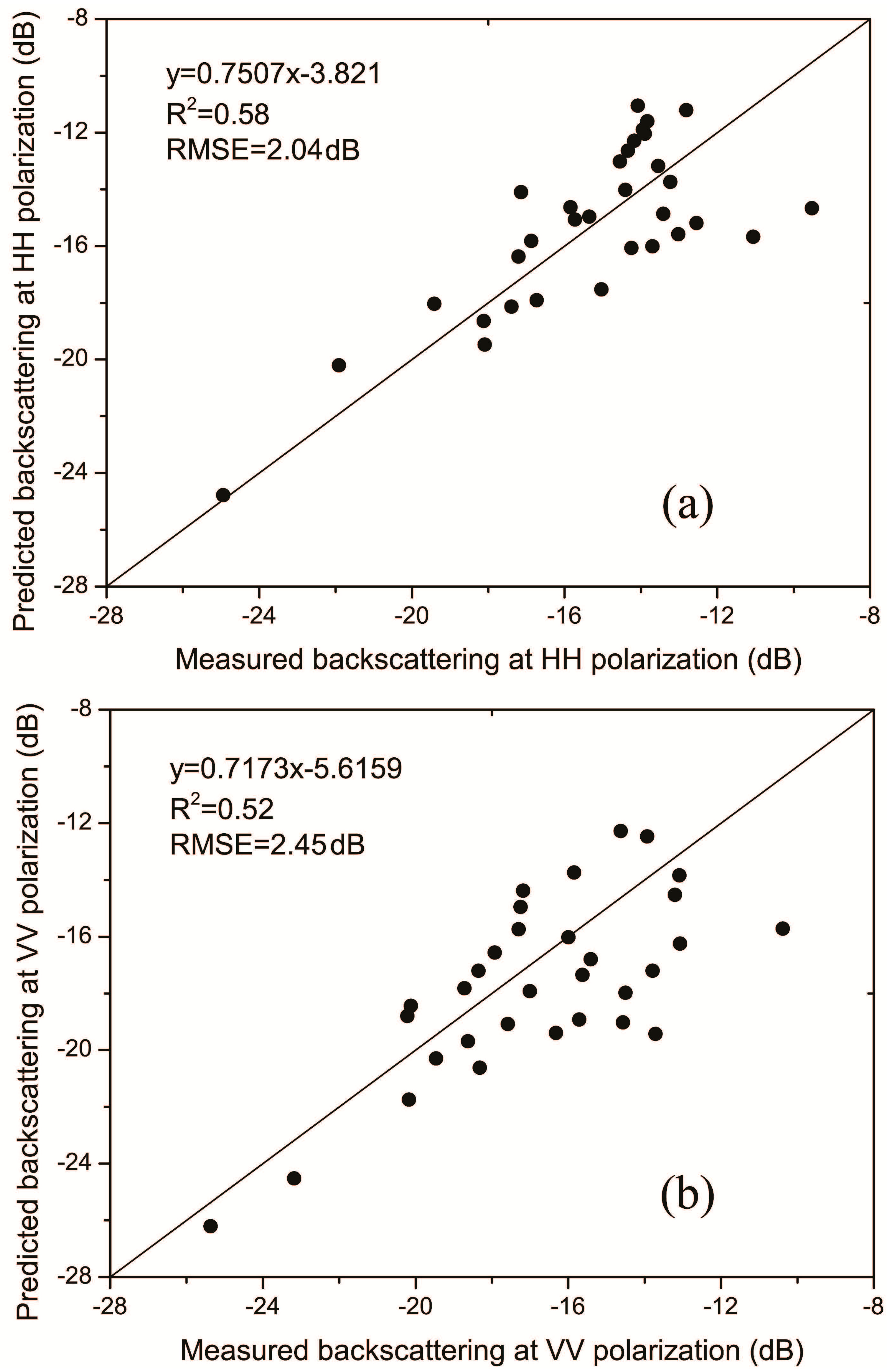
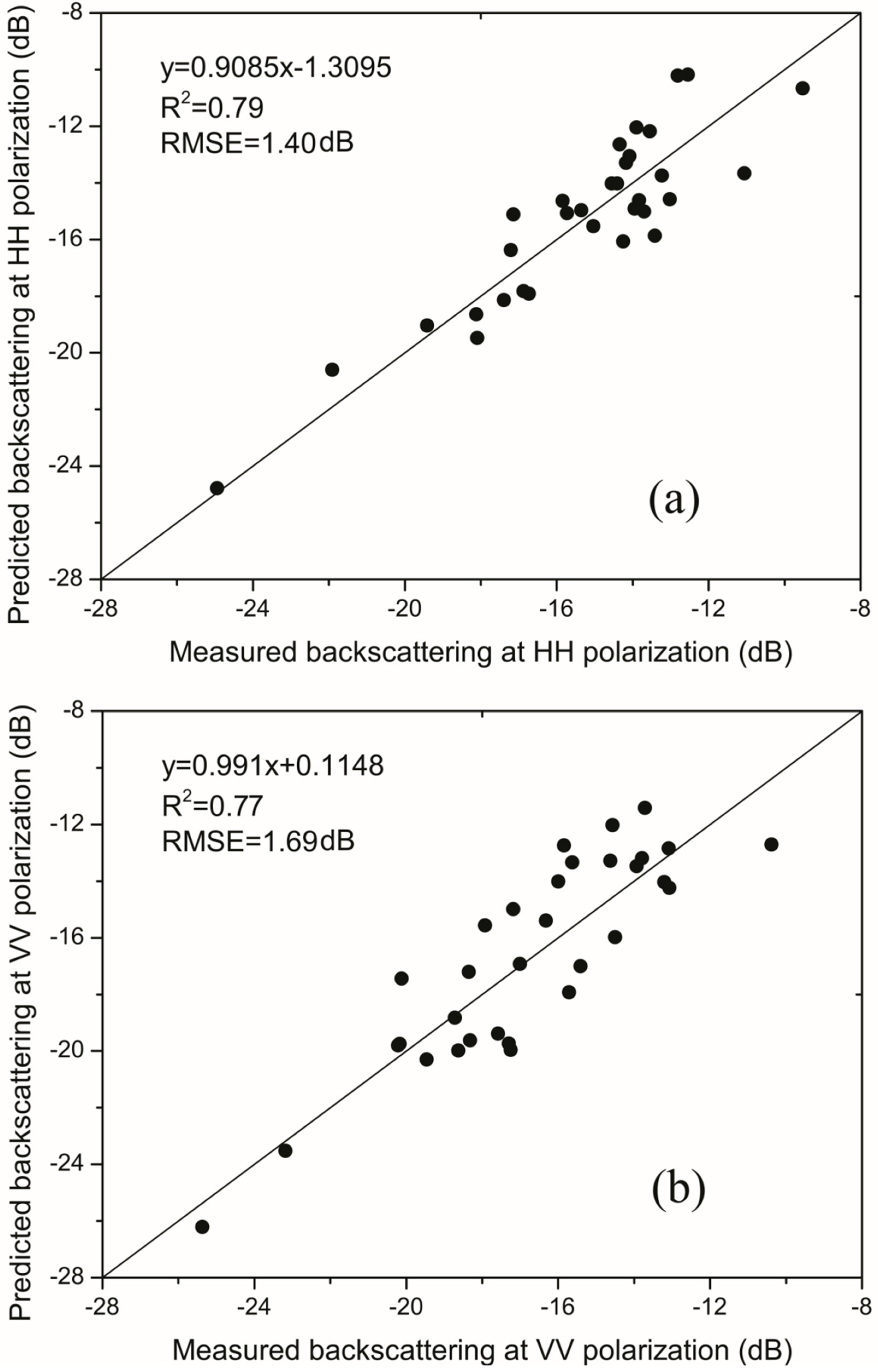
| Vegetation condition | Model | HH Polarization | VV Polarization | ||
|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | ||
| Density vegetation conditions | Basic model | 0.78 | 1.58 | 0.74 | 1.63 |
| Modified model | 0.81 | 1.23 | 0.78 | 1.61 | |
| Sparse vegetation conditions | Basic model | 0.25 | 2.65 | 0.15 | 2.93 |
| Modified model | 0.73 | 1.77 | 0.74 | 1.79 | |
4.2. Soil Moisture Estimation

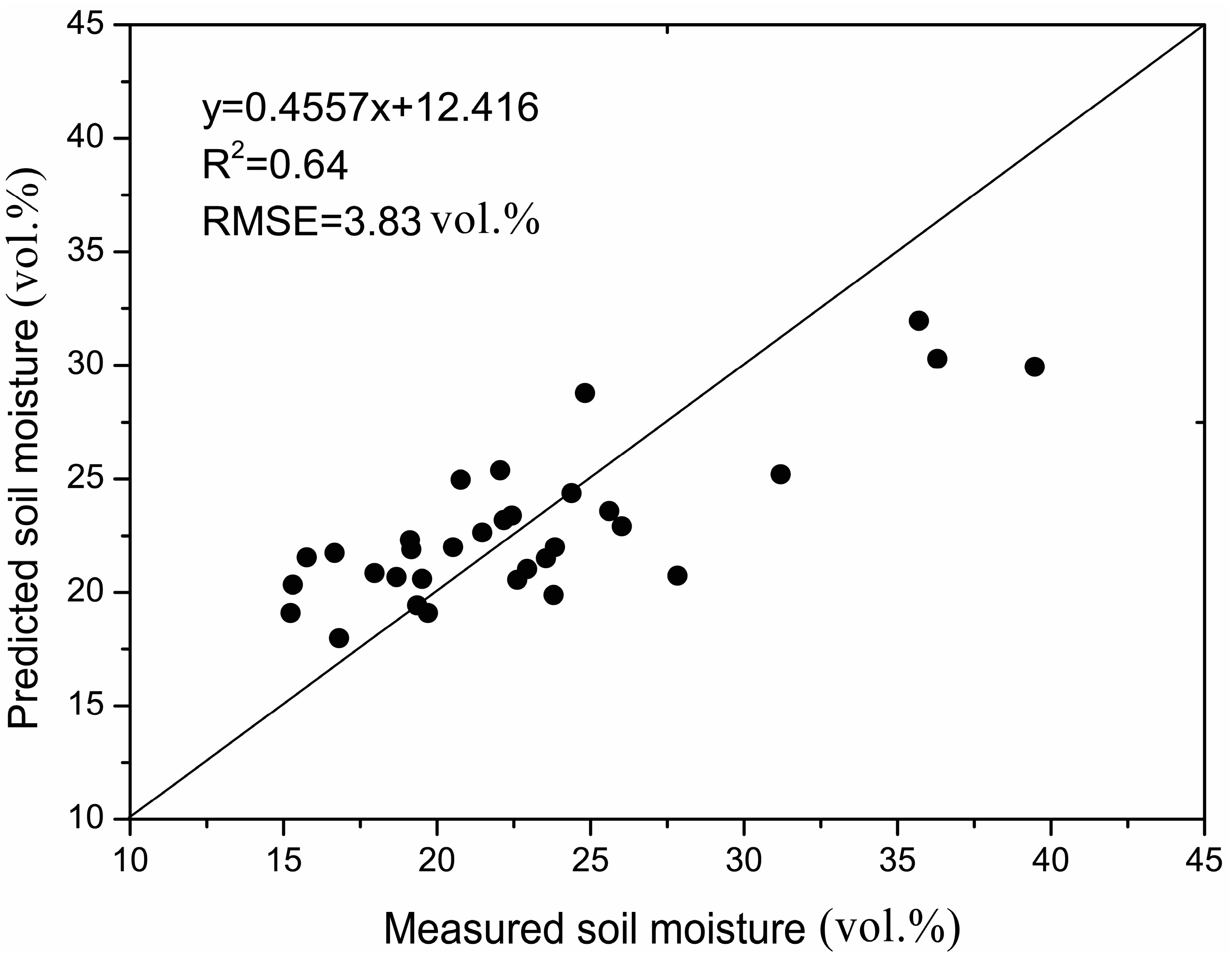
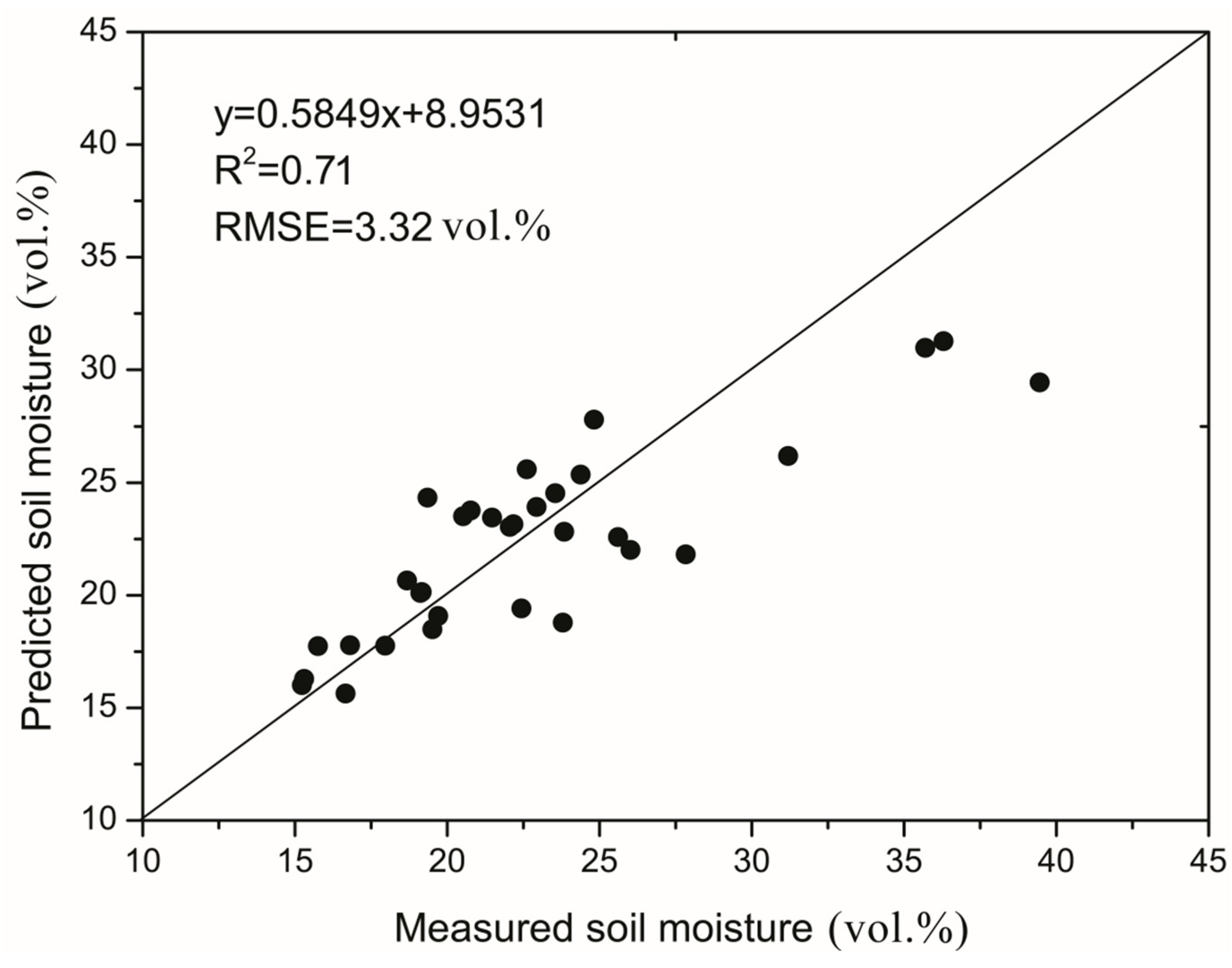
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Svoray, T.; Shoshany, M. Multi-scale analysis of intrinsic soil factors from SAR-based mapping of drying rates. Remote Sens. Environ. 2004, 92, 233–246. [Google Scholar] [CrossRef]
- Wang, C.; Qi, J.; Moran, S.; Marsett, R. Soil moisture estimation in a semiarid rangeland using ERS-2 and TM imagery. Remote Sens. Environ. 2004, 90, 178–189. [Google Scholar] [CrossRef]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. An empirical model and an inversion technique for radar scattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 1992, 30, 370–381. [Google Scholar] [CrossRef]
- Dubois, P.C.; van Zyl, J.; Engman, T. Measuring soil moisture with imaging radars. IEEE Trans. Geosci. Remote Sens. 1995, 33, 915–926. [Google Scholar] [CrossRef]
- Shi, J.; Wang, J.; Hsu, A.Y.; O’Neill, P.E.; Engman, E.T. Estimation of bare surface soil moisture and surface roughness parameter using L-band SAR image data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1254–1266. [Google Scholar] [CrossRef]
- Fung, A.K.; Li, Z.; Chen, K. Backscattering from a randomly rough dielectric surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
- Fung, A.K.; Chen, K. An update on the IEM surface backscattering model. IEEE Geosci. Remote Sens. Lett. 2004, 1, 75–77. [Google Scholar] [CrossRef]
- Chen, K.-S.; Wu, T.-D.; Tsang, L.; Li, Q.; Shi, J.; Fung, A.K. Emission of rough surfaces calculated by the integral equation method with comparison to three-dimensional moment method simulations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 90–101. [Google Scholar] [CrossRef]
- Zribi, M.; Dechambre, M. A new empirical model to retrieve soil moisture and roughness from C-band radar data. Remote Sens. Environ. 2003, 84, 42–52. [Google Scholar] [CrossRef]
- Prakash, R.; Singh, D.; Pathak, N.P. A fusion approach to retrieve soil moisture with SAR and optical data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 196–206. [Google Scholar] [CrossRef]
- Bindlish, R.; Barros, A.P. Parameterization of vegetation backscatter in radar-based, soil moisture estimation. Remote Sens. Environ. 2001, 76, 130–137. [Google Scholar] [CrossRef]
- Sang, H.; Zhang, J.; Lin, H.; Zhai, L. Multi-polarization ASAR backscattering from herbaceous wetlands in Poyang Lake region, China. Remote Sens. 2014, 6, 4621–4646. [Google Scholar] [CrossRef]
- Lakhankar, T.; Ghedira, H.; Temimi, M.; Azar, A.E.; Khanbilvardi, R. Effect of land cover heterogeneity on soil moisture retrieval using active microwave remote sensing data. Remote Sens. 2009, 1, 80–91. [Google Scholar] [CrossRef]
- Notarnicola, C.; Angiulli, M.; Posa, F. Use of radar and optical remotely sensed data for soil moisture retrieval over vegetated areas. IEEE Trans. Geosci. Remote Sens. 2006, 44, 925–935. [Google Scholar] [CrossRef]
- Gherboudj, I.; Magagi, R.; Berg, A.A.; Toth, B. Soil moisture retrieval over agricultural fields from multi-polarized and multi-angular RADARSAT-2 SAR data. Remote Sens. Environ. 2011, 115, 33–43. [Google Scholar] [CrossRef]
- Du, J.; Shi, J.; Sun, R. The development of HJ SAR soil moisture retrieval algorithm. Int. J. Remote Sens. 2010, 31, 3691–3705. [Google Scholar] [CrossRef]
- Lievens, H.; Verhoest, N.E.C. On the retrieval of soil moisture in wheat fields from L-band SAR based on Water Cloud modeling, the IEM, and effective roughness parameters. IEEE Geosci. Remote Sens. Lett. 2011, 8, 740–744. [Google Scholar] [CrossRef]
- Roo, R.D.D.; Du, Y.; Ulaby, F.T.; Dobson, M.C. A semi-empirical backscattering model at L-band and C-band for a soybean canopy with soil moisture inversion. IEEE Trans. Geosci. Remote Sens. 2001, 39, 864–872. [Google Scholar] [CrossRef]
- Wang, C.; Qi, J. Biophysical estimation in tropical forests using JERS-1 SAR and VNIR imagery. II. Aboveground woody biomass. Int. J. Remote Sens. 2008, 29, 6827–6849. [Google Scholar] [CrossRef]
- Mattar, C.; Wigneron, J.-P.; Sobrino, J.A.; Novello, N.; Calvet, J.-C.; Albergel, C.; Richaume, P.; Mialon, A.; Guyon, D.; Jiménez-Muñoz, J.C. A combined optical–microwave method to retrieve soil moisture over vegetated areas. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1404–1413. [Google Scholar] [CrossRef]
- Susan Moran, M.; Hymer, D.C.; Qi, J.; Sano, E.E. Soil moisture evaluation using multi-temporal synthetic aperture radar (SAR) in semiarid rangeland. Agric. For. Meteorol. 2000, 105, 69–80. [Google Scholar] [CrossRef]
- Santi, E.; Paloscia, S.; Pettinato, S.; Notarnicola, C.; Pasolli, L.; Pistocchi, A. Comparison between SAR soil moisture estimates and hydrological model simulations over the scrivia test site. Remote Sens. 2013, 5, 4961–4976. [Google Scholar] [CrossRef]
- Hosseini, M.; Saradjian, M. Soil moisture estimation based on integration of optical and SAR images. Can. J. Remote Sens. 2011, 37, 112–121. [Google Scholar] [CrossRef]
- Pasolli, L.; Notarnicola, C.; Bruzzone, L.; Bertoldi, G.; Della Chiesa, S.; Niedrist, G.; Tappeiner, U.; Zebisch, M. Polarimetric RADARSAT-2 imagery for soil moisture retrieval in alpine areas. Can. J. Remote Sens. 2011, 37, 535–547. [Google Scholar] [CrossRef]
- Paloscia, S.; Pettinato, S.; Santi, E.; Notarnicola, C.; Pasolli, L.; Reppucci, A. Soil moisture mapping using Sentinel-1 images: Algorithm and preliminary validation. Remote Sens. Environ. 2013, 134, 234–248. [Google Scholar] [CrossRef]
- Attema, E.; Ulaby, F.T. Vegetation modeled as a water cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Xiao, D.; Tian, B.; Tian, K.; Yang, Y. Landscape patterns and their changes in Sichuan Ruoergai Wetland National Nature Reserve. Acta Ecol. Sin. 2010, 30, 27–32. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanré, D.; Deuze, J.L.; Herman, M.; Morcette, J.J. Second simulation of the satellite signal in the solar spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Lee, J.-S.; Grunes, M.R.; de Grandi, G. Polarimetric SAR speckle filtering and its implication for classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2363–2373. [Google Scholar] [CrossRef]
- Loew, A.; Mauser, W. Generation of geometrically and radiometrically terrain corrected SAR image products. Remote Sens. Environ. 2007, 106, 337–349. [Google Scholar] [CrossRef]
- Van Zyl, J.J.; Chapman, B.D.; Dubois, P.; Shi, J. The effect of topography on SAR calibration. IEEE Trans. Geosci. Remote Sens. 1993, 31, 1036–1043. [Google Scholar] [CrossRef]
- Pairman, D.; Belliss, S.E.; McNeill, S.J. Terrain influences on SAR backscatter around Mt. Taranaki, New Zealand. IEEE Trans. Geosci. Remote Sens. 1997, 35, 924–932. [Google Scholar] [CrossRef]
- Zribi, M.; le Hégarat-Mascle, S.; Ottlé, C.; Kammoun, B.; Guerin, C. Surface soil moisture estimation from the synergistic use of the (multi-incidence and multi-resolution) active microwave ERS Wind Scatterometer and SAR data. Remote Sens. Environ. 2003, 86, 30–41. [Google Scholar] [CrossRef]
- Merzouki, A.; McNairn, H.; Pacheco, A. Mapping soil moisture using RADARSAT-2 data and local autocorrelation statistics. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 128–137. [Google Scholar] [CrossRef]
- Jacome, A.; Bernier, M.; Chokmani, K.; Gauthier, Y.; Poulin, J.; de Sève, D. Monitoring volumetric surface soil moisture content at the la grande basin boreal wetland by radar multi polarization data. Remote Sens. 2013, 5, 4919–4941. [Google Scholar] [CrossRef]
- Topp, G.; Davis, J.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Biftu, G.F.; Gan, T.Y. Retrieving near-surface soil moisture from Radarsat SAR data. Water Resour. Res. 1999, 35, 1569–1579. [Google Scholar] [CrossRef]
- Magagi, R.; Bernier, M.; Ung, C. Quantitative analysis of RADARSAT SAR data over a sparse forest canopy. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1301–1313. [Google Scholar] [CrossRef]
- Moran, M.S.; Vidal, A.; Troufleau, D.; Inoue, Y.; Mitchell, T.A. Ku-and C-band SAR for discriminating agricultural crop and soil conditions. IEEE Trans. Geosci. Remote Sens. 1998, 36, 265–272. [Google Scholar] [CrossRef]
- Prévot, L.; Champion, I.; Guyot, G. Estimating surface soil moisture and leaf area index of a wheat canopy using a dual-frequency (C and X bands) scatterometer. Remote Sens. Environ. 1993, 46, 331–339. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT+ SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009. [Google Scholar] [CrossRef]
- Inoue, Y.; Kurosu, T.; Maeno, H.; Uratsuka, S.; Kozu, T.; Dabrowska-Zielinska, K.; Qi, J. Season-long daily measurements of multifrequency (Ka, Ku, X, C, and L) and full-polarization backscatter signatures over paddy rice field and their relationship with biological variables. Remote Sens. Environ. 2002, 81, 194–204. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Sarabandi, K.; McDonald, K.; Whitt, M.; Dobson, M.C. Michigan microwave canopy scattering model. Int. J. Remote Sens. 1990, 11, 1223–1253. [Google Scholar] [CrossRef]
- Svoray, T.; Shoshany, M. SAR-based estimation of areal aboveground biomass (AAB) of herbaceous vegetation in the semi-arid zone: A modification of the water-cloud model. Int. J. Remote Sens. 2002, 23, 4089–4100. [Google Scholar] [CrossRef]
- Svoray, T.; Shoshany, M. Herbaceous biomass retrieval in habitats of complex composition: A model merging SAR images with unmixed Landsat TM data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1592–1601. [Google Scholar] [CrossRef]
- Xing, M.; He, B.; Li, X. Integration method to estimate above-ground biomass in arid prairie regions using active and passive remote sensing data. J. Appl. Remote Sens. 2014. [Google Scholar] [CrossRef]
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens. 1998, 19, 1533–1543. [Google Scholar] [CrossRef]
- Taconet, O.; Benallegue, M.; Vidal-Madjar, D.; Prevot, L.; Dechambre, M.; Normand, M. Estimation of soil and crop parameters for wheat from airborne radar backscattering data in C and X bands. Remote Sens. Environ. 1994, 50, 287–294. [Google Scholar] [CrossRef]
- Svoray, T.; Shoshany, M.; Curran, P.; Foody, G.M.; Perevolotsky, A. Relationship between green leaf biomass volumetric density and ERS-2 SAR backscatter of four vegetation formations in the semi-arid zone of Israel. Int. J. Remote Sens. 2001, 22, 1601–1607. [Google Scholar] [CrossRef]
- Imhoff, M.L. Radar backscatter and biomass saturation: Ramifications for global biomass inventory. IEEE Trans. Geosci. Remote Sens. 1995, 33, 511–518. [Google Scholar] [CrossRef]
- Bindlish, R.; Barros, A.P. Multifrequency soil moisture inversion from SAR measurements with the use of IEM. Remote Sens. Environ. 2000, 71, 67–88. [Google Scholar] [CrossRef]
- Joseph, A.; van der Velde, R.; O’Neill, P.; Lang, R.; Gish, T. Effects of corn on C-and L-band radar backscatter: A correction method for soil moisture retrieval. Remote Sens. Environ. 2010, 114, 2417–2430. [Google Scholar] [CrossRef]
- Zribi, M.; Baghdadi, N.; Holah, N.; Fafin, O. New methodology for soil surface moisture estimation and its application to ENVISAT-ASAR multi-incidence data inversion. Remote Sens. Environ. 2005, 96, 485–496. [Google Scholar] [CrossRef]
- Kasischke, E.S.; Bourgeau-Chavez, L.L. Monitoring south Florida wetlands using ERS-1 SAR imagery. Photogramm. Eng. Remote Sens. 1997, 63, 281–291. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, B.; Xing, M.; Bai, X. A Synergistic Methodology for Soil Moisture Estimation in an Alpine Prairie Using Radar and Optical Satellite Data. Remote Sens. 2014, 6, 10966-10985. https://doi.org/10.3390/rs61110966
He B, Xing M, Bai X. A Synergistic Methodology for Soil Moisture Estimation in an Alpine Prairie Using Radar and Optical Satellite Data. Remote Sensing. 2014; 6(11):10966-10985. https://doi.org/10.3390/rs61110966
Chicago/Turabian StyleHe, Binbin, Minfeng Xing, and Xiaojing Bai. 2014. "A Synergistic Methodology for Soil Moisture Estimation in an Alpine Prairie Using Radar and Optical Satellite Data" Remote Sensing 6, no. 11: 10966-10985. https://doi.org/10.3390/rs61110966
APA StyleHe, B., Xing, M., & Bai, X. (2014). A Synergistic Methodology for Soil Moisture Estimation in an Alpine Prairie Using Radar and Optical Satellite Data. Remote Sensing, 6(11), 10966-10985. https://doi.org/10.3390/rs61110966





