Estimation of Airborne Lidar-Derived Tropical Forest Canopy Height Using Landsat Time Series in Cambodia
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
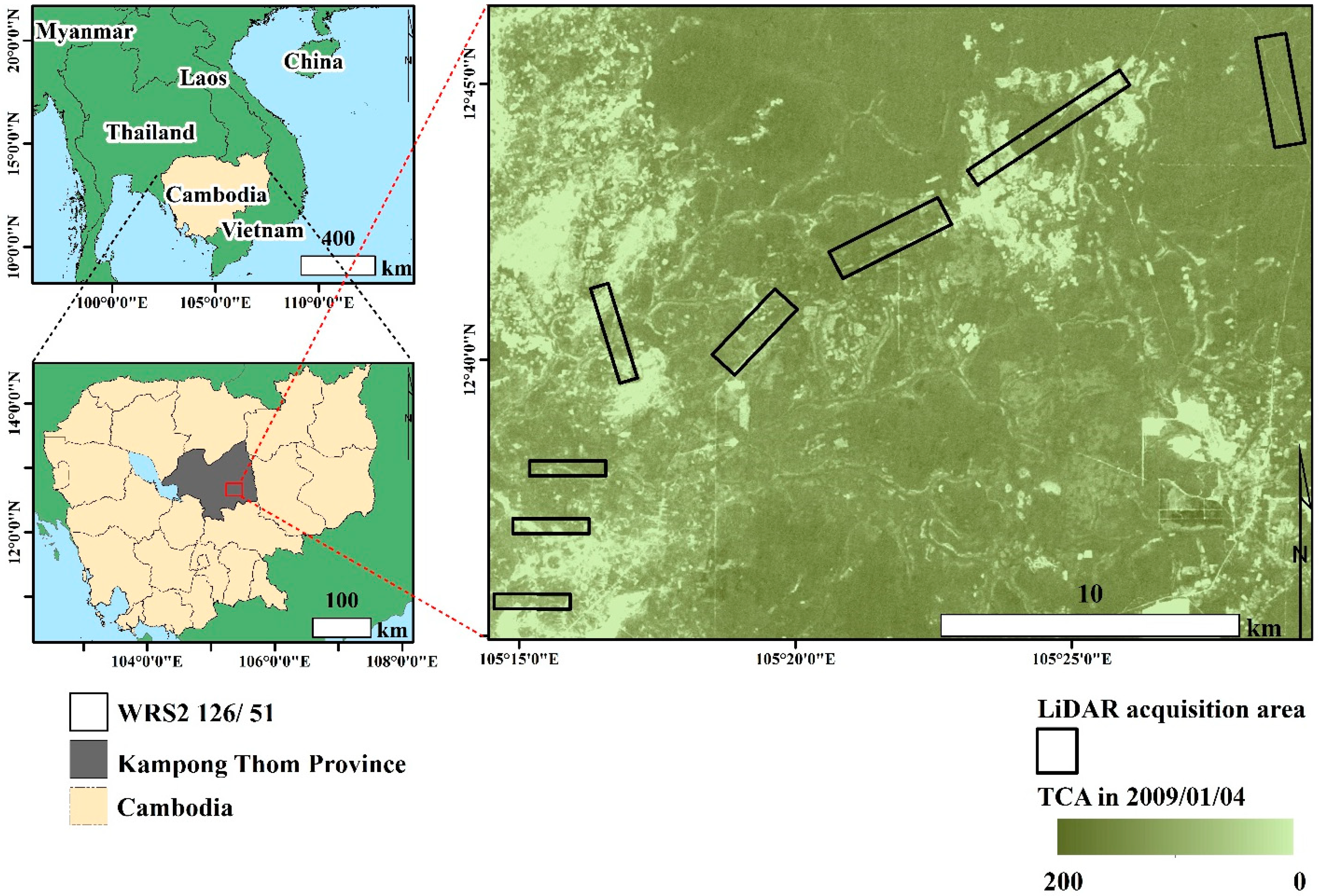
2.2. Landsat Data
| Year/Month/Day | Satellite |
|---|---|
| 1983/12/1 | Landsat 4 MSS |
| 1984/12/11 | Landsat 5 MSS |
| 1986/12/1 | Landsat 5 MSS |
| 1990/12/4 | Landsat 4 TM |
| 1994/11/21 | Landsat 5 TM |
| 1996/1/27 | Landsat 5 TM |
| 1997/1/13 | Landsat 5 TM |
| 2000/12/31 | Landsat 7 ETM+ |
| 2003/2/7 | Landsat 7 ETM+ |
| 2003/12/24 | Landsat 7 ETM+ |
| 2004/11/8 | Landsat 7 ETM+ |
| 2006/11/30 | Landsat 7 ETM+ |
| 2008/1/20 | Landsat 7 ETM+ |
| 2009/1/14 | Landsat 5 TM |
| 2009/12/24 | Landsat 7 ETM+ |
| 2010/12/27 | Landsat 7 ETM+ |
| 2011/12/30 | Landsat 7 ETM+ |
2.3. Airborne Lidar Data
| Parameter | Optech ALTM 3100 |
|---|---|
| Flight altitude (above ground) | 500 m |
| Flying Speed | 25 m/s |
| Pulse repetition frequency | 100 kHz |
| Scan frequency | 53 Hz |
| Laser beam divergence | 0.5 mrad |
| Wave length | 1064 nm |
2.4. Methods
2.4.1. Landsat Image Processing
2.4.2. Disturbance History from Landsat Spectral Trajectories
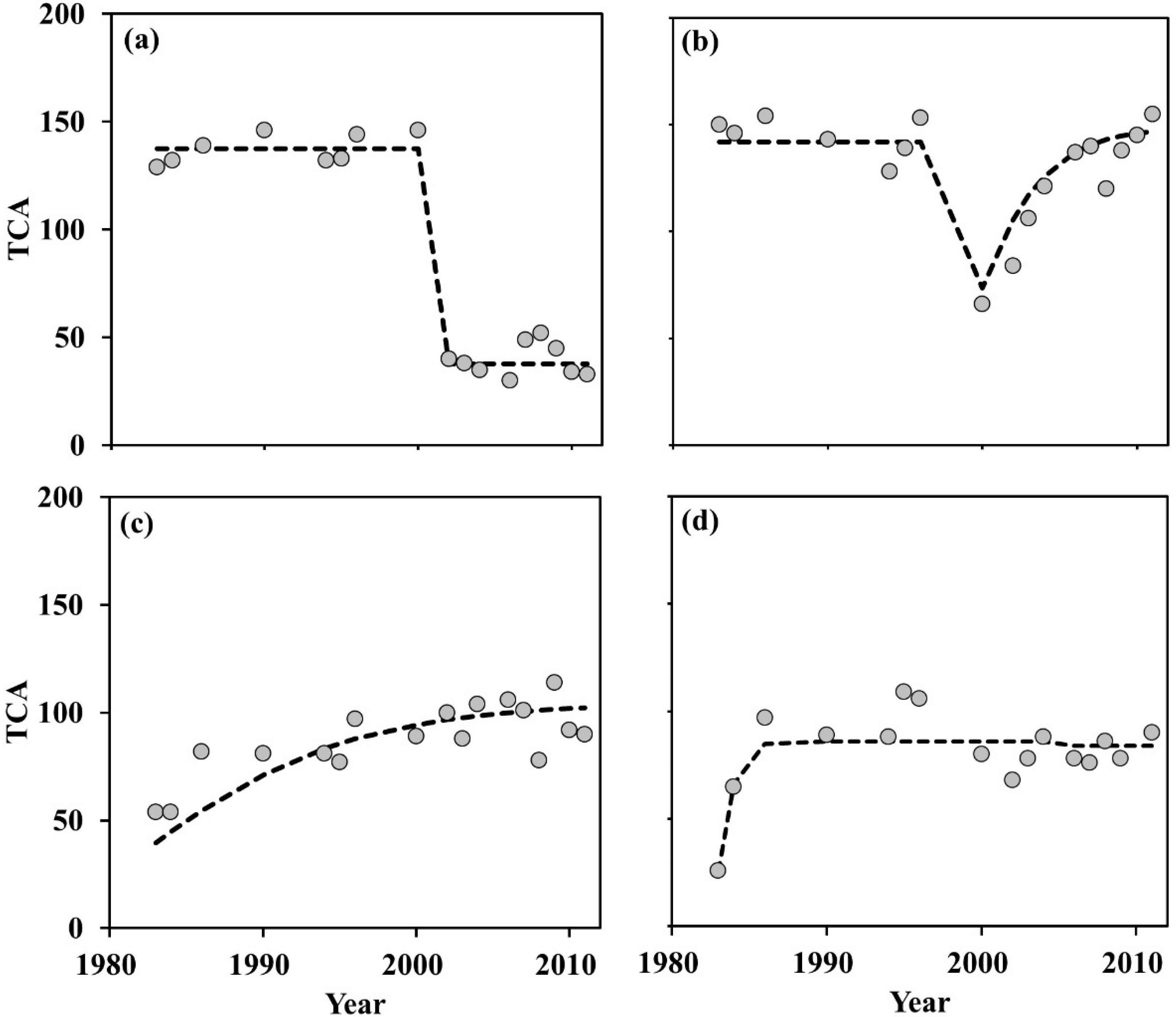
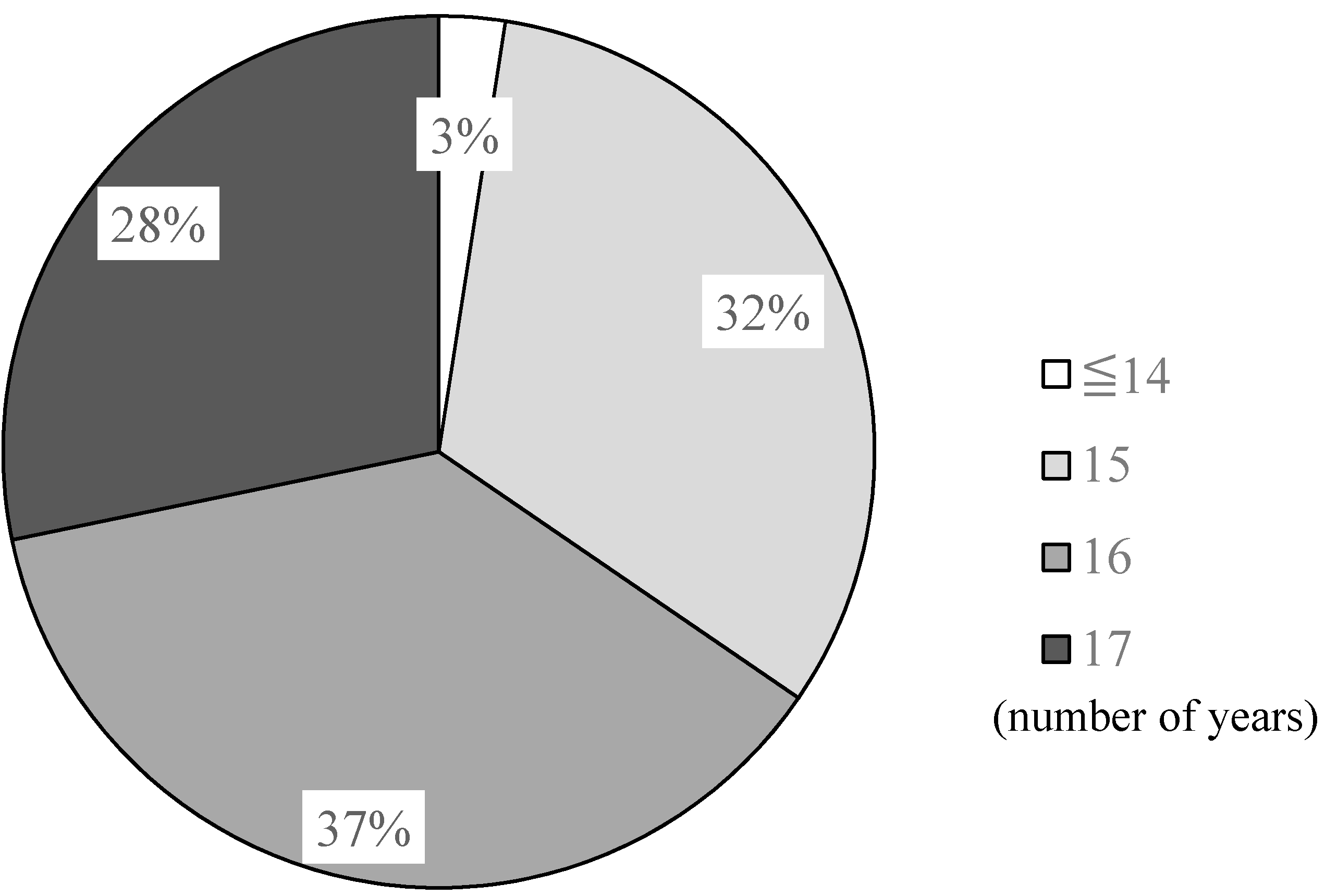
2.4.3. Datasets for Mean Canopy Height Estimation
2.4.4. Mean Canopy Height Estimation Using Multiple Regression and Random Forest
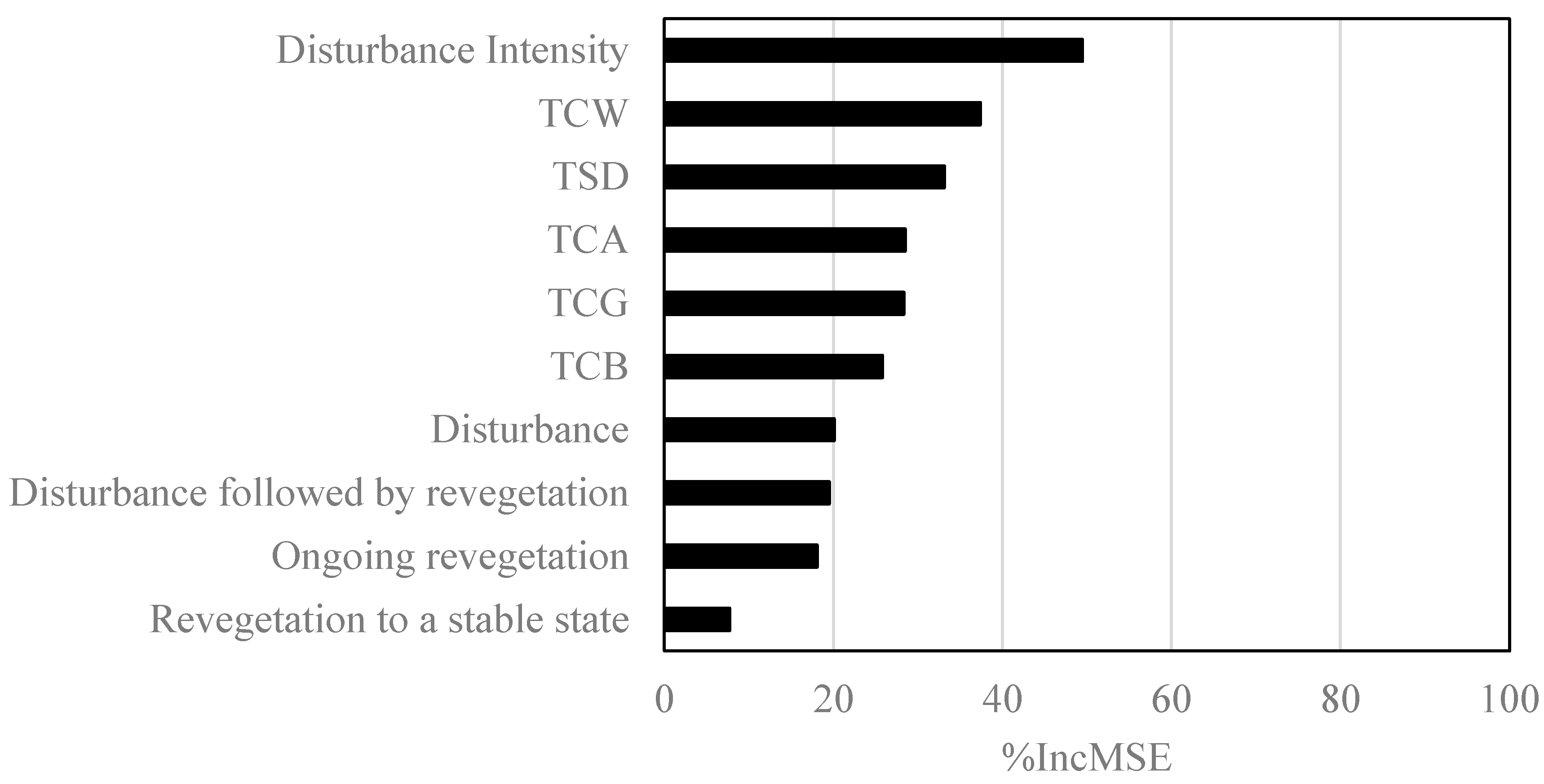
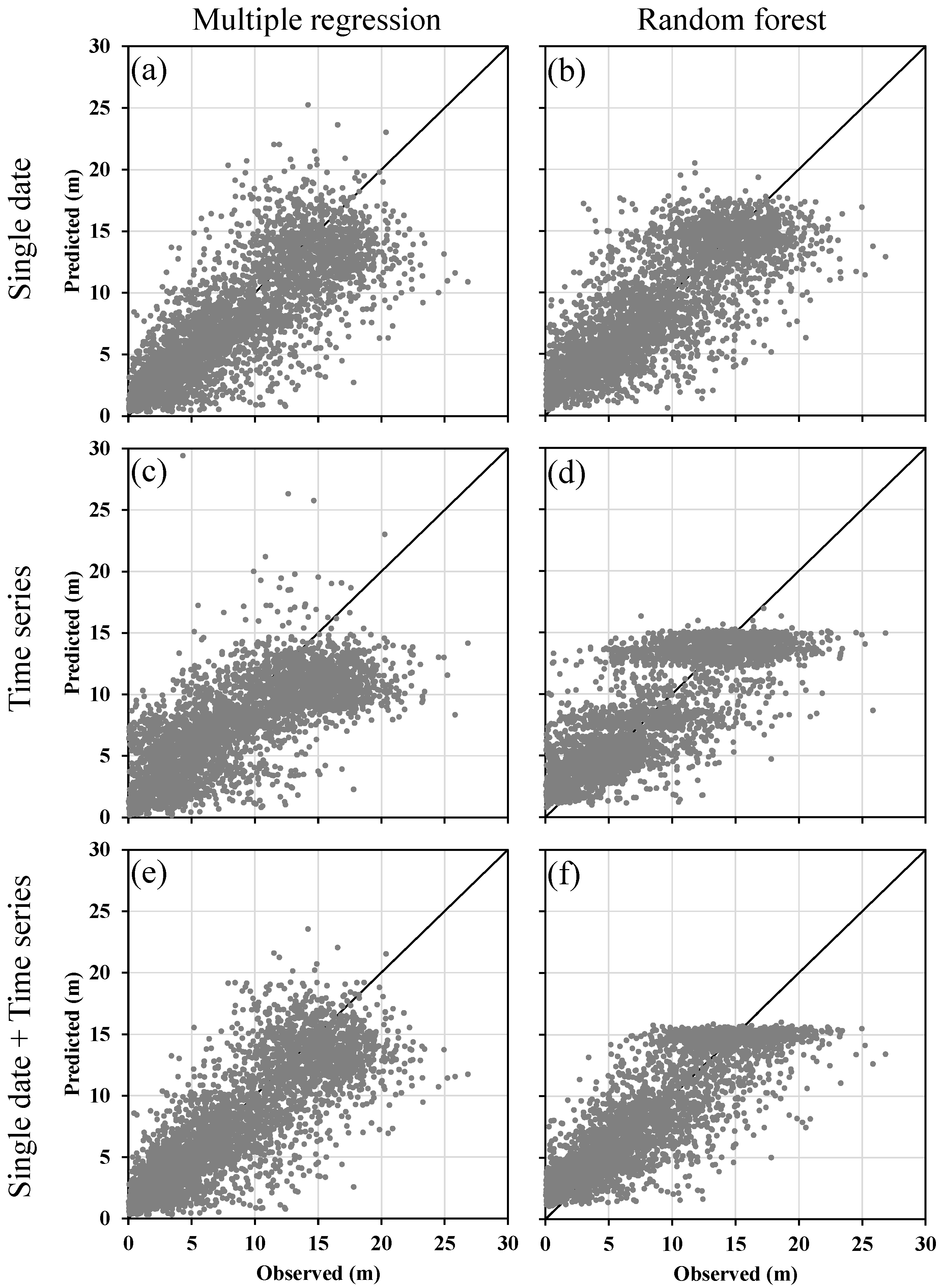
2.4.5. Comparison of Model Performance for Estimating Lidar-Measured Mean Canopy Height
3. Results
3.1. Trajectory-Based Characterization of Forest Disturbance
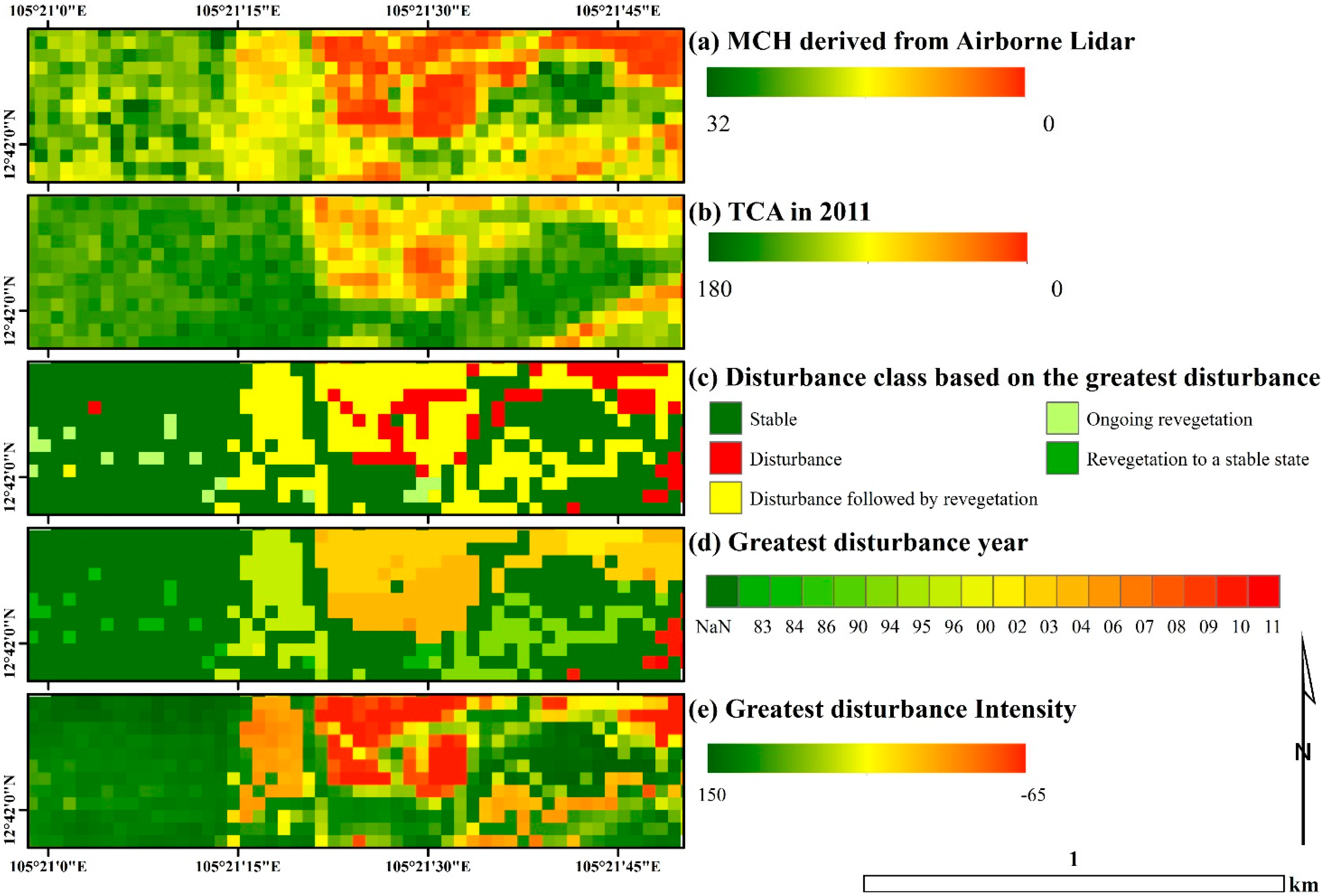
3.2. Performance of Canopy Height Models
| Variables | Correlation | |
|---|---|---|
| TCB | −0.70 | ** |
| TCG | 0.64 | ** |
| TCW | −0.73 | ** |
| TCA | 0.69 | ** |
| Disturbance Intensity | 0.64 | ** |
| TSD | 0.38 | ** |
| Model | Variables | R2 | RMSE | |||
|---|---|---|---|---|---|---|
| Random forest | Single date | 0.66 | 3.25 | |||
| Time series | 0.66 | 3.24 | ||||
| Single date | Disturbance Intensity | 0.72 | 2.97 | |||
| Single date | TSD | 0.68 | 3.14 | |||
| Single date | Class | 0.70 | 3.05 | |||
| Single date | Disturbance Intensity | TSD | 0.73 | 2.88 | ||
| Single date | Disturbance Intensity | Class | 0.74 | 2.87 | ||
| Single date | TSD | Class | 0.71 | 3.00 | ||
| Single date | Disturbance Intensity | TSD | Class | 0.75 | 2.81 | |
| Multiple regression | Single date | 0.65 | 3.38 | |||
| Time series | 0.55 | 3.91 | ||||
| Single date | Disturbance Intensity | 0.67 | 3.28 | |||
| Single date | TSD | 0.66 | 3.35 | |||
| Single date | Class | 0.66 | 3.35 | |||
| Single date | Disturbance Intensity | TSD | 0.67 | 3.28 | ||
| Single date | Disturbance Intensity | Class | 0.67 | 3.26 | ||
| Single date | TSD | Class | 0.66 | 3.25 | ||
| Single date | Disturbance Intensity | TSD | Class | 0.67 | 3.26 | |
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gibbs, H.K.; Brown, S.; Niles, J.O.; Foley, J.A. Monitoring and estimating tropical forest carbon stocks: Making REDD a reality. Environ. Res. Lett. 2007, 2, 1–13. [Google Scholar]
- Baccini, A.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, J.; Hackler, P.; Beck, P.S.A.; Dubayah, R.; Friedl, M.A.; et al. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nat. Clim. 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed]
- Geist, H.J.; Lambin, E.F. What Drives Tropical Deforestation? A Meta-Analysis of Proximate and Underlying Causes of Deforestation Based on Subnational Case Study Evidence; LUCC International Project Office: Louvain-la-Neuve, Belgium, 2001. [Google Scholar]
- Geist, H.J.; Lambin, E.F. Proximate causes and underlying driving forces of tropical deforestation. Bioscience 2002, 52, 143–150. [Google Scholar] [CrossRef]
- Wulder, M.A.; Franklin, S.E. Understanding Forest Disturbance and Spatial Pattern: Remote Sensing and GIS Approaches; Taylor and Francis: Boca Raton, FL, USA, 2007. [Google Scholar]
- Song, C.; Schroeder, T.A.; Cohen, W.B. Predicting temperate conifer forest successional stage distributions with multitemporal Landsat Thematic Mapper imagery. Remote Sens. Environ. 2007, 106, 228–237. [Google Scholar] [CrossRef]
- Hunter, M.O.; Keller, M.; Victoria, D.; Morton, D.C. Tree height and tropical forest biomass estimation. Biogeosciences 2013, 10, 8385–8399. [Google Scholar] [CrossRef]
- Stone, C.; Penman, T.; Turner, R. Determining an optimal model for processing Lidar data at the plot level: Results for a Pinus radiata plantation in New South Wales, Australia. New Zeal. J. For. Sci. 2011, 41, 191–205. [Google Scholar]
- Moesera, D.; Roubineka, J.; Schleppib, P.; Morsdorfc, F.; Jonasa, T. Canopy closure, LAI and radiation transfer from airborne LiDAR synthetic images. Agric. For. Meteorol. 2014, 197, 158–168. [Google Scholar] [CrossRef]
- Donoghue, D.N.M.; Watt, P.J.; Cox, N.J.; Wilson, J. Remote sensing of species mixtures in conifer plantations using Lidar height and intensity data. Remote Sens. Environ. 2007, 110, 509–522. [Google Scholar] [CrossRef]
- Ahmed, O.S.; Franklin, S.E.; Wulder, M.A. Integration of LiDAR and Landsat to estimate forest canopy cover in coastal British Columbia. Photogramm. Eng. Remote Sens. 2014, 80, 953–961. [Google Scholar] [CrossRef]
- Morsdorf, F.; Marell, A.; Koetz, B.; Cassagne, N.; Pimont, F.; Rigolot, E. Discrimination of vegetation strata in a multi-layered Mediterranean forest ecosystem using height and intensity information derived from airborne laser scanning. Remote Sens. Environ. 2010, 114, 1403–1415. [Google Scholar] [CrossRef]
- Falkowski, M.J.; Evans, J.S.; Martinuzzi, S.; Gessler, P.E.; Hudak, A.T. Characterizing forest succession with Lidar data: An evaluation for the Inland Northwest, USA. Remote Sens. Environ. 2009, 113, 946–956. [Google Scholar] [CrossRef]
- Palminteri, S.; Powell, G.V.N.; Asner, G.P.; Peres, C.A. LiDAR measurements of canopy structure predict spatial distribution of a tropical mature forest primate. Remote Sens. Environ. 2012, 127, 98–105. [Google Scholar] [CrossRef]
- Asner, G.P.; Clark, J.K.; Mascro, J.; Vaudry, R.; Chadwick, K.D.; Vieilledent, G.; Rasamoelina, M.; Balaji, A.; Kennedy-Bowdoin, T.; Maatoug, L.; et al. Human and environmental controls over aboveground carbon storage in Madagascar. Carbon Balance Manag. 2012, 7. [Google Scholar] [CrossRef]
- Asner, G.P.; Clark, J.K.; Mascaro, J.; Galindo García, G.A.; Chadwick, K.D.; Encinales, D.A.N.; Paez-Acosta, G.; Montenegro, E.C.; Kennedy-Bowdoin, T.; Duque, Á.; et al. High-resolution mapping of forest carbon stocks in the Colombian Amazon. Biogeosciences 2012, 9, 2683–2696. [Google Scholar] [CrossRef]
- Ahmed, O.S.; Franklin, S.E.; Wulder, M.A. Characterizing stand-level forest canopy cover and height using landsat time series, samples of airborne LiDAR, and the random forest algorithm. ISPRS J. Photogramm. Remote Sens. 2014. under review. [Google Scholar]
- Chen, G.; Hay, G.J. A support vector regression approach to estimate forest biophysical parameters at the object level using airborne Lidar transects and quick bird data. Photogramm. Eng. Remote Sens. 2011, 77, 733–741. [Google Scholar] [CrossRef]
- Hudak, A.T.; Lefsky, M.A.; Cohen, W.B.; Berterretche, M. Integration of lidar and Landsat ETM+ data for estimating and mapping forest canopy height. Remote Sens. Environ. 2002, 82, 397–416. [Google Scholar] [CrossRef]
- Wulder, M.A.; Seemann, D. Forest inventory height update through the integration of Lidar data with segmented Landsat imagery. Can. J. Remote Sens. 2003, 29, 536–543. [Google Scholar] [CrossRef]
- Cohen, W.B.; Fiorella, M.; Gray, J.; Helmer, E.; Anderson, K. An efficient and accurate method for mapping forest clearcuts in the Pacific Northwest using Landsat imagery. Photogramm. Eng. Remote Sens. 1998, 64, 293–300. [Google Scholar]
- Cohen, W.B.; Goward, S.N. Landsat’s role in ecological applications of remote sensing. Bioscience 2004, 54, 535–545. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Hay, G.J.; Castilla, G. Towards automated segmentation of forest inventory polygons on high spatial resolution satellite imagery. For. Chron. 2008, 84, 221–230. [Google Scholar] [CrossRef]
- Woodcock, C.E.; Allen, R.; Anderson, M.; Belward, A.; Bindschadler, R.; Cohen, W.; Gao, F.; Goward, S.N.; Helder, D.; Helmer, E.; et al. Free access to Landsat imagery. Science 2008, 320, 1011. [Google Scholar] [CrossRef] [PubMed]
- Wulder, M.A.; Masek, J.G.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Opening the archive: How free data has enabled the science and monitoring promise of Landsat. Remote Sens. Environ. 2012, 122, 2–10. [Google Scholar] [CrossRef]
- Kajisa, T.; Murakami, T.; Mizoue, N.; Yoshida, S. Differences in spectral trajectory with stand volume development between Japanese larch and Japanese oak in Hokkaido, Japan. J. For. Res. 2007, 12, 435–441. [Google Scholar] [CrossRef]
- Kajisa, T.; Murakami, T.; Mizoue, N.; Top, N.; Yoshida, S. Object-based forest biomass estimation using Landsat ETM+ in Kampong Thom Province, Cambodia. J. For. Res. 2009, 14, 203–211. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondízio, E.; Moran, E. Relationships between forest stand parameters and Landsat TM spectral responses in the Brazilian Amazon Basin. For. Ecol. Manag. 2004, 198, 149–167. [Google Scholar] [CrossRef]
- Powell, S.L.; Cohen, W.B.; Healey, S.P.; Kennedy, R.E.; Moisen, G.G.; Pierce, K.B.; Pierce, K.B.; Ohmann, J.L. Quantification of live aboveground forest biomass dynamics with Landsat time-series and field inventory data: A comparison of empirical modelling approaches. Remote Sens. Environ. 2010, 1145, 1053–1068. [Google Scholar] [CrossRef]
- Duncanson, L.I.; Niemann, K.O.; Wulder, M.A. Integration of GLAS and Landsat TM data for aboveground biomass estimation. Can. J. Remote Sens. 2010, 36, 129–141. [Google Scholar] [CrossRef]
- Gómez, C.; White, J.C.; Wulder, M.A. Characterizing the state and processes of change in a dynamic forest environment using hierarchical spatio-temporal segmentation. Remote Sens. Environ. 2011, 115, 1665–1679. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Cohen, W.B.; Schroeder, T.A. Trajectory-based changedetection for automated characterization of forest disturbance dynamics. Remote Sens. Environ. 2007, 110, 370–386. [Google Scholar] [CrossRef]
- Ahmed, O.S.; Franklin, S.E.; Wulder, M.A. The interpretation of forest disturbance using Landsat imagery time-series and airborne LiDAR-derived canopy cover data in British Columbia. Can. J. Remote Sens. 2014, 39, 521–542. [Google Scholar] [CrossRef]
- Pflugmacher, D.; Cohen, W.B.; Kennedy, R.E. Using Landsat-derived disturbance history 1972–2010 to predict current forest structure. Remote Sens. Environ. 2012, 122, 146–165. [Google Scholar] [CrossRef]
- Li, A.; Huang, C.; Sun, G.; Shi, H.; Toney, C.; Zhu, Z.; Rollins, M.G.; Goward, S.N.; Masek, J.G. Modeling the height of young forests regenerating from recent disturbances in Mississippi using Landsat and ICESat data. Remote Sens. Environ. 2011, 115, 1837–1849. [Google Scholar] [CrossRef]
- Helmer, E.H.; Ruzycki, T.S.; Wunderle, J.M.; Vogesser, S.; Ruefenacht, B.; Kwit, C.; Brandeis, T.J.; Ewert, D.N. Mapping tropical dry forest height, foliage height profiles and disturbance type and age with a time series of cloud-cleared Landsat and ALI image mosaics to characterize avian habitat. Remote Sens. Environ. 2010, 114, 2457–2473. [Google Scholar] [CrossRef]
- Hilker, T.; Wulder, M.A.; Coops, N.C. Update of forest inventory data with Lidar and high spatial resolution satellite imagery. Can. J. Remote Sens. 2008, 34, 5–12. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Olden, J.D.; Lawler, J.J.; Poff, N.L. Machine learning methods without tears: A primer for ecologists. Q. Rev. Biol. 2008, 83, 171–193. [Google Scholar] [CrossRef] [PubMed]
- Durbha, S.S.; King, R.L.; Younan, N.H. Support vector machines regression for retrieval of leaf area index from multi-angle imaging spectroradiometer. Remote Sens. Environ. 2007, 107, 348–361. [Google Scholar] [CrossRef]
- Hudak, A.T.; Cookston, N.; Evans, J.; Hall, D.; Falkowski, M. Nearest neighbor imputation of species-level, plot scale forest structure attributes from Lidar data. Remote Sens. Environ. 2008, 112, 2232–2245. [Google Scholar] [CrossRef]
- DFW. Forest Cover Assessment, Cambodia (in Khmer); Department of Forest and Wildlife: Phnom Penh, Cambodia, 1999.
- Bruun, T.B.; de Neergaard, A.; Lawrence, D.; Ziegler, A.D. Environmental consequences of the demise in Swidden cultivation in Southeast Asia: Carbon storage and soil quality. Hum. Ecol. 2009, 37, 375–388. [Google Scholar] [CrossRef]
- Padoch, C.; Coffey, K.; Mertz, O.; Leisz, S.J.; Fox, J.; Wadley, R.L. The demise of Swidden in Southeast Asia? Local realities and regional ambiguities. Geogr. Tidsskr. 2007, 107, 29–41. [Google Scholar] [CrossRef]
- Fox, J.; Vogler, J.B. Land-use and land-cover change in Montane Mainland Southeast Asia. Environ. Manag. 2005, 36, 394–403. [Google Scholar] [CrossRef]
- Markham, B.L.; Storey, J.C.; Williams, D.L.; Irons, J.R. Landsat sensor performance: History and current status. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2691–2694. [Google Scholar] [CrossRef]
- Axelsson, P. Processing of laser scanner data—Algorithms and applications. ISPRS J. Photogramm. Remote Sens. 1999, 54, 138–147. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.G.; Wolfe, R.E. Automated registration and orthorectification package for Landsat and Landsat-like data processing. J. Appl. Remote Sens. 2009, 3, 033515. [Google Scholar] [CrossRef]
- Chavez, P.S., Jr. Image-based atmospheric corrections—Revisited and improved. Photogramm. Eng. Remote Sens. 1996, 62, 1025–1036. [Google Scholar]
- Canty, M.J.; Nielsen, A.A.; Schmidt, M. Automatic radiometric normalization of multitemporal satellite imagery. Remote Sens. Environ. 2004, 91, 441–451. [Google Scholar] [CrossRef]
- Schroeder, T.A.; Cohen, W.B.; Song, C.; Canty, M.J.; Yang, Z. Radiometric correction of multi-temporal Landsat data for characterization of early successional forest patterns in western Oregon. Remote Sens. Environ. 2006, 103, 16–26. [Google Scholar] [CrossRef]
- Powell, S.L.; Cohen, W.B.; Yang, Z.; Pierce, J.D.; Alberti, M. Quantification of impervious surface in the Snohomish Water Resources Inventory Area of Western Washington from 1972–2006. Remote Sens. Environ. 2008, 112, 1895–1908. [Google Scholar]
- Gillanders, S.N.; Coops, N.C.; Wulder, M.A.; Gergel, S.E.; Nelson, T. Multitemporal remote sensing of landscape dynamics and pattern change: Describing natural and anthropogenic trends. Prog. Phys. Geog. 2008, 35, 502–528. [Google Scholar]
- Crist, E.P. A TM tasselled cap equivalent transformation for reflectance factor data. Remote Sens. Environ. 1985, 17, 301–306. [Google Scholar] [CrossRef]
- Cohen, W.B.; Spies, T.A.; Alig, R.A.; Oetter, D.R.; Maiersperger, T.K.; Fiorella, M. Characterizing 23 years (1972–1995) of stand replacement disturbance in Western Oregon forests with Landsat imagery. Ecosystems 2002, 5, 122–137. [Google Scholar] [CrossRef]
- Hansen, M.J.; Franklin, S.E.; Woudsma, C.G.; Peterson, M. Caribou habitat mapping and fragmentation analysis using Landsat MSS, TM, and GIS data in the North Columbia Mountains, British Columbia, Canada. Remote Sens. Environ. 2001, 77, 50–65. [Google Scholar] [CrossRef]
- Crist, E.P.; Cicone, R.C. A physically based transformation of Thematic Mapper data. The TM tasselled Cap. IEEE Trans. Geosci. Remote Sens. 1984, 22, 256–263. [Google Scholar] [CrossRef]
- Price, K.P.; Jakubauskas, M.E. Spectral retrogression and insect damage in lodgepole pine successional forests. Int. J. Remote Sens. 1998, 19, 1627–1632. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Gomez, C.; Stenhouse, G. A history of habitat dynamics: Characterizing 35 years of stand replacing disturbance. Can. J. Remote Sens. 2011, 37, 234–251. [Google Scholar] [CrossRef]
- R: A Language and Environment for Statistical Computing. Available online: http://www.R-project.org/ (accessed on 12 January 2013).
- Chen, G.; Hay, J.G.; Castilla, G.; St-Onge, B.; Powers, R. A multiscale geographic object-based image analysis to estimate Lidar measured forest canopy height using Quickbird imagery. Int. J. Geogr. Inf. Sci. 2010, 25, 877–893. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L.; Cutler, A. Random forests—Classification description: Random forests. Available online: http://www.stat.berkeley.edu/~breiman/RandomForests/cc_home.htm (accessed on 12 January 2013).
- McInerney, D.; Nieuwenhuis, M. Comparative analysis of kNN and decision tree methods for the Irish National Forest Inventory. Int. J. Remote Sens. 2009, 30, 4937–4955. [Google Scholar] [CrossRef]
- Gleason, C.J.; Im, J. Forest biomass estimation from airborne Lidar data using machine learning approaches. Remote Sens. Environ. 2012, 125, 80–91. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by random forest. R News 2002, 23, 18–22. [Google Scholar]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 285, 1–26. [Google Scholar]
- Duro, D.C.; Franklin, S.E.; Dubé, M.G. A comparison of pixel-based and object-based image analysis with selected machine learning algorithms for the classification of agricultural landscapes using SPOT-5 HRG imagery. Remote Sens. Environ. 2012, 118, 259–272. [Google Scholar] [CrossRef]
- Maltamo, M.; Eerikainen, K.; Packalen, P.; Hyyppa, J. Estimation of stem volume using laser scanning-based canopy height metrics. Forestry 2006, 79, 217–229. [Google Scholar] [CrossRef]
- Frazier, R.J.; Coops, N.C.; Wulder, M.A.; Kennedy, R. Characterization of aboveground biomass in an unmanaged boreal forest using Landsat temporal segmentation metrics. ISPRS J. Photogramm. Remote Sens. 2014, 92, 137–146. [Google Scholar] [CrossRef]
- Mon, M.S.; Mizoue, N.; Htun, N.Z.; Kajisa, T.; Yoshida, S. Factors affecting deforestation and forest degradation in selectively logged production forest: A case study in Myanmar. For. Ecol. Manag. 2012, 267, 190–198. [Google Scholar]
- Cohen, W.B.; Yang, Z.; Kennedy, R. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 2. TimeSync—Tools for calibration and validation. Remote Sens. Environ. 2010, 114, 2911–2924. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ota, T.; Ahmed, O.S.; Franklin, S.E.; Wulder, M.A.; Kajisa, T.; Mizoue, N.; Yoshida, S.; Takao, G.; Hirata, Y.; Furuya, N.; et al. Estimation of Airborne Lidar-Derived Tropical Forest Canopy Height Using Landsat Time Series in Cambodia. Remote Sens. 2014, 6, 10750-10772. https://doi.org/10.3390/rs61110750
Ota T, Ahmed OS, Franklin SE, Wulder MA, Kajisa T, Mizoue N, Yoshida S, Takao G, Hirata Y, Furuya N, et al. Estimation of Airborne Lidar-Derived Tropical Forest Canopy Height Using Landsat Time Series in Cambodia. Remote Sensing. 2014; 6(11):10750-10772. https://doi.org/10.3390/rs61110750
Chicago/Turabian StyleOta, Tetsuji, Oumer S. Ahmed, Steven E. Franklin, Michael A. Wulder, Tsuyoshi Kajisa, Nobuya Mizoue, Shigejiro Yoshida, Gen Takao, Yasumasa Hirata, Naoyuki Furuya, and et al. 2014. "Estimation of Airborne Lidar-Derived Tropical Forest Canopy Height Using Landsat Time Series in Cambodia" Remote Sensing 6, no. 11: 10750-10772. https://doi.org/10.3390/rs61110750
APA StyleOta, T., Ahmed, O. S., Franklin, S. E., Wulder, M. A., Kajisa, T., Mizoue, N., Yoshida, S., Takao, G., Hirata, Y., Furuya, N., Sano, T., Heng, S., & Vuthy, M. (2014). Estimation of Airborne Lidar-Derived Tropical Forest Canopy Height Using Landsat Time Series in Cambodia. Remote Sensing, 6(11), 10750-10772. https://doi.org/10.3390/rs61110750





