Diurnal Dynamics of Wheat Evapotranspiration Derived from Ground-Based Thermal Imagery
Abstract
: The latent heat flux, one of the key components of the surface energy balance, can be inferred from remotely sensed thermal infrared data. However, discrepancies between modeled and observed evapotranspiration are large. Thermal cameras might provide a suitable tool for model evaluation under variable atmospheric conditions. Here, we evaluate the results from the Penman-Monteith, surface energy balance and Bowen ratio approaches, which estimate the diurnal course of latent heat fluxes at a ripe winter wheat stand using measured and modeled temperatures. Under overcast conditions, the models perform similarly, and radiometric image temperatures are linearly correlated with the inverted aerodynamic temperature. During clear sky conditions, the temperature of the wheat ear layer could be used to predict daytime turbulent fluxes (root mean squared error and mean absolute error: 20–35 W·m−2, r2: 0.76–0.88), whereas spatially-averaged temperatures caused underestimation of pre-noon and overestimation of afternoon fluxes. Errors are dependent on the models’ ability to simulate diurnal hysteresis effects and are largest during intermittent clouds, due to the discrepancy between the timing of image capture and the time needed for the leaf-air-temperature gradient to adapt to changes in solar radiation. During such periods, we suggest using modeled surface temperatures for temporal upscaling and the validation of image data.1. Introduction
Aircraft and satellite sensors operating in the thermal infrared (TIR) region of the electromagnetic spectrum provide spatially comprehensive information on the radiometric surface temperature (Trad), which is derived from the thermal radiation emitted by the different surface components within the sensor’s field of view. The diurnal and seasonal cycles of the surface temperature are affected by the relative efficiency of the components of the surface energy balance (SEB) in dissipating the available energy. Thus, SEB key components, such as the turbulent latent (λE) and sensible (H) heat flux, are frequently inferred from observations of the radiometric temperature over a wide range of spatial and temporal scales [1–12].
Trad is commonly applied as a proxy for the aerodynamic temperature (Taero), a theoretical temperature at the thermal roughness height, which satisfies the bulk resistance formulation for the sensible heat transport [13,14]. For real canopies, the quantitative relation between the radiometric and the aerodynamic temperature is, however, complex and not understood in detail, yet [11,12]. Ambient conditions and canopy characteristics affect both variables differently, and they may have high spatial and temporal variability [11,13,15]. Consequently, uncertainties introduce errors in H and λE estimates [12]. Errors tend to be large for surfaces with partial vegetation cover, stressed vegetation and vegetation undergoing seasonal changes [8,16–18]. Furthermore, TIR-based studies often show a clear sky bias, since studies are predominantly carried out under clear sky conditions. Ground-based data for validating remotely sensed surface temperatures under variable cloud cover are needed [9,19]. An understanding of the dynamic thermal adaptation of canopies, i.e., for the critical early and the late growth stages, will improve the interpretation of model behavior [20]. Ground-based TIR cameras, allowing for a high observation frequency and for studying the spatial variability of temperatures, independently from ambient conditions, might provide a suitable tool for such studies.
The latent heat flux (λE) is one of the important SEB components where major attention is needed to improve the agreement between different climate models [21]. In this study, we test the integration of temperatures derived from ground-based TIR imagery in three different single-source (which do not distinguish between soil evaporation and transpiration) evapotranspiration models (Bowen ratio, surface energy balance (SEB) and Penman–Monteith) for reproducing the diurnal course of λE. We use latent heat flux measurements provided by an eddy covariance (EC) station for validation. Models require data on net radiation, ground heat flux and standard meteorological parameters. In this study, we use micrometeorological observations from an eddy covariance station.
In particular, we aim to: (1) study the relation of the temperature of the different surface components (based on thermal infrared image, radiometer and thermocouple measurements) to the aerodynamic temperature derived from EC measurements; (2) test the suitability of the different model and temperature combinations to capture the diurnal cycle of the integrated latent heat flux from the soil and the canopy; and (3) study the effect of cloud cover on the temperatures and model results. Contrasting with radiation thermometer measurements, thermal imagery provides not only the range, but also the distribution and relative contribution of temperatures from different parts of the canopy. We hypothesize that such observations provide a deeper understanding of the performance of different algorithms under variable ambient conditions and help to explain model deviations from the reference flux measurements.
2. Material and Methods
2.1. Research Site and Vegetation
The Merzenhausen research site was established by the Collaborative Research Center TR32 [22]. The site is located at 93 m a.s.l. (50°55′47″N, 06°17′47″E) in the intensively agriculturally used area around Jülich (Germany) with a temperate climate [23]. The mean annual air temperature is 10.2 °C, and the mean annual precipitation sum is 825 mm [24]. Measurements are performed from 19 July to 24 July 2012. The observed area, located within a 200 m by 360 m-wide field, is cropped with winter wheat (Triticum aestivum L. cv. Tobak; sowing density: 360 plants·m−2). Non-destructive LAI measurements (cf. Section 2.5) indicate an average leaf area index (LAI) of 4.0 (ranging from 3.3 to 5.4) and a vegetation height of 0.87 m (ranging from 0.84 to 0.9 m) during the measurement period. The observed winter wheat is in the stage of ripening (kernel formation completed) with the flag leaves being partly senescent, indicating that the bottom of the crop canopy is senescent [25] and that the plants are reaching maturity [26]. The underlying soil texture is classified as silt loam. The field was harvested on 2 August.
2.2. Experimental Set-Up
We mounted a FLIRA315 thermal imaging camera (FLIR Systems Inc., Wilsonville, OR, USA), sensitive at wavelengths of 7.5–13 μm, in a weatherproof housing at a height of 2.2 m over the soil surface. The accuracy reported for the camera is ±2 °C with a thermal sensitivity < 0.5 °C. Based on the results from preliminary field studies, the camera is tilted 36° below a horizontal line. The tilt angle was chosen to avoid the major influence of the soil on remotely sensed surface temperatures of a row-structured canopy with an erectophile leaf angle distribution. The camera’s field of view (FOV, 25° × 18.8°) is pointed towards the SE, observing an area of 1 m × 1 m (Figure 1). Images (16 bit, 320 × 240 pixels) are captured at a five-minute time interval. The camera is connected to a fanless embedded box PC (Bressner Technologies, Gröbenzell, Germany) running the control software (IRControl, Automation Technology, Bad Oldesloe, Germany).
2.3. Reference Temperature Measurements
The set-up for obtaining reference leaf temperatures consists of four type T (temperature) copper-constantan thermocouples with Teflon insulation (Omega Engineering, Stamford, CT, USA) connected to a temperature data adapting device (RedLab TEMP, Meilhaus Electronic, Alling, Germany). The sensors are attached to the lower side of winter wheat leaves using semi-permeable tape. The typical and the maximum error for the thermocouple measurements (including the error for the cold junction compensation sensor) are ±0.26 K and ±0.71 K, respectively. An infrared radiometer (Apogee SI-121, Apogee Instruments, Logan, UT, USA), sensitive at wavelengths of 8–14 μm (with a FOV of 18°), is mounted directly below the infrared camera housing and connected to a data logger (Combilog, Theodor Friedrichs & Co., Borgfelde, Germany). Using the same inclination as for the camera, it records the radiometric surface temperature of an area measuring 1.2 m in maximum length and 0.9 m in maximum width. The accuracy reported for the infrared radiometer is ±0.2 K (for object temperatures between −30 °C and +65 °C).
2.4. Thermal Image Data Processing
We calculated the percentage area contribution of the different surface components to the total image area by means of an unobserved K-means classification (ENVI software, Research Systems Inc., Boulder, CO, USA) of manually selected daytime and nighttime images. Wheat ears (Class I) cover 30%, mixed stem and leaf surfaces (Class II) 44% and the sum of deeper shaded areas and underlying soil (Class III, describing the background) 26% of the image. We manually selected image pixels corresponding to the surface Classes I and III and, using the software, IRControl (Automation Technology, Bad Oldesloe, Germany), derive the corresponding temperature values (Class I, Trad,WE; Class III, Trad,BG) for each time step. The temperature corresponding to Class II (Trad,mean) is assumed to be represented by the average image temperatures. This is motivated by the fact that stem and leaf surfaces form the largest area in the scenes and that their temperatures are usual identical to the average. Thermal infrared (8–14 μm) emissivity values between 0.93 for sparse canopies (including the effect of the underlying soil) and/or drier vegetation and 0.99 for dense, healthy vegetation canopies (with cavities trapping the radiation) have been reported [13,27–30]. Generally, the thermal emissivity of vegetation is assumed to be higher than 0.95 [30,31]. Considering the partly senescent leaves and the high fraction of dry wheat ears in the images, we apply an emissivity of 0.95 (the mean value of reported values, the lowest boundary reported for the thermal emissivity of vegetation). The applied linear spatial averaging of temperatures is less accurate than a retrieval of raw thermal emission for each pixel. However, since the manufacturer’s software does not provide radiances, we are confined to this procedure. The software corrects for the so-called “background radiation” (emitted by the surrounding objects and further reflected by the object) and the radiation emitted by the atmosphere. Considering the relatively high emissivity of the canopy and, consequently, the small effect of the background radiation on temperature estimates, the “background” or “reflected temperature” was approximated using measured air temperatures. The atmospheric transmission along the observation path is calculated by providing measured air temperature (in 5 °C intervals ranging from 5 °C to 30 °C) and relative humidity values (35%, 60%, 80%, 90% and 95%) from standard meteorological measurements for each image. Differences between the raw and the temperature- and humidity-corrected temperature values range up to ±1.5 K. We extracted the surface temperatures corresponding to the surface components (Trad,WE, Trad,BG) and the image mean (Trad,mean), minimum (Trad,min) and maximum temperatures (Trad,max). For the purpose of this study, to model the turbulent latent heat flux measured by eddy covariance (EC) instruments, half-hourly average values are computed.
2.5. Ecosystem Gas Exchange, Canopy Architecture and Meteorological Data
A micrometeorological station with turbulence sensors for measuring CO2 and H2O fluxes by the eddy covariance method is permanently located near the center of the wheat field, at a distance of approximately 12 m to the IR camera setup. Horizontal and vertical wind velocity are measured by a sonic anemometer (CSAT3, Campbell Scientific, Logan, UT, USA). CO2 and H2O concentrations are measured using an open-path infrared gas analyzer (LI7500, LI-COR, Lincoln, NE, USA) at a measurement height of 2 m [32]. Ground heat flux is measured by means of heat flux plates (Hukseflux Thermal Sensors B.V., Delft, The Netherlands) located at depths of 0.02–0.06 m and repeated measurements of near-surface heat capacity density (KD2 pro, Decagon, Pullman, WA, USA) [23]. Net and global radiation is measured with a net radiation sensor (NR-Lite, Kipp & Zonen, Delft, The Netherlands). Details on instruments, footprint analyses, data processing and quality filtering for estimating the turbulent latent and sensible heat fluxes are given in [24,32,33]. All data are aggregated to 30-min intervals. Field measurements of the Leaf Area Index (LAI) and canopy height were performed on 23 July. Nondestructive LAI measurements are obtained using a SunScan Canopy Analysis System (Delta T Devices, Cambridge, U.K.). For obtaining representative field estimates, the data from eight plot measurements are averaged to mean values. The cloud fraction (CF) is provided by a Total Sky Imager (TSI 880, YES Inc., Turners Falls, MA, USA) located at the Jülich Observatory for Cloud Evolution (JOYCE) located approximately 8 km from the research site. To test for inconsistencies in cloud cover between both sites, we investigate TSI images for the difference, ΔCF, of CF estimates in the sector towards Merzenhausen compared to the fraction around Jülich. The cloud fraction is determined from the images at an elevation of 30°, thus with a cloud base height at ∼2 km, giving information on CF at a distance of ∼4 km. The 10th and 90th percentiles of ΔCF lie at −0.12 and 0.14, respectively, indicating that most of the time CF towards Merzenhausen did not deviate by more than one octa from that observed at Jülich. During intermittent cloud cover, 80% of the ΔCF lies within −0.12 to 0.32 compared to −0.02 to 0.13 for clear sky and −0.02 to 0.05 for overcast conditions. We further compare daytime half hour averages of global radiation measured at Jülich and at Merzenhausen during the observation days. Differences (ΔG) can be as large as −140 W·m−2 and 220 W·m−2 for single half hour averages, in general; however, ΔG is much smaller, with 80% lying within the interval −31 to 63 W·m−2 and 50% in the interval −8 to 30 W·m−2. Differences are, as expected, largest during intermittent cloud cover (0.2 < CF < 0.8), with 80% of ΔG within −69 to 79 W·m−2, and smaller during overcast (−49 to 34 W·m−2) and clear sky (−17 to 35 W·m−2). Thus, radiation differences are, most of the time, much smaller than global radiation, and we therefore believe that the CF determined in Jülich is a sufficiently good estimate for Merzenhausen.
2.6. Latent Heat Flux Modeling Approaches
In this case study, three different evapotranspiration algorithms are evaluated (Table 1, [34–43]), which are commonly used to infer surface energy fluxes from thermal infrared images: (a) the surface energy balance-based approach (“SEB”); (b) the Bowen ratio energy balance-based method (“Bowen ratio”); and (d) the “Penman-Monteith” equation; in addition, we use modeled surface temperatures in the SEB-based calculation ((c) “T modeled”).
The surface energy budget, measured by the micrometeorological instruments, is usually not balanced. The evaluation of the energy balance closure was beyond the scope of our study. However, to avoid an effect of the residuum on model evaluations, we subtract it from the measured net radiation and derive the corrected net radiation Rnc (W·m−2):
2.6.1. Modeling Approach (a) “SEB”
The bulk aerodynamic or surface energy balance (SEB) method uses the bulk resistance formulation for the sensible heat flux (H, W·m−2), which is based on the near surface gradient of temperatures at the surface (Taero, °C) and the atmosphere (Tair, °C) [46]. The radiometric temperature (Trad, °C) can be used as a proxy for the aerodynamic temperature Taero [40]:
For Ri < −0.008 and Ri > 0.008, the aerodynamic resistance is calculated from:
To study the agreement between the unknown aerodynamic (Taero) and the remotely sensed surface temperature, we inverted the bulk formulation for the sensible heat flux using the sensible heat flux derived from eddy covariance measurements to compute the “inverted aerodynamic temperature” (Taero,inv) [49].
2.6.2. Modeling Approach (b) “Bowen Ratio”
The Bowen ratio energy balance method is a widely used micrometeorological method to estimate latent heat fluxes because of its simplicity and robustness [50,51]. At the ground level, it has been applied routinely to estimate latent and sensible heat fluxes for various land surface types, such as water, grassland, crops or forests [52]. However, with the increasing availability of atmospheric water and temperature profiles at larger scales (e.g., using polar orbiting satellite systems, like the Atmospheric Infrared Sounder (AIRS)), its application to satellite-based estimates of λE becomes feasible, as demonstrated by [53]. No information on surface characteristics is needed. The method is based on a rearrangement of the surface energy balance and the theory of the flux-gradient relationship [35]. For the calculation, humidity and temperature observations from two different heights, net radiation and ground heat flux estimates are required. The approach is based on the assumption of the similarity of the eddy diffusivities of heat and water vapor and of a balanced energy budget. Assuming that the net horizontal advection of energy can be neglected, we apply the simplified version to compute the Bowen ratio β and the latent heat flux as follows:
2.6.3. Modeling Approach (c) “T Modeled”
Approach (c) is similar to (a), but based on modeled surface temperatures (Tmodeled) instead of Trad. We applied the modified version of the Todorovic approach [54], suggested by [38], to derive Tmodeled. The Todorovic model is based on the assumption that the additional energy needed by the water vapor flux to overcome the stomatal resistance (rs) leads to a decrease in λE, which is balanced by an increase in the amount of H [37]. Thus, the additional H component describes the difference in energy needed for the water vapor flux at “wet” conditions (rs = 0) to the energy needed at actual conditions (rs > 0). The additional amount of energy leads to an increase in the canopy temperature (t, °C), causing a small increase in the sensible heat flux. The modified equation [38] includes the response of the stomatal conductance to the VPD [55]:
Accordingly, the canopy temperature at potential evapotranspiration TCp (°C) can be derived from:
The actual canopy temperature, Tmodeled, is computed by:
Subsequently, using Tmodeled, the actual sensible heat flux is derived from the bulk formulation of the sensible heat flux (Equation (2)), and the latent heat flux is derived from the SEB (Equation (7)), as described for (a).
2.6.4. Modeling Approach (d) “Penman-Monteith”
By combining energy balance and mass transfer approaches, the Penman–Monteith (PM) equation [41,60] allows for computing evaporative fluxes from standard meteorological data. An important scaling parameter of the PM equation is the surface resistance term, rC (s·m−1), describing the (bulk) canopy resistance that controls the transfer of water vapor from the leaves within the canopy to the surrounding air. This term can be derived from the canopy surface temperature. For computing rC, the following equation is applied [38,61]:
Subsequently, the latent heat flux is derived from the Penman-Monteith (PM) equation [39,41]:
2.7. Data Analyses and Model Error
Modeling and data analyses are performed using the R statistical programming language [62]. The latent heat flux measured by the EC instruments is used as a reference data set. The root mean square error (RMSE) is based on the sum of squared errors and commonly applied in climatological studies as a measure of the goodness of predicted values compared to the reference data values. Because the RMSE is sensitive to outliers, its interpretation can be misleading [63]. However, for comparison with the results from other studies, we computed the RMSE:
For estimating the overall precision of predicted latent heat fluxes, the mean absolute error (MAE), describing the absolute deviation of the modeled from measured data values with positive signs for both over- and under-estimations, is calculated as:
3. Results and Discussion
3.1. Ambient Conditions and Surface Temperatures
Micrometeorological data and the components of the surface energy balance (Figure 2) demonstrate the transition from cloudy conditions with occasional rainfall (19–21 July) to clear sky conditions with large temperature amplitudes (22–24 July). The similarity of the latent heat flux (λE) and the sensible heat flux (H) diurnal amplitudes indicate progressing senescence of the wheat plants [64] and hints at the progressing depletion of available soil water [65]. Daytime evaporative fractions, defined as the ratio of λE to available energy (Rn-G) [66], range from ∼0.3 to 0.5 during clear sky conditions (22–24 July) and from ∼0.4 to 0.8 during cloudy conditions (19–21 July) and show the typical parabolic shape during the diurnal cycle [67]. The horizontal wind speed was low to moderate (∼2 m·s−1) at reference height z (2 m), with the highest (∼5 m·s−1) and lowest (∼ 1 m·s−1) maximum daytime values recorded on 19 July and 22 July, respectively (Figure 2). Dew point temperature calculations indicate that dew was likely during morning hours on 22 July. Image-based surface temperatures (Trad) range from 3.4 °C to 36.4 °C with a mean value of ∼17 °C (Table 2) and a standard deviation of ∼6 °C. The infrared radiometer and the thermocouple records indicate a slightly smaller temperature range (3.9 °C to 28 °C and 4.7 °C to 30.1 °C, respectively). The statistics of Trad,WE and Trad,BG demonstrate differences in the thermal response, such as a higher thermal conductance of ripe wheat ears and dry leaves in the upper canopy layer, causing a faster response to changes in net radiation and a larger temperature amplitude, compared to the soil and deeper canopy layers (Table 2).
Pronounced daytime warming and nighttime cooling of the wheat ears (compared to Trad,BG) are demonstrated in the sample images (Figure 1). The image-based maximum temperatures clearly exceed those recorded by thermocouples (maximum temperature differences of +10 °C between Trad,max and Tleaf on July 22), whereas the spatially integrated temperatures from the radiometer are significantly lower than Tleaf, i.e., at night (Figures 2 and 3). Image-based surface temperatures generally exceed air temperatures (Tair) by 2 °C–3 °C (cloudy days) up to 5 °C (clear days), but around sunset and at night (Figure 2b).
Few studies examined the response of ear temperatures to ambient conditions [68–70], despite their major contribution to the upper canopy layer in agricultural areas for several weeks. It was shown that spike temperatures of non-irrigated cultivars can exceed ambient air temperatures after having reached physiological maturity by up to 10 °C [68]. Their position ensures that they receive a minimum of shading; thus, they are the major structures for absorbing light. Further, they have a low surface area-to-volume ratio, thus a limited ability to dissipate heat. We are, however, aware that uncertainties in the derived temperature values due to the surface thermal emissivity, changes in the reflective temperature (cf. Section 2.4) and the sun-sensor geometry have to be considered. The reflectivity of ripe wheat ears is high, resulting in a low absorption of net radiation. We account for senescent parts of the canopy by applying a comparable low emissivity value (ɛ = 0.95). However, the emissivity of dry leaves can be even lower [71], causing an underestimation of calculated surface temperatures. Furthermore, studies report decreasing radiometric temperatures at oblique viewing angles [72]. Directional effects are, however, dependent on incident radiation (by modifying the contribution of observed sunlit and shaded leaves), the LAI and leaf angle distribution parameters [6].
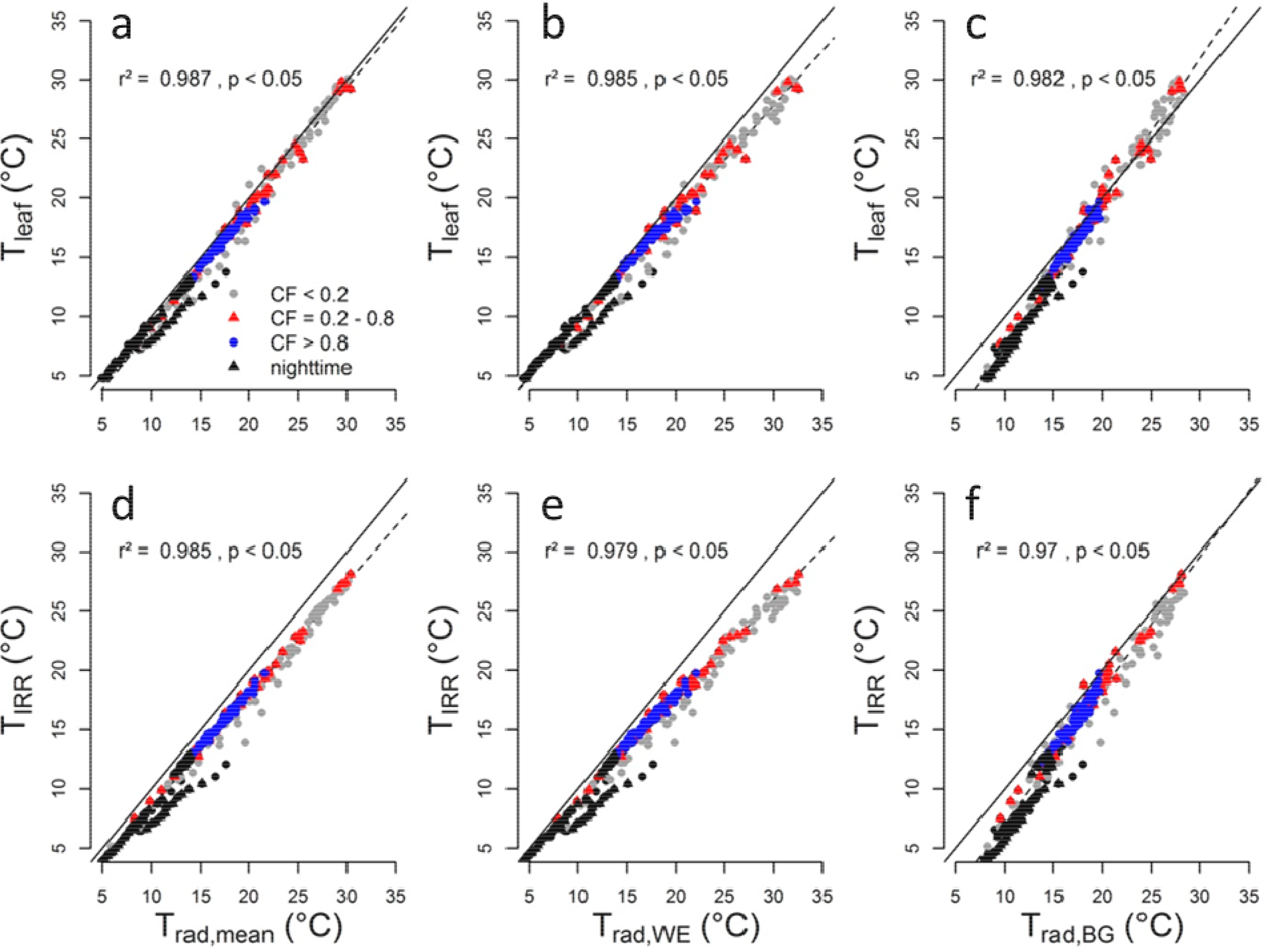
Despite these uncertainties, the correlation between image, point and spatially integrated temperature data is high. The highly linear correlation between Tleaf and Trad,mean (Figure 3a) indicates that the assumed emissivity, temperature and humidity corrections applied during image processing (cf. Section 2.5) are correct. Comparison of TIRR with Trad,mean (Figure 3d) shows an offset of about −1 °C and a slope of ∼0.96. As both measurement rely on the same physical principle, the differences should be negligible. They could be caused by small differences in the field of view and different correction algorithms (cf. Section 2.5). However, the most likely reasons are: (1) the default assumption of an emissivity of one for the derivation of TIRR; and (2) the immanent spatial averaging of radiation in the radiometer. The latter may lead to different results than arithmetically averaging temperatures from a camera image, as thermal radiation is not linearly related to the temperature. The inconsistency between TIRR and Trad,mean leads to equivalent offsets and smaller slopes in the relation between Trad,WE and Trad,BG to TIRR (Figure 3e,f) compared to the relation to Tleaf (Figure 3b,c). Linear regression fits show an increasing divergence at higher and lower temperature values (Figure 3) and for the nighttime data. Trad,WE is higher at temperatures ≥ 20 °C and Trad,BG lower at temperatures ≤ 15 °C compared to Tleaf and TIRR. Cloud cover has a low impact on the relation between measured temperatures (Figure 3); however, as expected, under overcast sky conditions (CF > 0.8), the linearity is highest and the temperature range is smallest.
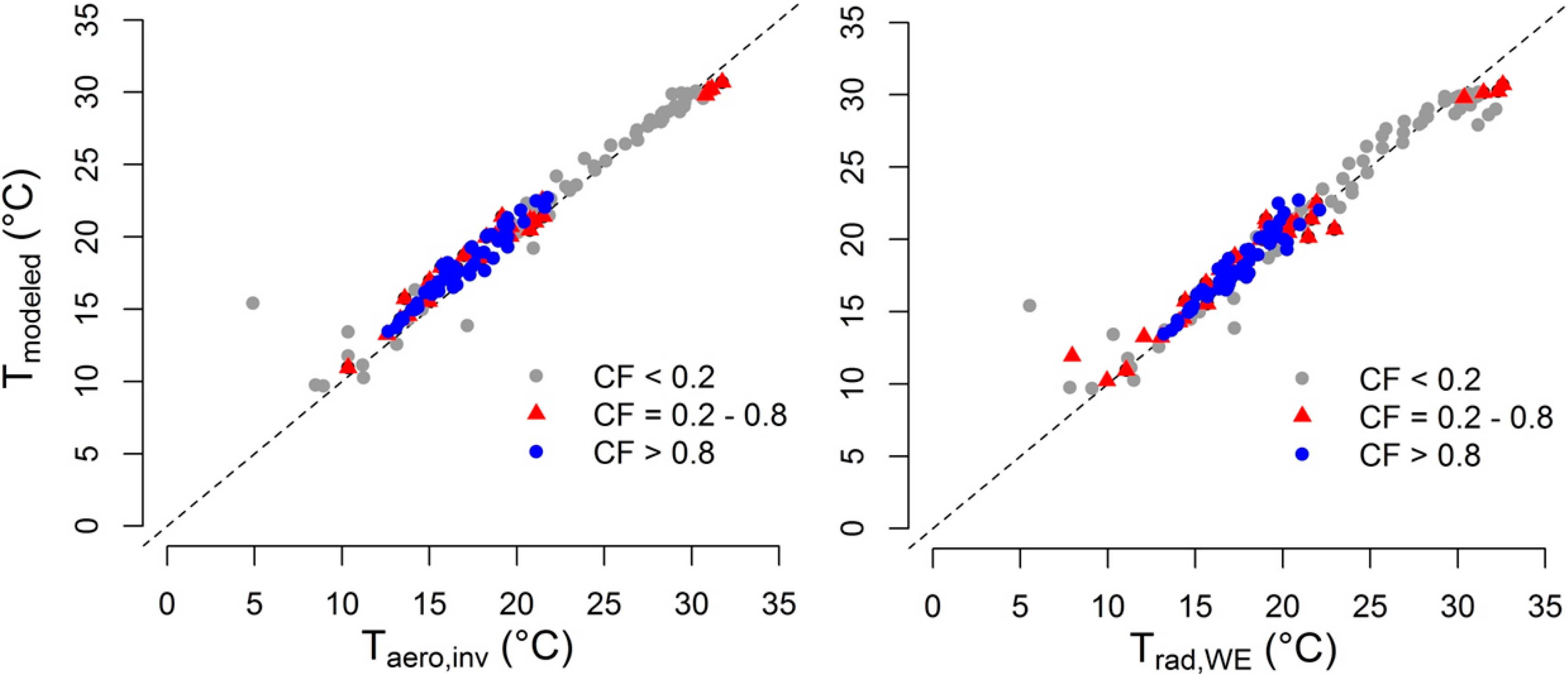
3.2. Radiometric Surface Temperatures versus the Inverted Aerodynamic Temperature
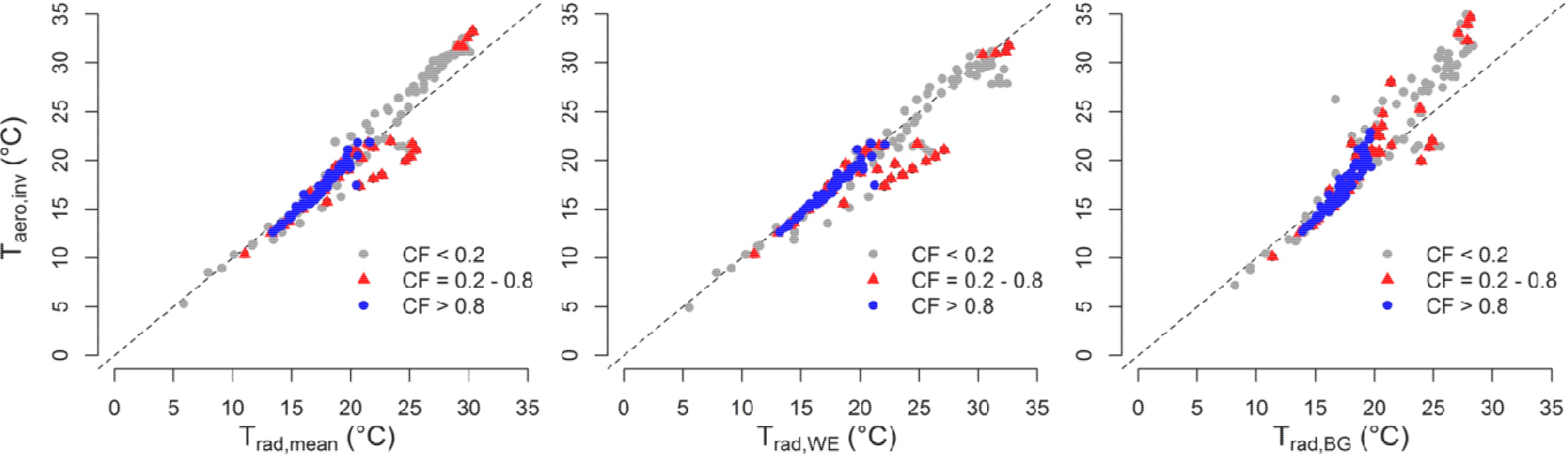
During overcast conditions (cloud fraction > 0.8) and for temperatures below ∼20 °C, the image-based temperatures are linearly related to the inverted aerodynamic temperature (Taero,inv, cf. Section 3.1), indicating a high suitability of Trad to predict the corresponding turbulent sensible heat flux (Figure 4). Trad,WE, receiving a maximum of solar radiation, responds faster to changes in net radiation than Trad,mean and Trad,BG. As a consequence, Trad,WE is more strongly correlated to Taero,inv at temperatures > 20 °C and during clear sky conditions (CF < 0.2), whereas Trad,mean and Trad,BG are underestimating Taero,inv (Figure 4). As a consequence, for the current viewing geometry and the applied emissivity and background temperature settings (cf. Section 2.4), Trad,WE is more suitable to predict the turbulent heat fluxes, giving preference to the use of a single surface component over spatially-averaged temperatures during such periods. Contrastingly, under overcast conditions, the use of spatially-averaged temperatures, based on thermal camera imagery, performs similar. Note that awnless ears (as in this study) respond more rapidly to changes in incoming radiation [73], whereas the presence of awns can cause a different microclimate around the canopy [74,75], restricting a generalization of our observations. Scatter plots indicate the weakest correlation of Trad and Taero,inv during intermittent clouds (Figure 4) when Trad,WE and Trad,mean mostly exceed Taero,inv (cf. Section 4.2.3). This can be related to the occurrence of frequent outliers. The most likely cause for these outliers is the occurrence of sunny intervals, which cause rapid fluctuations of turbulent fluxes in response to changes in available energy. Simultaneously, a rapid increase of leaf temperatures is induced, which depends on the plant-specific time constant for thermal equilibration [76]. This is, however, not captured using 30 min-averaged surface temperatures (raw data obtained at a resolution of 5 min). The timing of thermal image capture affects the suitability of derived Trad values to predict the measured flux data, which highlights the need for longer continuous observations to capture near-steady-state canopy temperatures and resulting temperature gradients [77–79]. Consequently, especially the relation between Taero,inv and Trad,WE is nonlinear during intermittent clouds (Figure 4).
3.3. Suitability of Model-Temperature Combinations to Predict Sub-Daily λE Dynamics
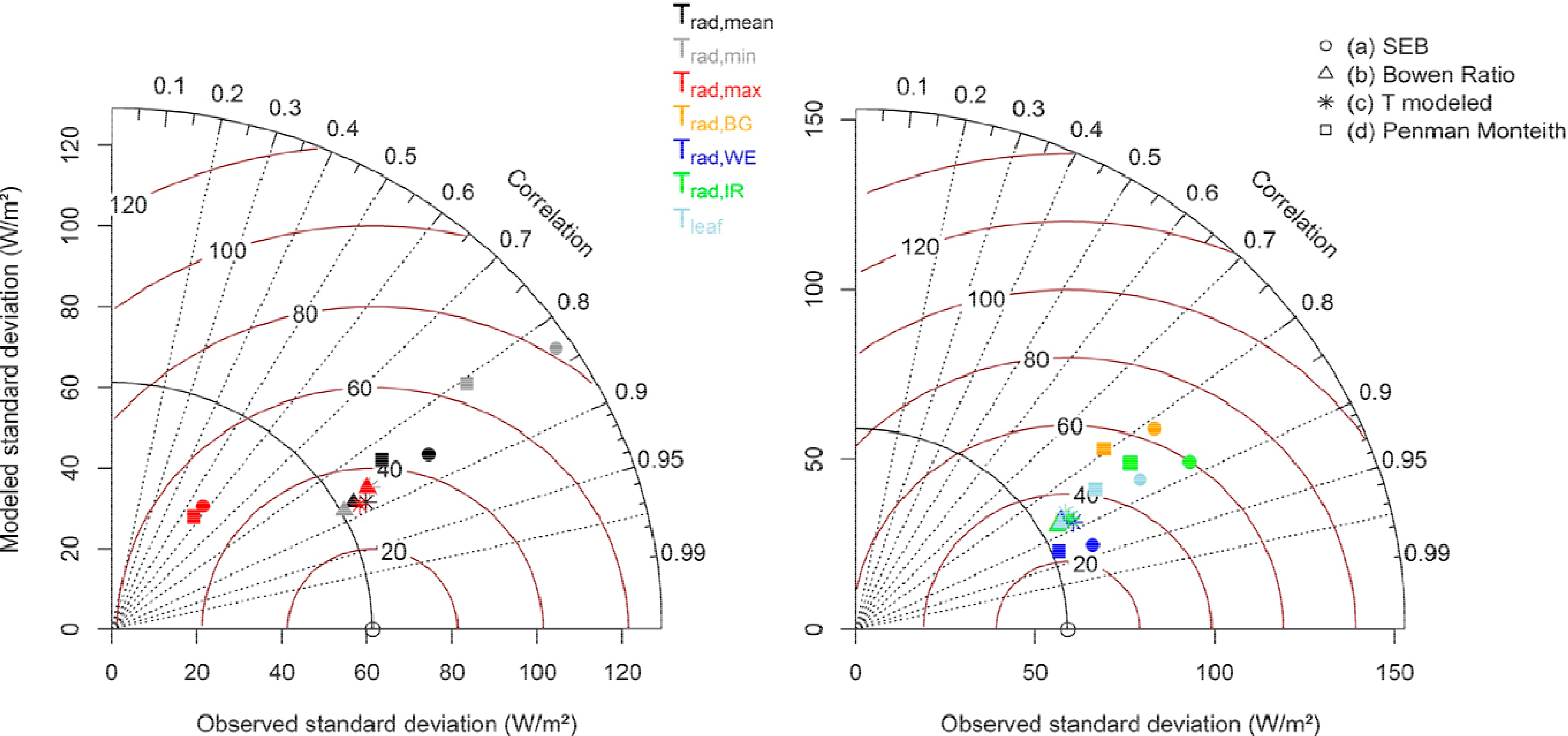
The Taylor diagram [80] graphically summarizes how closely the predicted values match the observed values in terms of their correlation, RMSE and standard deviation (Figure 5). Nighttime data is excluded from the diagrams to account for the uncertainty of nocturnal EC flux measurements. The EC technique measures the turbulent transfer of heat and water vapor from the soil and the canopy integrated over the footprint area of the eddy covariance tower. Thus, the unknown contribution of soil evaporation to the total latent heat flux restricts the use of EC-based observations as validation data for evapotranspiration models, which are based on canopy surface temperatures (as in this study). Further, the uncertainty caused by the forced energy balance closure has to be taken into account (adjusted available energy, cf. Section 2, Equation (1)). The diagram clearly shows that measured latent heat fluxes are most accurately simulated when using Trad,WE, describing the temperature of wheat ears. These results agree with the finding on the linear correlation between Trad,WE with Taero,inv (cf. Section 3.2).
On the one hand, this is related to the fast response of wheat ears to solar radiation (cf. Sections 3.1 and 3.2). On the other hand, there might be physiological reasons, related to soil water availability, for these findings, as described in the following text. During the observation period, the overall variability of soil water content is low; however, the fraction of available water (fAW) decreases to values < 50% (with fAW defined as the ratio of the difference between measured volumetric soil water content (SWCvol) and SWCvol at the wilting point to the difference between SWCvol at field capacity and SWCvol at the wilting point). For a winter wheat stand in China, [81] found that at an fAW below 50%, the plants experienced “water stress”, and stomatal conductance (gc) was decreasing linearly with fAW. Reports on the overall contribution of ear activity differ [82–84]. However, it was shown that the rate of ear photosynthesis can exceed that of the flag leaf, especially under water stress conditions [83,85]. Thus, under the observed moisture and phenological conditions, ears probably remain active for a longer time period and maintain a higher water content than flag leaves [84,86,87]. These studies give further reason to our findings on the suitability of ear temperatures to model turbulent fluxes during the observation period.
RMSE and MAE for the complete data set and for different subsets (nighttime: 21.00 h–03.00 h UTC, daytime: 6 h–18.00 h UTC, cloud fraction ≥ 0.8, cloud fraction ≥ 0.2–0.8, cloud fraction < 0.2) are computed (Tables 3 and 4). Calculated errors using Trad,WE and Trad,mean (20–35 W·m−2) are well below the values published for other studies (∼30–80 W·m−2, see [3,4] for recent reviews and [88–92] for studies using ground-based data) and below the range of errors reported for eddy covariance (EC) measurements [42], which are here used as reference data. The highest errors (up to 90%) in latent heat flux estimates (using the surface temperature to predict the sensible heat flux) have been reported for natural semiarid areas [8]. Most studies have been performed using aircraft or satellite data [4], thus restricting a comparison to our results. Further, it is worth noting that most TIR-based model evaluation studies exclude data from periods with higher fractions of cloud cover.
The results from the approaches “Bowen ratio” (b) and “T modeled” (c) show high correlation and low RMSE values and are insensitive to the input temperatures (Figure 4, Tables 3 and 4), providing robust estimates of evapotranspiration. Results suggest further investigation of the use of the Bowen ratio method for large-scale flux observations [53], despite its limitations due to the underlying assumptions [35,43]. Note that we accounted for the residual of the energy balance closure, which leads to inaccuracies of the Bowen ratio method.
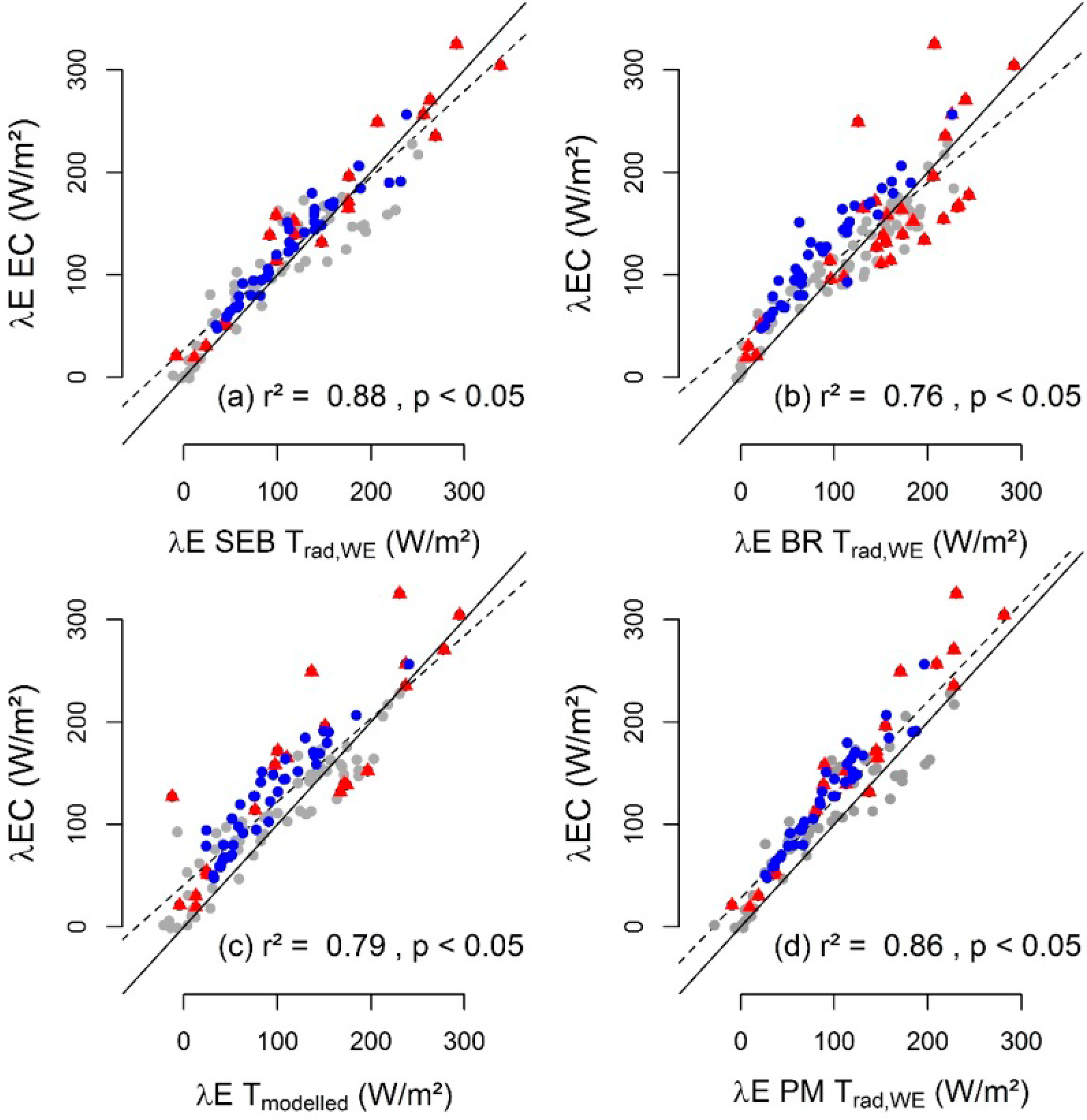
The approaches “Penman-Monteith” (d) and “SEB” (a) are more sensitive to the input temperature, especially during intermittent cloud cover and clear sky conditions. However, when parameterized with Trad,WE, the “Penman-Monteith” (d) and “SEB (a) algorithms show the lowest errors (RMSE and MAE ∼ 20, Table 3) and the highest coefficient of determination values of the linear regression fits (r2 = 0.83–0.85 (daytime data), Figure 6).
3.4. The Impact of Cloud Cover on Model Results
RMSE and MAE are highest during intermittent clouds (cloud fraction ≥ 0.2–0.8), with the RMSE values nearly doubled. This can be related to the occurrence of frequent outliers during sunny intervals (Figure 6, cf. Section 3.2) and the limited ability of images taken at specific intervals (5 min in this study) to capture rapid fluctuations of turbulent fluxes. The differences between the MAE for different cloud conditions are lower compared to those of the RMSE (Tables 3 and 4). This indicates that the models’ ability to resolve the diurnal cycle, rather than the ability to simulate the absolute flux magnitude, is diminished, the latter being more critical for temporal upscaling. Note that, resulting from the distance between the sensor and study site (cf. Section 2.5), the highest uncertainty in cloud fraction estimates occurs during intermittent cloud cover. Such inconsistencies in cloud fraction data might contribute to model errors during such periods.
This case study demonstrates the complex and interrelated effects of model structure, input temperature and cloud cover on modeled fluxes. Errors in land surface models’ to resolve sub-diurnal patterns of transpiration are often related to their diminished ability to simulate the natural diurnal hysteresis [93]. We hypothesize that the results demonstrate the model and surface temperature-specific ability to reproduce such hysteresis effects, which are strongly affected by local cloud cover. At the observation scale, the phase angle difference between VPD and net radiation causes a phase angle difference between VPD and latent heat flux [94]. Hysteresis arises from the well-known asymmetry between morning and afternoon data: for a given VPD in the morning, the stomatal conductance is higher compared to the afternoon, producing a clockwise rotation in the hysteresis curve (Figure 7). The decreasing slope at VPD values ≥ 1.5 kPa indicates the initiation of stomatal closure, giving reason to the value applied for VPD0 in Equation (10) (cf. Section 3.3). Generally, all models capture the hysteresis effect (Figure 7). The surface temperature integrates information on stomatal closure causing a similar hysteresis effect for Trad and latent heat fluxes. The diurnal variability of this effect (and the resulting half-hourly magnitude of the hysteresis) is, however, reproduced best by those models that explicitly use VPD data (Bowen ratio, T modeled and Penman-Monteith), highlighting its importance on the partitioning of available energy during the stage of crop maturity. A sample diurnal course of the hysteresis between VPD and latent heat fluxes shows the overestimation of afternoon fluxes, i.e., for the SEB approach, followed by the Penman-Monteith equation (Figure 7). These observations explain the lower performance of the SEB and the Penman-Monteith approach during clear sky conditions (where VPD becomes relevant and stomatal closure can be initiated), as demonstrated in the RMSE and MAE statistics (Tables 3 and 4). Under prevailing moisture conditions and for the current plant physiological stage, using Trad,WE allows capturing these effects, whereas image-averaged temperatures (Trad,mean, TIRR) underestimate pre-noon and overestimate afternoon fluxes during clear sky conditions.
The strong effect of the interrelations between model structure and cloud cover restricts the validity of our findings and highlights the need for longer time series obtained under variable cloud cover and for different plant phenological stages to study the performance of model and input temperature combinations. During the six observation days, fluxes are mainly driven by radiation. Adjusting the net radiation for energy balance closure minimizes errors for approaches that derive the latent heat flux as the residual from the energy balance (SEB approach). Therefore, error statistics shown have to be interpreted carefully. Further, note that errors that arise from the Sun-sensor geometry and the anisotropic behavior of thermal emission (i.e., during clear sky conditions) are not quantified. The fraction of the sunlit or and shaded side of the wheat ears seen by the sensor changes during the diurnal cycle [95]. More generally, average climate site conditions and genotype-specific characteristics, such as the leaf water content, stomatal behavior, morphological traits, the presence of awns, canopy structure and phenological stage, strongly affect leaf and canopy temperatures. Thus, a generalization of observed temperatures and model results is strongly limited. On the other hand, such genotype-specific characteristics allow for using thermal imagery as a tool for observing plant response to stress as part of non-invasive phenotyping approaches [96].
Results from our study contribute to the overall understanding of evapotranspiration model behavior for variable cloud cover conditions, when parameterized with remotely sensed surface temperatures. With increasing variability of precipitation and availability of water in the future, more comparative studies on model-specific abilities to accurately quantify evapotranspiration are needed. The integration of surface temperatures in large-scale estimates of the water balance, especially for irrigation purposes, has been used for several years. However, the availability of affordable ground-based thermal imagers and processing software has increased the possibilities of using such images to study plant response to stress and its impact on turbulent fluxes from a canopy [92]. In the framework of currently developing plant phenotyping networks (e.g., the European Plant Phenotyping Network (EPPN) [97], the significance of studying canopy temperatures has been recognized. We suggest using ground-based thermal image time series of a variety of plant types and under field conditions to further evaluate the suitability of surface temperature-evapotranspiration model combinations to quantify sub-diurnal dynamics of the water balance.
3.5. Modeled Surface Temperatures
Results from the modified Todorovic approach (“T modeled” (c)) [49] outperform most approaches, i.e., with respect to modeled standard deviations (note that the position in the Taylor diagram slightly changes due to the influence of surface temperatures on the aerodynamic resistance. This indicates the superiority of modeled surface temperatures (T,modeled) over observed temperatures (Trad) during certain time periods. Tmodeled is closely related to the inverted aerodynamic temperature; however, it overestimates this during the day (Figure 8), causing an overestimation of the daytime sensible heat flux. The linear regression fit between modeled and measured daytime (6 h–18.00 h UTC) λE shows the resulting consequent underestimation of measured latent fluxes (Figure 6, MAE ∼ 25 W·m−2). Since Tmodeled are calculated from micrometeorological data with the raw values obtained at a very high temporal resolution, they are more suitable to capture nonlinear processes and short-term fluctuations. This is the most likely reason for the high agreement between modeled and measured standard deviations found for the “T modeled” (c) approach. We suggest using modeled temperatures for validating thermal infrared data obtained at a lower temporal resolution (given the availability of meteorological data in an adequate temporal resolution).
4. Conclusions
In this study, we demonstrate the potential and the limitations of ground-based thermal images to study the behavior of single-source evapotranspiration models under variable cloud cover, when parameterized with remotely sensed surface temperatures. At a ripe winter wheat stand, the models performed best at resolving the evapotranspiration diurnal cycle when parameterized with the temperature of the wheat ears (root mean squared error and mean absolute error between modeled and measured fluxes: 20–35 W·m−2, r2: 0.76−0.88) and if integrating vapor pressure deficit data to account for natural hysteresis effects. Under clear sky conditions and for the prevailing site characteristics, which cause strong temperature differences between the different canopy layers and the soil, the simulation and the upscaling of turbulent fluxes can benefit from single-surface component temperatures. In contrast, under overcast conditions, spatially-averaged data provide similar model results. Large errors during intermittent clouds are related to the timing of thermal image capture, which affects the ability of derived surface temperatures to capture steady-state conditions of temperature gradients and causes a nonlinear relation between image-based radiometric and the aerodynamic temperature. Under such conditions, the use of discontinuous small-scale measurements to predict the complex, nonlinear processes of the surface energy balance is strongly limited, and consequently, the use of temperature-robust models is required. This further implicates that, for the temporal upscaling and the validation of remotely sensed surface temperatures, modeled temperatures based on standard meteorological data are more suitable. For future studies, we suggest using image time series obtained under a large range of environmental conditions and for a variety of plant types to further evaluate the performance of different surface temperature-model combinations to quantify sub-diurnal dynamics of the water balance and to study plant responses to abiotic stress.
Acknowledgments
We gratefully acknowledge financial support by the Transregional Collaborative Research Centre (SFB/TR) 32 “Pattern in Soil-Vegetation-Atmosphere Systems: Monitoring, Modelling and Data Assimilation” funded by the Deutsche Forschungsgemeinschaft (DFG). The authors would like to thank the IGB 2 Ecosystem Dynamics Research Group at Forschungszentrum Jülich GmbH (Germany) for technical support.
Author Contributions
Rainer Haseneder-Lind and Hella Ellen Ahrends designed and performed the experiments; Anja Stadler and Jan H. Schween contributed data and analyses tools; Hella Ellen Ahrends, Susanne Crewell and Uwe Rascher performed the analyses and the interpretation of the results; Hella Ellen Ahrends wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ 2012, 122, 50–65. [Google Scholar]
- Courault, D.; Seguin, B.; Olioso, A. Review on estimation of evapotranspiration from remote sensing data: From empirical to numerical modeling approaches. Irrig. Drain. Syst 2005, 19, 223–249. [Google Scholar]
- Glenn, E.P.; Doody, T.M.; Guerschman, J.P.; Huete, A.R.; King, E.A.; McVicar, T.R.; van Dijk, A.I.J.M.; van Niel, T.G.; Yebra, M.; Zhang, Y. Actual evapotranspiration estimation by ground and remote sensing methods: The Australian experience. Hydrol. Process 2011, 25, 4103–4116. [Google Scholar]
- Kalma, J.; McVicar, T.; McCabe, M. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys 2008, 29, 421–469. [Google Scholar]
- Kustas, W.; Anderson, M. Advances in thermal infrared remote sensing for land surface modeling. Agric. For. Meteorol 2009, 149, 2071–2081. [Google Scholar]
- Maes, W.H.; Steppe, K. Estimating evapotranspiration and drought stress with ground-based thermal remote sensing in agriculture: A review. J. Exp. Bot 2012, 63, 4671–4712. [Google Scholar]
- Merlin, O.; Chirouze, J.; Olioso, A.; Jarlan, L.; Chehbouni, G.; Boulet, G. An image-based four-source surface energy balance model to estimate crop evapotranspiration from solar reflectance/thermal emission data (SEB-4S). Agric. For. Meteorol 2014, 184, 188–203. [Google Scholar]
- Morillas, L.; García, M.; Nieto, H.; Villagarcia, L.; Sandholt, I.; Gonzalez-Dugo, M.P.; Zarco-Tejada, P.J.; Domingo, F. Using radiometric surface temperature for surface energy flux estimation in Mediterranean drylands from a two-source perspective. Remote Sens. Environ 2013, 136, 234–246. [Google Scholar]
- Tomlinson, C.J.; Chapman, L.; Thornes, J.E.; Baker, C. Remote sensing land surface temperature for meteorology and climatology: A review. Meteorol. Appl 2011, 18, 296–306. [Google Scholar]
- Van der Tol, C. Validation of remote sensing of bare soil ground heat flux. Remote Sens. Environ 2012, 121, 275–286. [Google Scholar]
- Kustas, W.; Anderson, M.; Norman, J.; Li, F. Utility of radiometric-aerodynamic temperature relations for heat flux estimation. Bound-Lay Meteorol 2007, 122, 167–187. [Google Scholar]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ 2013, 131, 14–37. [Google Scholar]
- Huband, N.D.S.; Monteith, J.L. Radiative surface temperature and energy balance of a wheat canopy. Bound-Lay Meteorol 1986, 36, 107–116. [Google Scholar]
- Kimes, D.S. Effects of vegetation canopy structure on remotely sensed canopy temperatures. Remote Sens. Environ 1980, 10, 165–174. [Google Scholar]
- Matsushima, D. Relations between aerodynamic parameters of heat transfer and thermal-infrared thermometry in the bulk surface formulation. J. Meteorol. Soc. Jpn. Ser. II 2005, 83, 373–389. [Google Scholar]
- Chehbouni, A.; Seen, D.L.; Njoku, E.G.; Lhomme, J.-P.; Monteny, B.; Kerr, Y.H. Estimation of sensible heat flux over sparsely vegetated surfaces. J. Hydrol 1997, 188–189, 855–868. [Google Scholar]
- Lagos, L.; Martin, D.; Verma, S.; Irmak, S.; Irmak, A.; Eisenhauer, D.; Suyker, A. Surface energy balance model of transpiration from variable canopy cover and evaporation from residue-covered or bare soil systems: Model evaluation. Irrig. Sci 2013, 31, 135–150. [Google Scholar]
- Rosenberg, N.; Blad, B.; Verma, S. Microclimate: The Biological Environment, 2nd ed; Wiley-Interscience: New York, NY, USA, 1983. [Google Scholar]
- Jin, M.; Dickinson, R.E. Land surface skin temperature climatology: Benefitting from the strengths of satellite observations. Environ. Res. Lett 2010, 5. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P.A. Climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 2. Surface moisture climatology. J. Geophys. Res 2007, 112. [Google Scholar] [CrossRef]
- Pitman, A.J.; Xia, Y.; Leplastrier, M.; Henderson-Sellers, A. The CHAmeleon surface model: Description and use with the PILPS phase 2(e) forcing data. Glob. Planet Change 2003, 38, 121–135. [Google Scholar]
- Vereecken, H.; Kollet, S.; Simmer, C. Patterns in soil-vegetation-atmosphere systems: Monitoring, modeling, and data assimilation. Vadose Zone J 2010, 9, 821–827. [Google Scholar]
- Graf, A.; Werner, J.; Langensiepen, M.; van de Boer, A.; Schmidt, M.; Kupisch, M.; Vereecken, H. Validation of a minimum microclimate disturbance chamber for net ecosystem flux measurements. Agric. For. Meteorol 2013, 174–175, 1–14. [Google Scholar]
- Baatz, R.; Bogena, H.R.; Hendricks Franssen, H.J.; Huisman, J.A.; Qu, W.; Montzka, C.; Vereecken, H. Calibration of a catchment scale cosmic-ray probe network: A comparison of three parameterization methods. J. Hydrol 2014, 516, 231–244. [Google Scholar]
- Dufranne, D.; Moureaux, C.; Vancutsem, F.O.; Bodson, B.; Aubinet, M. Comparison of carbon fluxes, growth and productivity of a winter wheat crop in three contrasting growing seasons. Agric. Ecosyst. Environ 2011, 141, 133–142. [Google Scholar]
- Hanft, J.M.; Wych, R.D. Visual indicators of physiological maturity of hard red spring wheat. Crop. Sci 1982, 22, 584–588. [Google Scholar]
- Chen, J.-M.; Zhang, R.-H. Studies on the measurements of crop emissivity and sky temperature. Agric. For. Meteorol 1989, 49, 23–34. [Google Scholar]
- Idso, S.B.; Jackson, R.D.; Ehrler, W.L.; Mitchell, S.T. A method for determination of infrared emittance of leaves. Ecology 1969, 50, 899–902. [Google Scholar]
- Jones, H.G. Application of thermal imaging and infrared sensing in plant physiology and ecophysiology. In Incorporating Advances in Plant Pathology; Callow, J.A., Ed.; Academic Press: London, UK, 2004; Volume 41, pp. 107–163. [Google Scholar]
- Smith, J. Matter-energy interaction in the optical region. In Manual of Remote Sensing, 2nd ed; American Society of Photogrammetry: Falls Church, VA, USA, 1983; Volume 1, pp. 61–113. [Google Scholar]
- Schmugge, T.J.; Kustas, W.P. Radiometry at infrared wavelengths for agricultural applications. Agronomie 1999, 19, 83–96. [Google Scholar]
- Schmidt, M.; Reichenau, T.G.; Fiener, P.; Schneider, K. The carbon budget of a winter wheat field: An eddy covariance analysis of seasonal and inter-annual variability. Agric. For. Meteorol 2012, 165, 114–126. [Google Scholar]
- Mauder, M.; Cuntz, M.; Drüe, C.; Graf, A.; Rebmann, C.; Schmid, H.P.; Schmidt, M.; Steinbrecher, R.A. Strategy for quality and uncertainty assessment of long-term eddy-covariance measurements. Agric. For. Meteorol 2013, 169, 122–135. [Google Scholar]
- Jackson, R.; Moran, M.S.; Gay, L.; Raymond, L. Evaluating evaporation from field crops using airborne radiometry and ground-based meteorological data. Irrig. Sci 1987, 8, 81–90. [Google Scholar]
- Bowen, I.S. The ratio of heat losses by conduction and by evaporation from any water surface. Phys. Rev 1926, 27, 779–787. [Google Scholar]
- Tanner, C.B. Energy balance approach to evapotranspiration from crops. Soil Sci. Soc. Am. J 1960, 24, 1–9. [Google Scholar]
- Verma, S.B. Micrometeorological methods for measuring surface fluxes of mass and energy. Remote Sens. Rev 1990, 5, 99–115. [Google Scholar]
- Li, L.; Yu, Q.; Su, Z.; van der Tol, C. A simple method using climatic variables to estimate canopy temperature, sensible and latent heat fluxes in a winter wheat field on the North China Plain. Hydrol. Process 2009, 23, 665–674. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; United Nations Food and Agriculture Organization: Rome, Italy, 1998. [Google Scholar]
- Jackson, R.D.; Idso, S.B.; Reginato, R.J.; Pinter, P.J. Canopy temperature as a crop water stress indicator. Water Resour. Res 1981, 17, 1133–1138. [Google Scholar]
- Monteith, J.L. Evaporation and the environment. Symp. Soc. Exp. Biol 1995, 19, 205–234. [Google Scholar]
- Foken, T.; Wimmer, F.; Mauder, M.; Thomas, C.; Liebethal, C. Some aspects of the energy balance closure problem. Atmos. Chem. Phys 2006, 6, 4395–4402. [Google Scholar]
- Liu, H.; Foken, T.A. Modified Bowen ratio method to determine sensible and latent heat fluxes. Meteorol. Z 2001, 10, 71–80. [Google Scholar]
- Foken, T. The energy balance closure problem: An overview. Ecol. Appl 2008, 18, 1351–1367. [Google Scholar]
- Mauder, M.; Desjardins, R.; Pattey, E.; Worth, D. An attempt to close the daytime surface energy balance using spatially-averaged flux measurements. Bound-Lay Meteorol 2010, 136, 175–191. [Google Scholar]
- Monteith, J.L.; Szeicz, G. Radiative temperature in the heat balance of natural surfaces. Q. J. Roy Meteor. Soc 1962, 88, 496–507. [Google Scholar]
- Monteith, J. Gas exchange in plant communities. Environ. Control Plant Growth 1963, 95, 112. [Google Scholar]
- Tolk, J.A.; Howell, T.A.; Steiner, J.L.; Krieg, D.R. Aerodynamic characteristics of corn as determined by energy balance techniques. Agron. J 1995, 87, 464–473. [Google Scholar]
- Chávez, J.; Neale, C.M.U.; Hipps, L.E.; Prueger, J.H.; Kustas, W.P. Comparing aircraft-based remotely sensed energy balance fluxes with eddy covariance tower data using heat flux source area functions. J. Hydrometeorol 2005, 6, 923–940. [Google Scholar]
- Gavilán, P.; Berengena, J. Accuracy of the Bowen ratio-energy balance method for measuring latent heat flux in a semiarid advective environment. Irrig. Sci 2007, 25, 127–140. [Google Scholar]
- Todd, R.W.; Evett, S.R.; Howell, T.A. The Bowen ratio-energy balance method for estimating latent heat flux of irrigated alfalfa evaluated in a semi-arid, advective environment. Agric. For. Meteorol 2000, 103, 335–348. [Google Scholar]
- Savage, M.J.; Everson, C.S.; Metelerkamp, B.R. Bowen ratio evaporation measurement in a remote montane grassland: Data integrity and fluxes. J. Hydrol 2009, 376, 249–260. [Google Scholar]
- Mallick, K.; Jarvis, A.; Wohlfahrt, G.; Gough, C.; Hirano, T.; Kiely, G.; Miyata, A.; Yamamoto, S. Components of near-surface energy balance derived from satellite soundings—Part 2: Latent heat flux. Atmos. Chem. Phys. Discuss 2010, 10, 14417–14443. [Google Scholar]
- Todorovic, M. Single-layer evapotranspiration model with variable canopy resistance. J. Irrig. Drain. Eng 1999, 125, 235–245. [Google Scholar]
- Leuning, R. A critical appraisal of a combined stomatal-photosynthesis model for C3 plants. Plant Cell Environ 1995, 18, 339–355. [Google Scholar]
- Isaac, P.R.; Leuning, R.; Hacker, J.M.; Cleugh, H.A.; Coppin, P.A.; Denmead, O.T.; Raupach, M.R. Estimation of regional evapotranspiration by combining aircraft and ground-based measurements. Bound-Lay Meteorol 2004, 110, 69–98. [Google Scholar]
- Yu, Q.; Liu, Y.; Liu, J.; Wang, T. Simulation of leaf photosynthesis of winter wheat on Tibetan Plateau and in North China Plain. Ecol. Model 2002, 155, 205–216. [Google Scholar]
- Danielsson, H.; Karlsson, G.P.; Karlsson, P.E.; Håkan Pleijel, H. Ozone uptake modelling and flux-response relationships—An assessment of ozone-induced yield loss in spring wheat. Atmos. Environ 2003, 37, 475–485. [Google Scholar]
- Mo, X.; Liu, S. Simulating evapotranspiration and photosynthesis of winter wheat over the growing season. Agric. For. Meteorol 2001, 109, 203–222. [Google Scholar]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci 1948, 193, 120–145. [Google Scholar]
- Silva, B.; Ramana Rao, T.V. The CWSI variations of a cotton crop in a semi-arid region of Northeast Brazil. J. Arid. Environ 2005, 62, 649–659. [Google Scholar]
- The R-Project for Statistical Computing. Available online: www.r-project.org (accessed on 9 October 2014).
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res 2005, 30, 79–82. [Google Scholar]
- Ingwersen, J.; Steffens, K.; Högy, P.; Warrach-Sagi, K.; Zhunusbayeva, D.; Poltoradnev, M.; Gäbler, R.; Wizemann, H.-D.; Fangmeier, A.; Wulfmeyer, V.; et al. Comparison of Noah simulations with eddy covariance and soil water measurements at a winter wheat stand. Agric. For. Meteorol 2011, 151, 345–355. [Google Scholar]
- Kim, J.; Verma, S.B.; Rosenberg, N.J. Energy balance and water use of cereal crops. Agric. For. Meteorol 1989, 48, 135–147. [Google Scholar]
- Bastiaanssen, W.G.M.; Wal, T.; Visser, T.N.M. Diagnosis of regional evaporation by remote sensing to support irrigation performance assessment. Irrig. Drain. Syst 1996, 10, 1–23. [Google Scholar]
- Gentine, P.; Entekhabi, D.; Heusinkveld, B. Systematic errors in ground heat flux estimation and their correction. Water Resour. Res 2012, 48. [Google Scholar] [CrossRef]
- Panozzo, J.F.; Eagles, H.A.; Cawood, R.J.; Wootton, M. Wheat spike temperatures in relation to varying environmental conditions. Aus. J. Agric. Res 1999, 50, 997–1006. [Google Scholar]
- Pararajasingham, S.; Hunt, L.A. Wheat spike temperature in relation to base temperature for grain filling duration. Can. J. Plant Sci 1991, 71, 63–69. [Google Scholar]
- Ayeneh, A.; van Ginkel, M.; Reynolds, M.P.; Ammar, K. Comparison of leaf, spike, peduncle and canopy temperature depression in wheat under heat stress. Field Crops Res 2002, 79, 173–184. [Google Scholar]
- French, A.N.; Schmugge, T.J.; Kustas, W.P. Discrimination of senescent vegetation using thermal emissivity contrast. Remote Sens. Environ 2000, 74, 249–254. [Google Scholar]
- Otterman, J.; Brakke, T.W.; Fuchs, M.; Lakshmi, V.; Cadeddu, M. Longwave emission from a plant/soil surface as a function of the view direction: Dependence on the canopy architecture. Int. J. Remote Sens 1999, 20, 2195–2201. [Google Scholar]
- Ferguson, H.; Eslick, R.F.; Aase, J.K. Canopy temperatures of barley as influenced by morphological characteristics1. Agron. J 1973, 65, 425–428. [Google Scholar]
- Hatfield, J.L.; Pinter, J.P., Jr.; Chasseray, E.; Ezra, C.E.; Reginato, R.J.; Idso, S.B.; Jackson, R.D. Effects of panicles on infrared thermometer measurements of canopy temperature in wheat. Agric. For. Meteorol 1984, 32, 97–105. [Google Scholar]
- Blum, A. The effect of heat stress on wheat leaf and ear photosynthesis. J. Exp. Bot 1986, 37, 111–118. [Google Scholar]
- Stone, L.R.; Kanemasu, E.T.; Horton, M.L. Grain sorghum canopy temperature as influenced by clouds. Remote Sens. Environ 1975, 4, 177–181. [Google Scholar]
- Wiegand, C.L.; Namken, L.N. Influences of plant moisture stress, solar radiation, and air temperature on cotton leaf temperature. Agron. J 1966, 58, 582–586. [Google Scholar]
- Wiegand, C.L.; Swanson, W.A. Time constants for thermal equilibration of leaf, canopy, and soil surfaces with change in insolation. Agron. J 1973, 65, 722–724. [Google Scholar]
- Pennington, D.A.; Heatherly, L. Effects of changing solar radiation on canopy-air temperatures of cotton and soybean. Agric. For. Meteorol 1989, 46, 1–14. [Google Scholar]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res 2001, 106, 7183–7192. [Google Scholar]
- Shen, Y.; Kondoh, A.; Tang, C.; Zhang, Y.; Chen, J.; Li, W.; Sakura, Y.; Liu, C.; Tanaka, T.; Shimada, J. Measurement and analysis of evapotranspiration and surface conductance of a wheat canopy. Hydrol. Process 2002, 16, 2173–2187. [Google Scholar]
- Bort, J.; Febrero, A.; Amaro, T.; Araus, J. Role of awns in ear water-use efficiency and grain weight in barley. Agronomie 1994, 14, 133–139. [Google Scholar]
- Abbad, H.; El Jaafari, S.; Bort Pie, J.; Araus Ortega, J.L. Comparison of flag leaf and ear photosynthesis with biomass and grain yield of durum wheat under various water conditions and genotypes. Agronomie 2004, 24, 19–28. [Google Scholar]
- Maydup, M.L.; Antonietta, M.; Guiamet, J.J.; Graciano, C.; López, J.R.; Tambussi, E.A. The contribution of ear photosynthesis to grain filling in bread wheat (Triticum aestivum L.). Field Crop. Res 2010, 119, 48–58. [Google Scholar]
- Zhang, Y.; Zhang, Y.; Wang, Z.; Wang, Z. Characteristics of canopy structure and contributions of non-leaf organs to yield in winter wheat under different irrigated conditions. Field Crop. Res 2011, 123, 187–195. [Google Scholar]
- Morgan, J.M. Possible role of abscisic acid in reducing seed set in water-stressed wheat plants. Nature 1980, 285, 655–657. [Google Scholar]
- Morgan, J.; King, R. Association between loss of leaf turgor, abscisic acid levels and seed set in two wheat cultivars. Funct. Plant Biol 1984, 11, 143–150. [Google Scholar]
- Anderson, M.; Norman, J.; Kustas, W.; Houborg, R.; Starks, P.; Agam, N. A thermal-based remote sensing technique for routine mapping of land-surface carbon, water and energy fluxes from field to regional scales. Remote Sens. Environ 2008, 112, 4227–4241. [Google Scholar]
- Colaizzi, P.D.; Kustas, W.P.; Anderson, M.C.; Agam, N.; Tolk, J.A.; Evett, S.R.; Howell, T.A.; Gowda, P.H.; O’Shaughnessy, S.A. Two-source energy balance model estimates of evapotranspiration using component and composite surface temperatures. Adv. Water Resour 2012, 50, 134–151. [Google Scholar]
- Gonzalez-Dugo, M.; Neale, C.; Mateos, L.; Kustas, W.; Prueger, J.; Anderson, M.; Li, F. A comparison of operational remote sensing-based models for estimating crop evapotranspiration. Agric. Forest Meteorol 2009, 149, 1843–1853. [Google Scholar]
- Kustas, W.P.; Norman, J.M. A two-source energy balance approach using directional radiometric temperature observations for sparse canopy covered surfaces. Agron. J 2000, 92, 847–854. [Google Scholar]
- Sánchez, J.; Kustas, W.; Caselles, V.; Anderson, M. Modelling surface energy fluxes over maize using a two-source patch model and radiometric soil and canopy temperature observations. Remote Sens. Environ 2008, 112, 1130–1143. [Google Scholar]
- Matheny, A.M.; Bohrer, G.; Stoy, P.C.; Baker, I.; Black, A.; Desai, A.R.; Dietze, M.; Gough, C.; Ivanov, V.; Jassal, P.; et al. Characterizing the diurnal patterns of errors in the prediction of evapotranspiration by several land-surface models: An NACP analysis. J. Geophys. Res 2014, 119, 1458–1473. [Google Scholar]
- Zhang, Q.; Manzoni, S.; Katul, G.; Porporato, A.; Yang, D. The hysteretic evapotranspiration—Vapor pressure deficit relation. J. Geophys. Res 2014, 119, 125–140. [Google Scholar]
- Nielsen, D.C.; Clawson, K.L.; Blad, B.L. Effect of solar azimuth and infrared thermometer view direction on measured soybean canopy temperature. Agron. J 1984, 76, 607–610. [Google Scholar]
- Prashar, A.; Jones, H.G. Infra-red thermography as a high-throughput tool for field phenotyping. Agronomy 2014, 4, 397–417. [Google Scholar]
- European Plant Phenotyping Network. Available online: http://www.plant-phenotyping-network.eu (accessed on 9 October 2014).



| Approach | Basic Principle | Basic Input Data | References |
|---|---|---|---|
| SEB | SEB-based approach, TIR-based calculation of H, λE derived as the residual of the SEB. | Air density, net radiation, ground heat flux, aerodynamic resistance, air temperature, surface temperature | [34] |
| Bowen ratio | Bowen ratio method, TIR-based calculation of heat and water vapor gradients. | net radiation, ground heat flux, air temperature, surface temperature humidity | [35–39] |
| T modeled | SEB-based approach, calculation of H based on modeled surface temperature (modified Todorovic approach), λE derived as the residual of the SEB. | Air density, net radiation, ground heat flux, humidity, aerodynamic resistance, air temperature, surface temperature | [40] |
| Penman Monteith | TIR-based parameterization of the (bulk) canopy resistance term of the PM equation. | Air density, net radiation, ground heat flux, humidity, aerodynamic resistance, air temperature, surface temperature | [41–43] |
| Temperature | Standard Deviation | Median | Mean | Minimum | Maximum |
|---|---|---|---|---|---|
| Trad.mean | 6.3 | 16.5 | 16.9 | 4.9 | 30.3 |
| Trad.min | 5.5 | 15.2 | 15.2 | 3.4 | 25.8 |
| Trad.max | 7.5 | 17.7 | 19.7 | 8.7 | 36.4 |
| Trad.WE | 6.9 | 16.5 | 17.2 | 4.3 | 32.6 |
| Trad.BG | 5.2 | 16.4 | 17.1 | 8.0 | 28.4 |
| Tleaf1 | 5.3 | 14.9 | 15.1 | 4.7 | 26.8 |
| Tleaf2 | 6.5 | 15.5 | 16.2 | 4.8 | 30.1 |
| Tleaf3 | 6.2 | 15.7 | 16.4 | 5.5 | 29.9 |
| Tleaf4 | 5.8 | 15.4 | 16.0 | 5.1 | 28.0 |
| TIRR | 6.0 | 14.7 | 15.2 | 3.9 | 28.1 |
| Taero,inv. | 6.6 | 16.5 | 17.7 | 3.7 | 33.2 |
| Tmodeled | 8.1 | 17.5 | 17.8 | −7.5 | 34.2 |
| Tair | 5.2 | 16.1 | 16.4 | 6.9 | 28.0 |
| Approach | All 1 | Night 2 | Day 3 | CF ≥ 0.8 4 | CF = 0.2–0.8 5 | CF < 0.2 6 |
|---|---|---|---|---|---|---|
| SEB | 21 (17) | 5 (7) | 22 (22) | 14 (16) | 24 (22) | 25 (22) |
| Bowen ratio | 27 (21) | 4 (4) | 29 (27) | 17 (33) | 45 (35) | 17 (17) |
| T modeled | 29 (24) | 5 (7) | 29 (31) | 16 (35) | 47 (43) | 22 (20) |
| Penman–Monteith | 23 (22) | 5 (6) | 24 (30) | 13 (33) | 24 (34) | 23 (22) |
1df > 157;221.00 h–03.00 h UTC, df > 25;36 h–18.00 h UTC, df > 108;4df > 39;5df > 23;6df > 58.
| Approach | All 1 | Night 2 | Day 3 | CF ≥0.8 4 | CF = 0.2–0.8 5 | CF <0.2 6 |
|---|---|---|---|---|---|---|
| SEB | 29 (29) | 5 (9) | 31 (39) | 13 (16) | 43 (36) | 13 (48) |
| Bowen ratio | 24 (21) | 4 (4) | 29 (27) | 16 (34) | 44 (33) | 18(17) |
| T modeled | 28 (23) | 5 (7) | 28 (31) | 16 (34) | 42 (40) | 20 (21) |
| Penman–Monteith | 32 (28) | 5 (7) | 34 (37) | 13 (30) | 47 (41) | 13 (34) |
1df > 157;221.00 h–03.00 h UTC, df > 25;36 h–18.00 h UTC; df > 108;4df > 39;5df > 23;6df > 58.
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahrends, H.E.; Haseneder-Lind, R.; Schween, J.H.; Crewell, S.; Stadler, A.; Rascher, U. Diurnal Dynamics of Wheat Evapotranspiration Derived from Ground-Based Thermal Imagery. Remote Sens. 2014, 6, 9775-9801. https://doi.org/10.3390/rs6109775
Ahrends HE, Haseneder-Lind R, Schween JH, Crewell S, Stadler A, Rascher U. Diurnal Dynamics of Wheat Evapotranspiration Derived from Ground-Based Thermal Imagery. Remote Sensing. 2014; 6(10):9775-9801. https://doi.org/10.3390/rs6109775
Chicago/Turabian StyleAhrends, Hella Ellen, Rainer Haseneder-Lind, Jan H. Schween, Susanne Crewell, Anja Stadler, and Uwe Rascher. 2014. "Diurnal Dynamics of Wheat Evapotranspiration Derived from Ground-Based Thermal Imagery" Remote Sensing 6, no. 10: 9775-9801. https://doi.org/10.3390/rs6109775
APA StyleAhrends, H. E., Haseneder-Lind, R., Schween, J. H., Crewell, S., Stadler, A., & Rascher, U. (2014). Diurnal Dynamics of Wheat Evapotranspiration Derived from Ground-Based Thermal Imagery. Remote Sensing, 6(10), 9775-9801. https://doi.org/10.3390/rs6109775





