Envisat/ASAR Images for the Calibration of Wind Drag Action in the Doñana Wetlands 2D Hydrodynamic Model
Abstract
:1. Introduction
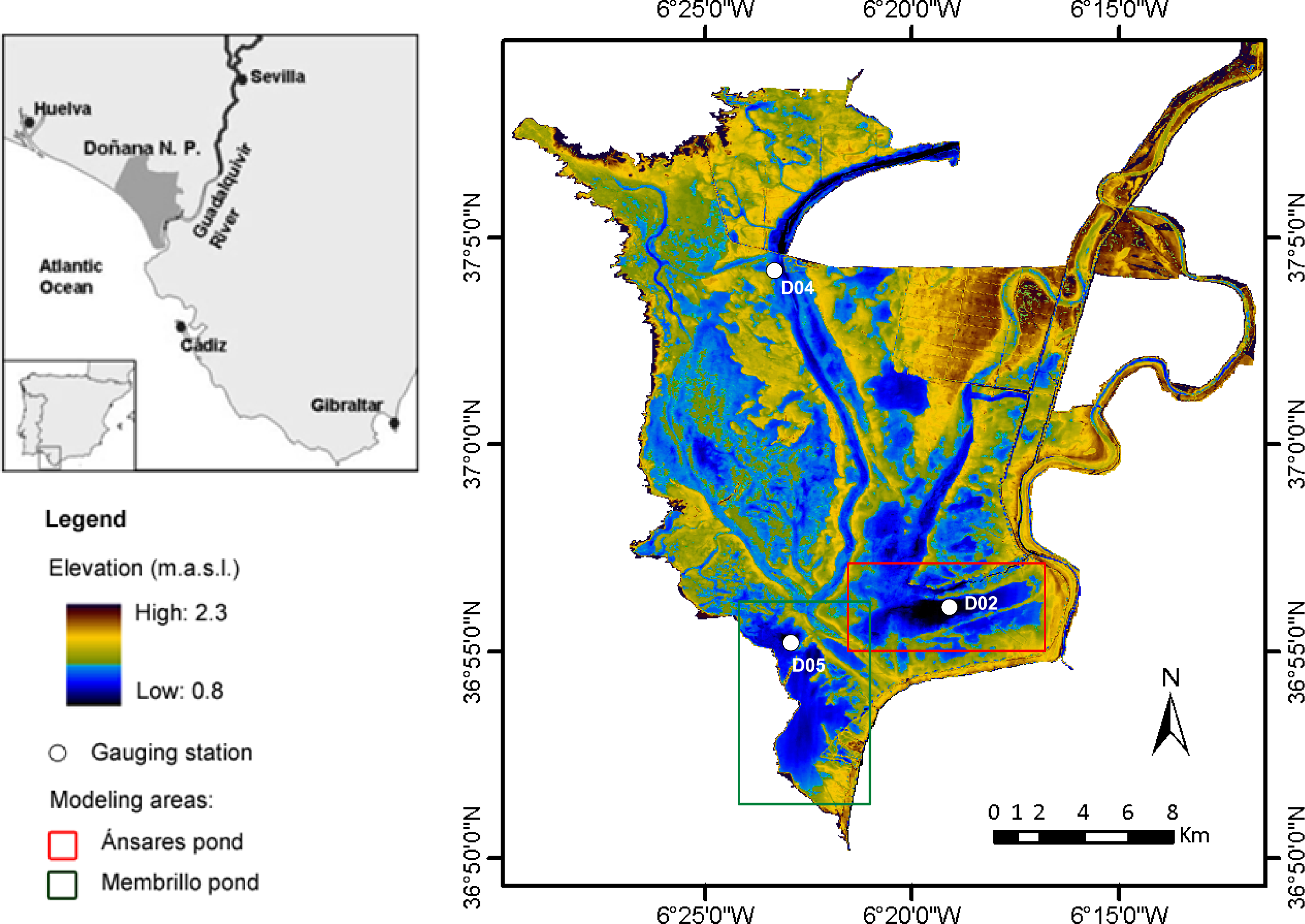
2. Study Area
3. Study Data
3.1. Envisat/ASAR Imagery
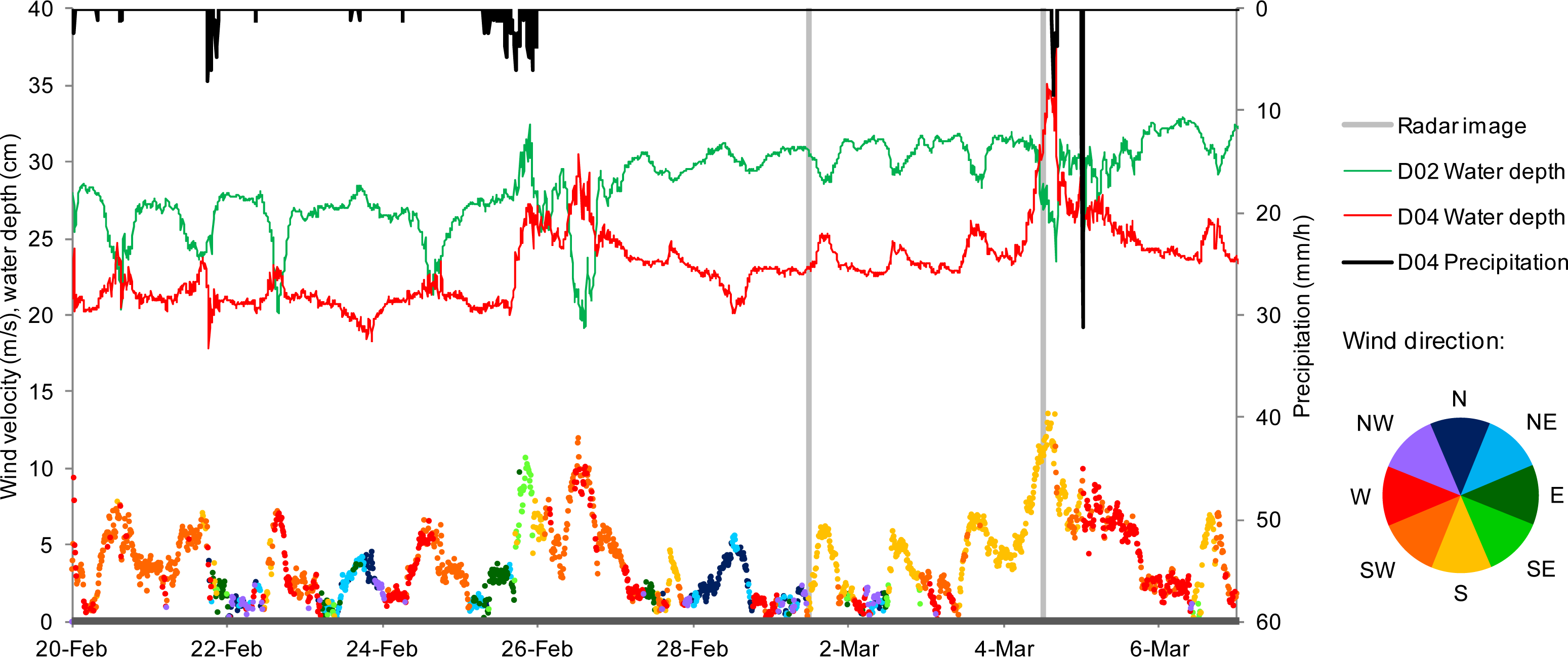
3.2. In Situ Hydrometeorological Measurements
- - For the Membrillo event, measuring station D05 was still not operational. Wind speed and direction, air temperature and precipitation concurrent with the ASAR scenes were recorded at station D04. Water temperature was available at station D02.
- - For the Ánsares event, wind speed, wind direction and precipitation concurrent with the ASAR scene were recorded at station D05. Water level was available at station D02.
4. Methodology
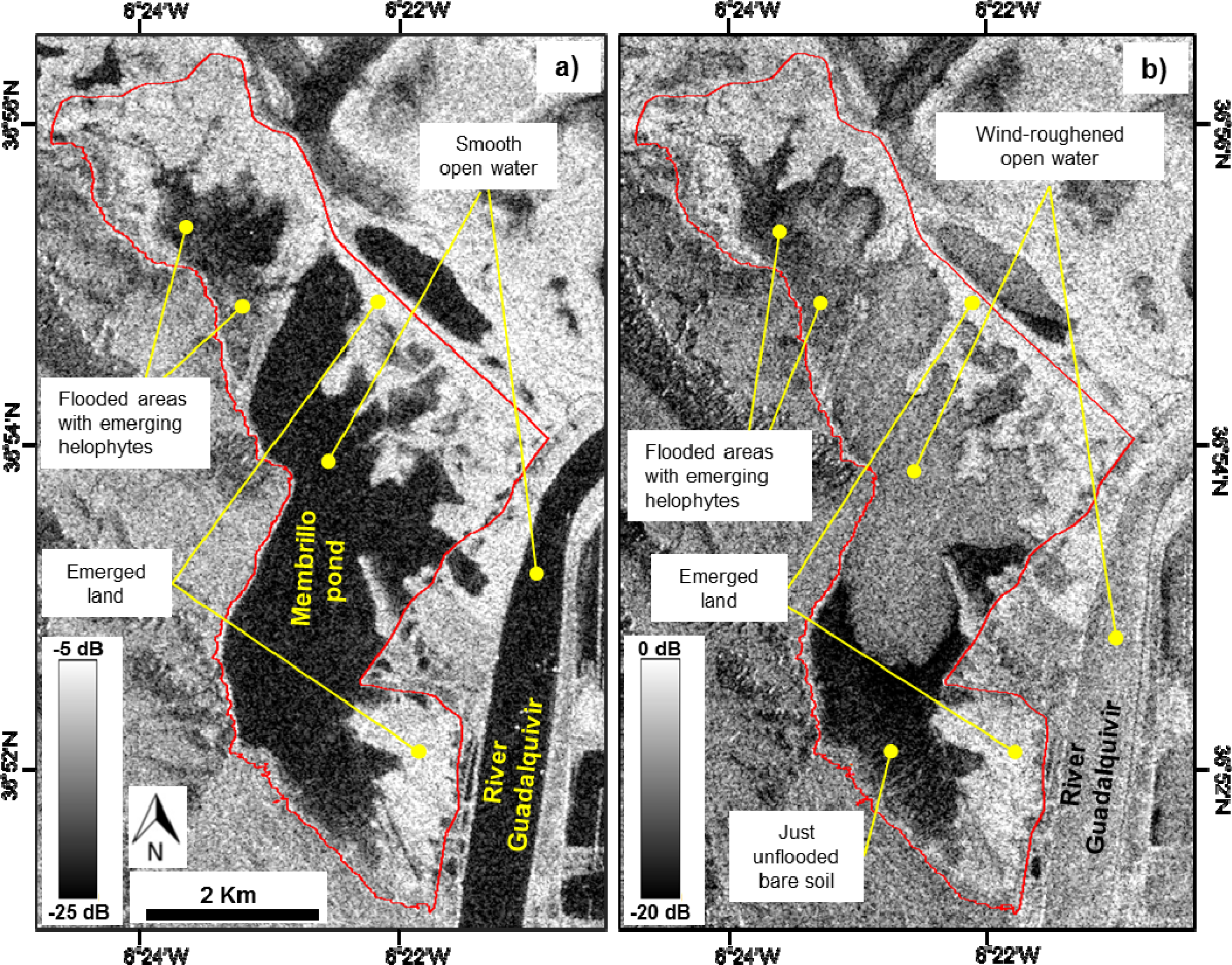
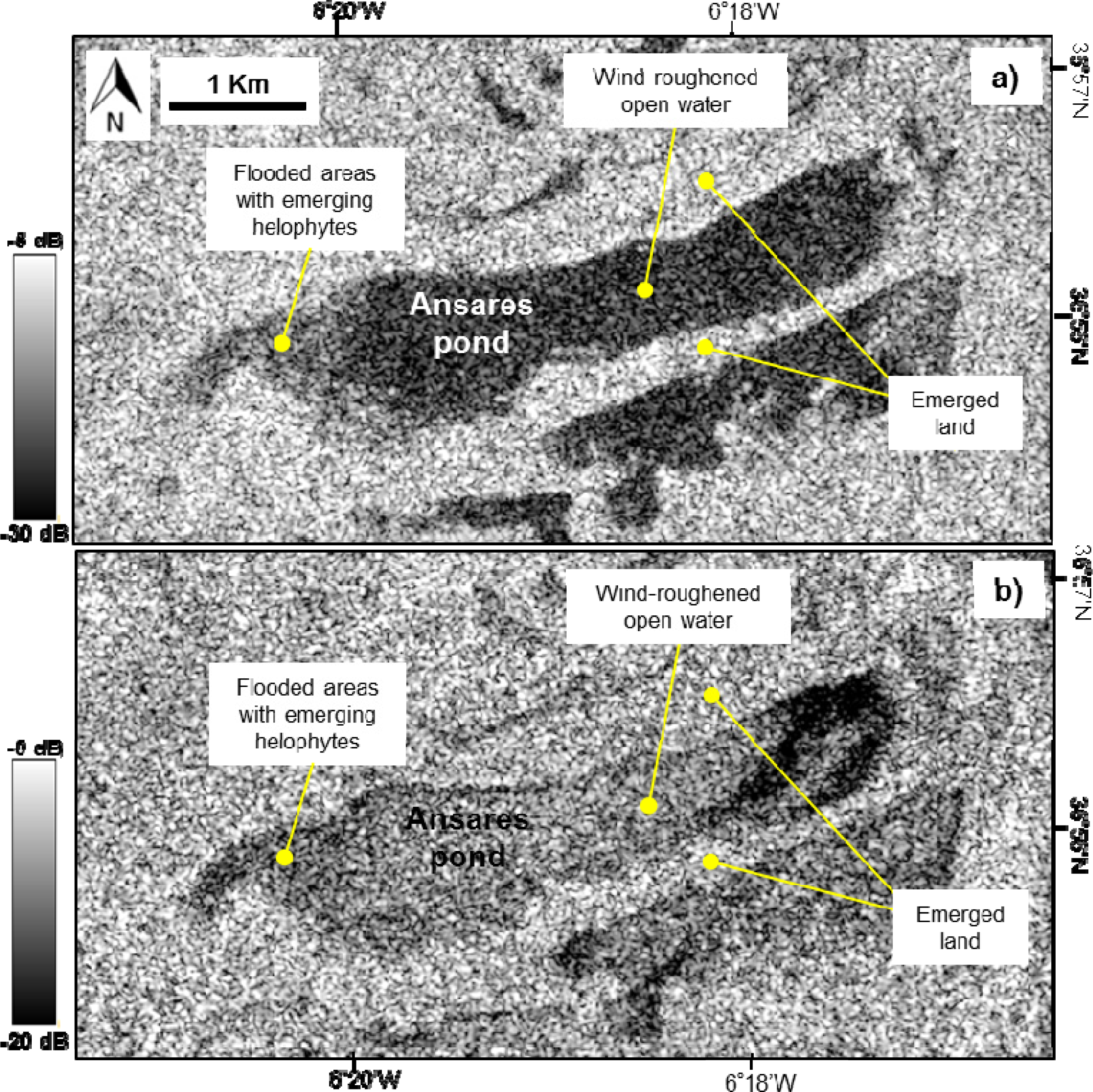
4.1. Flood Mapping from the ASAR Images
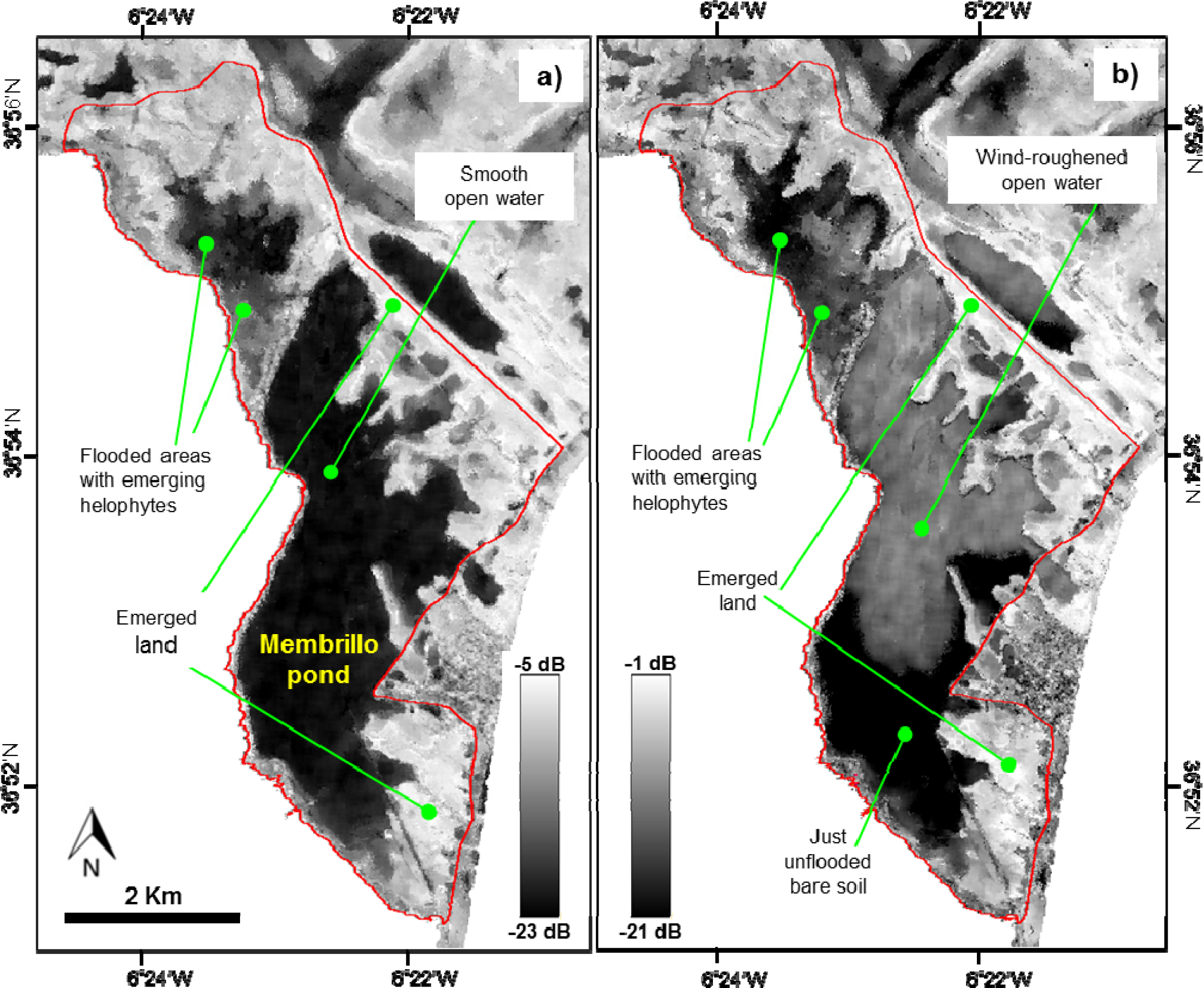
4.1.1. ASAR Image Interpretation
4.1.2. Image Filtering
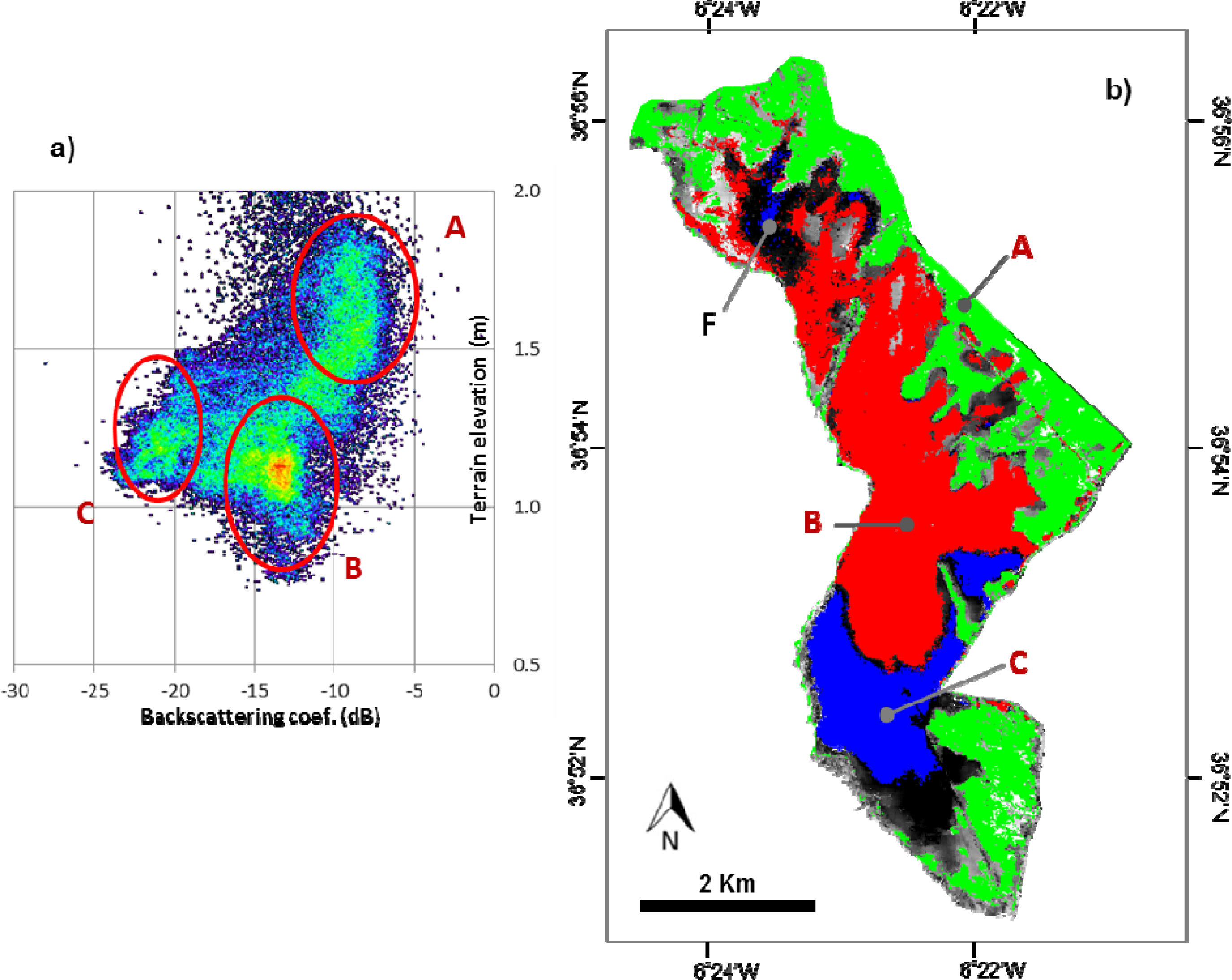
4.1.3. Flood Mapping
4.2. Hydrodynamic Modeling
4.2.1. Numerical Scheme
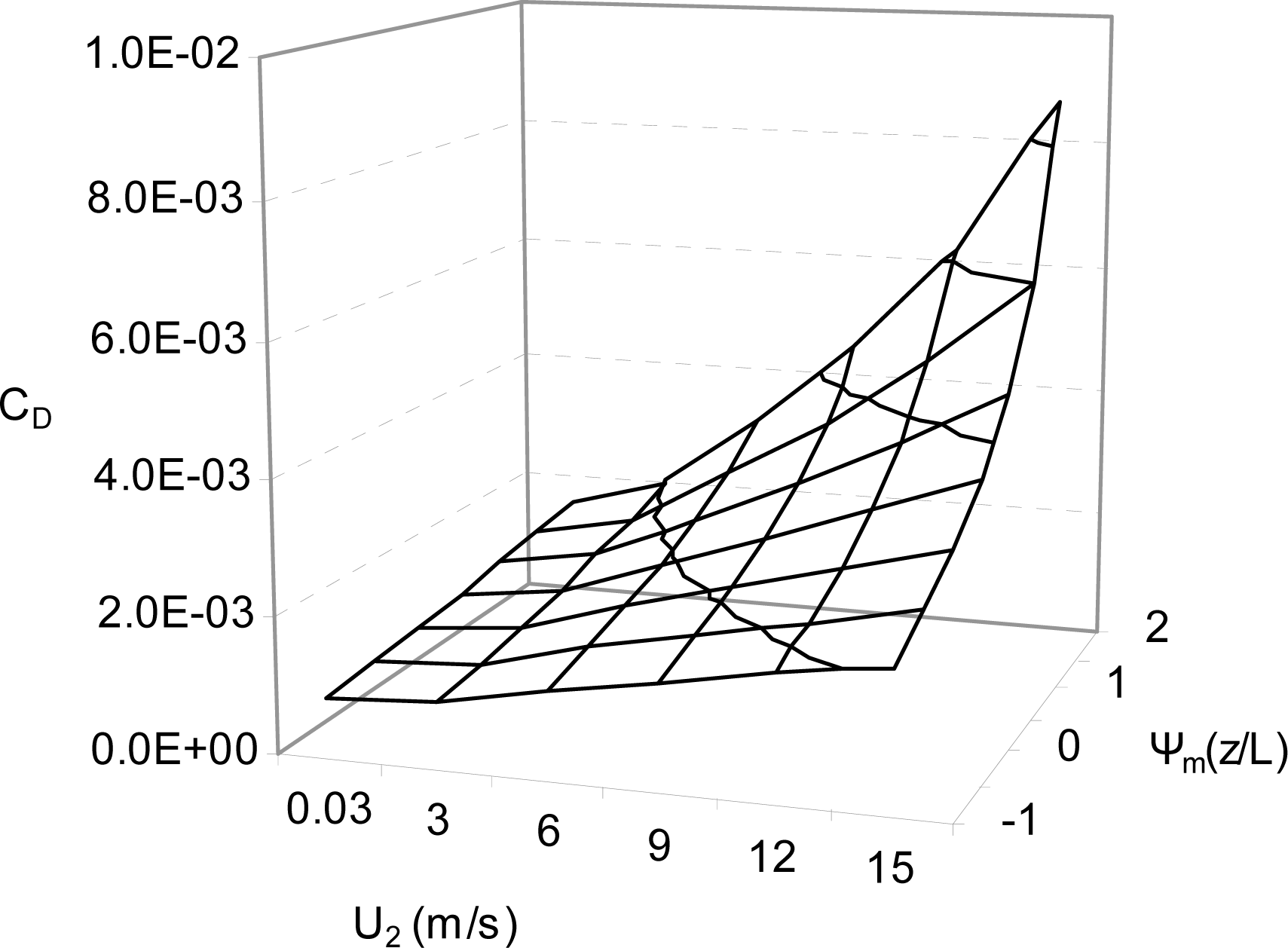
4.2.2. Wind Stress Formulations
4.2.3. Model Setup
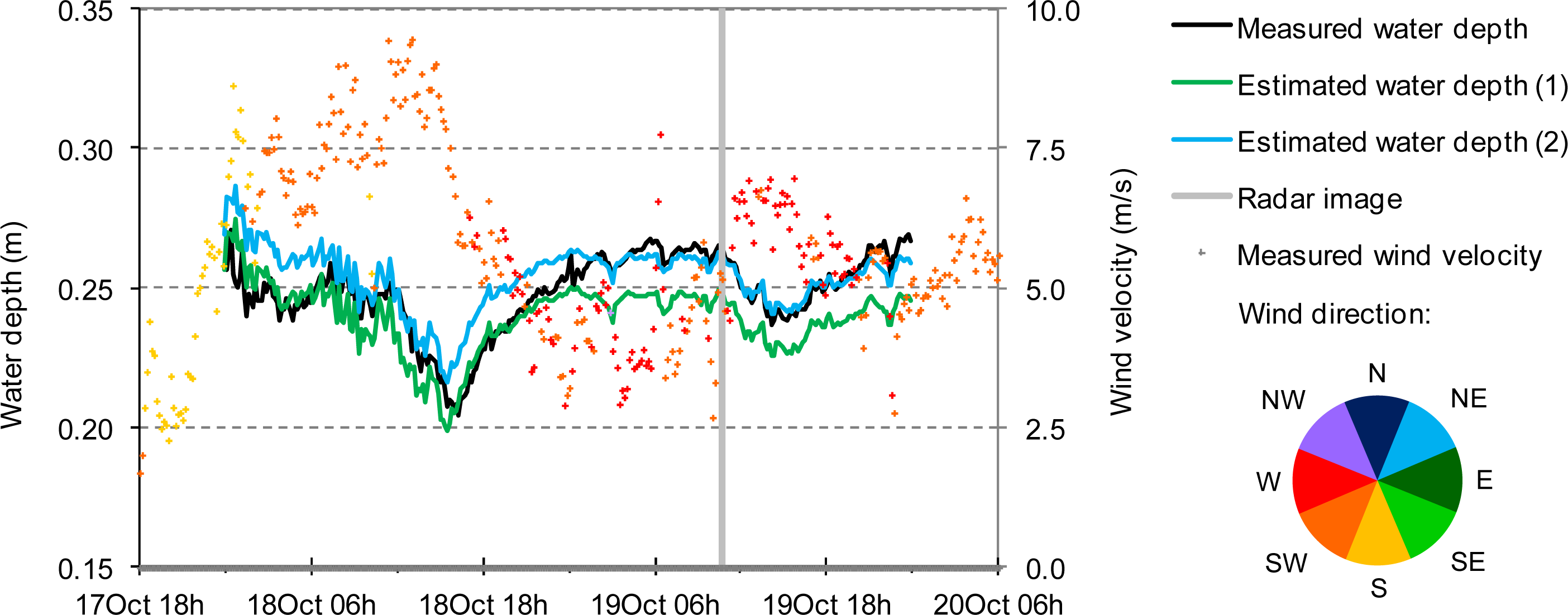
4.2.4. Model Performance
5. Results and Discussion
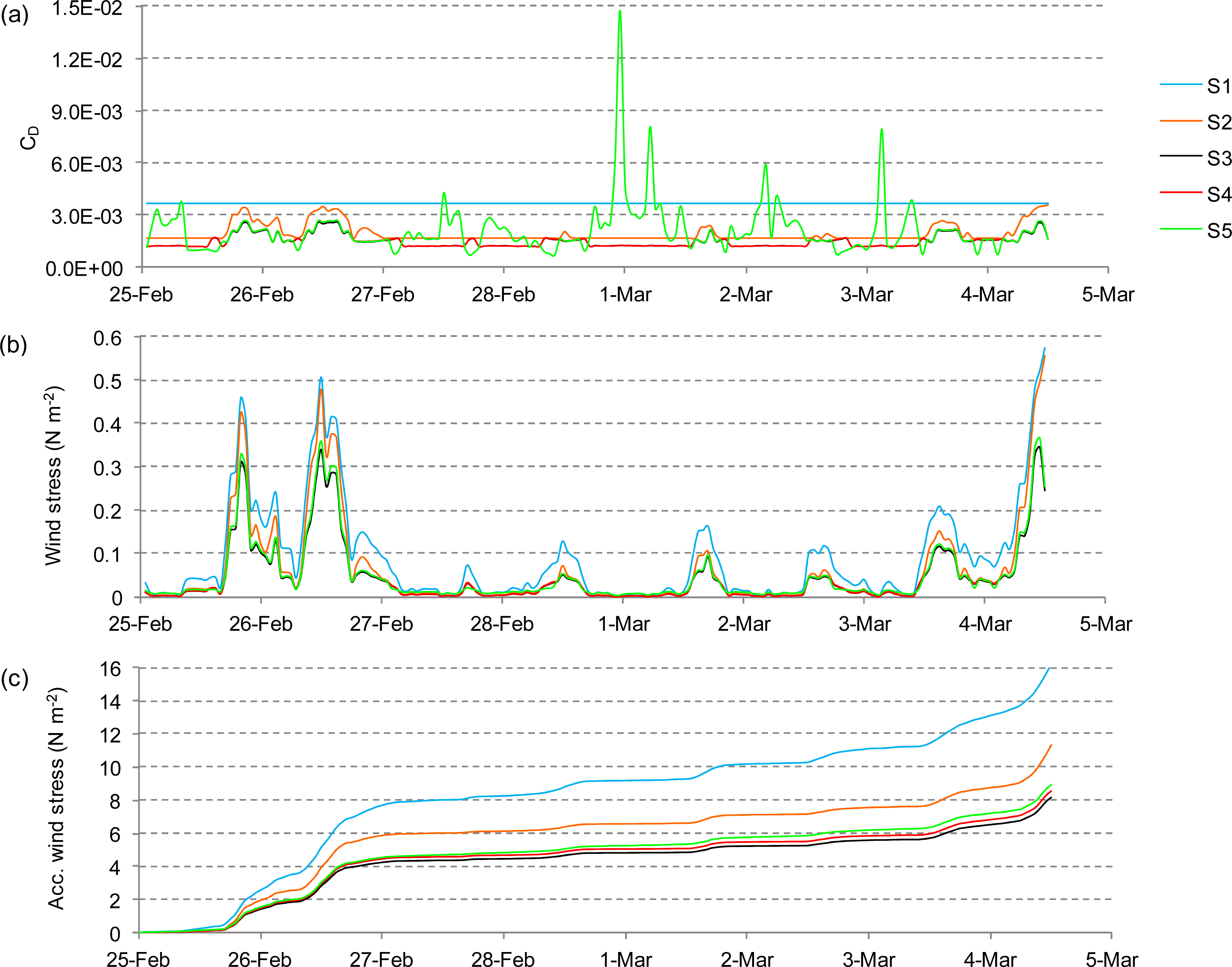
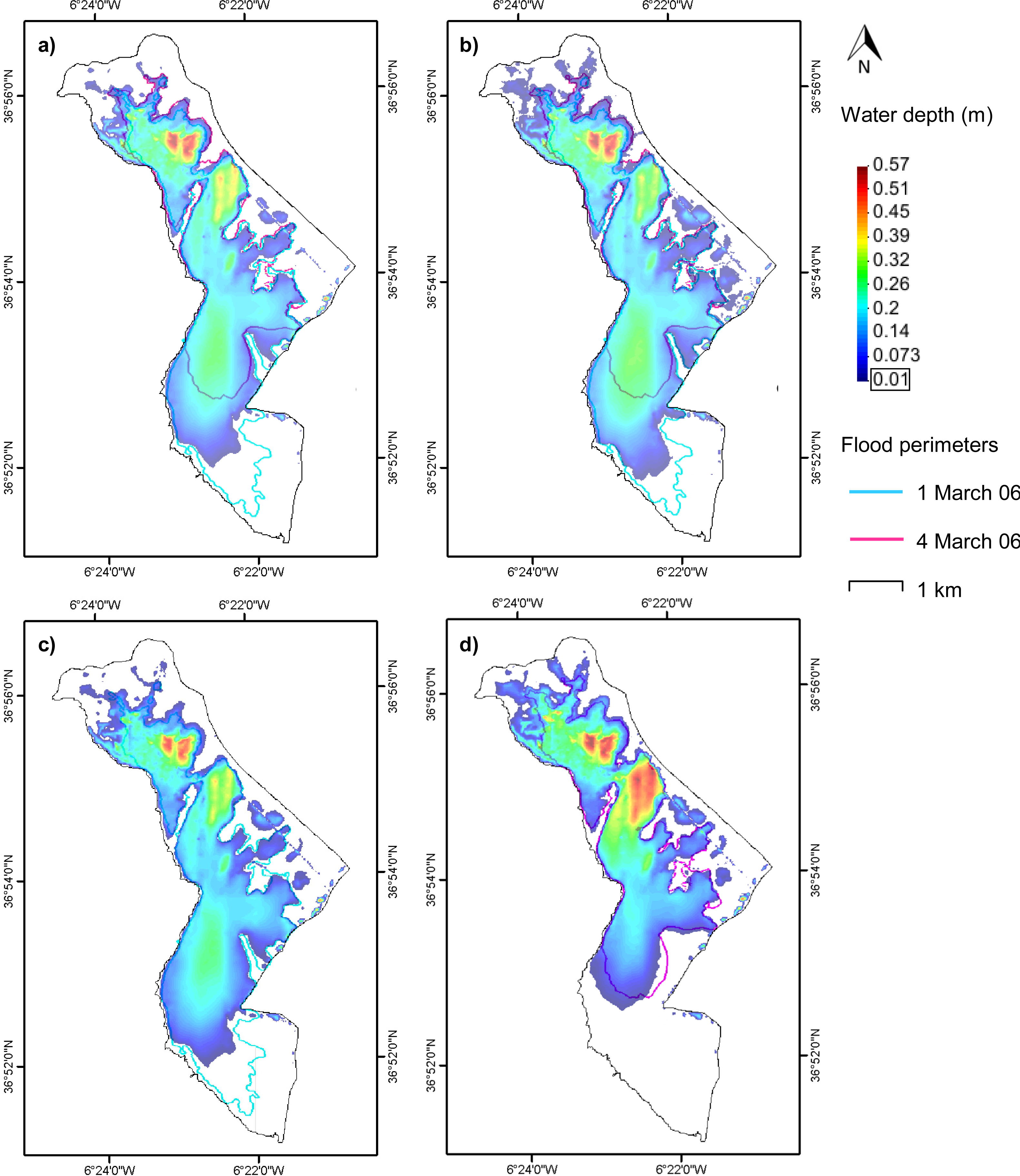
5.1. Comparison of Wind Stress Formulations, Membrillo Event
5.2. Modeling Results
5.2.1. Selection of the Wind Stress Formulation (Membrillo Event)
5.2.2. Analysis of the Membrillo Event
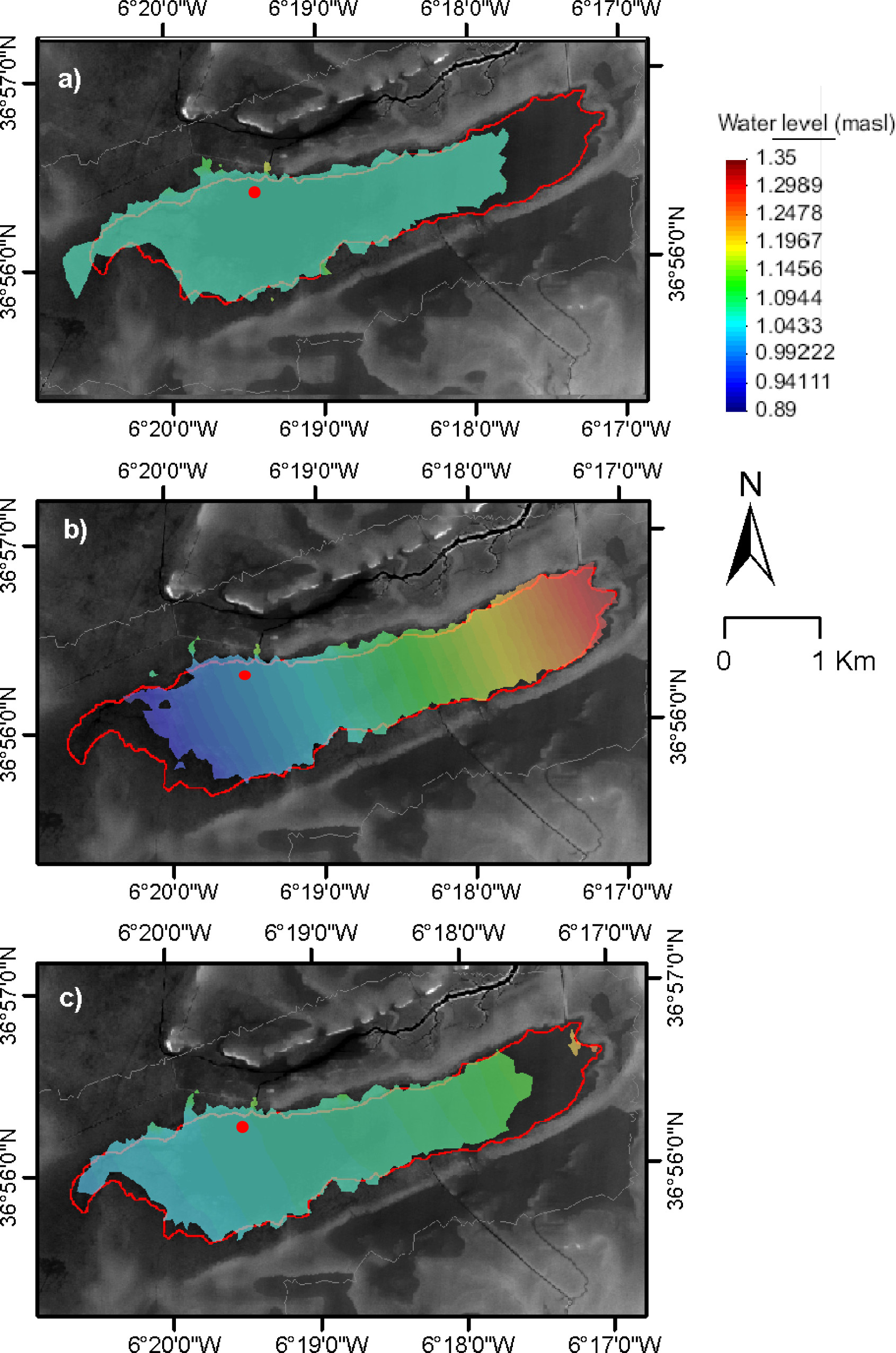
5.2.3. Analysis of the Ánsares Event
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- García-Novo, F.; Marín-Cabrera, C. Doñana: Agua y Biosfera; Ministerio de Medio Ambiente: Sevilla, Spain, 2005. [Google Scholar]
- Gómez-Rodríguez, C.; Bustamante, J.; Díaz-Paniagua, C. Evidence of hydroperiod shortening in a preserved system of temporary ponds. Remote Sens 2010, 2, 1439–1462. [Google Scholar]
- Suso, J.; Llamas, M.R. Influence of groundwater development on the Doñana-National-Park ecosystems (Spain). J. Hydrol 1993, 141, 239–269. [Google Scholar]
- Munñoz-Reinoso, J.C. Vegetation changes and groundwater abstraction in SW Donñana, Spain. J. Hydrol 2001, 242, 197–209. [Google Scholar]
- Menanteau, L. Evolución Histórica y Consecuencias Morfológicas de la Intervención Humana en las Zonas Húmedas: El Caso de las Marismas del Guadalquivir. In Las Zonas Húmedas en Andalucía; Dirección General de Medio Ambiente, Ministerio de Obras Públicas y Urbanismo: Madrid, Spain, 1984; pp. 43–76. [Google Scholar]
- Saura, J.; Bayán, B.; Casas, J.; Ruiz de Larramendi, A.; Urdiales, C. Documento Marco Para el Desarrollo del Proyecto Doñana 2005. Regeneración Hídrica de las Cuencas y Cauces Vertientes a las Marismas del Parque Nacional de Doñana; Ministerio de Medio Ambiente: Madrid, Spain, 2001. [Google Scholar]
- Bladé-Castellet, E.; Gómez, M. Modelación del Flujo en Lámina Libre Sobre Cauces Naturales. Análisis Integrado en una y dos Dimensiones (Monografía CIMNE, 97); CIMNE: Barcelona, Spain, 2006. [Google Scholar]
- European Space Agency. ASAR Product Handbook, Issue 2.2; ESA: Paris, France, 2007. [Google Scholar]
- Marti-Cardona, B.; Lopez-Martinez, C.; Dolz-Ripolles, J.; Bladé-Castellet, E. ASAR polarimetric, multi-incidence angle and multitemporal characterization of Doñana wetlands for flood extent monitoring. Remote Sens. Environ 2010, 114, 2802–2815. [Google Scholar]
- Ferrarin, C.; Umgiesser, G.; Scroccaro, I.; Matassi, G. Hydrodynamic modeling of the lagoons of Marano and Grado, Italy. GeoEcoMarina 2009, 15, 13–19. [Google Scholar]
- Kjerfve, B.; Magill, K.E. Geographic and hydrodynamic characteristics of shallow coastal lagoons. Mar. Geol 1989, 88, 187–199. [Google Scholar]
- Pasternack, G.B.; Hinnov, L.A. Hydrometeorological controls on water level in a vegetated Chesapeake Bay tidal freshwater delta. Estuar. Coast. Shelf Sci 2003, 58, 367–387. [Google Scholar]
- Reed, R.E.; Dickey, D.A.; Burkholder, J.M.; Kinder, C.A.; Brownie, C. Water level variations in the Neuse and Pamlico Estuaries, North Carolina due to local and remote forcing. Estuar. Coast. Shelf Sci 2008, 76, 431–446. [Google Scholar]
- Ramos-Fuertes, A. Hidrometeorología y Balance Térmico de la Marisma de Doñana. Universitat Politècnica de Catalunya, Escola Tècnica Superior d’Enginyers de Camins, Canals i Ports de Barcelona, Barcelona, Spain, 2012. [Google Scholar]
- Ji, Z.G.; Morton, M.R.; Hamrick, J.M. Wetting and drying simulation of estuarine processes. Estuar. Coast. Shelf Sci 2001, 53, 683–700. [Google Scholar]
- Marti-Cardona, B.; Steissberg, T.E.; Schladow, S.G.; Hook, S.J. Relating fish kills to upwellings and wind patterns in the Salton Sea. Hydrobiologia 2008, 604, 85–95. [Google Scholar]
- Mans, C.; Bramato, S.; Baquerizo, A.; Losada, M. Surface seiche formation on a shallow reservoir in complex terrain. J. Hydraul. Eng 2011, 137, 517–529. [Google Scholar]
- Somes, N.L.G.; Bishop, W.A.; Wong, T.H.F. Numerical simulation of wetland hydrodynamics. Environ. Int 1999, 25, 773–779. [Google Scholar]
- Min, J.; Wise, W.R. Depth-averaged, spatially distributed flow dynamic and solute transport modelling of a large-scaled, subtropical constructed wetland. Hydrol. Process 2010, 24, 2724–2737. [Google Scholar]
- Markfort, C.D.; Perez, A.L.S.; Thill, J.W.; Jaster, D.A.; Porté-Agel, F.; Stefan, H.G. Wind sheltering of a lake by a tree canopy or bluff topography. Water Resour. Res 2010, 46. [Google Scholar] [CrossRef]
- Cózar, A.; Gálvez, J.A.; Hull, V.; García, C.M.; Loiselle, S.A. Sediment resuspension by wind in a shallow lake of Esteros del Iberá (Argentina): A model based on turbidimetry. Ecol. Model 2005, 186, 63–76. [Google Scholar]
- Zijlema, M.; van Vledder, G.P.; Holthuijsen, L.H. Bottom friction and wind drag for wave models. Coast. Eng 2012, 65, 19–26. [Google Scholar]
- Martín, M.; López, J.A.; López, L.; Mantecón, R.; Cantos, R.; Coleto, I. Hidrogeologia del Parque Nacional de Donñana y su entorno; Instituto Tecnoìlogico Geominero de Espanña: Madrid, Spain, 1992. [Google Scholar]
- Siljeström, P.; Clemente, L.; Rodriguez-Ramirez, A. Clima. In Parque Nacional de Doñana; García Canseco, V., Ed.; Canseco Editores: Talavera de la Reina, Spain, 2002; pp. 43–56. [Google Scholar]
- Bayán, B.J.; Dolz, J. Las aguas superficiales y la marisma del Parque Nacional de Doñana. Revista de Obras Públicas 1995, 142, 17–29. [Google Scholar]
- Aragonés, D.; Díaz-Delgado, R.; Bustamante, J. Tratamiento de una Serie Temporal Larga de Imágenes Landsat Para la Cartografía de la Inundación Histórica de las Marismas de Doñana. Proceedings of the XI Congreso Nacional de Teledetección, Puerto de la Cruz, Tenerife, Spain, 21–23 September 2005; pp. 407–410.
- García, J.I.; Mintegui, J.A.; Robredo, J.C. La Vegetación en la Marisma del Parque Nacional de Doñana en Relación con su Régimen Hidráulico; Organismo Autónomo de Parques Nacionales: Madrid, Spain, 2005. [Google Scholar]
- Salvia, M.; Franco, M.; Grings, F.; Perna, P.; Martino, R.; Karszenbaum, H.; Ferrazzoli, P. Estimating flow resistance of wetlands using SAR images and interaction models. Remote Sens 2009, 1, 992–1008. [Google Scholar]
- Grings, F.; Ferrazzoli, P.; Karszenbaum, H.; Tiffenberg, J.; Kandus, P.; Guerriero, L.; Jacobo-Berrles, J.C. Modeling temporal evolution of junco marshes radar signatures. IEEE Trans. Geosci. Remote Sens 2005, 43, 2238–2245. [Google Scholar]
- Reschke, J.; Bartsch, A.; Schlaffer, S.; Schepaschenko, D. Capability of C-band SAR for operational wetland monitoring at high latitudes. Remote Sens 2012, 4, 2923–2943. [Google Scholar]
- Kuenzer, C.; Guo, H.; Huth, J.; Leinenkugel, P.; Li, X.; Dech, S. Flood mapping and flood dynamics of the Mekong delta: ENVISAT-ASAR-WSM based time series analyses. Remote Sens 2013, 5, 687–715. [Google Scholar]
- Kussul, N.; Shelestov, A.; Skakun, S. Flood Monitoring on the Basis of SAR Data. In Use of Satellite and in-situ Data to Improve Sustainability, NATO Science for Peace and Security Series C: Environmental Security; Kogan, F., Powell, A., Fedorov, O., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 19–29. [Google Scholar]
- Skakun, S. A neural network approach to flood mapping using satellite imagery. Comput. Inform 2010, 29, 1013–1024. [Google Scholar]
- Cossu, R.; Schoepfer, E.; Bally, P.; Fusco, L. Near real-time SAR-based processing to support flood monitoring. J. Real Time Image Process 2009, 4, 205–218. [Google Scholar]
- Ramos, A.; Martí-Cardona, B.; Rabadà, J.; Dolz, J. Hydrometeorology and Heat Balance in a Shallow Wetland: Contribution of Field Data and Remote Sensing to the Understanding of Doñana Marshes. Proceedings of the International Conference on Ecohydrology and Climate Change, Tomar, Portugal, 10–12 September 2009.
- Rosich, B.; Meadows, P. Absolute Calibration of ASAR Level 1 Products Generated with PF-ASAR; ESA-ESRIN: Frascati, Italy, 2004. [Google Scholar]
- Kozlov, I.E.; Kudryavtsev, V.N.; Johannessen, J.A.; Chapron, B.; Dailidiene, I.; Myasoedov, A.G. ASAR imaging for coastal upwelling in the Baltic Sea. Adv. Space Res 2012, 50, 1125–1137. [Google Scholar]
- Marti-Cardona, B.; Dolz-Ripolles, J.; Lopez-Martinez, C. Wetland inundation monitoring by the synergistic use of ENVISAT/ASAR imagery and ancilliary spatial data. Remote Sens. Environ 2013, 139, 171–184. [Google Scholar]
- Díaz-Delgado, R.; Bustamante, J.; Pacios, F.; Aragonés, D. Hydroperiod of Doñana Marshes: Natural or Anthropic Origin of Inundation Regime? Proceedings of the 1st GlobWetland Symposium: Looking at Wetlands from Space, Frascati, Italy, 19–20 October 2006.
- Marti-Cardona, B.; Dolz-Ripolles, J. On the Synergistic Use of Envisat/ASAR Imagery and Ancillary Spatial Data for Monitoring Doñana Wetlands. Proceedings of the ESA Living Planet Symposium, Edinburgh, UK, 9–13 September 2013.
- Marti-Cardona, B.; Dolz-Ripolles, J.; Lopez-Martinez, C. Imágenes SAR para la Cartografía de Doñana: Beneficios del Filtrado Asistido por Información Espacial Auxiliar. Proceedings of the XV Congreso de la Asociación Española de Teledetección, Madrid, Spain, 22–24 October 2013.
- Mahalanobis, P.C. On the generalized distance in statistics. Proc. Natl. Inst. Sci. (Calcutta) 1936, 2, 49–55. [Google Scholar]
- Luque, C.J.; Rubio-Casal, A.E.; Álvarez, A.A.; Muñoz, J.; Vecino, I.; Doblas, D.; Leira, P.; Redondo, S.; Castillo, J.; Mateos, E.; et al. Memoria de Vegetación: Parque Nacional de Doñana. Proyecto de Cartografía y Evaluación de la Flora y Vegetación Halófita y de los Ecosistemas de Marismas que se encuentren dentro de la Red de Espacios Naturales Protegidos de Andalucía; Consejería de Medio Ambiente de la Junta de Andalucía & Universidad de Sevilla: Sevilla, Spain, 2005. [Google Scholar]
- García-Murillo, P.; Fernández-Zamudio, R.; Cirujano, S.; Sousa, S. Flora y vegetacioìn de la marisma de Donñana en el marco del proyecto de restauracioìn ecoloìgica Donñana 2005. Limnetica 2007, 2, 319–330. [Google Scholar]
- Dolz, J.; Bladé Castellet, E.; Gili, J.A. Modelo Numérico de la Hidrodinámica de la Marisma de Doñana. In Doñana, Agua y Biosfera; García Novo, F., Marín Cabrera, C., Eds.; Confederación Hidrográfica del Guadalquivir, Ministerio de Medio Ambiente: Madrid, Spain, 2005; pp. 149–150. [Google Scholar]
- Iberaula. Available online: http://www.iberaula.es (accessed on 6 May 2013).
- Roe, P.L. Approximate Riemann, solvers, parameter vectors, and difference schemes. J. Comput. Phys 1981, 43, 357–372. [Google Scholar]
- Vázquez-Cendón, M.E. Improved treatment of source terms in upwind schemes for the shallow water equations in channels with irregular geometry. J. Comput. Phys 1999, 148, 497–526. [Google Scholar]
- Bladé, E.; Cea, L.; Corestein, G.; Escolano, E.; Puertas, J.; Vázquez-Cendón, E.; Dolz, J.; Coll, A. Iber—River modelling simulation tool. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería 2014, 30, 1–10. [Google Scholar]
- Bladé, E.; Gómez-Valentín, M.; Dolz, J.; Aragón-Hernández, J.L.; Corestein, G.; Sánchez-Juny, M. Integration of 1D and 2D finite volume schemes for computations of water flow in natural channels. Adv. Water Resour 2012, 42, 17–29. [Google Scholar]
- Munk, W.H. Wind stress on water: An hypothesis. Q. J. R. Meteorol. Soc 1955, 81, 320–332. [Google Scholar]
- Van Dorn, W.G. Wind stress on an artificial pond. J. Mar. Res 1953, 12, 249–276. [Google Scholar]
- Hsu, S.A.; Meindl, E.A.; Gilhousen, D.B. Determining the power-law wind-profile exponent under near-neutral stability conditions at sea. J. Appl. Meteorol 1994, 33, 757–765. [Google Scholar]
- Arya, S.P. Introduction to Micrometeorology, 2nd ed.; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Charnock, H. Wind stress on a water surface. Q. J. R. Meteorol. Soc 1955, 81, 639–640. [Google Scholar]
- Hsu, S.A. Estimating overwater friction velocity and exponent of power-law wind profile from gust factor during storms. J. Waterw. Port Coast. Ocean Eng 2003, 129, 174–177. [Google Scholar]
- Donelan, M. The Dependence of the Aerodynamic Drag Coefficient on Wave Parameters. Proceedings of the First International Conference on Meteorology and Air-Sea Interaction of the Coastal Zone, The Hague, The Netherlands, 1982; pp. 381–387.
- Bradley, E.F.; Coppin, P.A.; Godfrey, J.S. Measurements of sensible and latent heat flux in the western equatorial Pacific Ocean. J. Geophys. Res.: Ocean 1991, 96, 3375–3389. [Google Scholar]
- Yelland, M.; Taylor, P.K. Wind stress measurements from the open ocean. J. Phys. Oceanogr 1996, 26, 541–558. [Google Scholar]
- Mitsuta, Y.; Tsukamoto, O. Drag coefficients in light wind. Bull. Disaster Prev. Res. Inst 1978, 28, 25–32. [Google Scholar]
- Wüest, A.; Lorke, A. Small-scale hydrodynamics in lakes. Annu. Rev. Fluid Mech 2003, 35, 373–412. [Google Scholar]
- Ibáñez, E. Validación de Modelos Digitales del Terreno de Precisión a Partir de Datos Láser Escáner Aerotransportado. Aplicación a la Marisma del Parque Nacional de Doñana. Universitat Politècnica de Catalunya, Escola Tècnica Superior d’Enginyers de Camins, Canals i Ports de Barcelona, Barcelona, Spain, 2008. [Google Scholar]
- Prestininzi, P.; di Baldassarre, G.; Schumann, G.; Bates, P.D. Selecting the appropriate hydraulic model structure using low-resolution satellite imagery. Adv. Water Resour 2011, 34, 38–46. [Google Scholar]
- Bates, P.D.; de Roo, A.P.J. A simple raster-based model for flood inundation simulation. J. Hydrol 2000, 236, 54–77. [Google Scholar]
- Horritt, M.S.; Bates, P.D. Predicting floodplain inundation: Raster-based modelling versus the finite-element approach. Hydrol. Process 2001, 15, 825–842. [Google Scholar]

| Acquisition Date | ASAR Swath | Incidence Angle Range (°) | Acquisition Mode | Polarization Configuration |
|---|---|---|---|---|
| 19 October 2006 | IS1 | 15.0–22.9 | Alternated polarization | HH/HV |
| 1 March 2006 | IS4 | 31.0–36.3 | Image | HH |
| 4 March 2006 | IS2 | 19.2–26.7 | Image | HH |
| Simulation | Wind Profile | Drag Formulation | Atmospheric Stability | Low Wind Speed Correction |
|---|---|---|---|---|
| S1 | Exponential | Constant | Neutral | No |
| S2 | Exponential | Van Dorn | Neutral | No |
| S3 | Logarithmic | Charnock | Non-neutral | No |
| S4 | Logarithmic | Charnock | Neutral | No |
| S5 | Logarithmic (exponential for low wind) | Charnock, (Wuest and Lorke for low wind) | Neutral | Yes |
| Case of Study | Computational Mesh (TIN) | Initial Volume (m3) | Initial Time | Final Time | |||
|---|---|---|---|---|---|---|---|
| Num. of Elements | Num. of Nodes | Min. Element Size (m) | Max. Element Size (m) | ||||
| Membrillo | 52,348 | 27,381 | 12.5 | 200 | 1,956,337 | 25 February 2006 0000 h | 4 March 2006 1,200 h |
| Ánsares | 7,352 | 3,804 | 13.6 | 398 | 550,000/600,000 | 18 October 2006 0000 h | 20 October 2006 0000 h |
| ASAR 01Mar06 | ASAR 04Mar06 | F med | |
|---|---|---|---|
| S1 | 0.78 | 0.74 | 0.76 |
| S2 | 0.78 | 0.77 | 0.77 |
| S3 | 0.78 | 0.76 | 0.77 |
| S4 | 0.79 | 0.76 | 0.77 |
| S5 | 0.79 | 0.76 | 0.77 |
| F med | 0.78 | 0.76 | 0.77 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ramos-Fuertes, A.; Marti-Cardona, B.; Bladé, E.; Dolz, J. Envisat/ASAR Images for the Calibration of Wind Drag Action in the Doñana Wetlands 2D Hydrodynamic Model. Remote Sens. 2014, 6, 379-406. https://doi.org/10.3390/rs6010379
Ramos-Fuertes A, Marti-Cardona B, Bladé E, Dolz J. Envisat/ASAR Images for the Calibration of Wind Drag Action in the Doñana Wetlands 2D Hydrodynamic Model. Remote Sensing. 2014; 6(1):379-406. https://doi.org/10.3390/rs6010379
Chicago/Turabian StyleRamos-Fuertes, Anaïs, Belen Marti-Cardona, Ernest Bladé, and Josep Dolz. 2014. "Envisat/ASAR Images for the Calibration of Wind Drag Action in the Doñana Wetlands 2D Hydrodynamic Model" Remote Sensing 6, no. 1: 379-406. https://doi.org/10.3390/rs6010379
APA StyleRamos-Fuertes, A., Marti-Cardona, B., Bladé, E., & Dolz, J. (2014). Envisat/ASAR Images for the Calibration of Wind Drag Action in the Doñana Wetlands 2D Hydrodynamic Model. Remote Sensing, 6(1), 379-406. https://doi.org/10.3390/rs6010379





