Feasibility of Ocean Acoustic Waveguide Remote Sensing (OAWRS) of Atlantic Cod with Seafloor Scattering Limitations
Abstract
:1. Introduction
2. Data Collection
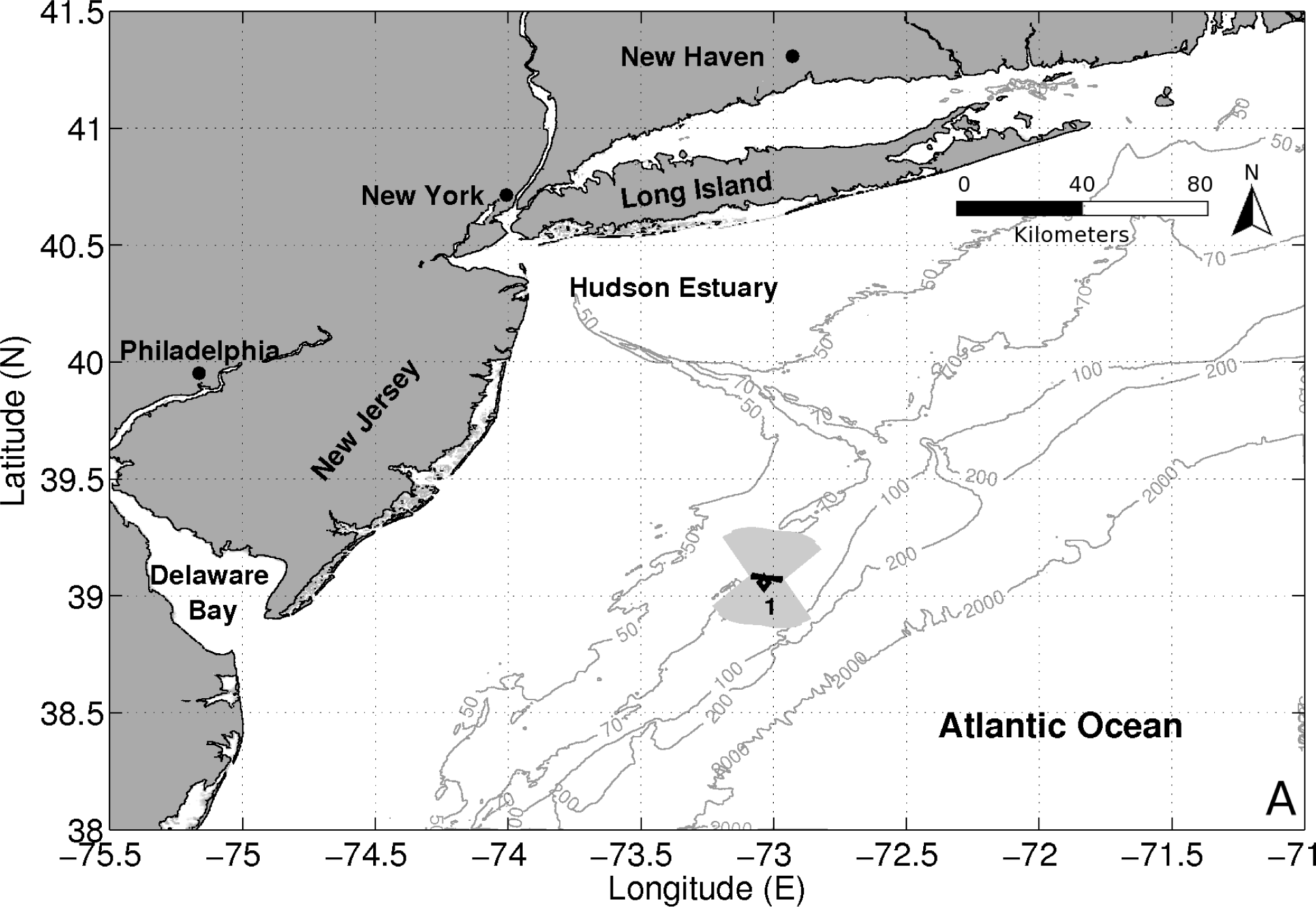
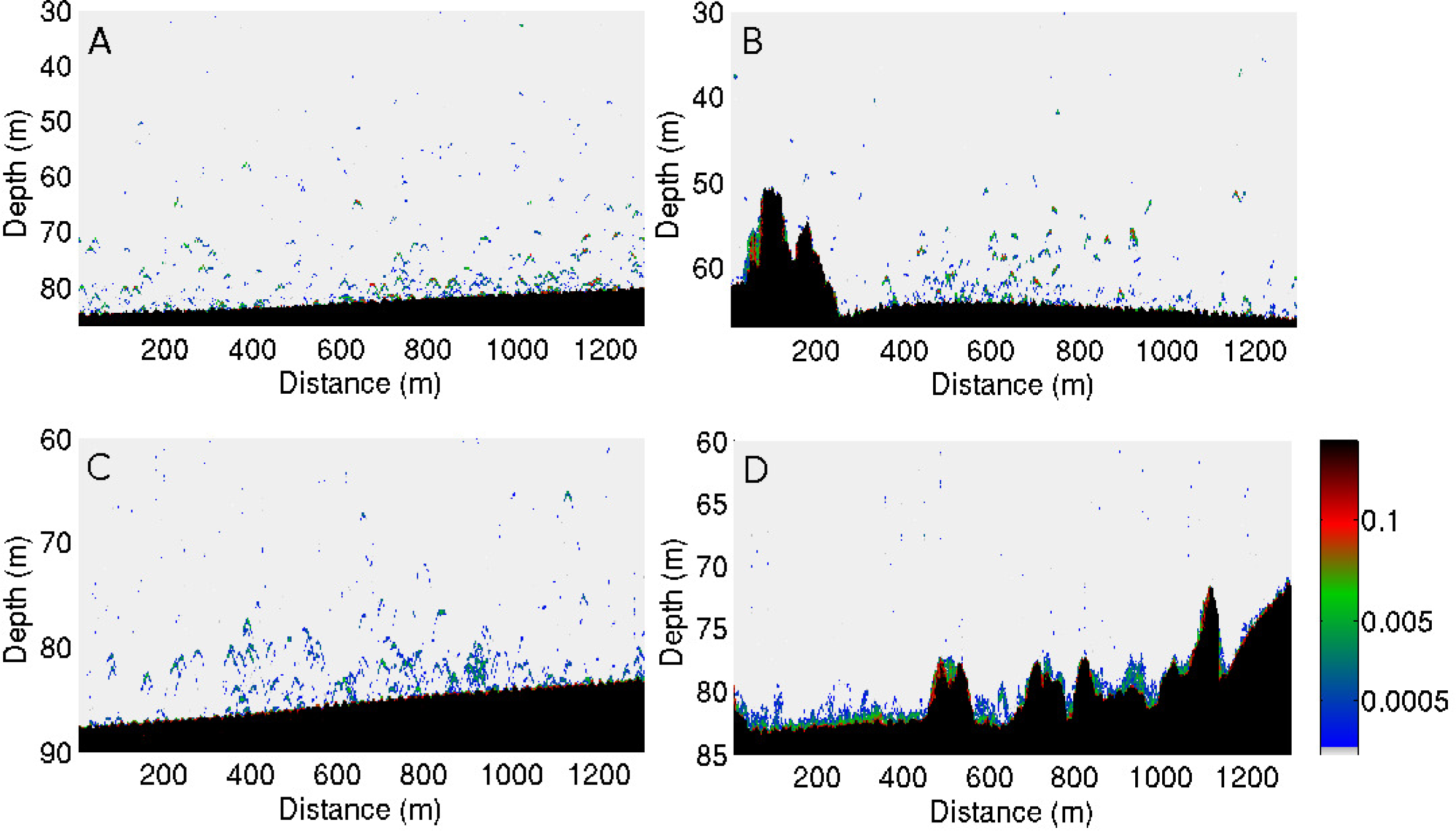
2.1. Seafloor Scattering Data Collection during OAWRS Experiments
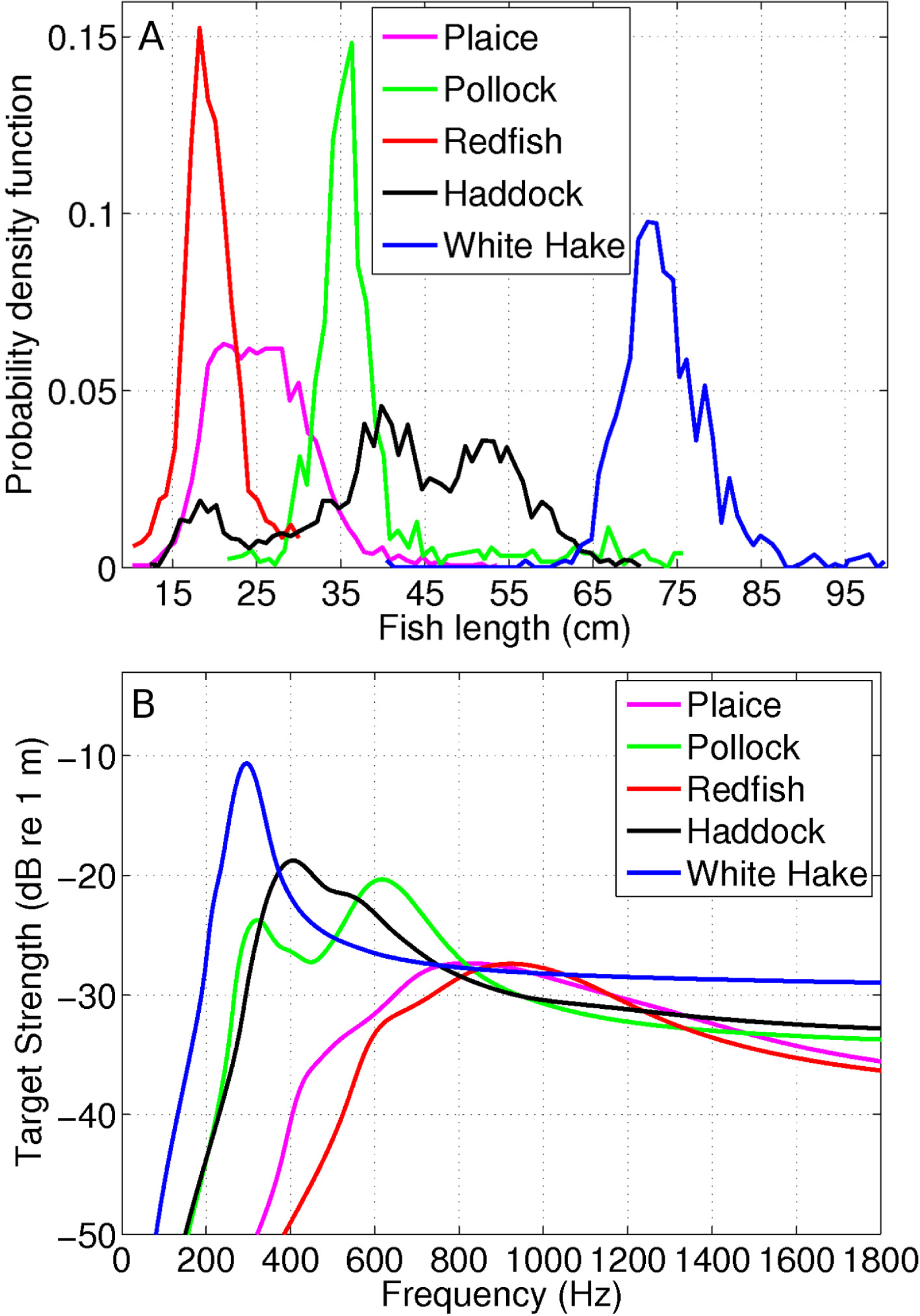
2.2. Measured Distribution of Atlantic Cod in Massachusetts State Waters
3. Methods
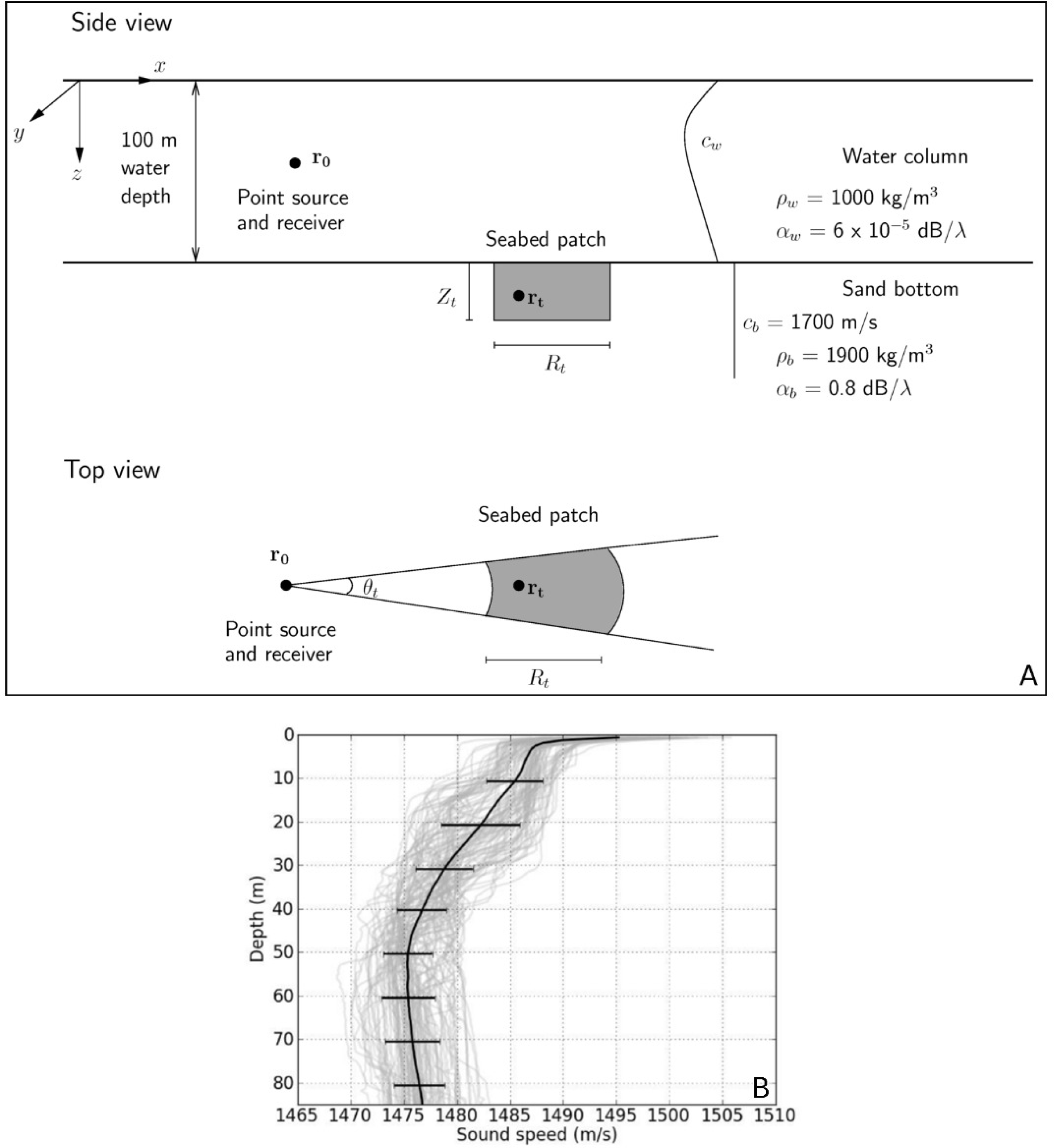
3.1. Estimation of Rayleigh–Born Seafloor Scattering Amplitude Statistics from Measured Seafloor Scattering
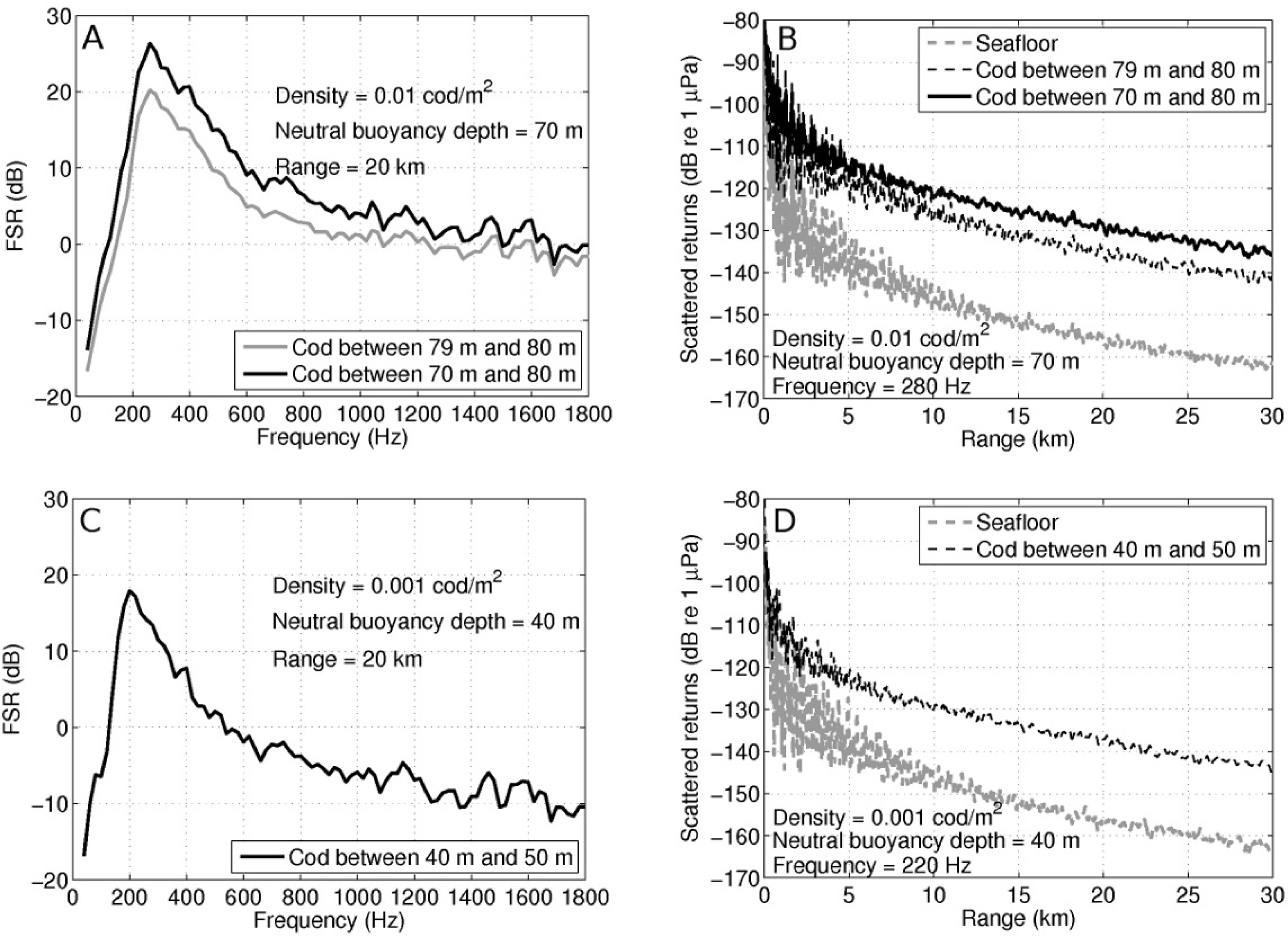
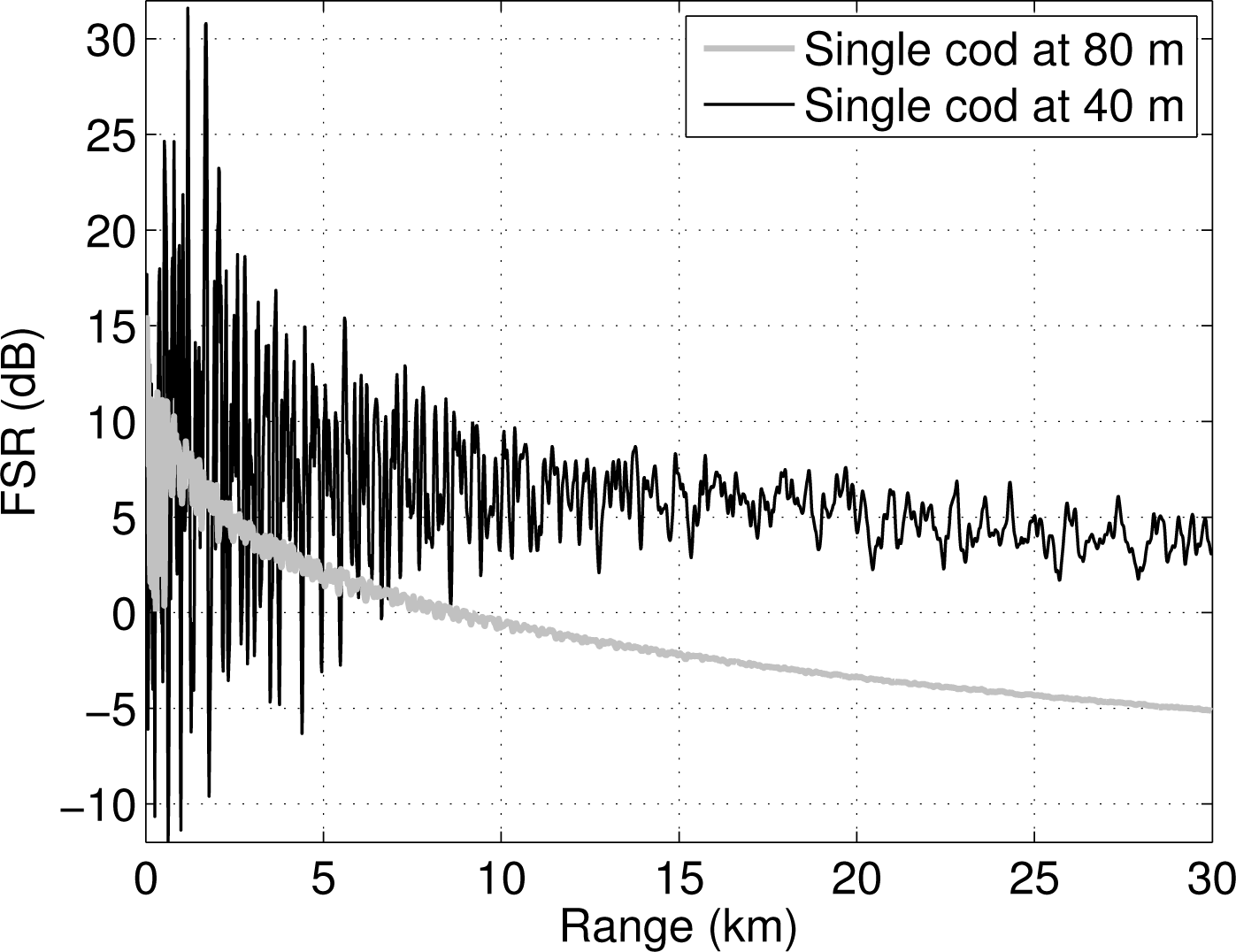
3.2. Fish-to-Seafloor Scattering Ratio
4. Results
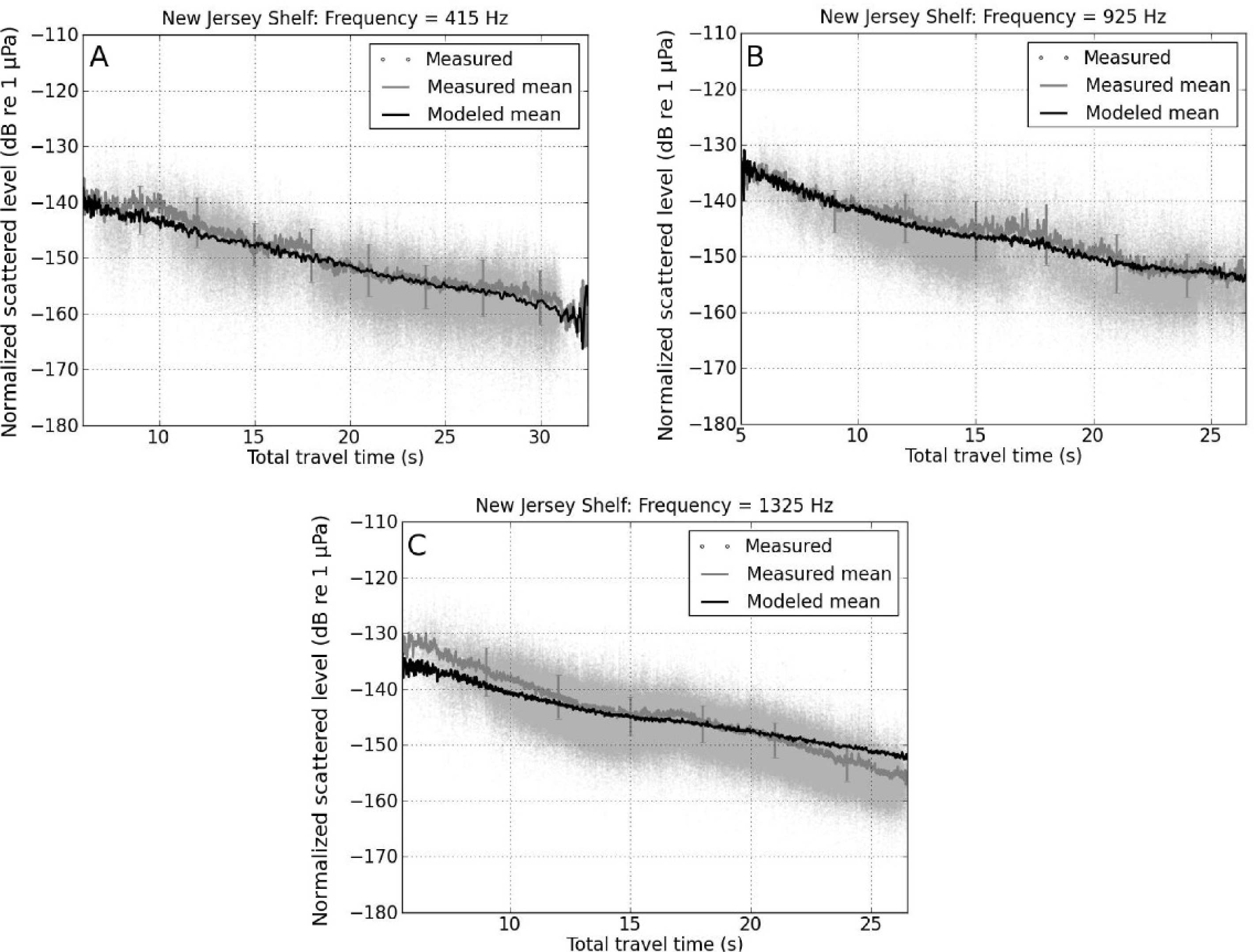
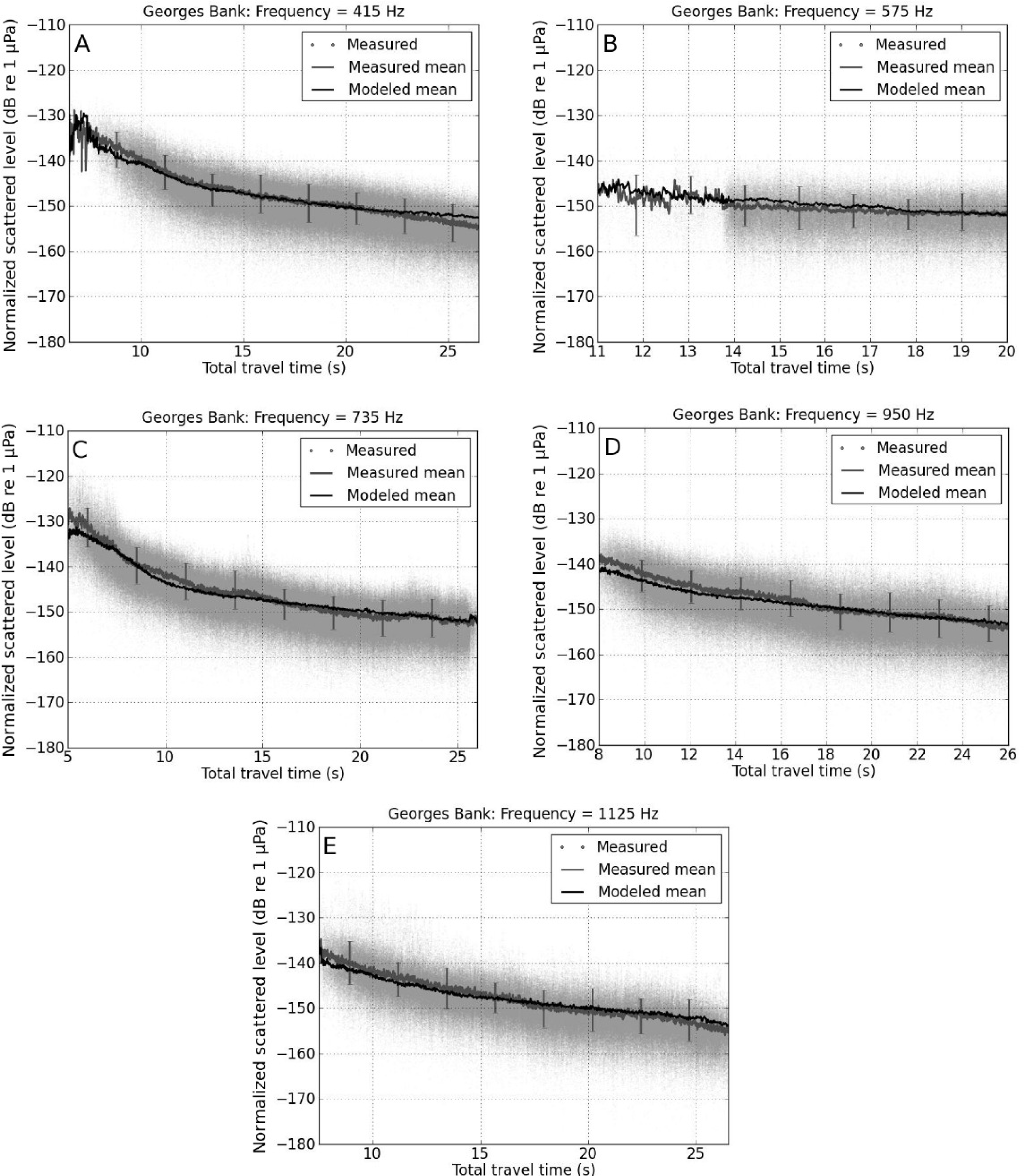
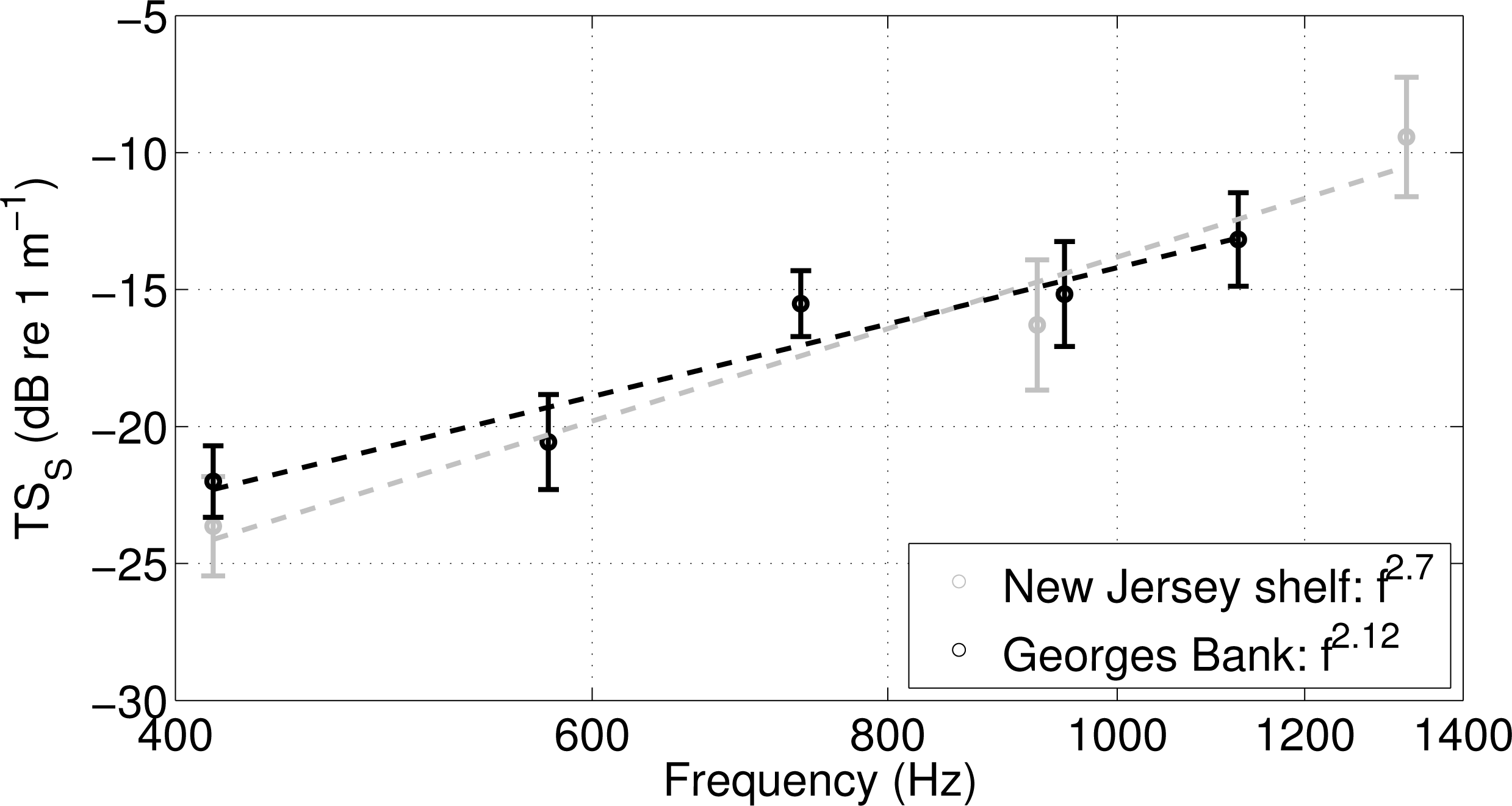
4.1. Experimental Estimation of Rayleigh-Born Seafloor Scattering Amplitude
4.2. OAWRS Detection of Atlantic Cod Aggregations and Individuals
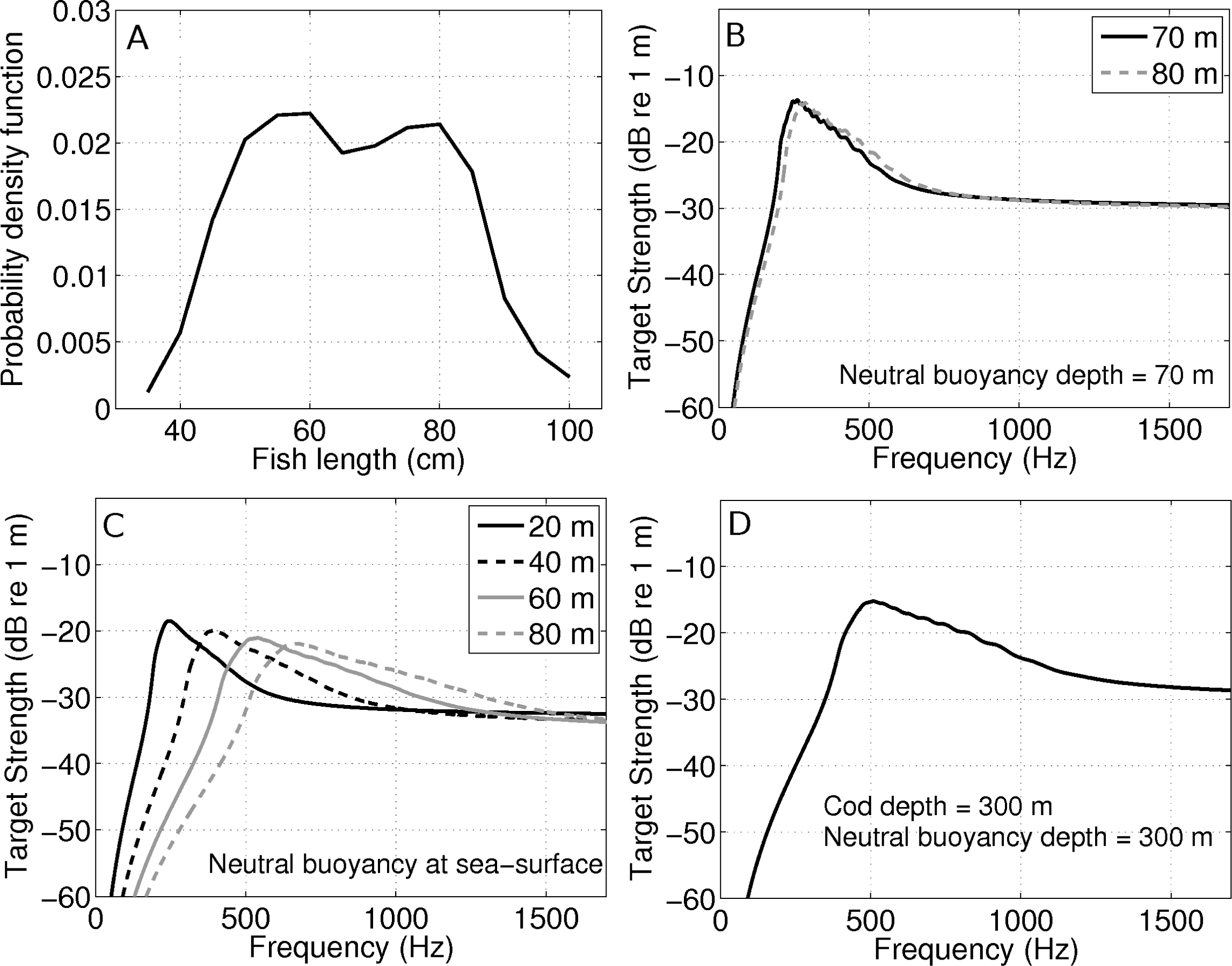
4.3. Theoretical Derivation of Rayleigh–Born Seafloor Scattering Amplitude
5. Discussion
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Northeast Fisheries Science Center. Ecology of the Northeast US Continental Shelf—Human Dimension; Technical Report; NFSC, National Oceanic And Atmospheric Administration: Woods Hole, MA, USA, 2012. [Google Scholar]
- Northeast Regional Office. 2011 Gulf of Maine Cod Baseline Assessment; Technical Report; Northeast Regional Office, National Oceanic And Atmospheric Administration: Gloucester, MA, USA, 2012. [Google Scholar]
- Northeast Fisheries Science Center. 55th Northeast Regional Stock Assessment Workshop (55th SAW): Assessment Summary Report; Ref Doc. 13-01; National Marine Fisheries Service: Woods Hole, MA, USA, 2013; p. 41. [Google Scholar]
- Myers, R.; Hutchings, J.; Barrowman, N. Hypotheses for the decline of cod in the North Atlantic. Mar. Ecol. Progr. Series 1996, 138, 293–308. [Google Scholar]
- Hutchings, J. Spatial and temporal variation in the density of northern cod and a review of hypotheses for the stock’s collapse. Can. J. Fish. Aquat. Sci 1996, 53, 943–962. [Google Scholar]
- Kerry, J. Following Field Hearing, Kerry Presses Urgent Next Steps to Aid Fishermen; Press Release: Washington, D.C., USA, 2011. [Google Scholar]
- Kerry, J. Kerry Urges New Cod Assessment, Preparations for Economic Relief; Press Release: Washington, D.C., USA, 2011. [Google Scholar]
- Hearing Before the Subcommittee on Oceans, Atmosphere, Fisheries, and Coast Guard, One Hundred Twelfth Congress, First Session US Senate Committe on Commerce, Science, and Transportation, March 8 2011; Technical Report; United States Senate, Govt. of United States: Washington, DC, USA, 2011.
- Makris, N.C.; Ratilal, P.; Jagannathan, S.; Gong, Z.; Andrews, M.; Bertsatos, I.; Godo, O.R.; Nero, R.W.; Jech, J.M. Critical population density triggers rapid formation of vast oceanic fish shoals. Science 2009, 323, 1734–1737. [Google Scholar]
- Makris, N.C.; Ratilal, P.; Symonds, D.T.; Jagannathan, S.; Lee, S.; Nero, R.W. Fish population and behavior revealed by instantaneous continental shelf-scale imaging. Science 2006, 311, 660–663. [Google Scholar]
- Christensen, V.; Guenette, S.; Heymans, J.; Walters, C.; Watson, R.; Zeller, D.; Pauly, D. Hundred-year decline of North Atlantic predatory fishes. Fish Fish 2003, 4, 1–24. [Google Scholar]
- Drinkwater, K. The response of Atlantic cod (Gadus morhua) to future climate change. ICES J. Mar. Sci. J. Conseil 2005, 62, 1327–1337. [Google Scholar]
- Hutchings, J.; Reynolds, J. Marine fish population collapses: Consequences for recovery and extinction risk. BioScience 2004, 54, 297–309. [Google Scholar]
- Ames, E. Atlantic cod stock structure in the Gulf of Maine. Fisheries 2004, 29, 10–28. [Google Scholar]
- Sund, O. Echo sounding in fishery research. Nature 1935, 135, 953. [Google Scholar]
- MacLennan, D.; Simmonds, E. Fisheries Acoustics; Chapman & Hall: London, UK, 1992. [Google Scholar]
- Misund, O. Underwater acoustics in marine fisheries and fisheries research. Rev. Fish Biol. Fisheries 1997, 7, 1–34. [Google Scholar]
- Medwin, H.; Clay, C. Fundamentals of Acoustical Oceanography; Academic Press: Waltham, MA, USA, 1997. [Google Scholar]
- Fish Stock Assessment 101 Series: Part 1Data Required for Assessing U.S. Fish Stocks; NOAA Fisheries: Silver Spring, MD, USA, 2012.
- Gerlotto, F.; Soria, M.; Fréon, P. From two dimensions to three: The use of multibeam sonar for a new approach in fisheries acoustics. Can. J. Fish. Aquat. Sci 1999, 56, 6–12. [Google Scholar]
- Freon, P.; Misund, O.A. Dynamics of Pelagic Fish Distribution and Behaviour-Effects on Fisheries and Stock Assessment; Fishing News Books: Cambridge, UK, 1999. [Google Scholar]
- Northeast Fisheries Science Center. 54th Northeast Regional Stock Assessment Workshop (54th SAW): Assessment Report; Ref Doc. 12–18; Northeast Fisheries Science Center, NOAA: Woods Hole, MA, USA, 2012; p. 600. [Google Scholar]
- Løvik, A.; Hovem, J.M. An experimental investigation of swim bladder resonance in fishes. J. Acoust. Soc. Am 1979, 66, 850–854. [Google Scholar]
- Urick, R.J. Principles of Underwater Sound; McGraw Hill: New York, NY, USA, 1983. [Google Scholar]
- Bucker, H.P. Wave propagation in a duct with boundary scattering (with application to a surface duct). J. Acoust. Soc. Am 1980, 68, 1768–1772. [Google Scholar]
- Ivakin, A.N. A unified approach to volume and roughness scattering. J. Acoust. Soc. Am 1998, 103, 827–837. [Google Scholar]
- Galinde, A.; Donabed, N.; Andrews, M.; Lee, S.; Makris, N.C.; Ratilal, P. Range-dependent waveguide scattering model calibrated for bottom reverberation in a continental shelf environment. J. Acoust. Soc. Am 2008, 123, 1270–1281. [Google Scholar]
- Morse, P.M.; Ingard, K.U. Theoretical Acoustics; Princeton University Press: New Jersey, NJ, USA, 1986. [Google Scholar]
- Andrews, M.; Chen, T.; Ratilal, P. Empirical dependence of acoustic transmission scintillation statistics on bandwidth, frequency, and range in New Jersey continental shelf. J. Acoust. Soc. Am 2009, 125, 111–124. [Google Scholar]
- Gong, Z.; Andrews, M.; Jagannathan, S.; Patel, R.; Jech, J.M.; Makris, N.C.; Ratilal, P. Low-frequency target strength and abundance of shoaling Atlantic herring (Clupea harengus) in the Gulf of Maine during the Ocean Acoustic Waveguide Remote Sensing 2006 Experiment. J. Acoust. Soc. Am 2010, 127, 104–123. [Google Scholar]
- Goff, J.A.; Kraft, B.J.; Mayer, L.A.; Schock, S.G.; Sommerfield, C.K.; Olson, H.C.; Gulick, S.P.S.; Nordfjord, S. Seabed characterization on the New Jersey middle and outer shelf: Correlatability and spatial variability of seafloor sediment properties. Mar. Geol 2004, 209, 147–172. [Google Scholar]
- Gurshin, C.; Howell, W.; Jech, J. Synoptic acoustic and trawl surveys of spring-spawning Atlantic cod in the Gulf of Maine cod spawning protection area. Fish. Res 2013, 141, 44–61. [Google Scholar]
- Howell, W. Synoptic Acoustic and Trawl Surveys to Characterize Biomass and Distribution of the Spring Spawning Aggregations of Atlantic Cod in Lpswich Bay, FY2009 Northeast Consortium Collaborative Research Award # 111675; Technical Report; 2011.
- Northeast Fisheries Science Center (NOAA). Northeast (NE) Multispecies Information Sheet Charter/Party and Recreational Fishing. Technical report, National Oceanic And Atmospheric Administration,. 2012. [Google Scholar]
- Advanced Sampling Technologies Research Group: Surveys, Northeast Fisheries Science Center.
- Love, R. Resonant acoustic scattering by swim bladder-bearing fish. J. Acoust. Soc. Am 1978, 64, 571–580. [Google Scholar]
- Jagannathan, S.; Bertsatos, I.; Symonds, D.; Chen, T.; Nia, H.; Jain, A.; Andrews, M.; Gong, Z.; Nero, R.; Ngor, L. others. Ocean acoustic waveguide remote sensing (OAWRS) of marine ecosystems. Mar. Ecol. Progr. Series 2009, 395, 137–160. [Google Scholar]
- Andrews, M.; Gong, Z.; Ratilal, P. High resolution population density imaging of random scatterers with the matched filtered scattered field variance. J. Acoust. Soc. Am 2009, 126, 1057–1068. [Google Scholar]
- Collins, M.D. A split-step Pade solution for the parabolic equation method. J. Acoust. Soc. Am 1993, 93, 1736–1742. [Google Scholar]
- Lawson, G.; Rose, G. The importance of detectability to acoustic surveys of semi-demersal fish. ICES J. Mar. Sci. J. Conseil 1999, 56, 370–380. [Google Scholar]
- Mello, L.G.; Rose, G. Using geostatistics to quantify seasonal distribution and aggregation patterns of fishes: An example of Atlantic cod (Gadus morhua). Can. J. Fish. Aquat. Sci. 2005, 62, 659–670. [Google Scholar]
- van der Kooij, J.; Righton, D.; Strand, E.; Michalsen, K.; Thorsteinsson, V.; Svedäng, H.; Neat, F.C.; Neuenfeldt, S. Life under pressure: Insights from electronic data-storage tags into cod swim bladder function. ICES J. Mar. Sci. J. Conseil 2007, 64, 1293–1301. [Google Scholar]
- Rose, G.; Porter, D. Target-strength studies on Atlantic cod (Gadus morhua) in Newfoundland waters. ICES J. Mar. Sci. J. Consei 1996, 53, 259–265. [Google Scholar]
- Arnold, G.; Walker, M. Vertical movements of cod (Gadus morhua L.) in the open sea and the hydrostatic function of the swim bladder. ICES J. Mar. Sci. J. Consei 1992, 49, 357–372. [Google Scholar]
- Harden Jones, F.; Scholes, P. Gas secretion and resorption in the swim bladder of the cod Gadus morhua. J. Comp. Physiol. B: Biochem. Syst. Environ. Physiol 1985, 155, 319–331. [Google Scholar]
- Lawson, G.L.; Rose, G.A. Seasonal distribution and movements of coastal cod (Gadus morhua L.) in Placentia Bay, Newfoundland. Fish. Res 2000, 49, 61–75. [Google Scholar]
- Brander, K. Spawning and Life History Information for North Atlantic Cod Stocks; Number 205; International Council for the Exploration of the Sea Copenhagen: Denmark, 1994. [Google Scholar]
- McQuinn, I.H.; Simard, Y.; Stroud, T.W.; Beaulieu, J.L.; Walsh, S.J. An adaptive, integrated “acoustic-trawl” survey design for Atlantic cod (Gadus morhua) with estimation of the acoustic and trawl dead zones. ICES J. Mar. Sci. J. Consei 2005, 62, 93–106. [Google Scholar]
- Gulf of Maine Area Census of Marine Life: Substrates.
- Rowe, S.; Hutchings, J.A. Sound production by Atlantic cod during spawning. Trans. Am. Fish. Soc 2006, 135, 529–538. [Google Scholar]
- Fudge, S.B.; Rose, G.A. Passive-and active-acoustic properties of a spawning Atlantic cod (Gadus morhua) aggregation. ICES J. Mar. Sci. J. Consei 2009, 66, 1259–1263. [Google Scholar]
- Pitcher, T. Behaviour of Teleost Fishes; Springer: Berlin/Heidelberg, Germany, 1992; Volume 7. [Google Scholar]
- Brawn, V.M. Sound production by the cod (Gadus callarias L.). Behaviour 1961, 18, 239–255. [Google Scholar]
- Ratilal, P.; Makris, N.C. A unified model for reverberation and submerged target scattering in shallow water. J. Acoust. Soc. Am 2000, 107, 2920–2920. [Google Scholar]
- Makris, N.C. The effect of saturated transmission scintillation on ocean acoustic intensity measurements. J. Acoust. Soc. Am 1996, 100, 769–783. [Google Scholar]
- Chen, T.; Ratilal, P.; Makris, N.C. Mean and variance of the forward field propagated through three-dimensional random internal waves in a continental-shelf waveguide. J. Acoust. Soc. Am 2005, 118, 3560–3574. [Google Scholar]
- Ratilal, P.; Makris, N.C. Mean and covariance of the forward field propagated through a stratified ocean waveguide with three-dimensional random inhomogeneities. J. Acoust. Soc. Am 2005, 118, 3532–3559. [Google Scholar]
- Lough, R. Essential fish habitat source document: Atlantic cod, Gadus morhua, life history and habitat characteristics. NOAA Tech. Memo. NMFS-NE 2004, 190, 94. [Google Scholar]
- Jensen, F.B.; Kuperman, W. A.; Porter, M. B.; Schmidt, H. Computational Ocean Acoustics; Springer Science+ Business Media: New York, NY, USA, 2011. [Google Scholar]
- Clay, C.S.; Medwin, H. Acoustical Oceanography; Wiley: New York, USA, 1977. [Google Scholar]
- Brekhovskikh, L.M.; Lysanov, I.P. Fundamentals of Ocean Acoustics; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- National Oceanic and Atmospheric Administration. Endangered and Threatened Species: Designation of Critical Habitat for Cook Inset Beluga Whale. Proposed Rules, Federal Register; Technical Report; 2011; 20179–20214.
- Allen, J.; Peterson, M.; Sharrard, G.; Wright, D.; Todd, S. Radiated noise from commercial ships in the Gulf of Maine: Implications for whale/vessel collisions. J. Acoust. Soc. Am 2012, 132, EL229–EL235. [Google Scholar]
- Arveson, P.; Vendittis, D. Radiated noise characteristics of a modern cargo ship. J. Acoust. Soc. Am 2000, 107, 118–129. [Google Scholar]
- Erbe, C. Underwater noise of whale-watching boats and potential effects on killer whales (Ornicus orca), based on an acoustic impact model. Mar. Mamm. Sci 2002, 18, 394–418. [Google Scholar]
- Au, W.W.; Hastings, M.C. Principles of Marine Bioacoustics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Medwin, H.; Blue, J.E. Sounds in the Sea: From Ocean Acoustics to Acoustical Oceanography; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Richardson, W. J.; Greene, C. R., Jr.; Malme, C. I.; Thomson, D.H. Marine Mammals and Noise; Academic Press Limited: London, UK, 1995. [Google Scholar]
- Division of Marine Fisheries. Industry-Based Survey for Gulf of Maine Cod, Pilot Study, Appendix G: Ancillary Data: Species of Interest Distribution Maps; Technical Report; Division of Marine Fisheries, Massachusetts Government: Boston, MA, USA, 2006. [Google Scholar]
- Mayo, R.; Terceiro, M. Assessment of 19 Northeast Groundfish Stocks through 2004. Proceedings of the 2005 Groundfish Assessment Review Meeting (2005 GARM), Northeast Fisheries Science Center, Woods Hole, MA, USA, 15–19 August 2005; pp. 15–19.
- State of Maine, Maine Department of Marine Resources. Interjurisdictional Fisheries Resource Monitoring and Assessment: Completion Report; Grant#NA05NMF4071035; Technical Report; Maine Department of Marine Resources: Augusta, ME, USA, 2010. [Google Scholar]
- Rayleigh, B.J.W.S. The Theory of Sound; Dover Publications: New York, NY, USA, 1945; Volume I and II. [Google Scholar]
A. Appendix

A.1. Analytical Formulation of Rayleigh–Born Volume Scattering from Seafloor
A.2. Efficient Estimation of Scattering from the Seafloor Field over Wide Areas
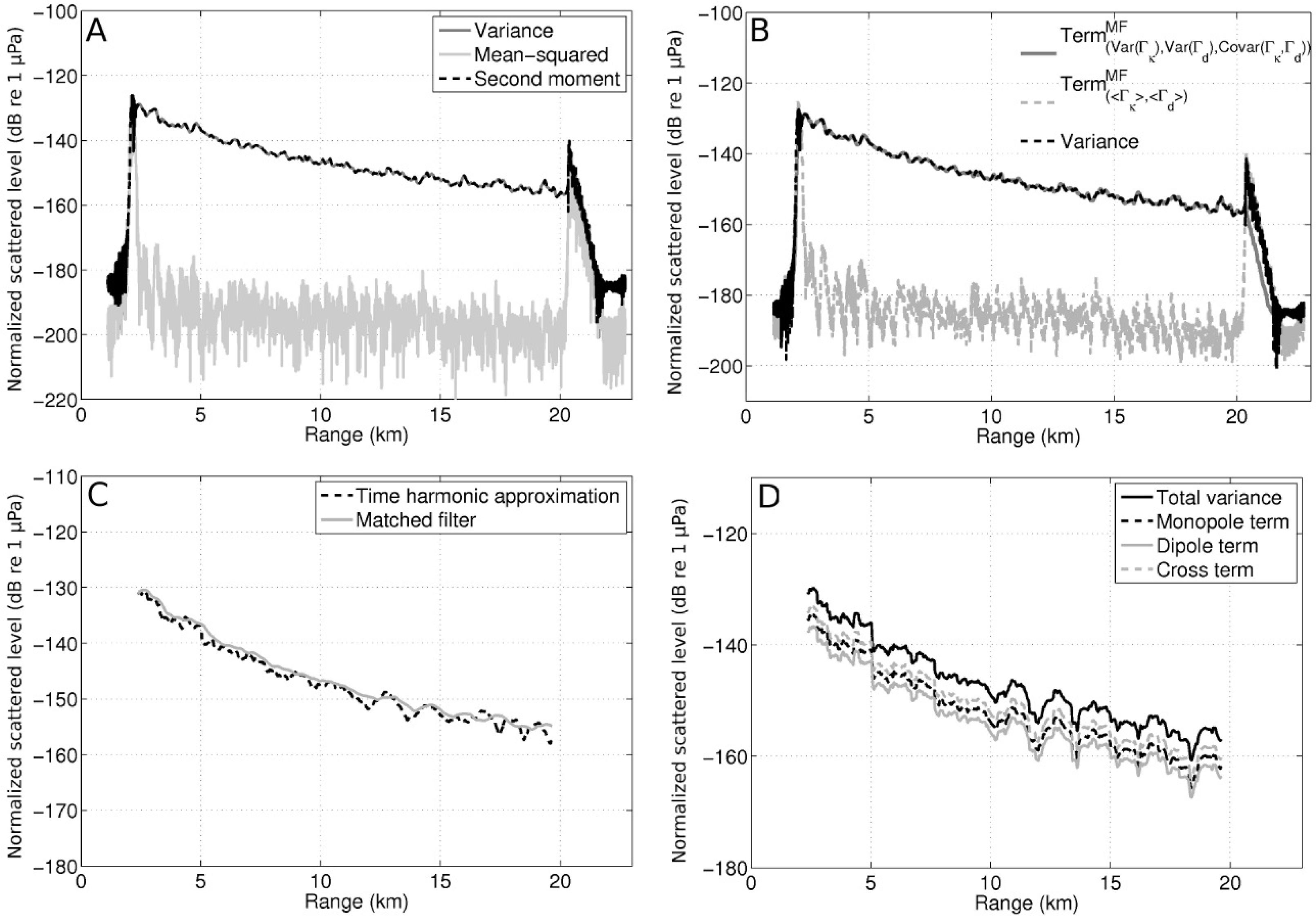
A.3. Full Analytical Expressions for the Total Moments of the Matched Filtered Scattered Field
A.4. Time Harmonic Approximation to the Matched Filtered Scattered Intensity

© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Jain, A.D.; Ignisca, A.; Yi, D.H.; Ratilal, P.; Makris, N.C. Feasibility of Ocean Acoustic Waveguide Remote Sensing (OAWRS) of Atlantic Cod with Seafloor Scattering Limitations. Remote Sens. 2014, 6, 180-208. https://doi.org/10.3390/rs6010180
Jain AD, Ignisca A, Yi DH, Ratilal P, Makris NC. Feasibility of Ocean Acoustic Waveguide Remote Sensing (OAWRS) of Atlantic Cod with Seafloor Scattering Limitations. Remote Sensing. 2014; 6(1):180-208. https://doi.org/10.3390/rs6010180
Chicago/Turabian StyleJain, Ankita D., Anamaria Ignisca, Dong Hoon Yi, Purnima Ratilal, and Nicholas C. Makris. 2014. "Feasibility of Ocean Acoustic Waveguide Remote Sensing (OAWRS) of Atlantic Cod with Seafloor Scattering Limitations" Remote Sensing 6, no. 1: 180-208. https://doi.org/10.3390/rs6010180
APA StyleJain, A. D., Ignisca, A., Yi, D. H., Ratilal, P., & Makris, N. C. (2014). Feasibility of Ocean Acoustic Waveguide Remote Sensing (OAWRS) of Atlantic Cod with Seafloor Scattering Limitations. Remote Sensing, 6(1), 180-208. https://doi.org/10.3390/rs6010180




