Delineating Individual Trees from Lidar Data: A Comparison of Vector- and Raster-based Segmentation Approaches
Abstract
: Light detection and ranging (lidar) data is increasingly being used for ecosystem monitoring across geographic scales. This work concentrates on delineating individual trees in topographically-complex, mixed conifer forest across the California’s Sierra Nevada. We delineated individual trees using vector data and a 3D lidar point cloud segmentation algorithm, and using raster data with an object-based image analysis (OBIA) of a canopy height model (CHM). The two approaches are compared to each other and to ground reference data. We used high density (9 pulses/m2), discreet lidar data and WorldView-2 imagery to delineate individual trees, and to classify them by species or species types. We also identified a new method to correct artifacts in a high-resolution CHM. Our main focus was to determine the difference between the two types of approaches and to identify the one that produces more realistic results. We compared the delineations via tree detection, tree heights, and the shape of the generated polygons. The tree height agreement was high between the two approaches and the ground data (r2: 0.93–0.96). Tree detection rates increased for more dominant trees (8–100 percent). The two approaches delineated tree boundaries that differed in shape: the lidar-approach produced fewer, more complex, and larger polygons that more closely resembled real forest structure.1. Introduction
Remote sensing has been established as one of the primary tools for broad-scale analysis of forest systems. Metrics relating to forest structure such as tree height, canopy cover and biomass can be estimated using remote sensing [1–3]. More recently, as sensor technology has improved and expanded to yield higher resolution optical data as well as light detection and ranging (lidar) data, it has become increasingly possible to detect individual trees. The successful detection and delineation of individual trees is critical in forest science, allowing for studies of individual tree demography and growth modeling [4–6], understanding of wildlife habitat and behavior [7,8], and more precise measures of biomass in forests [9,10].
Many approaches have been developed to detect and delineate individual trees from remotely sensed data (Figure 1). Early on, studies focused on assessing individual trees based on optical imagery. Sheng, et al. [11] used stereoscopic aerial photographs to identify, model, and measure a single coniferous tree using photogrammetric techniques. Later studies used a variation of local maxima [12] and adaptive binarization [13] for tree detection, as well as region-growing [14], edge detection [15], and valley-following [16] for tree delineation.
With the wide introduction of lidar into remote sensing, an increasing number of studies have undertaken individual tree detection [17,18]. Through time, these studies have shown increased complexity of analyses, increased accuracy of results, and a focus on the use of lidar data alone. A combination of variable window size filtering [19,20], spatial wavelet analysis [5], k-means clustering [21], and morphological analyses [22] were used to identify trees and estimate their biophysical parameters. Brandtberg et al. [23] Gaussian-smoothed a canopy height model (CHM) at numerous scales to create a scale-space structure and then detected trees which were represented as “blobs” in the scale-space structure, while Gleason and Im [24] combined object recognition, local maxima filtering, and hill climbing algorithms to delineate them. Most commonly, a variation of region-growing algorithms was applied for tree delineation from CHM [20,25–28]. The latter approach was later used to predict tree volume on a semi-individual tree level [29]. The efficacies of a few of the above methods were compared in a coastal foothill region of Oregon [30]. All of the region-growing studies relied on first identifying the tree tops with a local maximum filter. In one case where tropical canopy was thick, [31] manually delineated trees to classify them into tree species. Kaartinen et al. [17] provide a comprehensive review of 33 tree detection methods, and found automated methods outperformed manual ones, especially with high trees.
More recent studies focus on full exploitation of the point cloud and do not transform the lidar data into a raster. Lee et al. [32] implemented an adaptive clustering algorithm similar to watershed segmentation except that the method was applied to the 3D lidar points. Their algorithm relies on training data to perform segmentation based on supervised learning. Li et al. [33] designed and tested an individual tree segmentation approach that does not require such training data. Their algorithm exploits the spacing between the tops of trees to identify and group points into a single tree based on simple rules of proximity and likely tree shape.
Simultaneous with developments in lidar technology has been the increase in spatial resolution of optical image sensors. Classification algorithms developed for courser imagery often perform poorly at fine scales due to high local heterogeneity [34–36], and thus finer resolution imagery has necessitated a change in the way imagery is processed: from pixel-based to object-based image analysis (OBIA). The OBIA approach first segments imagery into meaningful objects through the use of spectral and spatial context. This allows for image processing and Geographic Information System (GIS) functionality [37]. The OBIA approach is inherently multi-scalar, as image segments are captured and operate hierarchically. At the landscape scale, studies have successfully extracted biophysical forest inventory parameters from imagery [38] and used lidar to classify land covers [39,40]. At stand-scale, Ke et al. [41] used a combination of lidar and optical imagery to classify tree species. A number of geospatial image segmentation programs are available, including BerkeleyImageSeg [42] and Trimble eCognition [43].
Less research has been done using OBIA to extract individual trees [35,44], and there have been few comparisons of OBIA-derived approaches and lidar point cloud segmentation (one exception is Kaartinen et al. [17]). In this work, we compare two paradigms of segmentation for individual tree delineation. The first approach uses 3D lidar point cloud segmentation algorithm developed by Li, Guo, Jakubowski and Kelly [33] (hereafter called “lidar-derived”), and the second uses an OBIA approach with surfaces derived from lidar data (hereafter called “OBIA”). The latter analysis uses a novel method for correcting artifacts in a CHM by filling in erroneous height values. We evaluate both types of tree polygons in terms of their area, shape index, compactness, and ability to predict ground reference tree height, all across a gradient of tree densities. Finally, we classify the tree objects into species and species type, and validate the results against ground reference data using a 10-fold cross-validation.
2. Methods
2.1. Study Area Description
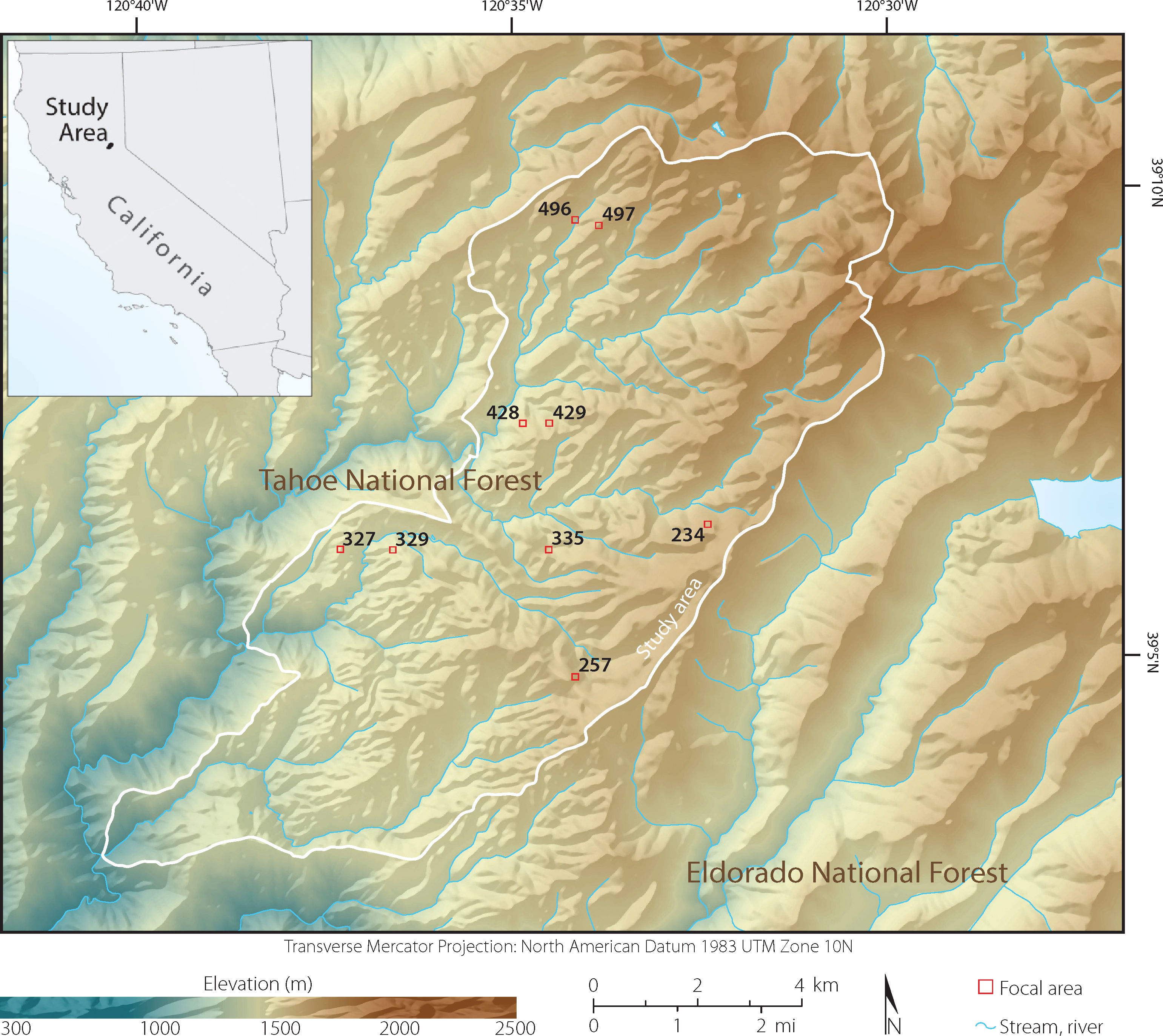
The study area (9,950 ha) is comprised of topographically complex mixed-conifer forest within California’s Sierra Nevada mountain range (center: 39°07’N, 120°36’W). The elevation varies from 600 to 2,186 m above sea level and much of the land is characterized by steep slopes (Figure 2). The forest is mostly managed by the US Department of Agriculture, Forest Service, with a few small private inholdings. The forest composition is predominantly conifer, with the dominant species being red and white fir (Abies magnifica and Abies concolor, respectively), sugar pine (Pinus lambertiana), ponderosa pine (Pinus ponderosa), and incense-cedar (Calocedrus decurrens). Less than 10 percent of the forest is non-conifer, dominated by the California black oak (Quercus kelloggii). Overall, the area experiences typical Mediterranean climate conditions: an average precipitation of 1,182 mm/year and frequent (5 to 15 year intervals) low-severity fires [45].
2.2. Ground Reference Data and Spatial Protocol
This experiment is part of a larger study—Sierra Nevada Adaptive Management Project—in which 411 circular plots (area = 500 m2) were established throughout the study area to characterize the fire and forest health ecology. The plots were centered at even coordinates (e.g., 700,000 m E, 4,333,000 m N; 700,500 m E, 4,333,500 m N, etc.) according to the Universal Transverse Mercator (UTM) system. In the work described here, we chose nine plots (Figures 2 and 3) representative of three overstory tree densities: low (<200 trees/ha), medium (≥200 to <400 trees/ha), and high (≥400 trees/ha). Plots were classified according to tree density. Within each plot, we geolocated trees according to a spatial protocol (described below), and collected measurements relating to trees (height, species, dominance, height to live crown, and diameter at breast height or DBH), shrub (species, and height), and fuels (fuel loads and ladder fuels). More information can be found in [46].
The trees were divided into three classes: overstory (DBH ≥ 19.5 cm), mid-size (5 ≤ DBH < 19.5) and small (DBH < 5 cm). All overstory trees were tagged with a unique identification number and georeferenced according to the spatial protocol. Although all trees within the plots were measured and described, in this work we only consider the overstory trees (n = 141) since the position of the smaller trees were not recorded. In addition to the overstory trees, we selectively measured and georeferenced large and/or isolated “marker” trees (n = 57) outside of the plots, for the purpose of improving the match between lidar and ground reference data. Both, the overstory and the marker trees (n = 198) were used in the analyses.
The plots and the trees were georeferenced in the following manner. First, we stabilized a Trimble GeoXH differential Global Positioning System (dGPS) in the most open canopy area within or near the plot (≤30 m from the plot center), where it recorded at least 300 measurements below positional dilution of precision (PDOP) of 5. In most circumstances, we recorded between 1,000 and 7,000 measurements for each plot position. We used a Trimble Zephyr antenna elevated 3 m from the ground to reduce multipath issues. The dGPS data were post-processed using University NAVSTAR Consortium (UNAVCO) and Continuously Operating Reference Stations (CORS), all located ≤20 km from the field measurements. To georeference the trees, we used an Impulse Laser Rangefinder and Impulse Electronic Compass. The electronic compass was carefully stabilized and calibrated on each plot before recording the trees’ positions. We used the “filter” option in the range finder, so that it would only record distances to a designated target (positioned on the measured trees). Since the rangefinder requires a clear line of sight to its target, some measurements were collected from two and sometimes three positions in plots with very high tree or shrub density. They were later combined in GIS. Since the error of the laser rangefinder is ≤2 cm, and the compass degree error ≤0.5 degrees, we only considered marker trees <50 m from the measuring unit. All tree positions were manually verified and in a few cases moved to increase the correspondence to the lidar data.
2.3. Multispectral Imagery
We used DigitalGlobe’s WorldView-2 data in the species prediction part of this work (described below). The imagery includes eight spectral and one panchromatic band (Table 1). A single image, acquired on June 14th, 2010 at 12:14 local time (sun elevation = 71.3°), was used for the analysis. The data was delivered in LV1B product level: 16-bit and radiometrically corrected. The sky was clear (cloud cover = 0.077 %) and no snow was present in any of the analyzed plots.
The data was orthorectified and then pan-sharpened before the analysis. The orthorectification was performed in EXELIS’s ENVI 5 [47] software using a combination of a Rational Polynomial Coefficients (RPC) sensor model and a 0.5 m digital elevation model (DEM) generated from the lidar data. The image and the DEM both used bilinear resampling. We used −24.557 m as the geoid offset based on National Geodetic Survey’s GEOID99 model computed at the center of the image scene. The data was projected into the UTM (zone 10S) coordinate system with respect to 1983 North American Datum (NAD83) at 50 cm pixel ground sample distance (GSD) to match the remainder of the data. We pan-sharpened the spectral data cube using the Gram-Schmidt algorithm and bilinear resampling [48].
2.4. LiDAR Data
Lidar data was acquired between 18 and 21 September 2008 by the National Center for Airborne Laser Mapping (NCALM) using the Optech GEMINI Airborne Laser Terrain Mapper (ALTM) sensor. Flying at an average height of 1,000 m AGL, the sensor collected up to 4 returns per pulse at an average of 9 and a minimum of 6 pulses/m2. We confirmed the horizontal accuracy to be 5.5–10 cm, and the average vertical accuracy to be 7.5 cm. The instrument was operated at a 70 kHz pulse rate frequency (PRF), with a 40 Hz scan frequency, and a ±20 degree scan angle. All even-numbered flight lines were flown twice in order to obtain high point density. The final point cloud often exceeded 20 points/m2 because of dense vegetation. All data were delivered in the UTM coordinate system with respect to NAD83 and the 1988 North American Vertical Datum using the NGS GEOID03 model. NCALM preprocessed the data to remove erroneous below-surface and air points. A 5 m search radius was used to identify and remove isolated points. The points were classified as ground and above-ground using TerraScan’s iterative triangle-building surface model classification [49]. From the entire point cloud, we extracted 100 m squares centered at plot centers.
2.5. Segmenting the Point Cloud into Individual Trees
Individual trees were segmented using a tree segmentation algorithm [33]. The algorithm exploits the spacing between the tops of trees to identify and group points into a single individual tree. An adaptive spacing threshold (dt) was used to improve the segmentation accuracy: dt = 2 and 1.5 m when tree heights were ≥15 and <15 m, respectively. This spacing threshold was chosen based on our knowledge of the forest in our study areas. We assume that the tree spacing at the upper lever is greater than 1 m, and that the taller trees have larger crown sizes and hence larger spacing. We did not use a minimum spacing rule or the shape index threshold as it did not improve the accuracy of the classification. Prior to the segmentation, the point cloud was normalized by subtracting the DEM ground values [32]. Following the segmentation, we converted the segmented point cloud into two-dimensional tree polygons by calculating the concave hull around the lidar points identified as a single tree (Figure 4). Further, each tree’s maximum-height point was extracted for later analysis.
2.6. Preparing the Data for Image Segmentation
We generated DSM (20 cm GSD) from the 100 m square point clouds using LAStools, which uses triangulated irregular network (TIN) interpolation to calculate the raster values. We determined that TIN interpolation was sufficient for generating these surfaces due to the very high spatial. LAStools used the maximum of all lidar points (ground and non-ground) within a moving kernel window to generate the DSM, whereas only the points classified as ground were used to generate the DEM. Preliminary analysis indicated that it was an appropriate resolution for accurate crown delineation—50 cm GSD surfaces were too course to create meaningful individual tree segments. We then generated a CHM by simple image subtraction (Equation (1)).
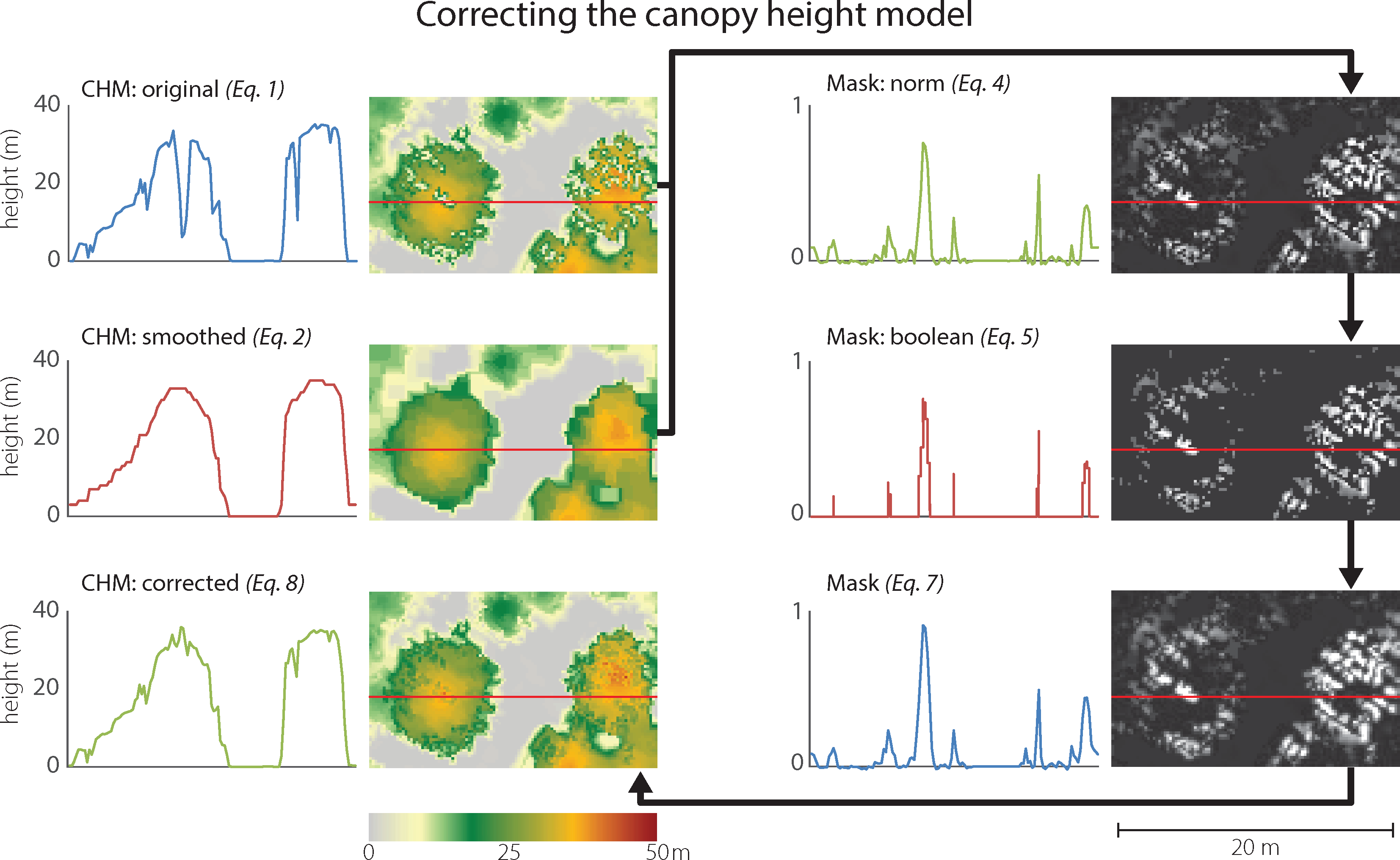
2.7. Correcting for CHM Artifacts
An accurate delineation of the tree crowns required generating a CHM at a high resolution (20 cm GSD), such that there was not always a lidar point within each pixel. As a result, the CHM contained a number of artifacts that prohibited successful segmentation using the OBIA framework. In particular, the CHM contained many severe elevation drops, especially in the middle of the canopy. The elevation drop artifacts are directly related to the scanning pattern of the lidar sensor, i.e., the z-value thin troughs are located in between the lines of lidar scans (Figure 5). The challenge is further complicated since the artifact pixels are not no-data values; rather their value is well within a typical CHM. This problem has been noted before, especially when attempting to delineate individual trees [50]. Filtering the image using a blurring or a median filter is one solution, albeit with negative consequences: the effective sharpness and thus the ability to identify the trees’ edges diminishes substantially (typically at least a 5 × 5 or a 7 × 7 kernel must be used to minimize the artifacts). Another option is to interpolate the surfaces at a higher pixel size, although that approach also suffers from similar consequences. We identified a new method to mitigate this problem.
First, a CHM was smoothed such that its continuity across tree crowns is restored and, simultaneously, the crowns’ distinct edges are preserved. This can be achieved with an adaptive enhanced Lee filter [51,52] or through morphological filtering [53]. The enhanced Lee filter reduces speckle while preserving texture. It uses the local coefficient of variation to classify pixels as either homogeneous, heterogeneous, or point targets, and then replaces the targeted pixels based on the classification. The second method uses two cycles of the morphological closing operator (dilation followed by erosion). Closing filtering fills the small holes and fuses thin troughs. In this work we used the morphology filter approach (Equation (2)) as it produced better results with our data.
Although the smoothed CHM was an improvement over the original, we strive to use the original CHM values as much as possible. The next few steps develop a technique that replaces the artifact pixels of the original CHM while preserving the surrounding original correct height values. Ultimately, we derived a continuous mask used to blend the two images: the correct pixels from CHM and the replaced artifact pixels from CHMsmooth.
First, a simple mask was generated by subtracting the artifact CHM from the smoothed CHM (Equation (3)). The simple mask was normalized (Equation (4)) to make the process reproducible for landscapes where the CHM values may vary to a smaller or larger degree.
A binary mask was created by reducing near-zero values to zero and all other values to one (Equation (5)). The Boolean mask was convolved with a simple matrix and the normalized mask was added (Equation (6)). To increase the impact of the normalized mask, we multiplied it by a constant, b. The convolution part of this operation ensures that no hard edges are generated when the smoothed CHM pixels are added to the original CHM. Setting b to a very high number decreases the feathering effect when adding back the smoothed CHM pixels.
The smoothed mask was normalized to create a standard mask range from zero to one (Equation (7)). The final CHM was compiled by removing the artifact pixels (via the inverse of Mask) and filling in smoothed CHM values where Mask permits (Equation (8)). Constant c was used to adjust the corrected values such that they match the original CHM. The process is further described and illustrated in Figure 5.
2.8. CHM Segmentation
We used the multi-resolution segmentation approach in eCognition 8.8 [43] to divide the CHM into individual trees. The segmentation process relies on user-specified parameters regarding the scale, shape and spectral criterion of homogeneity, and a compactness ratio. We used the estimation of scale parameter (ESP) tool to determine the optimal parameters [54], but the shape and the compactness were determined visually. All three parameters were altered depending on the particular segmentation resolution or purpose (e.g., segmenting small isolated trees vs. large clumped tree stands).
The CHM was first segmented into large, coarse objects, which were then subdivided into individual tree crowns and ground. The subdivision into tree crowns was an iterative process of classification and segmentation. The classification in this case was a means to an end rather than an attempt to produce correctly classified objects. For example, objects that were likely short trees surrounded by ground pixels (low mean z-values) were identified and segmented further into very small objects to discriminate between actual ground objects and the trees. The small tree objects were then merged together to produce meaningful tree polygons. Next, medium-height tree objects were identified at the coarse-level and similarly, steps were taken to transform them into meaningful polygons. This processed continued until all possible objects of interest were segmented. Baatz, Hoffmann and Willhauck [44] previously described this approach as “object-orient” OBIA, where meaningful objects are segmented, one object type at a time instead of trying to segment the entire image in one step. Various object metrics were used to isolate trees prior to each sub-segmentation (Table 2: segmentation). A single complicated rule set (74 steps) was developed and applied to the entire study area.
During preliminary analysis we determined that optical imagery did not improve the delineation of the tree crowns. We also did not use the lidar intensity as it was inconsistent across sensor acquisitions and varied depending on the gain control settings of the lidar sensor [55,56], the incidence angle, atmospheric dispersion and absorption, and bidirectional reflectance coefficients [57]. The segmentation was based on nine 90 × 90 m squares (8,100 m2) extracted from the corrected CHMs at plot centers to avoid any edge effects due to the raster filtering. The segments were smoothed by eCognition to remove the staircase-boundary effect, so that the polygon boundary no longer followed the edges of individual pixels.
2.9. Predicting Species
We used Waikato Environment for Knowledge Analysis (WEKA) software [58] to classify the segments into four individual tree species (Abies concolor, Pinus lambertiana, Pinus ponderosa, Psuedotsuga menziesii) and species types (e.g., pines vs. firs). WEKA is a collection of machine learning algorithms for data mining tasks developed by the Machine Learning Group at the University of Waikato. WEKA has proven to be an effective tool in classification, especially when many predictive attributes are available [59]. Two species, Calocedrus decurrens, and Quercus kelloggii, were eliminated from the analysis because of low sample size (n = 4, each).
We extracted a number of object metrics to feed the classification routines, including object shape, lidar, and multispectral image metrics (Table 2: classification). Additionally, we ran a feature optimization algorithm based on Pearson’s correlation coefficient to identify the most influential metrics (as measured by the correlation) and to avoid overfitting the classification models. All metrics were normalized prior to the classification. We identified two classifiers that best predicted the objects: LibLINEAR for individual species and the radial basis function (RBF) neural network for species type. LibLINEAR is a library for large-scale linear classification that supports logistic regression and linear support vector machines (SVM) [60]. We used the SVM classifier for predicting the tree species. An SVM classifier uses data close to the support vectors (class boundaries) to fit a hyperplane to the training data within the feature Space [61]. The RBF network uses k-means clustering to determine basis functions and then calculates logistic regression based on these functions. Multivariate Gaussian functions are then fitted to all classes [62].
2.10. Comparison of Segments
We compared the two segmentation approaches to each other and against the ground reference data. In validating the results to georeferenced trees, we evaluated the estimation of tree heights, species, and how tree detection varies across tree crown classes (e.g., dominant, intermediate, etc.).
In order to compare the two types of polygons, we first matched their tree height predictions to ensure that correct pairs of polygons were used for the comparison. Next, we compared the polygon shape characteristics by considering their area, shape index, and compactness. Shape index is a widely applicable measure of shape complexity as compared to a square: a higher index indicates a more complex polygon [63,64]. Jiao and Liu [65] found that, among other shape metrics, shape index is an effective descriptor of complexity. Similarly, compactness is a measure of complexity as compared to a circle [66]. Both metrics are described in Equations (9) and (10), where SI is shape index, C is compactness, P is perimeter, and A is area.
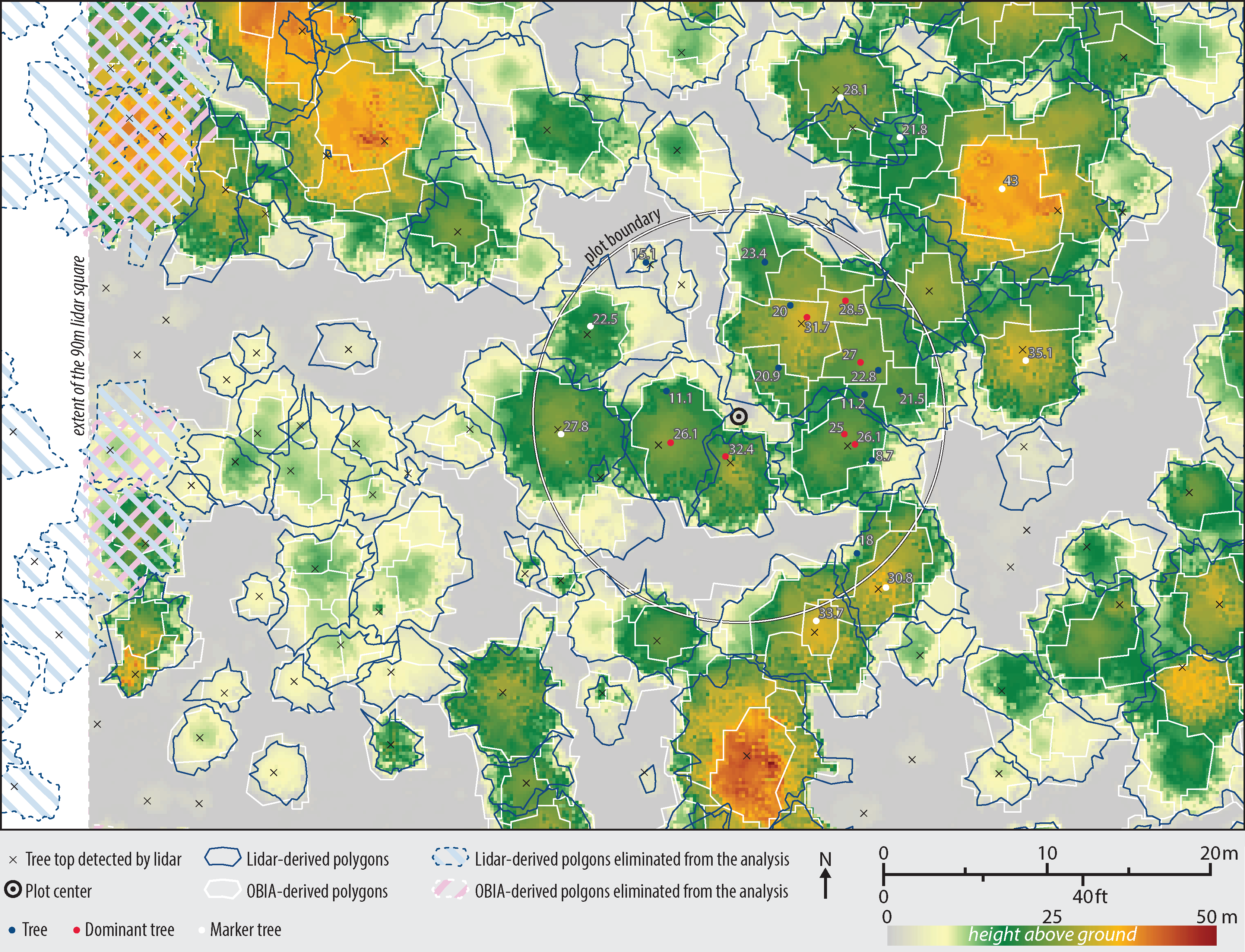
Since the lidar segmentation generated fewer polygons than OBIA, we used the former as a basis for comparison in order to avoid double-counting of the polygons. In particular, the tree top points as detected by the lidar segmentation algorithms were used to intersect and collect information from both types of polygons. All polygons that contact the 90 m CHM edges were eliminated from the analysis resulting in n = 949 (Figure 6).
3. Results
We used an OBIA approach to segment the CHM and a point cloud segmentation algorithm to segment the lidar data into individual trees. Segments at the edges of the considered areas were excluded from any of the analyses. Across all nine 90 × 90 m areas, a total of 2,875 objects were delineated using OBIA and 949 based on the lidar point cloud analysis. The OBIA method over-segmented many large trees, although in some cases, it correctly delineated smaller trees that the lidar approach had missed. This was especially true when the smaller trees were surrounded by large, taller species. Overall, the lidar-derived method produced larger polygons, especially for the tall and large trees. The agreements of tree height estimation between the ground reference data and the generated polygons were high for both methods. All dominant ground referenced trees were detected by both of the approaches; the tree detection rates dropped considerably for intermediate and suppressed trees, as well as for dead trees. Tree height accuracy declined in areas of high tree density.
3.1. Polygons vs. Ground Reference Data
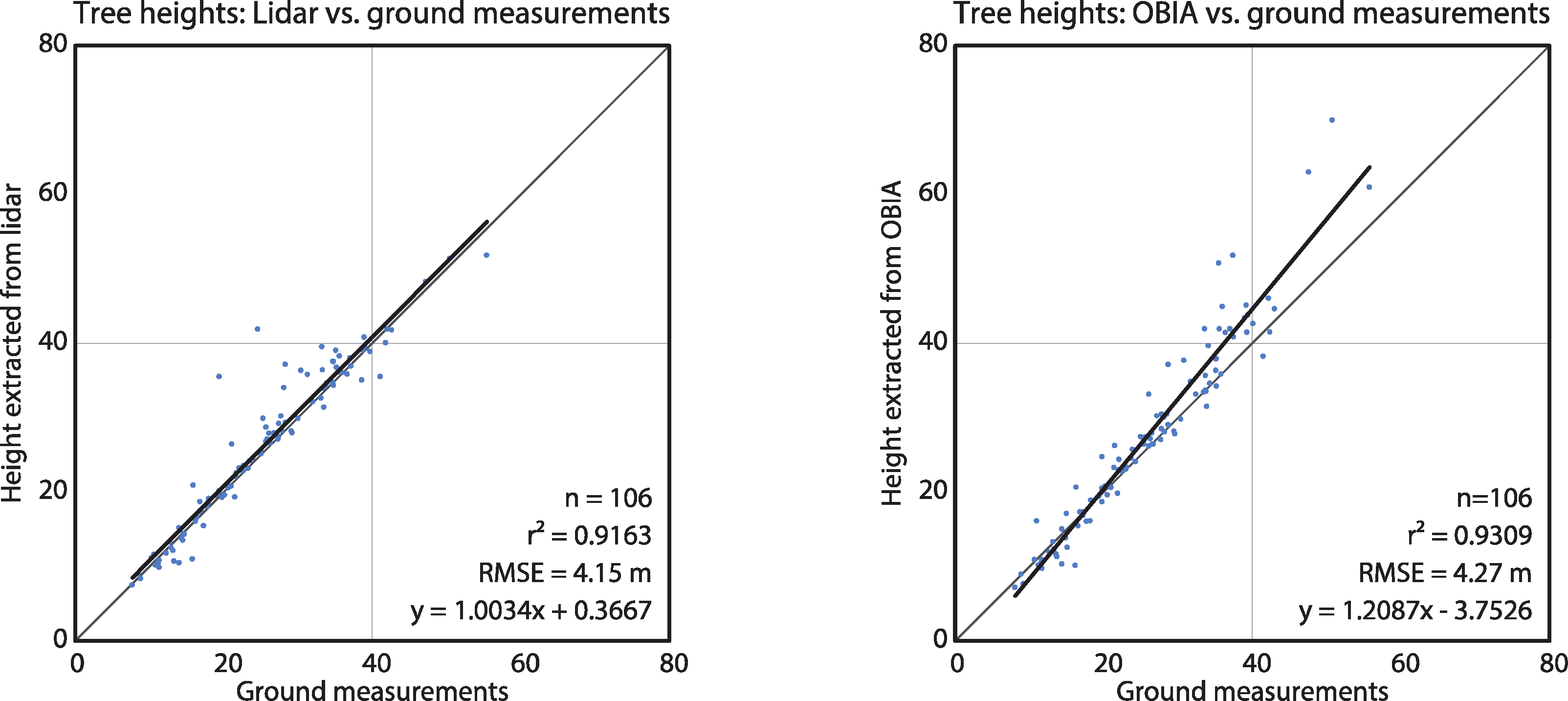
We intersected the ground reference tree points with lidar and OBIA polygons to validate the results. We cross referenced the tree heights measured on the ground against the maximum lidar z-value points within the lidar polygons, and the maximum pixel value of the corrected CHM within the OBIA polygons. In cases where there were more than one ground reference points within a polygon, we kept only the point that best matched the CHM height (n = 106). Pearson’s squared correlation coefficients for the lidar polygons and for the OBIA polygons vs. ground measurements were r2 = 0.9163 and r2 = 0.9309, respectively (Figure 7).
We also analyzed the rate of tree detection by both methods in various crown classes (Figure 8). All dominant overstory trees (DBH ≥ 19.5 cm) were detected by both of the segmentation approaches (n = 16). However, the rate of detection dropped when trees were occluded by taller or bigger trees. The OBIA method detected a larger percentage of the non-dominant trees. Both methods detected less than 50 percent of dead trees.
We used the tree-top points, as detected by the lidar point cloud segmentation algorithm, to cross reference the lidar and OBIA polygons. We present the results as a function of (1) the method used to derive the polygons and (2) tree density.
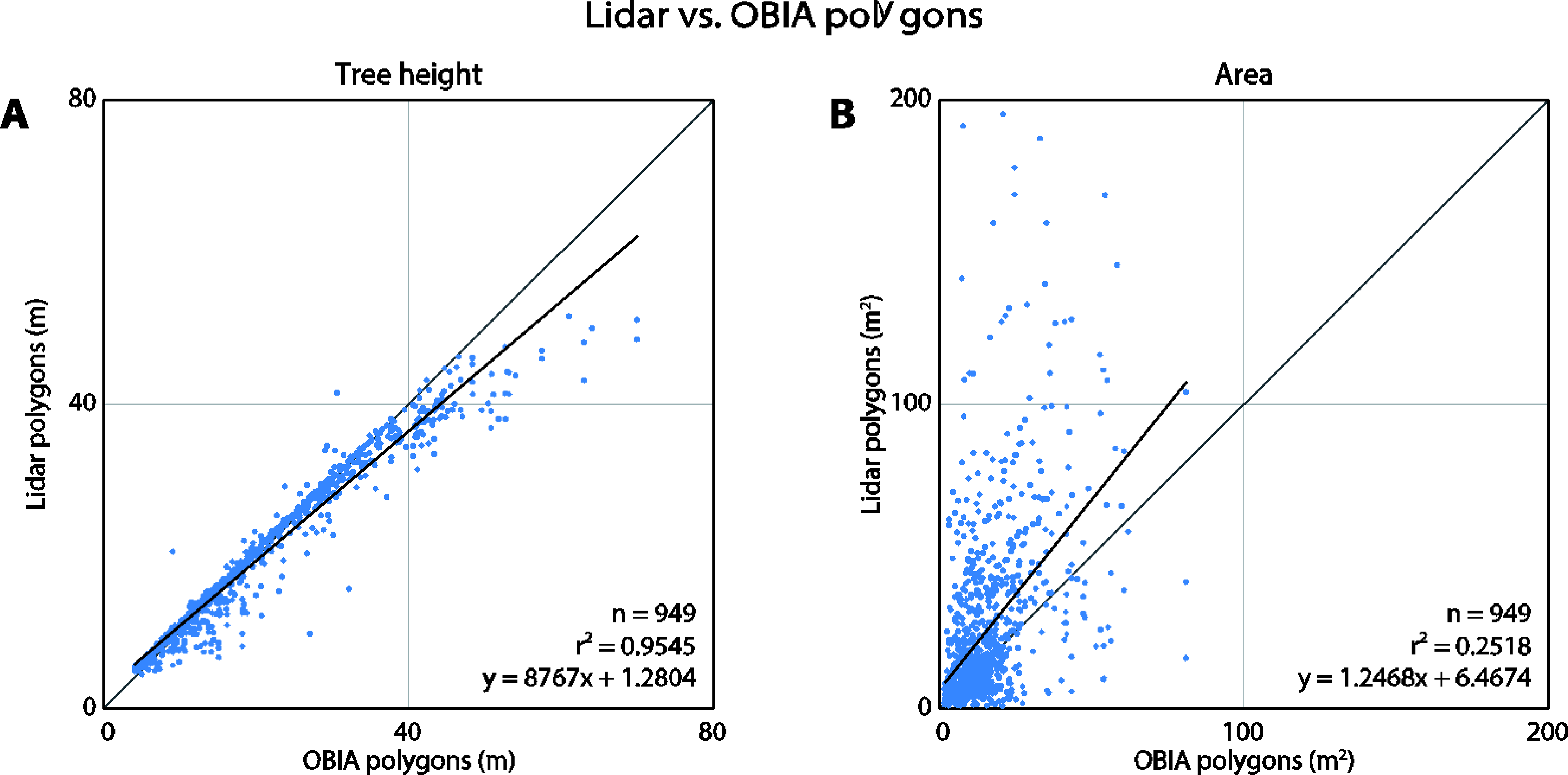
The tree heights derived by both methods correlate very well (r2 = 0.9545) indicating that the polygons detected the same trees (Figure 9). The OBIA approach estimated higher tree heights when predicting the tallest trees. The area, shape index, and compactness metrics differed significantly between the two methods. The area plot (Figure 9B) clearly reveals that the lidar-derived polygons tend to be larger than the OBIA polygons. The range of lidar polygons is twice that of the OBIA polygons. In general, the compactness and shape index plots indicate that the lidar polygons are more complex. Both approaches produced polygons that were much more complex than simple geometric polygons (circle or a square).
3.2. Tree Density Effects
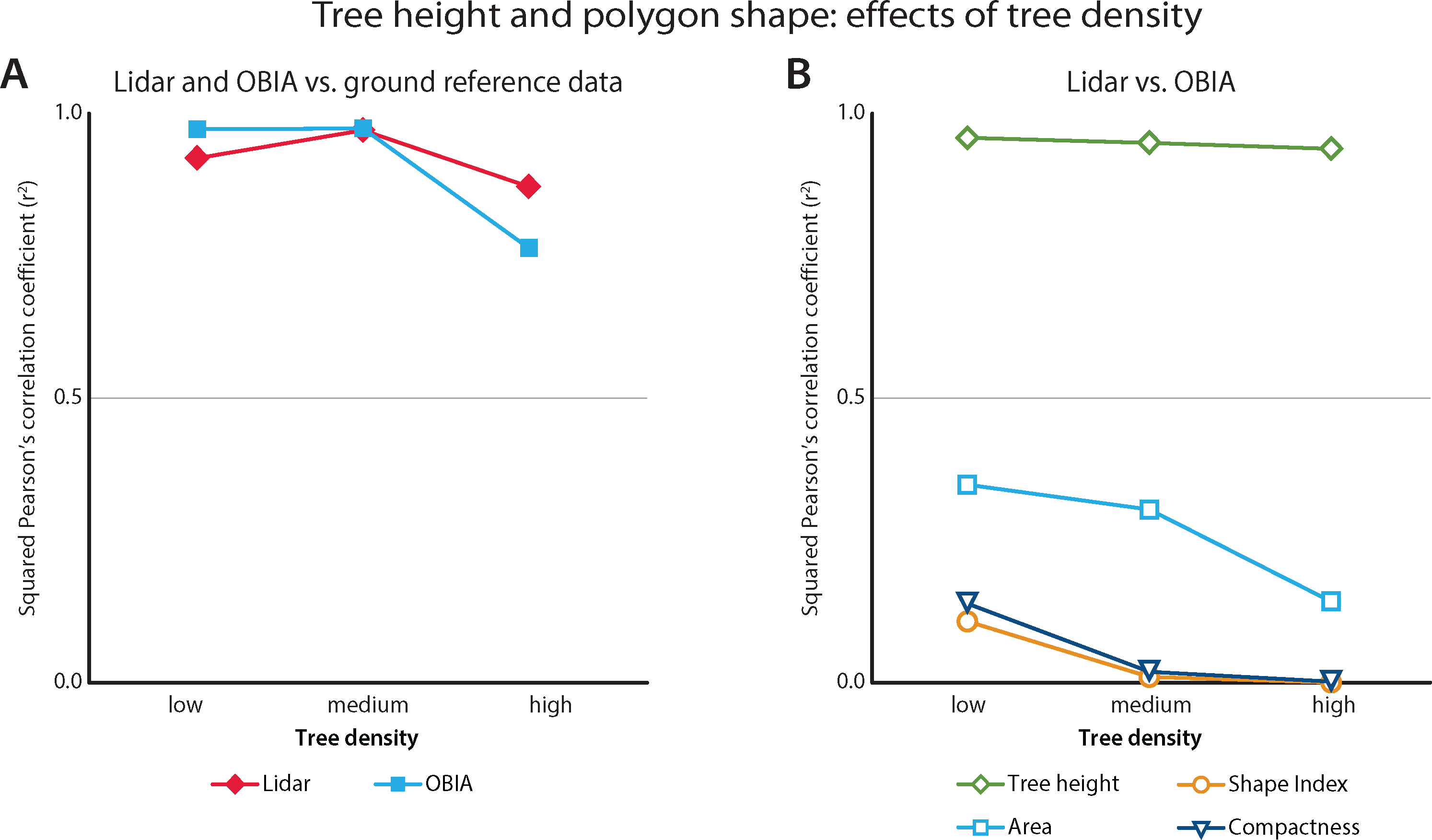
As expected, the tree density also affected tree height correlations. We summarize these effects with squared correlation coefficients as a function of tree density (Figure 10). Both methods performed best in areas with medium tree density when predicting the tree height. However, the OBIA method worked slightly better in low density areas, and considerably worse in high density areas.
The agreement between tree height predictions slightly declined in high tree density areas, but for the most part remained constant (r2 = 0.9596 vs. r2 = 0.9401 in low and high tree densities, respectively). The shape characteristics of the two polygon types were less correlated than the tree heights. The area correlation declined at high tree densities, where the lidar polygons were consistently larger than the OBIA polygons. OBIA polygons increased in complexity at higher tree densities and were therefore less similar to the lidar polygons.
3.3. Predicting Tree Species
We used all polygon features (Table 2) to predict individual species using the SVM algorithm from the LibLINEAR approach. The individual species predictions were poor: only 56 percent were correctly classified. However, the RBF neural network algorithm was able to correctly classify up to 75 percent of the species types (e.g., pines vs. firs). In the latter case, we used only six predictive metrics based on the suggestion from a feature optimization algorithm.
4. Discussion
The high Pearson’s squared correlation coefficients between tree polygons and the ground reference data indicate that both lidar and OBIA methods detected individual trees well: r2 = 0.9163 for the lidar-derived and r2 = 0.9309 for the OBIA-derived polygons. Further, the good fit with the OBIA approach also indicates that the CHM correction method worked well. While the lidar segmentation polygons were usually detected and delineated correctly, the locations of the tops of trees did not always match those of the ground reference data (Figure 6). This may be a result of trees that are leaning or not straight, as ground-reference positions were measured at the tree trunks, at breast-height level (1.3 m from the ground), as suggested by Brokaw and Thompson [67].
All of the dominant and most of the co-dominant trees were detected by both methods (Figure 8). Although the OBIA approach had a higher detection rate for non-dominant trees than the lidar approach, this is likely due to the oversegmentation found with the OBIA approach. Consequently, these optimistic OBIA results should be explored further. This caution is supported by the tree height vs. ground data fits: the overall fit of the lidar-derived tree heights is tighter (Figure 7). The dominant tree detection rates of both methods were higher than those previously reported [28] possibly due to the higher point density in our data.
In comparing the ability of each method to delineate trees, one conclusion clearly stands out: while the detection rate and evaluated tree heights were comparable, the shapes of the derived objects were very different. Besides a few outlier points, the main discrepancy between lidar- and OBIA-derived tree heights was due to the tallest trees (>50 m), where the OBIA approach tended to overestimate height. This is likely due to the constants, a, b and c, used to correct the CHM surface. Previous studies [5,19] have shown that tree heights derived from traditional CHM tend to be underestimated and thus, future research should evaluate whether the tall-tree heights derived from the corrected CHM are true.
It is clear from visual inspection that the lidar and OBIA polygons differ in shape (Figure 6). This was further verified by the comparison of their areas and shape complexities (Figure 9 and 10). One explanation for the compactness of the OBIA polygons is that the segmentation algorithm does not allow polygon overlap. In contrast, the lidar-derived tree canopy polygons often overlapped because lidar points classified as one tree may be on top of, underneath, or within another tree in the x-y space (Figure 4). This is a more realistic representation of real forest canopy, especially in complex, dense forests such as those in our study area. Another reason for why the lidar polygons were more complex may be because of the way the concave hulls were constructed. Concave hulls that do not follow the lidar points as closely (by changing the α parameter when generating an alpha-shape) would lead to a simpler tree crown boundary and thus a simpler shape.
In general, the lidar polygons were larger than the OBIA polygons, as is evident in the area comparison plot (Figure 9). Effectively, this means that the lidar segmentation method tended to under-segment and under-detect trees, while the OBIA method over-segmented the trees. In particular, the lidar segmentation algorithm sometimes erroneously grouped trees into one segment when the trees were very close together (i.e., their crowns were merged or intertwined) or when the tops of the trees were not clearly detectable [33]. Correct segmentation in such circumstances (especially when canopy cover > 50 percent) is still problematic regardless of the used method; it is an active area of research [5]. This is further evident when taking the tree density into consideration. In high tree density areas where trees grow in clusters, the disagreement between the area of the lidar- and OBIA-derived polygons increased and the overall accuracy of tree heights (as compared to ground truth) decreased (Figure 10). This is consistent with previous research where individual tree detection accuracy decreased in densely vegetated areas [26]. The lidar polygons were created from concave hulls around the segmented lidar points, and this could be another reason for why the lidar polygons were larger.
The low accuracy of individual tree species classification is not surprising considering the study area. Even on the ground, the four classified species (Douglas fir, white fir, sugar pine, and ponderosa pine) can be easily misidentified by an untrained eye. On the other hand, the overall shape of firs vs. pines is more discernable, and more accurately classified: the firs are more conical and the pines are more oval, especially in mature species. This is evident in the improved accuracy of tree type classification for firs vs. pines. Including hyperspectral data as a predictor would likely improve the results even further, and possibly help with the individual tree species classification. It is also possible that the classification results would improve had the lidar and WorldView-2 data been collected in closer temporal proximity. Although we took great care to spatially match the two datasets, and no major ecological event occurred in between the two data collections, it is possible that lidar and optical data collected simultaneously would yield better classification of the species. We should note that many other algorithms were tested during the preliminary analysis, including rule-based, decision tree and other machine learning classifiers; only the best results are presented here.
One of key challenges during the OBIA CHM segmentation process was the assignment of the correct scale, shape, and compactness parameters to obtain meaningful objects. Using previously established methods [54] to determine the scale factor helped in the choice of these parameters; however, as Suarez, et al. [68] discusses, designing an effective rule-set is still a largely manual process with potentially unlimited trial-and-error iterations. Efforts in future OBIA research will likely concentrate on designing processes to make the segmentation process less reliant on analyst input, and thus more deterministic and repeatable.
5. Conclusions
The successful detection and delineation of individual trees is critical in forest science, allowing for multi-scale analysis of the role of trees in forest functioning. There are many possible methods to delineate trees with remotely sensed data. In this work, we compared two segmentation algorithms for individual tree delineation: a lidar-derived method that uses 3D lidar points, and an OBIA approach that make use of the lidar canopy height model. First, we segmented a lidar point cloud into trees using a 3D segmentation algorithm. Next, we developed a new technique to produce a CHM without common lidar artifacts in order to segment it using an OBIA-derived method. The two methods were compared in x-y space in terms of their agreement to ground referenced tree heights, as well as tree detection across crown class and tree density. The overall tree height agreements of the OBIA- and the lidar-derived polygons were high (r2 = 0.9309 and r2 = 0.9163, respectively) and decreased in densely vegetated areas. The two types of objects were different in terms of polygon area and shape complexity. The OBIA objects were more likely to over-segment while the lidar objects were more likely to under-segment the trees, although the latter produced polygons more similar in shape to real tree crowns. Further research is necessary to automate the OBIA segmentation process and to improve 3D segmentation of the point cloud in dense forests.
Acknowledgments
This is SNAMP Publication #24. The Sierra Nevada Adaptive Management Project is funded by USDA Forest Service Region 5, USDA Forest Service Pacific Southwest Research Station, US Fish and Wildlife Service, California Department of Water Resources, California Department of Fish and Game, California Department of Forestry and Fire Protection, and the Sierra Nevada Conservancy.
Conflict of Interest
The authors declare no conflict of interest.
References and Notes
- Hyyppä, J.; Hyyppä, H.; Yu, X.; Kaartinen, H.; Kukko, A.; Holopainen, M. Forest Inventory Using Small-Footprint Airborne Lidar. In Topographic Laser Ranging and Scanning: Principles and Processing; Shan, J., Toth, C.K., Eds.; Taylor & Francis Group: New York, NY, USA, 2009; pp. 335–370. [Google Scholar]
- Jensen, J.R. Remote Sensing of the Environment: An Earth Resource Perspective, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2007; pp. 1–591. [Google Scholar]
- Lefsky, M.A.; Cohen, W.B.; Harding, D.J.; Parker, G.G.; Acker, S.A.; Gower, S.T. Lidar remote sensing of above-ground biomass in three biomes. Glob. Ecol. Biogeogr 2002, 11, 393–399. [Google Scholar]
- Clark, M.L.; Clark, D.B.; Roberts, D.A. Small-footprint lidar estimation of sub-canopy elevation and tree height in a tropical rain forest landscape. Remote Sens. Environ 2004, 91, 68–89. [Google Scholar]
- Falkowski, M.J.; Smith, A.M.S.; Gessler, P.E.; Hudak, A.T.; Vierling, L.A.; Evans, J.S. The influence of conifer forest canopy cover on the accuracy of two individual tree measurement algorithms using lidar data. Can. J. Remote Sens 2008, 34, 338–350. [Google Scholar]
- Vepakomma, U.; St-Onge, B.; Kneeshaw, D. Response of a boreal forest to canopy opening: assessing vertical and lateral tree growth with multi-temporal lidar data. Ecol. Appl 2011, 21, 99–121. [Google Scholar]
- Garcia-Feced, C.; Temple, D.; Kelly, M. Characterizing California Spotted Owl nest sites and their associated forest stands using Lidar data. J. For 2011, 108, 436–443. [Google Scholar]
- Zhao, F.; Sweitzer, R.A.; Guo, Q.; Kelly, M. Characterizing habitats associated with fisher den structures in the Southern Sierra Nevada, California using discrete return lidar. Forest Ecol. Manag 2012, 280, 112–119. [Google Scholar]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Measuring individual tree crown diameter with lidar and assessing its influence on estimating forest volume and biomass. Can. J. Remote Sens 2003, 29, 564–577. [Google Scholar]
- Zhao, F.; Guo, Q.; Kelly, M. Allometric equation choice impacts lidar-based forest biomass estimates: A case study from the Sierra National Forest, CA. Agric. For. Meteorol 2012, 165, 64–72. [Google Scholar]
- Sheng, Y.; Gong, P.; Biging, G.S. Model-based conifer-crown surface reconstruction from high-resolution aerial images. Photogramm. Eng. Remote Sensing 2001, 67, 957–965. [Google Scholar]
- Maltamo, M.; Mustonen, K.; Hyyppä, J.; Pitkänen, J.; Yu, X. The accuracy of estimating individual tree variables with airborne laser scanning in a boreal nature reserve. Can. J. Forest Res 2004, 34, 1791–1801. [Google Scholar]
- Pitkänen, J. Individual tree detection in digital aerial images by combining locally adaptive binarization and local maxima methods. Can. J. Forest Res 2001, 31, 832–844. [Google Scholar]
- Wang, L.; Gong, P.; Biging, G.S. Individual tree-crown delineation and treetop detection in high-spatial-resolution aerial imagery. Photogramm. Eng. Remote Sensing 2004, 70, 351–358. [Google Scholar]
- Brandtberg, T.; Walter, F. Automated delineation of individual tree crowns in high spatial resolution aerial images by multiple-scale analysis. Mach. Vis. Appl 1998, 11, 64–73. [Google Scholar]
- Gougeon, F.A.; Leckie, D.G. The individual tree crown approach applied to Ikonos images of a coniferous plantation area. Photogramm. Eng. Remote Sensing 2006, 72, 1287–1297. [Google Scholar]
- Kaartinen, H.; Hyyppä, J.; Yu, X.; Vastaranta, M.; Hyyppä, H.; Kukko, A.; Holopainen, M.; Heipke, C.; Hirschmugl, M.; Morsdorf, F.; Næsset, E.; Pitkänen, J.; Popescu, S.; Solberg, S.; Wolf, B.M.; Wu, J.-C. An International Comparison of Individual Tree Detection and Extraction Using Airborne Laser Scanning. Remote Sens 2012, 4, 950–974. [Google Scholar]
- Hyyppä, J.; Inkinen, M. Detecting and estimating attributes for single trees using laser scanner. Photogramm. J. Finl 1999, 16, 27–42. [Google Scholar]
- Popescu, S.C.; Wynne, R.H. Seeing the trees in the forest: using lidar and multispectral data fusion with local filtering and variable window size for estimating tree height. Photogramm. Eng. Remote Sensing 2004, 70, 589–604. [Google Scholar]
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating individual trees in a savanna woodland using small footprint LIDAR data. Photogramm. Eng. Remote Sensing 2006, 72, 923–932. [Google Scholar]
- Morsdorf, F.; Meier, E.; Kötz, B.; Itten, K.I.; Dobbertin, M.; Allgöwer, B. LIDAR-based geometric reconstruction of boreal type forest stands at single tree level for forest and wildland fire management. Remote Sens. Environ 2004, 92, 353–362. [Google Scholar]
- Kwak, D.A.; Lee, W.K.; Lee, J.H.; Biging, G.S.; Gong, P. Detection of individual trees and estimation of tree height using LiDAR data. J. Forest Res 2007, 12, 425–434. [Google Scholar]
- Brandtberg, T.; Warner, T.A.; Landenberger, R.E.; McGraw, J.B. Detection and analysis of individual leaf-off tree crowns in small footprint, high sampling density lidar data from the eastern deciduous forest in North America. Remote Sens. Environ 2003, 85, 290–303. [Google Scholar]
- Gleason, C.J.; Im, J. A fusion approach for tree crown delineation from LiDAR data. Photogramm. Eng. Remote Sensing 2012, 78, 679–692. [Google Scholar]
- Koch, B.; Heyder, U.; Weinacker, H. Detection of individual tree crowns in airborne lidar data. Photogramm. Eng. Remote Sensing 2006, 72, 357–363. [Google Scholar]
- Yu, X.; Hyyppä, J.; Vastaranta, M.; Holopainen, M.; Viitala, R. Predicting individual tree attributes from airborne laser point clouds based on the random forests technique. ISPRS J. Photogramm 2011, 66, 28–37. [Google Scholar]
- Hyyppä, J.; Kelle, O.; Lehikoinen, M.; Inkinen, M. A segmentation-based method to retrieve stem volume estimates from 3-D tree height models produced by laser scanners. ISPRS J. Photogramm 2001, 39, 969–975. [Google Scholar]
- Solberg, S.; Naesset, E.; Hanssen, K.H.; Christiansen, E. Mapping defoliation during a severe insect attack on Scots pine using airborne laser scanning. Remote Sens. Environ 2006, 102, 364–376. [Google Scholar]
- Breidenbach, J.; Næsset, E.; Lien, V.; Gobakken, T.; Solberg, S. Prediction of species specific forest inventory attributes using a nonparametric semi-individual tree crown approach based on fused airborne laser scanning and multispectral data. Remote Sens. Environ 2010, 114, 911–924. [Google Scholar]
- Edson, C.; Wing, M.G. Airborne light Detection and Ranging (LiDAR) for individual tree stem location, height, and biomass measurements. Remote Sens 2011, 3, 2494–2528. [Google Scholar]
- Féret, J.-B.; Asner, G.P. Semi-supervised methods to identify individual crowns of lowland tropical canopy species using imaging spectroscopy and LiDAR. Remote Sens 2012, 4, 2457–2476. [Google Scholar]
- Lee, H.; Slatton, K.C.; Roth, B.E.; Cropper, W.P. Adaptive clustering of airborne LiDAR data to segment individual tree crowns in managed pine forests. Int. J. Remote Sens 2010, 31, 117–139. [Google Scholar]
- Li, W.; Guo, Q.; Jakubowski, M.; Kelly, M. A new method for segmenting individual trees from the lidar point cloud. Photogramm. Eng. Remote Sensing 2012, 78, 75–84. [Google Scholar]
- Cleve, C.; Kelly, M.; Kearns, F.R.; Moritz, M. Classification of the wildland–urban interface: A comparison of pixel-and object-based classifications using high-resolution aerial photography. Compu. Environ. Urban Syst 2008, 32, 317–326. [Google Scholar]
- Guo, Q.C.; Kelly, M.; Gong, P.; Liu, D. An object-based classification approach in mapping tree mortality using high spatial resolution imagery. GIScience Remote Sens 2007, 44, 24–47. [Google Scholar]
- Kelly, M.; Blanchard, S.; Kersten, E.; Koy, K. Object-based analysis of imagery in support of public health: new avenues of research. Remote Sens 2011, 3, 2321–2345. [Google Scholar]
- Blaschke, T. Object-based image analysis for remote sensing. ISPRS J. Photogramm 2010, 65, 2–16. [Google Scholar]
- Chubey, M.S.; Franklin, S.E.; Wulder, M.A. Object-based analysis of Ikonos-2 imagery for extraction of forest inventory parameters. Photogramm. Eng. Remote Sensing 2006, 72, 383–394. [Google Scholar]
- Brennan, R.; Webster, T. Object-oriented land cover classification of lidar-derived surfaces. Can. J. Remote Sens 2006, 32, 162–172. [Google Scholar]
- Antonarakis, A.S.; Richards, K.S.; Brasington, J. Object-based land cover classification using airborne LiDAR. Remote Sens. Environ 2008, 112, 2988–2998. [Google Scholar]
- Ke, Y.; Quackenbush, L.J.; Im, J. Synergistic use of QuickBird multispectral imagery and LIDAR data for object-based forest species classification. Remote Sens. Environ 2010, 114, 1141–1154. [Google Scholar]
- Clinton, N.; Holt, A.; Scarborough, J.; Yan, L.; Gong, P. Accuracy assessment measures for object-based image segmentation goodness. Photogramm. Eng. Remote Sensing 2010, 76, 289–299. [Google Scholar]
- Trimble. eCognition Developer; Version 8.8; Trimble: Munich, Germany, 2012. [Google Scholar]
- Baatz, M.; Hoffmann, C.; Willhauck, G. Progressing from Object-Based to Object-Oriented Image Analysis. In Object-Based Image Analysis: Spatial Concepts for Knowledge-Driven Remote Sensing Applications; Blaschke, T., Lang, S., Hay, G.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 29–42. [Google Scholar]
- Stephens, S.L.; Collins, B.M. Fire regimes of mixed conifer forests in the north-central Sierra Nevada at multiple spatial scales. Northwest Sci 2004, 78, 12. [Google Scholar]
- Jakubowski, M.K.; Guo, Q.; Kelly, M. Tradeoffs between lidar pulse density and forest measurement accuracy. Remote Sens. Environ 2013, 130, 245–253. [Google Scholar]
- Exelis. ENVI Software; Exelis: McLean, VA, USA, 2012. [Google Scholar]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. US Patent No. 6,011,875,. 4 January 2000. [Google Scholar]
- Chang, Y.; Habib, A.; Lee, D.; Yom, J. Automatic classification of lidar data into ground and non-ground points. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2008, 37, 463–468. [Google Scholar]
- Leckie, D.; Gougeon, F.; Hill, D.; Quinn, R.; Armstrong, L.; Shreenan, R. Combined high-density lidar and multispectral imagery for individual tree crown analysis. Can. J. Remote Sens 2003, 29, 633–649. [Google Scholar]
- Lee, J.-S. Digital Image Enhancement and Noise Filtering by Use of Local Statistics. IEEE Trans. Pattern Anal. Mach. Intell. 1980, PAMI–2, 165–168. [Google Scholar]
- Lopes, A.; Touzi, R.; Nezry, E. Adaptive speckle filters and scene heterogeneity. IEEE Trans. Geosci. Remote Sens 1990, 28, 992–1000. [Google Scholar]
- Haralick, R.M.; Sternberg, S.R.; Zhuang, X. Image analysis using mathematical morphology. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 532–550. [Google Scholar]
- Drǎguţ, L.; Tiede, D.; Levick, S.R. ESP: a tool to estimate scale parameter for multiresolution image segmentation of remotely sensed data. Int. J. Geogr. Inf. Sci 2010, 24, 859–871. [Google Scholar]
- Leonard, J. Technical Approach for LIDAR Acquisition and Processing; EarthData Inc.: Frederick, MD, USA, 2005; pp. 1–20. [Google Scholar]
- Im, J.; Jensen, J.R.; Hodgson, M.E. Object-based land cover classification using high-posting-density LiDAR data. GIScience Remote Sens 2008, 45, 209–228. [Google Scholar]
- Baltsavias, E.P. Airborne laser scanning: basic relations and formulas. ISPRS J. Photogram 1999, 54, 199–214. [Google Scholar]
- Frank, E.; Hall, M.; Holmes, G.; Kirkby, R.; Pfahringer, B.; Witten, I.H.; Trigg, L. Weka—A Machine Learning Workbench for Data Mining. In Data Mining and Knowledge Discovery Handbook; Maimon, O., Rokach, L., Eds.; Springer: New York, NY, USA, 2010; pp. 1269–1277. [Google Scholar]
- Jakubowski, M.K.; Guo, Q.; Collins, B.; Stephens, S.; Kelly, M. Predicting surface fuel models and fuel metrics using lidar and imagery in dense, mountainous forest. Photogramm. Eng. Remote Sensing 2013, 79, 37–50. [Google Scholar]
- Fan, R.E.; Chang, K.W.; Hsieh, C.J.; Wang, X.R.; Lin, C.J. LIBLINEAR: A library for large linear classification. J. Mach. Learn. Res 2008, 9, 1871–1874. [Google Scholar]
- Keerthi, S.S.; Shevade, S.K.; Bhattacharyya, C.; Murthy, K.R.K. Improvements to Platt's SMO algorithm for SVM classifier design. Neural Comput 2001, 13, 637–649. [Google Scholar]
- Buhmann, M.D. Radial basis functions. Acta Numer 2000, 9, 1–38. [Google Scholar]
- Forman, R.T.T.; Godron, M. Landscape Ecology; JohnWiley and Sons: New York, NY, USA, 1986; pp. 1–619. [Google Scholar]
- McGarigal, K.; Cushman, S.A.; Neel, M.C.; Ene, E. FRAGSTATS: Spatial Pattern Analysis Program for Categorical Maps; Version 4; University of Massachusetts Amherst: MA, USA, 2002. [Google Scholar]
- Jiao, L.; Liu, Y. Analyzing the shape characteristics of land use classes in remote sensing imagery. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, I-7, 135–140. [Google Scholar]
- Trani, M.K.; Giles, R.H., Jr. An analysis of deforestation: Metrics used to describe pattern change. Forest Ecol. Manag 1999, 114, 459–470. [Google Scholar]
- Brokaw, N.; Thompson, J. The H for DBH. Forest Ecol. Manag 2000, 129, 89–91. [Google Scholar]
- Suarez, J.C.; Ontiveros, C.; Smith, S.; Snape, S. Use of airborne LiDAR and aerial photography in the estimation of individual tree heights in forestry. Comput. Geosci 2005, 31, 253–262. [Google Scholar]





| Band | Spectral Region | GSD (nadir) | GSD (20° off nadir) |
|---|---|---|---|
| 1 (Coastal) | 400–450 nm | 185 cm | 207 cm |
| 2 (Blue) | 450–510 nm | 185 cm | 207 cm |
| 3 (Green) | 510–580 nm | 185 cm | 207 cm |
| 4 (Yellow) | 585–625 nm | 185 cm | 207 cm |
| 5 (Red) | 630–690 nm | 185 cm | 207 cm |
| 6 (Red edge) | 705–745 nm | 185 cm | 207 cm |
| 7 (NIR1) | 770–895 nm | 185 cm | 207 cm |
| 8 (NIR2) | 860–1040 nm | 185 cm | 207 cm |
| Panchromatic | 450–800 nm | 46 cm | 52 cm |
| Object Metric | Segmentation | Classification | Feature Optimized |
|---|---|---|---|
| Border Shape | × | ||
| Compactness | × | ||
| Density | × | ||
| Length/width Ratio | × | × | × |
| Square Pixel | × | × | |
| Roundness | × | ||
| Shape Index | × | ||
| User Defined* | × | × | |
| Area | × | × | |
| Neighbor Proximity (ground) | × | ||
| Maximum Lidar Height | × | × | × |
| Mean Lidar Height | × | × | × |
| Minimum Lidar Height | × | ||
| Mean Difference to Neighbor | × | × | × |
| 8 Metrics: Mean(WV2 band i) | × | ||
| 8 Metrics: Standard Deviation(WV2 band i) | × | ||
| NDVI (Maximum) | × | × | |
| NDVI (Mean) | × | × |
*User Defined = (border index) × (shape index) × (compactness) × (roundness).
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Jakubowski, M.K.; Li, W.; Guo, Q.; Kelly, M. Delineating Individual Trees from Lidar Data: A Comparison of Vector- and Raster-based Segmentation Approaches. Remote Sens. 2013, 5, 4163-4186. https://doi.org/10.3390/rs5094163
Jakubowski MK, Li W, Guo Q, Kelly M. Delineating Individual Trees from Lidar Data: A Comparison of Vector- and Raster-based Segmentation Approaches. Remote Sensing. 2013; 5(9):4163-4186. https://doi.org/10.3390/rs5094163
Chicago/Turabian StyleJakubowski, Marek K., Wenkai Li, Qinghua Guo, and Maggi Kelly. 2013. "Delineating Individual Trees from Lidar Data: A Comparison of Vector- and Raster-based Segmentation Approaches" Remote Sensing 5, no. 9: 4163-4186. https://doi.org/10.3390/rs5094163
APA StyleJakubowski, M. K., Li, W., Guo, Q., & Kelly, M. (2013). Delineating Individual Trees from Lidar Data: A Comparison of Vector- and Raster-based Segmentation Approaches. Remote Sensing, 5(9), 4163-4186. https://doi.org/10.3390/rs5094163






