1. Introduction
Mapping shallow water bathymetry from ships by sonar is a quite an expensive task. Many shallow water areas are not accessible by hydrographic ships due to rocks, coral reefs or simply the shallowness of the water. Active or passive remote sensing from aircraft and/or satellites could be the tools to solve the problem [
1–
4]. However, the active systems (Lidar) are very expensive to operate and their study area is small. Airborne passive sensors (CASI, HySpex) are cheaper than and cover a wider area per flight than Lidars. There are also high spatial resolution satellites (WorldView-2, QuickBird) suitable for shallow water bathymetry mapping. However, the airborne systems and high resolution satellite data may not be easily accessible in every part of the world. Freely available Landsat data may be the only option for many countries.
There are different methods for retrieving water depth from remote sensing data. For example, Lyzenga [
5] proposed a method for removing water column effects to obtain bottom reflectance parameters from remote sensing imagery. This method can also be used to retrieve water depth. On the other hand, the method assumes identical water quality all over the imaged area and a homogeneous bottom in each pixel. Neither assumption may be valid in optically complex waters with highly variable bottom habitats. Few researchers developed different methods to be able to model effects of environmental factors such as bottom material, vegetation, pollution, algae cover, turbulence, tributaries,
etc. on reflectance sourced solely by depth [
6–
9]. Leu and Chang [
10] used two dimensional wave spectrums to estimate water depths based on the principle that while waves propagate toward the shoreline, their wave lengths decrease due to decrements in water depth. Fonstad and Marcus [
11] combined remote sensing imagery and open channel flow principals to estimate water depths in clear rivers. Ceyhun and Yalçın [
12] proposed artificial neural networks (ANN) to estimate water depths in shallow waters. ANNs allow the methodology to consider the nonlinear multi-parameter relationship between reflectance from different spectral bands and water depths. These algorithms attempt to isolate water attenuation and hence depth from other factors by using different combinations of spectral bands. These multiple band techniques depend upon large amounts of ground truth data and a resolution fine enough to discriminate bottom types. Also, Abileh and Vignudelli [
13] used least-square fit on fusing shoreline contours from 58 Landsat images with water levels from the various satellite radar altimeters to determine near-shore bathymetry of Lake Nasser, Egypt, and the fitted function is then used to assign a relative depth to each Landsat image shoreline.
Using of a physics-based approach that allows to map both water depth and bottom type simultaneously has been proposed by several authors [
14–
17]. The method is based on modeled spectral libraries that are created using bio-optical or radiative transfer models. Full modeled spectra are compared with the measured reflectance spectra and it is assumed that the water depth and bottom type used in the modeling correspond to those in nature when the modeled and measured reflectance matches. More sophisticated versions of the method [
18] also allow retrieving optical water properties besides the water depth and bottom type. The spectral library approach does not require the collecting of
in situ data during the image acquisition and it can work without any
in situ data. However, some preliminary knowledge on the dominating benthic habitats and their optical properties, as well as optical water properties, is needed in the first stages of applying this method when creating the modeled spectral library.
Unfortunately, there is not much in situ data available for the Iranian coastal zone research. There is a small amount of ground truth knowledge pertaining to the depth and/or bottom type in the Southern Caspian Sea. On the other hand, many coastal zone studies in the Southern Caspian Sea, such as those examining near-shore fisheries, coastal erosion, water quality, or recreation activities, require bathymetry information from shallow coastal waters. In this study, we therefore test the possibility to map water depth in the southeast of the Caspian Sea with satellite imagery.
2. Material and Methods
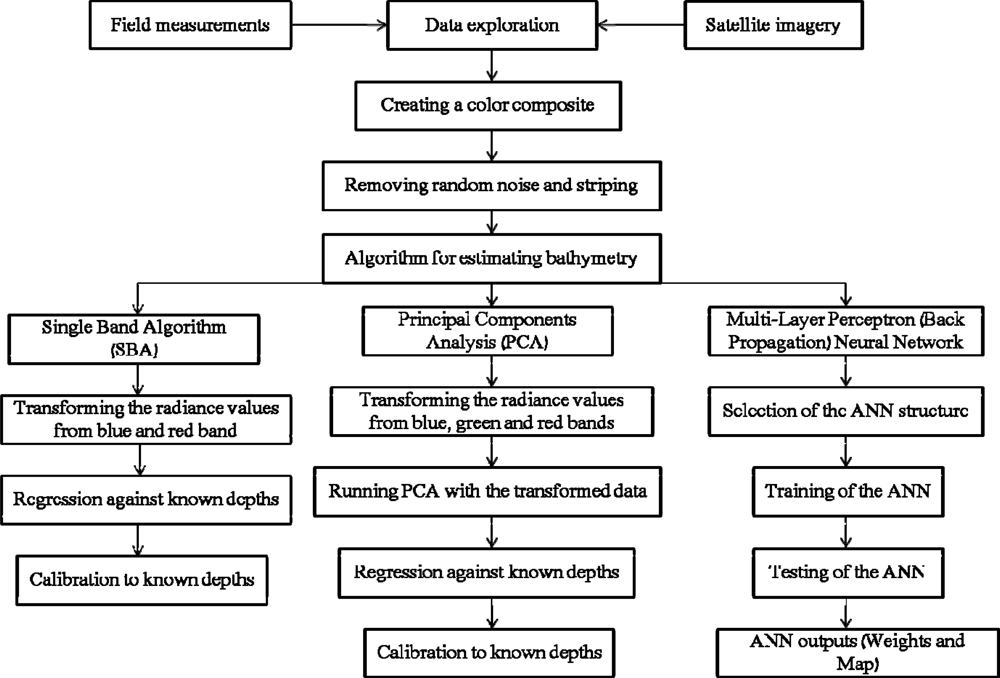
Three different methods were tested for retrieving water depth from Landsat 5 TM data. Firstly, we used a single band algorithm calibrated against known depths. The algorithm [
19] is one of the families of algorithms that have been used to estimate bathymetry [
20,
21]. These algorithms are based on the fact that radiance is, to varying degrees, attenuated by the water column. The light attenuation coefficient is a function of wavelength, sea bottom types, and water column properties. However, we do have available the shortest of the visible wavelengths (blue), and we want to take full advantage of its water penetrating properties. For these reasons we will use a single band algorithm (SBA) which assumes a constant attenuation coefficient and requires the least amount of ancillary information.
The second procedure utilizes several bands of imagery and principal components analysis (PCA). This method is analogous to a multi-band algorithm that accounts for varying attenuation coefficients for different bottom types as it calculates water depth, unlike the single band algorithm [
22].
The third procedure utilizes MLP to perform a regression analysis between input variables (visible bands) and one dependent variable with the output containing one output neuron (bathymetry) [
12]. The multi-layer perceptron with the back-propagation (BP) learning algorithm is used as neural network model.
The different stages of methodology have been shown in
Figure 1. In this study, we used visible bands of Landsat TM imagery collected over the southeastern part of the Caspian Sea on 6 October 2011. Depth data was collected in 31 sampling points (
Figure 2). The Speedtech SM-5 Depthmate portable sounder was used. The position of sampling locations was recorded using Garmin 62S Global Positioning System (GPS) receiver. The shallow points are located in the area called Gorgan Bay. Gorgan Bay is a large (23,800 ha) shallow inlet at the extreme southeastern corner of the Caspian Sea, north and east of the town of Behshahr, almost totally cut off from the open sea by the Miankaleh Peninsula (24,200 ha). It is low and sandy with a chain of dunes 50 m wide paralleling the Caspian Sea coast. The Gorgan Bay is brackish and receives freshwater inflow from a number of small rivers and streams rising on the humid north slope of the Alborz Mountains to the south. Some freshwater marshes occur at the western end of the bay, where inflow is greatest.
There are two very important procedures that must be undertaken prior to bathymetric analysis. First, the image must be geometrically registered so that corresponding pixels in the entire image refer to exactly the same place on the ground. Resampling was done with a set of ground control points to make the image match a base map. The second pre-analysis procedure involved removal of random noise and stripping. Both the single band algorithm and the PCA method are sensitive to random noise and striping within the raw imagery. Therefore, the image has been enhanced with a low-pass (mean) filter.
The algorithm used for depth estimation was following:
where,
Z = depth;
V = observed signal radiance;
Vs = portion of signal resulting from scattering of radiation in the atmosphere, water column and water surface;
κ = water attenuation coefficient;
Vo = sensitivity factor consisting of contributions from solar irradiance at the surface, the bottom reflectance, atmospheric transmission, and sensor equipment.
If we assume that the actual observed radiance (
V) changes exponentially with water depth then after the removal of scattering component (
Vs) the radiance can be logarithmically transformed to a linear function of depth. The result can then be put back into the
Equation (1). The equation now takes the form of
depth = slope (X) + constant. The line this equation describes is the best fit of a simple linear regression using known depth measurements as the dependent variable and the transformed radiance values (
X) as the independent variable. The slope of this line is related to the water attenuation coefficient such that
, and the constant value is given by
By first calculating the transformed radiance values and then regressing them against control points of known depth, all of the variables in the
Equation (2) are known and the depth of water can be calculated.
The transformed radiance values were calculated by taking the values from blue and red bands in SBA algorithm, subtracting
Vs, and then taking the natural log of the result. The
Vs was estimated from the spectral properties of the deepest water area in the image where the water depth is known to be greater than 50 m. A polygon file has been provided that outlines the known deep water area to estimate
Vs. Assuming that such deep water should have virtually zero radiance values in the blue band, any reflectance registered must be due to scattering. Then, the average value of the pixels that lie in known deep water was taken and one standard deviation was subtracted. There are 31 locations across the image where we measured water depth (
Figure 2). This allows us to calibrate the water depth algorithm by regression analysis.
Principal components analysis (PCA) is related to factor analysis and can be used to transform a set of image bands such that the new bands (called
components) are uncorrelated with one another and are ordered in terms of the amount of image variation that they can explain [
23]. The input images into the PCA are the Landsat visible bands transformed, just as described above. While in the single band method it is assumed that the transformed blue band corresponds directly to water depth, the PCA assumes that the first component from the analysis using all three bands (transformed) will correspond to water depth. It is the first component result that then can be calibrated to known water depths.
Because the PCA requires that input files be of a byte/binary format, transformed blue, green and red bands stretched to a value range of 0–255. Then, to make analysis more accurate, the land areas were masked for all three stretched images and use the results as the input files for the PCA. The first component has been produced using forward T-Mode PCA showing the sources of variation in the data set. PCA method assumes that change in depth explains the most variance and other factors, such as a changing bottom type, will be secondary sources of variation [
24]. The first component image values at the known site locations were extracted. Knowing the slope and constant values from the regression, it was easy to calibrate the transformed data to depth. Finally, the first component was calibrated with known depths.
We used MLP to perform a regression analysis between input variables (visible bands) and one dependent variable with the output containing one output neuron (bathymetry). The multi-layer perceptron used in the back-propagation (BP) learning algorithm is one of the most widely used neural network models. Research indicates that a three-layered BP network can approximate any polynomial function, then the used BP network contains one input layer (three nodes), one output layer (one output neuron) and one hidden layer (six nodes). The values of the output-predicted image is the activation level of the output layer node (scaled to the original data range),
i.e.,
where,
where
wjk represents the weight between node
j (hidden layer neuron) and node
k (output layer neuron), and
oj is the output from node
j (hidden layer neuron). The function
f is usually a nonlinear sigmoidal function that is applied to the weighted sum of inputs before the signal passes to the next layer. Once the forward pass is finished, the activities of the output nodes are compared with their expected activities. The actual output will differ from the desired outcome and the difference is associated with error in the network. This error is then propagated backward with weights for relevant connections corrected via a relation known as the delta rule:
where
η is the learning rate,
δ is the computed error, and
α is the momentum factor.
The forward and backward passes continue until the network has “learned” the characteristics of pattern. The main training parameters consist of learning rate (the change rate of the weights) between 0.01 and 0.2, momentum factor (0.5 and 0.6) and sigmoid function constant “α”. The R square reported by regression MLP is based on a “leave 50% out” rule, which dynamically updates over the training procedure and indicates goodness of the prediction, i.e., the percent variance explained by independent variables.
There are two main assumptions in the presented methodology:
The single band algorithm (SBA) assumes that the transformed blue band corresponds directly to water depth, while PCA assumes that the first component using all three transformed bands corresponds to water depth.
Assuming that known deep water should have virtually zero radiance values in the blue band, any reflectance registered must be due to scattering.
3. Results
For estimating
Vs, the mean value of known optically deep water is 54.93 for blue band, 18.58 for green band and 11.71 for red band. The standard deviation is 0.91, 0.53 and 0.31, respectively. Subsequently, the estimated values of
Vs are 54.02, 18.04 and 11.40, respectively. The difference between the original band and the transformed band is striking (
Figures 3 and
4).
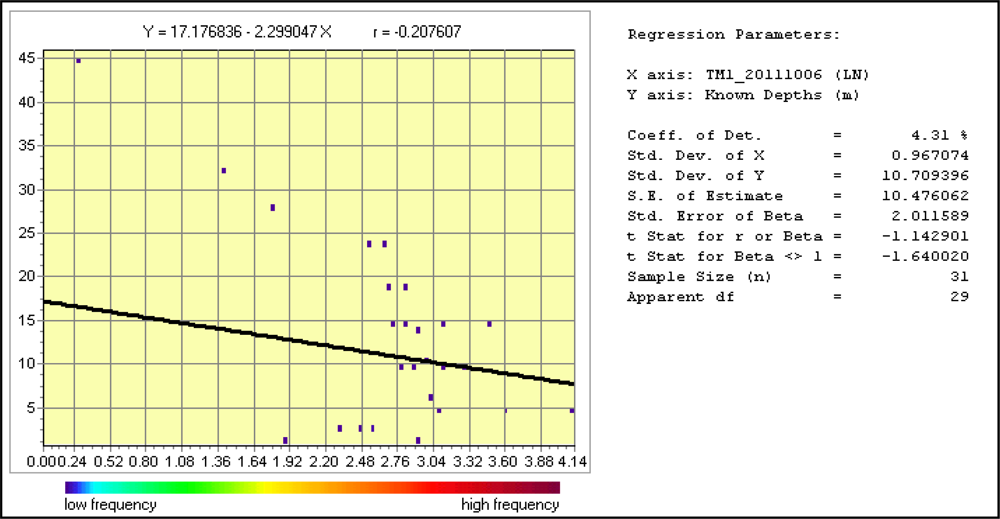
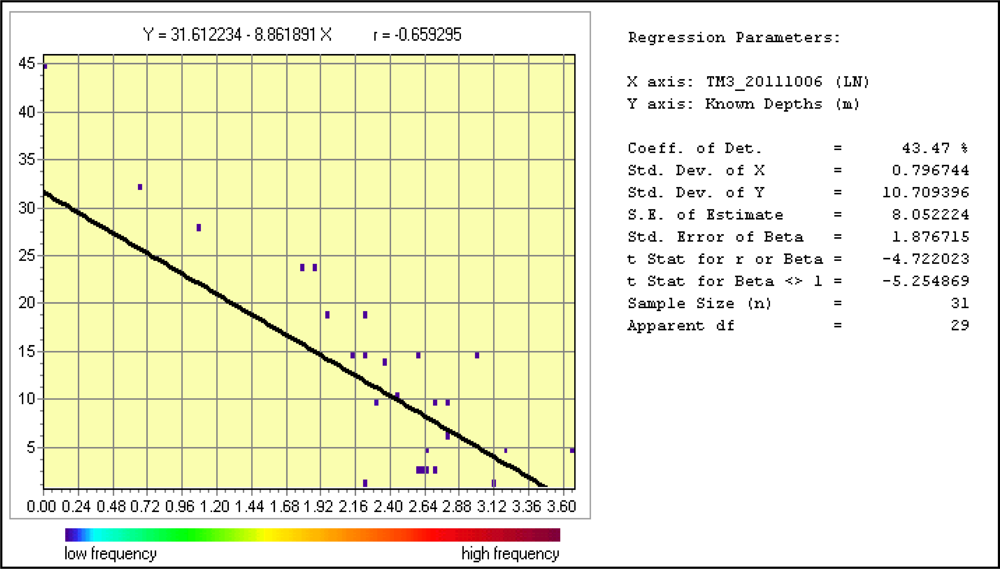
After regressing the transformed blue and red band
versus known depths (
Figures 5,
6,
7 and
8), the correlation coefficient (
r) is −0.2 and −0.65 for blue and red bands, respectively, thereby indicating an inverse relationship between these bands and the known depths. The sum of the squared residuals (35,439.49 for blue band, 20,937.41 for red band) subtracted from the total sum of squares (37,035.76 for both bands) gives the explained part of the regression (the regression sum of squares: 1,596.27 for the blue band, 16,098.35 for the red band). The explained part divided by the total sum of squares yields the coefficient of determination (
R-squared) that represents the extent of variability in the known depths explained by the transformed bands. In our case, 4.31% and 43.47% of the variance in the depths is explained by transformed blue and red bands respectively. The F value in regression (1.31 for the blue band, 22.30 for the red band) is compared to the
F value given in the table (4.18) and hence, the overall regression for the blue band is not significant, but for the red band, it is significant. Also, in our case, the
t-statistic has to exceed the 3.396 critical value in order for the bands to be significant: at a 99% confidence level. The coefficient has a t-statistic of −1.143 for the blue band and −4.722 for the red band, thus indicating that the coefficient for the blue band is not significant (99%), but is significant for the red band. The
t-statistic and the F statistic combined are the most common tests indicating that the regression between the transformed blue band and known depths is not significant.
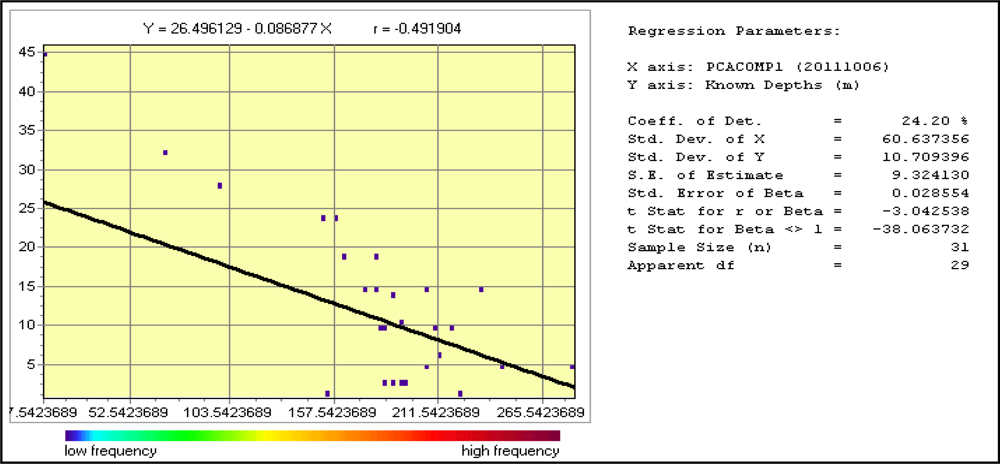
Regressing the first component of PCA and known depths (
Figures 9 and
10), we found that the correlation coefficient (
r) is only −0.49. In our case, only 24.20% of the variance in the known depths is explained by the first component of PCA because the coefficient of determination (
R-squared) is 0.24. The
F value in this regression (9.26) is greater than the
F value given in the table (4.18) and hence, the overall regression is significant. The coefficient has a t-statistic of −3.043 indicating that the coefficient is not significant (99%). The
t-statistic and the
F statistic combined are the most common tests indicating that regression between the first component of PCA and known depths is significant.
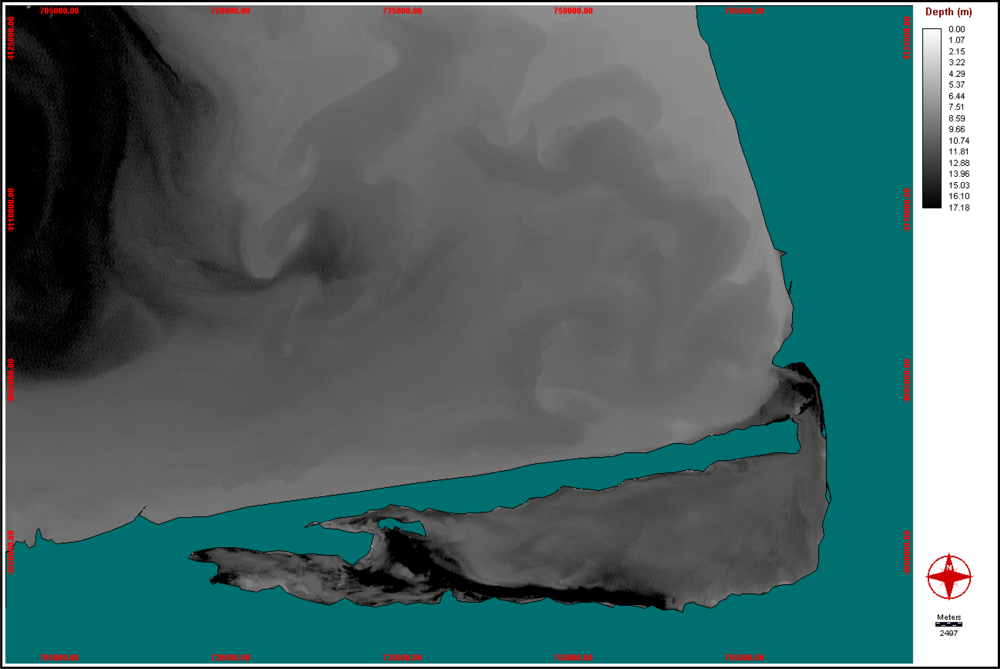
The outputs from the neural network are obtained by fuzzying the signals into values in the range of 0–1 with the activation function and then scaled to the original data range (
Figure 11). In fact, the values of the output MLP predicted image is the activation level of the bathymetry.
4. Discussion
Neither the true color or false color composite image nor any of the original bands can be used as an index of depth without some further processing.
Table 1 shows that the single band algorithm for transformed red band produces quite reasonable depth estimates. It is not surprising as the absorption coefficient of water increases exponentially in the red part of spectrum and, consequently, small changes in water depth have significant impact on the water leaving signal. However, the absorption of light by water molecules is so strong that there is no bottom effect in reflectance if the water is deeper than 5–6 m [
25,
26]. This applies both to optically clear and turbid waters. Consequently, the red band is the best for mapping depth in waters less than 5 m deep, but cannot be used for estimating water depth in waters deeper than 5–6 m.
In relatively clear waters, light penetrates the deepest in the blue part of spectrum and information in the blue band can be used for bathymetry estimation. However, in coastal and inland waters, both colored dissolved organic matter and phytoplankton absorb light strongly in the blue band. Thus, the blue band provides information about the optically active constituents in water rather than allows to estimate the water depth. This explains also the low correlation (R = −0.2) between the blue band radiance and water depth observed by us in the southern part of the Caspian Sea.
The single band algorithm and many other methods require extensive ground truth information. This method used a single band algorithm and assumed a constant water attenuation coefficient throughout the blue and red bands. To assume otherwise would have required more ground truth knowledge about bottom type than was available. When such data is available, there are a number of algorithms that might be used to effectively isolate changes in depth from changes in other factors. When not available, the single band method works well as a rough estimate of bathymetry, as our analysis has shown.
The second method used principal components analysis (PCA) in an attempt to adjust for varying water attenuation coefficients without additional ground truth data. This procedure is based on the assumption that the first component result of PCA, which explains most of the variance in the data set, will be a depth-dependent variable that is independent of other sources of variation such as bottom type. After producing the first component image and calibrating it to known depths, we compared the results to the algorithm method. The PCA method produces a depth-dependent variable (independent of bottom type) without ground truth data. The first component of PCA, using the three TM bands of imagery, should approximate relative water depth given the assumption that depth explains the most variance between two or more bands of information.
The third method is based on nonlinear optimization techniques and machine learning methods such as artificial neural networks (ANNs) that provide an interesting alternative to examine complex coastal waters and to handle multivariate data. Models based on these methods determine the output values (e.g., the bathymetric values) from input data (e.g., water reflectance at various wavelengths) through nonlinear multidimensional parametric functions. The determination of the model parameters, as well as the assessment of the model performance, rely on a reference data set.
From the methods tested by us, the MLP-ANNs method seems to be performing the best as it produces the highest correlation (r = −0.94) with the
in situ depth data. Spatial patterns shown in
Figures 6 and
8 indicate that both of the single band algorithms describe patterns well in terms of water quality rather than the water depth. The two may be related as some of the water turbidity is caused by re-suspension from the bottom rather than transport from the adjacent land or other shallow areas. Many optically active substances affect the water, leaving radiance in the blue band and contribution of the bottom signal is relatively low there. This explains why the single blue band algorithm does not perform well (
r = −0.21). All bottom types from bare sand to vegetation have relatively higher reflectance in the red part of the spectrum [
25,
27]. On the other hand, water absorption coefficient increases exponentially in the red part of the spectrum. Consequently, the changes in water color due to variable water depth are more prominent in this part of the spectrum. This explains better performance of the single red band algorithm (
r = −0.66).
Radiometric resolution of previous Landsat sensors is just eight bit. This means that the whole range between the darkest objects (usually water) and the brightest objects (clouds, snow) has to be described with only 256 gray levels. Just a few levels can be used to describe the whole variability in water leaving signal. Nevertheless, our results show that rough estimates of water depth can be produced from Landsat data. Landsat 8 was launched recently and the launch of Sentinel-2 is planned soon. Although both are again designed for land applications, they will still provide a better platform for bathymetric mapping. In fact, bathymetric retrieval from the new generation multi or hyperspectral imagery is very feasible because of the very high spatial resolution capabilities and significantly improved radiometric resolutions of the optical remote sensing images and the reliability of results due to the frequent presence of optimal clear waters. In such settings, a reduced set of measured elevation can be effectively used to derive a continuous and accurate DEM based on empirical approaches [
28].
The complexity of coastal waters, as well as the atmosphere above, requires more complex algorithms capable of handling bathymetric modeling. The atmospheric correction process is applied to remove the effects of the atmosphere that contribute to the signal measured by a satellite sensor. The objective of this process is the discrimination, from top-of-atmosphere radiance, of the signal emerging from the sea carrying information on the materials suspended and dissolved in seawater. However, several studies focusing on water quality remote sensing using the Landsat sensors [
29,
30] have shown that it is actually better to use Landsat top-of-atmosphere radiances (atmospherically uncorrected data) rather than reflectance (atmospherically corrected data). This can be explained by the small number of gray levels (usually less than 10) available for describing the whole variability in optical water properties. Atmospheric correction can introduce and extra error, but the number of available gray levels remains the same.
Also, the shallow waters have negative influences on the accuracy of bathymetric modeling. We have repeated methodology for two clusters (known depths less and greater than 5 m, which is almost 15 feet). As, the values less than 5 m are removed, the coefficient of determination increases. Therefore, the shallow waters lead to some errors in methodology. Unfortunately, there is not enough data about optically active constituents (OACs) in this region. The correction of data in these shallow waters is challenged by the presence of continental aerosols, bottom reflectance, and adjacency of land. Minimizing these perturbing effects, which generally are site specific, requires knowledge of the regional aerosol and bottom optical properties. Specifically, effects of continental aerosols are minimized by properly accounting for their scattering phase function and single scattering albedo; the increase in radiance due to bottom reflectance can be removed through iterative processes knowing the water depth and spectral reflectance of the seabed, and the adjacency effects are minimized by determining the reduction in image contrast as a function of the aerosol and of the land reflectance [
31].
5. Conclusions
Landsat series sensors were not designed for water studies. For example, the radiometric resolution of previous Landsat sensors is merely eight bit. This means that the whole range between the darkest objects (usually water) and the brightest objects (clouds, snow) has to be described with just 256 gray levels. Only a few levels can be used to describe the entire variability of the water leaving signal. Nevertheless, our results show that rough estimates of water depth can be produced from Landsat data. Landsat 8 was launched recently and the launch of Sentinel-2 is planned in 2014. Although both are again designed for land applications, they will still provide a better platform for bathymetric mapping as their radiometric resolution, and signal-to-noise ratio and other technical parameters are more suitable for aquatic remote sensing.
In this research, we produced images of absolute bathymetry using three different but related methods. For any method, one must be aware of the possibility for error at each of the steps involved and continually question the results. While the dynamic nature of the coast makes precision in bathymetric estimation difficult (e.g., tides, waves, lack of ground truth information), it also makes such analyses essential if we are to have recent and/or time series data for the coastal zone.
We may thus conclude that the artificial neural network method and the single band method using red Landsat band can produce reasonably good depth estimates in shallow coastal waters even with a relatively small amount of in situ data to calibrate the algorithms and relatively poor sensor that is not designed for remote sensing of such dark objects like water bodies. In addition, the large variability in time and space of the bulk properties of coastal waters hampers any implementation of a single and global algorithm that would work with the same efficiency in all regions.
In summation, this study provides the empirical algorithm as the first step for the development and validation of bathymetric algorithms in the southeastern Caspian Sea. It is quite evident that in shallow waters and in spectral regions where the upwelling light is influenced by multiple parameters, the signal from the bottom can only be separated from the signal from the water column by more detailed optical modeling. The collection of IOP and reflectance measurements and the set-up of such models and inversion schemes for developing bathymetric algorithms specific to the Caspian Sea are thus recommended for further study.