A Sample-Based Forest Monitoring Strategy Using Landsat, AVHRR and MODIS Data to Estimate Gross Forest Cover Loss in Malaysia between 1990 and 2005
Abstract
:1. Introduction
2. Methods
2.1. Data and Forest Loss Characterization
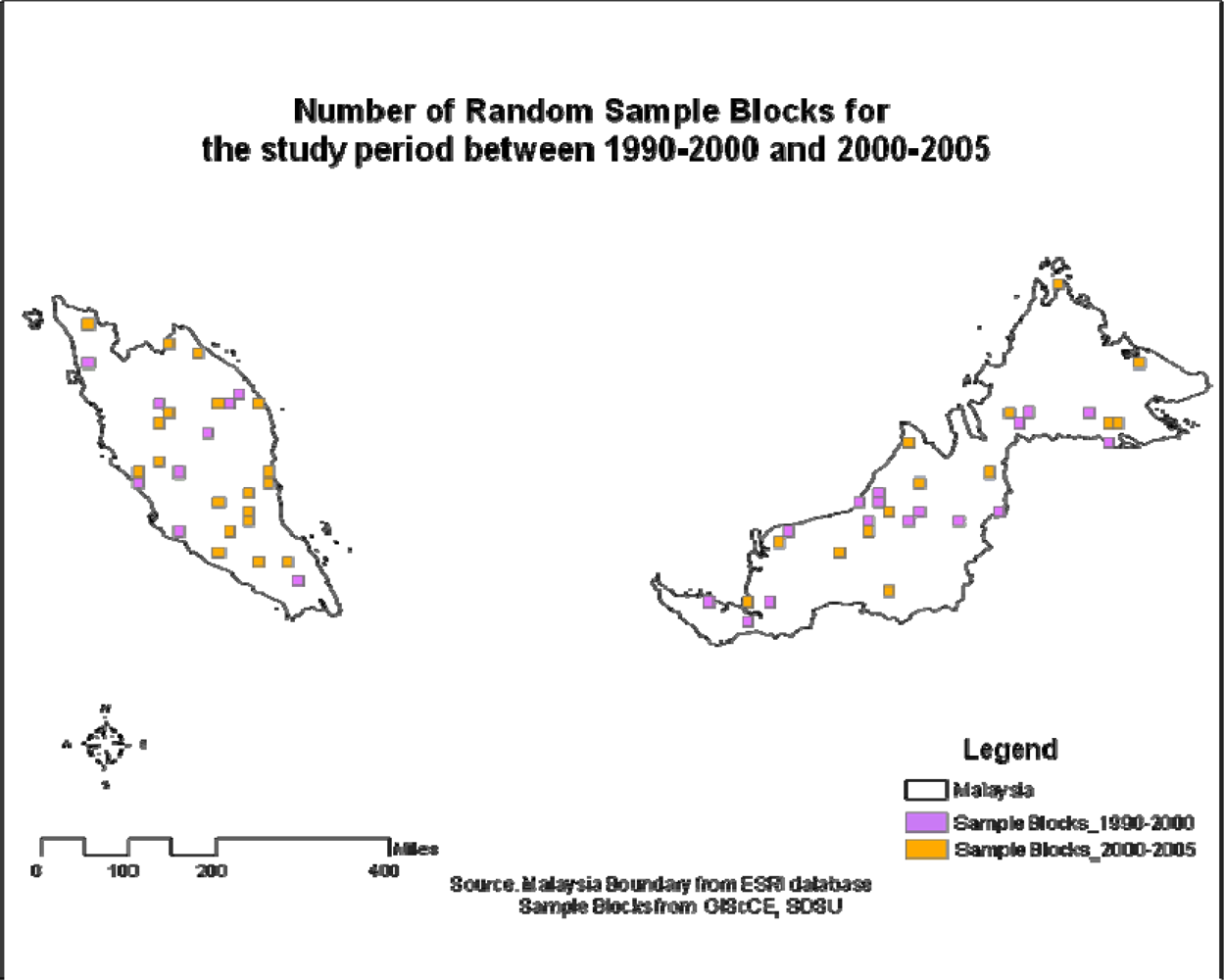
2.2. Sampling Design
2.3. Estimation
3. Results and Discussion
3.1. Discussion of Trends in Forest Cover Loss between Malaysia and Indonesia
3.2. Discussion of Sampling Design
4. Conclusions
References
- Hansen, M.C.; Stehman, S.V.; Potapov, P.V.; Loveland, T.R.; Townshend, J.R.G.; de Fries, R.S.; Pittman, K.W.; Arunarwati, B.; Stolle, F.; Steininger, M.K.; et al. Humid tropical forest clearing from 2000 to 2005 quantified by using multitemporal and multiresolution remotely sensed data. Proc. Natl. Acad. Sci. USA 2008, 105, 9439–9444. [Google Scholar]
- Grainger, A. Rates of deforestation in the humid Tropics: Estimates and measurements. Geogr. J 1993, 159, 33–44. [Google Scholar]
- Tucker, C.J.; Townshend, J.R.G. Strategies for monitoring tropical deforestation using satellite data. Int. J. Remote Sens 2000, 21, 1461–1471. [Google Scholar]
- Allen, J.C.; Barnes, D.F. The causes of deforestation in developing countries. Ann. Assoc. Am. Geogr 1985, 75, 163–184. [Google Scholar]
- Achard, F.; Eva, H; Mayaux, P. Tropical forest mapping from coarse spatial resolution satellite data. Int. J. Remote Sens 2001, 22, 2741–2762. [Google Scholar]
- Dauvergne, P. Loggers and Degradation in Asia-Pacific; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Mayaux, P.; Holmgren, P.; Achard, F.; Eva, H.; Stibig, H.-J.; Branthomme, A. Tropical forest cover change in the 1990s and options for future monitoring. Phil. Trans. Biol. Sci 2005, 360, 373–384. [Google Scholar]
- Salahuddin, J.S. Asia-Pacific Forestry Sector Outlook Study Working Paper Series. Working Paper No: APFSOS/WP/07. Country Report-Malaysia. Available online: ftp://ftp.fao.org/docrep/fao/003/W7701E/W7701E00.pdf (accessed on 1 December 2012).
- ITTO. Status of Tropical Forest Management 2005: Country Profile Malaysia. Available online: http://www.itto.int/sfm_detail/id=12410000 (accessed on 1 December 2012).
- McMorrow, J.; Talip, M.A. Decline of forest area in Sabah, Malaysia: Relationship to state policies, land code and land capability. Glob. Environ. Chang 2001, 11, 217–230. [Google Scholar]
- Aiken, R.S.; Leigh, C.H. On the declining fauna of Peninsular Malaysia in the post colonial period. R. Swed. Acad. Sci 1985, 14, 15–22. [Google Scholar]
- Eva, H.D.; Belward, A.S.; de Miranda, E.E.; di Bella, C.M.; Gond, V.; Huber, O.; Jones, S.; Sgrenzaroli, M.; Fritz, S. A land cover map of South America. Glob. Chang. Biol 2004, 10, 731–744. [Google Scholar]
- FAO. Global Forest Resources Assessment 2010. Available online: http://www.fao.org/docrep/013/i1757e/i1757e.pdf (accessed on 1 December 2012).
- Friedl, M.A.; McIver, D.K.; Hodges, J.C.F.; Zhang, X.Y.; Muchoney, D.; Strahler, A.H.; Woodcock, C.E.; Gopal, S.; Schneider, A.; Cooper, A.; et al. Global land cover mapping from MODIS: Algorithms and early results. Remote Sens. Environ 2002, 83, 287–302. [Google Scholar]
- Hansen, M.C.; Stehman, S.V.; Potapov, P.V.; Arunarwati, B.; Stolle, F.; Pittman, K. Quantifying changes in the rates of forest clearing in Indonesia from 1990 to 2005 using remotely sensed data sets. Environ. Resour. Lett. 2009. [Google Scholar] [CrossRef]
- Hansen, M.C.; Stehman, S.V.; Potapov, P.V. Quantification of global gross forest cover loss. Proc. Natl. Acad. Sci. USA 2010, 107, 8650–8655. [Google Scholar]
- Innes, J.L.; Koch, B. Forest biodiversity and its assessment by remote sensing. Glob. Ecol. Biogeogr. Lett 1998, 7, 397–419. [Google Scholar]
- Achard, F.; Eva, H.D.; Stibig, H.-J.; Mayaux, P.; Gallego, J.; Richards, T.; Malingreau, J.-P. Determination of deforestation rates of the world’s humid tropical forests. Science 2002, 297, 999–1002. [Google Scholar]
- FAO. Forest Resources Assessment 1990: Survey of Tropical Forest Cover and Study of Change Processes; FAO Forestry Paper 130; Food and Agriculture Organization of the United Nations: Rome, Italy, 1996. [Google Scholar]
- FAO. The 2010 Global Forest Resources Assessment Remote Sensing Survey: An Outline of Objectives, Data, Methods, and Approach; Forest Resources Assessment Working Paper 155; Food and Agriculture Organization of the United Nations: Rome, Italy, 2009. [Google Scholar]
- Richards, T.; Gallego, J.; Achard, F. Sampling for forest cover change assessment at the pan-tropical scale. Int. J. Remote Sens 2000, 21, 1473–1490. [Google Scholar]
- Duveiller, G.; Defourny, P.; Desclée, B.; Mayaux, P. Deforestation in Central Africa: Estimates at regional, national and landscape levels by advanced processing of systematically-distributed Landsat extracts. Remote Sens. Environ 2008, 112, 1969–1981. [Google Scholar]
- Potapov, P.; Hansen, M.C.; Stehman, S.V.; Loveland, T.R.; Pittman, K. Combining MODIS and Landsat imagery to estimate and map boreal forest cover loss. Remote Sens. Environ 2008, 112, 3708–3719. [Google Scholar]
- Broich, M.; Stehman, S.V.; Hansen, M.C.; Potapov, P.; Shimabukuro, Y.E. A comparison of sampling designs for estimating deforestation from Landsat imagery: A case study of the Brazilian Legal Amazon. Remote Sens. Environ 2009, 113, 2448–2454. [Google Scholar]
- Broich, M.; Hansen, M.C.; Stolle, F.; Potapov, P.; Arunarwati Margono, B.; Adusei, B. Remotely sensed forest cover loss shows high spatial and temporal variation across Sumatra and Kalimantan, Indonesia 2000–2008. Environ. Res. Lett. 2011. [Google Scholar] [CrossRef]
- Hansen, M.C.; de Fries, R.S. Detecting long term global forest change using continuous fields of tree cover maps from 8 km AVHRR data for the years 1982–1999. Ecosystems 2004, 7, 695–716. [Google Scholar]
- Gutman, G.; Byrnes, R.; Masek, J.; Covington, S.; Justice, C.; Franks, S.; Headley, R. Towards monitoring land cover and land-use changes at a global scale: The Global Land Survey 2005. Photogramm. Eng. Remote Sensing 2008, 74, 6–10. [Google Scholar]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Wadsworth and Brooks/Cole: Monterey, CA, USA, 1984. [Google Scholar]
- Stehman, S.V.; Hansen, M.C.; Broich, M.; Potapov, P.V. Adapting a global stratified random sample for regional estimation of forest cover change derived from satellite imagery. Remote Sens. Environ 2011, 115, 650–658. [Google Scholar]
- Greenpeace International. Roadmap to Recovery: The World’s Last Intact Forest Landscapes; Greenpeace International: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Stehman, S.V. Sampling Strategies for Forest Monitoring from Global to National Levels. In Global Forest Monitoring from Earth Observation; Achard, F., Hansen, M.C., Eds.; Chapter 5; Taylor & Francis: New York, NY, 2012; pp. 79–106. [Google Scholar]
- Särndal, C.-E.; Swensson, B.; Wretman, J. Model-Assisted Survey Sampling; Springer-Verlag: New York, NY, USA, 1992. [Google Scholar]
- Lohr, S.L. Sampling: Design and Analysis, 2nd ed.; Brooks/Cole: Boston, MA, USA, 2010. [Google Scholar]
- Stehman, S.V.; Sohl, T.L.; Loveland, T.R. An evaluation of sampling strategies to improve precision of estimates of gross change in land use and land cover. Int. J. Remote Sens 2005, 26, 4941–4957. [Google Scholar]
- Brewer, K.R.W.; Hanif, M. Sampling with Unequal Probabilities; Springer-Verlag: New York, NY, USA, 1983. [Google Scholar]
- Stehman, S.V.; Overton, W.S. Comparison of variance estimators of the Horvitz-Thompson estimator for randomized variable probability systematic sampling. J. Am. Stat. Assoc 1994, 89, 30–43. [Google Scholar]
- Overton, W.S.; Stehman, S.V. The Horvitz-Thompson theorem as a unifying perspective for probability sampling: With examples from natural resource sampling. Am. Stat 1995, 49, 261–268. [Google Scholar]
- FWI/GFW. The State of the Forest: Indonesia; Forest Watch Indonesia: Bogor, Indonesia, Global Forest Watch: Washington, DC, USA; 2002. [Google Scholar]
- FAO. Global Forest Resources Assessment 2000; FAO Forestry Paper No. 140; Food and Agriculture Organization of the United Nations: Rome, Italy, 2001. [Google Scholar]
- Cochran, W.G. Sampling Techniques, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1977. [Google Scholar]
- Achard, F.; Stibig, H.-J.; Eva, H.; Mayaux, P. Tropical forest cover monitoring in the humid tropics—TREES project. Int. Soc. Trop. Ecol 2002, 43, 9–20. [Google Scholar]
- Achard, F.; de Fries, R.; Eva, H.; Hansen, M.C.; Mayaux, P.; Stibig, H.-J. Pan tropical monitoring of deforestation. Environ. Res. Lett 2007, 4, 1–11. [Google Scholar]
- Eva, H.D.; Achard, F.; Beuchle, R.; de Miranda, E.; Carboni, S.; Seliger, R.; Vollmar, M.; Holler, W.A.; Oshiro, O.T.; Arroyo, V.B.; et al. Forest cover changes in tropical South and Central America from 1990–2005 and related carbon emissions and removals. Remote Sens 2012, 4, 1369–1391. [Google Scholar]

| Period | n | Percent Area of Forest Cover (SE) | Percent of Land Area Cleared (SE) | Total Area (Mha) of Gross Forest Cover Loss (SE) | Annual Mean (Mha/yr) Gross Forest Cover Loss (SE) |
|---|---|---|---|---|---|
| 1990–2000 | 25 | 81.0 (3.9) | 13.0 (2.4) | 4.25 (0.78) | 0.42 (0.08) |
| 2000–2005 | 35 | 72.8 (4.3) | 9.8 (1.7) | 3.20 (0.55) | 0.64 (0.11) |
| Period | Estimated Annual Mean Gross Forest Cover Loss (Mha/yr) (SE in Parentheses) | |
|---|---|---|
| Malaysia | Indonesia * | |
| 1990–2000 | 0.42 (0.08) | 1.78 (0.14) |
| 2000–2005 | 0.64 (0.11) | 0.71 (0.09) |
| Stratum | Nh | nh | Mean Forest Cover Loss as % of Land Area (Standard Deviation) | Percent Contribution to Estimated Variance | |
|---|---|---|---|---|---|
| MODIS | Landsat | ||||
| 1 | 95 | 2 | 0.00 (0.00) | 2.78 (2.98) | 1.5 |
| 2 | 649 | 10 | 0.37 (0.66) | 9.39 (7.76) | 94.0 |
| 3 | 165 | 13 | 4.50 (2.07) | 12.41 (7.15) | 3.7 |
| 4 | 47 | 8 | 16.02 (5.55) | 19.40 (9.33) | 0.7 |
| 5 | 2 | 2 | 47.00 (1.41) | 33.55 (12.09) | 0.0 |
Share and Cite
Giree, N.; Stehman, S.V.; Potapov, P.; Hansen, M.C. A Sample-Based Forest Monitoring Strategy Using Landsat, AVHRR and MODIS Data to Estimate Gross Forest Cover Loss in Malaysia between 1990 and 2005. Remote Sens. 2013, 5, 1842-1855. https://doi.org/10.3390/rs5041842
Giree N, Stehman SV, Potapov P, Hansen MC. A Sample-Based Forest Monitoring Strategy Using Landsat, AVHRR and MODIS Data to Estimate Gross Forest Cover Loss in Malaysia between 1990 and 2005. Remote Sensing. 2013; 5(4):1842-1855. https://doi.org/10.3390/rs5041842
Chicago/Turabian StyleGiree, Namita, Stephen V. Stehman, Peter Potapov, and Matthew C. Hansen. 2013. "A Sample-Based Forest Monitoring Strategy Using Landsat, AVHRR and MODIS Data to Estimate Gross Forest Cover Loss in Malaysia between 1990 and 2005" Remote Sensing 5, no. 4: 1842-1855. https://doi.org/10.3390/rs5041842
APA StyleGiree, N., Stehman, S. V., Potapov, P., & Hansen, M. C. (2013). A Sample-Based Forest Monitoring Strategy Using Landsat, AVHRR and MODIS Data to Estimate Gross Forest Cover Loss in Malaysia between 1990 and 2005. Remote Sensing, 5(4), 1842-1855. https://doi.org/10.3390/rs5041842





