Integrating Solar Induced Fluorescence and the Photochemical Reflectance Index for Estimating Gross Primary Production in a Cornfield
Abstract
:1. Introduction
2. Methods
2.1. Study Site and Field Data Collection
2.2. Spectral Data Processing
2.3. Flux Data, LUE and GPP Modeling
2.4. Cross-Validation
3. Results
3.1. Diurnal and Seasonal Courses of GPP, PRI, and SIF
3.2. LUE and GPP Modeling
3.3. Cross-Validation
4. Discussion
5. Conclusions
Acknowledgments
Disclaimer
Conflict of Interest
References
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rodenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar]
- Grace, J.; Disney, C.J.N.M.; Lewis, P.; Quaife, T.; Bowyer, P. Can we measure terrestrial photosynthesis from space directly, using spectral reflectance and fluorescence? Glob. Chang. Biol 2007, 13, 1484–1497. [Google Scholar]
- Middleton, E.M.; Huemmrich, K.F.; Cheng, Y.-B.; Margolis, H.A. Spectral Bioindicators of Photosynthetic Efficiency and Vegetation Stress. In Hyperspectral Remote Sensing of Vegetation; Thenkabail, P.S., Lyon, J.G., Huete, A., Eds.; CRC Press: Boca Raton, FL, USA, 2011; pp. 265–288. [Google Scholar]
- Tucker, C.J.; Sellers, P.J. Satellite remote sensing of primary production. Int. J. Remote Sens 1986, 7, 1395–1416. [Google Scholar]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. BioScience 2004, 54, 547–560. [Google Scholar]
- Peng, Y.; Gitelson, A.A. Remote estimation of gross primary productivity in soybean and maize based on total crop chlorophyll content. Remote Sens. Environ 2012, 117, 440–448. [Google Scholar]
- Cheng, Y.-B.; Wharton, S.; Ustin, S.L.; Zarco-Tejada, P.J.; Falk, M.; Paw U, K.T. Relationships between Moderate Resolution Imaging Spectroradiometer water indexes and tower flux data in an old growth conifer forest. J. Appl. Remote Sens. 2007, 1. [Google Scholar] [CrossRef]
- Xiao, J.; Zhuang, Q.; Law, B.E.; Chen, J.; Baldocchi, D.D.; Cook, D.R.; Oren, R.; Richardson, A.D.; Wharton, S.; Ma, S.; et al. A continuous measure of gross primary production for the conterminous United States derived from MODIS and AmeriFlux data. Remote Sens. Environ 2010, 114, 576–591. [Google Scholar]
- Houborg, R.; Anderson, M.C.; Daughtry, C.S.T.; Kustas, W.P.; Rodell, M. Using leaf chlorophyll to parameterize light-use-efficiency within a thermal-based carbon, water and energy exchange model. Remote Sensing Environ 2011, 115, 1694–1705. [Google Scholar]
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore, B., III. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ 2004, 89, 519–534. [Google Scholar]
- Sellers, P.J.; Dickinson, R.E.; Randall, D.A.; Betts, A.K.; Hall, F.G.; Berry, J.A.; Collatz, G.J.; Denning, A.S.; Mooney, H.A.; Nobre, C.A.; et al. Modeling the exchange of energy, water, and carbon between continents and the atmosphere. Science 1997, 275, 502–509. [Google Scholar]
- Zhang, Q.; Middleton, E.M.; Margolis, H.A.; Drolet, G.G.; Barr, A.A.; Black, T.A. Can a satellite-derived estimate of the fraction of PAR absorbed by chlorophyll (FAPARchl) improve predictions of light-use efficiency and ecosystem photosynthesis for a boreal aspen forest? Remote Sens. Environ 2009, 113, 880–888. [Google Scholar]
- Campbell, P.K.E.; Middleton, E.M.; Thome, K.J.; Kokaly, R.F.; Huemmrich, K.F.; Lagomasino, D.; Novick, K.A.; Brunsell, N.A. EO-1 hyperion reflectance time series at calibration and validation sites: Stability and sensitivity to seasonal dynamics. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2013, 6, 276–290. [Google Scholar]
- Gitelson, A.A.; Peng, Y.; Masek, J.G.; Rundquist, D.C.; Verma, S.; Suyker, A.; Baker, J.M.; Hatfield, J.L.; Meyers, T. Remote estimation of crop gross primary production with Landsat data. Remote Sens. Environ 2012, 121, 404–414. [Google Scholar]
- Monteith, J.L. Solar-radiation and productivity in tropical ecosystems. J. Appl. Ecol 1972, 9, 747–766. [Google Scholar]
- Monteith, J.L. Climate and the efficiency of crop production in Britain. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci 1977, 281, 277–294. [Google Scholar]
- Cheng, Y.-B.; Middleton, E.M.; Hilker, T.; Coops, N.C.; Krishnan, P.; Black, T.A. Dynamics of spectral bio-indicators and their correlations with light use efficiency using directional observations at a Douglas-fir forest. Meas. Sci. Technol. 2009, 20. [Google Scholar] [CrossRef]
- Middleton, E.M.; Cheng, Y.-B.; Hilker, T.; Black, T.A.; Krishnan, P.; Coops, N.C.; Huemmrich, K.F. Linking foliage spectral responses to canopy level ecosystem photosynthetic light use efficiency at a Douglas-fir forest in Canada. Can. J. Remote Sens 2009, 35, 166–188. [Google Scholar]
- Nichol, C.J.; Huemmrich, K.F.; Black, T.A.; Jarvis, P.G.; Walthall, C.L.; Grace, J.; Hall, F.G. Remote sensing of photosynthetic-light-use efficiency of boreal forest. Agric. For. Meteorol 2000, 101, 131–142. [Google Scholar]
- Drolet, G.G.; Middleton, E.M.; Huemmrich, K.F.; Hall, F.G.; Amiro, B.D.; Barr, A.G.; Black, T.A.; McCaughey, J.H.; Margolis, H.A. Regional mapping of gross light-use efficiency using MODIS spectral indices. Remote Sens. Environ 2008, 112, 3064–3078. [Google Scholar]
- Hall, F.G.; Hilker, T.; Coops, N.C. Data assimilation of photosynthetic light-use efficiency using multi-angular satellite data: I. Model formulation. Remote Sens. Environ 2012, 121, 301–308. [Google Scholar]
- Hilker, T.; Hall, F.G.; Tucker, C.J.; Coops, N.C.; Black, T.A.; Nichol, C.J.; Sellers, P.J.; Barr, A.; Hollinger, D.Y.; Munger, J.W. Data assimilation of photosynthetic light-use efficiency using multi-angular satellite data: II Model implementation and validation. Remote Sens. Environ 2012, 121, 287–300. [Google Scholar]
- Heinsch, F.A.; Zhao, M.; Running, S.W.; Kimball, J.S.; Nemani, R.R.; Davis, K.J.; Bolstad, P.V.; Cook, B.D.; Desai, A.R.; Ricciuto, D.M.; et al. Evaluation of remote sensing based terrestrial productivity from MODIS using regional tower eddy flux network observations. IEEE Trans. Geosci. Remote Sens 2006, 44, 1908–1925. [Google Scholar]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Running, S.W.; Zhao, M.; Costa, M.H.; Kirschbaum, A.A.; Ham, J.M.; Saleska, S.R.; et al. Evaluation of MODIS NPP and GPP products across multiple biomes. Remote Sens. Environ 2006, 102, 282–292. [Google Scholar]
- Turner, D.P.; Urbanski, S.; Bremer, D.; Wofsy, S.C.; Meyers, T.; Gower, S.T.; Gregory, M. A cross-biome comparison of daily light use efficiency for gross primary production. Glob. Chang. Biol 2003, 9, 383–395. [Google Scholar]
- Damm, A.; Elbers, J.; Erler, A.; Gioli, B.; Hamdi, K.; Hutjes, R.; Kosvancova, M.; Meroni, M.; Miglietta, F.; Moersch, A.; et al. Remote sensing of sun-induced fluorescence to improve modeling of diurnal courses of gross primary production (GPP). Glob. Chang. Biol 2010, 16, 171–186. [Google Scholar]
- Demmig, B.; Winter, K.; Krüger, A.; Czygan, F.-C. Photoinhibition and zeaxanthin formation in intact leaves: A possible role of the xanthophyll cycle in the dissipation of excess light energy. Plant Physiol 1987, 84, 218–224. [Google Scholar]
- Demmig-Adams, B.; Adams, W.W. Photosynthesis: Harvesting sunlight safely. Nature 2000, 403, 371–374. [Google Scholar]
- Gamon, J.A.; Serrano, L.; Surfus, J.S. The photochemical reflectance index: An optical indicator of photosynthetic radiation use efficiency across species, functional types, and nutrient levels. Oecologia 1997, 112, 492–501. [Google Scholar]
- Li, X.-P.; Bjorkman, O.; Shih, C.; Grossman, A.R.; Rosenquist, M.; Jansson, S.; Niyogi, K.K. A pigment-binding protein essential for regulation of photosynthetic light harvesting. Nature 2000, 403, 391–395. [Google Scholar]
- Demmig-Adams, B.; Adams, W.W., III. The role of xanthophyll cycle carotenoids in the protection of photosynthesis. Trends Plant Sci 1996, 1, 21–26. [Google Scholar]
- Gamon, J.A.; Field, C.B.; Bilger, W.; Björkman, O.; Fredeen, A.L.; Peñuelas, J. Remote sensing of the xanthophyll cycle and chlorophyll fluorescence in sunflower leaves and canopies. Oecologia 1990, 85, 1–7. [Google Scholar]
- Yamamoto, H.Y. Biochemistry of the violaxanthin cycle in higher plants. Pure Appl. Chem 1979, 51, 639–648. [Google Scholar]
- Gamon, J.A.; Penuelas, J.; Field, C.B. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ 1992, 41, 35–44. [Google Scholar]
- Peñuelas, J.; Filella, I.; Gamon, J.A. Assessment of photosynthetic radiation-use efficiency with spectral reflectance. New Phytol 1995, 131, 291–296. [Google Scholar]
- Peñuelas, J.; Gamon, J.A.; Fredeen, A.L.; Merino, J.; Field, C.B. Reflectance indices associated with physiological changes in nitrogen- and water-limited sunflower leaves. Remote Sens. Environ 1994, 48, 135–146. [Google Scholar]
- Peñuelas, J.; Llusia, J.; Pinol, J.; Filella, I. Photochemical reflectance index and leaf photosynthetic radiation-use-effeciency assessment in Mediterranean trees. Int. J. Remote Sens 1997, 18, 2863–2868. [Google Scholar]
- Filella, I.; Amaro, T.; Araus, J.L.; Peñuelas, J. Relationship between photosynthetic radiation-use efficiency of barley canopies and the photochemical reflectance index (PRI). Physiol. Plant 1996, 96, 211–216. [Google Scholar]
- Inoue, Y.; Peñuelas, J. Relationship between light use efficiency and photochemical reflectance index in soybean leaves as affected by soil water content. Int. J. Remote Sens 2006, 27, 5109–5114. [Google Scholar]
- Trotter, G.M.; Whitehead, D.; Pinkney, E.J. The photochemical reflectance index as a measure of photosynthetic light use efficiency for plants with varying foliar nitrogen contents. Int. J. Remote Sens 2002, 23, 1207–1212. [Google Scholar]
- Gamon, J.A.; Bond, B. Effects of irradiance and photosynthetic downregulation on the photochemical reflectance index in Douglas-fir and ponderosa pine. Remote Sens. Environ 2013, 135, 141–149. [Google Scholar]
- Sims, D.A.; Luo, H.; Hastings, S.; Oechel, W.C.; Rahman, A.F.; Gamon, J.A. Parallel adjustments in vegetation greenness and ecosystem CO2 exchange in response to drought in a Southern California chaparral ecosystem. Remote Sens. Environ 2006, 103, 289–303. [Google Scholar]
- Drolet, G.G.; Huemmrich, K.F.; Hall, F.G.; Middleton, E.M.; Black, T.A.; Barr, A.G.; Margolis, H.A. A MODIS-derived photochemical reflectance index to detect inter-annual variations in the photosynthetic light-use efficiency of a boreal deciduous forest. Remote Sens. Environ 2005, 98, 212–224. [Google Scholar]
- Barton, C.V.M.; North, P.R.J. Remote sensing of canopy light use efficiency using the photochemical reflectance index: Model and sensitivity analysis. Remote Sens. Environ 2001, 78, 264–273. [Google Scholar]
- Gamon, J.; Field, C.; Fredeen, A.; Thayer, S. Assessing photosynthetic downregulation in sunflower stands with an optically-based model. Photosynth. Res 2001, 67, 113–125. [Google Scholar]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ 2002, 81, 337–354. [Google Scholar]
- Stylinski, C.D.; Gamon, J.A.; Oechel, W.C. Seasonal patterns of reflectance indices, carotenoid pigments and photosynthesis of evergreen chaparral species. Oecologia 2002, 131, 366–374. [Google Scholar]
- Hernández-Clemente, R.; Navarro-Cerrillo, R.M.; Suárez, L.; Morales, F.; Zarco-Tejada, P.J. Assessing structural effects on PRI for stress detection in conifer forests. Remote Sens. Environ 2011, 115, 2360–2375. [Google Scholar]
- Nichol, C.J.; Grace, J. Determination of leaf pigment content in Calluna vulgaris shoots from spectral reflectance. Int. J. Remote Sens 2010, 31, 5409–5422. [Google Scholar]
- Garbulsky, M.F.; Peñuelas, J.; Gamon, J.; Inoue, Y.; Filella, I. The photochemical reflectance index (PRI) and the remote sensing of leaf, canopy and ecosystem radiation use efficiencies: A review and meta-analysis. Remote Sens. Environ 2011, 115, 281–297. [Google Scholar]
- Peñuelas, J.; Garbulsky, M.F.; Filella, I. Photochemical reflectance index (PRI) and remote sensing of plant CO2 uptake. New Phytol 2011, 191, 596–599. [Google Scholar]
- Van der Tol, C.; Verhoef, W.; Rosema, A. A model for chlorophyll fluorescence and photosynthesis at leaf scale. Agric. For. Meteorol 2009, 149, 96–105. [Google Scholar]
- Baker, N.R. Chlorophyll fluorescence: A probe of photosynthesis in vivo. Annu. Rev. Plant Biol 2008, 59, 89–113. [Google Scholar]
- Meroni, M.; Rossini, M.; Guanter, L.; Alonso, L.; Rascher, U.; Colombo, R.; Moreno, J. Remote sensing of solar-induced chlorophyll fluorescence: Review of methods and applications. Remote Sens. Environ 2009, 113, 2037–2051. [Google Scholar]
- Joiner, J.; Yoshida, Y.; Vasilkov, A.P.; Corp, L.A.; Middleton, E.M. First observations of global and seasonal terrestrial chlorophyll fluorescence from space. Biogeosciences 2011, 8, 637–651. [Google Scholar]
- Middleton, E.M.; Corp, L.A.; Campbell, P.K.E. Comparison of measurements and FluorMOD simulations for solar-induced chlorophyll fluorescence and reflectance of a corn crop under nitrogen treatments. Int. J. Remote Sens 2008, 29, 5193–5213. [Google Scholar]
- Corp, L.A.; Middleton, E.M.; McMurtrey, J.E.; Entcheva Campbell, P.K.; Butcher, L.M. Fluorescence sensing techniques for vegetation assessment. Appl. Opt 2006, 45, 1023–1033. [Google Scholar]
- Mohammed, G.H.; Binder, W.D.; Gillies, S.L. Chlorophyll fluorescence: A review of its practical forestry applications and instrumentation. Scand. J. For. Res 1995, 10, 383–410. [Google Scholar]
- Lichtenthaler, H.K. Vegetation stress: An introduction to the stress concept in plants. J. Plant Physiol 1996, 148, 4–14. [Google Scholar]
- Meroni, M.; Rossini, M.; Picchi, V.; Panigada, C.; Cogliati, S.; Nali, C.; Colombo, R. Assessing steady-state fluorescence and PRI from hyperspectral proximal sensing as early indicators of plant stress: The case of ozone exposure. Sensors 2008, 8, 1740–1754. [Google Scholar]
- Zarco-Tejada, P.J.; Miller, J.R.; Mohammed, G.H.; Noland, T.L.; Sampson, P.H. Estimation of chlorophyll fluorescence under natural illumination from hyperspectral data. Int. J. Appl. Earth Obs. Geoinf 2001, 3, 321–327. [Google Scholar]
- Zarco-Tejada, P.J.; Miller, J.R.; Mohammed, G.H.; Noland, T.L. Chlorophyll fluorescence effects on vegetation apparent reflectance: I. Leaf-level measurements and model simulation. Remote Sens. Environ 2000, 74, 582–595. [Google Scholar]
- Zarco-Tejada, P.J.; Miller, J.R.; Mohammed, G.H.; Noland, T.L.; Sampson, P.H. Chlorophyll fluorescence effects on vegetation apparent reflectance: II. Laboratory and airborne canopy-level measurements with hyperspectral data. Remote Sens. Environ 2000, 74, 596–608. [Google Scholar]
- Zarco-Tejada, P.J.; Pushnik, J.C.; Dobrowski, S.; Ustin, S.L. Steady-state chlorophyll a fluorescence detection from canopy derivative reflectance and double-peak red-edge effects. Remote Sens. Environ 2003, 84, 283–294. [Google Scholar]
- Dobrowski, S.Z.; Pushnik, J.C.; Zarco-Tejada, P.J.; Ustin, S.L. Simple reflectance indices track heat and water stress-induced changes in steady-state chlorophyll fluorescence at the canopy scale. Remote Sens. Environ 2005, 97, 403–414. [Google Scholar]
- Maier, S.W.; Günther, K.P.; Stellmes, M. Sun-Induced Fluorescence: A New Tool for Precision Farming. In Digital Imaging and Spectral Techniques: Applications to Precision Agriculture and Crop Physiology; VanToai, T., Major, D., McDonald, M., Schepers, J., Tarpley, L., Eds.; American Society of Agronomy: Madison, WI, USA, 2003; pp. 209–222. [Google Scholar]
- Meroni, M.; Busetto, L.; Colombo, R.; Guanter, L.; Moreno, J.; Verhoef, W. Performance of spectral fitting methods for vegetation fluorescence quantification. Remote Sens. Environ 2010, 114, 363–374. [Google Scholar]
- Alonso, L.; Gomez-Chova, L.; Vila-Frances, J.; Amoros-Lopez, J.; Guanter, L.; Calpe, J.; Moreno, J. Improved Fraunhofer Line Discrimination method for vegetation fluorescence quantification. IEEE Geosci. Remote Sens. Lett 2008, 5, 620–624. [Google Scholar]
- Meroni, M.; Colombo, R. Leaf level detection of solar induced chlorophyll fluorescence by means of a subnanometer resolution spectroradiometer. Remote Sens. Environ 2006, 103, 438–448. [Google Scholar]
- Damm, A.; Erler, A.; Hillen, W.; Meroni, M.; Schaepman, M.E.; Verhoef, W.; Rascher, U. Modeling the impact of spectral sensor configurations on the FLD retrieval accuracy of sun-induced chlorophyll fluorescence. Remote Sens. Environ 2011, 115, 1882–1892. [Google Scholar]
- Louis, J.; Ounis, A.; Ducruet, J.-M.; Evain, S.; Laurila, T.; Thum, T.; Aurela, M.; Wingsle, G.; Alonso, L.; Pedros, R.; et al. Remote sensing of sunlight-induced chlorophyll fluorescence and reflectance of Scots pine in the boreal forest during spring recovery. Remote Sens. Environ 2005, 96, 37–48. [Google Scholar]
- Moya, I.; Camenen, L.; Evain, S.; Goulas, Y.; Cerovic, Z.G.; Latouche, G.; Flexas, J.; Ounis, A. A new instrument for passive remote sensing: 1. Measurements of sunlight-induced chlorophyll fluorescence. Remote Sens. Environ 2004, 91, 186–197. [Google Scholar]
- Rossini, M.; Meroni, M.; Migliavacca, M.; Manca, G.; Cogliati, S.; Busetto, L.; Picchi, V.; Cescatti, A.; Seufert, G.; Colombo, R. High resolution field spectroscopy measurements for estimating gross ecosystem production in a rice field. Agric. For. Meteorol 2010, 150, 1283–1296. [Google Scholar]
- Rossini, M.; Cogliati, S.; Meroni, M.; Migliavacca, M.; Galvagno, M.; Busetto, L.; Cremonese, E.; Julitta, T.; Siniscalco, C.; Morra di Cella, U.; et al. Remote sensing-based estimation of gross primary production in a subalpine grassland. Biogeosciences 2012, 9, 2565–2584. [Google Scholar]
- Daumard, F.; Champagne, S.; Fournier, A.; Goulas, Y.; Ounis, A.; Hanocq, J.F.; Moya, I. A field platform for continuous measurement of canopy fluorescence. IEEE Trans. Geosci. Remote Sens 2010, 48, 3358–3368. [Google Scholar]
- Meroni, M.; Picchi, V.; Rossini, M.; Cogliati, S.; Panigada, C.; Nali, C.; Lorenzini, G.; Colombo, R. Leaf level early assessment of ozone injuries by passive fluorescence and photochemical reflectance index. Int. J. Remote Sens 2008, 29, 5409–5422. [Google Scholar]
- Zarco-Tejada, P.J.; Berni, J.A.J.; Suárez, L.; Sepulcre-Cantó, G.; Morales, F.; Miller, J.R. Imaging chlorophyll fluorescence with an airborne narrow-band multispectral camera for vegetation stress detection. Remote Sens. Environ 2009, 113, 1262–1275. [Google Scholar]
- Zarco-Tejada, P.J.; Catalina, A.; González, M.R.; Martín, P. Relationships between net photosynthesis and steady-state chlorophyll fluorescence retrieved from airborne hyperspectral imagery. Remote Sens. Environ 2013, 136, 247–258. [Google Scholar]
- Zarco-Tejada, P.J.; Morales, A.; Testi, L.; Villalobos, F.J. Spatio-temporal patterns of chlorophyll fluorescence and physiological and structural indices acquired from hyperspectral imagery as compared with carbon fluxes measured with eddy covariance. Remote Sens. Environ 2013, 133, 102–115. [Google Scholar]
- Agati, G.; Mazzinghi, P.; Fusi, F.; Ambrosini, I. The f685/f730 chlorophyll fluorescence ratio as a tool in plant physiology: Response to physiological and environmental factors. J. Plant Physiol 1995, 145, 228–238. [Google Scholar]
- Amoros-Lopez, J.; Gomez-Chova, L.; Vila-Frances, J.; Calpe, J.; Alonso, L.; Moreno, J.; del Valle-Tascon, S. Study of the diurnal cycle of stressed vegetation for the improvement of fluorescence remote sensing. Proc. SPIE 2006, 6359. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.C.; Wulder, M.A.; Black, T.A.; Guy, R.D. The use of remote sensing in light use efficiency based models of gross primary production: A review of current status and future requirements. Sci. Total Environ 2008, 404, 411–423. [Google Scholar]
- Rascher, U.; Agati, G.; Alonso, L.; Cecchi, G.; Champagne, S.; Colombo, R.; Damm, A.; Daumard, F.; de Miguel, E.; Fernandez, G.; et al. CEFLES2: The remote sensing component to quantify photosynthetic efficiency from the leaf to the region by measuring sun-induced fluorescence in the oxygen absorption bands. Biogeosciences 2009, 6, 1181–1198. [Google Scholar]
- Cheng, Y.-B.; Middleton, E.M.; Huemmrich, K.F.; Zhang, Q.; Campbell, P.K.E.; Corp, L.A.; Russ, A.L.; Kustas, W.P. Utilizing in situ directional hyperspectral measurements to validate bio-indicator simulations for a corn crop canopy. Ecol. Inform 2010, 5, 330–338. [Google Scholar]
- Cheng, Y.-B.; Middleton, E.M.; Zhang, Q.; Corp, L.A.; Dandois, J.; Kustas, W.P. The photochemical reflectance index from directional cornfield reflectances: Observations and simulations. Remote Sens. Environ 2012, 124, 444–453. [Google Scholar]
- Plascyk, J.A. The MK II Fraunhofer Line Discriminator (FLD-II) for airborne and orbital remote sensing of solar-stimulated luminescence. OPTICE 1975, 14, 339–330. [Google Scholar]
- Munger, J.; Loescher, H. Guidelines for Making Eddy Covariance Flux Measurements; Ameriflux; Oak Ridge, TN, USA, 2006. [Google Scholar]
- Cook, B.D.; Davis, K.J.; Wang, W.; Desai, A.; Berger, B.W.; Teclaw, R.M.; Martin, J.G.; Bolstad, P.V.; Bakwin, P.S.; Yi, C.; et al. Carbon exchange and venting anomalies in an upland deciduous forest in northern Wisconsin, USA. Agric. For. Meteorol 2004, 126, 271–295. [Google Scholar]
- Carter, G.A.; Jones, J.H.; Mitchell, R.J.; Brewer, C.H. Detection of solar-excited chlorophyll a fluorescence and leaf photosynthetic capacity using a fraunhofer line radiometer. Remote Sens. Environ 1996, 55, 89–92. [Google Scholar]
- Chappelle, E.W.; Corp, L.A.; McMurtrey, J.E.; Kim, M.S.; Daughtry, C.S.T. Fluorescence: A diagnostic tool for the detection of stress in plants. Proc. SPIE 1997, 2959, 14–23. [Google Scholar]
- Demmig-Adams, B. Linking the xanthophyll cycle with thermal energy dissipation. Photosynth. Res 2003, 76, 73–80. [Google Scholar]
- Valentini, R.; Cecchi, G.; Mazzinghi, P.; Mugnozza, G.S.; Agati, G.; Bazzani, M.; Deangelis, P.; Fusi, F.; Matteucci, G.; Raimondi, V. Remote-sensing of chlorophyll-a fluorescence of vegetation canopies. 2. Physiological significance of fluorescence signal in response to environmental stresses. Remote Sens. Environ 1994, 47, 29–35. [Google Scholar]
- Rosema, A.; Snel, J.F.H.; Zahn, H.; Buurmeijer, W.F.; van Hove, L.W.A. The relation between laser-induced chlorophyll fluorescence and photosynthesis. Remote Sens. Environ 1998, 65, 143–154. [Google Scholar]
- Flexas, J.; Escalona, J.M.; Medrano, H. Water stress induces different levels of photosynthesis and electron transport rate regulation in grapevines. Plant Cell Environ 1999, 22, 39–48. [Google Scholar]
- Cerovic, Z.G.; Goulas, Y.; Gorbunov, M.; Briantais, J.M.; Camenen, L.; Moya, I. Fluorosensing of water stress in plants: Diurnal changes of the mean lifetime and yield of chlorophyll fluorescence, measured simultaneously and at distance with a tau-LIDAR and a modified PAM-fluorimeter, in maize, sugar beet, and Kalanchoe. Remote Sens. Environ 1996, 58, 311–321. [Google Scholar]
- Agati, G.; Cerovic, Z.G.; Moya, I. The effect of decreasing temperature up to chilling values on the in vivo F685/F735 chlorophyll fluorescence ratio in phaseolus vulgaris and pisum sativum: The role of the photosystem I contribution to the 735 nm fluorescence band. Photochem. Photobiol 2000, 72, 75–84. [Google Scholar]
- Pieruschka, R.; Klimov, D.; Kolber, Z.S.; Berry, J.A. Monitoring of cold and light stress impact on photosynthesis by using the laser induced fluorescence transient (LIFT) approach. Funct. Plant Biol 2010, 37, 395–402. [Google Scholar]
- Yaryura, P.; Cordon, G.; Leon, M.; Kerber, N.; Pucheu, N.; Rubio, G.; Garcia, A.; Lagorio, M.G. Effect of phosphorus deficiency on reflectance and chlorophyll fluorescence of cotyledons of oilseed rape (Brassica napus L.). J. Agron. Crop Sci 2009, 195, 186–196. [Google Scholar]
- McMurtney, J.E.; Middleton, E.M.; Corp, L.A.; Campbell, P.K.E.; Butcher, L.M.; Chappelle, E.W.; Cook, W.B. IEEE Fluorescence Responses from Nitrogen Plant Stress in 4 Fraunhofer Band Regions. Proceedings of IEEE International Geoscience and Remote Sensing Symposium, 2002 (IGARSS ’02), Toronto, Canada, 24–28 June 2002; 3, pp. 1538–1540.
- Subhash, N.; Mohanan, C.N. Laser-induced red chlorophyll fluorescence signatures as nutrient stress indicator in rice plants. Remote Sens. Environ 1994, 47, 45–50. [Google Scholar]
- Schachtl, J.; Huber, G.; Maidl, F.-X.; Sticksel, E. Laser-Induced Chlorophyll Fluorescence Measurements for Detecting the Nitrogen Status of Wheat (Triticum aestivum L.) Canopies. In Precision Agriculture; Wageningen Academic Publishers: Wageningen, The Netherlands, 2005; Volume 6, pp. 143–156. [Google Scholar]
- Silva, E.A.; Gouveia-Neto, A.S.; Oliveira, R.A.; Moura, D.S.; Cunha, P.C.; Costa, E.B.; Camara, T.J.R.; Willadino, L.G. Water deficit and salt stress diagnosis through LED induced chlorophyll fluorescence analysis in Jatropha curcas L. J. Fluoresc 2012, 22, 623–630. [Google Scholar]
- Zhang, H.; Hu, H.; Zhang, X.B.; Wang, K.L.; Song, T.Q.; Zeng, F.P. Detecting Suaeda salsa L. chlorophyll fluorescence response to salinity stress by using hyperspectral reflectance. Acta Physiol. Plant 2012, 34, 581–588. [Google Scholar]
- Middleton, E.; McMurtney, J.E.; Campbell, P.K.; Corp, L.A.; Butcher, L.M.; Chappelle, E.W. Optical and fluorescence properties of corn leaves from different nitrogen regimes. Proc. SPIE 2003, 4879, 72–83. [Google Scholar]
- Meroni, M.; Panigada, C.; Rossini, M.; Picchi, V.; Cogliati, S.; Colombo, R. Using optical remote sensing techniques to track the development of ozone-induced stress. Environ. Pollut 2009, 157, 1413–1420. [Google Scholar]
- Perez-Priego, O.; Zarco-Tejada, P.J.; Miller, J.R.; Sepulcre-Canto, G.; Fereres, E. Detection of water stress in orchard trees with a high-resolution spectrometer through chlorophyll fluorescence in-filling of the O2-A band. IEEE Trans. Geosci. Remote Sens 2005, 43, 2860–2869. [Google Scholar]
- Zarco-Tejada, P.J.; Gonzalez-Dugo, V.; Berni, J.A.J. Fluorescence, temperature and narrow-band indices acquired from a UAV platform for water stress detection using a micro-hyperspectral imager and a thermal camera. Remote Sens. Environ 2012, 117, 322–337. [Google Scholar]
- Joiner, J.; Guanter, L.; Lindstrot, R.; Voigt, M.; Vasilkov, A.P.; Middleton, E.M.; Huemmrich, K.F.; Yoshida, Y.; Frankenberg, C. Global monitoring of terrestrial chlorophyll fluorescence from moderate spectral resolution near-infrared satellite measurements: Methodology, simulations, and application to GOME-2. Atmos. Meas. Tech. Discuss 2013, 6, 3883–3930. [Google Scholar]




 ), 2010 (
), 2010 (
 ), 2011 (
), 2011 (
 ), 2012(
), 2012(
 ) in the USDA BARC cornfield.
) in the USDA BARC cornfield.
 ), 2010 (
), 2010 (
 ), 2011 (
), 2011 (
 ), 2012(
), 2012(
 ) in the USDA BARC cornfield.
) in the USDA BARC cornfield.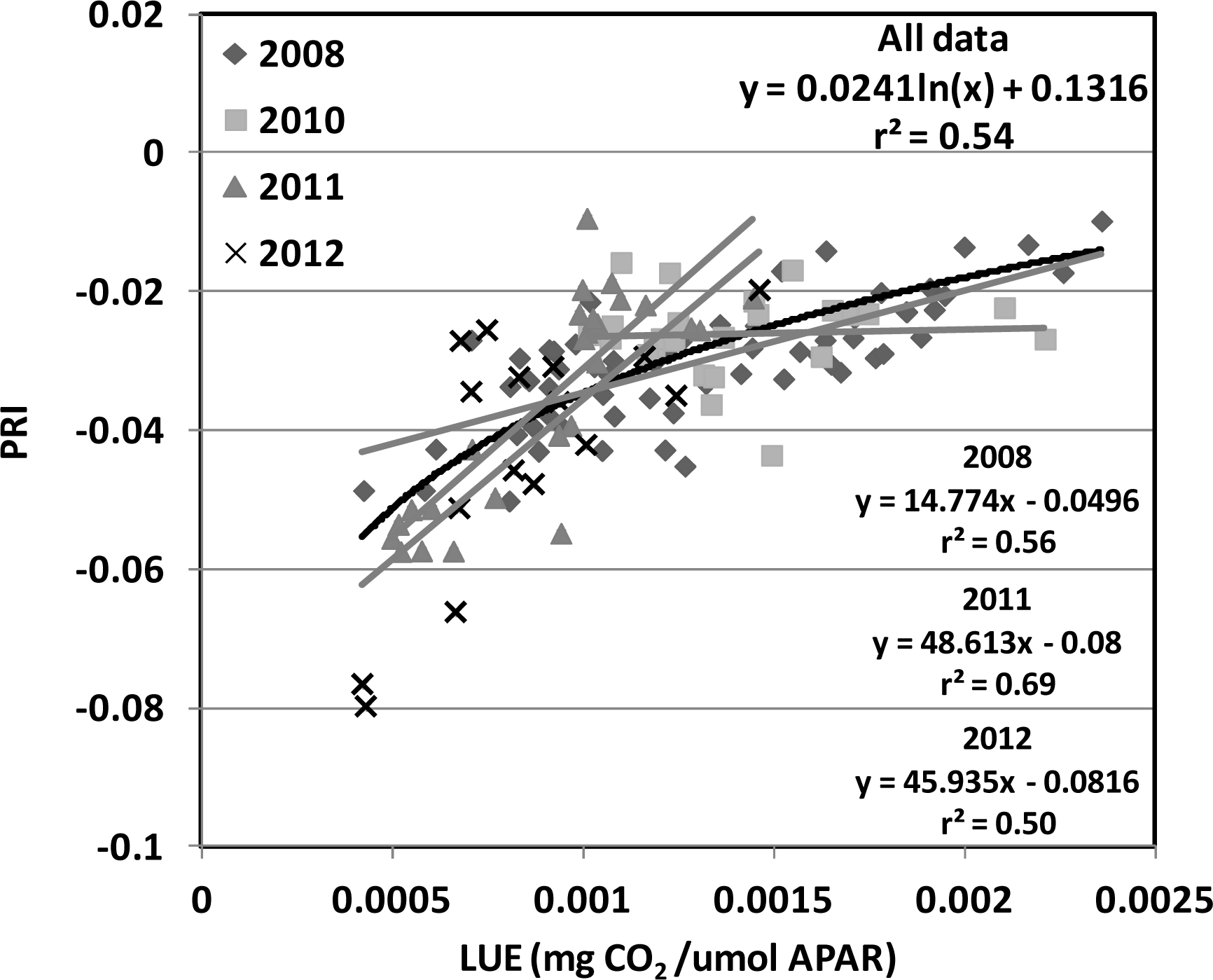
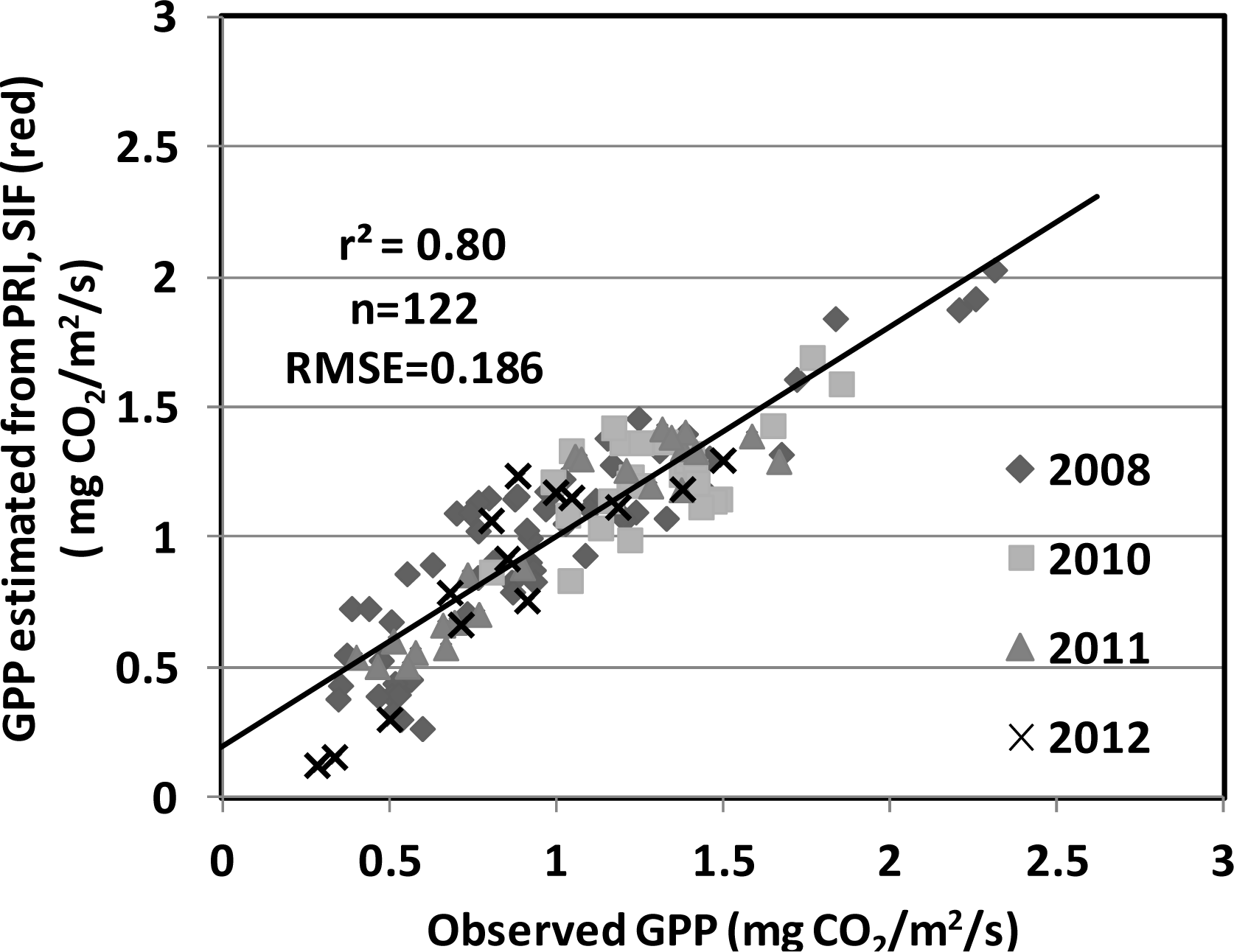
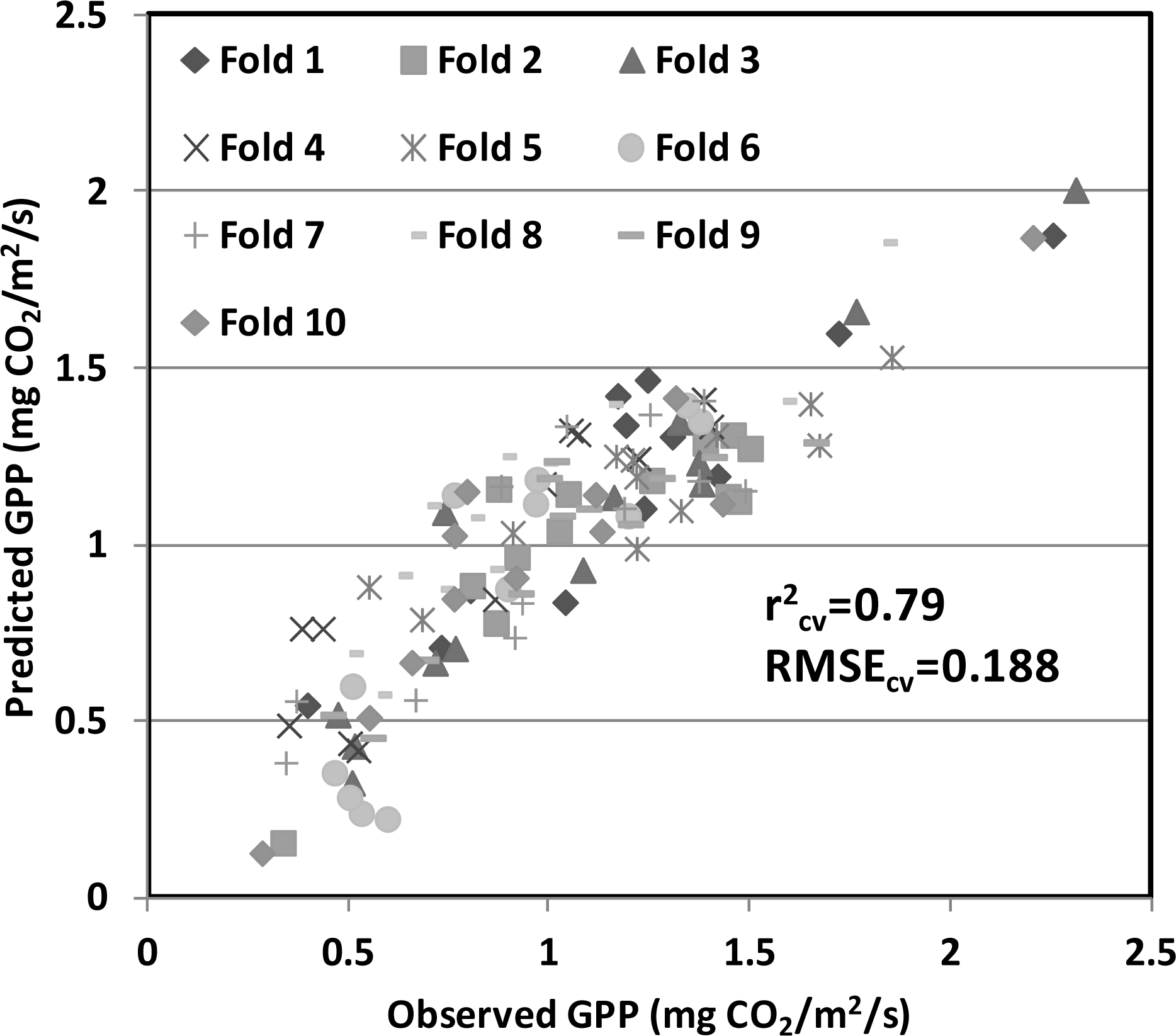
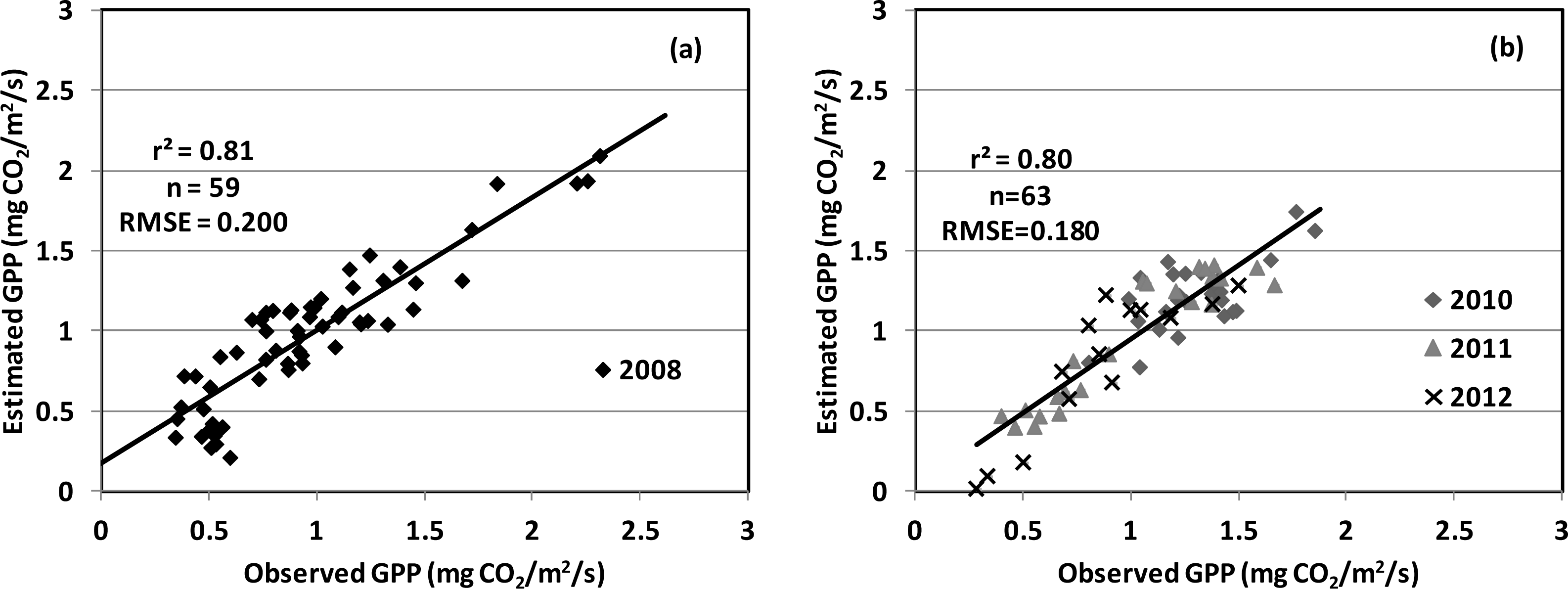
| Year | Planting Date | Varieties | Maximum LAI | Maximum GPP; Date | Total Precipitation (mm) | Average Temperature (°C) |
|---|---|---|---|---|---|---|
| 2008 | 180 | TA 560-00 | 3.27 | 73.98; 214 | 256.54 | 20.80 |
| 2010 | 136 | Pioneer 35F37 | 2.48 | 75.17; 199 | 410.22 | 23.22 |
| 2011 | 145 | Pioneer 35K09 | 2.79 | 60.81; 192 | 354.08 | 24.51 |
| 2012 | 138 | Dekalb 57-67 | 3.42 | 59.66; 208 | 291.09 | 22.97 |
| Output Variable | Predictor Variable | Formula |
|---|---|---|
| LUE | PRI | LUE = a + b × PRI |
| SIF | LUE = a + b × SIF | |
| PRI, SIF | LUE = a + b × PRI + c × SIF + d × PRI × SIF | |
| GPP | PRI | GPP = a + b × PRI |
| SIF | GPP = a + b × SIF | |
| PRI, SIF | GPP = a + b × PRI + c × SIF + d × PRI × SIF | |
| Output Variable | Predictor Variable | r2 | RMSE (mg CO2/μmol PAR) |
|---|---|---|---|
| LUE | PRI | 0.45 (0.54 Logarithm Fit) | 0.000324 (0.000322 Logarithm Fit) |
| SIF (red) | 0.12 | 0.000409 | |
| SIF (far-red) | 0.01 | 0.000435 | |
| SIF (red) yield | 0.29 | 0.000368 | |
| SIF (far-red) yield | 0.06 | 0.000424 | |
| PRI, SIF (red) | 0.55 | 0.000297 | |
| PRI, SIF (far-red) | 0.48 | 0.000317 | |
| PRI, SIF (red) yield | 0.61 | 0.000275 | |
| PRI, SIF (far-red) yield | 0.53 | 0.000301 | |
| Output Variable | Predictor Variable | r2 | RMSE (mg CO2/m2/s) |
|---|---|---|---|
| GPP | PRI | 0.54 | 0.2770 |
| SIF (red) | 0.31 | 0.3598 | |
| SIF (far-red) | 0.28 | 0.3891 | |
| SIF (red) yield | 0.21 | 0.3877 | |
| SIF (far-red) yield | 0.20 | 0.4107 | |
| PRI, SIF (red) | 0.80 | 0.1894 | |
| PRI, SIF (far-red) | 0.78 | 0.1994 | |
| PRI, SIF (red) yield | 0.67 | 0.2055 | |
| PRI, SIF (far-red) yield | 0.66 | 0.2099 | |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Cheng, Y.-B.; Middleton, E.M.; Zhang, Q.; Huemmrich, K.F.; Campbell, P.K.E.; Corp, L.A.; Cook, B.D.; Kustas, W.P.; Daughtry, C.S. Integrating Solar Induced Fluorescence and the Photochemical Reflectance Index for Estimating Gross Primary Production in a Cornfield. Remote Sens. 2013, 5, 6857-6879. https://doi.org/10.3390/rs5126857
Cheng Y-B, Middleton EM, Zhang Q, Huemmrich KF, Campbell PKE, Corp LA, Cook BD, Kustas WP, Daughtry CS. Integrating Solar Induced Fluorescence and the Photochemical Reflectance Index for Estimating Gross Primary Production in a Cornfield. Remote Sensing. 2013; 5(12):6857-6879. https://doi.org/10.3390/rs5126857
Chicago/Turabian StyleCheng, Yen-Ben, Elizabeth M. Middleton, Qingyuan Zhang, Karl F. Huemmrich, Petya K. E. Campbell, Lawrence A. Corp, Bruce D. Cook, William P. Kustas, and Craig S. Daughtry. 2013. "Integrating Solar Induced Fluorescence and the Photochemical Reflectance Index for Estimating Gross Primary Production in a Cornfield" Remote Sensing 5, no. 12: 6857-6879. https://doi.org/10.3390/rs5126857
APA StyleCheng, Y.-B., Middleton, E. M., Zhang, Q., Huemmrich, K. F., Campbell, P. K. E., Corp, L. A., Cook, B. D., Kustas, W. P., & Daughtry, C. S. (2013). Integrating Solar Induced Fluorescence and the Photochemical Reflectance Index for Estimating Gross Primary Production in a Cornfield. Remote Sensing, 5(12), 6857-6879. https://doi.org/10.3390/rs5126857





