Abstract
Interpretation of remote sensing reflectance from coastal waters at different wavelengths of light yields valuable information about water column constituents, which in turn, gives information on a variety of processes occurring in coastal waters, such as primary production, biogeochemical cycles, sediment transport, coastal erosion, and harmful algal blooms. The Hyperspectral Infrared Imager (HyspIRI) is well suited to produce global, seasonal maps and specialized observations of coastal ecosystems and to improve our understanding of how phytoplankton communities are spatially distributed and structured, and how they function in coastal and inland waters. This paper draws from previously published studies on high-resolution, hyperspectral remote sensing of coastal and inland waters and provides an overview of how the HyspIRI mission could enable the retrieval of new aquatic biophysical products or improve the retrieval accuracy of existing satellite-derived products (e.g., inherent optical properties, phytoplankton functional types, pigment composition, chlorophyll-a concentration, etc.). The intent of this paper is to introduce the development of the HyspIRI mission to the coastal and inland remote sensing community and to provide information regarding several potential data products that were not originally part of the HyspIRI mission objectives but could be applicable to research related to coastal and inland waters. Further work toward quantitatively determining the extent and quality of these products, given the instrument and mission characteristics, is recommended.
1. Introduction
Coastal ecosystems are among the most productive ecosystems in the world, playing a major role in water, carbon, nitrogen, and phosphorous cycles between land and sea. Furthermore, coastal regions are home to about two thirds of the world’s population [1]. In the USA, coastal counties alone contribute nearly 40% of the country’s Gross Domestic Production [2]. The social and economic wellbeing of human communities living in these regions depends significantly on the health of the surrounding coastal ecosystem. Studies of coastal and inland aquatic ecosystems and water quality are critical to understanding and protecting these valuable resources. These marginal regions between land and sea support valuable ecotones that are highly vulnerable to shifts in the environment, whether from climate change and its consequences (e.g., sea level rise), human activities (e.g., eutrophication or changes to existing watershed hydrology), or natural disturbances (e.g., storms or tsunamis). As these drivers of change can occur on large scales or even globally, spaceborne remote sensing is a key tool for studying these environments.
Observations of the visible portion of the water-leaving radiance from a spaceborne platform started at the end of the 1970s with the launch of the Coastal Zone Color Scanner (CZCS) on Nimbus-7. CZCS had a spatial resolution of 825 m at nadir and five channels spanning 443–750 nm. The sensor was primarily used to map the biomass of the ocean, which was achieved with great success [3]. Following CZCS, a number of multispectral sensors have been launched by various space agencies, with a number of bands in the visible and infrared regions, such as the Ocean Color Monitor (OCM), with eight bands and the Global Imager (GLI), with 36 bands. The spatial resolution at nadir of such multispectral ocean color sensors has ranged from 250 m (e.g., the MODerate spectral resolution Imaging Spectroradiometer (MODIS)) to a few kilometers (e.g., the POLarization and Directionality of the Earth’s Reflectances (POLDER) instrument, with 6 km spatial resolution).
As coastal aquatic ecosystems exhibit extreme variations in areal extent, spatial dynamics, and bio-optical complexity, studying and monitoring their biophysical features and processes require imagery with high spatial and spectral resolutions [4]. Lee et al. [5] have suggested a minimum requirement of 17 bands (see Table 2 in [5]) located between 400 and 800 nm to observe subtle changes in the remote sensing reflectance from water. The so-called “Decadal Survey” [6] has defined the need for a global mission for studying coastal aquatic ecosystems using a spaceborne hyperspectral sensor. Recent advances in sensor technology have enabled the development and launch of spaceborne hyperspectral sensors, which has opened a new era in the remote sensing of the inland, estuarine, and coastal environments. Remote sensing retrievals can benefit from more spectral information, making it possible to acquire more information over a greater range of conditions and reduce the effect of noise in the data by choosing different but correlated regions of the spectrum or using information from a combination of bands with a known relationship. Hyperspectral sensors open the possibility of the retrieval of a large number of aquatic biophysical products, such as phytoplankton concentration, concentration of dissolved organic matter, diffuse attenuation coefficient, backscattering coefficient, suspended sediment concentration, or phytoplankton community structure. The National Aeronautics and Space Administration (NASA) launched the first spaceborne hyperspectral sensor, Hyperion, with 220 contiguous spectral bands, in 2000. The European Space Agency launched the Compact High Resolution Imaging Spectrometer (CHRIS), a programmable sensor with up to 63 bands, in 2001. The Naval Research Laboratory built and launched the Hyperspectral Imager for the Coastal Ocean (HICO) in 2009. Except for HICO, none of the spaceborne hyperspectral sensors launched so far was designed to have a Signal-to-Noise Ratio (SNR) that is optimized for the optically complex coastal aquatic environment. HICO is a low cost, prototype sensor that was developed as a demonstration mission with on-demand image acquisition and was not designed to be capable of providing global coverage on a regular basis.
The Decadal Survey has recommended the development of the Hyperspectral Infrared Imager (HyspIRI) mission. Although originally developed as a terrestrial ecosystem mission, HyspIRI is well suited to produce global maps of coastal ecosystems and improve our understanding of how phytoplankton communities are distributed and structured and how they function.
As shown in Table 1, the current design plan for HyspIRI includes a hyperspectral Visible Short Wave Infrared (VSWIR) imaging spectrometer with 213 spectral channels between 0.38 and 2.5 μm at 0.01 μm spectral resolution and a multispectral Thermal Infrared (TIR) imager with eight spectral channels (one centered at 4 μm and seven located between 7.5 and 12 μm) [7]. Both instruments will have a spatial resolution of 60 m at nadir. The spacecraft is planned to fly in an ascending polar orbit, crossing the equator at 11:00 a.m. local time. The equatorial revisit times will be 19 and five days for the VSWIR and TIR instruments, respectively [7]. The instrument will have 14-bit radiometric resolution, 2% polarization sensitivity, and a 4° westward tilt to reduce specular solar reflectance.

Table 1.
Key characteristics of the Hyperspectral Infrared Imager (HyspIRI) mission.
Figure 1 compares the spectral resolution and range of HyspIRI’s VSWIR spectrometer to those of traditional spaceborne ocean color instruments used for open ocean remote sensing. With more than 30 bands in the spectral range 400–800 nm, HyspIRI would be capable of capturing subtle changes in the reflectance due to bio-optical variations in the water and provide new information that cannot be obtained from current multispectral sensors. For example, the spectral bands between 710 and 750 nm will provide critical information necessary for accurately retrieving high concentrations of chlorophyll-a (chl-a) [8]. The high spectral resolution of HyspIRI would also result in redundancy of information due to strong correlation between some bands, which would improve retrievals of water column properties when the measurements contain errors [9]. Using the high spectral resolution of HyspIRI, we can expect to not only improve the accuracy of the retrieval of existing products (e.g., chl-a concentration, inherent optical properties, etc.), but also derive new products that could not be retrieved using multispectral sensors (e.g., pigment composition). Moreover, the spectral range of HyspIRI includes wavelengths between 1 and 2.5 microns, which are important for atmospheric correction and can be used to significantly improve the retrieval of surface reflectance in coastal and inland waters. The projected SNR of HyspIRI is better than that of Hyperion, comparable to that of HICO, and is considered reasonably adequate for accurately retrieving hyperspectral reflectance from water surface for typical coastal or inland water conditions. Even with a temporal revisit cycle as long as 19 days, the regular global coverage offered by HyspIRI at high spatial and spectral resolutions will support studies of global coastal waters that require detailed information about the spatial extent and distribution of surface, sub-surface, or bottom features.
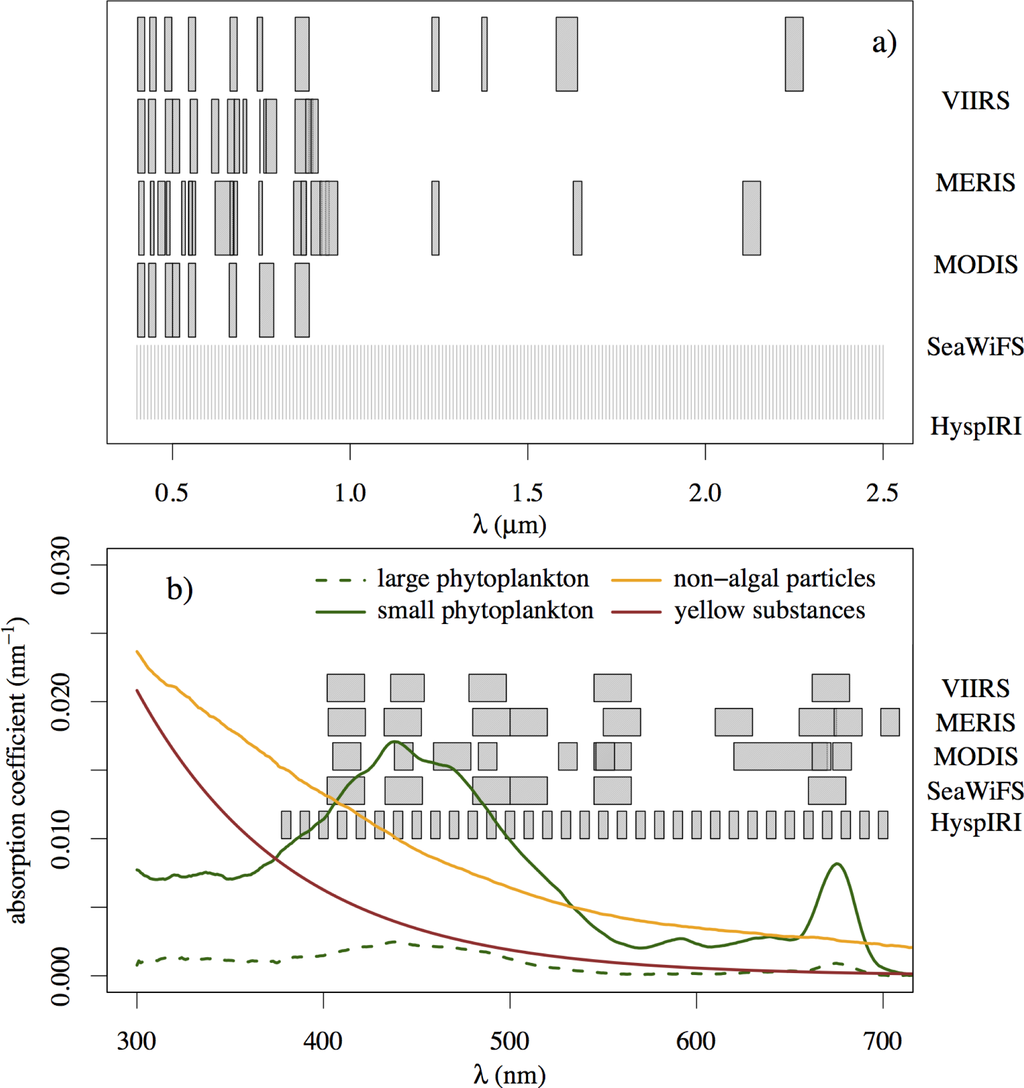
Figure 1.
(a) Spectral coverage of HyspIRI and standard ocean color sensors in the VSWIR region; (b) Absorption coefficients of phytoplankton (small and large cells), non-algal particles, and yellow substances, and the spectral coverage of the aforementioned sensors in the visible region. All bands are shown for MODIS and MERIS (MEdium Resolution Imaging Spectrometer), some of which overlap. However, only the moderate resolution bands are shown for VIIRS (Visible Infrared Imaging Spectrometer).
This paper discusses the retrieval of various optical and bio-optical properties routinely measured by multispectral ocean color sensors and the improvements that could be achieved when using hyperspectral data such as what will be collected by HyspIRI.
2. Candidate Algorithms and Coastal and Inland Water Data Products
Though there are different types of retrieval algorithms, within a given type, the retrieval algorithms are often essentially similar and their primary difference lies only in the choice of wavelengths used for the retrieval. Therefore, the choice of wavelengths at which a retrieval algorithm is applied is a critical factor, as the goal is to capture and take advantage of the unique spectral signature of the bio-optical product of interest. Hyperspectral data offer more choices of wavelengths and consequently better capability to capture spectral signatures of the bio-optical products of interest. This paper addresses the use of various types of algorithms for retrieving various bio-optical products from remote sensing reflectance and the expected improvement in their performance with the use of higher number of wavelengths. The approaches for the development of these algorithms can be classified into two broad categories, namely, empirical and analytical. Empirical algorithms are fundamentally data-driven and include band ratios [10,11], band differences [12], Principal Component Analysis (PCA) [13,14] and Artificial Neural Networks (ANN) [15,16], with implicit or explicit empirical expressions that relate remote sensing reflectance (Rrs) to the bio-physical product of interest. The analytical algorithms are theoretically driven and include techniques based on spectral inversion [17,18], spectral optimization [19], and look-up-tables [20,21]. These algorithms encompass a wide range of complex approaches but are generally derived from the following basic radiative transfer equation that relates Rrs to the optical properties of water [22]:
where a(λ) and bb(λ) are the bulk absorption and backscattering coefficients of water and its constituents, respectively, and G(λ) is a scaling factor that accounts for geometrical conditions, bidirectional effects and the state of the air-water interface.
Many algorithms are based on a combination of empirical and analytical approaches. For example, empirical algorithms such as ANN use datasets that are developed based on the radiative transfer model; some algorithms based on the analytical radiative transfer model are empirically parameterized using datasets collected in situ [23]. Such algorithms are often referred to as semi-empirical or semi-analytical algorithms.
A discussion of the merits and demerits of each algorithm for each product is beyond the scope of this paper. The following is a brief discussion on how HyspIRI could possibly improve retrieval accuracies over what is currently achievable using multispectral data from conventional ocean color sensors, without discriminating in favor of or against any particular algorithm. It is the authors’ recommendation that further work be done with data simulation and other analysis strategies to quantitatively predict the quality of these data products and their applicability to specific science questions.
2.1. Inherent and Apparent Optical Properties
The optical properties of water are conventionally divided into two classes, (1) inherent optical properties (IOPs) and (2) apparent optical properties (AOPs). The inherent optical properties depend only on the medium (i.e., water) and are independent of the ambient light field within the medium, while the apparent optical properties depend on the medium as well as the geometric structure of the ambient light field within the medium.
2.1.1. Absorption
Total absorption and backscattering are the two main drivers of the magnitude and shape of the reflectance signal; they are crucial parameters for the characterization and inversion of the water-leaving radiance. A number of algorithms have been developed to derive either the total absorption coefficient or the individual absorption coefficients of the primary absorptive components, namely, pure seawater, phytoplankton, and yellow substances [24]. The retrieval of the absorption coefficient is performed at a given set of wavelengths or over the entire visible spectrum. The absorptions by detritus and yellow substances are often combined into a single component due to the similarity of their spectral shapes. Semi-empirical and analytical algorithms will see an immediate gain from the increased number of wavelengths at which the absorption coefficient could be retrieved; for example, the quasi-analytical algorithm developed by Lee et al. [18] can now provide the total absorption and phytoplankton absorption coefficient at all visible wavelengths of HyspIRI [25]. Subsequent decomposition into absorptions by individual components would therefore be more accurate as the number of wavelengths available to characterize the absorption would significantly outnumber the number of individual components. Figure 1 shows the absorption coefficients of various marine components in the visible and near-infrared regions. The measured reflectance spectrum is roughly inversely proportional to the total absorption spectrum, and, hence, is marked by spectral features due to absorption by water-column constituents. The high spectral resolution of HyspIRI can resolve details that cannot be resolved by multispectral sensors—details such as the secondary peaks of absorption by phytoplankton (e.g., at 640 nm for chl-c1,2). In general, optimization methods derive a limited number of parameters (aph(443), ay(443) and bbp(443)) as dictated by the number of wavelengths available. Access to hyperspectral information would increase the number of retrievable parameters (i.e., slope of spectral dependence of yellow substances) by exploiting different parts of the spectra depending on the parameter of interest. Using hyperspectral information, one can expect to distinguish between the contributions from detritus and yellow substances to the total absorption coefficient. ANN analyses would benefit from the supplementary information contained in hyperspectral data (over what is contained in multispectral data), resulting in a better characterization of the magnitude and shape of the total absorption coefficient and, consequently, a better decomposition of the total absorption signal into the individual components. For example, Schofield et al. [26] showed that the hyperspectral information on the total absorption coefficient could be de-convolved into absorption by three groups of phytoplankton representative pigments (chl-a-c, phycobilin and chl-a-b), yellow substances, and detritus. This type of approach, only applicable to hyperspectral data, infers valuable information to describe coastal ecosystem processes and the fate of biogeochemical components in the coastal shelf.
2.1.2. Backscattering
Total backscattering coefficient is often described as the sum of the backscattering coefficients of pure seawater and particulates. The particulate backscattering includes backscattering by living (phytoplankton, viruses, and bacteria) and non-living (mineral) particles. Although ignored in current algorithms, it has been shown that scattering and, therefore, backscattering by pure seawater is affected by water temperature and salinity [27]. The presence of a thermal infrared sensor in addition to the VSWIR sensor would enable testing and possibly correcting for the effect of variations in the temperature and result in improved retrieval of the backscattering coefficient of pure seawater. Two aspects of the particle backscattering coefficients provide useful information on the marine constituents: the magnitude and the spectral dependence, the former being related to the concentration of particles and the latter to the size distribution of the particles. In open ocean waters, where phytoplankton is the main driver of the optical variability, a value of one for the slope of the spectral dependence (described as a power law) is commonly accepted. In coastal areas, this assumption becomes invalid and the slope of the spectral dependence can vary from −1 to 3 in extreme cases [28,29]. Algorithms for retrieving backscattering coefficients (some algorithms retrieve both absorption and scattering coefficients) would gain in accuracy for the same reasons as described earlier for the retrieval of the absorption coefficients. Improved accuracy in the retrieval of the spectral slope of the backscattering coefficient would yield, in theory, improved information on particle size distribution [28,30], a key parameter when studying biogeochemical cycles. The magnitude of the slope of the spectral dependence changes from the visible to the near infrared due to particulate absorption [31]. Using hyperspectral data, we can develop methods that would account for this change in the magnitude of the slope of the backscattering coefficient in the visible and near infrared regions. Doxaran et al. [31] proposed a model based on hyperspectral measurements to account for absorption by particles in the near infrared when retrieving the backscattering coefficient, which could only be applied to data collected by a hyperspectral sensor, such as HyspIRI.
2.1.3. Diffuse Attenuation Coefficient (Kd(λ))
The diffuse attenuation coefficient (Kd) is calculated to estimate the penetration of light in the water column. This coefficient is important for studying biological processes and water turbidity. One of the earliest methods to derive the diffuse attenuation coefficient from remotely sensed data was based on a ratio of water-leaving radiances, developed by Austin and Petzold [32]. They showed that Kd(490) could be derived using a simple linear regression of the ratio of water-leaving radiances at two wavebands, centered at 443 and 550 nm. Later, Mueller and Trees [33] replaced the waveband at 443 nm with one at 490 nm and the waveband at 550 nm with one at 555 nm to improve the retrieval of Kd(490); their algorithm was selected to retrieve the standard Kd(490) product for the Sea-viewing Wide Field-of-view Sensor (SeaWiFS). The higher number of wavebands available with HyspIRI would give more opportunities to test different combinations of wavelengths and undoubtedly improve the accuracy with which Kd(490) could be retrieved. Moreover, a simple linear regression or a more complex formulation [34] of band ratios against Kd(490), or algorithms based on more than two wavelengths [35,36], could be used to improve the retrieval of Kd(490) in coastal waters. Given the number of wavebands available on HyspIRI, the diffuse attenuation coefficients could also be derived at other wavelengths besides 490 nm using simple mathematical formulations. Fichot et al. [35] proposed a method based on principal component analysis to derive Kd at 320, 340, 380, 412, 443, and 490 nm using data from the multispectral bands of SeaWiFS. Similarly, Jamet et al. [36] used an ANN-based algorithm to compute Kd(490) in coastal waters using multispectral remote sensing reflectance. The use of hyperspectral data would certainly improve the retrieval of the diffuse attenuation coefficient for statistically based approaches, provided that the training dataset is large enough and encompasses a variety of optical environments such as those encountered in coastal waters. The algorithm from Fichot et al. [35] would certainly gain in accuracy from remote sensing reflectance collected in the ultraviolet (UV) region (HyspIRI will collect radiances starting at 380 nm), as the primary goal for that algorithm was to derive Kd at those wavelengths. Applications that depend on photochemistry (e.g., photodegradation of yellow substances) would benefit significantly from the measurements in the UV region. To summarize, irrespective of the method used (i.e., simple regression or advanced statistics), the use of hyperspectral data would allow the derivation of the diffuse attenuation coefficient with better accuracy than what is achievable using multispectral data.
A limitation of empirical or semi-empirical algorithms is that they omit or ignore the impact of sun elevation on the retrieval of Kd. The diffuse attenuation coefficient is an apparent optical property that can vary by ∼30% between when the sun is at the zenith and when it is 60° off zenith. Consequently, empirical band ratio algorithms overestimate Kd when the sun is close to the zenith and underestimate Kd when the sun is close to the horizon. The semi-analytical approach based on inherent optical properties [37] overcomes this limitation by explicitly including the solar angle in the calculation of Kd, and it is found that this algorithm works fine for both oceanic and coastal waters [38,39]. In particular, this algorithm is applicable to both multispectral and hyperspectral data, which would be extremely useful for a HyspIRI-type sensor.
2.2. Retrieving Optically Active Constituents
2.2.1. Absorption by Yellow Substances
In coastal waters that are subject to river run-off and re-suspension from hydrodynamic forcing, colored dissolved organic matter (CDOM) and gelbstoff often represent a large fraction of the organic material. They play an important role in the biogeochemical cycles through re-mineralization by photochemistry and by altering the light available for photosynthesis by phytoplankton and the subsequent biological production. With a high spatial resolution, HyspIRI would enable an accurate mapping of coastal waters that are under the influence of CDOM. The hyperspectral information available from HyspIRI would make it possible to test new band ratios and improve upon existing methods, such as the algorithm developed by Morel and Gentili [40], which retrieved CDOM concentration from the reflectance ratios Rrs(412)/Rrs(443) and Rrs(490)/Rrs(555). Their algorithm, initially developed for open oceans, could be adapted to coastal waters by testing the use of reflectance at other bands such as 400 nm, where the absorption by CDOM is strong.
Similarly, Bélanger et al. [41] used a polynomial expression to derive the ratio of CDOM absorption to the total absorption at 412 nm as a function of Rrs(555), Rrs(412)/Rrs(555) and Rrs(490)/Rrs(555). Such empirical algorithms could be further tested with more band combinations, provided hyperspectral data are available. Hyperspectral data would also improve the retrieval of the absorption coefficient of CDOM using spectral inversion schemes, as described in Section 2.1.1. Algorithms such as the Garver-Siegel-Maritorena (GSM) model, which in its original version uses six wavelengths, would theoretically yield more accurate results when applied to 30 or more wavelengths. Similarly, Schofield et al. [26] developed a method to infer the optical concentrations of three phytoplankton populations (chl-a-c, chl-a-b, and phycobilin-containing phytoplankton), gelbstoff and detritus from the total absorption measured at 9 wavelengths in the visible region. Their method assumed predetermined spectral shapes for the absorption by the three phytoplankton populations, and allowed some variation in the spectral slopes of absorptions by gelbstoff and detritus. An optimization scheme was used to derive the contribution of each component to the total absorption by minimizing the squared difference between the reconstructed spectra and the measured spectra. Fichot et al. [42] showed that the concentration of terrigenous dissolved organic matter (tDOM) could be unambiguously derived from the slope of their absorption spectra between 275 and 295 nm (inferred from reflectances at longer wavelengths), which was extrapolated from MODIS reflectance in the visible region. These two methods [26,42] would benefit from the use of hyperspectral data because an increase in the number of available wavelengths could strengthen the underlying spectral relationships on which these methods are based.
2.2.2. Suspended Particulate Matter
Suspended Particulate Matter (SPM), also referred to as the Total Suspended Matter (TSM), is a critical parameter when studying coastal erosion, sediment transport (for applications such as the optimization of dredging operations) and assessing the impact of offshore developments. The nature and concentration of TSM in water are highly related to the bulk optical properties of the water [43]. Whereas phytoplankton drives the optical properties in open ocean waters, TSM plays a significant role in coastal waters where detritus and mineral particles contribute to a significant fraction of the water-leaving radiance. Approaches based on the relationships between IOPs and TSM would benefit from the use of hyperspectral data. First, we can expect the accuracy of the retrieved TSM to increase if the IOPs are retrieved with a better accuracy. Numerous studies [31,44–46] have demonstrated the usefulness of near infrared and infrared bands to assess TSM concentration in turbid coastal waters, estuaries and rivers, as long as spatial resolution criteria are sufficiently met. For example, Sterckx et al. [45], using hyperspectral data from the Advance Hyperspectral Sensor (AHS), showed that TSM was related to the logarithm-linear relationship of the difference between the reflectances at 833 and 1004 nm (r2 = 0.83; RMSE = 15.53 mg/L) for TSM concentrations up to 350 mg/L. Their approach used the insensitivity of the band at 1004 nm to TSM concentration to remove contaminations from cirrus clouds and adjacency effects. Doxaran et al. [46] also found a significant relationship between TSM and the ratio of Rrs(780) to Rrs(560). Linear regression of the derived TSM concentration against the measured TSM concentration showed an r2 of 0.98 with a slope of 0.94 and an RMSE of 6.1 mg/L. These two examples of simple algorithms illustrate the need for hyperspectral observations when dealing with turbid waters. The visible part of the spectrum can be exploited for moderate-to-high levels of TSM (less than 50 mg/m3). However, as the concentration of TSM increases, reflectance in the near infrared and infrared bands will yield better retrievals of the TSM concentration. HyspIRI would be a valuable asset for retrieving TSM concentration in turbid and very turbid waters, and would allow testing of different combinations of reflectances in the visible and near infrared regions to not only estimate the concentration of TSM but also remove adverse environmental effects, such as adjacency effects, contamination from high altitude clouds, and sun glint.
2.2.3. Chlorophyll-a Concentration
The concentration of chl-a in water is a strong indicator of the trophic status of a water body [47,48]. Continuous monitoring of the biophysical status of a water body requires a regular estimation of its primary productivity, usually indicated in the form of chl-a concentration. With its ubiquity in surface waters and ease of measurement in a laboratory setting, chl-a concentration is a convenient and reliable indicator of water quality and is used routinely for monitoring marine and lacustrine waters. In fact, remote sensing of ocean color for water quality analysis has been historically focused on estimating chl-a concentration [49]. Various algorithms have been developed for estimating chl-a concentration in open ocean, coastal, estuarine, and inland waters using remotely sensed data. In the open ocean, phytoplankton dominates the optical properties of water, and algorithms based on simple ratios of reflectance in the blue and green spectral regions have been commonly used to retrieve accurate estimates of chl-a concentration from satellite data [10,11]. In most inland, estuarine, and coastal waters, however, Dissolved Organic Matter (DOM) and SPM occur in relative abundance besides phytoplankton, resulting in complex optical properties, which render the simple blue-green algorithms unreliable in accurately estimating chl-a concentration. For such waters, algorithms based on reflectance in the red and near-infrared (NIR) regions [23,50] are preferred, due to the decreased effects of DOM and SPM at these spectral regions.
Matthews [51], and Odermatt et al. [52] have provided reviews of many recently developed chl-a algorithms. Most of the algorithms were developed for application to multispectral data and have produced chl-a estimates with varying degrees of accuracy for open ocean, coastal, estuarine, and inland waters, limited primarily by the inability to resolve from multispectral data the complex, overlapping spectral features from various constituents in turbid productive waters. The hyperspectral data offered by HyspIRI would enable the resolution of fine spectral features due to chl-a, leading to more accurate estimates of chl-a concentration.
The two-band NIR-red model [50]:
and the three-band NIR-red model [23]:
where Rλ is the remote sensing reflectance at the spectral channel centered at λ nm, have been shown to yield accurate estimates of chl-a concentration in optically deep inland and coastal waters in North America, Asia, and Europe [53–56], with the spectral band positions of the models fixed at MERIS’ spectral channels centered at 665 nm, 708 nm, and 753 nm. These MERIS-based NIR-red algorithms have yielded chl-a estimates with consistently high accuracies on the order of 90% or more for waters with a wide range of chl-a concentrations. The hyperspectral data from HyspIRI would provide increased flexibility in the choice of spectral bands for these models and could potentially lead to different band combinations. Such an adapted (or adaptive) algorithm could provide more accurate estimates of chl-a concentration than what has been achieved using the spectral bands of MERIS. For instance, MERIS does not have a spectral band centered between 708 nm and 753 nm; therefore, λ for the three-band model has to be set at 753 nm. However, the spectral band centered at 753 nm is susceptible to significant effects due to instrument noise and imperfect atmospheric correction, which significantly affects the performance of the three-band model [8]. The hyperspectral data from HyspIRI would enable the use of a shorter wavelength for λ3, which could improve the performance of the three-band NIR-red model. The hyperspectral data would also enable the use of algorithms based on sophisticated, numerically driven approaches such as the Levenberg Marquardt multivariate optimization for estimating water quality parameters [57,58].
For optically shallow waters, algorithms such as those based on spectral inversion techniques [19,59] or Look-Up-Tables [21] have been used to minimize the effect of reflectance from the bottom and retrieve the chl-a concentration in water. The use of hyperspectral data will help improve the isolation of contributions from the bottom and lead to more accurate retrievals of chl-a concentration.
Davis et al. [60] used data from the spaceborne hyperspectral sensor Hyperion and several airborne hyperspectral sensors to evaluate the spatial resolution required to study coastal waters, with a specific focus on detecting algal bloom patches, and concluded that a spatial resolution less than 100 m is required to adequately capture the spatial dynamics of heterogeneous coastal waters. With a spatial resolution of 60 m, HyspIRI would be capable of adequately capturing the spatial variability in coastal waters.
HyspIRI’s temporal revisit cycle of 19 days (for the visible and short wave infrared sensor) is too long for operational monitoring of short-term algal blooms in inland and coastal waters. However, the hyperspectral data offered by HyspIRI at 60 m spatial resolution, though only in the form of sporadic snapshots, can be used to develop and/or improve techniques for resolving the complex spatial and spectral dynamics of inland and coastal waters, and can thereby indirectly aid water quality monitoring and management efforts. Such high-accuracy snapshots provide reliable data that can be treated as “ground truth” and assimilated into algal bloom forecasting models to improve the predictive capabilities of models that characterize complex biophysical dynamics and the ecosystem response.
2.2.4. Phytoplankton Functional Types (PFTs)
The HyspIRI mission will provide the scientific community with hyperspectral observations that will lead to a more robust chl-a product and the opportunity to detect various accessory pigments that can be utilized to identify biogeochemically important PFTs. Understanding the spatial and temporal distribution of PFTs will allow the scientific community to improve its knowledge of biologically mediated fluxes of elements that contribute to the carbon cycle [61]. Information on biodiversity provides a valuable quantitative database for structuring sophisticated predictive models that include taxonomic phytoplankton community information, such as size spectra, probability distributions of certain taxa, and upper trophic level estimations, such as fisheries productivity [62,63]. Determining the spatial variability and concentrations of various PFTs is critical to improving primary productivity estimates and understanding the feedbacks of climate change [64].
Hyperspectral techniques, which can enhance the discernment of subtle features in hyperspectral data, could also enable the detection of marker pigments. The reflectance is converted to total absorption using an algorithm (e.g., based on inversion of a water-column radiative transfer model) and the total absorption is then separated into absorptions by individual endmembers. High-resolution reflectance spectra will facilitate the retrieval of total absorption at high resolution. Determining the total absorption at a high resolution can lead to better discrimination between relative concentrations of photosynthetic and photo-protective pigments, which serve as taxonomic marker pigments and provide a proxy for the physiological function of the phytoplankton community.
Figure 2 shows the in vivo absorption spectra of the photoproductive and photosynthetic pigments in solution. The weight-specific absorption coefficients were derived by measuring the absorption spectra of individual pigments in solvent and shifting the maxima of the solvent according to the method described by Bidigare et al. [65]. The spectra on Figure 2 were generated using data published by Bricaud et al. [66]. Not all pigments shown are easily discernable, but certain key marker pigments (or groups of pigments) can be distinguished and used to identify functional types present in the water column. Chl-a, chl-b and chl-c are characterized by sharp absorption bands, whereas the carotenoids have a broader absorption spectrum. Carotenoids can be further divided into several photosynthetic pigments (fucoxanthin, peridinin, 19’-Hexanoyloxyfucoxanthin and 19’-butanoyloxyfucoxanthin), whose maximum absorption occurs around 490–500 nm and non-photosynthetic pigments (zeaxanthin, diadinoxanthin, alloxanthin, and β-carotene), which have two absorption peaks around 460 and 500 nm. Methods based on phytoplankton absorption have been used successfully to obtain information using the unique spectral signatures of pigments such as chl-b, chl-c, photosynthetic and non-photosynthetic carotenoids [67,68], and fucoxanthin [69].
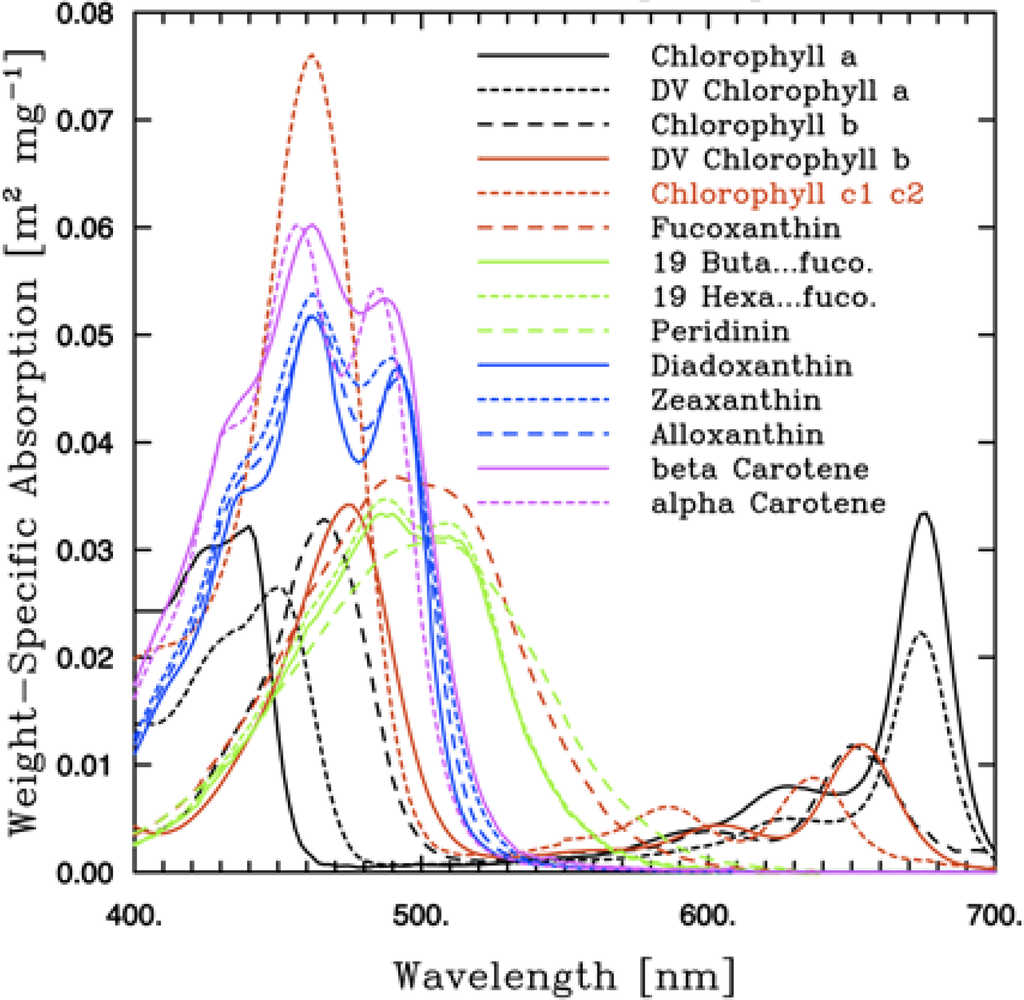
Figure 2.
Weight-specific in vitro absorption spectra of various pigments,
, derived from measuring the absorption spectra of individual pigments in solvent and shifting the maxima of the spectra according to the method described by Bidigare et al. [65]. The spectra were generated using data published by Annick Bricaud [66].
Historically, algorithm development for detecting PFTs has been based on the apparent and inherent optical properties and their relationship to marker pigments for phytoplankton taxa or groups within a community. Development of algorithms for detecting PFTs in the coastal ocean has been a challenge due to the optical complexity caused by sediment re-suspension, coastal runoff, and bottom reflectance. However, successful modeling of the absorption has led to the development of mathematical approaches to estimate photo-protective and photosynthetic pigments that vary with cell size, carbon content, and pigment packaging effects [70–73]. More recently, algorithms have been developed to distinguish phytoplankton groups, such as Phaeocystis and diatoms [72,74]. A number of approaches based on phytoplankton absorption to retrieve pigment composition [26,72] or phytoplankton size distribution [75–78] would show great improvements when applied to HyspIRI data. Applications such as PHYSAT (PHYtoplankton groups from SATellites [79]) and PhytoDOAS (Phytoplankton Differential Optical Absorption Spectroscopy [80,81]) use spectrally resolved reflectance to interpret changes in community structure and reduce the noise due to the presence of yellow substances or suspended minerals, and are well suited for coastal observations. Lubac et al. [82] demonstrated the advantage of using a hyperspectral sensor over a multispectral sensor to detect Phaeocystis globosa spp. in turbid coastal waters based on the second derivative of Rrs(λ).
Algorithms for detecting PFTs have also been developed based on the incorporation of ecological and geographic knowledge of ocean color, bio-optical characteristics, and remotely sensed physical parameters, such as Sea Surface Temperature (SST), Photosynthetically Active Radiation (PAR), and sun-induced fluorescence [83–85]. The incorporation of ecological and geographic knowledge with ocean color, bio-optical characteristics, and remotely sensed physical parameters is a powerful approach to capturing variability due to environmental conditions. The simultaneous measurements of visible (phytoplankton) and infrared (SST) radiation is a step towards such an approach. For instance, it is known that some species, such as Alexandrium spp., require favorable environmental conditions to germinate [85]. Such information could be provided by the TIR bands on HyspIRI.
2.2.5. Fluorescence
Sun-induced fluorescence emission by phytoplankton, modeled as a Gaussian curve centered around 683 nm, can be used to infer phytoplankton concentration [86–88]. Approaches that use fluorescence to derive phytoplankton concentration have been promoted for ocean color applications in coastal areas since the portion of the spectrum that they exploit is only moderately impacted by other marine constituents besides phytoplankton. Ocean color sensors like MERIS and MODIS carry specific wavebands to record the fluorescence emission embedded in the reflectance signal. The reflectance signal in the near infrared also carries information on the absorption and elastic scattering. A simple model to derive the magnitude of fluorescence, referred to as the fluorescence line height (FLH), was developed to reduce the contribution from elastic scattering to the total reflectance signal. This approach is based on a baseline reflectance formed linearly between two wavelengths where the fluorescence is negligible (e.g., 667 and 748 nm for MODIS [89]; 665 and 709 nm for MERIS [84,86]), which is then subtracted from the total reflectance signal at the sensor’s “fluorescence” band (678 nm for MODIS and 681 nm for MERIS) to yield the FLH. For MERIS, the same approach was developed to take account of the shift in the reflectance peak to longer wavelengths for highly productive waters to derive a maximum chlorophyll index (MCI) [90]. Although these approaches are relatively insensitive to perturbations of CDOM [91,92], in highly turbid waters FLH suffers from interference from the high turbidity [92,93]. Therefore, more sophisticated approaches have been used to derive the fluorescence signal based on the radiative transfer theory [87]. The use of hyperspectral data will allow for a better characterization of the fluorescence signature in the reflectance data, especially when choosing the baseline wavelengths and the peak wavelength. Mischaracterization of the baseline may lead to negative estimation of the FLH, and shifts in the reflectance peak wavelength may result in reduced sensitivity of the current multispectral sensors in quantifying the fluorescence signal. The availability of more bands could lead to more advanced schemes of inversion of the reflectance signal.
In addition to providing information on chl-a concentration, FLH also provides a powerful tool to assess the physiological state of the phytoplankton community, when combined with other data [94,95]. FLH is an excellent indicator of factors that control phytoplankton primary productivity, such as pigment concentration, non-photochemical quenching, and pigment packaging effects. Both laboratory and field studies have demonstrated that these physiological indicators change on rapid time scales and represent new avenues for understanding primary productivity and carbon flow globally [96,97]. The fluorescence quantum yield (Φf) may vary by an order of magnitude in marine environments, especially in the coastal ocean, due to variations in the taxonomic composition of phytoplankton, nutrient availability, temperature, and light [95]. Changes in Φf and FLH may emphasize linkages between phytoplankton physiology and environmental variability, which was a key point in the Decadal Survey. With accurate characterization of FLH in the coastal regions, HyspIRI will provide unprecedented coverage of changing phytoplankton community response to coastal issues such as eutrophication, ecosystem health, and changing nutrient ratios [98].
2.2.6. Coastal Fronts and Plumes
The combination of hyperspectral and thermal imagery provides an opportunity to better detect and map coastal fronts and plumes at high spatial resolution, leading to a unique data product with useful applications. Coastal plumes produced by the continuous discharge of rivers and estuaries are common features in shelf and coastal waters and contain harmful runoff from land. They influence various aspects of the coastal environment, from circulation patterns to biogeochemical processes causing eutrophication, turbidity, and spread of harmful pollutants [99,100]. The complex behaviour of coastal plumes is determined by various factors, including river discharge characteristics, topography/bathymetry, and wind and tidal effects [101–103]. Estuarine and ocean fronts result when denser water under-rides lighter water, giving rise to an inclined interface and a strong convergence at the surface, which can concentrate phytoplankton and pollutants, such as oil slicks.
To detect and map fronts and plumes, remote sensors exploit their differences in turbidity, color, temperature, and salinity from the background water. Due to their high turbidity and color gradients, most estuarine fronts and coastal plumes can be detected by satellites, such as SeaWiFS, MODIS, and Landsat TM [104]. The lower salinity and temperature of some shelf features, such as the Mississippi and La Plata River plumes, have been mapped with airborne scanning microwave radiometers and spaceborne thermal infrared scanners. Open ocean fronts, such as the Iceland-Faroes front, often have strong temperature gradients, while coastal upwelling fronts can be detected by their colder temperatures and colors due to high chl-a concentration.
With its relatively high spatial resolution, hyperspectral VSWIR channels and TIR channels, HyspIRI will improve our ability to identify and analyze coastal plumes and oceanic fronts. Combining HyspIRI’s high-resolution data with Synthetic Aperture Radar (SAR) and multispectral imagery from other satellites should provide the temporal and spatial resolution required for imaging the location, extent, composition, and dynamics of coastal plumes, fronts, and oil slicks. Series of images from various satellites, such as SeaWiFS, MODIS, AVHRR, and RADARSAT SAR, have enabled researchers to study coastal plume and front variability under a wide range of tidal and wind forcing conditions. The consistency found among different sensors proved important for remote sensing studies in which a single sensor cannot meet all requirements for spatial and temporal resolution, especially in areas where cloud cover reduces the temporal resolution.
In addition, the high spectral resolution of HyspIRI will enable us to estimate the concentrations of biogeochemical constituents in the plumes and fronts [105,106]. The biogeochemical constituents vary according to their origin, which can be river runoff or wind-induced upwelling. As a result, HyspIRI data can help us to analyze water quality, nutrient loads, and changes in fisheries due to natural and human-induced stress on marine ecosystems at fine spatial scales.
3. Challenges, Limitations, and Potential Solutions
There are a few aspects that should be considered regarding the characteristics of the HyspIRI mission and its applicability to remote retrievals of the water column parameters discussed in this paper. The sun glint presents a problem that has to be addressed if one wants to exploit the full potential of HyspIRI. Examination of MODIS scenes indicated that a 4° westward tilt at an 11:00 a.m. ascending equatorial crossing could result in a maximum glint signal that is between 20% and 100% of the magnitude of the surface reflectance at 488 nm [107]. In operational processing of ocean color products, sun glint is often flagged by applying thresholds for water-leaving radiance. Such flags can be used to mask a large portion of an image. For HyspIRI, this would result in a substantial loss of opportunities to observe the water column at low latitudes. However, new algorithms, such as POLYMER [108], which processes the atmospheric and oceanic signals simultaneously through optimization schemes, have proven efficient at removing sun glint. Given HyspIRI’s high spectral resolution and spectral coverage extending into the SWIR region, improved performances of algorithms such as POLYMER is expected, provided that the initial conditions (i.e., spectral dependence of marine and atmospheric components) have been properly addressed. Figure 3 illustrates the correction of sun glint by the POLYMER algorithm.

Figure 3.
MERIS false color image acquired off the coast of Portugal on 21 June 2005 (left) and chl-a concentration derived by the POLYMER algorithm (right). The algorithm was able to retrieve chl-a concentration in the presence of thin clouds and sun glint (Courtesy of F. Steinmetz).
The 19-day equatorial revisit cycle (shorter at higher latitudes) of the HyspIRI mission is inadequate to monitor or map short-term events such as the development and movement of harmful algal blooms or enhanced production following a storm event [109]. Nevertheless, the revisit time would be adequate to map coastal in-water constituents and their optical properties for long term monitoring (on seasonal or annual scales). Detailed snapshots of inland, estuarine, and coastal waters, though acquired infrequently, can be used in conjunction with data from multispectral sensors that provide almost daily global coverage to provide a better understanding of the temporal evolution of aquatic ecosystem processes. Moreover, as described in previous sections, the detailed snapshots can also lead to the development of improved techniques for retrieving bio-optical products. The primary general application of HyspIRI would be to look at persistent, long-term water quality issues and relate them to spatial processes (e.g., nutrient or sediment discharge hotspots along the coasts). HyspIRI might also provide information on seasonal succession of species in estuaries and inland waters or snapshots of responses to episodic events. At high latitudes, the revisit time reduces to only a few days, thereby improving the temporal resolution greatly. Provided the signal strength is sufficiently strong, HyspIRI might be able to coarsely observe phytoplankton bloom dynamics in polar systems.
The final accuracy of the biophysical products retrieved from satellite data depends on a number of factors, such as the ability of the particular bio-optical model to correctly relate variations in the biophysical parameter of interest to the measured reflectance without being sensitive to effects caused by variations in other optically active constituents in the water, the accuracy of atmospheric correction, the reliability of radiometric calibration, and the inherent noise in the sensor. Regardless of the improvements that can be achieved in the rest of the factors, the total noise in the sensor, as commonly indicated by the SNR, sets a constraint on the minimum error that would be invariably present in the retrieved biophysical product. A high SNR is essential for the ability to detect fine spectral features of low magnitude, as would be required to discriminate among PFTs or estimate the absorption coefficient of phytoplankton. Fisher [110] has shown that the number of independent quantities retrieved from remote sensing reflectance would significantly decrease when the noise increases. Moreover, spectral inversion techniques that rely on accurate absolute reflectance require high SNR. The projected SNR of HyspIRI [111] is better than that of Hyperion [112], comparable to that of HICO [58,113], and is considered reasonably adequate for accurately retrieving hyperspectral reflectance from the water surface and, consequently, the aquatic biophysical parameters described here.
Finally, hyperspectral algorithms will require a large in situ dataset for development and validation activities, such as the SeaBASS/NOMAD dataset [114,115]. The aggregation of such a dataset would require tremendous effort from the ocean color/hyperspectral community, especially in coastal areas, which are known to be under-documented even for multispectral applications. In addition, to derive PFTs, a library of pigments and specific IOP spectra will be required to validate the existing algorithms (e.g., to provide endmembers for unmixing the absorption spectra) and explore potential candidates for identification. An effort is underway to collect data from the community and develop a spectral library to support the HyspIRI mission. However, further plans to expand this effort will need to be put in place within the next few years to assure that sufficient specific absorption spectra are collected and processed for use with algorithms, perhaps in preparation for a broader HyspIRI validation program.
4. Conclusions
Currently, there are no civilian spaceborne hyperspectral instruments designed to globally observe coastal and inland waters at high spatial and spectral resolution. However, the upcoming HyspIRI mission will offer these capabilities. In this article, we have provided a brief summary of the characteristics of HyspIRI and discussed the valuable benefits from the use of HyspIRI for coastal aquatic remote sensing. HyspIRI data can be used to develop new techniques or improve existing techniques to retrieve aquatic data products at a level of spatial and spectral detail and accuracy that is not achievable with multispectral data. The increased spectral resolution in the visible region will allow for more accurate retrievals for water quality assessment using data products such as the diffuse attenuation coefficient (an indicator of turbidity), chl-a concentration (an indicator of eutrophication), primary production (an indicator of the functions of an ecosystem), backscattering coefficient and TSM concentration (indicators of the nature and size distribution of particles and sediment transport), and PFTs (indicators of harmful algal blooms and the state of the ecosystem). As the increased complexity of the ecosystem is resolved, the HyspIRI mission will provide highly resolved spatial measurements of the Carbon Cycle as it relates to seasonal to decadal time scales.
A few studies have already illustrated the use of spaceborne hyperspectral data for studying the coastal aquatic environment. Hyperion initially showed potential for coastal aquatic studies [116]. However, problems due to the radiometric instability of the sensor and low SNR have made Hyperion unreliable for accurate, quantitative analysis of aquatic ecosystems [6]. HICO has been shown to provide accurate estimates of the concentrations of optically active components in coastal waters [54,117,118]. HICO is a demonstration mission on the International Space Station (ISS), with on-demand image acquisition. The orbital constraints on the ISS platform prevent HICO from providing either regular or global coverage. Except for HICO, there is no spaceborne hyperspectral sensor designed specifically for coastal waters currently in operation or scheduled to be launched in the near future. With an SNR that is comparable to that of HICO’s, HyspIRI’s regular high-resolution snapshots can be used for seasonal monitoring of global coastal waters.
A salient strength of HyspIRI for coastal and inland water applications is its high resolution—both spatial and spectral. Specifically, issues of scale and interactions between complex biophysical dynamics and ecosystem response could provide input into modeling studies for important biogeochemical constituents. Studies of scale could lead to better algorithms or enhanced understanding of the uncertainties encountered in coarser-resolution ocean color instruments. The three-year HyspIRI mission could establish techniques that are transferrable to future missions that would provide potentially near-real time operational support for inland and coastal water resource management.
Further work toward determining the extent and quality of HyspIRI-derived bio-optical products, taking into account the instrument and mission characteristics, is recommended and would need to be chiefly carried out by the research community, as the mission is not scoped to produce any scientific products beyond surface reflectance and temperature. It is our hope that researchers in the community who are interested in the development and use of these products put forward their analyses and views regarding the quality of HyspIRI-derived aquatic data products or their applicability to specific science questions as they relate to primarily in the Carbon Cycle and Ecosystem and Earth Surface and Interior focus areas.
Acknowledgments
We are grateful for the input provided by members of the HyspIRI Aquatic Study Group and for the support of the HyspIRI project in the development of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cracknell, A.P. Remote sensing techniques in estuaries and coastal zones—An update. Int. J. Remote Sens 1999, 19, 485–496. [Google Scholar]
- Kildow, J.T.; Colgan, C.S.; Scorse, J. State of the U.S. Ocean and Coastal Economies—2009. Report of the National Ocean Economics Program (NOEP);. 2009, pp. 1–60. Available online: http://www.OceanEconomics.org/nationalreport (accessed on 03 December 2013).
- Yentsch, C. CZCS—Its Role in the Study of the Growth of Oceanic Phytoplankton. In Ocean. Colour: Theory and Applications; Barale, V., Ed.; Springer: Berlin, Germany, 2013. [Google Scholar]
- Klemas, V.V. Airborne remote sensing of coastal features and processes. J. Coast. Res 2013, 29, 239–255. [Google Scholar]
- Lee, Z.P.; Carder, K.; Arnone, R.; He, M. Determination of primary spectral bands for remote sensing of aquatic environments. Sensors 2007, 7, 3428–3441. [Google Scholar]
- National Research Council. Earth Science and Applications from Space: National Imperatives for the Next Decade and Beyond; Committee on Earth Science and Applications from Space: A Community Assessment and Strategy for the Future; The National Academic Press: Washington, DC, USA, 2007; pp. 1–456. [Google Scholar]
- Roberts, D.A.; Quattrochi, D.A.; Hulley, G.C.; Hook, S.J.; Green, R.O. Synergies between VSWIR and TIR data for the urban environment: An evaluation of the potential for the Hyperspectral Infrared Imager (HyspIRI) Decadal Survey mission. Remote Sens. Environ 2012, 117, 83–101. [Google Scholar]
- Moses, W.; Gitelson, A.; Berdnikov, S.; Povazhnyy, V. Satellite estimation of chlorophyll-a concentration using the red and NIR bands of MERIS—The Azov Sea case study. IEEE Geosci. Remote Sens. Lett 2009, 6, 845–849. [Google Scholar]
- IOCCG. Minimum Requirements for an Operational Ocean-Colour Sensor; Reports of the International Ocean.-Colour. Coordinating Group No.1; IOCCG: Dartmouth, NS, Canada, 1998. [Google Scholar]
- Gordon, H.R.; Clark, D.K.; Brown, J.W.; Brown, O.B.; Evans, R.H.; Broenkow, W.W. Phytoplankton pigment concentrations in the Middle Atlantic Bight: comparison of ship determinations and CZCS estimates. Appl. Opt 1983, 22, 20–36. [Google Scholar]
- O’Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res 1998, 103, 24937–24953. [Google Scholar]
- Hu, C.; Lee, Z-P.; Franz, B. Chlorophyll a algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Craig, S.E.; Jones, C.T.; Li, W.K.W.; Lazin, G.; Horne, E.; Caverhill, C.; Cullen, J.J. Deriving optical metrics of coastal phytoplankton biomass from ocean colour. Remote Sens. Environ 2012, 119, 72–83. [Google Scholar]
- Sathyendranath, S.; Hoge, F.E.; Platt, T.; Swift, R.N. Detection of phytoplankton pigments from ocean color: Improved algorithms. Appl. Opt 1994, 33, 1081–1089. [Google Scholar]
- Schiller, H.; Doerffer, R. Neural network for emulation of an inverse model operational derivation of Case II water properties from MERIS data. Int. J. Remote Sens 1999, 20, 1735–1746. [Google Scholar]
- Ioannou, I.; Gilerson, A.; Gross, B.; Moshary, F.; Ahmed, S. Neural network approach to retrieve the inherent optical properties of the ocean from observations of MODIS. Appl. Opt 2011, 50, 3168–3186. [Google Scholar]
- Hoge, F.E.; Lyon, P.E. Satellite retrieval of inherent optical properties by linear matrix inversion of oceanic radiance models: An analysis of model and radiance measurement errors. J. Geophys. Res. 1996, 101. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt 2002, 41, 5755–5772. [Google Scholar]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. 2. Deriving bottom depths and water properties by optimization. Appl. Opt 1999, 38, 3831–3843. [Google Scholar]
- Carder, K.L.; Hawes, S.K.; Baker, K.A.; Smith, R.C.; Steward, R.G.; Mitchell, B.G. Reflectance model for quantifying chlorophyll a in the presence of productivity degradation products. J. Geophys. Res 1991, 96, 20599–20611. [Google Scholar]
- Mobley, C.D.; Sundman, L.K.; Davis, C.O.; Bowles, J.H.; Downes, T.V.; Leathers, R.A.; Montes, M.J.; Bissett, W.P.; Kohler, D.D.; Reid, R.P.; et al. Interpretation of hyperspectral remote-sensing imagery by spectrum matching and look-up tables. Appl. Opt 2005, 44, 3576–3592. [Google Scholar]
- Gordon, H.R.; Brown, O.B.; Jacobs, M.M. Computed relationships netween the inherent and apparent optical properties of a flat homogeneous ocean. Appl. Opt 1975, 14, 417–427. [Google Scholar]
- Dall’Olmo, G.; Gitelson, A.A. Effect of bio-optical parameter variability on the remote estimation of chlorophyll-a concentration in turbid productive waters: Experimental results. Appl. Opt 2005, 44, 412–422. [Google Scholar]
- IOCCG. Remote Sensing of Inherent Optical Properties: Fundamentals, Tests of Algorithms, and Applications; IOCCG: Dartmouth, NS, Canada, 2006. [Google Scholar]
- Lee, Z-P.; Rhea, W.J.; Arnone, R.; Goode, W. Absorption coefficients of marine waters: Expanding multiband information to hyperspectral data. IEEE Trans. Geosci. Remote Sens 2005, 43, 118–124. [Google Scholar]
- Schofield, O.; Bergmann, T.; Oliver, M.J.; Irwin, A.; Kirkpatrick, G.; Bissett, P.W.; Moline, M.A.; Orrico, C. Inversion of spectral absorption in the optically complex coastal waters of the Mid-Atlantic Bight. J. Geophys. Res. 2004. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, L. Effects of temperature and salinity on light scattering by water. Proc. SPIE 2010. [Google Scholar] [CrossRef]
- Loisel, H.; Nicolas, J.-M.; Sciandra, A.; Stramski, D.; Poteau, A. Spectral dependency of optical backscattering by marine particles from satellite remote sensing of the global ocean. J. Geophys. Res. Oceans 2006, 111. [Google Scholar] [CrossRef]
- Martinez-Vicente, V.; Land, P.E.; Tilstone, G.H.; Widdicombe, C.; Fishwick, J.R. Particulate scattering and backscattering related to water constituents and seasonal changes in the Western English Channel. J. Plankton Res 2010, 32, 577–583. [Google Scholar]
- Kostadinov, T.S.; Siegel, D.A.; Maritorena, S. Retrieval of the particle size distribution from satellite ocean color observations. J. Geophys. Res.: Oceans 2009, 114, 2156–2202. [Google Scholar]
- Doxaran, D.; Ruddick, K.; McKee, D.; Gentili, B.; Tailliez, D.; Chami, M.; Babin, M. Spectral variations of light scattering by marine particles in coastal waters, from the visible to the near infrared. Limnol. Oceanogr 2009, 54, 1257–1271. [Google Scholar]
- Austin, R.W.; Petzold, T. The determination of the diffuse attenuation coefficient of sea water using the Coastal Zone Color Scanner. Oceanogr. Space 1981, 13, 239–256. [Google Scholar]
- Mueller, J.L.; Trees, C.C. Revised SeaWiFS Prelaunch Algorithm for the Diffuse Attenuation Coefficient Kd(490). In Case Studies for SeaWiFS Calibration and Validation, Part 4; NASA Tech. Memo. 104566; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 1997; pp. 18–21. [Google Scholar]
- Loisel, H.; Poteau, A. Chapter 5. Inversion of IOP Based on Rrs and Remotely-Retrieved Kd; Reports of the International Ocean.-Colour. Coordinating Group, No. 5; IOCCG: Dartmouth, NS, Canada, 2006; pp. 1–89. [Google Scholar]
- Fichot, C.; Sathyendranath, S.; Miller, W.L. SeaUV and SeaUVC, Algorithms for the retrieval of UV/Visible diffuse attenuation coefficients from ocean colour. Remote Sens. Environ 2008, 112, 1584–1602. [Google Scholar]
- Jamet, C.; Loisel, H.; Dessailly, D. Retrieval of the spectral diffuse attenuation coefficient Kd.(λ) in open and coastal ocean waters using a neural network inversion. J. Geophys. Res.: Oceans 2012, 117, 2012. [Google Scholar] [CrossRef]
- Lee, Z-P.; Darecki, M.; Carder, K.L.; Davis, C.O.; Stramski, D.; Rhea, W.J. Diffuse attenuation coefficient of downwelling irradiance: An evaluation of remote sensing methods. J. Geophys. Res.: Oceans 2005, 110. [Google Scholar] [CrossRef]
- Zhao, J.; Barnes, B.; Melo, N.; English, D.; Lapointe, B.; Muller-Karger, F.; Schaeffer, B.; Hu, C. Assessment of satellite-derived diffuse attenuation coefficients and euphotic depths in south Florida coastal waters. Remote Sens. Environ 2013, 131, 38–50. [Google Scholar]
- Cunningham, A.; Ramage, L.; McKee, D. Relationships between inherent optical properties and the depth of penetration of solar radiation in optically complex coastal waters. J. Geophys. Res.: Oceans 2013, 118, 2169–9291. [Google Scholar]
- Morel, A. Are the empirical relationships describing the bio-optical properties of case 1 waters consistent and internally compatible? J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Bélanger, S.; Babin, M.; Larouche, P. An empirical ocean color algorithm for estimating the contribution of chromophoric dissolved organic matter to total light absorption in optically complex waters. J. Geophys. Res.: Oceans 2008, 113. [Google Scholar] [CrossRef]
- Fichot, C.G.; Kaiser, K.; Hooker, S.B.; Amon, R.M.W.; Babin, M.; Bélanger, S.; Walker, S.A.; Benner, R. Pan-Arctic distributions of continental runoff in the Arctic Ocean. Sci. Rep 2013, 3, 2045–2322. [Google Scholar]
- Astoreca, R.; Doxaran, D.; Ruddick, K.; Rousseau, V.; Lancelot, C. Influence of suspended particle concentration, composition and size on the variability of inherent optical properties of the Southern North Sea. Cont. Shelf Res 2012, 35, 117–128. [Google Scholar]
- Ritchie, J.C.; Schiebe, F.R.; McHenry, J.R. Remote sensing of suspended sediment in surface water. Photogramm. Eng. Remote Sens 1976, 42, 1539–1545. [Google Scholar]
- Sterckx, S.; Knaeps, E.; Bollen, M.; Trouw, K.; Houthuys, R. Retrieval of suspended sediment from advanced hyperspectral sensor data in the scheldt estuary at different stages in the tidal cycle. Mar. Geod 2007, 30, 97–108. [Google Scholar]
- Doxaran, D.; Ehn, J.; Bélanger, S.; Matsuoka, A.; Hooker, S.; Babin, M. Optical characterisation of suspended particles in the Mackenzie River plume (Canadian Arctic Ocean) and implications for ocean colour remote sensing. Biogeosciences 2012, 9, 3213–3229. [Google Scholar]
- Falkowski, P.G.; Raven, J.A. Aquatic Photosynthesis; Blackwell Scientific Publishers: Oxford, UK, 1997; pp. 1–375. [Google Scholar]
- Schalles, J.F.; Gitelson, A.A.; Yacobi, Y.Z.; Kroenke, A.E. Estimation of Chlorophyll a from time series measurements of high spectral resolution reflectance in an eutrophic lake. J. Phycol 1998, 34, 383–390. [Google Scholar]
- IOCCG. Status and Plans for Satellite Ocean-Colour Missions: Considerations for Complimentary Missions. In Reports of the International Ocean.-Colour. Coordinating Group, No. 2; Yoder, J.A., Ed.; IOCCG: Dartmouth, NS, Canada, 1999; p. 43. [Google Scholar]
- Gitelson, A.A. The peak near 700 nm on radiance spectra of algae and water: relationships of its magnitude and position with chlorophyll concentration. Int. J. Remote Sens 1992, 13, 3367–3373. [Google Scholar]
- Matthews, M.W. A current review of empirical procedures of remote sensing in inland and near-coastal transitional waters. Int. J. Remote Sens 2011, 32, 6855–6899. [Google Scholar]
- Odermatt, D.; Gitelson, A.; Brando, V.E.; Schaepman, M. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remote Sens. Environ 2012, 118, 116–126. [Google Scholar]
- Gilerson, A.A; Gitelson, A.A.; Zhou, J.; Gurlin, D.; Moses, W.J.; Ioannou, I.; Ahmed, S.A. Algorithms for remote estimation of chlorophyll-a in coastal and inland waters using red and near infrared bands. Opt. Express 2010, 18, 24109–24125. [Google Scholar]
- Gitelson, A.A.; Gao, B-C.; Li, R.-R.; Berdnikov, S.; Saprygin, V. Estimation of chlorophyll-a concentration in productive turbid waters using a Hyperspectral Imager for the Coastal Ocean—the Azov Sea case study. Environ. Res. Lett. 2011, 6. [Google Scholar] [CrossRef]
- Gurlin, D.; Gitelson, A.A.; Moses, W.J. Remote estimation of chl-a concentration in turbid productive waters—Return to a simple two-band NIR-red model? Remote Sens. Environ 2011, 115, 3479–3490. [Google Scholar]
- Moses, W.J.; Gitelson, A.A.; Berdnikov, S.; Saprygin, V.; Povazhnyi, V. Operational MERIS-based NIR-red algorithms for estimating chlorophyll-a concentrations in coastal waters—The Azov Sea case study. Remote Sens. Environ 2012, 121, 118–124. [Google Scholar]
- Pozdnyakov, D.; Korosov, A.; Grassl, H.; Pettersson, L. An advanced algorithm for operational retrieval of water quality from satellite data in the visible. Int. J. Remote Sens 2005, 26, 2669–2687. [Google Scholar]
- Moses, W.J.; Bowles, J.H.; Lucke, R.L.; Corson, M.R. Impact of signal-to-noise ratio in a hyperspectral sensor on the accuracy of biophysical parameter estimation in case II waters. Appl. Opt 2012, 20, 4309–4330. [Google Scholar]
- Lee, Z-P.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. I. A Semi-analytical model. Appl. Opt 1998, 37, 6329–6338. [Google Scholar]
- Davis, C.O.; Kavanaugh, M.; Letelier, R.; Bissett, W.P.; Kohler, D. Spatial and spectral resolution considerations for imaging coastal waters. Proc. SPIE 2007, 6680. [Google Scholar] [CrossRef]
- Falkowski, P.G.; Katz, M.E.; Knoll, A.H.; Quigg, A.; Raven, J.A.; Schofield, O. The evolution of modern eukaryotic phytoplankton. Science 2004, 305, 354–360. [Google Scholar]
- Chesson, P.L.; Case, T.J. Nonequilibrium community theories: Chance, variability, history, and coexistence. Community Ecol 1986, 1, 229–239. [Google Scholar]
- DeAngelis, D.; Waterhouse, J.C. Equilibrium and nonequilibrium concepts in ecological models. Ecol. Monogr 1987, 57, 1–21. [Google Scholar]
- Moisan, T.; Sathyendranath, S.; Bouman, H.A. Ocean Color Remote Sensing of Phytoplankton Functional Types. In Remote Sensing of Biomass—Principles and Applications; InTech: Morn Hill, Winchester, UK, 2012; pp. 101–124. [Google Scholar]
- Bidigare, R.R.; Latasa, M.; Johnson, Z.; Barber, R.T.; Trees, C.C.; Balch, W.M. Observation of a Synechococcus.-dominated cyclonic eddy in open-oceanic waters of the Arabian Sea. Proc. SPIE 1990, 2963, 260–265. [Google Scholar]
- Bricaud, A.; Claustre, H.; Ras, J.; Oubelkheir, K. Natural variability of phytoplanktonic absorption in oceanic waters: Influence of the size structure of algal population. J. Geophys. Res.: Oceans 2004, 109. [Google Scholar] [CrossRef]
- Hoepffner, N.; Sathyendranath, S. Determination of the major groups of phytoplankton pigments from the absorption spectra of total particulate matter. J. Geophys. Res 1993, 98, 22789–22803. [Google Scholar]
- Bricaud, A.; Mejia, C.; Blondeau-Patissier, D.; Claustre, H.; Crepon, M.; Thiria, S. Retrieval of pigment concentrations and size structure of algal populations from their absorption spectra using multilayered perceptrons. Appl. Opt 2007, 46, 1251–1260. [Google Scholar]
- Chazottes, A.; Crepon, M.; Bricaud, A.; Ras, J.; Thiria, S. Statistical analysis of absorption spectra of phytoplankton and of pigment concentrations observed during three POMME cruises using a neural network clustering method. Appl. Opt 2007, 46, 3790–3799. [Google Scholar]
- Balch, W.; Holligan, PM.; Ackleson, SG.; Voss, KJ. Biological and optical properties of mesoscale coccolithophore blooms. Limnol. Oceanogr 1991, 36, 629–643. [Google Scholar]
- Subramanian, A.; Carpenter, E.J.; Karentz, P.G.; Falkowski, P.G. Optical properties of the marine diazotrophic cyanobacteria Trichodesmium. spp. I. Absorption and spectral photosynthetic characteristics. Limnol. Oceanogr 1999, 44, 608–617. [Google Scholar]
- Sathyendranath, S.; Watts, L.; Devred, E. Discrimination of diatoms from other phytoplankton using ocean-colour data. Mar. Ecol. Prog. Ser 2004, 272, 59–68. [Google Scholar]
- Whitmire, A.L.; Pegau, W.S.; Karp-Boss, L.; Boss, E.; Cowles, T.J. Spectral backscattering properties of marine phytoplankton cultures. Opt. Express 2010, 18, 1680–1690. [Google Scholar]
- Moisan, J.R.; Moisan, T.A.H; Linkswiler, M.A. Estimating phytoplankton pigment concentrations from phytoplankton absorption spectra. J. Geophys. Res.: Oceans 2011, 116, 0148–0227. [Google Scholar]
- Devred, E.; Sathyendranath, S.; Stuart, V.; Maass, H.; Ulloa, O.; Platt, T. Bio-optics of the ocean: A two-component model of absorption by phytoplankton. J. Geophys. Res.: Oceans 2006, 111. [Google Scholar] [CrossRef]
- Ciotti, A.M.; Bricaud, A. Retrievals of a size parameter for phytoplankton and spectral light absorption by Colored detrital matter from water-leaving radiances at SeaWiFS channels in a continental shelf region off Brazil. Limnol. Oceanogr. Methods 2006, 4, 237–253. [Google Scholar]
- Hirata, T.; Aiken, J.; Hardman-Mountford, N.; Smyth, T.J.; Barlow, R. An absorption model to determine phytoplankton size classes from satellite ocean colour. Remote Sens. Environ 2008, 112, 3153–3159. [Google Scholar]
- Devred, E.; Sathyendranath, S.; Stuart, S.; Platt, T. Absorption-derived phytoplankton cell size: Application to satellite ocean-colour data in the Northwest Atlantic. Remote Sens. Environ 2011, 115, 2255–2266. [Google Scholar]
- Alvain, S.; Moulin, C.; Dandonneau, Y. Remote sensing of phytoplankton groups in Case 1 waters from global SeaWiFS imagery. Deep Sea Res 2005, 52, 1989–2004. [Google Scholar]
- Bracher, A.; Vountas, M.; Dinter, T.; Burrows, J.P.; Röttgers, R.; Peeken, I. Quantitative observation of cyanobacteria and diatoms from space using PhytoDOAS on SCIAMACHY data. Biogeosciences 2009, 6, 751–764. [Google Scholar]
- Sadeghi, A.; Dinter, T.; Vountas, M.; Taylor, B.; Peeken, I.; Altenburg Soppa, M.; Bracher, A. Improvements to the PhytoDOAS method for identification of coccolithophores using hyperspectral satellite data. Ocean Sci 2012, 8, 1055–1070. [Google Scholar]
- Lubac, B.; Loisel, H.; Guiselin, N.; Astoreca, R.; Artigas, L.F.; Mériaux, X. Hyperspectral versus multispectral remote sensing approach to detect phytoplankton blooms in coastal waters: Application to a Phaeocystis globosa bloom. J. Geophys. Res.: Oceans 2008, 113. [Google Scholar] [CrossRef]
- Raitsos, D.E.; Lavender, S.J.; Maravelias, C.D.; Haralambous, J.; Richardson, A.J.; Reid, P.C. Identifying phytoplankton functional groups from space: an ecological approach. Limnol. Oceanogr 2008, 53, 605–613. [Google Scholar]
- Hu, C.; Cannizzaro, J.; Carder, K.L.; Muller-Karger, F.E.; Hardy, R. Remote detection of Trichodesmium blooms in optically complex coastal waters: Examples with MODIS full-spectral data. Remote Sens. Environ 2010, 114, 2048–2058. [Google Scholar]
- Anderson, D.M.; Alpermann, T.J.; Cembella, A.D.; Collos, Y.; Masseret, E.; Montresor, M. The globally distributed genus Alexandrium.: Multifaceted roles in marine ecosystems and impacts on human health. Harmful Algae 2012, 14, 10–35. [Google Scholar]
- Gower, J.; Doeffer, R.; Borstad, G. Interpretation of the 685 nm peak in water leaving radiance spectra in terms of fluorescence, absorption and scattering, and its observation by MERIS. Int. J. Remote Sens 1999, 20, 1771–1786. [Google Scholar]
- Huot, Y.; Brown, C.A.; Cullen, J.J. Retrieval of phytoplankton biomass from simultaneous inversion of reflectance, the diffuse attenuation coefficient, and sun-induced fluorescence in coastal waters. J. Geophys. Res.: Oceans 2005, 112. doi: 10.10292006JC003794. [Google Scholar]
- Huot, Y.; Babin, M.; Bruyant, F.; Grob, C.; Twardowski, M.S.; Claustre, H. Does chlorophyll a provide the best index of phytoplankton biomass for primary productivity studies? Biogeosciences 2007, 4, 853–868. [Google Scholar]
- Abbott, M.R.; Letelier, R.M. Algorithm Theoretical Basis Document Chlorophyll Fluorescence. MODIS Product Number 20; 1999. p. 42. Available online: http://modis.gsfc.nasa.gov/data/atbd/atbd_mod22.pdf (accessed on 03 December 2013).
- Gower, J.; King, S.; Goncalves, P. Global monitoring of plankton blooms using MERIS MCI. Int. J. Remote Sens 2008, 29, 6209–6216. [Google Scholar]
- Hu, C.; Müller-Karger, F.E.; Taylor, C.J.; Carder, K.L.; Kelble, C.; Johns, E.; Heil, C.A. Red tide detection and tracking using MODIS fluorescence data: A regional example in SW Florida coastal waters. Remote Sens. Environ 2005, 97, 311–321. [Google Scholar]
- McKee, D.; Cunningham, A.; Wright, D.; Hay, L. Potential impacts of nonalgal materials on water-leaving sun induced chlorophyll fluorescence signals in coastal waters. Appl. Opt 2007, 46, 7720–7729. [Google Scholar]
- Gilerson, A.; Zhou, J.; Hlaing, S.; Ioannou, I.; Schalles, J.; Gross, B.; Moshary, F; Ahmed, S. Fluorescence component in the reflectance spectra from coastal waters. Dependence on water composition. Opt. Express 2007, 15, 15702–15721. [Google Scholar]
- Falkowski, P.G.; Kiefer, D.A. Chlorophyll a fluorescence in phytoplankton: Relationship to photosynthesis and biomass. J. Plankton Res 1985, 7, 715–731. [Google Scholar]
- Behrenfeld, M.J.; Westberry, T.K.; Boss, E.; O’Malley, R.T.; Siegel, D.A.; Wiggert, J.D.; Franz, B.A.; McClain, C.R.; Feldman, G.C.; Doney, S.C.; et al. Satellite-detected fluorescence reveals global physiology of ocean phytoplankton. Biogeosciences 2009, 6, 779–794. [Google Scholar]
- Cleveland, J.S.; Perry, M.J. Quantum yield, relative specific absorption and fluorescence in nitrogen limited, Chaetoceros gracilis. Mar. Biol 1987, 94, 489–497. [Google Scholar]
- Moisan, T.A.; Olaizola, M.; Mitchell, B.G. Xanthophyll Cycling in Phaeocystis. antarctica Karsten.: Changes in Cellular Fluorescence. Mar. Ecol. Progr. Ser 1998, 169, 113–121. [Google Scholar]
- Westberry, T.K.; Siegel, D.A. Phytoplankton natural fluorescence in the Sargasso Sea: Prediction of primary production and eddy induced nutrient fluxes. Deep Sea Res 2003, 50, 417–434. [Google Scholar]
- Mestres, M.; Sierra, J.P.; Sánchez-Arcilla, A. Factors influencing the spreading of a low discharge river plume. Cont. Shelf Res 2007, 27, 2116–2134. [Google Scholar]
- Riegl, B.M.; Purkis, S.J. Model of coral population response to accelerated bleaching and mass mortality in a changing climate. Ecol. Model 2009, 220, 192–208. [Google Scholar]
- Stumpf, R.P.; Gelfenbaum, G.; Pennock, J.R. Wind and tidal forcing of a buoyant plume, Mobile Bay, Alabama. Cont. Shelf Res 1993, 13, 1281–1301. [Google Scholar]
- Wiseman, W.J., Jr.; Garvine, R.W. Plumes and coastal currents near large river mouths. Estuaries 1995, 18, 509–517. [Google Scholar]
- Blanton, J.; Amft, J.; Tisue, T. Response of a small-scale bottom-attached estuarine plume to wind and tidal dissipation. J. Coast. Res 1997, 13, 349–362. [Google Scholar]
- Purkis, S.; Klemas, V. Remote Sensing and Global Environmental Change; Wiley-Blackwell: Oxford, UK, 2011; pp. 1–384. [Google Scholar]
- Chang, G.C.; Dickey, T.D.; Schofield, O.M.; Weidemann, A.D.; Boss, E.; Pegau, W.S.; Moline, M.A.; Glenn, S.M. Nearshore physical processes and bio-optical properties in the New York Bight. J. Geophys. Res.: Oceans 2002, 107, 3133. [Google Scholar]
- Brando, V.E.; Dekker, A.G. Satellite hyperspectral remote sensing for estimating estuarine and coastal water quality. IEEE Trans. Geosci. Remote Sens 2003, 41, 1378–1387. [Google Scholar]
- Hochberg, E.J.; Mobley, C.D.; Park, Y.; Goodman, J.; Turpie, K.R.; Gao, B-C.; Bruce, C.F.; Green, R.O.; Knox, R.G.; Muller-Karger, F.E.; et al. HyspIRI Sunglint Subgroup Report; NASA White Paper, 2011; pp. 1–72. Available online: http://hyspiri.jpl.nasa.gov/downloads/2011_Sunglint_Report/2011_HyspIRI_Sunglint_Report_11-4.pdf (accessed on 03 December 2013).
- Steinmetz, F.; Deschamps, P-Y.; Ramon, D. Atmospheric correction in presence of sun glint: Application to MERIS. Opt. Express 2011, 19, 9783–9800. [Google Scholar]
- Babin, S.M.; Carton, J.A.; Dickey, T.D.; Wiggert, J.D. Satellite evidence of hurricane-induced phytoplankton blooms in an oceanic desert. J. Geophys. Res.: Oceans 2004, 109. [Google Scholar] [CrossRef]
- Fischer, J. On the information content of multispectral radiance measurements over an ocean. Int. J. Remote Sens 1985, 6, 773–786. [Google Scholar]
- Gao, B-C. HyspIRI Visible to Short Wavelength Infrared (VSWIR) Water Leaving Reflectance. Algorithm Theoretical Basis Document;. 2010. Available online: http://hyspiri.jpl.nasa.gov/downloads/Algorithm_Theoretical_Basis/HyspIRI_Gao_ATBD-VSWIR_Water_8_2010_101109.pdf (accessed on 03 December 2013).
- Hu, C.; Feng, L.; Lee, Z-P.; Davis, C.O.; Mannino, A.; McClain, C.R.; Franz, B.A. Dynamic range and sensitivity requirements of satellite ocean color sensors: Learning from the past. Appl. Opt 2012, 51, 6045–6062. [Google Scholar]
- Lucke, R.L.; Corson, M.; McGlothlin, N.R.; Butcher, S.D.; Wood, D.L.; Korwan, D.R.; Li, R.R.; Snyder, W.A.; Davis, C.O.; Chen, D.T. Hyperspectral Imager for the Coastal Ocean: instrument description and first images. Appl. Opt 2011, 50, 1501–1516. [Google Scholar]
- Fargion, G.S.; McClain, C.R. The SeaWiFS Bio-optical Archive and Storage System (SeaBASS): Current Architecture and Implementation; NASA Tech. Memo. 2002–211617; Fargion, G.S.; McClain, C.R. NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2002; pp. 1–45. [Google Scholar]
- Werdell, P.J.; Bailey, S.W. An improved in situ data set for bio-optical algorithm development and ocean color satellite validation. Remote Sens. Environ 2005, 98, 122–140. [Google Scholar]
- Nikolakopoulos, K.G.; Karathanassi, V.; Rokos, D. Hyperspectral data and methods for coastal water mapping. Proc. SPIE 2006, 6359. [Google Scholar] [CrossRef]
- Braga, F.; Giardino, C.; Bassani, C.; Matta, E.; Candiani, G.; Strombeck, N.; Adamo, M.; Bresciani, M. Assessing water quality in the northern Adriatic Sea from HICO™ data. Remote Sens. Lett 2013, 4, 1028–1037. [Google Scholar]
- Moses, W.J.; Gitelson, A.A.; Berdnikov, S.; Bowles, J.H.; Povazhnyi, V.; Saprygin, V.; Wagner, E.J.; Patterson, K.W. HICO-based NIR-red models for estimating chlorophyll-a concentration in productive coastal waters. IEEE Geosci. Remote Sens. Lett. 2013. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).