1. Introduction
Cyanobacteria commonly known as blue-green (BG) algae are an important phytoplankton class [
1] and have received increasing attention because of their occurrence in inland eutrophic waters around the world [
2]. The abundant growth of cyanobacteria in aquatic systems creates problems for water resource managers and policy makers due to their capacity to produce toxins also known as “cyanotoxins”, which are a major concern for human health [
3,
4]. Some of the genera of these BG algae produce toxins which cause hepatotoxic, neurotoxic and dermatotoxic effects and general inhibition of protein synthesis in animals and humans [
3]. One of the first cases of human fatalities associated with cyanobacteria and their toxins occurred in 1996 at Caruaru, PE, Brazil, where exposure through renal dialysis led to the death of approximately fifty patients [
4]. Besides their toxic characteristic, Cyanobacterial Harmful Algal Blooms (CHABs) also degrade aquatic habitats due to their malodorousness [
3,
5] and the appearance of a scum layer or thick mat on the surface of water.
Tropical aquatic systems such as Brazilian reservoirs are some of the most suitable places where BG algae can multiply very rapidly. It is because the temperature range (25–35 °C) required to achieve BG algae maximal specific rates of growth matches with the average temperature of these aquatic systems [
6]. Several BG algae have confirmed their apparent high carbon affinities since they could maintain slow net growth even at pH > 10 [
7]. Light and nutrient availability are also characteristics which promote CHABs [
5]. These facts enhance the importance of monitoring BG algae presence in water supply and recreational reservoirs. However, traditional monitoring methods consist of collection of field samples, laboratory analysis, and manual cell counts. These methods are time-consuming, labor intensive and costly [
8]. Efficient alternative methods should be developed in order to improve the monitoring of CHABs and remote sensing has been proved as a valuable tool for this application [
9].
For remote sensing techniques, phycocyanin (PC) which is a characteristic photosynthetic pigment in inland BG algae, has been used as a proxy due to its distinct optical characteristic (absorption peak at ∼620 nm) [
5,
10–
12]. Initially, cyanobacterial biomass was estimated mostly from chlorophyll-
a (chl-
a) concentration since it is the primary and dominant photosynthetic pigment in BG algae [
13]. However, recent studies have documented that chl-
a is not an accurate estimator of cyanobacterial biomass since it is common to almost all phytoplankton groups [
14]. Therefore, recent studies have evaluated the utility of PC to estimate BG algae abundance, particularly when BG algae are associated with other non-harmful phytoplankton groups [
15]. Most of the researchers have been exploiting the PC absorption feature between 615 and 630 nm to develop empirical and semi-analytical models to detect presence of BG algae in water bodies. However, Mishra
et al. [
5] proposed the use of a band at 600 nm since it has less influence of chl-
a absorption when compared to 620 nm and it also has a significant absorption component by PC.
Thus far, five different algorithms have been proposed for the quantification of BG by exploiting the PC absorption feature: a semi-empirical baseline algorithm (DE93) [
16], a single reflectance band ratio algorithm (SC00) [
17], a nested semi-empirical band ratio algorithm (SI05) [
10], a new single reflectance band ratio algorithm (MI09) [
5] and a three band algorithm (HU10) [
11]. The baseline algorithm [
16] adds reflectance at two wavelengths (600 and 648 nm) to draw a reference baseline, and subtracts the reflectance at 624 nm which is the absorption maximum of PC. The single reflectance ratio [
17] uses a PC fluorescence peak of around 650 nm and the PC absorption peak around 625 nm. The nested band ratio [
10] algorithm was developed for the Medium Resolution Imaging Spectrometer (MERIS) sensor from the European Space Agency (ESA). To match the MERIS band configuration, it uses 620 nm as the PC absorption maximum and estimates PC concentrations from a semi-analytical inversion procedure using the 620 nm band. The model also addresses the chl-
a influence at the PC absorption band (620 nm). The new single reflectance ratio [
5] uses reflectance at 700 nm as reference, and targets PC absorption at 600 nm in order to minimize the chl-
a interference. The three band algorithm [
11] uses 725 nm as reference and targets the PC absorption by using the difference in the reflectance at 600 nm and 615 nm.
All these algorithms were developed for eutrophic waters involving various study sites worldwide with different optical properties. DE93 used coefficients of inherent optical properties in 10 shallow eutrophic lakes in The Netherlands. SC00 dataset was obtained from a hypereutrophic lake, Carter Lake, in Nebraska, USA. SI05 was developed from datasets from two lakes in The Netherlands: Lake Loosdrecht and Lake Ijsselmeer. MI09 was developed in laboratory using two different laboratory cultured cyanobacterial species. HU10 was developed using data from two shallow eutrophic lakes in the United Kingdom. However, all these algorithms were developed for latitudes higher than 35° and they have not been validated for low latitude areas such as the tropical reservoir in Brazil used in this study. In this research, we have intensively reviewed the performance of the aforementioned algorithms using two unique datasets collected from a tropical reservoir in Brazil and aquaculture ponds in Mississippi, USA. The specific objectives of this research are: (1) to compare and evaluate the performance of the existing reflectance based PC algorithms in two different environmental settings with very high and very low concentrations of chl-a and PC, (2) to apply the existing PC algorithms to a synthetic dataset that was simulated using a Gaussian function as the spectral response function of Hyperion, Compact High-Resolution Imaging Spectrometer (CHRIS) and Hyperspectral Infrared Imager (HyspIRI), and (3) to examine the influence of chl-a on the performance of these algorithms.
2. Materials and Methods
2.1. Study Sites
We collected field data from two study sites. The first dataset was acquired from the Funil Reservoir located in Itatiaia, RJ, Brazil during 2–5 April 2013, and the second dataset was collected from catfish aquaculture ponds located at the Thad Cochran National Warmwater Aquaculture Center, Stoneville, MS, USA during 13–16 July 2010 and 28–29 April 2011. A summary of study sites, the field campaigns and descriptive statistics of pigments and nutrient concentrations are shown in
Table 1.
Funil Reservoir was constructed during the late 1960s by the damming of the Paraíba do Sul River in Southeast Brazil. This hydrographic basin connects three economically important Brazilian states including Minas Gerais, Rio de Janeiro, and São Paulo. It serves as the primary source of drinking water for domestic supply, irrigation, industrial self-supply systems, aquaculture, and hydroelectric power generation [
18]. The reservoir receives waste from one of the main Brazilian industrial areas that has enhanced the eutrophication process in recent decades, consequently causing frequent and intense cyanobacterial blooms [
19].
The water for all catfish aquacultures in northwest Mississippi comes from wells pumping the Mississippi River Alluvial Aquifer [
12]. It is also known that commercial pond culture of channel catfish is practical only in regions with the proper temperature regime—around 25–30°C—for reproduction and rapid growth. According to Tucker [
20], the region has the appropriate climatic condition, soil type and water supply for a successful pond culture of channel catfish. However, management practice such as addition of excessive nutrients in the form of commercial catfish food causes phytoplankton blooms dominated by cyanobacteria during warm periods.
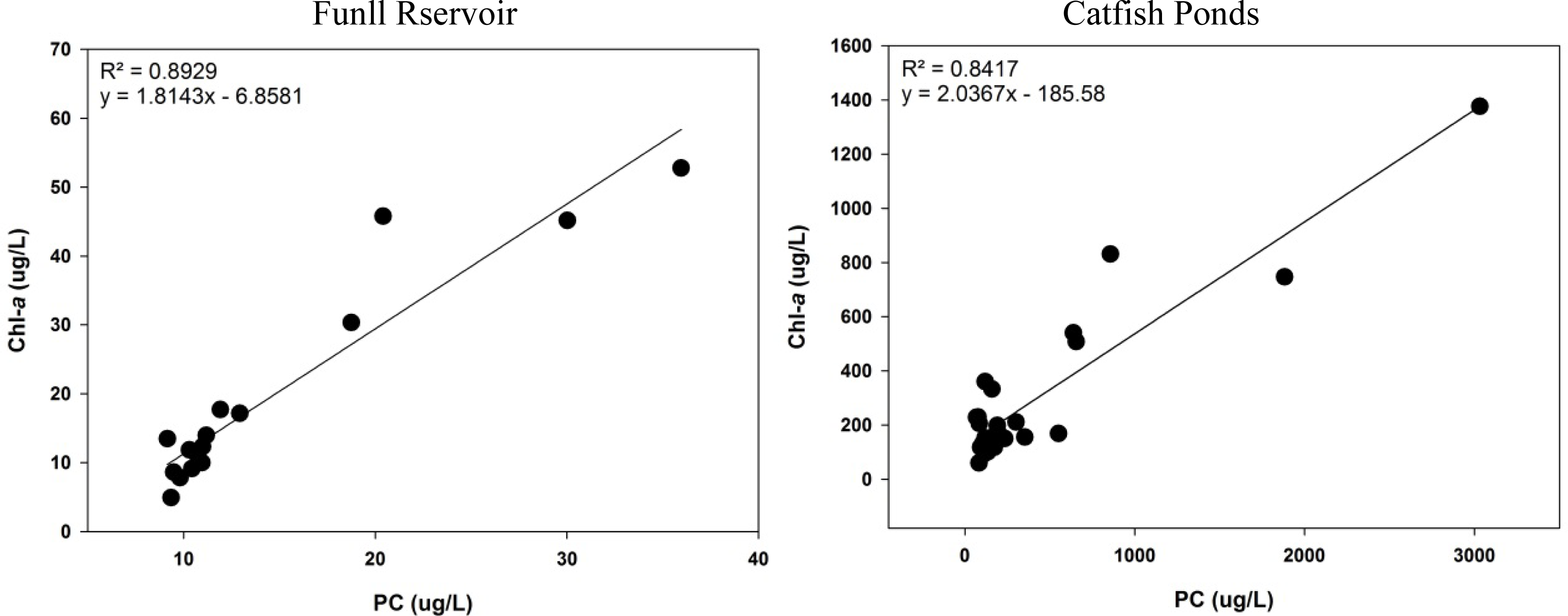
The datasets collected from the two study sites represent extreme range of chl-
a and PC concentrations and are suitable for performance evaluations of the PC algorithms. For example, average PC in Funil Reservoir was found to be 14.52 (μg/L), whereas the catfish pond average PC reading was 241.51 (μg/L) (
Table 1). Similar extremes were observed for chl-
a as well (
Table 1). The observed standard deviation among datasets was helpful in reviewing the performance of the above algorithms at very low and very high concentration ranges and also at a varying chl-
a absorption range.
2.2. Remote Sensing Reflectance
Field radiometric measurements in the Funil Reservoir, Brazil were acquired during 2–5 April, 2013. Radiance and irradiance measurements were carried out using the RAMSES hyperspectral radiometers (TriOS GmbH, Oldenburg, Germany). Measurements were acquired in the visible and near-infrared range of the spectrum (360–900 nm) with 3.3 nm spectral resolution (0.3 nm accuracy). Six sensors were used, two irradiance and four radiance sensors, acquiring data simultaneously. The two irradiance sensors centered at nominal (excluding effects of wave motion) viewing zenith angle (θv) of 90° pointed upward (for downwelling irradiance, Ed) and downward (for upwelling irradiance, Eu) directions. A radiance sensor was also pointed downward to measure the upwelling radiance (Lu). These three measures were collected above and below (below the air-water interface, 1m, 2m and 3m) the water surface. On the top of the boat, a radiometer with an optical fiber and cosine diffuser (yielding a hemispherical field of view, FOV), pointed upward to acquire the incident spectral irradiance (Es). The other two radiometers with a 7° FOV were also on the top of the boat and were centered at nominal θv of 40° in two different directions: upward for the sky radiance (Ls) and downward direction for the radiance received by the sensor pointed at the water surface (Lw).
For the catfish ponds, a dual sensor-system with two inter-calibrated Ocean Optics spectroradiometers (Ocean Optics Inc., Dunedin, FL, USA) were used to acquire remote sensing reflectance (Rrs) data in the range 400–900 nm with a sampling interval of 0.3 nm. The first radiometer was equipped with a 25° FOV optical fiber pointed downward to measure the upwelling radiance just below the air-water interface, expressed in digital numbers (DNLu(λ)). The second radiometer was equipped with an optical fiber and cosine diffuser (yielding a 180° FOV), pointed upward to acquire above surface downwelling irradiance, also expressed in digital numbers (DNEd(λ)). The inter-calibration of the radiometers was accomplished by measuring the upwelling radiance of a white Spectralon reflectance standard (Labsphere, Inc., North Sutton, NH, USA) simultaneously with incident irradiance. The two radiometers were inter-calibrated immediately before and after measurements in each sampling site.
R
rs for the optical measures was calculated based on Mobley [
21]. For Funil Reservoir, R
rs was calculated based on
Equation 1 and for catfish ponds based on
Equation 2.
where,
t is the transmittance at the air-water interface (0.98);
n is the refractive index of water (1.34); and
Fi (λ) is the spectral immersion coefficient [
22].
where,
DNLu,ref and
DNEd,ref are digital numbers representing upwelling radiance and downwelling irradiance over the white Spectralon panel;
ρref is the irradiance reflectance of the Spectralon panel.
The spectral immersion coefficient for each sensor was derived by following
Equation (3) [
22].
where,
nw is the wavelength-dependent refractive index of freshwater and can be estimated using
Equation (4) [
23].
ng is the corresponding index of the glass window of the radiance sensor.
At both study sites, for each sample point, multiple reflectance measurements were acquired and for which the average spectrum was calculated by using either
Equation (1) or
(2). The spectra of R
rs were resampled at 1 nm for further analysis. A synthetic dataset was also created by resampling Rrs measurements matching Hyperion and CHRIS bandwidths using a Gaussian function as the spectral response functions of both sensors.
2.3. Limnological Parameters
2.3.1. Chlorophyll-a
For the Brazilian dataset, water samples were collected from the subsurface, approximately 10 cm below the water surface, and were kept at cool temperatures until delivery to the laboratory for analysis with the duplicates. The method of chl-
a analysis consisted of filtering the collected samples using GF/F filters (Whatman, 0.7 μm pore size) and then extracting the samples from the filters using 90% acetone and measuring the absorbance in a Varian Cary 50 Conc UV-VIS spectrophotometer (Agilent Technologies, Santa Clara, CA, USA) [
24]. Concentration of chl-
a from the spectrophotometric absorbance data was calculated using the equation from Lorenzen [
25].
For the North American ponds, the chl-
a concentrations were analyzed from the water samples collected in 1 L Niskin bottles and immediately filtered onto GF/F filters (Whatman, 0.7 μm pore size) under low vacuum (<12.7 cm of Mercury). Samples were extracted in triplicates using acetone extraction procedure and concentrations were measured using HPLC following the Environmental Protection Agency (EPA) method 447 [
26].
2.3.2. Phycocyanin
During the Brazilian field campaign in April 2013, an in situ fluorometer called FluoroProbe (bbe Moldeanke, GmbH), was used to measure temperature and phytoplankton concentrations. The FluoroProbe data was used to distinguish phytoplankton into four groups: (1) Chlorophyta, (2) PC-rich Cyanobacteria, (3) Diatoms, and (4) Cryptophyta. All data were time stamped and archived on a field handheld personal computer. To measure PC concentration, we used a fluorometer (Turner Designs, model 10-AU-005) with a PC optical kit which uses the excitation and emission wavelengths at 600 nm and 640 nm, respectively.
During catfish pond field campaigns, water samples were filtered immediately after collection through 0.2 μm nucleopore membrane filters (Millipore) under low vacuum. The filters were stored in a 15 mL falcon tube frozen at −80 °C until analysis at the laboratory. For the analysis, filters were transferred to 50 ml polycarbonate centrifuge tubes in order to reach ambient room temperature, and then suspended in 5 mL of 50 mM phosphate buffer. Samples were homogenized using a sonicator [
27] and an ice-bath was used to avoid the destruction of pigments from localized heating. The tip of the sonicator was rinsed twice with 5 mL of 50 mM phosphate buffer each time and the rinse was collected in the centrifuge tube. Samples were centrifuged at 5 °C, 27,200 g for 25 min. This process was repeated one more time using the same settings. The supernatant was collected and absorbance was measured using a Perkin Elmer lambda 850 spectrophotometer (Perkin Elmer Inc., Waltham, MA, USA). Concentration of PC was calculated using the equation from Bennett and Bogorad [
28].
2.4. Model Calibration and Validation
Three sets of calibration and validations were performed including one on the Funil Reservoir’s data, one on the Catfish Pond’s data, and the third on a mixed dataset. As the Funil Reservoir and Catfish Pond datasets have significantly different concentration ranges (
Table 1), a third dataset was created by mixing the two and then randomly dividing into two datasets, one to be used for calibration (60%) and the other for validation (40%). Models were calibrated using the hyperspectral R
rs and the formulas listed in
Table 2. For each model and each dataset, a linear calibration curve was set between the model values and the PC concentration. We did not use the best fit functions, which were mainly non-linear functions, to avoid an out of range calibration/validation problem because the range of PC concentration in both datasets was extreme without any overlap (
Table 1).
A cross-validation procedure was adopted, if any, by developing linear calibration using one dataset and validating with the two remaining datasets (
Table 3). Validations were analyzed by plotting PC Measured
versus PC Predicted.
2.5. Error Analysis
Error analysis was performed by comparing measured and predicted PC concentrations. Bias, Mean Square Error (MSE), Mean Absolute Error (MAE), and Root Mean Square Error (RMSE) were used to evaluate model performance and were calculated according to
Table 4.
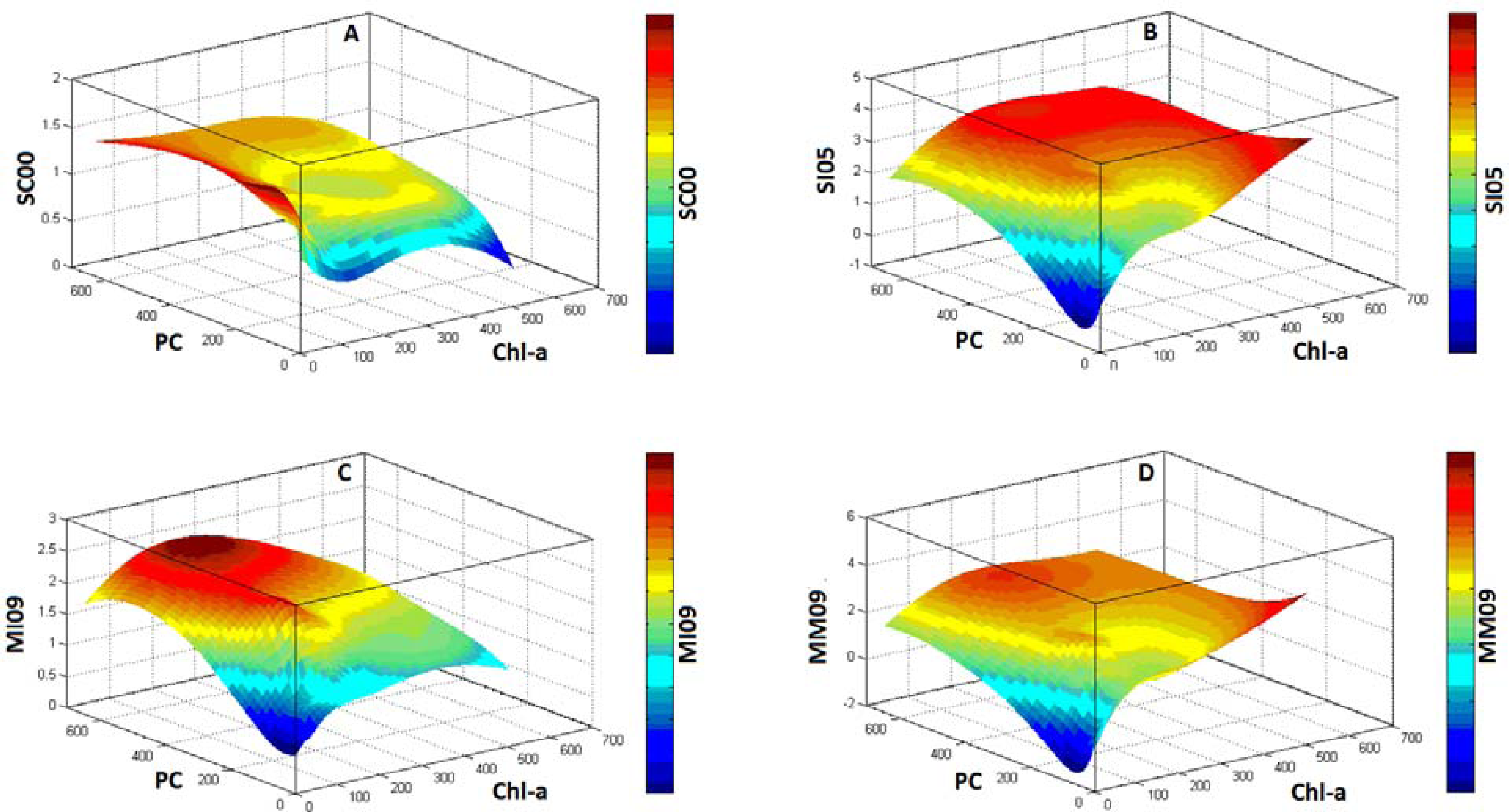
2.6. Sensitivity Analysis
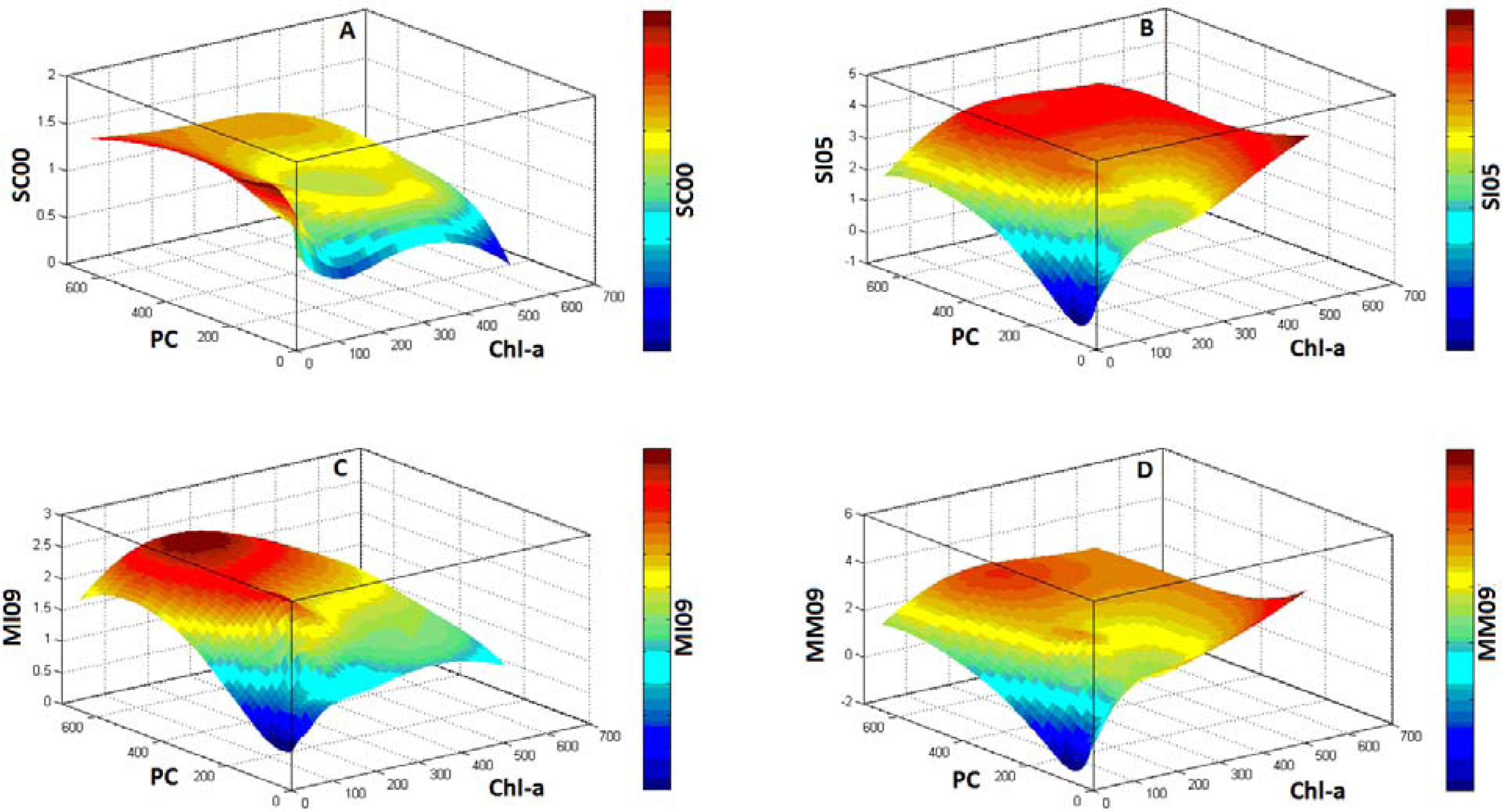
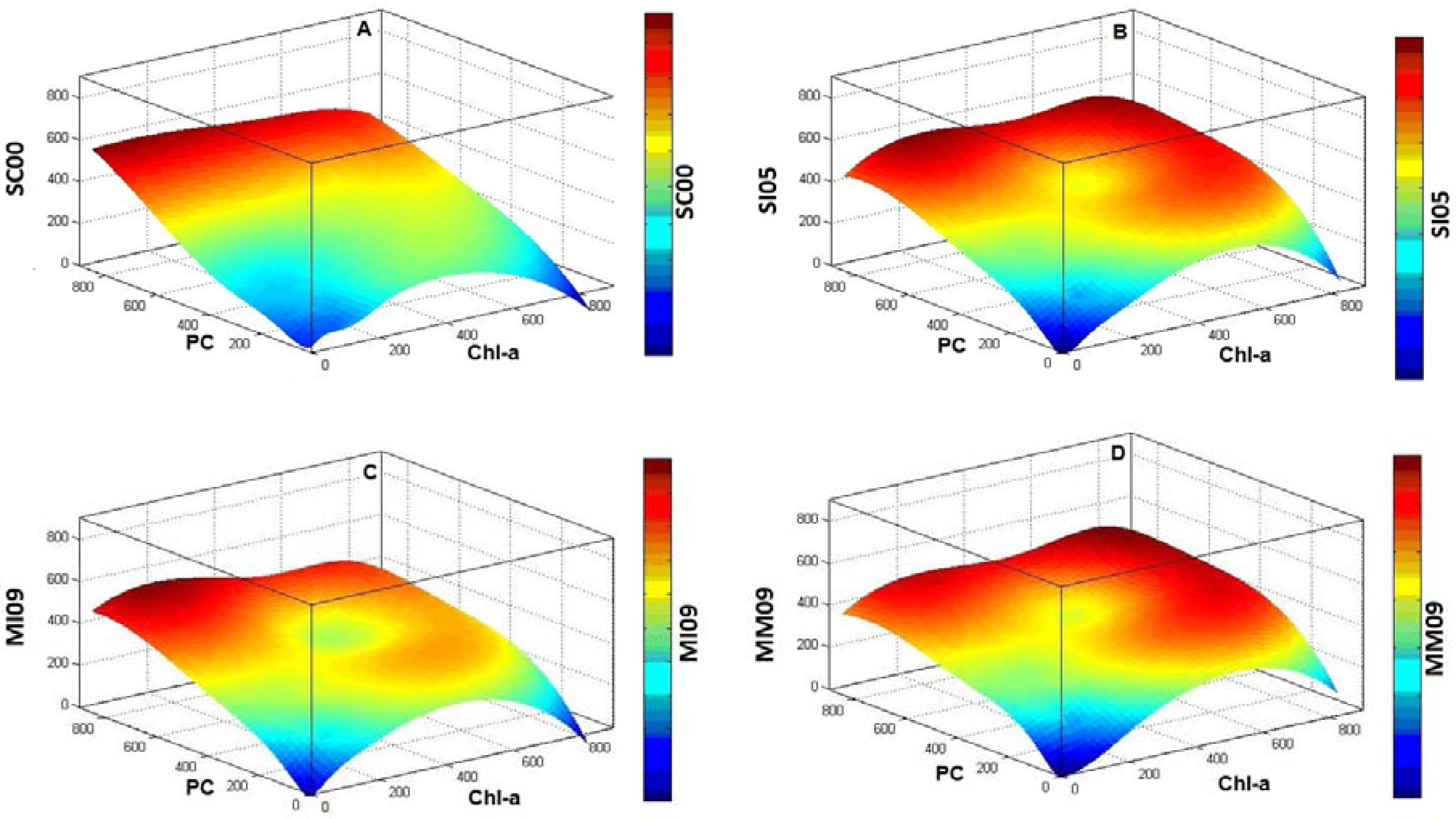
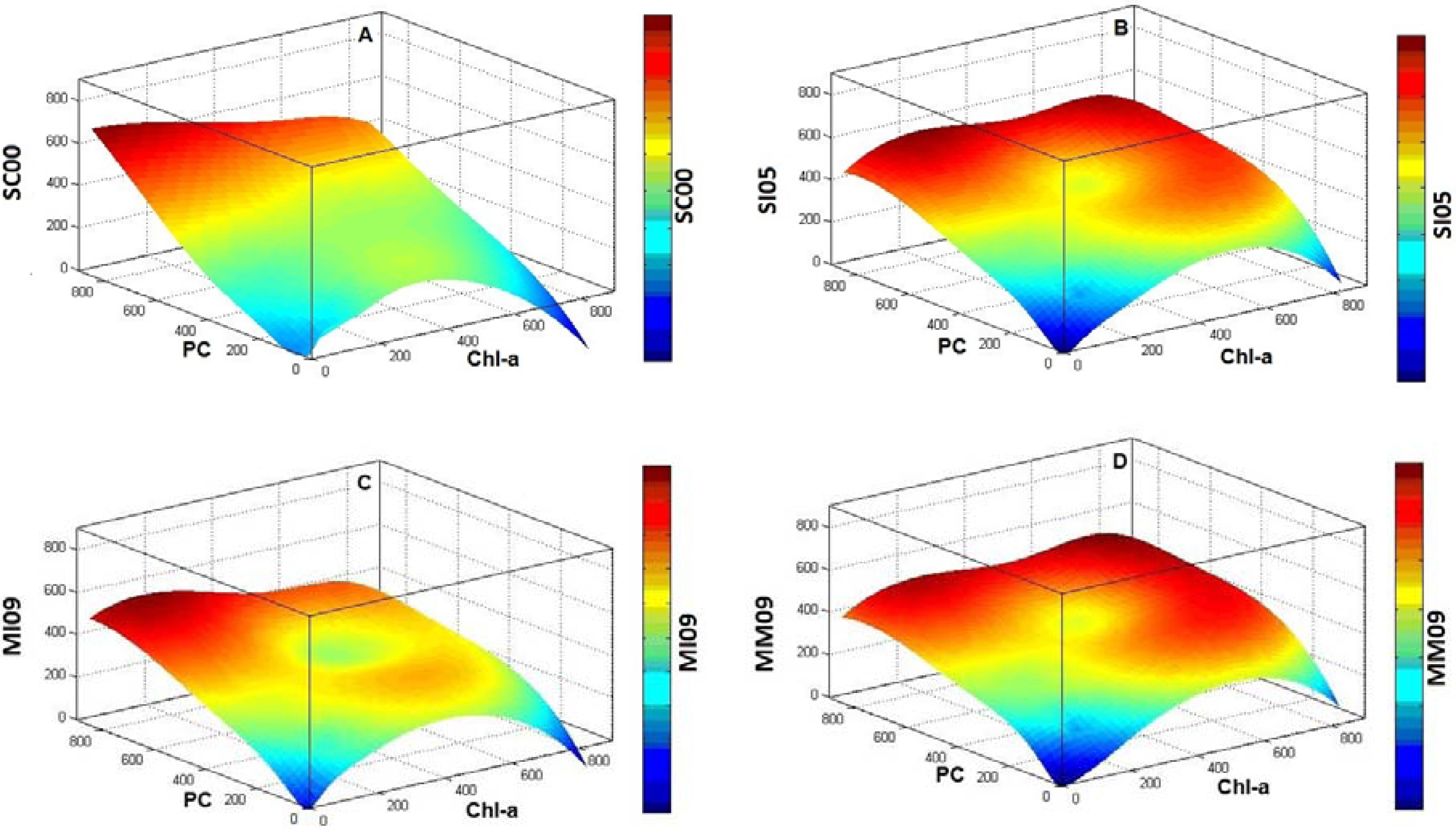
Sensitivity analysis was carried out for the models with the lowest errors and the best validation plots for the simulated data representing the hyperspectral satellite sensors. This analysis was performed to study chl-
a interference on the aforementioned PC detection algorithms. The sensitivity analysis was realized using the values derived from PC detection algorithms (
Table 2), chl-
a, and PC concentrations. Surface plots were generated using these three parameters. They were analyzed according to the slope in each axes and the color scale of the surface which represents the PC detection algorithms.
4. Conclusions
In this paper, we have reviewed and discussed the performance of all available reflectance based algorithms to predict phycocyanin (PC) content in waters with wide ranges of pigment concentration. All PC algorithms analyzed in this paper used different wavelength regions in the reflectance spectra including an absorption peak of around 600–620 nm, a fluorescence peak of around 650 nm, and a chl-
a reflectance peak between 700 and 724 nm. We applied seven reflectance based bio-optical algorithms including Dekker [
16], Schalles & Yacobi [
17], Simis
et al. [
10], Mishra
et al. [
5], Mishra [
29], Modified Mishra
et al. [
5], and Hunter
et al. [
11] (
Table 2) for calibration and validation using three datasets that contained observations from two study sites (Catfish Ponds, MS, USA and Funil Reservoir, RJ, Brazil). Overall, we conclude that the use of chl-
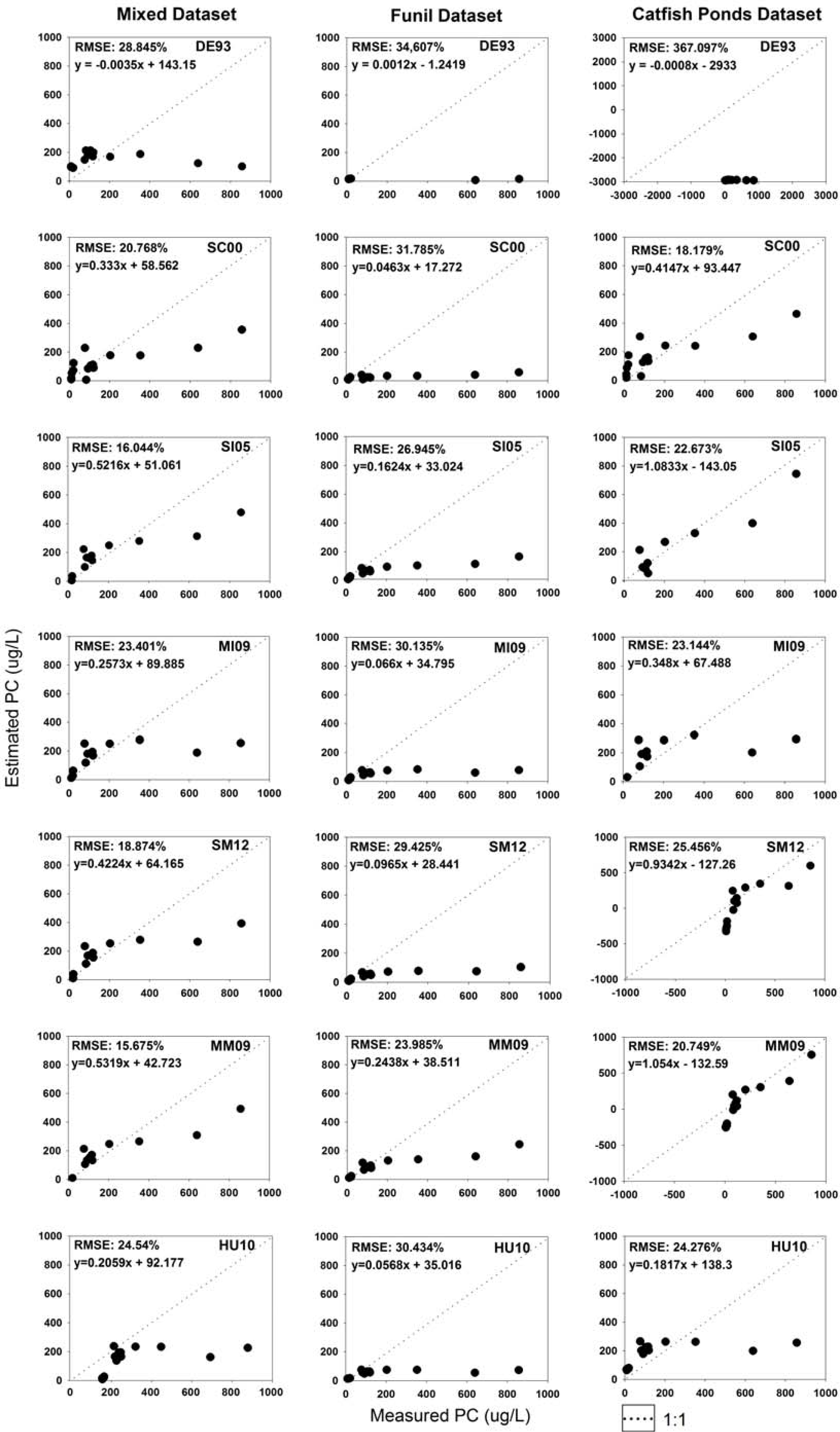
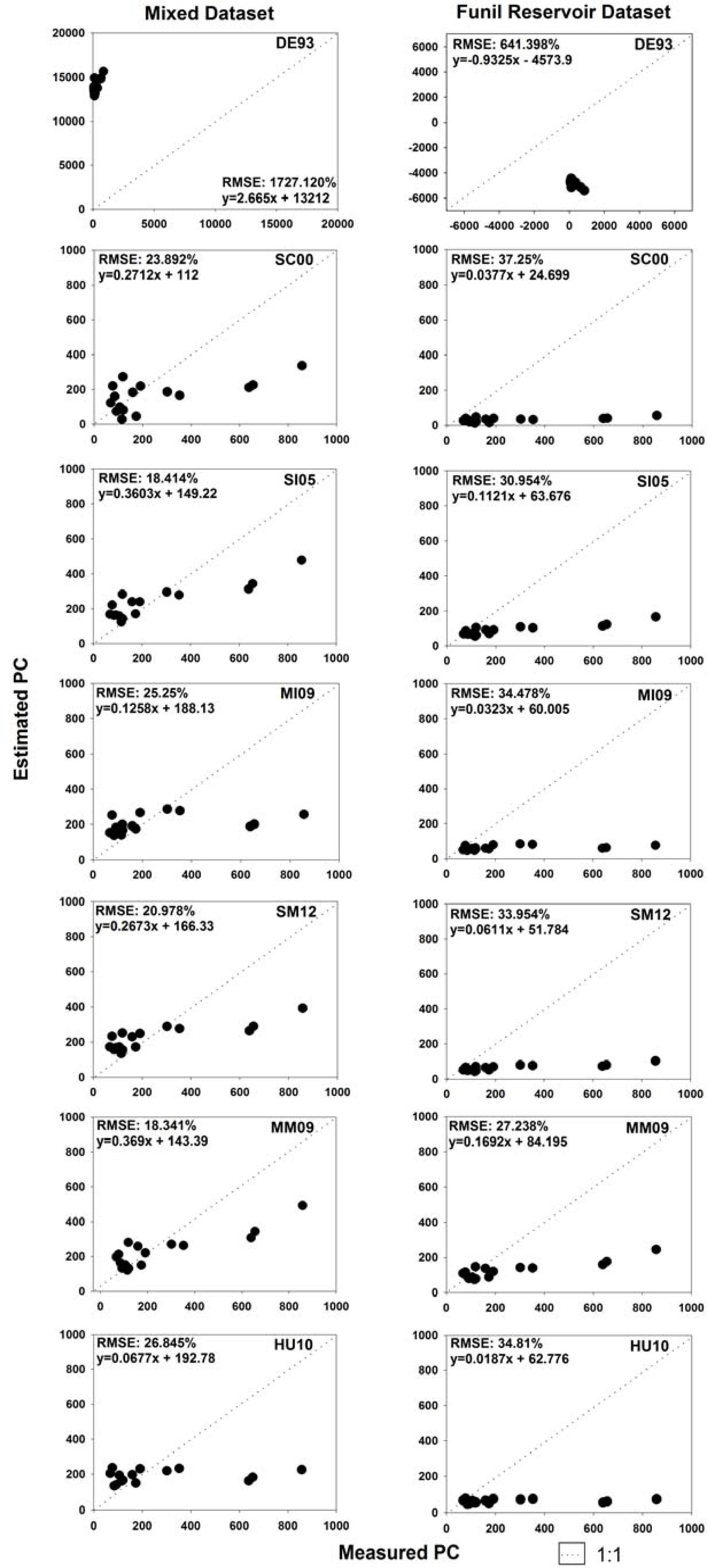
a reflectance peak near 700 nm and PC absorption at 600 nm is the best combination to be used in a PC prediction algorithm The Dekker [
16] algorithm showed the highest RMSE for all the datasets. Its best performance occurred in the mixed dataset (RMSE of 28.845%) where it showed a linear relationship at low PC concentrations, however, at very high PC concentration, this relationship was no longer linear. The relatively high errors produced by the Dekker [
16] algorithm in the three datasets suggest that an empirical parameterization in the calibration dataset could improve its performance. The Schalles & Yacobi [
17] algorithm showed its best performance in the high PC concentrations datasets, probably because it was developed using optical data obtained in eutrophic, cyanobacteria-dominated lakes [
17].
However, the use of the 650 nm band contaminates this model with strong interference from chl-
a, thus decreasing its PC prediction capacity. Similarly, Simis
et al. [
10] showed the lowest error values for the high PC dataset, and for the low PC dataset, it did not have the same accuracy. In our datasets, chl-
a concentration was high for the data points with low PC (
i.e., PC:chl-
a ratio was low for low PC points) and therefore, interference of chl-
a at 620 nm for low PC points was higher and affected the accuracy of the algorithm by Simis
et al. [
10]. Mishra
et al. [
5] showed the highest accuracy among all models and the least interference from chl-
a because of the use of a band at 600 nm, and by moving away from the PC absorption maxima at 620 nm. Its derivatives, Mishra [
29] and Modified Mishra
et al. [
5], used bands at 709 and 724 nm instead of at 700 and they produced mixed results with a higher sensitivity to chl-
a compared to Mishra
et al. [
5]. Hunter
et al. [
11] showed the lowest %RMSE for the low PC data points. However, for the high PC data points, it produced high errors due to the use of two bands (600 and 615 nm) in the PC absorption region.
Overall, the sensitivity analyses were crucial in determining the efficiency of each algorithm, since it was possible to observe the interference of chl-
a in these algorithms. Mishra
et al. [
5] appeared to be the most insensitive algorithm to chl-
a concentration, which also confirmed the fact that PC absorption at 600 nm has less influence of chl-
a absorption as compared to that at 620 nm. However, the residual errors found in Mishra
et al. [
5] could be due to the enhanced interference of another water constituent,
i.e., the total suspended solids (TSS). More research is needed to quantify the interference of TSS at 600 nm and isolate the errors observed in Mishra
et al. [
5].
In addition, we evaluated the performance of all the PC algorithms for two spaceborne hyperspectral sensors and the upcoming HyspIRI sensor using simulated in situ hyperspectral data. From the analysis, it has been concluded that the three sensors can potentially be used to quantify and map PC concentration using some of the reflectance based algorithms considered in this study. However, CHRIS bands appeared to be more sensitive to chl-a due to its narrow bandwidth around the chl-a reflectance peak. Variations in the bandwidth proved to be a determinant for the accuracy of bio-optical models. Overall, results demonstrate that reflectance based algorithms can be applied to infer PC concentrations and distributions accurately using any of the three sensors.
One of the unique factors of this review paper is the datasets used in comparing the performance of various models. The datasets represent two significantly different waters in terms of their bio-optical properties, one acquired from a tropical reservoir representing oligotrophic conditions and the other from catfish ponds representing hyper-eutrophic conditions. Performance evaluation of PC detection algorithms in a tropical reservoir has not been done previously, demonstrating the presence of a research gap for low latitude areas. For example, Matthew and Bernard [
38] stressed the importance of studying lower latitudes by advising future studies to focus on water types in different low latitude geographical regions of the world, mainly where data are lacking. Therefore, inclusion of a dataset from a tropical reservoir in our analysis created a significant difference in the two datasets which allowed us to test the performance and sensitivity of the reflectance based models at very low and very high PC and chl-
a presence. We summarize that the influence of chl-
a absorption determines the performance of a reflectance based PC prediction model, and that interference is higher at the PC absorption maxima near 620 nm than at 600 nm. Therefore, Mishra
et al. [
5] algorithm, which uses a band near 600 nm, showed the highest overall PC prediction accuracy. We conclude that for comprehensive water quality monitoring including accurate prediction of cyanobacteria content in water, a band at 600 nm is imperative in future multispectral and hyperspectral sensors.