1. Introduction
Tropical rainforests are centers of high species diversity and play a critical role in global biogeochemical processes, such as carbon dynamics [
1,
2]. Remote sensing with medium to coarse spatial resolution (
i.e., 30 to 1,000 m), multispectral (
i.e., <20 bands) satellites has played an increasingly important role in mapping broad-scale patterns of forest change in the humid tropics [
3]. Digital images from very high-spatial resolution (<4 m, VHR) satellite or airborne sensors now offer the prospect of mapping finer-scale forest properties, such as upper-canopy individual tree crowns (ITCs) [
4–
6], over larger areas than has been possible with aerial photographs or traditional field surveys. One desired capability from VHR imagery is automated ITC species mapping, especially with detailed spectral information offered by imaging spectrometers, or hyperspectral sensors [
7–
11]. This capability is in the initial stages of development, and is particularly difficult in tropical forests, where high plant species diversity leads to high spectral diversity [
12,
13]. Nonetheless, the ability to map individual canopy species would open the path to regional analyses not easily undertaken with field plots or coarser-resolution sensors, such as mapping beta-diversity, plant species assemblages, and changes in populations due to climate or land-use change.
Spectral variation among tree species is primarily controlled by their tissue chemistry, structure and the changes in these factors through time [
12–
14]. Tissues such as leaves, flowers, fruits, and woody branches have chemical properties that create distinct absorption features in reflectance spectra. In green leaves, photosynthetic (chlorophyll a and b) and accessory pigments (e.g., carotenoids) dominate absorption features in the visible spectrum (VIS: 400–700 nm) [
15] and water creates absorption features in the near-infrared (NIR: 700–1,327 nm) at 970 nm and 1,200 nm, respectively [
14,
16]. In the shortwave infrared (SWIR: 1,467–2,500 nm), relatively low reflectance and strong absorption by water in green leaves often masks other chemical absorption features, such as lignin, cellulose, and nitrogen, that can otherwise appear in dry tissues [
14,
17–
19]. Besides chemistry, factors that influence a species spectral response are tissue internal and surface structures that affect multiple-scattering and transmission of photons within canopies [
12,
20–
22], and the structural arrangement of tissues in crowns, measured through leaf and branch density, angular distribution, and clumping [
20]. For example, multiple-scattering of photons in canopies can enhance the expression of absorption features, such as NIR liquid water bands [
23]. Layered on top of these factors is phenology, with species variation in leaf aging, leaf drop, flowering and fruiting affecting the relative proportions and structural arrangement of chemicals exposed to the sensor through time [
24–
27]. A guiding hypothesis driving spectral species discrimination is that species differ in chemistry and structure enough to create consistently unique and detectable spectral signatures among species at one or multiple times through a year.
Recent research with spectral and chemical analysis of leaves from different humid tropical forests supports this hypothesis [
28–
31]. An initial study in Australia by Asner
et al. [
28] found that unique species-level chemical-structural properties can be detected in spectral features across the VIS to SWIR. More recent research by this team sought to classify species based on their chemical components, rather than directly from spectral reflectance [
29–
31]. In this approach, field spectra were scaled to canopy reflectance with radiative transfer (RT) models, and then partial least squares regression (PLSR) was used to estimate a large portfolio of plant chemicals from full-range (400–2,500 nm) canopy reflectance data. The best PLSR models were then applied to modeled canopy reflectance to estimate chemicals (e.g., photosynthetic pigments, water, nitrogen, cellulose, lignin, phenols) for species, and linear discriminate analysis (LDA) was used to classify species from their estimated chemical concentrations. This technique was proven to be very accurate over a range of humid tropical forests, with varying site conditions, taxonomic composition and phylogenetic history. However, it has yet to be implemented with airborne hyperspectral datasets, which will have more mixed chemical and spectral signatures (e.g., bark, lianas on trees) in the sensor instantaneous field of view (IFOV). The technique also requires a library of leaf spectral measurements with coincident chemical assays, which can be costly and difficult to acquire, especially in remote tropical forest locations.
Other studies have taken a more traditional approach, where species were classified directly from hyperspectral reflectance spectra without integrated chemical estimation. These analyses, mostly based on leaf spectra, typically involve a data reduction/feature-extraction step, including principal component analysis (PCA) and wavelet transforms [
32,
33], stepwise band selection [
8,
22,
34], and narrowband indices [
34,
35], that seeks to reduce noise and target discriminating spectral features. These reduced sets of predictor variables have been used with supervised classifiers, including spectral angle mapper [
8,
36], maximum likelihood [
8], LDA [
8,
9,
34,
37], decision trees, neural networks, log linear, quadratic and k-nearest neighbor [
9,
22,
32,
33,
35]. However, findings to date are difficult to generalize as these studies are mostly non-overlapping in species studied, tropical forest type (dry to wet), season, spatial scale (leaf to crown), sensor characteristics, sample sizes and processing techniques. There is certainly scope in the field to explore new analytical techniques. In particular, studies that use band ratios and reflectance bands [
8,
9,
34,
37] do not take advantage of a unique property of hyperspectral data—band contiguity. Techniques such as spectral derivatives and absorption-based spectroscopy can use band contiguity effectively and provide additional “hyperspectral metrics” related to plant chemistry and structure.
In this study, we revisit our multi-scale analysis of hyperspectral data from a tropical rainforest in Costa Rica [
8], in which we classified seven species with optimally-selected reflectance bands and a LDA classifier. In our new analysis, we move beyond isolated bands by including spectroscopic metrics based on spectral contiguity. Our follow-up analysis is organized at tissue, pixel and crown scales and has the following objectives:
Derive a suite of hyperspectral metrics related to vegetation chemical absorptions and structure.
Assess species classification accuracy when using these metrics in a Random Forests [
38] classifier.
Identify and discuss important metrics that distinguish species to gain a better understanding of the underlying factors that influence spectral variability and our ability to discriminate species.
This study is different than past tropical tree species discrimination studies in these ways: (1) we apply four different techniques to derive hyperspectral metrics: narrowband indices, absorption-based, derivative analysis, and spectral mixture analysis; (2) many metrics have not yet been used in tropical forests, especially with airborne data, and some derivative metrics are new derivations; (3) metrics are analyzed at tissue, pixel, and crown scales, as in Clark
et al. [
8], yet here we include laboratory bark spectra since these tissues can be an important contribution to overall spectral properties; (4) the Random Forests classifier is an untested technique for tropical tree discrimination; and, (5) we use Random Forests to rank metric importance, thereby gaining a better understanding of dominant underlying chemical and structural properties that aid species discrimination. Below we describe some of the metrics used in our analysis, with an emphasis on studies from tropical forests.
5. Discussion
5.1. Species Phenology Detected by Metrics from Hyperspectral Imagery
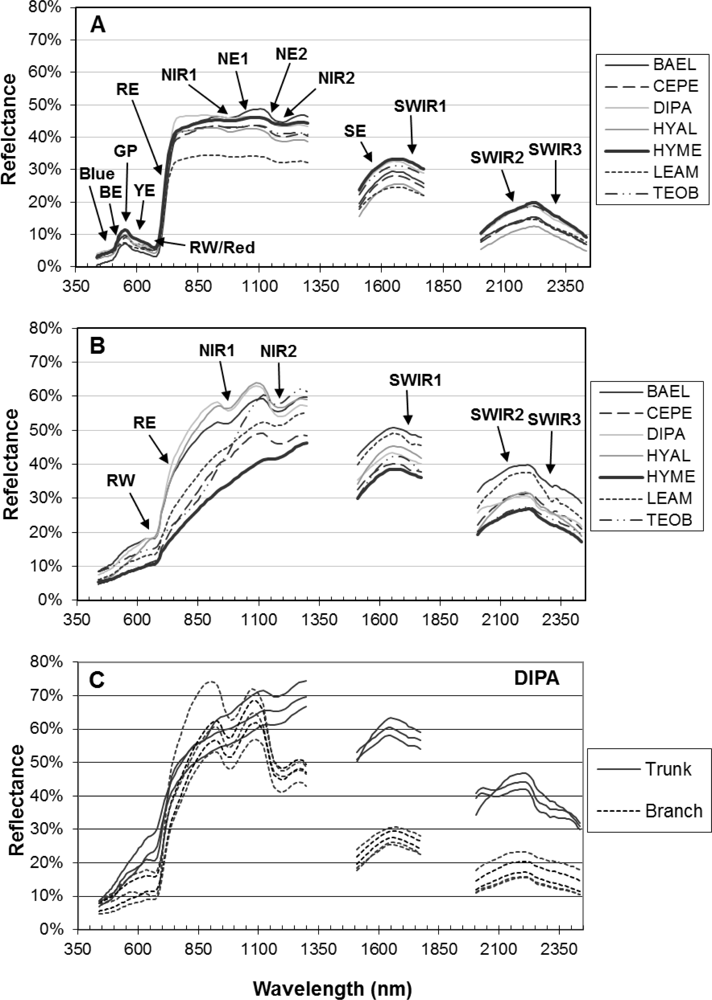
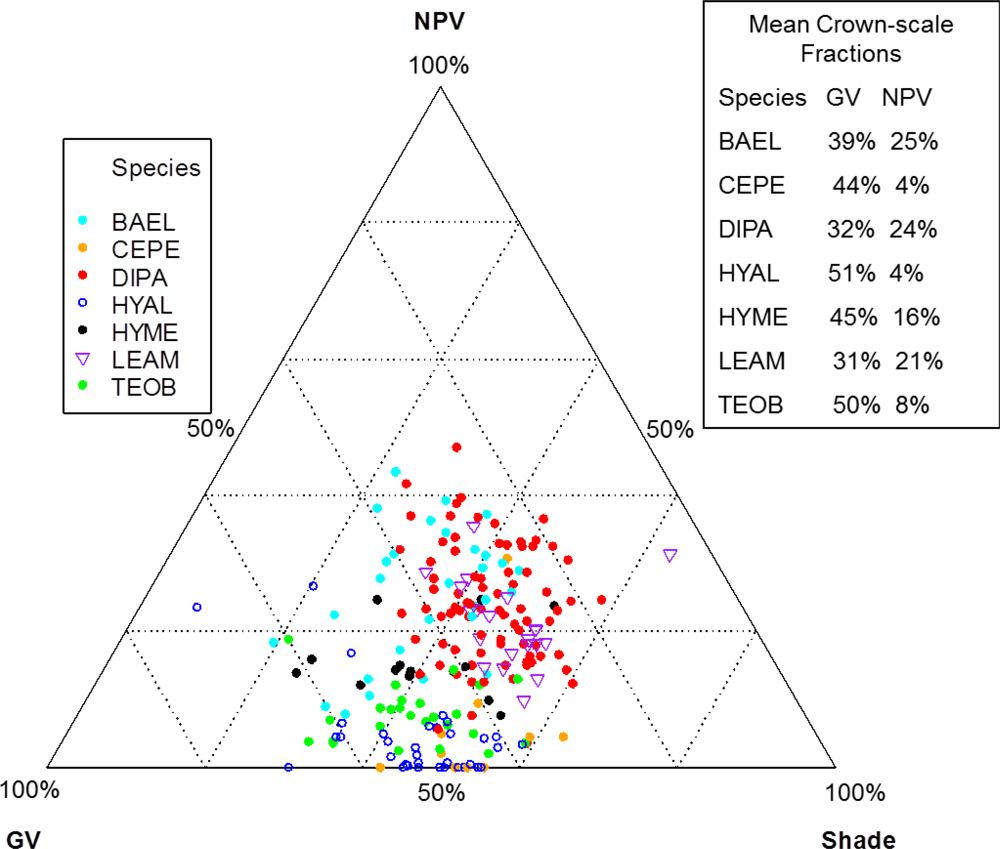
Individuals of BAEL, DIPA and LEAM had crowns with relatively high percentages of NPV compared to other species (
Figures 5 and
7), which can be attributed to bark tissues exposed to the sensor [
25]. The deciduous DIPA and LEAM trees in our study area had low LAI at the time of image acquisition, while individuals of BAEL had relatively high amounts of NPV because of their architectural properties—compound leaves with fine leaflets, sparse arrangement of leaves, and conspicuous white bark mostly free of other organisms. Crowns with low LAI (e.g., DIPA)
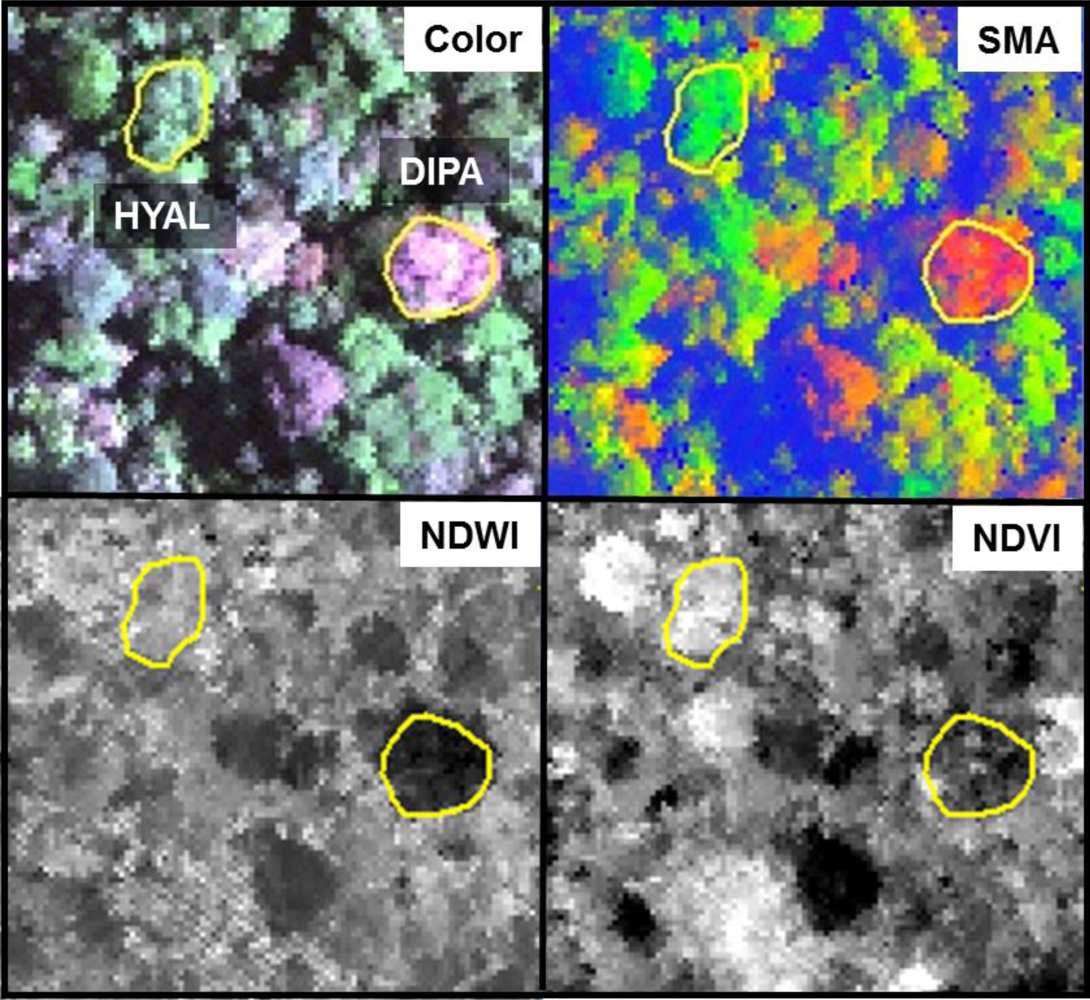
, were easily identified in both the hyperspectral reflectance imagery (
Figure 8; natural color) and the images of hyperspectral metrics (
Figure 8; SMA fractions, NDWI, NDVI). In the SMA false-color image, crowns with low leaf-area were clearly seen as groups of pixels with high NPV (red) in a matrix of high-GV canopy (green) and high-shade gaps (blue).
5.2. Species Differences in VIS to NIR Metrics Sensitive to Pigments, Structure and Stress
The RF classifier identified the red-edge as important for discriminating our set of species at tissue scales. The RE-Wvl and RVSI metrics were key variables for leaves. These results are consistent with work by Cochrane [
36], Clark
et al. [
8] and Rivard
et al. [
34], who also found this region useful for distinguishing leaves from moist tropical forest trees. The shape of the red edge is heavily influenced by photon absorption and florescence from chlorophyll in tissues [
15,
21]. Research has shown that high concentrations of chlorophyll in leaves widens and deepens red-well absorption and shifts the red-edge inflection point toward longer wavelengths [
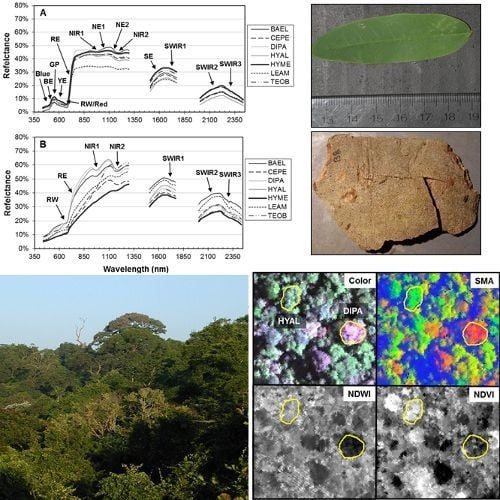
83]. In our study, BAEL and DIPA had a red edge at longer wavelengths than other species (
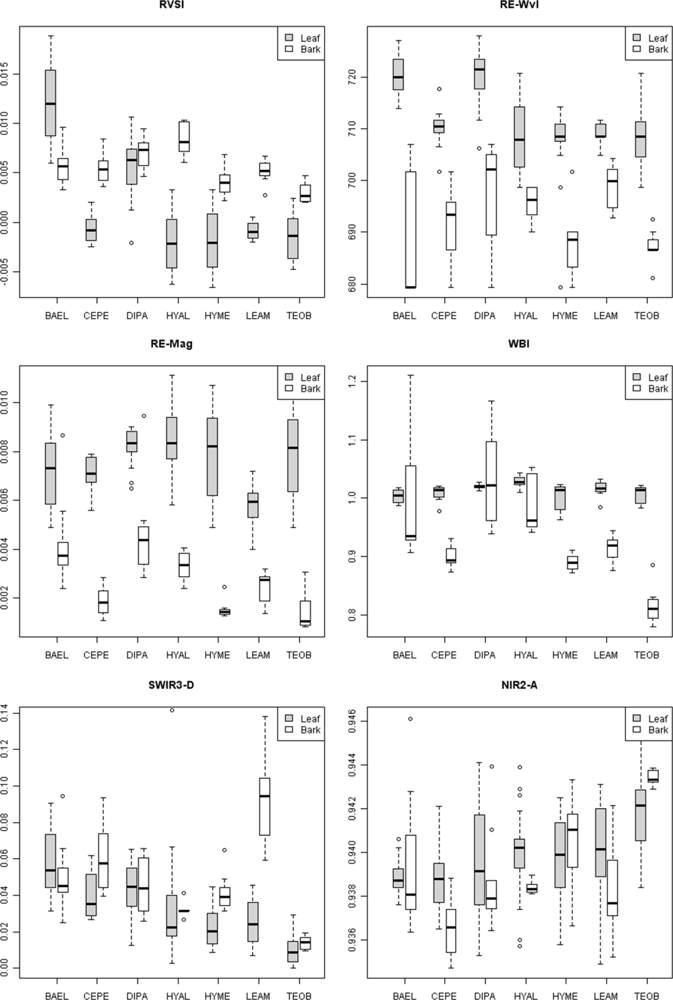
Figure 4, RE-Wvl), and the red absorption depth (Red-D) was also high for these species, suggesting that relatively high chlorophyll concentration for these species helps distinguish them from other species. The RVSI was designed to detect red-edge curve concavity or convexity relative to a baseline. The index was originally used to track vegetation communities through time, not spectral properties of tissues. We found that leaf-scale RVSI was not well correlated with any other red and red-edge metrics, and the metric does provide unique information for separating species using leaf spectra.
The red-edge magnitude, rather than inflection wavelength, was an important metric for discriminating species using bark spectra. Compared to leaves, bark had low to no chlorophyll and so there was relatively low red-well absorption, increased red-well reflectance (RW-Refl), decreased slope of the red-edge (lower magnitude, RE-Mag), and a shift in the red-edge inflection point toward shorter wavelengths (
Figure 1, online
supplement Table S4). We found that BAEL and DIPA bark had the highest RE-Mag values, while TEOB bark had the lowest values (
Figure 5). BAEL and DIPA bark specimens from young branches were mottled green and a PCA showed they had distinct spectral properties, likely due to photosynthesis and water absorption. An example of the greener branches is shown for DIPA (
Figure 1(c)). The branches have well-defined red absorption features and a steeply sloped red-edge, which translates into higher RE-Mag values overall (
Figure 1(b), BAEL, DIPA;
Figure 4, BAEL, DIPA). In contrast, TEOB bark samples were mostly dark brown with minimal green mottling, and their red-edge had a relatively shallow slope (
Figure 1(b), TEOB).
Metrics in the VIS-NIR that were important at the tissue scale were not predictive of metric importance at the pixel and crown scale. At these broader scales, metrics describing the red/chlorophyll absorption feature shape (e.g., depth) and position (e.g., red well wavelength) were important, rather than the red edge. Crown architecture and tree phenology were important factors in determining the amounts and exposure of bark, as well as lichens, bryophytes, epiphytes and other canopy components. High leaf-area species, such as HYAL and TEOB, had high red depth (Red-D), presumably due to chlorophyll absorption; these species also had relatively high NIR reflectance, likely due to multiple scattering among transmittant leaves [
8], and consequently their SR and NDVI values were relatively high (
Figure 8). In contrast, low leaf-area BAEL, DIPA and LEAM had a higher concentration of bark in the sensor’s IFOV, which translated into relatively high red-well reflectance due to lower chlorophyll absorption and low NIR reflectance due to less photon scattering; and thus, Red-D, SR, and NDVI values were relatively low for these species.
5.3. Species Differences in NIR Metrics Sensitive to Water and Structure
The NIR1 and NIR2 water-sensitive metrics, especially area, were important for distinguishing species leaves. Internal leaf structure, such as the air-cell wall interfaces in the spongy mesophyll, scatters NIR photons, increasing the expression of absorption features [
21]. Species differences in water absorption depth, width and area may thus result from a combination of factors that affect internal leaf photon scattering and absorption, such as leaf thickness, water content and the distribution of air-cell wall interfaces.
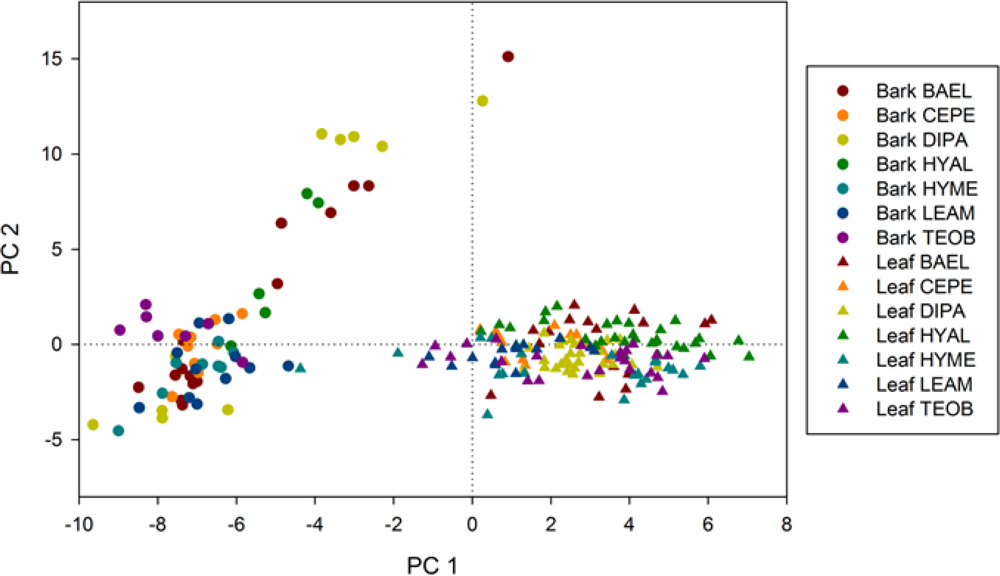
Bark specimens were generally less wet than leaves, as indicated by significantly lower WBI and NDWI values and clustering of bark on the PC1 axis side that indicated less water absorption. However, there was variability among and within species in water-related metrics. For example, much of the within-species bark variability comes from spectral differences between branch and trunk bark, as seen in VIS-NIR metrics. Our results thus indicate that bark spectral properties can vary considerably within a population of tropical tree species, even on a single individual, without considering increased spectral variance from surface lichens, bryophytes, etc. In temperate forests, Williams [
84] found that first-year twig spectra for conifer and hardwood species showed evidence of chlorophyll and NIR water absorption, and the depth of these features decreased considerably in second-year twigs from the conifer species, which were more woody. In our data, it appears that bark chlorophyll and NIR water absorption features are correlated because young branches have relatively more live tissues near the bark surface.
The depth, width and area of NIR water absorption features increased from the centimeter spatial scales of leaf and bark laboratory spectra to the 1.6-m scale of image pixels (
Table S4). The depth of these features can be partly attributed to poor radiometric calibration and signal-to-noise in the HYDICE sensor (discussed in Clark
et al. [
8]). However, the three-dimensional stacking of leaves and branches within the crown, which increases the path length of photons and increases their multiple-scattering and absorption, is expected to accentuate tissue-level chemical and structural properties [
12,
14,
17,
23]. Water absorption metrics calculated at pixel and crown scales should thus respond to the combination of water content of GV and NPV tissues and the structural distribution of these tissues within the crown [
62–
64]. The water absorption signal should be greater with more LAI relative to branch area because leaves tend to be wetter, and they are more transmittive, thereby permitting more photon scattering. This effect can be observed in
Figure 5, where a low leaf-area DIPA had relatively low NDWI relative to leaf-on HYAL, and
Figure 8, where pixels within DIPA crowns formed dark crowns in the NDWI image. In terms of RF metric importance, species differences in both NIR water absorption metrics were important at all scales. However, pixels and crown RF had more importance for NDWI (targets the NIR2 feature) and NIR1 area, whereas leaf and bark RF gave WBI (targets NIR1 feature) and NIR2 area more importance.
5.4. Species Differences in SWIR Metrics Sensitive to Non-Pigment Chemicals, Water and Structure
Metrics incorporating the area, asymmetry and width of SWIR1 and SWIR2 features were among the top-ranked metrics at pixel and crown scales. While the SWIR3 metrics were important at tissue scales, they were likely less important at pixel and crown scales due to low signal-to-noise in the HYDICE sensor and low reflectance in the region [
8,
74]. The SWIR1 feature is associated with lignin (primarily), starch, protein and nitrogen absorption and the SWIR2 feature is associated with protein and nitrogen (primarily), starch and cellulose absorption [
17]. The SWIR1 and SWIR2 absorption features were detected more in bark
vs. leaves: 70% and 15% of bark spectra, 5% and 7% of laboratory leaf spectra, respectively. These results suggest that bark has more of these chemical constituents than leaves, but differences could be related to less SWIR water absorption in bark. Radiative transfer models show that, with closed-canopy tropical forest, photons in SWIR wavelengths do not penetrate deeply into the canopy due to strong water absorption, and thus hyperspectral sensors only sense upper-canopy chemicals [
12,
20]. However, PLSR models based on leaf spectra from humid tropical forests indicate that SWIR is vitally important for accurately predicting a range of foliar chemicals, such as carbon, phenols, tannins, N, P, and K, as well as water [
20,
29,
31]. In addition, research in chaparral communities showed that SWIR indices lost predictive capacity for bulk canopy lignin and nitrogen when senesced vegetation was included in the analysis [
67]. The reason why SWIR1 and SWIR2 metrics were important for species discrimination at pixel and crown scales is thus likely related to LAI variation in crowns. In our pixel-scale data, we found the width of all three SWIR absorption features increased (
i.e., broadened) with higher NPV (
i.e., lower LAI), while depth only slightly increased for SWIR1 and SWIR2 features. This broadening and slight deepening, appears to have created important species-level differences in SWIR1 feature asymmetry (left to right area ratio), as species with low LAI (DIPA, LEAM) had lower median SWIR1-As (
Figure 5). It is not clear why low-LAI crowns have broad SWIR features, as RT models have not considered bark chemical-biophysical interactions. However, we speculate that crowns with lower LAI have less influence by water absorption and more expression of overlapping SWIR chemical absorptions.
5.5. Individual Tree Crown Classification with Random Forests
Our data show that leaf and bark tissues have distinct spectral characteristics as detected by hyperspectral metrics, which translates into higher spectral variability within an individual tree, within a species, and ultimately among species. The relative abundance and arrangement of these tissues in a crown, in turn, will determine the variability of metrics at broader spatial scales, and through seasonal phenological cycles. Given this spatio-temporal variability, spectral metrics do not necessarily have uni-modal distributions within a single crown, let alone among individuals in a species, and especially not at pixel sizes of VHR sensors.
A decision tree classifier is an intuitive technique for discovering multiple, non-linear pathways through the metrics to arrive at species labels. We found the tree-based RF classifier particularly useful for species discrimination based on spectral metrics in that it: (1) could handle non-parametric data and a multi-modal decision space; (2) generated hundreds of decision trees through random sampling of the data, instead of relying on just one—potentially overfit—model; (3) used all data for training, yet produced an unbiased measure of accuracy based on a cross-validation approach (OOB); (4) discovered the best metrics to use in the classification, without an optimization step; and, (5) produced a rank of important metrics, which we used for inferring chemical and structural differences among species.
At all spatial scales, the RF classifier had better performance when all metrics were included, through iterative random sampling, the most important metrics are selected in decision rules (
Table 4). The top-ten metrics in RF at all scales were derived from narrowband indices, absorption-based and derivative techniques (
Table 6); and, VIS, NIR and SWIR spectral features all appeared in these top-ranking metrics. This result concurs with other studies using PLSR and leaf spectra [
28,
29,
31] in that the whole 400–2,500 nm spectrum should be considered when classifying tree species from hyperspectral imagery.
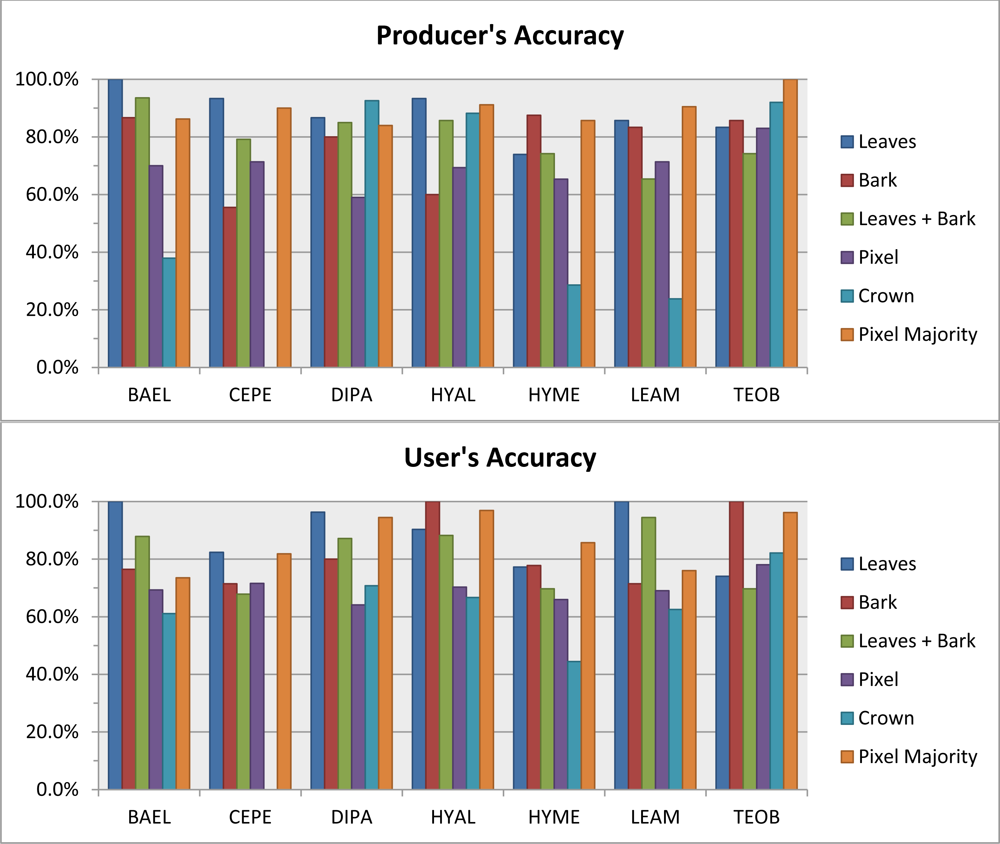
Leaf spectral metrics could discriminate species with 87% overall accuracy. Overall accuracy dropped only 2% when metrics from leaf and bark samples were combined in a single RF—which is impressive considering the extreme spectral variability introduced by bark. At the 1.6-m scale of our imagery, the RF classifier based on all metrics from randomly-sampled pixels within crowns had roughly the same performance (∼70% overall accuracy) as when using the average spectra from crowns, however the pixel-majority classification had much better accuracy, at 87% overall. The 88% Producer’s and 90% User’s accuracies for DIPA from the pixel-majority technique (
Table 5) are encouraging for mapping this species of high conservation value [
8]. Confusion of DIPA with BAEL and LEAM (
Table 5) was likely due to similar LAI from architecture and phenology, resulting in fractions of GV and NPV tissues and comparable photon scattering environments that created similar responses in our chemical-structure metrics.
The pixel-majority technique can accommodate within-crown spectral variation from VHR imagery, such as from pixels with a mix of bark, leaf, liana or epiphyte spectral properties, and still identify the correct species of the ITC. On average, correctly classified ITCs had 75% of their within-crown pixels correctly classified. Some crowns received the correct species label, but with only a fourth of the pixels correctly classified, indicating that ITCs can have high internal spectral variability. The 72% overall accuracy of the pixel-scale RF shows that it can handle some spectral variation among pixels within a species. By taking the majority vote of pixels within ITCs, the error from any misclassified pixels within a crown is minimized. However, a major caveat is that our data only include seven species. The pixel-scale RF performance, and thus crown pixel-majority accuracy, would likely decrease in mapping an entire tropical rainforest due to increased spectral diversity from hundreds of species.
5.6. Comparison with Past Research
The pixel-majority approach to classifying ITC tree species with spectral metrics was superior to using crown-scale metrics (87.4%
vs. 70.6%). In our previous analysis [
8], which used the same hyperspectral data as a starting point, we found that optimally-selected reflectance bands and a LDA classifier had 92.1% classification accuracy with crown-scale spectra, while the LDA pixel-majority classification had 83.6% overall accuracy. The LDA classifier also achieved better overall accuracy with leaf- and pixel-scale reflectance data [
8]. Why did LDA and reflectance data outperform Random Forests and spectral metrics at leaf, pixel and crown scales? The LDA classifier considers all predictor variables simultaneously to build a decision space using predictor variable covariance. In contrast, the decision space of a tree in RF is built one variable at time, and decisions at terminal nodes are dependent upon those at higher nodes. The decision tree is thus more susceptible to misclassification errors when data variability causes many different possible splits. The RF classifier attempts to minimize errors from a single decision tree through random sampling, generating hundreds of decision trees, and deriving the class label from a majority vote; and thus, RF should be fairly robust in the face of spectral variability. Another factor to consider is the difference in using reflectance data versus spectral metrics derived from reflectance. Illumination can influence spectral differences among species, and it is best captured by reflectance spectra as opposed to hyperspectral metrics, which minimize brightness variation from continuum removal, derivative analysis or band ratios. If illumination was the dominant factor in distinguishing species, we would have expected the SMA shade fraction to be among the top metrics in RF. Instead, Shade ranked 31 and 26 out of 66 metrics in pixel and crown RF, respectively (online
supplement Table S3). These results suggest that illumination variation is not a principal factor in discriminating species. In general, our metrics were not well correlated with shade (data not shown), indicating that species were mostly separated according to chemical absorptions and structure rather than illumination.
In many respects, our comparison of the LDA and RF classifiers for species discrimination is imperfect given the small sample size and lack of an independent test dataset. Our previous results with LDA are likely positively biased because they rely on band optimization using all available data and “leave-one-out” cross validation, whereas in RF there is no optimization step, 1/3 of the data can be randomly chosen and held out of each tree for accuracy assessment, and there were 1999 decision trees—as opposed to one LDA classifier. Given its ability to handle intra- and inter-class spectral variability, the RF classifier may prove more robust and less prone to over-fitting when applied to datasets with even higher spectral variability, as when including more species or using higher spatial resolution imagery.
5.7. Recommendations for Future Research
What the LDA and RF classifiers did find in common was that spectral information should come from across the VIS, NIR, and SWIR regions [
8]. Several of the most important reflectance bands and spectral metrics were found in NIR and SWIR; and thus, we recommend that future species discrimination research use hyperspectral sensors that cover the full 400 to 2,500 nm range. Engineering improvements in sensor signal-to-noise in the SWIR region should lead to a greater ability to discriminate species with distinct phenology or structure. The research community would greatly benefit from more datasets from technologically-advanced sensors flown over tropical forests, especially from sites with high species diversity, various land-cover types, and rich field data.
There are several limitations to our analyses in this and the Clark
et al. [
8] study that could be addressed through future research. Ideally, we would have used an independent validation dataset instead of OOB or cross-validation accuracy statistics. However, tropical forests typically have high species diversity, but with low population densities, making it difficult to collect enough samples for training, let alone for testing. Partly due to sampling issues, we limited our analyses to seven out of hundreds of tree species that occur at our study site, and individuals analyzed were relatively large, canopy-emergent trees with well-exposed crowns. An operational approach to mapping target species across a forest canopy will need to include a much broader range of species, including those with smaller and canopy-level crowns. For a pixel-majority technique, an appropriate image segmentation algorithm must be found to delineate crown objects [
6,
9,
10], a task that may benefit from canopy structure information provided by coincident lidar data. Alternatively, dominant species or species richness mapping may be more successful through per-pixel estimation techniques [
60,
70].
Another limitation of our study was that we had no tissue chemical assays from our study species, and so our discussion of chemical properties detected by spectral metrics is speculative. A more instructive study would entail linking chemical compounds in leaves and other canopy components to airborne hyperspectral data, preferably acquired near the same time. Unfortunately, this was not possible in our study as we analyzed the imagery many years after it was acquired. Recent research with high-fidelity spectral, chemical and structure measurements from leaves of tropical forest trees has made great strides in scaling species chemical-spectral diversity from the leaf to canopy scales with modeling techniques [
12,
28–
31].
Many of our results indicate that leaf phenology is a major factor in distinguishing species, as it changes the chemical-structural properties that influence their spectra. Here we have inferred phenological state and associated structural properties of trees based on field data and observations not directly linked to our individual study trees. This limits the conclusions we can draw from our results. We recommend that future studies acquire ITC estimates of crown structure (e.g., leaf and branch area) and other biological information, like liana cover, epiphyte cover, and flower density through either field observations or interpretation of VHR color imagery. Both tissue chemical assays and phenological data, acquired at the time of image acquisition, will permit a deeper understanding of the within- and among-species spectral variation that is expressed in a crown’s reflectance spectra or hyperspectral metrics.
6. Conclusions
In this study we explored a method to classify tropical rainforest tree species from full-range (400–2,500 nm) hyperspectral data acquired at tissue, pixel and crown scales. We focused on seven canopy-emergent species (Balizia elegans, Ceiba pentandra, Dipteryx panamensis, Hymenolobium mesoamericanum, Hyeronima alchorneoides, Lecythis ampla, and Terminalia oblonga) from a site in Costa Rica. Our study was unique for hyperspectral research focused on tropical species discrimination in several ways. First, at the tissue scale we analyzed bark spectra in addition to a traditional analysis of leaf spectra. Second, we used the non-parametric Random Forests classifier, which had not been previously used for tropical forest species classification. Finally, rather than use reflectance bands for predictor variables, we used a suite of hyperspectral metrics that should respond to vegetation chemical (e.g., pigments, water, lignin, cellulose, and nitrogen) and structural properties (e.g., LAI). Some of the narrowband indices were adaptations from broad-band formulations, yet most metrics used were specific to hyperspectral data. In particular, derivative and absorption-based indices relied on band contiguity, a unique characteristic of hyperspectral data, to describe spectral shape and extract information.
Metrics exhibited multi-modal data distributions, yet Random Forests was well-suited to this classification problem across scales. For tissue spectra measured in the laboratory, overall accuracies were 86.8% for leaves and 74.2% for bark, respectively. One important finding was that overall accuracy was only slightly less for leaf and bark metrics combined (84.9%) than with leaves alone; considering the different chemical-structural effects of these tissues on increased within- and among-species spectral variability, this result is an impressive testament to Random Forests ability to handle multi-modal distributions. With airborne hyperspectral data, overall accuracies for individual tree crowns were 71.5% for pixel spectra and 70.6% crown-mean spectra. Using the RF classifier and an object-based pixel-majority vote achieved an impressive 87.4% overall accuracy, and confusion was mainly between low leaf-area species.
Since the RF classifier can rank metrics by importance, it was a powerful tool to decipher the fundamental chemical, structural and phenological factors that drive spectral differences among species. In general, we found that metrics sensitive to chemicals and structure across the visible to shortwave infrared (SWIR) spectrum were useful to discriminate species from centimeter scales of leaf and bark tissue to pixel or crown scales measured by the airborne sensor, although the important metrics varied with scale. For example, the top-three metrics chosen by Random Forests for classifying leaves and bark were sensitive to near infrared (NIR) water absorption (NIR2-A, WBI) and a SWIR feature (SWIR3-D); the pixel-scale top-three metrics were also sensitive to NIR and SWIR absorption features (NIR1-A, SWIR1-As) as well as an anthocyanin feature (ARI2) in the visible spectrum; and, the crown-scale top-three metrics were sensitive to SWIR features (SWIR1-W, SWIR2-A) and the red chlorophyll absorption feature (Red-D). We found that variation in leaf and bark metrics is explained primarily along an axis of red absorption related to photosynthesis in leaves and another axis distinguishing SWIR chemical and NIR water absorption features, attributed to photosynthetic (wet) properties of younger green bark in some species. At pixel and crown scales, tree structure and phenology at the time of image acquisition were driving factors on spectral separability of species.
Much more research is needed to achieve operational mapping of tropical forest tree species, and our suite of hyperspectral metrics and object-based classification approach should be tested with many more species, at other sites, and with improved sensors. However, our results show that our seven tropical tree species were reliably discriminated with hyperspectral metrics selected by the Random Forests classifier, whose strength lies in its ability to accommodate the within-species spectral variability found in tropical forests. Our results also corroborate those from other studies that have found statistical separation of tropical forest species based on analysis of hyperspectral data [
8,
22,
34,
36,
37]. Adding to this, there is mounting evidence that tropical tree species have unique leaf chemical signatures that manifest as distinct hyperspectral signatures [
28–
31], and overall canopy species richness may track spectral-chemical diversity measured by full-range hyperspectral sensors [
12,
28]. Therefore, despite the many challenges that tropical rainforests present to operational species mapping, we conclude that imaging spectroscopy is the most credible technology for attaining this goal.