A Phase-Offset Estimation Method for InSAR DEM Generation Based on Phase-Offset Functions

Abstract

This paper presents a novel method for estimating the absolute phase offset in interferometric synthetic aperture radar (SAR) measurements for digital elevation model (DEM) generation. The method is based on “phase-offset functions (POF),” relating phase offset to topographic height, and are computed for two different overlapping interferometric data acquisitions performed with considerably different incidence angles over the same area of interest. For the purpose of extended mapping, opposite viewing directions are preferred. The two “phase-offset functions” are then linearly combined, yielding a “combined phase-offset function (CPOF)”. The intersection point of several straight lines (CPOFs), corresponding to different points in the overlap area allows for solving the phase offset for both acquisitions. Aiming at increasing performance and stability, this intersection point is found by means of averaging many points and applying principal component analysis. The method is validated against traditional phase offset estimation with corner reflectors (CR) using real OrbiSAR-1 data in X- and P-band.

1. Introduction

SAR interferometry is a well-known technique used to generate a Digital Elevation Model (DEM), which converts the absolute interferometric phase data into height data [1–4]. The absolute interferometric phase data can be obtained by removing the ambiguity of 2π from the measured interferometric phase using a phase-unwrapping algorithm [5–8]. For InSAR data there is a residual phase–offset value in the interferogram after phase unwrapping, which is a constant value for the whole scene, and which must be estimated. This phase component comes mainly from the phase induced by the interferometric SAR processing strategy, a not well-determined internal delay, and from the ratio between the range resolution and the wavelength used.

The absolute interferometric phase estimation is often solved by using ground control points (GCPs) within the scene or through the use of an already calibrated area. Automatic methods have also been proposed, based on spectral diversity [9–11] and on a maximum likelihood estimator [12]. By using GCPs, one can estimate the phase-offset values with great accuracy, making the generation of high accuracy DEMs possible. However, in certain regions of dense forest or in fluvial regions, it can be difficult to have access to appropriate areas to deploy the corner reflectors (GCPs). Dispensing the GCPs can lead not only to lower implementation cost, but also to a decrease in environmental impact associated with corner deployment.

This paper describes a method to estimate the phase-offset value automatically using a pair of unwrapped interferometric phases, whose data have been acquired in opposite flight directions and with an overlap area between the tracks. For a selected point in the overlapped area, a function relating phase-offset value to height value, called here phase-offset function (POF), can be built for each acquisition within a known height interval. The POFs of both acquisitions can be combined through a linear combination to remove its dependency on height, creating a combined phase-offset function (CPOF), whose slope is range dependent. The same procedure can be extended to a set of points spread over the overlapped area, creating a set of CPOFs whose intersections provide the estimate of the phase-offset values for both acquisitions. The performance of this method has been evaluated using data from the OrbiSAR-1 System in X and P bands; the results are compared with those obtained by using ground control points. This method has also been tested with OrbiSAR-1 data from an Amazon forest area without the use of GCPs to evaluate its performance in this environment for topographic mapping.

2. Proposed Method

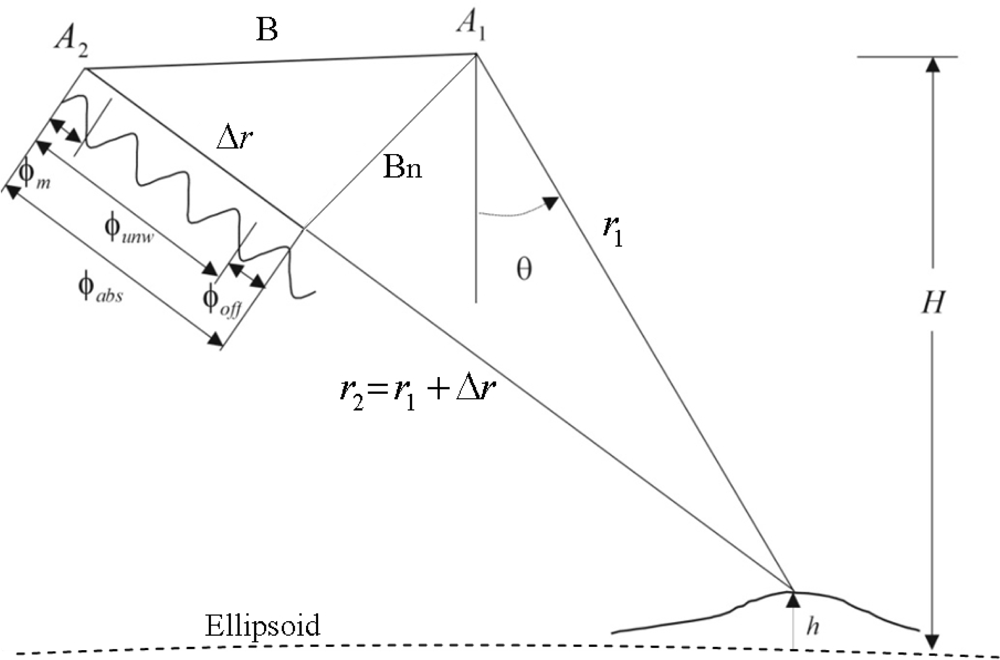
SAR Interferometry is based on the measurement of the phase difference from the complex-valued resolution elements of two co-registrated images, acquired by two separated antennas (baseline B) as shown in Figure 1. The measured interferometric phase is wrapped in 2π, represented by ϕ_m in Figure 1. The grid of the wrapped phase values is transformed into a grid of unwrapped phase values by using a phase-unwrapping algorithm that adds to each measured phase value a constant integer multiple of 2π, represented by ϕ_unw in Figure 1.

The phase-offset value, represented by ϕ_off in Figure 1, is a constant phase component for the whole scene that must be estimated and added to the unwrapped phase in order to obtain the absolute interferometric phase ϕ_abs, from which a digital elevation model (DEM) can be generated. The phase-offset value can be positive or negative, and is sometimes greater than 2π, depending on the interferometric SAR processing strategy used.

The proposed method to estimate the phase-offset value for an InSAR airborne system is based on the following assumptions: the interferometric SAR images are generated in zero-Doppler geometry [13], and the atmospheric effects are negligible. Considering the previous assumptions and taking antenna A₁ as the reference (Figure 1), the following equations can be written

$${\varphi }_{\mathit{abs}\hspace{0.17em}}=\hspace{0.17em}\hspace{0.17em}{\varphi }_{\mathit{unw}}\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}{\varphi }_{\mathit{off}},$$

(1)

$$\mathrm{\Delta }r=\frac{\lambda \hspace{0.17em}p}{4\pi }{\varphi }_{\mathit{abs}\hspace{0.17em}},$$

(2)

$$r_1=\hspace{0.17em}{r}_2-\hspace{0.17em}\mathrm{\Delta }r\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}{r}_2\hspace{0.17em}-\hspace{0.17em}\frac{\lambda \hspace{0.17em}p}{2\pi }{\varphi }_{\mathit{abs}\hspace{0.17em}},$$

(3)

with p = 1 for monostatic acquisitions and p = 2 for bistatic acquisitions schemes.

Assuming a flat-earth geometry, for sake of simplicity, the terrain height can be represented by:

$$h=H-r_1\hspace{0.17em}\text{cos}\theta$$

(4)

From the Equations (2) and (3), the Equation (4) can be rewritten as

$$h=H-\left(\hspace{0.17em}{r}_2-\frac{\lambda \hspace{0.17em}p}{2\pi }{\varphi }_{\mathit{abs}}\right)\hspace{0.17em}\text{cos}\theta ,$$

(5)

where h is the terrain height, H is the platform altitude and θ the look-angle for the antenna A₁.

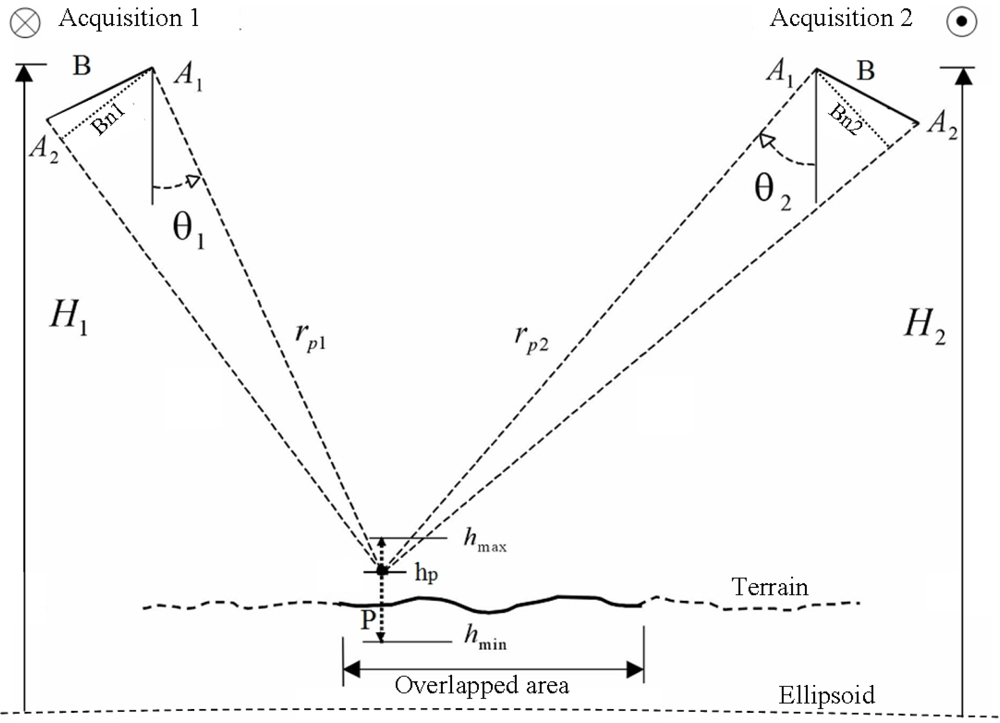
The proposed method is based on the acquisition mode shown in Figure 2, where two InSAR acquisitions, using the same SAR configuration, are done in opposite flight directions, over a common area, which represents the usual mode for systematic mapping to diminish the shadow and layover effects. In Figure 2, the height h_p of a point P in the overlapped area can be written, for both acquisitions, based on the Equation (5), by:

$$h_p=H_1-\left(r_{p1}\hspace{0.17em}-\frac{\lambda \hspace{0.17em}p}{2\pi }{\varphi }_{\mathit{abs}1}\right)\hspace{0.17em}\text{cos}{\theta }_1\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}{H}_2-\left(r_{p2}\hspace{0.17em}-\frac{\lambda \hspace{0.17em}p}{2\pi }{\varphi }_{\mathit{abs}2}\right)\hspace{0.17em}\text{cos}{\theta }_2$$

(6)

where ϕ_abs1 and ϕ_abs2 are the absolute phase of the first and second acquisition, respectively.

Equation (6) can be rewritten as

$$(H_1-r_{p1}\hspace{0.17em}\text{cos}{\theta }_1)\hspace{0.17em}+\frac{\lambda \hspace{0.17em}p}{2\pi }{\varphi }_{\mathit{abs}1}\text{cos}{\theta }_1=(H_2-r_{p2}\text{cos}{\theta }_2)\hspace{0.17em}+\frac{\lambda \hspace{0.17em}p}{2\pi }{\varphi }_{\mathit{abs}2}\text{cos}{\theta }_2,$$

(7)

$$h_p\hspace{0.17em}+\frac{\lambda \hspace{0.17em}p}{2\pi }{\varphi }_{\mathit{abs}1}\text{cos}{\theta }_1=\hspace{0.17em}\hspace{0.17em}{h}_p\hspace{0.17em}+\frac{\lambda \hspace{0.17em}p}{2\pi }{\varphi }_{\mathit{abs}2}\text{cos}{\theta }_2,$$

(8)

$${\varphi }_{\mathit{asb}1}\text{cos}{\theta }_1=\hspace{0.17em}\hspace{0.17em}{\varphi }_{\mathit{abs}2}\text{cos}{\theta }_2$$

(9)

Equation (9) shows that the absolute phases of both acquisitions, for a point P with height h_p, are only related by their incident angles. From this equation, the phase-offset ϕ_{off 1} can be related as a function of ϕ_{off 2}, as follows:

$${\varphi }_{\mathit{asb}1}\text{cos}{\theta }_1=\hspace{0.17em}\hspace{0.17em}{\varphi }_{\mathit{abs}2}\text{cos}{\theta }_2=\hspace{0.17em}({\varphi }_{\mathit{unw}1}+{\varphi }_{\mathit{off}1})\hspace{0.17em}\text{cos}{\theta }_1\hspace{0.17em}=\hspace{0.17em}({\varphi }_{\mathit{unw}2}+{\varphi }_{\mathit{off}2})\hspace{0.17em}\text{cos}{\theta }_2,$$

(10)

$${\varphi }_{\mathit{unw}1}\text{cos}{\theta }_1+{\varphi }_{\mathit{off}1}\text{cos}{\theta }_1=\hspace{0.17em}\hspace{0.17em}{\varphi }_{\mathit{unw}2}\text{cos}{\theta }_2+{\varphi }_{\mathit{off}2}\text{cos}{\theta }_2,$$

(11)

$${\varphi }_{\mathit{off}1}=\hspace{0.17em}\hspace{0.17em}{\varphi }_{\mathit{off}2}(\text{cos}{\theta }_2/\text{cos}{\theta }_1)\hspace{0.17em}\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}{\varphi }_{\mathit{unw}2}(\text{cos}{\theta }_2/\text{cos}{\theta }_1)-\hspace{0.17em}\hspace{0.17em}{\varphi }_{\mathit{unw}1},$$

(12)

$${\varphi }_{\mathit{off}1}=\hspace{0.17em}\hspace{0.17em}{\varphi }_{\mathit{off}2}\hspace{0.17em}{K}_{\theta }\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}{R}_{ph},$$

(13)

with

$$K_{\theta }=\hspace{0.17em}\text{cos}{\theta }_2/\text{cos}{\theta }_1\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}{R}_{ph}\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}{\varphi }_{\mathit{unw}2}\hspace{0.17em}{K}_{\theta }-\hspace{0.17em}\hspace{0.17em}{\varphi }_{\mathit{unw}1}$$

(14)

Considering that K_θ and R_ph are constant values at the position P with the height h_p, the phase-offset value ϕ_{off 1} can be seen as a linear combination of ϕ_{off 2}, depending on the relation of the incident angle and the unwrapped phase difference between the two acquisitions.

In order to build up the phase-offset function, we first consider the absolute phase value of a generic point P_i selected, based on its geographic coordinate, with a Cartesian coordinate of (x_p, y_p, z_p) and height equal to h_p relative to an ellipsoid, as shown in Figure 3, whose value depends on the knowledge of the slant range distances, r₁ and r₂, where for a monostatic SAR system, is given by

$$\mathrm{\Delta }{\varphi }_{\mathit{abs}{P}_i}\hspace{0.17em}=\hspace{0.17em}\frac{2\pi }{\lambda }\hspace{0.17em}(r_2-r_1)$$

(15)

The slant range distances, r₁ and r₂, can be found through the Cartesian distance from P_i(x_p, y_p, z_p) to A₁(x₁, y₁, z₁) and from P_i(x_p, y_p, z_p) to A₂(x₂, y₂, z₂), respectively, where A₁(x₁, y₁, z₁) and A₂(x₂, y₂, z₂) represent the coordinates of the two antenna phase centers, derived from the state vector of the platform, (V⃗, S⃗), shown in Figure 3. The corresponding unwrapped phase value of P_i(x_p, y_p, z_p), ϕ_unwPi, in the grid of unwrapped phase ϕ_{unw i}, can be determined by using the backward geocoding technique [14].

The phase-offset value of P_i(x_p, y_p, z_p), with height h_p, can be calculated by taking the difference from the absolute phase value calculated by using the slant range difference and the unwrapped phase value at this point, as follows

$${\varphi }_{\mathit{off}{P}_i}\hspace{0.17em}=\hspace{0.17em}\mathrm{\Delta }{\varphi }_{\mathit{abs}{P}_i}\hspace{0.17em}-\hspace{0.17em}{\varphi }_{\mathit{unw}{P}_i}$$

(16)

The phase-offset value found in Equation (16) would be the correct one if the P_i true height were h_p, which is the case when it uses the position and height of a corner reflector to calculate the phase-offset value. As the true height of the point P_i is unknown, a procedure based on function that relates phase-offset to height, applied in a height interval of h_min to h_max (Figure 2), was adopted to estimate the true phase-offset values for both acquisitions, assuming that the true height h_i of the point P_i is within [h_min, h_max].

Attributing a height for P_i from h_min to h_max in N steps, as shown in Figure 2, and applying the same procedure discussed previously to calculate the phase-offset value for each step, one can create a set of N phase-offset values for the first acquisition. The same procedure can be applied for the second acquisition, creating another set of phase-offset values related to the same height interval. The two set of phase-offset values calculated for the point P_i can be represented by functions, the phase-offset functions (POFs), as follows

$$f_{\mathit{off}1}^{Pi}\hspace{0.17em}=\hspace{0.17em}{\mathrm{\Phi }}_{\mathit{off}1}^{Pi}(h),$$

(17)

$$f_{\mathit{off}2}^{Pi}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}{\mathrm{\Phi }}_{\mathit{off}2}^{Pi}(h),$$

(18)

where h varies from h_min to h_max in N height steps.

Considering that the true height h_t of the point P_i is unknown, the phase-offset values cannot be determined from the POFs$f_1^{Pi}$ and $f_2^{Pi}$. In order to overcome this problem, the following procedure was used to estimate the phase-offset values of both acquisitions:

• - Firstly, as the POFs represented by the Equations (17) and (18) are generated within the same height interval, [h_min, h_max], one can combine them creating a new function g_i, the combined phase-offset function (CPOF), which relates the phase-offset values in the space Φ_{off 1} × Φ_{off 2} for the point P_i. A CPOF can be represented by a function that relates the phase-offset values of both acquisitions, for each height step, through the relation based on the Equation (13), as follows

  $${\mathrm{\Phi }}_{\mathit{off}1}(h)={\mathrm{\Phi }}_{\mathit{off}2}(h)\hspace{0.17em}.\hspace{0.17em}{K}_{{\theta }_{(h)}}+\hspace{0.17em}{R}_{p{h}_{(h)}},$$

  (19)

  with

  $$K_{{\theta }_{(h)}}=\hspace{0.17em}\text{cos}{\theta }_{2(h)}/\text{cos}{\theta }_{1\hspace{0.17em}(h)}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{R}_{p{h}_{(h)}}=\hspace{0.17em}{\varphi }_{\mathit{unw}2}\hspace{0.17em}{K}_{{\theta }_{(h)}}-\hspace{0.17em}{\varphi }_{\mathit{unw}1}$$

  (20)

  The terms K_θ and R_ph of the Equation (19) can be considered quite constant when computed in a short height interval for the same point P_i. Based on that, one can suppose without loss of generality, that Equation (19) represents a linear function of Φⁱ_{off 1} with respect to ⁱ_{off 2}, where the term K_θ represents the angular coefficient and the term R_ph represents the constant value of this linear function. The coefficients K_θ and R_ph change according to the range position selected for a point in the overlapped area.
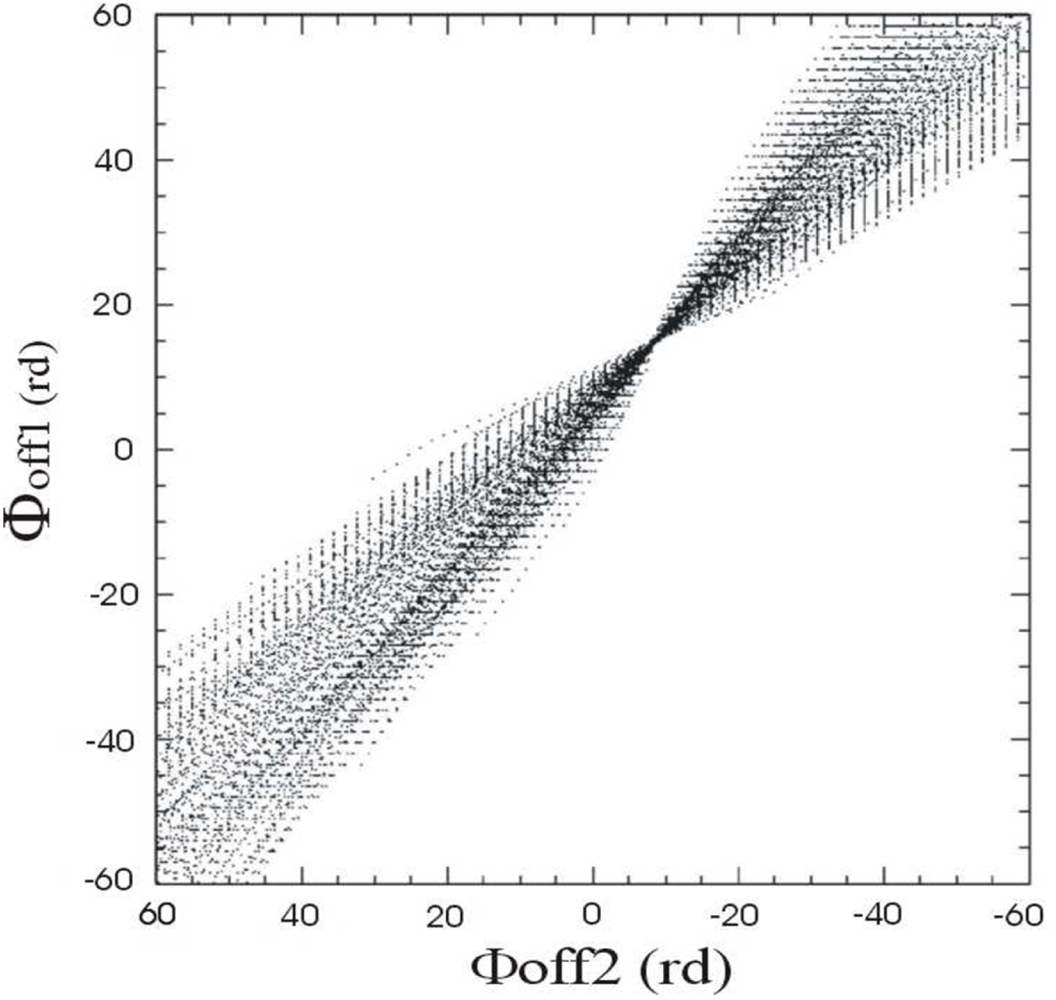
• - Secondly, considering another point P_k in the overlapped area, with a different range position from P_i, another two POFs, one for each acquisition, can be created for the point P_k. These two new functions can be combined, creating another CPOF, the g_k, that relates the phase-offset values of both acquisition in the space Φ_{off 1} × Φ_{off 2} for the point P_k.
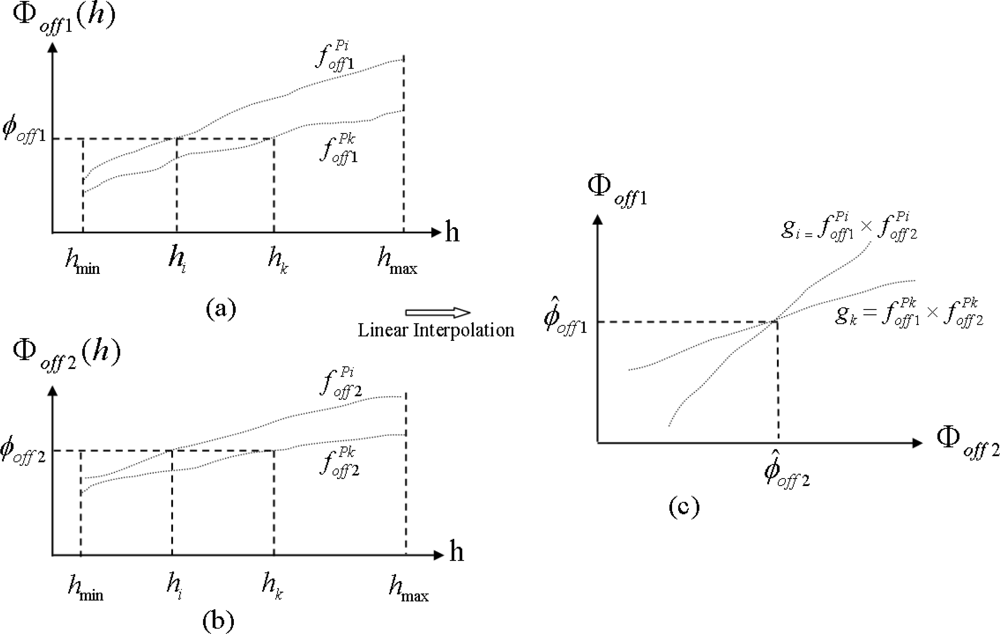
• - Finally, as the CPOFs g_i and g_k are generated using the same height interval in different range positions, represented in the space Φ_{off 1} × Φ_{off 2}, they have different angular coefficients, ensuring an intersection point between them, from where the phase-offset values for both acquisitions can be estimated, as illustrated in Figure 4. The coordinates of the intersection point in Φ_{off 1} × Φ_{off 2}, shown in Figure 4(c), represent the estimate values of the phase-offset for the first acquisition, ϕ̂_{off 1}, and for the second acquisition, ϕ̂_{off 2}.

In order to get an accurate estimation of the phase-offset values, instead of two points, a set of points in the overlapped area, with different range positions, can be used to produce a set of CPOFs in the space Φ_{off 1} × Φ_off, with a common intersection point. Due to noise presence in the interferometric unwrapped phase, or to abrupt variation of the phase, the common point of the intersection is not unique but has a cluster of points, very close together, from where the phase-offset values can be estimated.

3. Processing Sequence

Figure 5 shows the processing sequence used to estimate the phase-offset values of the two overlapped acquisitions. The interferometric unwrapped phase images ϕ_unw1 and ϕ_unw2 are filtered in three steps. Firstly, they are filtered, based on a coherence threshold from Coh₁ and Coh₂ images, respectively, to discard points with low coherence—the threshold value is an input parameter which should be chosen according to the characteristics of the terrain and the acquisition; this filter is crucial to improve the accuracy of the estimation. Secondly, a morphological erosion filter [15] is applied on the interferometric unwrapped phases to discard very small regions in order to decrease the disrupting effects during the POF generation. Finally, an average filter with window size fixed according to the image resolution is used to reduce phase noise on the interferometric unwrapped phase images. To gain computation time, only boxes around the points of interest are filtered. After the filtering steps, the positions of the set of points in the overlapped area are selected to carry out the generation of the POFs.

To illustrate the processing step that generates the POFs shown in Figure 5, a processing sequence was performed in a pair of the InSAR data gathered by the OrbiSAR-1 X-band system shown in Figure 6. The generation of the POFs f₁ and f₂ for a selected point in the overlapped area, shown in Figure 5, is based on the approach previously described and represented by Equations (17) and (18); in the next step of the processing chain, the POFs are combined through a linear combination, creating a CPOF g_comb in the space Φ_{off 1} × Φ_{off 2}.

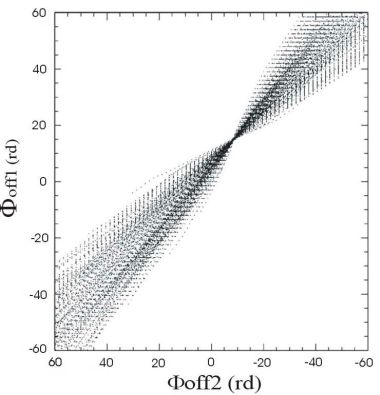
Carrying out the same operations for a set of points in the overlapped area, a set of functions g_comb can be created from where the intersection point can be estimated. Figure 7 shows the set of CPOF for 100 points scanned in the overlapped area in a height interval [h_max − h_min] equal to 200 m, based on the knowledge of the terrain topography from the SRTM DEM data, and a height step δ_h equal to 2 m.

The CPOFs have a linear behavior close to the intersection point. However, disturbing effects related to noise, terrain irregularities and the presence of range waves [16], among others, can make the offset-functions have a non-linear behavior. To avoid the use of the disrupted functions, a filter based on the linearity of the function g_comb (Figure 5) was introduced. This filter performs a linear approximation of the curves and uses the chi-square goodness of fit statistics [17] to decide which ones will be used for the estimation and which ones will be discarded.

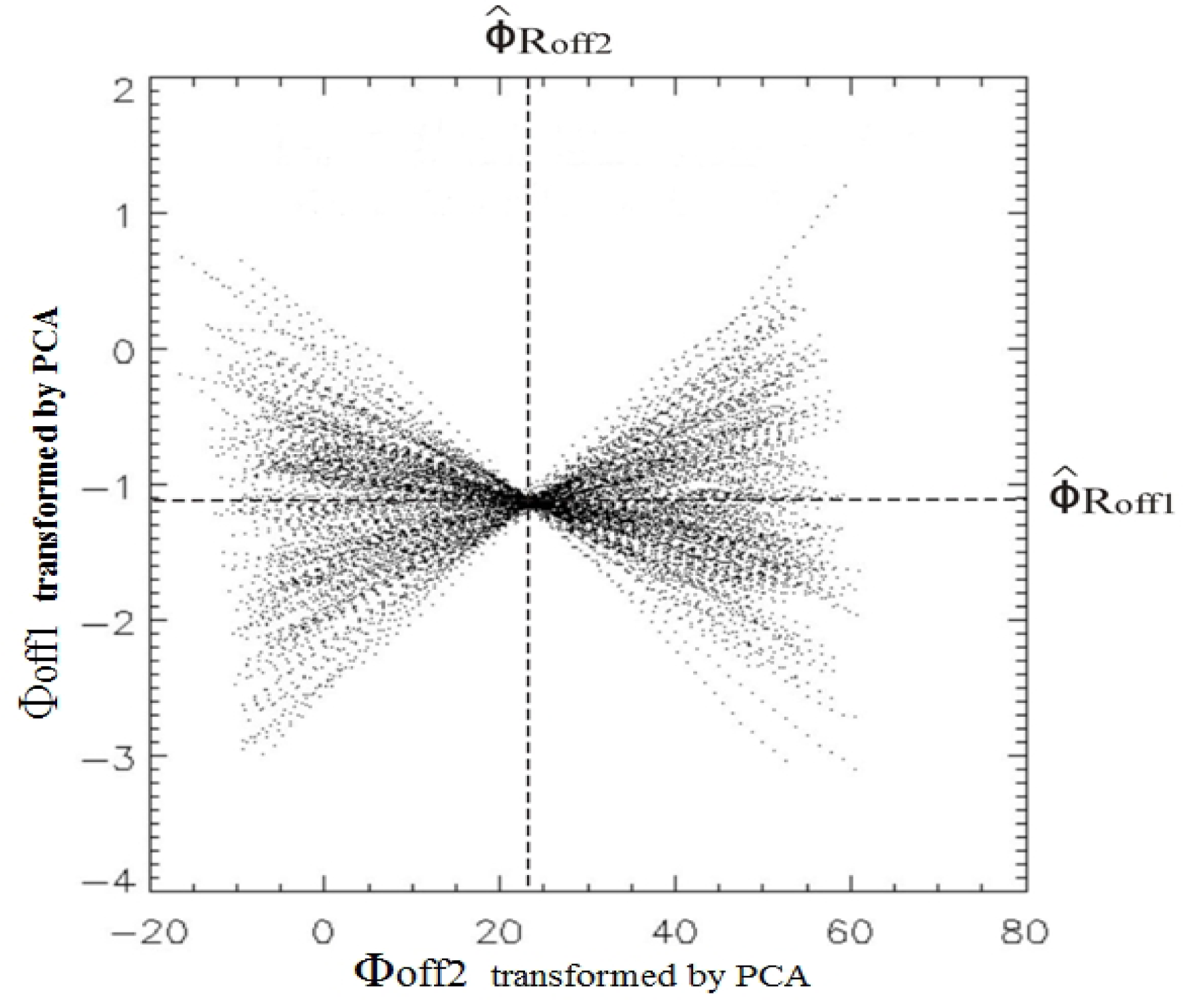
In order to make it easier to determine the intersection point of the CPOFs, the CPOFs are rotated using the Principal Components Analysis (PCA) [18], which is a mathematical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables, in this case the set of CPOFs g_comb, into a set of values of uncorrelated variables called Principal Components.

Figure 8 shows the CPOFs transformed by PCA. We can notice that PCA uncorrelates the functions, causing a spread and rotation of the g_comb functions, allowing an easy determination of the crossing point by finding the minimum dispersion value of these transformed functions on the horizontal axis, from where the transformed phase-offset values can be determined. Finally, the transformed phase-offset values are transformed back using the Principal Components Coefficients, providing an estimation of the phase-offset values for both acquisitions, ϕ̑_{off 1} and ϕ̑ _{off 2}. From these estimated phase-offset values, the absolute interferometric phase for both acquisitions can be determined by using the Equation (1).

This method works basically in two iterations. Firstly, the coarse phase-offsets values are estimated using a height interval [h_max − h_min] and a height step δ_h, according to the knowledge of the terrain mean height from the SRTM DEM data. Secondly, the coarse phase-offsets estimated values, ϕ̑_{off 1} and ϕ̑ _{off 2} (Figure 5) are used to decrease the height interval and the height step for the second iteration to allow a fine estimation. In some cases, a third iteration can be tried to improve the estimation. For each iteration the accuracy of the phase-offset values can be evaluated through the root mean square error between the DEMs in the overlapped area, ɛ_DEM12, of both acquisitions (Figure 5), which should be very small when the phase-offset values are well estimated.

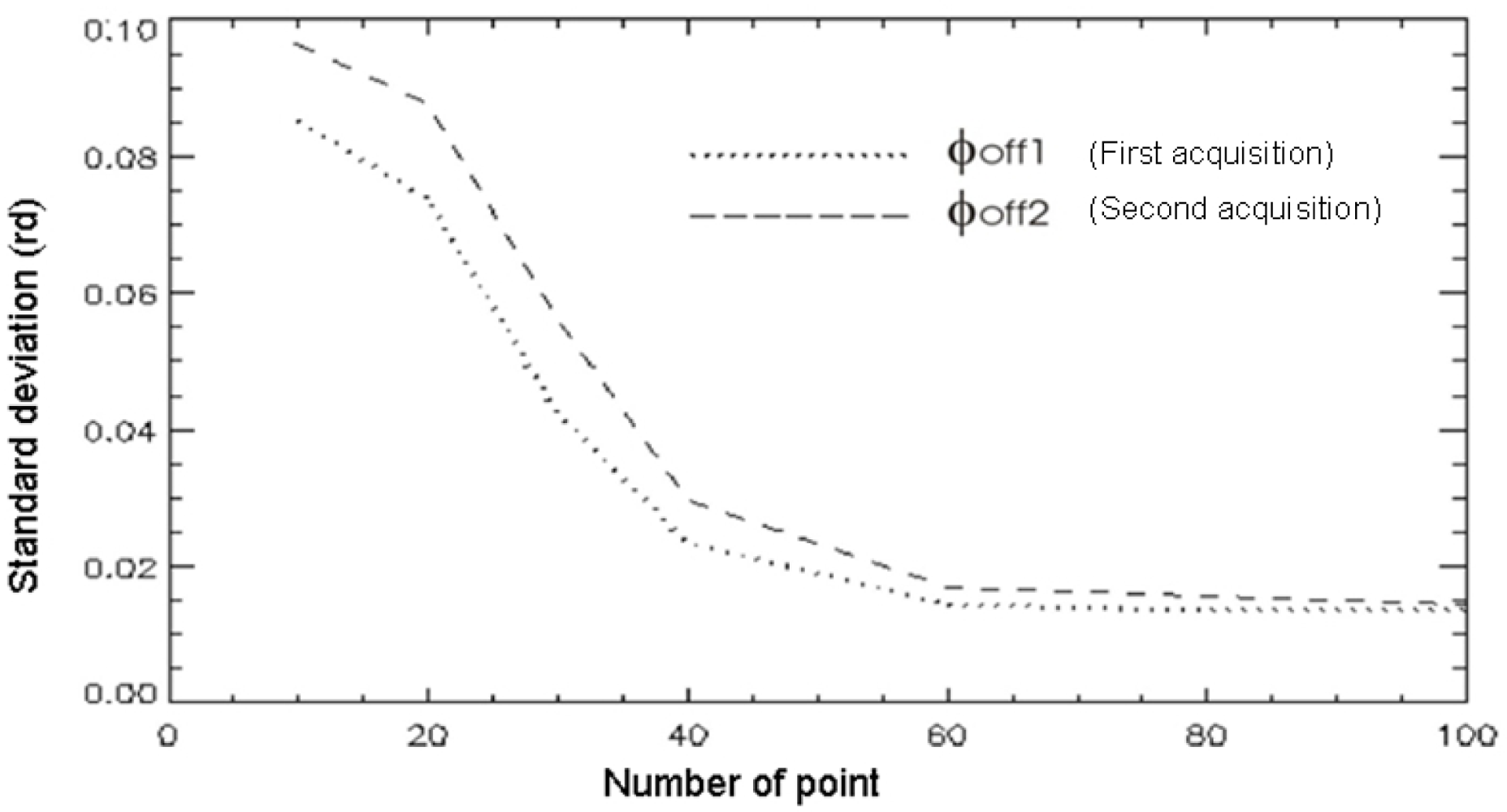
An important issue regarding the accuracy of the phase-offset estimation using the proposed method, is the number of points selected in the overlapped area used to build up the POFs. A statistical simulation using points randomly distributed in the overlapped area showed that the phase-offset values become stable after 60 points, as shown in Figure 9. This simulation was performed using a pair of unwrapped interferograms shown in Figure 6, whose area is characterized by hills and vegetation, presenting a diversity of coherence values.

The performance of the proposed method regarding the size of the overlapped area in range direction was checked by changing the overlap percentage in a range direction, varying from 20% to 90% of the swath width. For each fixed percentage, the algorithm was executed ten times. For each execution, the points used by the algorithm were randomly distributed in the overlapped area within a fixed range. The phase-offset mean values and standard deviations for the X-band of the first acquisition for each fixed percentage used are shown in

Table 1. Performance regarding the percentage of the area used in range direction.

Phase-offset	Percentage of Overlapped the Area in Range Direction
	20	30	40	50	60	70	80	90
Mean value [rd]	1.05	0.97	0.98	0.99	0.99	0.97	0.99	1.00
Std. dev. [rd]	0.06	0.04	0.03	0.03	0.03	0.03	0.02	0.05

.

It can be noted from Table 1 that the performance of the method regarding the percentage used is quite robust; percentages lower than 40% and higher than 80% present a slightly larger standard deviation. We noticed that for percentages less than 30%, the incident angle diversity is low, generating the intersection of noisy CPOFs. For percentage greater than 80% the disrupting effects in the POFs were more pronounced due to the presence of residual undulations in far range regions of the interferograms, caused by the receiving of delayed signal components from multiple reflections [16], thus decreasing the accuracy of the estimation. The flight configuration should be planned to ensure that the overlapped area in range direction is within the percentage interval of 40% to 80%, corresponding to an incidence angle difference between the two acquisitions of 9 to 21 degrees, ensuring an incidence angle diversity to give the necessary angular coefficient to the POFs, allowing an easier determination of the crossing point for the estimates of the phase-offset values.

4. Results and Discussion

The presented method validation was carried out in a test site area in the south-west of Brazil, Cachoeira Paulista, São Paulo state, using data from the OrbiSAR-1 system in X- and P-bands, with the parameters shown in

Table 2. OrbiSAR-1 System-flight parameters.

Parameter	Band
	X	P
Wavelength (λ) [m]	0.031228	0.713791
Flight altitude (H) [Km]	5.6	5.6
Incident angle (θ)—mid swath [deg]	50	50
Normal Baseline (Bn)—mid swath [m]	2.16	35.3
Swath width [Km]	7.0	7.0
Chirp bandwidth [MHz]	200	50
DEM spatial resolution [m]	2.0	2.0

. Four corner reflectors were deployed to the test site area to provide an accurate phase-offset estimation, which was used as a reference.

To evaluate the performance of the presented method, firstly, the corner reflectors were used to estimate the phase-offset values, followed by the absolute phase determination and the DEM generation for X- and P-bands. The same procedure was performed using the proposed method to estimate the phase-offset values, considering an overlapped area of approximately 60% of the swath width and a coherence threshold of 0.6 for X-band and 0.5 for P band. About 80 points randomly distributed in the overlapped area were used to build up the POFs in this estimation. The DEMs and geocoded images were generated with a spatial resolution of 2 m. Figure 10 shows part of the geocoded images and DEMs of X-band and P-band, generated by using the phase-offset values estimated with the proposed method.

The quality of the results regarding the estimate of the phase-offset values, the first based on corner reflectors at the scene and the second based on the proposed method, are presented in

Table 3. Phase-offset error between the two phase-offset estimation methods.

Statistics	Phase-Offset Value Difference (Corner Reflector–Proposed Method)
	X-band	P-band
Mean difference [rd]	0.047	0.051
Std. dev. [rd]	0.0152	0.0191

, showing that both methodologies provide quite close results. In this analysis, the phase errors induced by the temporal, baseline and volume decorrelation were not considered, since the contribution of these phase errors was embedded on the grid of unwrapped phase used in both methods.

The X-band and P-band DEMs generated with both phase-offset estimation methods were evaluated in 16 GCPs measured with GPS survey: the results are shown in

Table 4. DEM error in relation to 16 GCPs in the test site area measured with GPS survey.

Statistics Using 16 GCPs	Phase-Offset Estimation
	Corner Reflectors		Proposed Method
	X-Band DEM Difference	P-Band DEM Difference	X-Band DEM Difference	P-Band DEM Difference
Mean: μh [m]	1.1127	0.7641	1.1378	0.8265
Std. dev.: σh [m]	1.4720	0.6999	1.4709	0.7094

. The results in terms of mean and standard deviation are quite similar for both bands and methods used, showing that the proposed method for phase-offset estimation is a reliable automatic tool for generating accurate DEMs based on SAR interferometry.

The results shown in Table 4 reinforce the results presented in Table 3, where quite similar phase-offset values found with the two methods collaborate to generate quite similar DEMs. It can be noted from Table 4 that despite the fact that corner reflectors can provide the best phase-offset estimation, the DEMs from X- and P-band present errors when compared to GCPs. That could be explained from phase error mentioned before, which is not evaluated in the present work. In Table 4 we also notice that the mean difference and the standard deviation regarding the 16 GCPs for X-band are greater than those for P-band; this can be explained by the fact that the DEM generation process is more affected in vegetated areas, which is more pronounced for X-band data due to its low penetration into the vegetation.

4.1. Error Analysis

The height derived from the interferometric phase is very sensitive to phase errors. According to [19], the height error is related to phase error by:

$${\sigma }_h^{\theta }(m)=\frac{\lambda \hspace{0.17em}\hspace{0.17em}r\text{sin}\theta }{4\pi B_n}{\sigma }_{\varphi \hspace{0.17em}u}$$

(21)

where σ_ϕu is the phase uncertainty, B_n is the normal baseline, θ the incident angle, r the slant range distance and λ the wavelength.

The standard phase error and the phase uncertainty with 95% of confidence level, according to [17], are given respectively by:

$${\sigma }_{\varphi \hspace{0.17em}e}(rd)=\hspace{0.17em}{\sigma }_{\varphi }/\sqrt{N}$$

(22)

and

$${\sigma }_{\varphi \hspace{0.17em}u}(rd)\hspace{0.17em}=\hspace{0.17em}{\mu }_{\varphi }\hspace{0.17em}\pm \hspace{0.17em}2.0\hspace{0.17em}\times {\sigma }_{\varphi \hspace{0.17em}e}$$

(23)

where σ_ϕ is the standard deviation of the interferometric phase, N is the number of measurement and μ_ϕ is the mean phase error.

Table 5. Statistics regarding the phase-offset estimation error of the proposed method for X- and P-band.

Parameters and Statistics	Band
	X	P
Wavelength: (λ) [m]	0.0313918	0.713791
Measurement (GCPs) : (N)	16	16
Mean phase error : μϕ [rd]	0.0470	0.0510
Phase Std. dev. σϕ [rd]	0.0152	0.0191
Phase uncertainty (95%): Max(|σϕu|) [rd]	0.0508	0.0558
Mean height error: μh[m]	0.327	0.702
Height Std. dev. σh [m]	0.059	0.203
Height uncertainty (95%): Max(|σhu|) [m]	0.445	1.108

shows the height error regarding the phase-offset estimation difference between the two methods, with corner reflectors and with the presented method, shown in Table 3, considering that the estimation using the previous method leads to the best estimation. Taking into account only the phase-offset estimation error of this proposed method, leads to a height uncertainty of around 0.5 m for X-band and 1.1 m for P-band, with a 95% confidence level, as shown in the last row of Table 5 for the test carried out in Cachoeira Paulista.

4.2. Test Result without Using Corner Reflectors

The advantage of not using corner reflectors (GCPs) to estimate the phase-offset values on forested areas is tremendous. Dispensing the reflectors can lead not only to lower costs but it can also diminish the environmental impact associated with corner reflector deployment. In certain regions, like the dense Amazon forest or in fluvial regions, access to appropriate areas to deploy the reflectors can be difficult. Based on that, a test was performed in the Amazon rainforest area characterized by quite flat relief, without the use of corner reflectors. Several tracks were flown so that they crossed each other to compute the DEM difference in the intersection areas. The data were acquired with the same characteristics shown in Table 2. The phase-offset values were estimated using an overlapped area of approximately 50% of the swath width, where about 100 points randomly distributed in this overlapped area were used to build up the POFs for the phase-offset estimations. The coherence threshold used to select points was 0.6 for X-band and 0.5 for P-band. The DEM of X-band and P-band were generated with a spatial resolution of 2.5 m. The goal of this test was to verify if the phase-offset values would be well estimated for each track, enabling the generation of quite similar DEMs on the intersection areas. 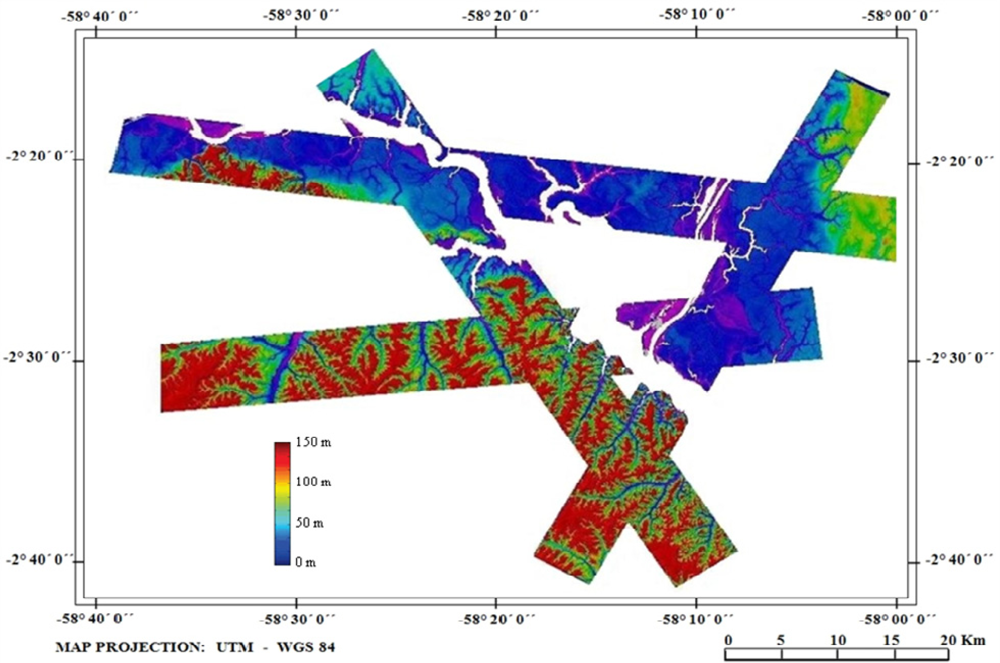Figure 11 shows the X-band DEMs of the tracks in color scale.

Table 6. Computed statistics between the DEMs in the intersection areas of all tracks.

Computed Statistics between the DEMs	DEM
	X-Band	P-Band
Mean value of the difference: μDEM[m]	0.520	0.640
Std. dev. of the difference: σDEM [m]	3.170	2.520
Std. dev. of the range slope: σrg [m]	0.003	0.360
Std. dev. of the azimuth slope: σaz [m]	0.008	0.310
Height standard error: σhe [m]	1.124	1.127
Height uncertainty (95%): Max(|σhu|) [m]	2.768	2.904

shows the computed statistics between the DEMs for X-band and P-band in the intersection areas of all tracks. It can be noted from Table 6 that the mean value differences are small for both bands, while the standard deviations have significant values, caused mainly by the high variation in the DEMs due to the forest structure, aggravated by the different looking angles in the intersection areas; this is more pronounced for X-band due to its low penetration into the forest, which makes it more susceptible to canopy variation. The standard deviations of the slope in range and azimuth directions were quite small for both bands. The estimates of height uncertainty at the 95% confidence level were around 3 m for both bands. In this computed statistics, all phase errors that contribute to lower the accuracy of DEMs were taken into account.

5. Conclusions

The method for phase-offset estimation, based on phase-offset functions presented in this work, has good potential for operational application, as it does not require the presence of GCP or a priori information, and at the same time is able to provide the accuracy requested for DEM generation.

The results presented in Table 3 and Table 4 using OrbiSAR-1 data show that the estimation of the phase-offset values generated quite similar results to those produced through the use of the corner reflectors, for X-band and P-band, indicating that the phase-offset estimation can be automatically done, leading to a lower cost and a faster estimation. Taking into account only the phase-offset estimation error, shown in Table 3, the height uncertainty regarding this error, shown in Table 5, indicates that the generation of X-band and P-band DEMs could be carried out in the scale of up to 1:5,000 m, according to [20].

The potential for mapping rainforest area was checked and the results are presented in Table 6, indicating that the proposed method can provide reliable phase-offset estimation to generate X-band and P-band DEMs in the scale of up to 1:12,000 m, with a vertical accuracy at the 95% confidence level equal to 2.768 m for X-band and 2.904 m for P-band.

The results presented in Tables 5 and 6 show that P-band has a somewhat larger height uncertainty than X-band, caused probably by the different scatter center positions of the pixels for the two acquisitions, since the penetration of the microwaves in the vegetation changes according to the incidence angle, which is more pronounced for P-band, increasing the error in estimating the sphase-offset values.