A New Algorithm for the Satellite-Based Retrieval of Solar Surface Irradiance in Spectral Bands
Abstract
:1. Introduction
2. Outline of the Method for the Retrieval of Spectrally Resolved Irradiance
3. Clear Sky Approach for the Retrieval of Spectrally Resolved Irradiance
3.1. Basis LUT: Treatment of Aerosols
3.2. Treatment of Water Vapor and Ozone Variations
3.3. Treatment of Surface Albedo
3.4. Sensitivity on Atmospheric Background Profiles
3.5. Summary of Clear Sky Approach
4. All Sky Approach for the Retrieval of Spectrally Resolved Irradiance
4.1. Retrieval of Effective Cloud Albedo
4.2. Spectral Correction of Cloud Effect
4.3. Used Input on the Atmospheric State
5. Irradiance on a Tilted Surface
6. Validation of the Retrieved Spectral Solar Surface Irradiance
6.1. Measurements of the Solar Spectral Surface Irradiance
6.2. Validation Results
7. Discussion
8. Conclusions
Acknowledgments
References
- Schmetz, J.; Pili, Tjemkes, P.S.; Just, D.; Kerkmann, J.; Rota, S.; Ratier, A. An introduction to Meteosat Second Generation (MSG). Bull. Am. Met. Soc 2002, 83, 977–992. [Google Scholar]
- GCOS, The Second Report on the Adequacy of the Global Observing Systems for Climate in Support of the UNFCCC; Vol. Rep. GCOS-82; WMO: Geneva, Switzerland, 2003.
- Woick, H.; Dewitte, S.; Feijt, A.; Gratzki, A.; Hechler, P.; Hollmann, R.; Karlsson, K.G.; Laine, V.; Loewe, P.; Nitsche, H.; et al. The satellite application facility on climate monitoring. Adv. Space Res 2002, 30, 2405–2410. [Google Scholar]
- Schulz, J.; Albert, P.; Behr, H.; Caprion, D.; Deneke, H.; Dewitte, S.; Dürr, B.; Fuchs, P.; Gratzki, A.; Hechler, P.; et al. Operational climate monitoring from space: The EUMETSAT satellite application facility on climate monitoring (CM-SAF). Atmos. Chem. Phys. Discuss 2008, 8, 8517–8563. [Google Scholar]
- Babst, F.; Mueller, R.; Hollmann, R. Verification of NCEP reanalysis shortwave radiation with mesoscale remote sensing data. IEEE Geosci. Remote Sens. Lett 2008, 5, 34–37. [Google Scholar]
- Perez, R.; Renne, D.; Seals, R.; Zelenka, A. The strengths of satellite based solar resource assessment. In Production of Site/Time-Specific Irradiances from Satellite and Ground Data; Report 98-3. New York State Energy Research and Development Authority: Albany, NY, USA, 1998. [Google Scholar]
- Möser, W.; Raschke, E. Incident solar radiation over Europe estimated from METEOSAT data. J. Climate Appl. Meteor 1984, 23, 166–170. [Google Scholar]
- Cano, D.; Monget, J.; Albuisson, M.; Guillard, H.; Regas, N.; Wald, L. A method for the determination of the global solar radiation from meteorological satellite data. Solar Energy 1986, 37, 31–39. [Google Scholar]
- Bishop, J.K.B.; W.B.R. Spatial and temporal variability of global surface solar irradiance. J. Geophys. Res 1991, 96, 839–858. [Google Scholar]
- Pinker, R.; Laszlo, I. Modelling surface solar irradiance for satellite applications on a global scale. J. Appl. Meteor 1992, 31, 166–170. [Google Scholar]
- Darnell, W.; Staylor, W.; Gupta, S.; Ritchey, N.; Wilber, A. Seasonal variation of surface radiation budget derived from ISCCP-C1 data. J. Geophys. Res 1992, 97, 15741–15760. [Google Scholar]
- Rigolier, M.; Levefre, M.; Wald, L. The method Heliosat-2 for deriving shortwave solar radiation from satellite images. Solar Energy 2004, 77, 159–169. [Google Scholar]
- Mueller, R.; Matsoukas, C.; Gratzki, A.; Hollmann, R.; Behr, H. The CM-SAFoperational scheme for the satellite based retrieval of solar surface irradiance—A LUT based eigenvector hybrid approach. Remote Sens. Environ 2009, 113, 1012–1022. [Google Scholar]
- Hammer, A.; Heinemann, D.; Hoyer, C.; R., K.; Lorenz, E.; Mueller, R.; Beyer, H. Solar Energy Assessment Using Remote Sensing Technologies. Remote Sens. Environ 2003, 86, 423–432. [Google Scholar]
- Posselt, R.; Mueller, R.; Stöckli, R.; Trentmann, J. Spatial and temporal homogeneity of solar surface irradiance across satellite generations. Remote Sens 2011, 3, 1029–1046. [Google Scholar]
- Stammes, K.; Tsay, S.; Wiscombe, W.; Jayaweera, K. Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media. Appl. Opt 1988, 27, 2502–2509. [Google Scholar]
- Mayer, B.; Kylling, A. Technical note: The libRadtran software package for radiative transfer calculations—Description and examples of use. Atmos. Chem. Phys 2005, 5, 1855–1877. [Google Scholar]
- Koepke, P.; Bais, A.; Balis, D.; Buchwitz, M.; de Backer, H.; de Cabo, X.; Eckert, P.; Eriksen, P.; Gillotay, D.; Koskela, T.; Lapeta, V.; Litynska, Z.; Lorente, J.; Mayer, B.; Renauld, A.; Ruggaber, A.; Schauberger, G.; Seckmeyer, G.; Seifert, P.; Schmalwieser, A.; Schwander, H.; Vanicek, K.; Weber, M. Comparison of models used for UV index calculations. Photochem. Photobiol 1998, 67, 657–662. [Google Scholar]
- Mayer, B.; Seckmeyer, G.; Kylling, A. Systematic long-term comparison of spectral UV measurements and UVSPEC modeling results. J. Geophys. Res 1997, 102, 8755–8767. [Google Scholar]
- Kato, S.; Ackerman, T.; Mather, J.; Clothiaux, E. The k-distribution method and correlated-k approximation for a short-wave radiative transfer. J. Quant. Spectrosc. Radiat. Transfer 1999, 62. [Google Scholar]
- Mueller, R.; Trentmann, J.; Träger-Chatterjee, C.; Posselta, R.; Stöckli, R. The Role of the Effective Cloud Albedo for Climate Monitoring and Analysis. Remote Sens 2011, 3, 2305–2320. [Google Scholar]
- Mueller, R.; Dagestad, K.; Ineichen, P.; Schroedter-Homscheidt, M.; Cros, S.; Dumortier, D.; Kuhlemann, R.; Olseth, J.; Piernavieja, G.; Reise, C.; Wald, L.; Heinemann, D. Rethinking satellite based solar irradiance modelling. The SOLIS clear-sky module. Remote Sens. Environ 2004, 91, 160–174. [Google Scholar]
- Ineichen, P. Comparison of eight clear sky broadband models against 16 independent data banks. Solar Energy 2006, 80, 468–478. [Google Scholar]
- Shettle, P.; Fenn, R.W. Models of the Atmospheric Aerosols and Their Optical Properties. AGARD Conference Proceedings No. 183, Optical Propagation in the Atmosphere, Lyngby, Denmark; 1976. [Google Scholar]
- Shetlle, E. Models of Aerosols, Clouds and Precipitation for Atmospheric Propagation Studies. AGARD Conference Proceedings No. 454, Atmospheric Propagation in the UV, Visible, IR and MM-Wave Region and Related Systems Aspects, Copenhagen, Denmark, 9–13 October 1989.
- Lenoble, J. Modeling of the influence of snowreflectance on ultraviolet irradiance for cloudless sky. Appl. Opt 1998, 37, 2441–2447. [Google Scholar]
- Loveland, T.R.; Belward, A.S. The IGBP-DIS Global 1 km Land Cover Data Set, DISCover first results. Int. J. Remote Sens 1997, 18, 3289–3295. [Google Scholar]
- Brown, J.F.; Loveland, T.; Merchant, J.W.; Reed, B.C.; Ohlen, D.O. Using multi-source data in global land-cover characterization: concepts, requirements, and methods. Photogramm. Eng. Remote Sensing 1993, 59, 977–987. [Google Scholar]
- Dickinson, R.E. Land surface processes and climate—Surface albedos and energy balance. Adv. Geophys 1983, 25, 305–353. [Google Scholar]
- Lindfors, A.; Arola, A. On the wavelength-dependent attenuation of UV radiation by clouds. Geophys. Res. Lett 2008, 35, L05806. [Google Scholar]
- Kinne, S.; Schulz, M.; Textor, C.; Guibert, S.; Balkanski, Y.; Bauer, S.E.; Berntsen, T.; Berglen, T.F.; Boucher, O.; Chin, M.; et al. An AeroCom initial assessment—Optical properties in aerosol component modules of global models. Atmos. Chem. Phys 2006, 6, 1815–1834. [Google Scholar]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanré, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ 1998, 66, 1–16. [Google Scholar]
- Hess, M.; Koepke, P.; Schult, I. Optical properties of aerosols and clouds: The software package OPAC. Bull. Amer. Meteor. Soc 1998, 79, 831–844. [Google Scholar]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Amer. Meteor. Soc 1996, 77, 437–471. [Google Scholar]
- Dee, D.P.; Uppala, S. Variational bias correction of satellite radiance data in the ERA-interim reanalyis. Q. J. Roy. Meteor. Soc 2009, 135, 1830–1841. [Google Scholar]
- Betts, A.K.; Ball, J.H.; Bosilovich, M.; Viterbo, P.; Zhang, Y.; Rossow, W.B. Intercomparison of water and energy budgets for five Mississippi subbasins between ECMWF re-analysis (ERA-40) and NASA Data Assimilation Office fvGCM for 1990–1999. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Ziemke, J.R.; Chandra, S.; Labow, G.J.; Bhartia, P.K.; Froidevaux, L.; Witte, J.C. A global climatology of tropospheric and stratospheric ozone derived from Aura OMI and MLS measurements. Atmos. Chem. Phys 2011, 11, 9237–9251. [Google Scholar]
- Klucher, T. Evaluation of models to predict insolation on tilted surfaces. Solar Energy 1979, 23, 111–114. [Google Scholar]
- Temps, R.C.; Coulson, K.L. Solar Radiation Incident Upon Slopes of Different Orientations. Solar Energy 1977, 19, 179–184. [Google Scholar]
- Drews, A.; Beyer, H.; Rindelhardt, U. Quality of performance assessment of PV plants based on irradiance maps. Solar Energy 2008, 82, 1067–1075. [Google Scholar]
Appendix
Meaning of Eigenvector Approach
Applied Error Measures

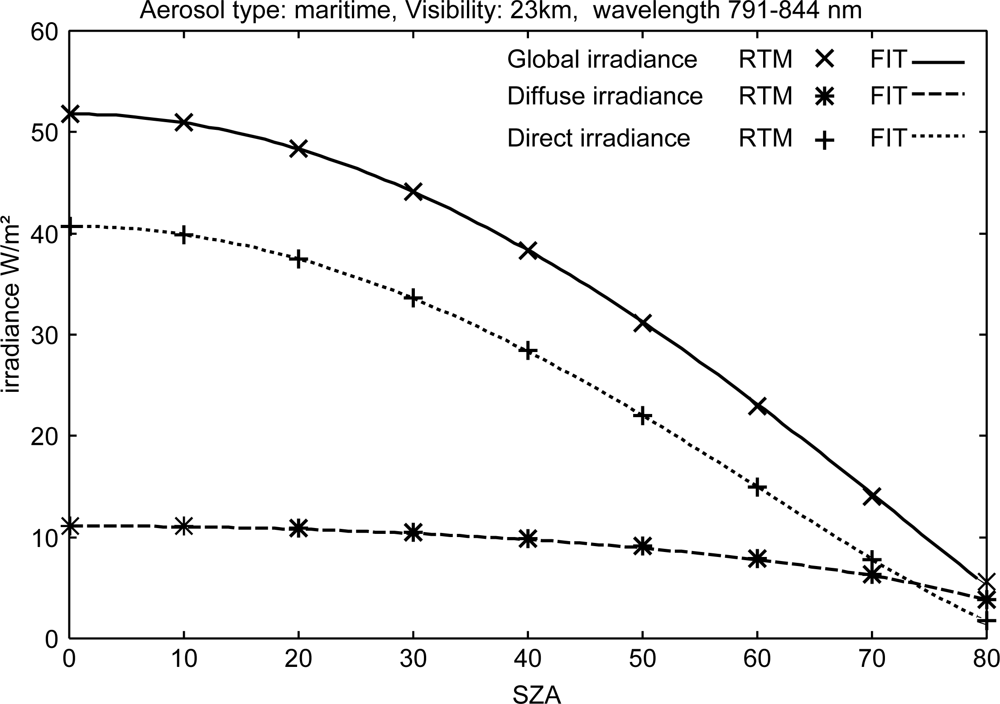
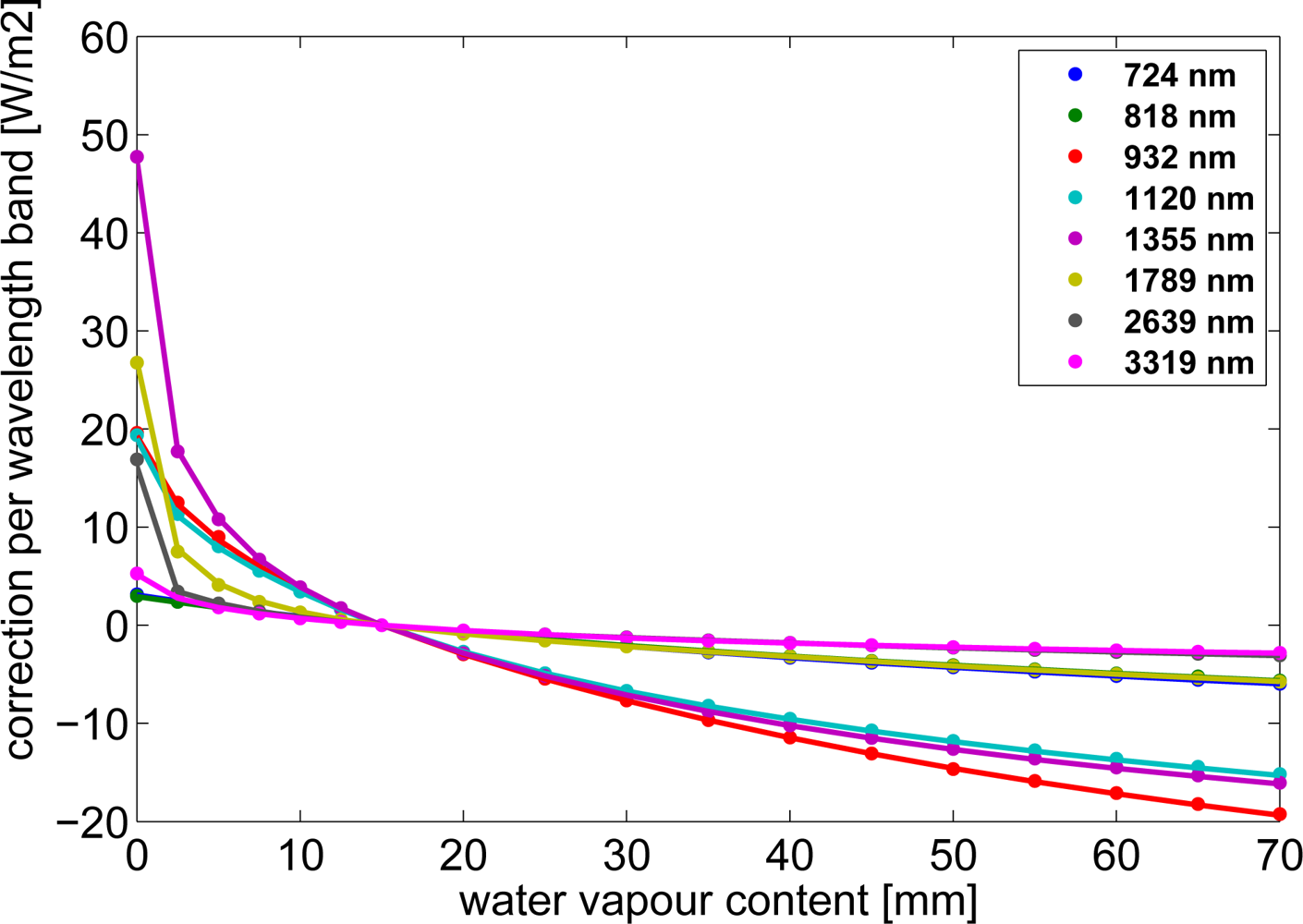
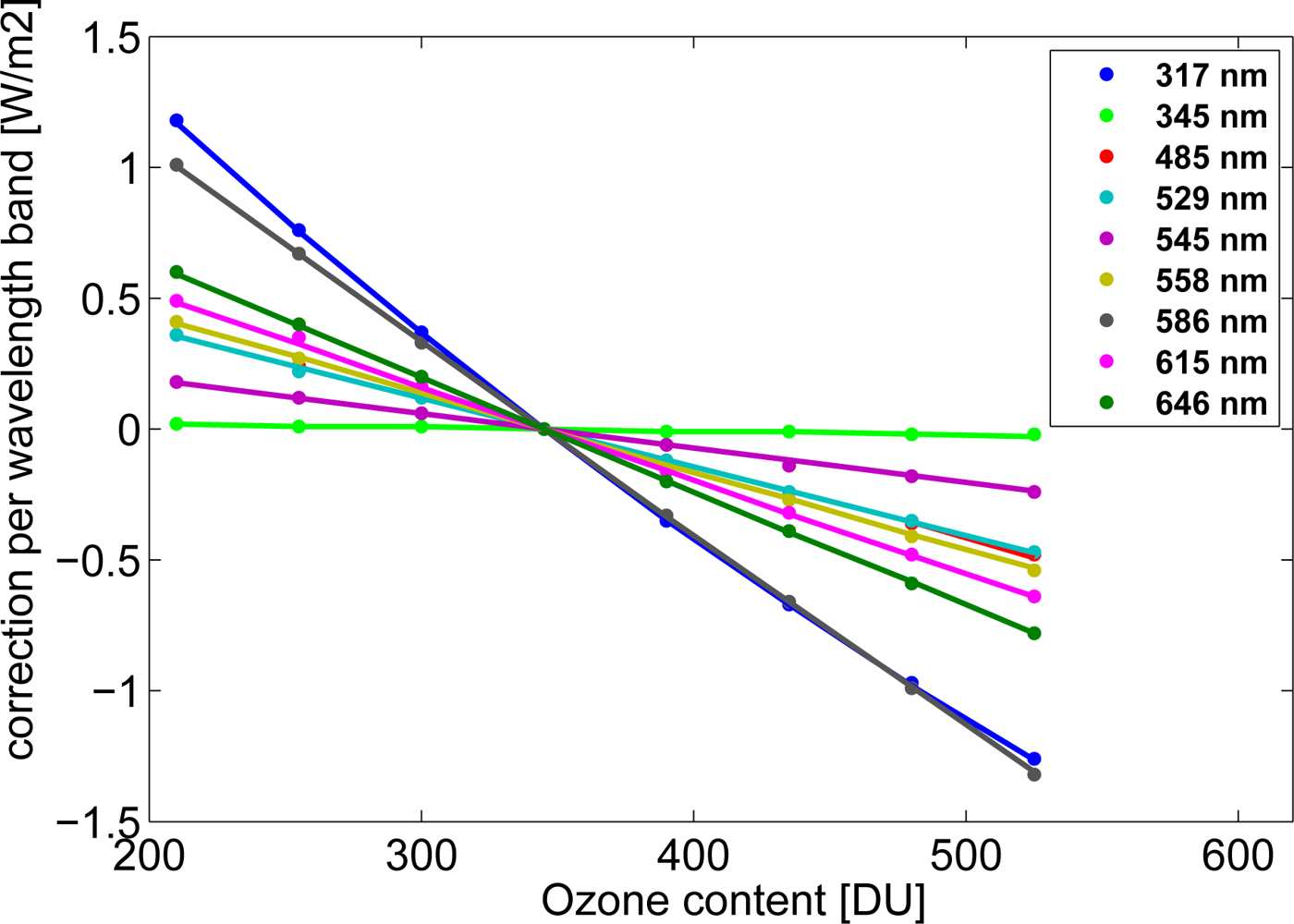
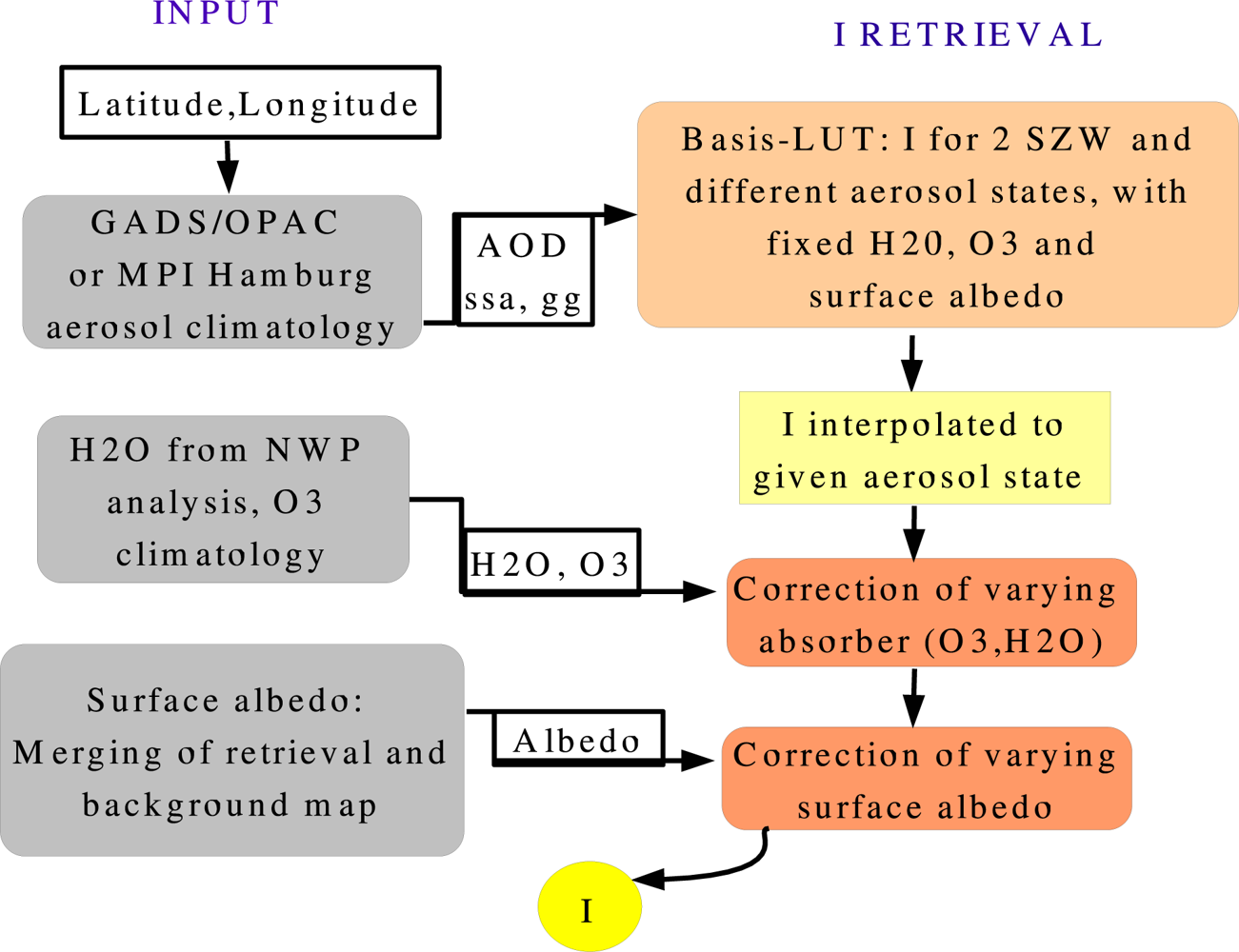
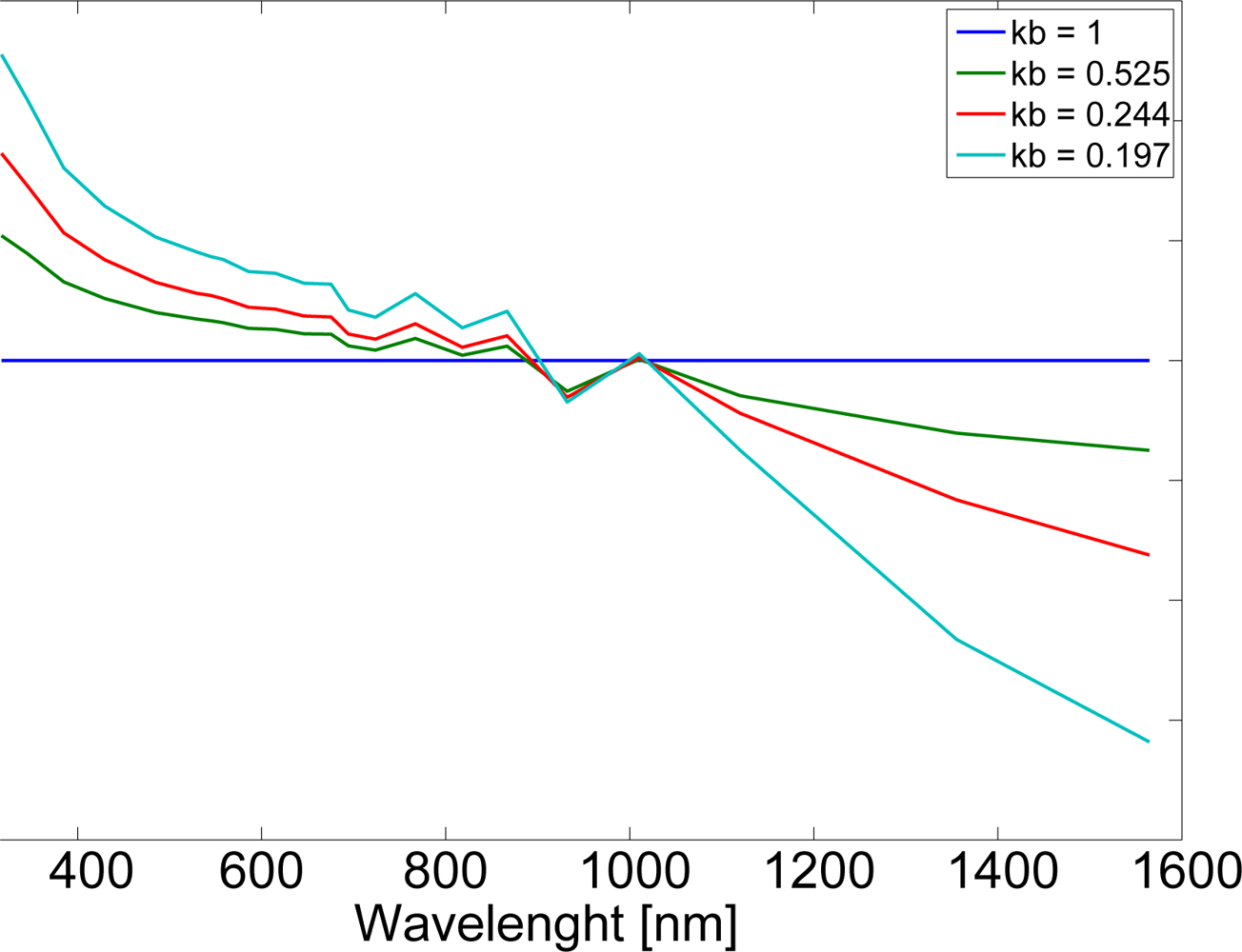
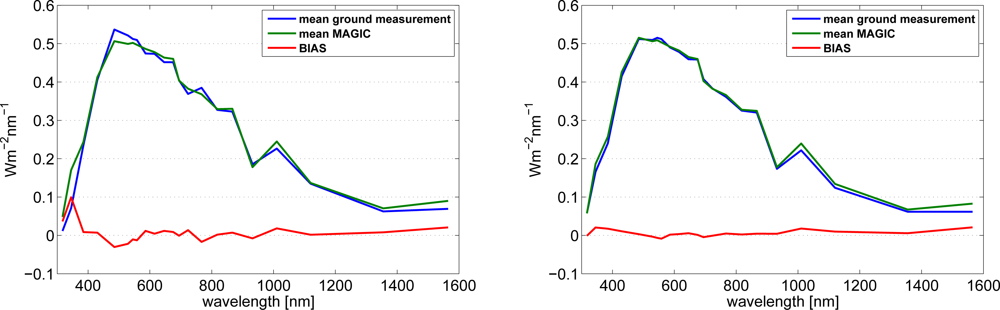

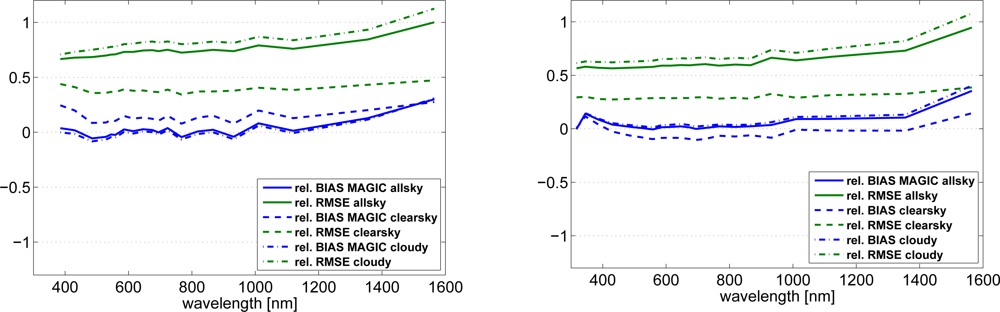


| Katoband Λ[nm] | Width [nm] | Deviation Relative to RTM [W/m2/band] | Dito [W/m2/nm] | |
|---|---|---|---|---|
| 724 | 38.2 | IΛ | −0.74 | −0.019 |
| 932 | 86.0 | IΛ | −2.11 | −0.025 |
| 1,335 | 321.8 | IΛ | −0.73 | −0.0023 |
| 932 | 86.0 | BΛ | −1.93 | −0.022 |
| Katoband Λ[nm] | Width [nm] | Deviation Relative to RTM [W/m2/band] | Dito [W/m2/nm] | |
|---|---|---|---|---|
| 317 | 20.9 | IΛ | −0.19 | −0.0091 |
| 586 | 38.4 | IΛ | −0.20 | −0.0052 |
| 646 | 41.7 | IΛ | −0.09 | −0.0022 |
| 317 | 20.9 | BΛ | −0.028 | −0.0013 |
| 646 | 41.7 | BΛ | −0.12 | −0.0028 |
| Parameter | RTM Runs broadband prototype | RTM Runs broadband new concept | RTM Runs 32 spectral bands new concept | Method |
|---|---|---|---|---|
| Background atmosphere | 5 | 1 | 1 | RIA |
| Aerosol AOD and type | ×10 × 8 | ×10 × 3 × 2 | ×23 × 3 × 2 | ssa and gg instead of 8 types |
| SZA | ×8 | ×2 | ×2 | MLB function |
| H2O, O3 | ×10 × 5 | +10 +3 | +18 +8 | parameterization |
| SAL | ×8 | +0 | +0 | parameterization |
| Totel number | 1,280,000 | 133 | 302 |
| Dataset | Loughborough | Stuttgart |
|---|---|---|
| Location | 52.77°N, −1.23°E | 48.75°N, 9.11°E |
| Provided by | CREST, Loughborough University | IPE, Stuttgart University |
| Period | Sep 2003–Aug 2004 | 2008 |
| Apparatus | Horiba, custom build | Stellarnet EPP 2000C UV-VIS, EPP 2000 NIR INGAS |
| Temporal resolution | 2 min scan, every 10 min | 1 min scan every min., delivered as 15 min average |
| Spectral resolution | 10 nm | 1 nm |
| Spectral range | 300 to 1,700 nm | 300 to 1,700 nm |
| Orientation | 20° East | South |
| Tilt | 52° | 33° |
| Completeness original data | 40% | 98% |
| Completeness hourly data | 35% | 97% |
Share and Cite
Mueller, R.; Behrendt, T.; Hammer, A.; Kemper, A. A New Algorithm for the Satellite-Based Retrieval of Solar Surface Irradiance in Spectral Bands. Remote Sens. 2012, 4, 622-647. https://doi.org/10.3390/rs4030622
Mueller R, Behrendt T, Hammer A, Kemper A. A New Algorithm for the Satellite-Based Retrieval of Solar Surface Irradiance in Spectral Bands. Remote Sensing. 2012; 4(3):622-647. https://doi.org/10.3390/rs4030622
Chicago/Turabian StyleMueller, Richard, Tanja Behrendt, Annette Hammer, and Axel Kemper. 2012. "A New Algorithm for the Satellite-Based Retrieval of Solar Surface Irradiance in Spectral Bands" Remote Sensing 4, no. 3: 622-647. https://doi.org/10.3390/rs4030622
APA StyleMueller, R., Behrendt, T., Hammer, A., & Kemper, A. (2012). A New Algorithm for the Satellite-Based Retrieval of Solar Surface Irradiance in Spectral Bands. Remote Sensing, 4(3), 622-647. https://doi.org/10.3390/rs4030622





