Photorealistic Building Reconstruction from Mobile Laser Scanning Data
Abstract
:1. Introduction
2. Applied Data
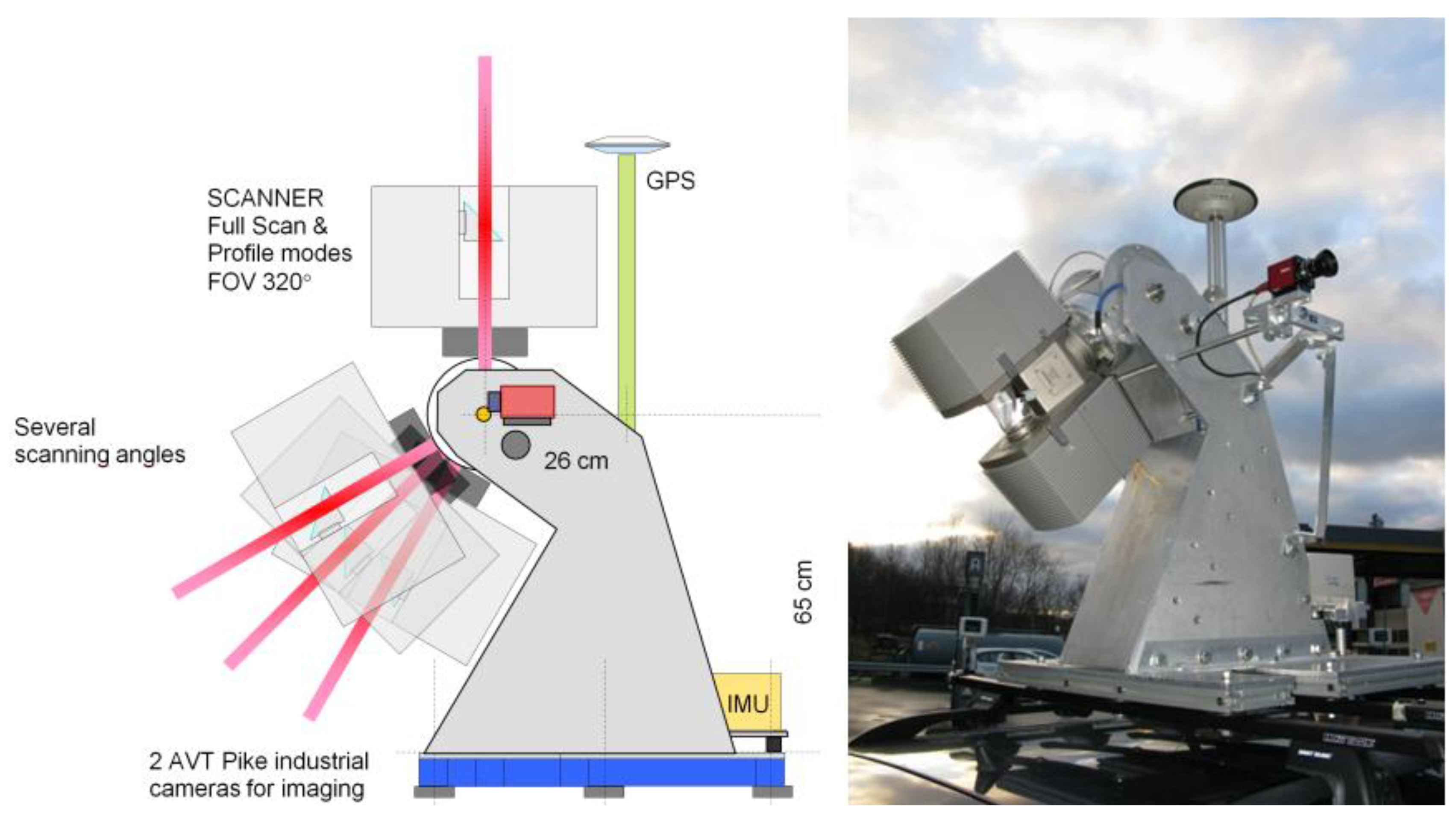
| Date | 12 May 2010 |
| Laser scanner | Faro Photon™ 120 |
| Navigation system | NovAtel SPAN™ |
| Laser point measuring frequency | 244 kHz |
| IMU frequency | 100 kHz |
| GPS frequency | 1 Hz |
| Data synchronization | Synchronizer by FGI, scanner as master |
| Cameras | Two AVT Pike |
| Profile measuring frequency | 49 Hz |

3. Geometry Reconstruction
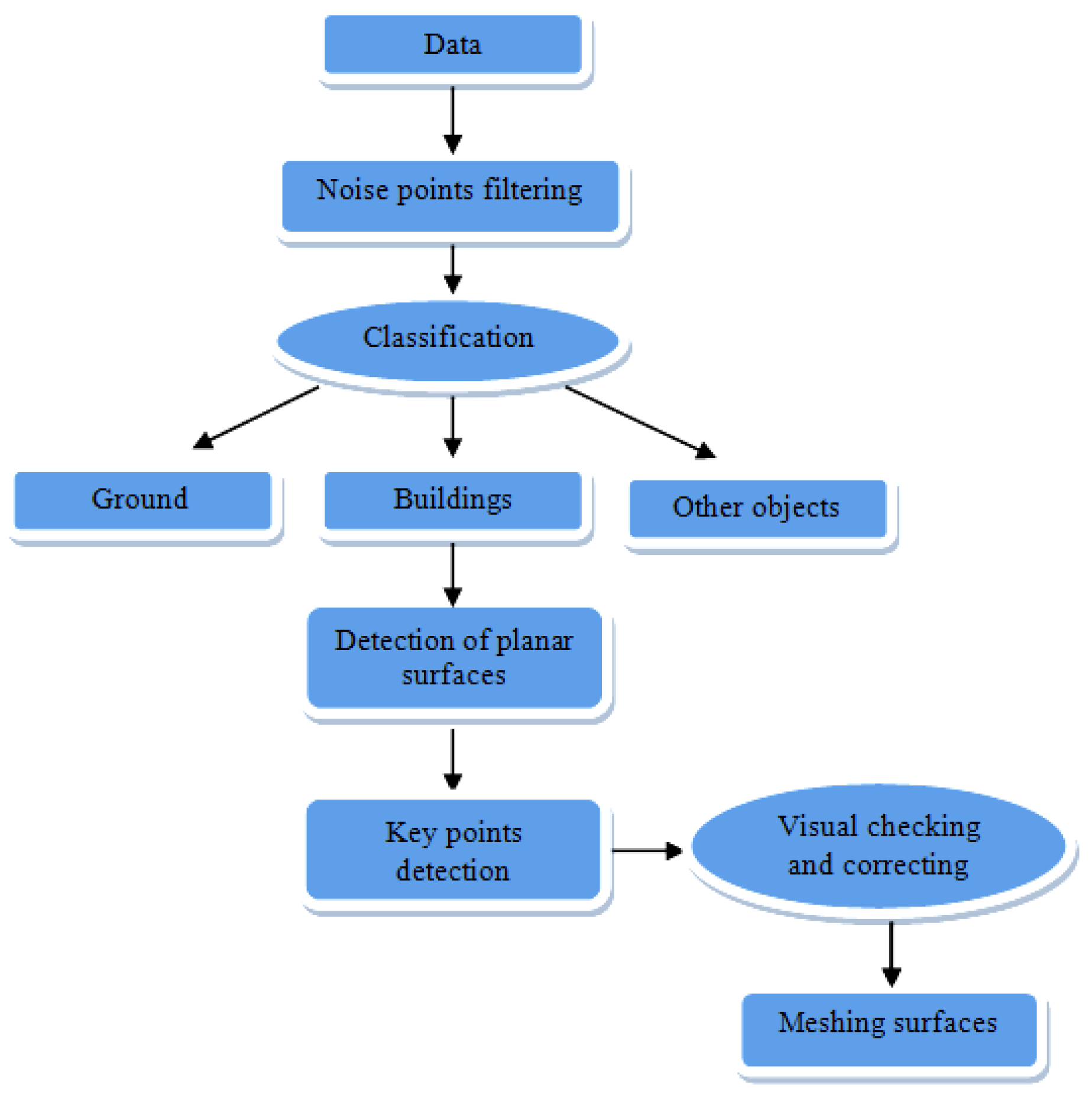
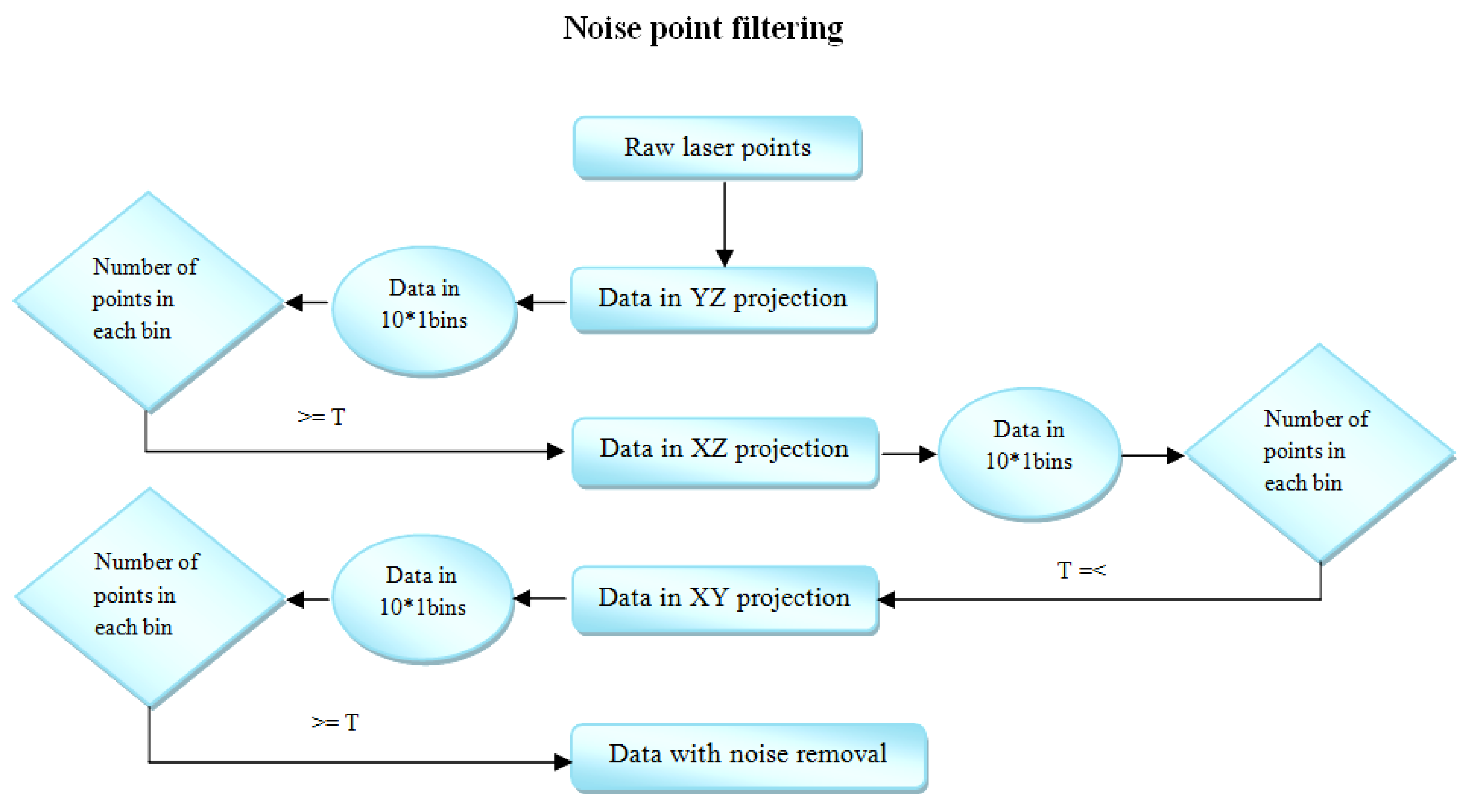
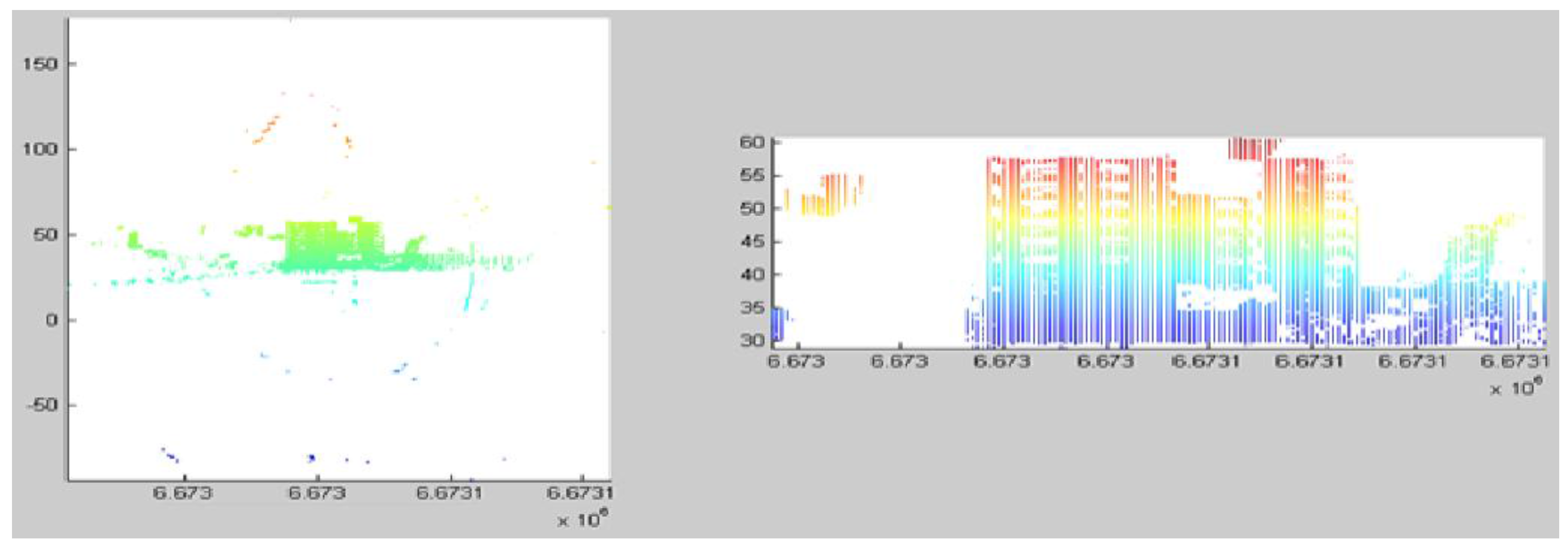
3.1. Noise Point Filtering
3.2. Object Classification
3.2.1. Ground Point Classification
| Abbreviation | Description |
|---|---|
| Zf_data | The most frequently occurring height value for data in one file; |
| Zf_grid | The most frequently occurring height value for data in each grid; |
| Z_min | The minimum height value for the data in one file; |
| Zmin_grid | The minimum height value for the data in the grid; |
| Zd | The difference between Zf_data and Zmin_grid |
| Algorithm 1 Ground point classification | |
| 1: Calculate Zf_data: mode (height value of data) | |
| 2: Compare the difference between Zf_data and Z_min | |
| 3: if the difference <= 1m then points with the height value <= Zf_data +0.25m accepted as ground points 4: else grid points in XY plane into 10*10 bins | |
| 5: for each bin calculate Zf_grid and absolute value of Zd: abs(Zd) 6: if abs(Zd) <= 3m then compare the difference between Zf_grid and Zmin_grid 8: if the difference <= 0.25m then points with the height value <= Zf_grid + 0.25 m as ground points 9: else | |
| points with the height value <= Zmin_grid + 0.25 m as ground points 10: end if 11: end if 12: end for 13: merge all ground points from each bin 14: end if | |
3.2.2. Building Point Classification
| Name | Description |
|---|---|
| Z_max | Maximum height value in the data (one file); |
| Z_min | Minimum height value in the data (one file); |
| Z_mid | Equals to (Z_max+Z_min)/2-2m; |
| Zg | The average height of ground points; |
- (1)
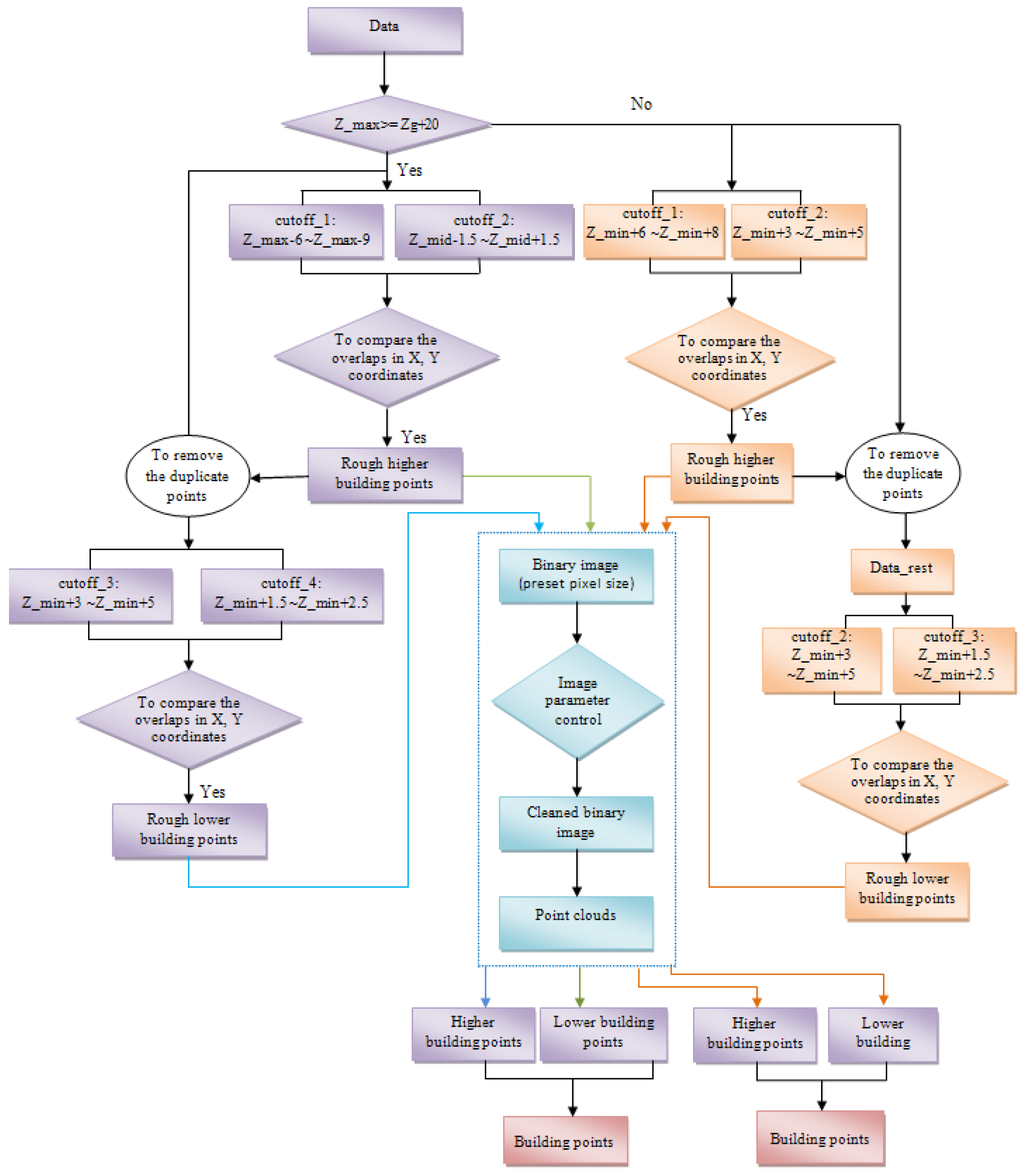
- Algorithm for data in which the maximum height of the buildings is greater than 20 m.
- (i)
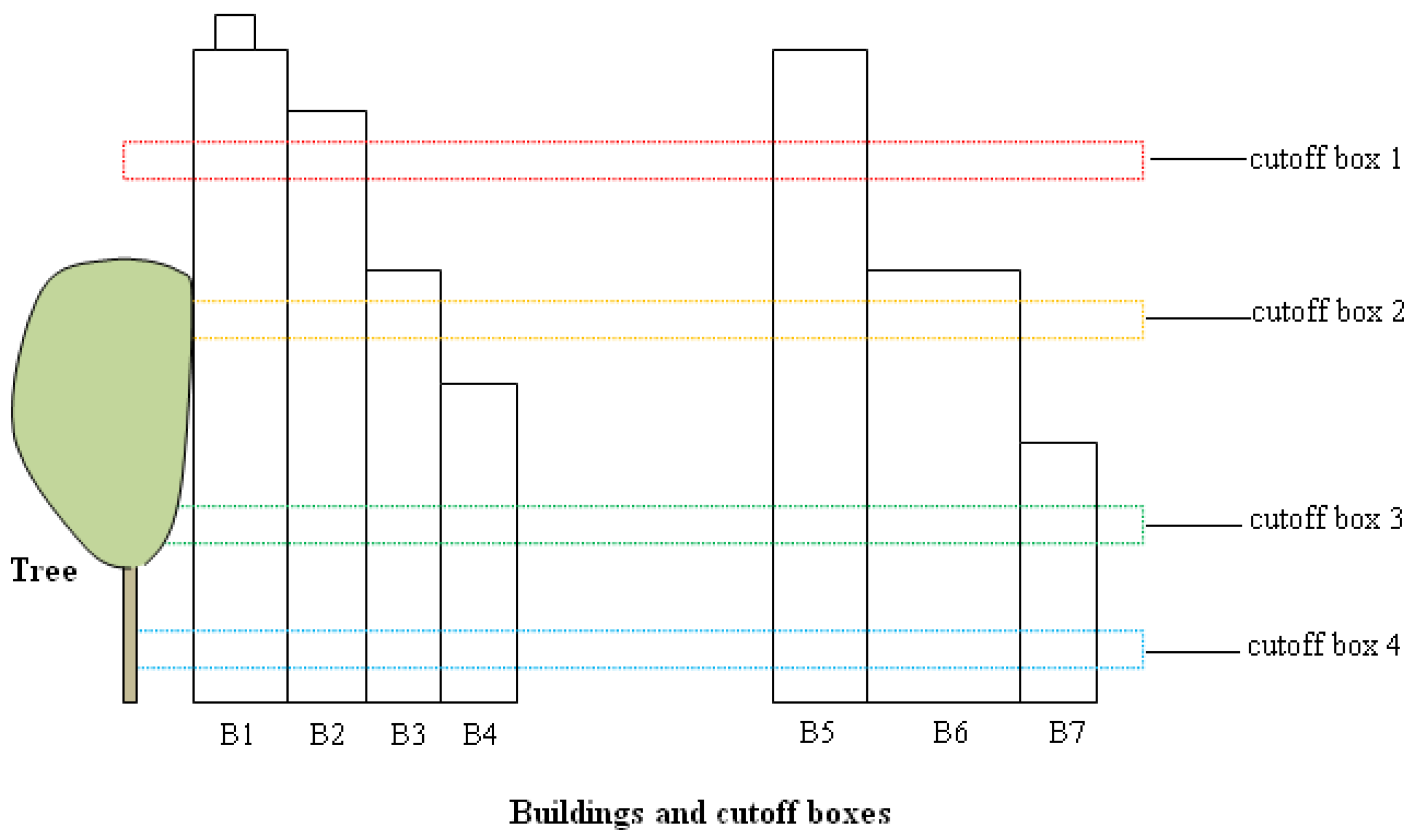
- Roughly extract higher buildings by obtaining points from two cutoff boxes (cutoff_1 and cutoff_2) and comparing the X and Y coordinates of points between the boxes.Firstly, two cutoff boxes are set to extract the points: cutoff_1: Z_max − 6 m~Z_max − 9 m; cutoff_2: Z_mid − 1.5 m~Z_mid + 1.5 m. The threshold for cutoff_1 is set mainly considering that on the top of some buildings, there are some prominent parts, for example, elevator tower, roof windows, and water tanks, which are the parts of the buildings, but these points cannot be used as parts of the continuous buildings. In some cases, noise points from the top of the buildings could not be completely removed (Figure 5). Therefore we start to obtain points from the setting threshold: Z_max − 6 m. For this threshold, it works whatever there exist prominent parts or noise points on the buildings or not. Due to the cutoff_1 starts from Z_max – 6 m, therefore the Z_mid is set to (Z_max+Z_min)/2 − 2 m. Since buildings are always continuous, the overlaps of the two sets of cutoff data in XY coordinates can be derived by:
- TF1 = ismember (cutoff_2 (:, [x, y]), cutoff_1(:, [x, y]), ‘rows’);
- Idx1 = find (TF1 == 1);
- Part_highBuilding = cutoff_2 (Idx1, [x, y, z]);
- TF2 = ismember (objectPoints (x,y), Part_highBuilding (x,y), ‘rows’);
- Idx2 = find (TF2 == 1);
- highBuilding = objectPoints (Idx2,[x, y, z]);
Thus, the higher buildings were extracted roughly. As a result, the whole building is extracted, not only a part of the building. However, in these data, there were still some other points besides building points, e.g., tree points. It will be further processed on the step (iii). - (ii)
- Similarly, roughly extract lower buildings by obtaining points from two cutoff boxes (cutoff_3 and cutoff_4) and comparing the X and Y coordinates of points between two boxes.After the higher buildings had been roughly extracted on the step (i), these points were removed from the data. Then we set two more cutoff boxes for detecting lower building. Cutoff_3: Z_min + 3 m~Z_min + 5 m; cutoff_4: Z_min + 1.5 m~Z_min + 2.5 m. As we know, the smaller the height of cutoff box, the less the number of the points in the box. The separation of building points from trees is easier. However, we have to consider that if there are windows in the cutoff area, it would lead to incomplete building extraction. For example, in one cutoff box, there are points on the wall and another cutoff box has less points or is even empty due to window reflection. After comparing the overlap between them, the result would lead to the missing of this building facade. Therefore, in order to avoid this context, the height of the cutoff boxes should be set properly. By applying the similar method as the step (i), overlaps of XY coordinates in the cutoff_3 and cutoff_4 datasets were obtained. Consequently, lower buildings were roughly extracted. But there were still other points included besides these building points. Therefore, further process will be performed on the step (iii).
- (iii)
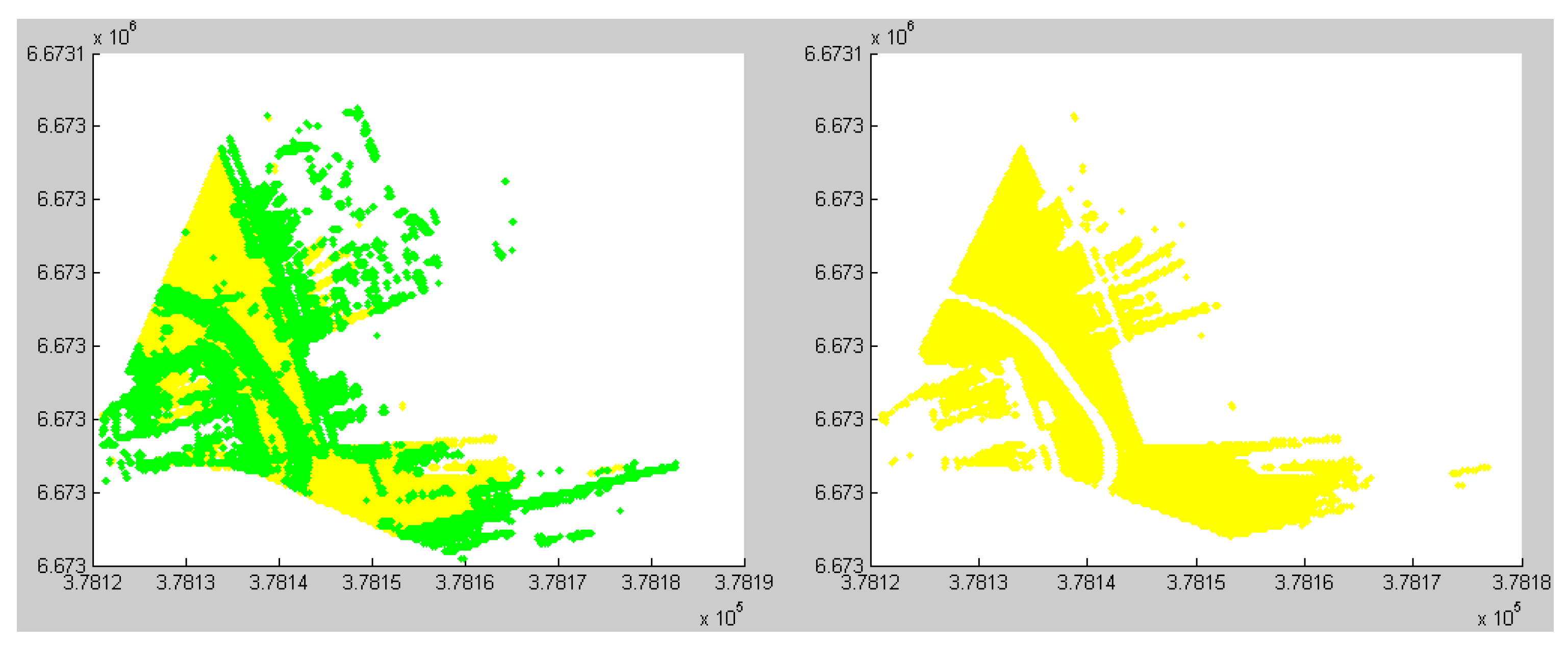
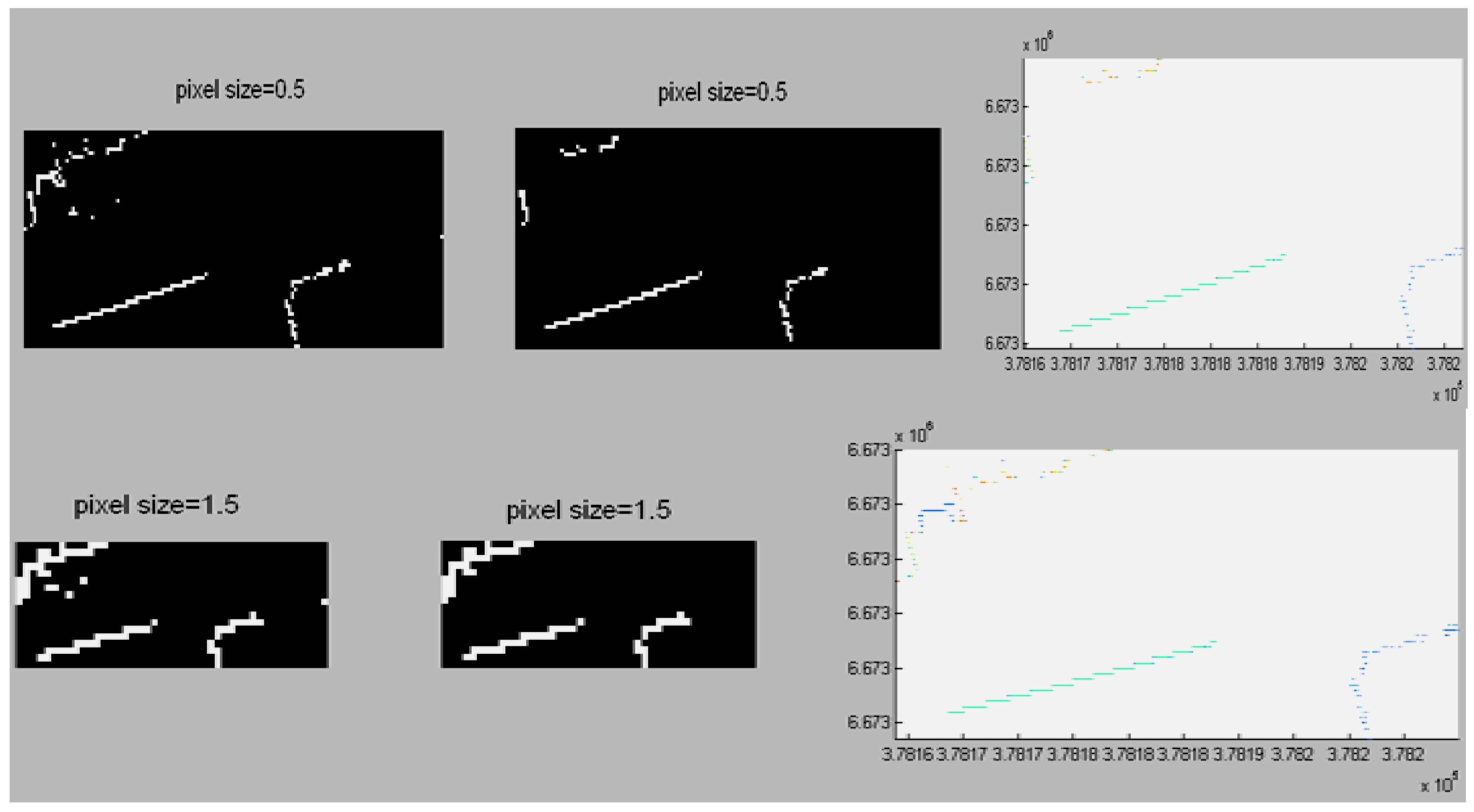
- By transforming these roughly detected building points into binary images, image parameters could be set to remove the non-building points.The purpose of this step was to remove non-building points by means of image processing technology. Firstly, the pixel size for binary image was predefined. Then we defined the size of the binary image from the XY coordinates of the extracted rough building points. A binary image could be formed by setting objects as 1 and empty as 0 from the roughly-detected building points from step (i) and (ii). In order to eliminate small and irregular areas (non-building areas) from the image, it is possible to set the thresholds for region properties, e.g., area size and eccentricity. For example, when the eccentricity value of an area is close to 1, it implies that the shape of the area is close to a line. When the eccentricity value is close to 0, the shape of the area is close to a circle. Usually, the shape is close to a line when a building facade is seen from the top, but a tree is close a circle (see Figure 9). For a square-like building, the eccentricity value can be set to a small value e.g., 0.3~0.5. However, it is possible that some tree points cannot be effectively separated. Thus, we can also utilize other parameters e.g., area size and other shape parameters (explain later on) to restrict it. Usually the MLS data are collected along the streets. Large dataset, in order to avoid sudden heavy computation or the situation of being out of memory, is processed usually by separating into several groups according to the number of profiles. Therefore, one group may contain only a part of a building e.g., one facade or two facades. Thus, the parameter ‘eccentricity’ can be effectively applied to these cases. As regards the shape of an area, besides the eccentricity, we can also use the region properties of major axis length and minor axis length to remove some irregular areas. An example of the pseudo codes:
- LabeledImage = bwlabel (binaryImage, 8);
- Stats = regionprops (LabeledImage, ‘Area’, ‘Eccentricity’, ‘MajorAxisLength’, ‘MinorAxisLength’);
- Find objects with Stats.Area > 4m2 and Stats.Eccentricity = 0.8 and Stats.MajorAxisLength < 15 m and Stats.MinorAxisLength > 4 m.
As we have mentioned in the above, there were a lot of trees very close to the building facades. It is challenging work to separate and classify buildings from trees by only applying region properties. Therefore, we created a morphological line structuring element. A morphological structure element can be constructed by a specific shape such as a line or a disk. For a line structure element, the length of the line and the angle of the line as measured in a counterclockwise direction from the horizontal axis should be predefined. In our case, the angle of the line structure element was set approximately to the building edge direction e.g., 10°. The line structure element can be set as: se = strel (‘line’, the length of line, the direction of line). This enabled the adhesion parts between building edges and trees to be effectively separated. - (iv)
- The processed binary image was transformed back into point cloud.
- (v)
- Applying steps (iii) and (iv) to the results derived from step (i) and step (ii), and merging the points, the buildings were finally extracted.

- (2)
- Algorithm for data in which the maximum height of the buildings is less than 20 m.
- (a)
- Set three cutoff boxes: cutoff_1: Z_min + 6 m~Z_min + 8 m; cutoff_2: Z_min + 3 m~Z_min + 5 m; cutoff_3: Z_min + 1.5 m~Z_min + 2.5 m.
- (b)
- Derive the overlap points between cutoff_1 and cutoff_2 and remove the overlap points from the data:
- P_overlap1= {P(x, y) cutoff_1 & P(x, y) cutoff_2 | P all points};
- P_1(x, y, z) = {P (x, y) ==P_overlap1(x, y) | P all points};
- Data_rest (x, y, z) = {~ (P_1 all points)}.
- (c)
- Derive the overlap points between cutoff_2 and cutoff_3 from ‘Data_rest’:
- P_overlap2= {P(x, y) cutoff_2 & P(x, y) cutoff_3 | P data_rest};
- P_2(x, y, z) = {P (x, y) == P_overlap2(x, y) | P Data_rest};
- (d)
- Apply step (iii) and step (iv) in the previous algorithm to P_1 and P_2 and merge the resulting building points.
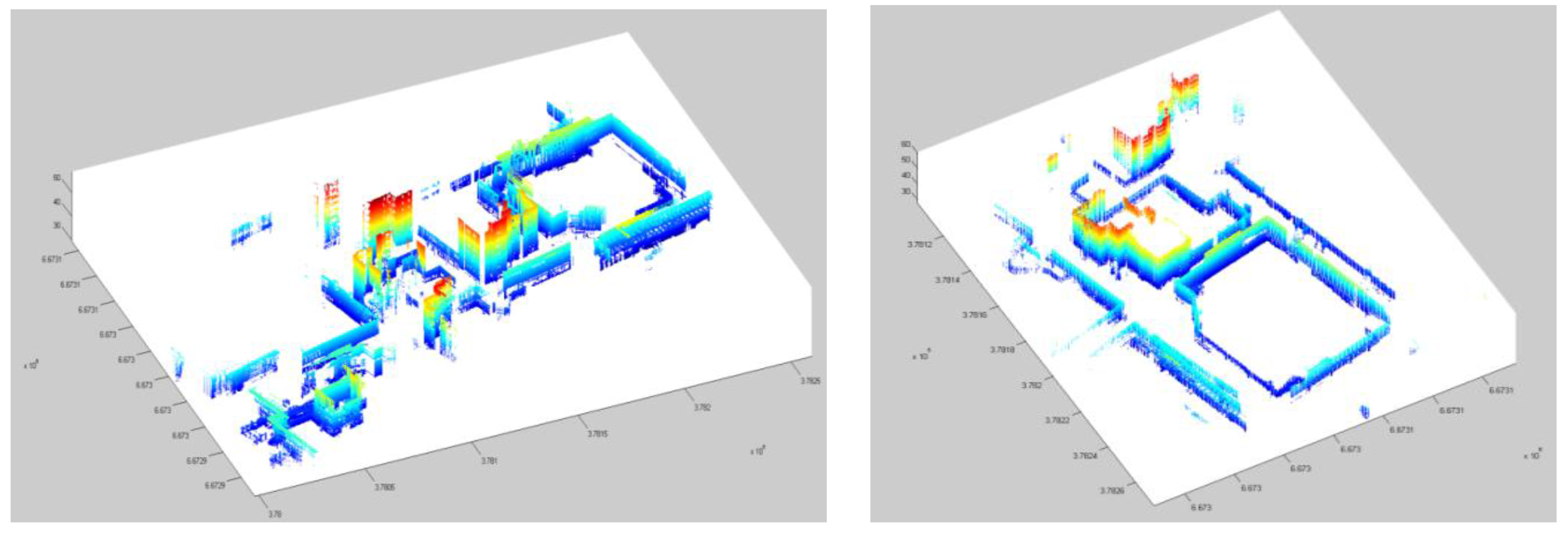
3.3. Key Point Extraction and Surface Meshes
3.3.1. Identifying Each Building Facade
- (1)
- Two neighbor points (P1, P2) were selected randomly to form a vector (V1).
- (2)
- A third point (P3) was added to form the vector V2 with P1. If V2 was not parallel to V1, then it was considered to be the basic plane.
- (3)
- If V2 and V1 were collinear, then this point (P3) was taken as a coplanar point. If not, then the next step was taken.
- (4)
- P4 is any point in the dataset. P4 and P2 formed vector V3. Does it satisfy the coplanar condition V3(V1 × V2) = 0? If yes, it is a coplanar point.
- (5)
- When a plane was identified, the points of this plane were removed from the dataset.
- (6)
- Steps (1) to (5) were repeated until all points were allocated to a certain plane (Figure 12).

3.3.2. Key Point Extraction

4. Texture Preparation and 3D Mapping
4.1. Texture Preparation
- (1)
- Images were taken at a certain oblique angle to the building facades requiring perspective correction.When objects obstruct the line of sight in front of a building or if buildings are high, the images have to be taken at an oblique angle. In addition, even if images were taken at approximately right angles to the building facade, they still need some perspective correction.
- (2)
- With large building facades, several images are needed for a single texture, and consequently image mosaicing was needed.Due to the limited field of view of the camera when covering a large building facade, one image only covered part of the building facade. Thus, several images needed to be combined to create an image mosaic of the facade. The texture shown in Figure 14 is a mosaic of seven images from left to right; with high buildings, images needed to be combined from the upper part and the lower part.
- (3)
- Due to some objects causing occlusions, e.g., trees close to buildings, there is noise, e.g., tree shadows, in the images of the building facades. This noise needs to be removed from the image.In this test area, as mentioned above, there are a lot of trees. Some of them are very close to the building facades (see the middle image of Figure 2). In this context, tree shadows on the building facades needed to be removed from the images for the sake of the high quality texture. Figure 14 is an example showing the original images taken at a certain oblique angle due to some objects obstructing the direct line of sight to the building. The Figure 14 also shows the texture from multi-image mosaic. In addition, in the lower part of the first image of Figure 14, some noise was removed for the final texture (see the lower image of Figure 14).

4.2. Texture Mapping

5. Results and Discussions
- (1)
- Automated process: We developed automated algorithms for noise point filtering, ground classification, building point classification, detection of planar surfaces, and building key point extraction. The result produced by building point classification had the greatest impact on the follow-up processes. Due to reflection from objects, the data from the laser scanner is subject to discontinuities. When some small area data were filtered out as noise points, it occasionally causes incompleteness of the building. In our method, we utilized binary images to clean the noise. The area and shape of an area were constrained to certain threshold values. Therefore, it was important to decide appropriate thresholds for non-building point filtering. The work load in manual checking and correction for model completeness depends on not only the quality of original data but also the results from the automated process.
- (2)
- The process of texture preparation. This step was processed manually. As the images were taken separately from the MLS system, there was no orientation information for automatic process. In addition, object occlusions on images, especially tree occlusions, resulted in the unpleasant appearance of building facades. This caused a lot of work in texture preparation.

- (1)
- By integrating with the ALS data.The degree of building completeness can be considerably improved during the process of geometry reconstruction by integrating the MLS data with the ALS data. This will mean a reduced work load in manual correction. However, new problems would rise from data integrating due to different data sources. ALS and MLS provide data with different resolutions, and probably from different years. And different geometry matching would lead to accuracy lost.
- (2)
- By utilizing images from cameras mounted on the platform of our ROAMER system.As regards building textures, we used cameras with wide fields of view and proper viewing angles from our ROAMER system, and synchronized time from GPS, IMU. The scanner and cameras can be used for identifying the corresponding relationships between point clouds and images so that automated texture mapping could be achieved by applying orientation information from images. Object occlusions on the images could be improved by employing images taken from different viewing angles or by detecting the location of windows on building facades from point clouds and applying consistent textures for the building walls.
6. Conclusions
Acknowledgements
References and Notes
- Toth, C. R&D of Mobile Mapping and Future Trends. In Proceedings of the ASPRS Annual Conference, Baltimore, MD, USA, 9–13 March 2009.
- Cornelis, N.; Leibe, B.; Cornelis, K.; Van Gool, L. 3D urban scene modeling integrating recognition and reconstruction. Int. J. Comput. Vis. 2008, 78, 121–141. [Google Scholar] [CrossRef]
- Chen, R.; Kuusniemi, H.; Hyyppä, J.; Zhang, J.; Takala, J.; Kuittinen, R.; Chen, Y.; Pei, L.; Liu, Z.; Zhu, L.; et al. Going 3D, Personal Nav and LBS. GPS World 2010, 21, 14–18. [Google Scholar]
- NAVTEQ Acquires PixelActive Acquisition Reinforces the Company’s Commitment to Leadership in 3D Mapping. 17 December 2010. Available online: http://corporate.navteq.com/webapps/NewsUserServlet?action=NewsDetail&newsId=946&lang=en&englishonly=false (accessed on 17 December 2010).
- Pollefeys, M.; Nister, D.; Frahm, J.M.; Akbarzadeh, A.; Mordohai, P.; Clipp, B.; Engels, C.; Gallup, D.; Kim, S.J.; Merrell, P.; et al. Detailed real-time urban 3D reconstruction from video. Int. J. Comput. Vis. 2008, 78, 143–167. [Google Scholar] [CrossRef]
- El-Sheimy, N. An overview of mobile mapping systems. In Proceedings of FIG Working Week 2005 and GSDI-8—From Pharaos to Geoinformatics, FIG/GSDI, Cairo, Egypt, 16–21 April 2005; p. 24.
- Brenner, C. Building reconstruction from images and laser scanning. Int. J. Appl. Earth Obs. Geoinf. 2005, 6, 187–198. [Google Scholar] [CrossRef]
- Petrie, G. An introduction to the technology, mobile mapping systems. Geoinformatics 2010, 13, 32–43. [Google Scholar]
- Baltsavias, E.P. Object extraction and revision by image analysis using existing geodata and knowledge: Current status and steps towards operational systems. ISPRS J. Photogramm. Remote Sens. 2004, 58, 129–151. [Google Scholar] [CrossRef]
- Kaartinen, H.; Hyyppä, J. EuroSDR-Project Commission 3 “Evaluation of Building Extraction”. Final Report; In EuroSDR: European Spatial Data Research, Official Publication; EuroSDR: Dublin, Ireland, 2006; Volume 50, pp. 9–77. [Google Scholar]
- Haala, N.; Kada, M. An update on automatic 3D building reconstruction. ISPRS J. Photogramm. Remote Sens. 2010, 65, 570–580. [Google Scholar] [CrossRef]
- Remondino, F.; El-Hakim, S. Image-based 3D modelling: A review. Photogramm. Rec. 2006, 21, 269–291. [Google Scholar] [CrossRef]
- Becker, S.; Haala, N. Combined Feature Extraction for Facade Reconstruction. In Proceedings of the ISPRS Workshop Laser Scanning 2007 and SilviLaser 2007, Espoo, Finland, 12–14 September 2007; pp. 241–247.
- Tian, Y.; Gerke, M.; Vosselman, G.; Zhu, Q. Knowledge-based building reconstruction from terrestrial video sequences. ISPRS J. Photogramm. Remote Sens. 2010, 65, 395–408. [Google Scholar] [CrossRef]
- Zhao, H.; Shibasaki, R. Reconstructing a textured CAD model of an urban environment using vehicle-borne laser range scanners and line cameras. Mach. Vis. Appl. 2003, 14, 35–41. [Google Scholar] [CrossRef]
- Früh, C.; Zakhor, A. An automated method for large-scale, ground-based city model acquisition. Int. J. Comput. Vis. 2004, 60, 5–24. [Google Scholar] [CrossRef]
- Kukko, A. Road Environment Mapper—3D Data Capturing with Mobile Mapping. Licentiate’s Thesis, Helsinki University of Technology, Espoo, Finland, 2009; p. 158. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhu, L.; Hyyppä, J.; Kukko, A.; Kaartinen, H.; Chen, R. Photorealistic Building Reconstruction from Mobile Laser Scanning Data. Remote Sens. 2011, 3, 1406-1426. https://doi.org/10.3390/rs3071406
Zhu L, Hyyppä J, Kukko A, Kaartinen H, Chen R. Photorealistic Building Reconstruction from Mobile Laser Scanning Data. Remote Sensing. 2011; 3(7):1406-1426. https://doi.org/10.3390/rs3071406
Chicago/Turabian StyleZhu, Lingli, Juha Hyyppä, Antero Kukko, Harri Kaartinen, and Ruizhi Chen. 2011. "Photorealistic Building Reconstruction from Mobile Laser Scanning Data" Remote Sensing 3, no. 7: 1406-1426. https://doi.org/10.3390/rs3071406
APA StyleZhu, L., Hyyppä, J., Kukko, A., Kaartinen, H., & Chen, R. (2011). Photorealistic Building Reconstruction from Mobile Laser Scanning Data. Remote Sensing, 3(7), 1406-1426. https://doi.org/10.3390/rs3071406





