Comparison of the Noise Robustness of FVC Retrieval Algorithms Based on Linear Mixture Models
Abstract
:1. Introduction
2. LMM-Based Algorithms
2.1. Algorithm-1: Reflectance-Based LMM
2.2. Algorithm-2: VI-Based LMM
2.3. Algorithm-3: Isoline-Based LMM
3. Error Propagation in FVC
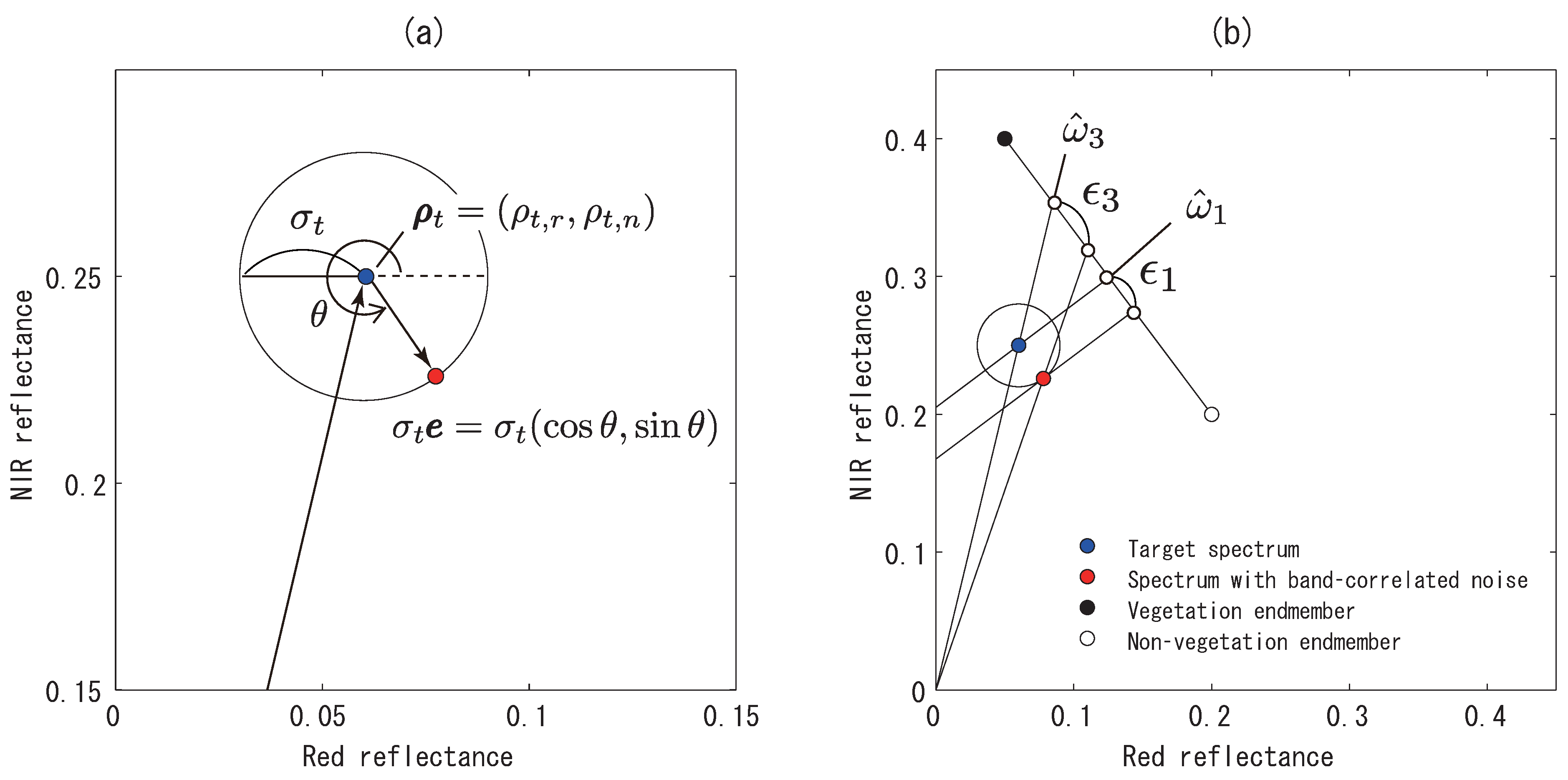
3.1. Measurement Errors in the Reflectance Spectra and Propagated Errors in the FVC
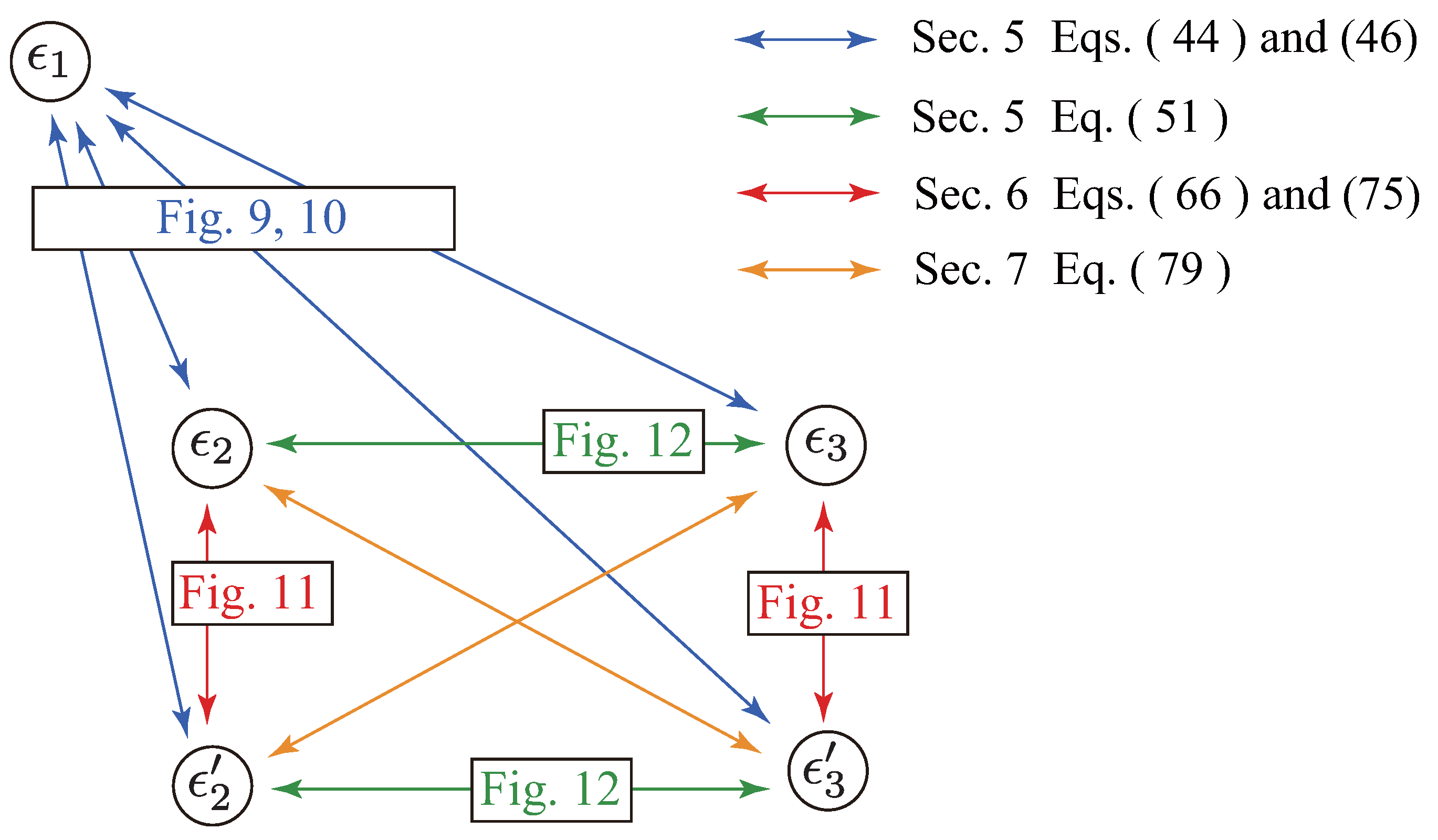
3.2. Relationships Among the Errors Propagated in the FVC
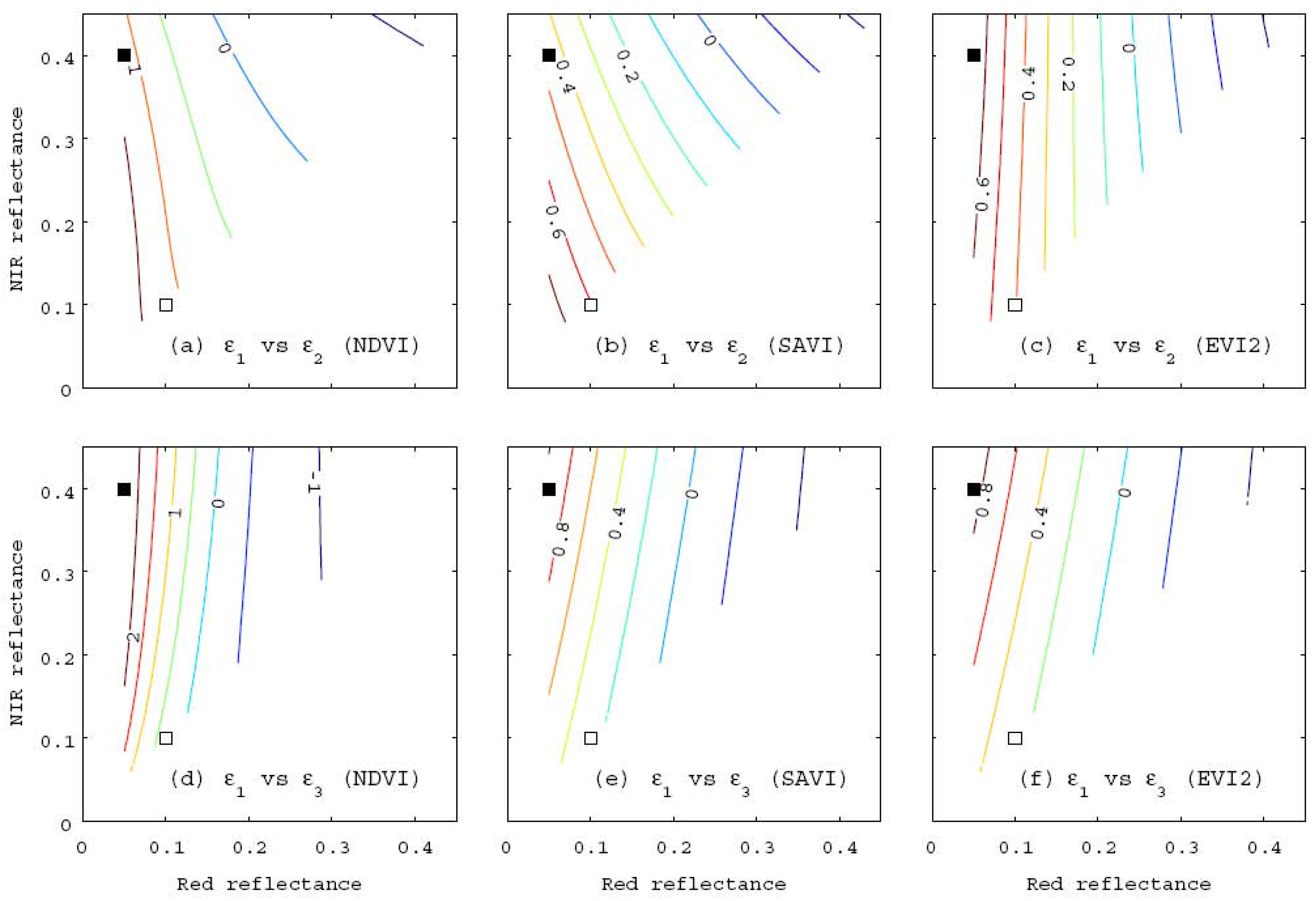
4. Comparison of the Propagated Errors
4.1. Derivation of the Angle
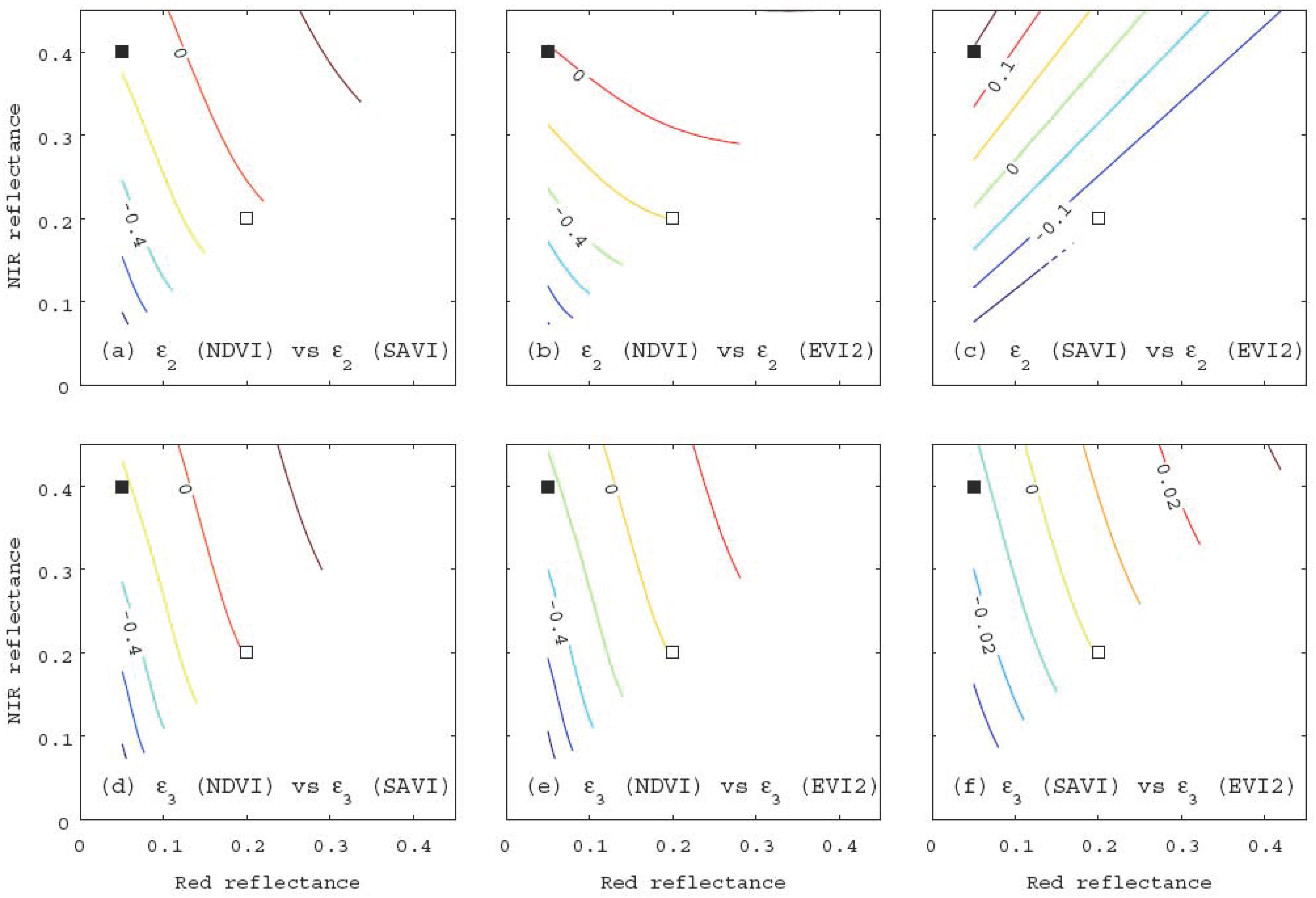
5. Comparison between Algorithms-2 and -3 under Identical VI Conditions
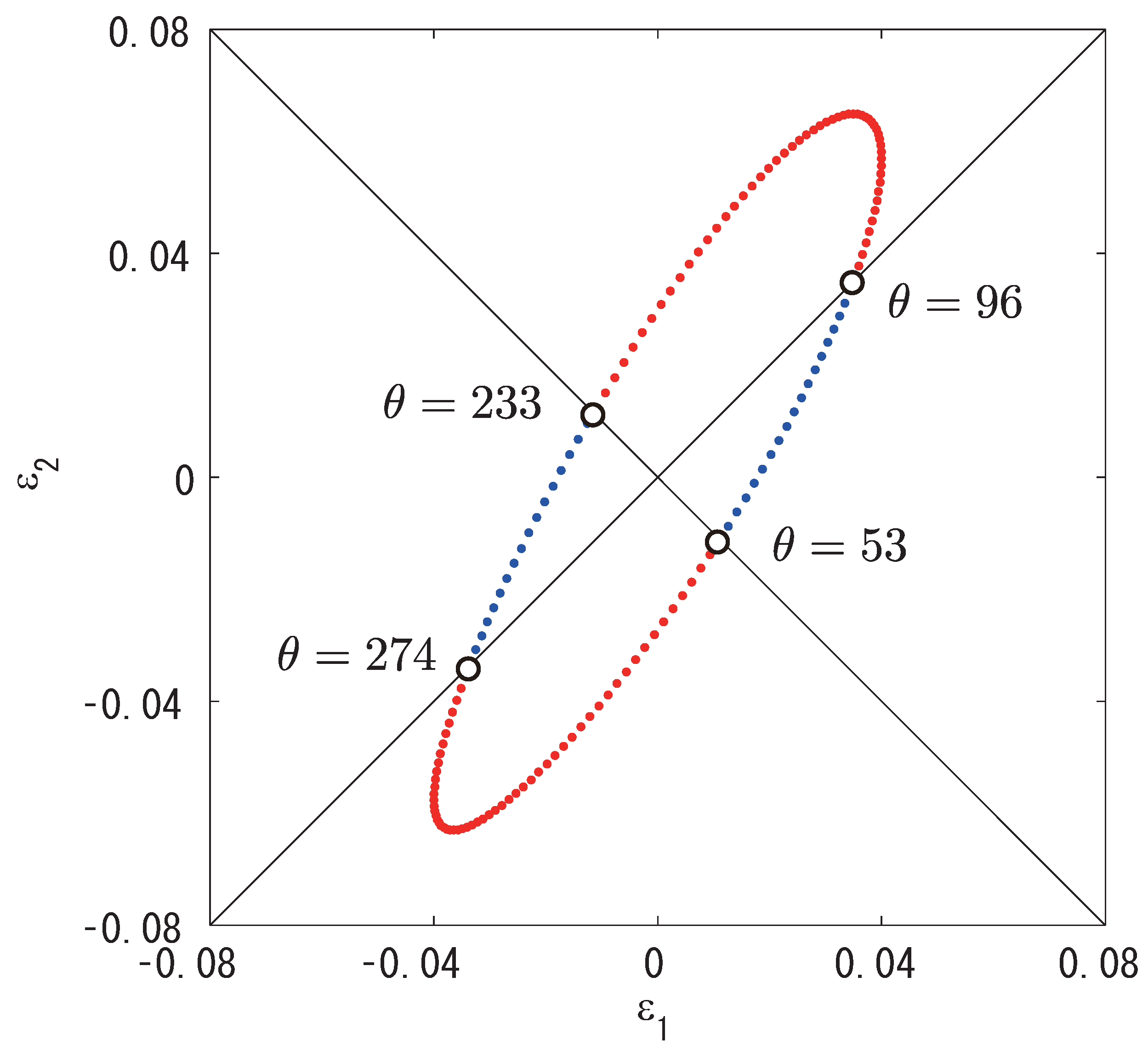
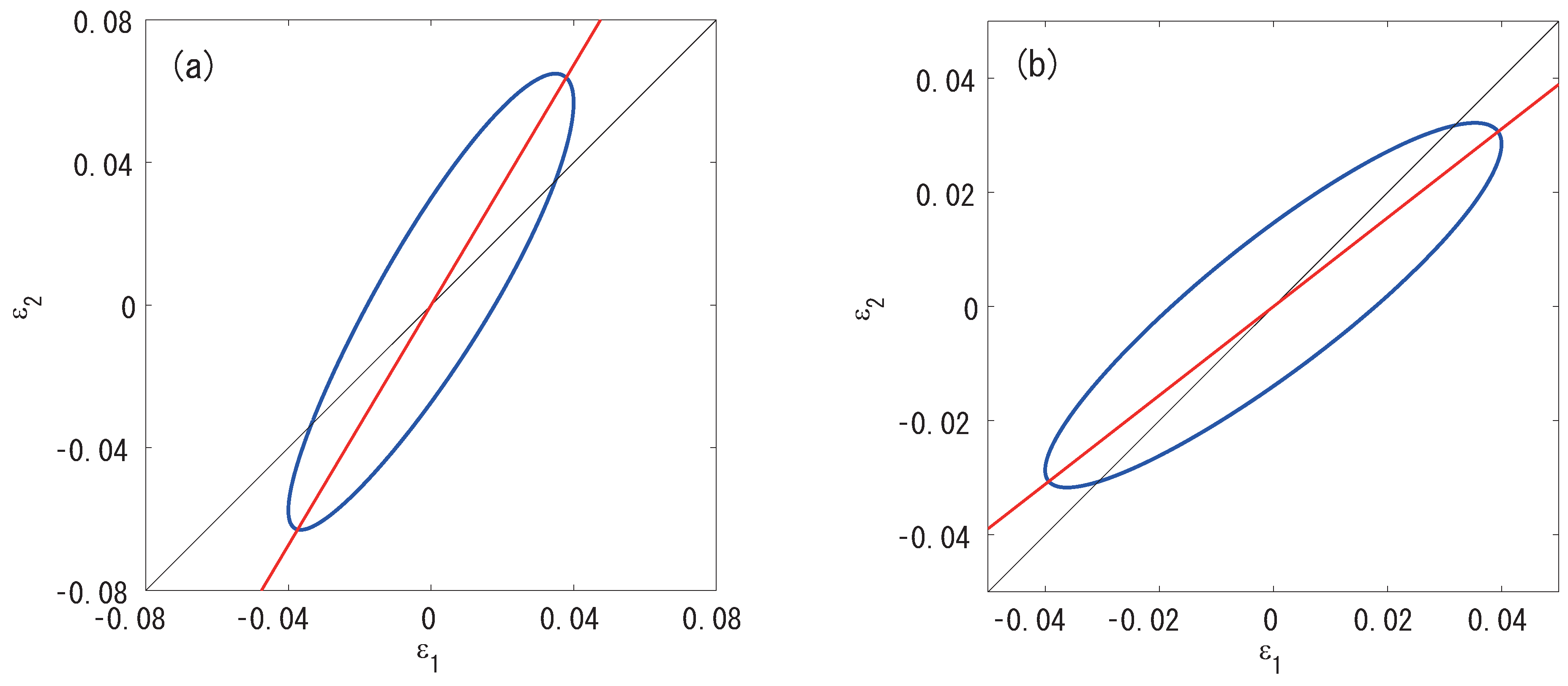
6. Numerical Demonstrations
7. Conclusions
Acknowledgements
Appendix
References
- Myneni, R.B.; Maggion, S.; Iaquinta, J.; Privette, J.L.; Gobron, N.; Pinty, B.; Kimes, D.S.; Verstreate, M.M.; Williams, D.L. Optical remote sensing of vegetation: Modeling, caveats, and algorithms. Remote Sens. Environ. 1995, 51, 169–188. [Google Scholar] [CrossRef]
- Hall, F.G.; Townshend, J.R.; Engman, E.T. Status of remote sensing algorithms for estimation of land surface state parameters. Remote Sens. Environ. 1995, 51, 138–156. [Google Scholar] [CrossRef]
- Wang, C.; Qi, J.; Cochrane, M. Assessment of Tropical Forest Degradation with Canopy Fractional Cover from Landsat ETM+ and IKONOS Imagery. Earth Interact. 2005, 9, 1–18. [Google Scholar] [CrossRef]
- Carlson, T.N.; Arthur, S.T. The impact of land use-land cover changes due to urbanization on surface microclimate and hydrology: A satellite perspective. Global Planet Change 2000, 25, 49–65. [Google Scholar] [CrossRef]
- Lobell, D.B.; Asner, G.P.; Law, B.E.; Treuhaft, R.N. Subpixel canopy cover estimation of coniferous forests in Oregon using SWIR imaging spectrometry. J. Geophys. Res. 2001, 106, 5151–5160. [Google Scholar] [CrossRef]
- Barlage, M.; Zeng, X. The Effects of observed fractional vegetation cover on the land surface climatology of the community land model. J. Hydrometeorol. 2004, 5, 823–830. [Google Scholar] [CrossRef]
- Zhang, J.; Walsh, J.E. Thermodynamic and hydrological impacts of increasing greenness in northern high latitudes. J. Hydrometeorol. 2006, 7, 1147–1163. [Google Scholar] [CrossRef]
- Foody, G.M.; Cox, D.P. Sub-pixel land cover composition estimation using a linear mixture model and fuzzy membership functions. Int. J. Remote Sens. 1994, 15, 619–631. [Google Scholar] [CrossRef]
- Wittich, K.P.; Hausing, O. Area-averaged vegetative cover fraction estimated from satellite data. Int. J. Biometeorol. 1995, 38, 209–215. [Google Scholar] [CrossRef]
- Small, C. Estimation of urban vegetation abundance by spectral mixture analysis. Int. J. Remote Sens. 2001, 22, 1305–1334. [Google Scholar] [CrossRef]
- Bateson, C.A.; Asner, G.P.; Wessman, C.A. Endmember bundles: A new approach to incorporating endmember variability into spectral mixture analysis. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1083–1094. [Google Scholar] [CrossRef]
- Xiao, J.; Moody, A. A comparison of methods for estimating fractional green vegetation cover within a desert-to-upland transition zone in central New Mexico, USA. Remote Sens. Environ. 2005, 98, 237–250. [Google Scholar] [CrossRef]
- Van de Voorde, T.; Vlaeminck, J.; Canters, F. Comparing different approaches for mapping urban vegetation cover from landsat ETM+ data: A case study on Brussels. Sensors 2008, 8, 3880–3902. [Google Scholar] [CrossRef] [PubMed]
- Horwitz, H.M.; Nalepka, R.F.; Hyde, P.D.; Morgenstern, J.P. Estimating the Proportions of Objects Within a Single Resolution Element of a Multispectral Scanner; Technical Report NASA Contract NAS-9-9784; University Michigan: Ann Arbor, MI, USA, 1971. [Google Scholar]
- Settle, J.J.; Drake, N.A. Linear mixing and the estimation of ground cover proportions. Int. J. Remote Sens. 1993, 14, 1159–1177. [Google Scholar] [CrossRef]
- Ichoku, C.; Karnieli, A. A review of mixture modeling techniques for sub-pixel land cover estimation. Rmote Sens. Rev. 1996, 13, 161–186. [Google Scholar] [CrossRef]
- Smith, M.O.; Johnson, P.E.; Adams, J.B. Quantitative determination of mineral types and abundances from reflectance spectra using principal components analysis. J. Geophys. Res., Suppl. 1985, 90, C797–C804. [Google Scholar] [CrossRef]
- Adams, J.B.; Smith, M.O.; Johnson, P.E. Spectral mixture modeling: A new analysis of rock and soil types at the Viking Lander 1 site. J. Geophys. Res. 1986, 91, 8098–8112. [Google Scholar] [CrossRef]
- Chang, C.I.; Zhao, X.L.; Althouse, M.; Pan, J.J. Least squares subspace projection approach to mixed pixel classification for hyperspectral images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 898–912. [Google Scholar] [CrossRef]
- Cochrane, M.A.; Souza, C.M. Linear mixture model classification of burned forests in the Eastern Amazon. Int. J. Remote Sens. 1998, 19, 3433–3440. [Google Scholar] [CrossRef]
- Gillespie, A.R. Spectral mixture analysis of multispectral thermal infrared images. Remote Sens. Environ. 1992, 42, 137–145. [Google Scholar] [CrossRef]
- Smith, M.O.; Ustin, S.L.; Adams, J.B.; Gillespie, A.R. Vegetation in deserts: I. A regional measure of abundance from multispectral images. Remote Sens. Environ. 1990, 31, 1–26. [Google Scholar] [CrossRef]
- Jasinski, M.F. Estimation of subpixel vegetation density of natural regions using satellite multispectral imagery. IEEE Trans. Geosci. Remote Sens. 1996, 34, 804–813. [Google Scholar] [CrossRef]
- Kallel, A.; Héarat-Mascle, S.L.; Ottlé, C.; Hubert-Moy, L. Determination of vegetation cover fraction by inversion of a four-parameter model based on isoline parametrization. Remote Sens. Environ. 2007, 111, 553–566. [Google Scholar] [CrossRef]
- Carpenter, G.A.; Gopal, S.; Macomber, S.; Martens, S.; Woodcock, C.E. A neural network method for mixture estimation for vegetation mapping. Remote Sens. Environ. 1999, 70, 138–152. [Google Scholar] [CrossRef]
- Guilfoyle, K.J.; Althouse, M.L.; Chang, C.-I. A quantitative and comparative analysis of linear and nonlinear spectral mixture models using radial basis function neural networks. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2314–2318. [Google Scholar] [CrossRef]
- Jimenéz-Muñoz, J.C.; Sobrino, J.A.; Plaza, A.; Guanter, L.; Moreno, J.; Martinez, P. Comparison between fractional vegetation cover retrievals from vegetation indices and spectral mixture analysis: Case study of PROBA/CHRIS data over an agricultural area. Sensors 2009, 9, 768–793. [Google Scholar] [CrossRef] [PubMed]
- Obata, K.; Yoshioka, H. Inter-algorithm relationships for the estimation of the fraction of vegetation cover based on a two endmember linear mixture model with the VI constraint. Remote Sens. 2010, 2, 1680–1701. [Google Scholar] [CrossRef]
- Obata, K.; Yoshioka, H. Relationships between errors propagated in fraction of vegetation cover by algorithms based on a two-endmember linear mixture model. Remote Sens. 2010, 2, 2680–2699. [Google Scholar] [CrossRef]
- Goward, S.N.; Markham, B.; Dye, D.G.; Dulaney, W.; Yang, J. Normalized difference vegetation index measurements from the advanced very high resolution radiometer. Remote Sens. Environ. 1991, 35, 257–277. [Google Scholar] [CrossRef]
- Miura, T.; Huete, A.; Yoshioka, H. Evaluation of sensor calibration uncertainties on vegetation indices for MODIS. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1399–1409. [Google Scholar] [CrossRef]
- Gong, P.; Zhang, A. Noise effect on linear spectral unmixing. Ann. GIS 1999, 5, 52–57. [Google Scholar] [CrossRef]
- Barducci, A.; Mecocci, A. Theoretical and experimental assessment of noise effects on least-squares spectral unmixing of hyperspectral images. Opt. Eng. 2005, 44, 087008. [Google Scholar]
- Soffer, R.J.; Neville, R.A.; Staenz, K.; White, H.P. Sensitivity of Spectral Unmixing Analysis to a Spectrally Dependent Gain Error in Hyperspectral Data. In Proceedings of the IEEE International Conference on Geoscience and Remote Sensing Symposium, IGARSS 2006, Denver, CO, USA, 31 July–4 August 2006; pp. 1130–1133.
- Shimabukuro, Y.E.; Smith, J.A. The least-squares mixing models to generate fraction images derived from remote sensing multispectral data. IEEE Trans. Geosci. Remote Sens. 1991, 29, 16–20. [Google Scholar] [CrossRef]
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens. 1998, 19, 1533–1543. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS. In Proceedings of the Third Earth Resources Technology Satellite-1 Symposium, Washington, DC, USA, 1974; pp. 309–317.
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Zeng, X.; Dickinson, R.E.; Walker, A.; Shaikh, M.; Defries, R.S.; Qi, J. Derivation and evaluation of global 1-km fractional vegetation cover data for land modeling. J. Appl. Meteorol. 2000, 39, 826–839. [Google Scholar] [CrossRef]
- Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Yoshioka, H.; Huete, A.; Miura, T. Derivation of vegetation isoline equations in red-NIR reflectance space. IEEE Trans. Geosci. Remote Sens. 2000, 38, 838–848. [Google Scholar] [CrossRef]






| Type of algorithm | Endmember model | Constraint |
|---|---|---|
| Reflectance-based LMM | reflectance spectrum | reflectance spectrum |
| VI-based LMM | VI | VI |
| Isoline-based LMM | reflectance spectrum | VI |
| NDVI | 1 | 0 | 1 | 1 | 0 | |
| SAVI | 0 | 1 | 1 | L | ||
| EVI2 | 0 | 1 | 1 |
| Class | Vegetation | Non-vegetation | ||
| Band | Red | NIR | Red | NIR |
| EM1 | 0.05 | 0.4 | 0.2 | 0.2 |
| EM2 | 0.05 | 0.4 | 0.1 | 0.1 |
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Obata, K.; Yoshioka, H. Comparison of the Noise Robustness of FVC Retrieval Algorithms Based on Linear Mixture Models. Remote Sens. 2011, 3, 1344-1364. https://doi.org/10.3390/rs3071344
Obata K, Yoshioka H. Comparison of the Noise Robustness of FVC Retrieval Algorithms Based on Linear Mixture Models. Remote Sensing. 2011; 3(7):1344-1364. https://doi.org/10.3390/rs3071344
Chicago/Turabian StyleObata, Kenta, and Hiroki Yoshioka. 2011. "Comparison of the Noise Robustness of FVC Retrieval Algorithms Based on Linear Mixture Models" Remote Sensing 3, no. 7: 1344-1364. https://doi.org/10.3390/rs3071344
APA StyleObata, K., & Yoshioka, H. (2011). Comparison of the Noise Robustness of FVC Retrieval Algorithms Based on Linear Mixture Models. Remote Sensing, 3(7), 1344-1364. https://doi.org/10.3390/rs3071344





