1. Describing Real Properties
We define a “real property” by one or sometimes multiple parcels as they are recorded in cadastral maps. It consists of a piece of land, sometimes defined by a fence, on which are one or more buildings, impervious surfaces, garages, trees and other vegetation. A property may also contain only the portion of a multi-unit building, for example in dense urban cores where buildings are connected.
The description of a real property consists of a table with coordinates and numbers. These define the number of buildings, type of building from a stored list of candidates, building height and footprint, number of floors, number and types of windows, presence of a basement floor, type of attic, roof type and roof details such as an eave, skylights, chimneys, presence of a garage and its size, types and extent of impervious surfaces, such as a driveway and parking spaces, and statements about the type and size of elements of vegetation, the presence of a water body, the existence and type of a fence, exposure to the sun and effects of shadows, the quality of views from a window, etc.
We expect that such information per parcel, for all properties of a city, will be useful for a broad range of applications in city administrations, commercial location-based services and searches on the Internet [
1]. There will, however, be concern about the cost of data creation. An economically favorable approach would build first of all on the wealth of already existing routine aerial photography justified by other applications, not insignificantly in connection with innovative location-aware global Internet sites such as
Google Maps and
Microsoft’s Bing Maps, or the innumerable regional sites. Secondly, such property-descriptions will need to be developed automatically, with little manual support.
Therefore we have designed a processing framework which focuses on using pre-existing high resolution vertical aerial images and cadastral data. These two sources need to be conflated into a common coordinate system. The aerial images themselves in turn are the source of terrain models, image camera poses and classifications. One may possibly also involve street vectors. The process first builds an integrated geometry and semantic object data set which can then be analyzed for the development of descriptors. Our initial results concern the definition of building details. We show that, for vertical aerial photography, we have achieved an accuracy in counting floors of 93%, and for windows 86%.
2. Inspiration from the Location-Aware Internet
2.1. Evolving from Digital Geodata to Location-Awareness
A location-aware Internet [
2,
3,
4,
5] has evolved since about 2005. Internet-search has been a driving force in the rapid development of detailed 2-dimensional maps and also 3-dimensional urban models. “Internet maps” in this context consist of street-maps used for car navigation, augmented by the terrain shape in the form of the Bald Earth and all this accompanied by photographic texture from ortho photos. This is currently available for large areas of the industrialized World when calling up the websites
maps.google.com or
www.bing.com/maps, and also from a number of regional Internet mapping services, for example the French
www.geoportail.fr or the German
www.klicktel.de/kartensuche.
The transition from the first availability of digital map data to today’s interactive location-based search on the Internet spans about 30 years. One may divide the evolution into several distinct stages:
- (1)
The massive transition to digital geo data dates back to the time when computing facilities were first able to cope with the data quantity implied in the geo-application and began with the scanning of paper maps and their subsequent vectorization in the late 1970s. This improved the storage, retrieval, transmission and printing of such data.
- (2)
The availability of digital data led to an early form of pre-Internet e-commerce by shipping shrink-wrapped Geodata to interested experts.
- (3)
Road maps became available for trip planning in the mid 1990s, initially for transportation systems, later for the general public in the form of car navigation. It required the broad acceptance of personal computing. Geodata were transported on digital media.
- (4)
The Internet was the major enabler of the widespread commerce with Geodata greatly improving the convenience in exchanging orthophotos, aerial and satellite photography. Shrink-wraps were replaced by online services.
- (5)
The GPS (Global Positioning System) inspired a further increase in the usefulness of digital Geodata and resulted in the transition to true real-time navigation from about the mid 1990s onwards, based on street maps.
- (6)
The latest stage of this evolution was the introduction of Geodata into the novel search-application via the Internet. Global location awareness was introduced into Internet search via
maps.google.com and
www.bing.com/maps. 3D urban building models came into being in November 2006 with
Microsoft’s announcement of the availability of
Virtual Earth in 3D [
6].
- (7)
We see today the emergence of smart telephones and a refined interest in locations, not only in cars but now also for pedestrian applications.
An interesting transition occurred along the way from Geodata as a realm of experts, into routine use by everyone. This separate evolutionary track began with a very early idea, namely the invention of the GIS (Geographic Information Systems) in about 1962 [
7]. The idea was born well ahead of the ability to realize it in the form of large area systems. While of course entirely predicated on the availability of the computer, it took the personal computer to make the idea a practical reality. However, the GIS did not change the basic limitations of “Geodata for the experts”. That change became very visible with the development of car navigation systems for regular passenger cars. It signaled for the first time a transition from experts to everyone. This development accelerated with the location-aware Internet search, so that today almost every Internet user is also a user of Geodata, inspecting and judging aerial photography, oblique imagery, 3D building models and, most recently, also street-side images and their various methods of supporting a Geo-naïve user.
Urban 3D models have been a research topic since the mid 1990s [
8,
9,
10,
11,
12]. The initial introduction into Internet-search at
Bing Maps (then
Virtual Earth) employed man-made buildings as triangulated point clouds with a visual embellishment by photographic texture. Since April 2008, vegetation is being classified and identified, and computer-generated vegetation is being placed on top of the Bald Earth [
5].
3D urban models are still in their infancy and are provided over large areas only by
Bing Maps, with an example presented in
Figure 1 in its “classic” version from www.bing.com/maps. Recently, the emphasis has shifted at
Microsoft from a full 3D urban model to the use of 2D street-side imagery that has undergone some limited 3D processing (see
www.bing.com/maps/explore). While Internet-search may be the most visible and also initial driving application, there are of course others. Often mentioned are city planning, virtual tourism, disaster preparedness, military or police training and decision making [
13], or 3D car navigation [
14]. In Germany, 3D building models are being considered of such municipal relevance that a fairly complex and all-encompassing CityGML data standard has been developed to guide the creation of 3D building models at various levels of detail, ranging from a basic L0 through to a virtual reality level L4 with indoor 3D modeling [
15]. This standard has been adopted by the international
Open Geospatial Consortium (OGC) [
16].
Figure 1.
Typical 3D content in support of an Internet search, taken from
www.bing.com/maps. The focus is on providing a pleasant “user experience”. The example is the
Colorado State Capitol. The geometry is from vertical aerial photography, the photo-texture from separate aerial oblique imagery. The vegetation has been classified and computer generated trees have been placed at the locations classified as trees.
Figure 1.
Typical 3D content in support of an Internet search, taken from
www.bing.com/maps. The focus is on providing a pleasant “user experience”. The example is the
Colorado State Capitol. The geometry is from vertical aerial photography, the photo-texture from separate aerial oblique imagery. The vegetation has been classified and computer generated trees have been placed at the locations classified as trees.
2.2. Towards Semantically Interpreted Urban Models
So-called 3D-location awareness of the Internet serves to please the user’s eye—one could speak of “eye candy”—but cannot be used as part of the search itself. This is unlike the 2D content with its street map and address codes that can be searched. An interpreted urban 3D model would support searches in geometry data, not just in alphanumeric data. Certain characteristics may be interest, such as: the number of buildings higher than four floors in a certain district, a built-up floor area in excess of 500 m2, impervious areas at less than 30% of the land area, large window surfaces in excess of 30% of the wall surface, a certain minimum sun exposure during the day, with attractive views of the distant urban landscape.
We can search for such objects if we augment the Internet with descriptions of real properties. Image contents must not merely be shown on a monitor, but they must get interpreted. For this to be accomplished at low cost, it must be done automatically and from easily available sources. We are facing a research challenge for computer vision [
4,
17].
2.3. Growing from Location-Awareness towards Ambient Intelligence
While applications like
Bing Maps or
Google Earth are currently driven to engage the public in using the associated Internet-search systems via attractive location awareness, there is a deeper justification in light of the emerging opportunities created by the Internet-of-Things and Ambient Intelligence. Both concepts need location awareness [
18]. Already in 1991, Marc Weiser authored his much quoted prediction for computing in the 21st century and postulated that location will be one of two issues of crucial importance: “ubiquitous computers must know where they are” [
19].
Weiser’s sketch of the future has morphed from ubiquitous computing to ambient intelligence. We expect the geometry of the elementary parts of an entire urban environment to be available at a human scale to be searched; we foresee that this becomes the basis for locations of fixed sensors, or moving GPS-tracked sensors, to read the RFID- and other tags of goods to be placed inside buildings, even inside individual rooms. In analogy, triangulated cell phones as well as tags can also place persons inside buildings and rooms. A semantically interpreted 3D city model could help find one’s briefcase, an errant person, the nearest copying machine and will affect the use and behavior of all sorts of computer-driven gadgets.
3. Going through a Processing Framework
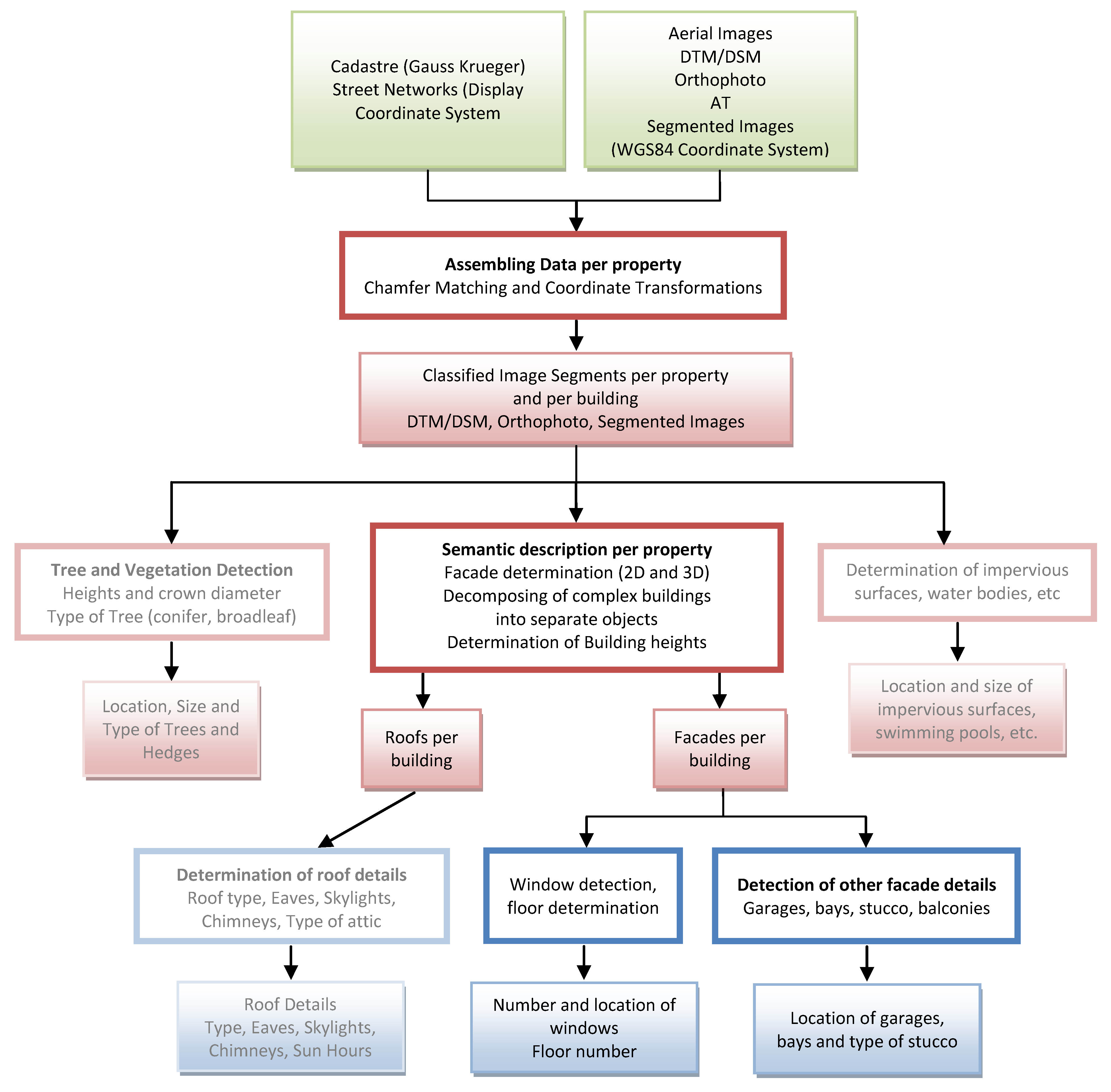
Low cost by automation and a reliance on pre-existing sources has led us to define a general processing framework (
Figure 2). We start out by conflating (merging) geometric data from essentially two sources: the aerial imagery and the cadastral information.
Figure 3 and
Figure 4 cover an example of a 400 m × 400 m urban test area in the city of
Graz (Austria). Conflation defines each property as a separate entity for further analysis, not unlike previous authors have proposed [
20]. The cadastral data may also contain preliminary information about a 2D building footprint. Conflation is part of a pre-processing workflow and results in all geometric data being available per property and in a single geometric reference system.
We now proceed towards the use of the dense 3D point clouds associated with the aerial photography and extracted from it by means of a dense matcher applied to the triangulated aerial photographs [
21]. “Dense” refers to the fact that each image pixel gets assigned a terrain elevation value. The surface model is thus at a spacing equal to the Ground Sampling Distance (GSD) of the images. The extraction of data per building and per element of vegetation comes first. This finds the areas occupied by a building as well as its height. For vegetation we need to find the type, its location, the height and the crown diameter. The building footprints get refined
vis-à-vis the cadastral prediction using image segmentation and classification to define roof lines.
From the building, one proceeds to the facades: building footprints become facade baselines. A decision is needed on the number of facades. We segment a single building shape so that the footprints of its parts all consist of simple rectangular shapes. This is the basis for addressing the facades. For each facade we must find its intersection with the ground—its footprint. This is the basis for an extraction of the facade in 3D by intersecting it with elevation data. We compute the corner points of each facade. These can then be projected into the block of overlapping aerial photography. We can search all aerial images for the best representation of the facade details; typically this will be the image with the maximum number of pixels for a given facade. Since there are multiple facade images, we prepare for a multi-view process.
Figure 2.
Diagram of the proposed work flow to characterize real properties from aerial images and associated cadastral data (performed processing steps highlighted).
Figure 2.
Diagram of the proposed work flow to characterize real properties from aerial images and associated cadastral data (performed processing steps highlighted).
What follows is a search for rows and columns of windows in the overlapping (i.e., “redundant”) photographic imagery. First of all, this serves to establish the number of floors. Second, we also are interested in the windows location themselves, as well as in their size. And finally, we want to take a look at attics and basement windows to establish whether there is an attic or basement.
While
Figure 2 summarizes the workflow, subsequent sections of this paper will fill in the details based on sample data from
Figure 3 and
Figure 4 from the City of
Graz to explain the approach. The aerial coverage is taken with a ground sampling distance at 10 cm and with overlaps of 80% forward and 60% sideward. Our aim is to show that an automated property characterization is feasible, not least due to the fact that the overlaps produce a10-image coverage of each terrain point.
Figure 3.
True Orthophoto of the city of Graz, 400 m × 400 m, at a ground sampling distance of 10 cm. “True” in that orthophoto implies the aerial photograph has been re-projected considering the elevation of the buildings, so that one cannot see any of the building facades. Shown here are 216 building details: Brockmanngasse, Kopernikusgasse; UltraCamX, acquired in 2007 [Courtesy of Microsoft-Graz].
Figure 3.
True Orthophoto of the city of Graz, 400 m × 400 m, at a ground sampling distance of 10 cm. “True” in that orthophoto implies the aerial photograph has been re-projected considering the elevation of the buildings, so that one cannot see any of the building facades. Shown here are 216 building details: Brockmanngasse, Kopernikusgasse; UltraCamX, acquired in 2007 [Courtesy of Microsoft-Graz].
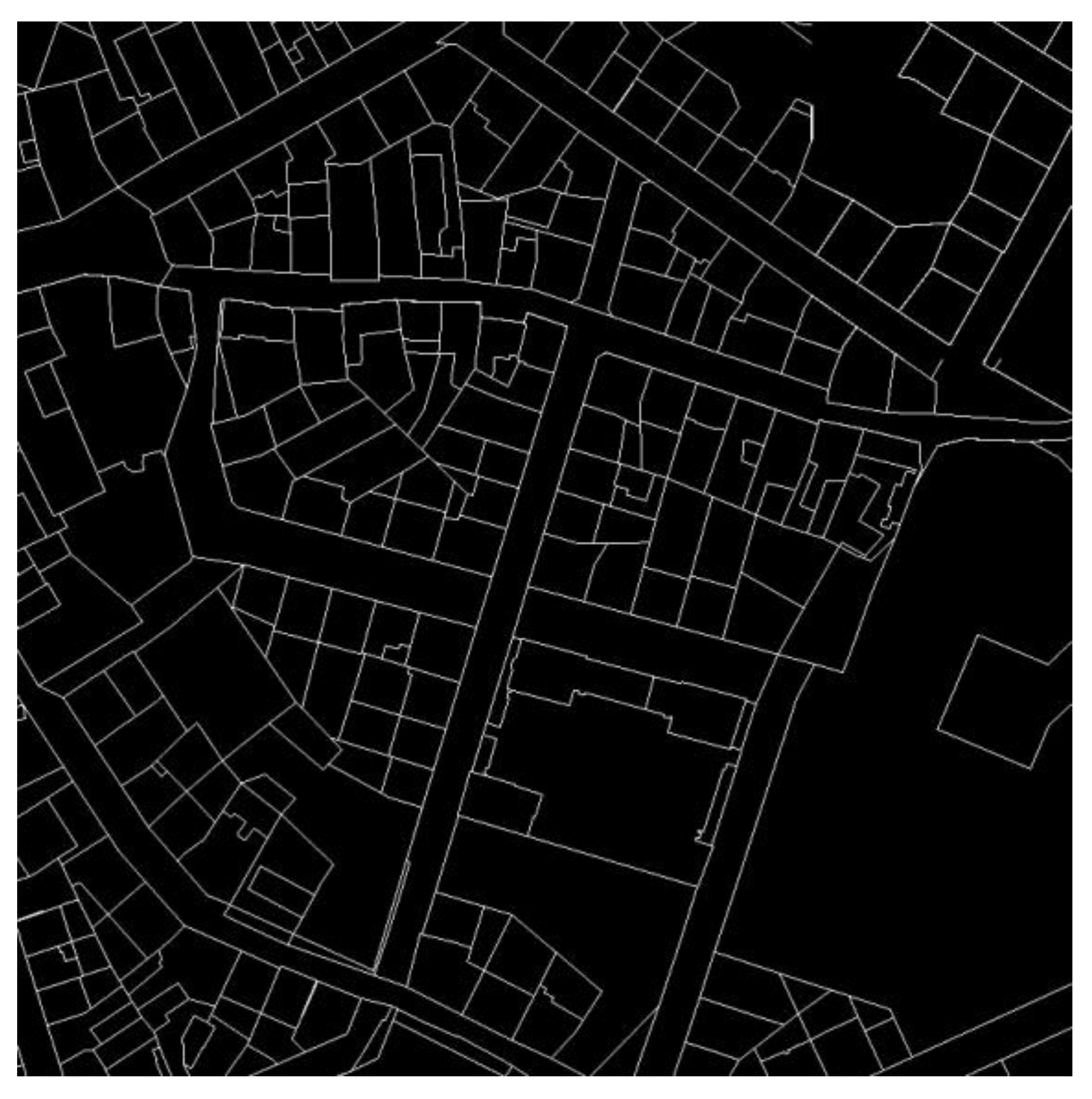
Figure 4.
Cadastral map of
Graz with legal property boundaries is shown for the same area in
Figure 3. The original data is in vector format that has been converted to a raster image at a GSD of 10 cm. Shown are 300 separate parcels [Courtesy of BEV-Austria].
Figure 4.
Cadastral map of
Graz with legal property boundaries is shown for the same area in
Figure 3. The original data is in vector format that has been converted to a raster image at a GSD of 10 cm. Shown are 300 separate parcels [Courtesy of BEV-Austria].
A US-Internet application associates its commercial value with each property (
www.zillow.com), by linking into the public property tax records. In the absence of such records, one would characterize a property before assessing its value. It is this characterization that is the focus of this contribution and may be essential in assessing any value. The characterization of vegetation and roof details [
22] are not discussed in this paper. For more information about vegetation and tree detection please read Hirschmugl
et al. [
23].
4. Source Data
4.1. A Wide Range of Potential Sources for Geo-Data
One can observe a growing avalanche of digital Geodata from imagery, but also from records of GNSS/GPS traces or cellular phone triangulations. The diversity of geo-data is summarized in
Table 1. The association with a geometric resolution or accuracy shows a range between ±2 cm and ±10 m.
Table 1.
The major providers of urban sources for geo-data with typical geometric resolution. A considerable dynamic exists to conflate image, vector and address data, to create updating mechanisms for street-level and address data (Google blog on conflation and updating, [
24]).
Table 1.
The major providers of urban sources for geo-data with typical geometric resolution. A considerable dynamic exists to conflate image, vector and address data, to create updating mechanisms for street-level and address data (Google blog on conflation and updating, [24]).
| OVERHEAD SOURCES | URBAN GSD |
|---|
| 1. Satellite Imagery | 0.5 m |
| 2. Aerial Imagery, vertical | 0.1 m |
| 3. Aerial imagery, oblique | 0.1 m |
| 4. Aerial Laser Scanning (LIDAR) | 0.1 m |
| STREET SIDE SOURCES | |
| 5. Street Side Imagery from Industrial Systems | 0.02 m |
| 6. Street Side Lasers | 0.02 m |
| 7. Crowd-Sourced Images (FLICKR, Photosynth) | 0.02 m |
| 8. Location Traces from Cell Phones and GNSS/GPS | 5 m |
| OTHER DOCUMENTS | |
| 9. Cadastral Maps, Parcel Maps | 0. 1 m |
| 10. Street Maps from Car Navigation | 5 m |
| 11. Address codes with geographic coordinates | 10 m |
The geometry of large urban areas is mapped by aerial photography. While it may be feasible in the distant future that a continuous stream of perennially fresh GPS/GNSS-tagged collections of crowd-sourced imagery will do away with any need for aerial photography, that time has yet to arrive. A coordinate reference is thus being established by an automatically triangulated block of aerial photographs to within a fraction of a pixel across an entire urban space. As previously stated, that reference, in the demonstration area in Graz, is within ±0.5 pixels or ±5 cm.
From the wide range of possible source data in
Table 1, our approach for the property characterization employs subsets “2” and “9” only, namely the original aerial images and cadastral maps. However, the aerial images are used to compute digital elevation data, orthophotos and image classifications. We anticipate that the addition of street network data “10” will augment the characterization result by information about traffic flows. It is worth noting that such data have become widely available at no cost off the Internet.
4.2. Vertical Aerial Images
At the core of the approach are vertical aerial images. In the current test environment we specifically use images from the
UltraCamX [
25]. This, like most digital aerial cameras, produces images in the four colors red, green, blue, and near infrared (NIR), and also collects a separate panchromatic channel. The images often have ~13 bits of radiometric range; this is encoded into 16 bits per color channel [
26,
27]. The entire administrative area of the city of
Graz consists of 155 km
2 and covers the dense urban core and rural outlying areas. This surface area is covered by 3,000 aerial photographs that have been flown with along-track overlaps at 80% and across-track at 60% with a GSD of 10 cm. This large number of aerial photographs far exceeds, by an order of magnitude, what one would have captured with a film camera and manual processing. The overlaps would have been at 60% and 20%, and the geometric GSD would have been at 20 cm, largely driven by concerns about the cost of film and of manual processing scaling with the number of film images.
Standard photogrammetric processing is being applied to such a block of digital photography using the
UltraMap-AT processing system. The word “standard” is applicable in terms of the principle of photo-triangulation itself, but the procedure is far from standard when considering the data quantities and the level of automation [
28]. Full automation is achieved first because of the high image overlaps; a second factor is the use of a very much larger number of tie-points than traditional approaches have been using. The aerial triangulation process therefore results not only in a pose for each aerial photograph, but also in a sparse cloud of terrain points, since about 1,000 tie-points are found per aerial photograph [
29,
30]. The accuracy of the triangulation is in the sub-pixel range of ±4 cm in planimetry and ±6 cm in height [
27]. The sparse cloud of terrain points may be at 20,000 per km
2.
4.3. Oblique Aerial Images
There is a need for simple measurements in urban spaces by non-expert users in municipal administrations. This combines with the appeal of a bird’s eye view of a neighborhood and has led to the introduction of oblique aerial photography [
30]. One application for this type of imagery has been in support of the location aware Internet, so far mainly in
www.bing.com/maps, and in the regional site
www.klicktel.de.
Because the viewing angles of facades are typically at 45° and thus larger in oblique than in vertical photography with its 27° at the image’s edges, one might be tempted to consider oblique sources in the facade analysis. Taking oblique images off the Internet allows one to compare the vertical and oblique views of specific facades (see
Figure 5). We will show that occlusions due to these large angles are severe and prevent one from obtaining useful floor and window counts from oblique aerial sources especially in historic cities like the city of Graz in Austria. For a more detailed description about this topic please read Meixner
et al. [
31].
Figure 5.
Oblique aerial image at 45° look angle taken from Bing Maps (left); Vertical aerial image obtained from UltraCamX at a look angle of 27° (right). The marked sections in the original image segments (above) have been rectified (below).
Figure 5.
Oblique aerial image at 45° look angle taken from Bing Maps (left); Vertical aerial image obtained from UltraCamX at a look angle of 27° (right). The marked sections in the original image segments (above) have been rectified (below).
4.4. Derived from Vertical Aerial Images: DSM and DTM Data
The Digital Surface Model (DSM) is created by “dense matching”. The input consists of the triangulated aerial photographs. In this process, one develops point clouds from subsets of the overlapping images and then merge (fuse) the separately developed point clouds of a given area. The process is described by Klaus in [
21]. For property classification, the elevation data are considered as input. Data used in our property-related experiments have been obtained from work at
Microsoft Graz [
27]. The conversion of the surface model DSM into a Bald Earth Digital Terrain Model (DTM) is a post-process of dense matching and has been described by Zebedin
et al. [
32].
The postings of the DSM and DTM are at 2 pixel intervals, and result in about 25 million points per km
2, far denser than traditional photogrammetry rules would support. However, because the overlaps of 80% and 60% result in 10 images per ground point, one is observing a type of “super-resolution” that supports a very dense sampling of terrain points. It has been shown that the vertical accuracy of such DSMs is in the range of about ±0.5 pixels [
33], provided the surface is well defined.
4.5. Derived from Vertical Aerial Images: True Orthophoto
The DSM is the reference surface onto which each aerial photograph is projected. The DSM and its associated photographic texture are then projected orthogonally into the XY-plane and result in what is denoted as a “true” orthophoto. In this data product, the buildings are only shown by their roofs, not however by their facades. Given the overlaps of the source images, the orthophoto can be constructed in such a way that all occlusions are avoided. Image detail in the orthophoto is therefore taken from multiple aerial images in a manner that would not be customary in traditional film-based orthophotography.
In the current context, the true orthophoto is an auxiliary tool for visual inspection of intermediate results. One could also use traditional orthophotos that have been projected not onto the DSM but onto the Bald Earth DTM instead. The traditional orthophoto would, however, show far less concurrence with the cadastral map. For further details about this method see Zebedin
et al. [
32] and Oda
et al. [
34]. Another possibility of generating true orthophotos is to use a fusion step where massive redundant image data is transformed to a common (ortho) view and processed with e.g., variational methods as described by Zach
et al. [
35] or Kluckner
et al. [
36].
4.6. Derived from Aerial Images: Classification into Segmented Images
Any urban area of interest can be covered by multiple color aerial images. These can be subjected to an automated classification to develop information layers about the area. We consider these as input for our characterization procedures. The classification approach used here has been described by Gruber-Geymayer
et al. [
37] and Zebedin
et al. [
32]. However, classification and segmentation methods are topics of intense research. For example Kluckner
et al. [
38] have proposed alternative novel methods with good results specifically interpreting urban scenes imaged by the
UltraCam digital aerial camera.
Standard classifications of 4-channel digital aerial photography typically lead to seven separate data layers: buildings; grass; trees; sealed surfaces; bare earth; water; other objects (“unclassified”). The unclassified areas may show lamp posts, cars, buses, people,
etc. Gruber-Geymayer
et al. [
39] report typical classification accuracies in the range of 90%: this means that a 10% error is being made either by assigning a class in error or not assigning any class.
4.7. Cadaster for Property Boundaries
Since a “property boundary” is a legal concept, it is not typically visible in the field and from the air. Also image segmentation algorithms cannot properly distinguish between buildings when they are physically attached to one another. It will be the rare exception that attached buildings can be separated from aerial imagery, for example if the roof styles differ, building heights vary or the colors of the roofing tiles differ. Obviously then one needs to introduce the cadastral map.
Cadastral information has a long history that is reflected in a need to consider its national circumstances and historical development to avoid negative surprises. The accuracy and the historical development of the Austrian land register can be considered to be at a rather highly developed level not found in many countries.
For the study area in the city of
Graz we have cadastral data available from the year 2008, provided by the Austrian Federal Mapping Agency
Bundesamt für Eich- und Vermessungswesen (BEV, see
Figure 4). The cadastral information addresses property boundaries, and not necessarily building footprints, although such building data may be provided from the cadastral sources, albeit with some uncertainty and oftentimes somewhat dated. The cadastral accuracy is quoted at ±10 cm which is equivalent to the range of the aerial photography’s pixel size and thus sufficient for the purpose of characterizing real properties [
40].
4.8. Optional Street Network and Address Data
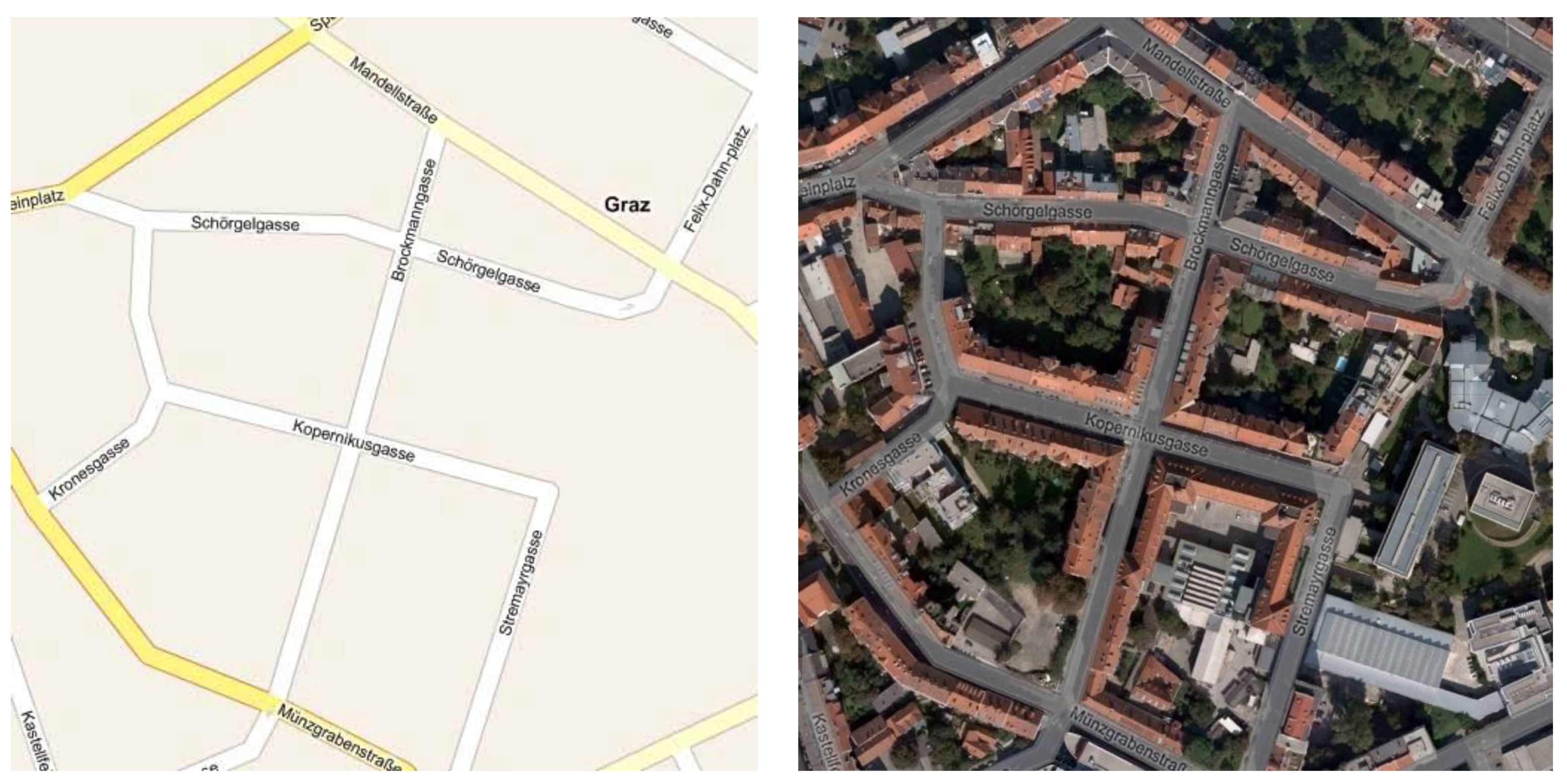
Car navigation has been the driver for the global development of digital street maps. They also support location awareness of Internet searches. Since the vector format of street maps is not available free of charge, it is at times re-engineered from the raster display off the Internet [
41]. The example for the
Graz study site, in
Figure 3 and
Figure 4, illustrates the scarcity of street map. And yet it can add unique information about traffic and traffic-related property-characteristics. Of course the street maps would take on a much elevated importance if there was no cadastral data (
Figure 6).
Figure 6.
Street layer for the area in
Figure 3 taken off the Internet search system
Bing Maps (Microsoft, November 2009). The raster GSD has been resampled to fit the aerial imagery sources at a GSD of 10 cm. To the right is a “hybrid” view of the street layer superimposed onto the orthophoto.
Figure 6.
Street layer for the area in
Figure 3 taken off the Internet search system
Bing Maps (Microsoft, November 2009). The raster GSD has been resampled to fit the aerial imagery sources at a GSD of 10 cm. To the right is a “hybrid” view of the street layer superimposed onto the orthophoto.
Address information is encoded in the form of a point and its geographic latitude and longitude. This is valuable when attaching alphanumeric information to a property. Again, this source is of elevated importance when one needs to cope with the absence of a cadaster. Between the street map, address data and the orthophoto, one will have to devise a strategy for approximating cadastral information.
4.9. Comments
All image-based source data for the proposed property work are the result of extensive computation and data processing, some of which constitutes the outcome of considerable recent innovations, such as dense image matching and fully automated aerial triangulation. However, none of this processing is specific to the property characterization; therefore we do not address it in this paper.
The growing diversity of Geodata sources has recently been discussed by Blumenthal [
24] with respect to efforts made at
Google. Two innovative phenomena stand out: crowd sourced imagery and motion traces. Both may have an impact on the property characterization as such data becomes increasingly more available. The detail from crowd sourced imagery (also denoted as Community Photo Collections CPC) will probably exceed by a level of magnitude that of aerial imagery. The developments in this domain hold great promise [
42,
43,
44]. Even new words are being introduced to deal with these changes, for example “neo-geographer” [
45]. A separate novel type of Geodata is the motion trace offering the option of modeling noise from traffic.
The Graz study area is 400 m × 400 m and contains 216 buildings situated on 321 parcels. This suggests that multiple parcels may combine into a single property.
5. Assembling Data per Property
5.1. Chamfer-Matching the Cadastral Map with the Building Classification
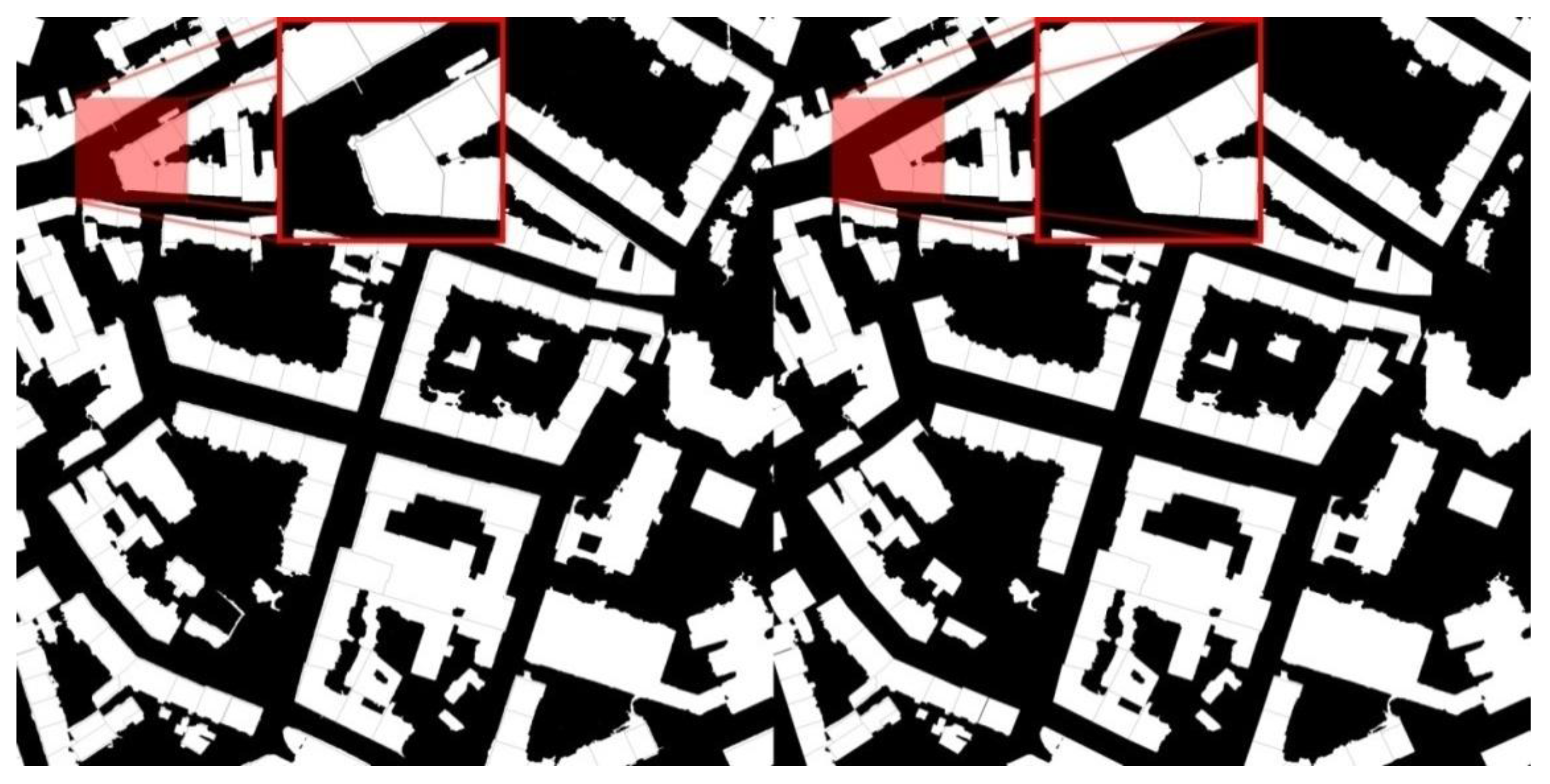
Most cadastral maps, including the Austrian cadastre, basically present a 2D data base and ignore the 3rd dimension. This causes issues when relating the cadastral data to the aerial photography and its inherently 3D data products. Co-registration therefore may be accomplished using the 2D building classification and a match between this and the 2D-cadastral map. Once this co-registration is achieved, the cadastral data are also geometrically aligned with all the orthophoto and other photo-derived data sets.
A 2-step process serves to match the 2D cadastral vector map (in its own coordinate system) and the 2D orthophoto (with its different coordinate reference). In a first step, the cadastral point coordinates simply get converted from their
Gauss-Krüger M34 values to the building classification’s
Universal Transverse Mercator UTM system. In an ideal world, this would solve the registration problem. However, it does not, as illustrated in
Figure 7 (left).
Figure 7.
Overlaying the cadastral map over the orthophoto will leave some small errors that need to be found and removed. Left is the overlay after step 1 of the registration, namely the coordinate transformation from the Gauss-Krüger to the UTM system. To the right is the result after a Chamfer-match has been applied. The area is a segment of the study area in
Figure 3.
Figure 7.
Overlaying the cadastral map over the orthophoto will leave some small errors that need to be found and removed. Left is the overlay after step 1 of the registration, namely the coordinate transformation from the Gauss-Krüger to the UTM system. To the right is the result after a Chamfer-match has been applied. The area is a segment of the study area in
Figure 3.
A second step is thus needed to achieve a fine alignment of the cadastre and the building classification. This is because small projection errors exist in the range of a few pixels (some tens of cm).
This adjustment is accomplished by a so-called Chamfer-match, here implemented after Borgefors [
46]. The algorithm converts the vector image of the cadastral map into a raster image and assigns a grey value to each pixel as a function of the distance from the nearest vector. This is denoted as a distance image. The resulting raster image from the cadastre is shown in
Figure 8. In a similar fashion, the building classification is transformed into an edge image. Chamfer-matching now employs these two computed auxiliary raster images by overlapping them to find small geometric changes to make them fit optimally. In our case this linear alignment is computed for the entire image patch. For this data set no non-linear misalignments like shearing or rotation occur, they are all solved in the first step.
Figure 7 (right) supports the conclusion that discrepancies have been reduced from their previous ±7 pixels down to a mere ±2 pixels (GSD = 10 cm).
Figure 8.
Cadastral raster image in the format of a computed distance transform image
(left) and the edges of the segmented image
(right), both used as an input to the Chamfer-match after Borgefors [
46].
Figure 8.
Cadastral raster image in the format of a computed distance transform image
(left) and the edges of the segmented image
(right), both used as an input to the Chamfer-match after Borgefors [
46].
5.2. Class-Specific Segmentation per Individual Properties
The image segmentation result has the same coordinate system as the orthophoto. Therefore the cadastral map can be used directly to cut a classification map into data per property.
Figure 9 illustrates the result.
An evaluation of the automated segmentation is based on manually developed ground truth. For the example of the building information, the result confirms that the classification approach implemented by Gruber-Geymayer
et al. [
37] and Zebedin
et al. [
32] delivers an accuracy of 90%. Classification uncertainties are caused by mismatches between cadastral line work and the building outlines when a cadastral boundary line coincides with a building facade. We may find facade details such as balconies, or roof extensions in the form of eaves that violate cadastral delineations. Having the cadaster available offers one the option of changing the segmentation and classification along building and property boundaries.
Figure 9.
Three separate sample properties and the source data per property. To the left in column (a) are the orthophoto segments. In column (b) are the elevation data (DSM), in column (c) are the elevations on top of the Bald Earth. Column (d) shows the classification result with seven object classes.
Figure 9.
Three separate sample properties and the source data per property. To the left in column (a) are the orthophoto segments. In column (b) are the elevation data (DSM), in column (c) are the elevations on top of the Bald Earth. Column (d) shows the classification result with seven object classes.
While we assume that these small differences will be insignificant in the application to a property characterization, we do want to understand and hopefully reduce or remove them. A roof’s eave causes a small parallel shift
vis-à-vis the cadastral data to make them fit the segmentation result. The inconsistencies from bay windows or balconies also would disappear if one were to redraw the classification boundaries. These interventions would affect the classification results and rate of misclassifications. These considerations create the need for methods to automatically improve the alignment of the cadastral line work and the segmentation boundaries. This could be possible e.g., by using a variational boundary regularization. Until such algorithms are developed and implemented, we perform such minor improvements by hand.
Figure 10 illustrates the discrepancies and their removal.
Figure 10.
Overlay of segmented image and cadastre for one of the samples in
Figure 9. Left is with the discrepancies due to roof eaves and facade detail, to the right is a manually cleaned-up version.
Figure 10.
Overlay of segmented image and cadastre for one of the samples in
Figure 9. Left is with the discrepancies due to roof eaves and facade detail, to the right is a manually cleaned-up version.
5.3. Dense Point Clouds per Property and per Building
In the current test area, the DSM/DTM are an elevation raster in the coordinate system of the photogrammetric block and at a posting interval of 20 cm. Cutting the large area dense DSM/DTM data set along property boundaries is trivial and based on the cadastral data after Chamfer refinement. A per-property presentation of the various map data is shown in
Figure 9.
Elevation values associated with the classification layer “building” will provide a visual impression of the building shape. Similarly, elevations associated with a vegetation layer will describe the shape of trees. This seems analogous to the processing performed for the current search-driven 3D “eye candy” of
Figure 1. However, in those data sets, the property boundaries do not play any role.
5.3. Discussion
The cadaster-based separation of the images, classification results and elevation data is fundamental to achieve the description per property. In the absence of a well-developed and accurate cadastral system, one would have to devise an approach with street maps and address points. Each address point would be a seed pixel in the imagery which point the area of a property can be defined. The street map would delimit the properties vis-à-vis public spaces. Properties would have to be defined from these approximations and rely on image content. Cadastral information without a cadastral survey would be required and this represents a future research challenge.
6. Development of a Description per Property
As a by-product of the data segmentation per property one obtains several important features: land area, areas used up by buildings, vegetation, water bodies, and impervious surfaces. We have previously established that the areas are at an accuracy of within 90%, largely due to limitations of the classification process.
By introducing the 3rd dimension in the form of the dense point cloud, one adds relevant property information and improves the accuracy of area measurements previously obtained in the 2D classification. An overriding role is associated with buildings; therefore they are the focus of our initial efforts. Going through each property, we add descriptive information about its buildings.
6.1. Finding the Footprint of Facades in 2D
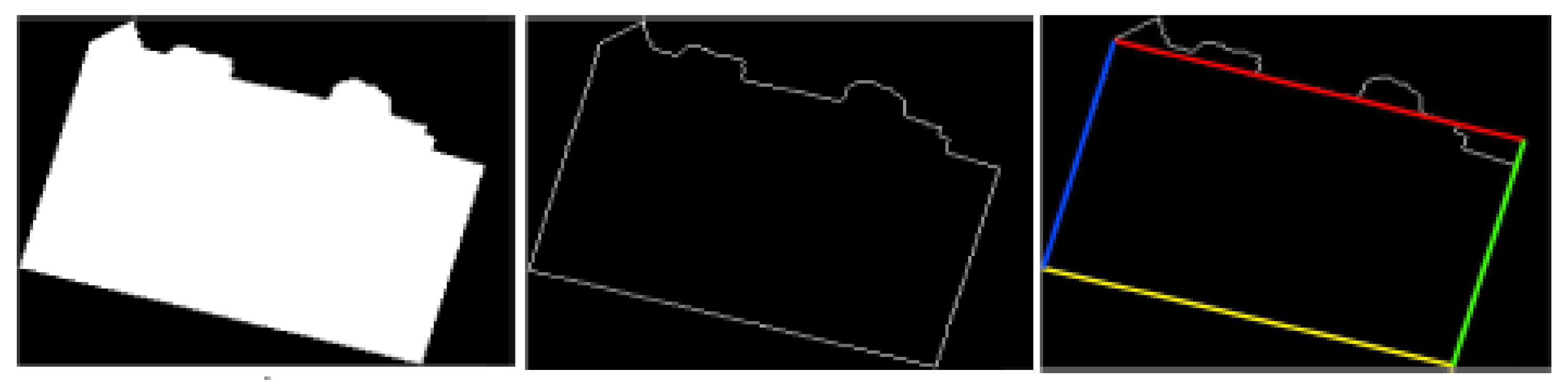
(a) Vectorizing the Building Contour
The contours of building objects from the image classification approximate the intersection of the facades with the ground. Initial contours need to be vectorized. This process is developed, for example in the Douglas-Peucker algorithm [
47] in 1973. It replaces the contour pixels by straight lines, each extended line segment defining a facade, as illustrated in
Figure 11.
Figure 11.
The classification layer “building” is based on color and texture. The left shows the binary layer, center is its contour in raster, and finally on the right is the geometric figure of the footprint.
Figure 11.
The classification layer “building” is based on color and texture. The left shows the binary layer, center is its contour in raster, and finally on the right is the geometric figure of the footprint.
(b) Vectorizing the Points along the Vertical Elements in the DSM
A second independent information source for a facade is the DSM. The first derivatives of the Z-values along X-rows and Y-columns of the dense point cloud represent the surface tangents. Where this is vertical, one will have a facade point.
(c) Fusing two Facade Data Sets: Segmentation Contours and DSM-Derivatives
The facade footprints from the image classification based on 2D color and texture need to be fused with the footprint from the 3D point cloud of the DSM. One initial approach is to simply use the mean between the two largely independent measures.
(d) A Property Boundary Cutting through two Connected Buildings
In the special case where a property boundary cuts through a building or through connected buildings, one does not have a facade. Such cases need to be recognized. We achieved this by means of the 3rd dimension, as discussed below in
Section 6.3.
At the end of steps (a) through (d) one obtains a series of straight line segments, each representing the footprint in 2D of a particular facade.
6.2. Decomposing a Building into Separate Building Objects
At issue is the number of a building’s facades and thus the building’s complexity. The simplest building will have four facades at right angles. However, there is no limit to the complexity of building shapes and thus of the number of facades, and also of the angles formed between adjacent facades.
The option exists to fit the pattern of facade footprints into a series of predefined shapes of (rectangular) building footprints. In the process one hopes to develop a set of separate non-overlapping basic building objects or “sub-buildings”. This could be obtained via a segmentation of the building footprint. However, one could also review the roof shapes. Having more than one local maximum in the roof height is an indication that the single building has a complex shape and should be segmented into multiple building objects or sub-buildings. This is of course not the case for all roof types e.g., gabled roofs.
6.3. Adding the 3rd Dimension to the Facade
Along the footprints of the facade one finds elevation values in the DSM. These attach a 3rd dimension to the facade. The simplest facade shape is a rectangle. Depending on the shape of the roof, a facade could also have a complex shape. Should the elevations change along the facade footprint, we could be facing a sloping ground or a varying roof line, or a combination of both. The slope of the ground is known from the DTM. Variations of the roof line are available from the difference between the DSM and the DTM. For use as a property descriptor, one might be satisfied with a single elevation value for each facade. Therefore we initially associate a vertical rectangle to each facade.
We have previously mentioned connected buildings and a property line cutting through buildings, leading to virtual facades. These can be identified via a look at the dense point cloud. The elevation values above the Bald Earth along a facade footprint will be zero at one side of the footprint. If they are not, then this facade will be marked as “virtual”.
6.4. From the Facade to the Height of a Building and Its Roof
As a minimum, we want to use two elevations values for each building: the height of the roof line and the height of the roof’s highest point. But given that a building has multiple facades, possibly built on a sloping ground and does not have a single roof line, one is faced with a more complex issue than expected. For simplicity, we initially average the multiple facade heights to a single value, and we define the roof height as the elevation difference between the highest point on the roof and the computed facade height.
6.5. Occlusions
Parts of buildings may be occluded by vegetation, other buildings or other objects such as cars or people. Any detailing of building information must be built with an understanding of the existence of occlusions. We see two approaches to deal with this issue. The first is the reliance on the known incidence angles defined by the camera station and neighborhood facade footprints. As one processes overlapping images and obtains different results, these differences themselves can indicate the effect of occlusions and cause a second look to be given to identify an occlusion. A second approach is a geometric process using the facade footprints, the DSM and the camera station. Occlusions get computed by Z-buffering or ray tracing.
7. Counting Floors and Windows
7.1. Vertical Aerial Photography
We proceed from the basic building description to an analysis of the facades. Work on building facades would intuitively build on street level photography or at least oblique aerial imagery. However, our interest is in understanding how well one can study facades in (cost free) vertical aerial photography. The facade detail of interest is a floor count, a window count and a description of the window’s location and size.
The facade’s geometry is assumed to be quadrilateral and has been produced from the intersection of the facade footprint with the DSM. This delivers four facade corner points in 3D object coordinates and gets projected using a perspective projection into the aerial imagery, as illustrated in
Figure 12. The rectification of the image content is applied by using a 2D bilinear interpolation to resample the image in a novel view. Typically, overlaps cause many aerial images to show the texture of a given facade.
Figure 13 presents four images of one of the two separate facades of the building in
Figure 12. The projection is based on the pose values of each image from the aerial triangulation.
Figure 12.
Two facades of one building are shown in the original vertical aerial photograph (above) and rectified into a facade plane (below). The facade quadrilateral is superimposed over the aerial photography to obtain the photo texture for further analysis.
Figure 12.
Two facades of one building are shown in the original vertical aerial photograph (above) and rectified into a facade plane (below). The facade quadrilateral is superimposed over the aerial photography to obtain the photo texture for further analysis.
Figure 13.
From a single facade of the building in
Figure 11, one will obtain multiple segments of vertical aerial images. These have been rectified into a facade coordinate system. From an aerial image block showing typically 10 images for each object point, not all will contain useful data for a specific vertical facade. Selected here are the four best, where “best” is defined as the largest area of a facade quadrilateral projected into an image.
Figure 13.
From a single facade of the building in
Figure 11, one will obtain multiple segments of vertical aerial images. These have been rectified into a facade coordinate system. From an aerial image block showing typically 10 images for each object point, not all will contain useful data for a specific vertical facade. Selected here are the four best, where “best” is defined as the largest area of a facade quadrilateral projected into an image.
7.2. Floors
From the building’s appearance, floors normally get defined by windows. Where this fails may be in industrial plants or some contemporary public architecture. In any event, windows will always be a defining element of any facade, and will also be associated with floors. A procedure for finding a floor count has been developed using the steps in
Table 2. It addresses a facade in a single plane and without significant extrusions.
Table 2.
Procedure for floor detection in simple planar facades.
Table 2.
Procedure for floor detection in simple planar facades.
The approach of
Table 2 is illustrated in
Figure 14. A floor count can be applied to each of a set of overlapping facade images. If there was a discrepancy in the result, some logic would need to be applied to resolve the ambiguity. To solve these ambiguities, we introduce constraints like minimum floor height, minimum distance between two floors and the maximum number of floors according to the facade height. Another limitation may exist when the edge histogram fails to have a distinct extremum. This might indicate that the facade/building is complex and that a refined approach should be used. One such option is the development of a 3D facade point cloud, as discussed below.
Figure 14.
Binary Prewitt edges in (a) are vertical, in (b) horizontal. The sums of edge values are shown in (c) as a count of the number of floors.
Figure 14.
Binary Prewitt edges in (a) are vertical, in (b) horizontal. The sums of edge values are shown in (c) as a count of the number of floors.
7.3. Windows
Window detection has been of some interest in recent years. Algorithms like boosting have been applied by Grabner
et al. [
48] to detect cars in aerial photography and windows in street-level images. Cech and Sara [
49] have developed a window detection based on a library of window shapes, analyzing street-level photography, as did Lee and Nevatia [
50] who based their approach on edge images. Other examples in the field of window detection are the works from Reznik and Mayer [
51] or Wenzel and Förstner [
52]. These approaches have been subjected to only limited experimental analysis, but are generally reported to find windows in a rather robust manner. In the current application we need to deal with vertical aerial photography and source data with more noise than street level images have.
Given our floor counts, we are reusing the intermediate Prewitt edges to also find the windows per floor. An approach that simply “intersects” the locations along the pixel rows and columns with the maximum edge sums will work if all windows are regularly arranged. While this is often the case, it is not always true. Therefore Lee and Nevatia [
50] have proposed a variation of the approach. To refine the locations of the windows a one dimensional search for the four sides of a window is performed. For every side of a window one hypothesizes a straight line segment and moves this in the two cardinal directions for a best fit with the image texture.
We find this method applicable to images with lower resolution, as is the case in facades imaged in vertical aerial photography. Also not only rectangular windows but other window designs can be automatically detected as well and rather quickly, without training the program in advance. The window count is applicable in each image segment of a given facade, separately. Or one might want to merge the edge data sets and apply single window detection to the sum of all edges. A comparison of the various different methods for window detection is pending and will be subject of ongoing work.
7.4. Multiple Facades per Building
We may find different floor numbers from the multiple facades of one building. It is possible that a building has different floor counts on a sloping terrain. Since the Bald Earth as well as the slope of a building footprint is known, this must enter into the floor count.
We have redundant information also from overlapping images all showing one and the same facade.
Figure 15 illustrates four results for one single facade imaged four times. The window locations are defined to within ±3 pixel in both horizontal as well as vertical directions, converting to a value of ±0.3 m vertically and ±0.3 m horizontally. In this example all 28 windows of the facade were found in all four aerial images.
Figure 15.
Four images on one facade from
Figure 12 lead to independent floor and window counts. It is to be noted that the floor counts and the number of windows concur with the visual inspection.
Figure 15.
Four images on one facade from
Figure 12 lead to independent floor and window counts. It is to be noted that the floor counts and the number of windows concur with the visual inspection.
7.5. Experimental Results
The Graz test area with 400 m × 400 m, containing 216 buildings is imaged onto 20 aerial photographs. From the available buildings we randomly chose 104 with a total of 225 facades in vertical aerial photography. Facade images with look angles below 5° were eliminated from further analysis. Each facade is typically imaged at the edge of the vertical aerial photos using look angles between 20° and 27°.
Considering oblique images from bing.com/maps, we also have 120 facades in the test area shown at look angles of around 45°. While a given facade is only imaged onto a single oblique image, they are imaged on average on four vertical images, even if eliminating the small look angles. As a result we have 870 facade images of the given 225 facades. It is very quickly obvious that in any quantitative analysis, oblique images will be seriously compromised by occlusions. In the case of vertical images, occlusions are reduced as the look angles become steeper. And since we operate with four or more vertical images of each facade, we can exploit the redundancy to find a most likely correct floor and window count.
Table 3 summarizes the results of the experimental work. With the workflow described earlier, each of the 870 image segments of the 225 facades is processed. Similarly, the oblique images are also processed. Then the facade images are classified by their look angles and a count takes place of the number of images in which the floor counts, and separately the window counts, were correct. In the look angle segment between 15° and 20° one finds 103 facades, and in 79 of those, the floor count was correct. Similarly, in the same look angle range, the window counts were correct in 174 of the 221 image segments.
Table 3.
Correct number of floors (above) and number of windows (below) from vertical images versus look angles. Right shows oblique result: Floor counts are compromised by occlusions.
Table 3.
Correct number of floors (above) and number of windows (below) from vertical images versus look angles. Right shows oblique result: Floor counts are compromised by occlusions.
| Angle [deg] | < 5 | 5–10 | 10–15 | 15–20 | 20–25 | >25 | Oblique |
|---|
| Floors | 0 | 7 of 21 | 79 of 103 | 191 of 221 | 255 of 279 | 228 of 246 | 90 of 120 |
| Floors, % | 0 | 33 | 77 | 86 | 91 | 93 | 75 |
| Windows | 0 | 6 of 21 | 69 of 103 | 174 of 221 | 233 of 279 | 212 of 246 | 79 of 120 |
| Windows, % | 0 | 29 | 67 | 79 | 83 | 86 | 66 |
These numbers can be condensed into a single figure of merit, for example if one decides on a single floor and window count per building from multiple values in overlapping images. In total the 104 test buildings have 387 floors and 2,646 windows. One finds the following:
| Accuracy of building detection | 100% | all 104 buildings were detected; |
| Accuracy of floor count | 93% | of all 397 floors counted; |
| Accuracy of window count | 86% | of all 2,646 windows counted. |
Consideration of the cause of failures finds occlusions as the major culprit, followed by facades deviating from the assumption that they are within a single facade plane, and that windows are unobstructed by balconies or awnings.
8. Introducing 3D Facade Point Clouds
8.1. 3D Detail in Facades
Facades are not always in a single plane.
Figure 16 presents a typical example of a building side consisting of various details such as extruding staircases and awnings. The application of the previous workflow to this type of facade will fail because there will not be useable edge histograms, and the process will deliver a failed classification. A possible elimination of these problems could be a splitting of the facades into multiple facade fragments. However, for our experimental data set of 104 buildings with 225 facades this method would result in a quadruple number of facades, and each image would only show a small element. One will have to cope with ambiguities because of the small size of the facade elements. The biggest problem is that the building classification that is used for the determination of building footprints is not always accurate enough due to misclassifications.
A solution to these types of facades may be in the analysis of 3D facade point clouds.
Figure 16.
To the left is a rectified facade image with its depth structure. To the right is a failed count of windows using the workflow that assumes that a facade is in a single plane. Abandoning this restriction will create a need for 3D point clouds of facades.
Figure 16.
To the left is a rectified facade image with its depth structure. To the right is a failed count of windows using the workflow that assumes that a facade is in a single plane. Abandoning this restriction will create a need for 3D point clouds of facades.
One will have to examine whether 3D facade point clouds can be produced in sufficient detail and resolution from vertical aerial imagery, so that facades can be successfully analyzed. “Success” will be achieved if the 3D point cloud: (a) improves the segmentation of a facade into facade planes; (b) then produces well defined values for the floor and window counts on these facade parts; and (c) finally supports the reconciliation of the facade parts into a single window and floor count for that building.
8.2. Creation of a 3D Facade Point Cloud
Performing a photogrammetric 3D process on a set of overlapping images of a facade taken from the street level is a widely studied endeavor [
53]. The challenge in the current context is different since we rely on vertical aerial photography where facades suffer from major geometric deformations and non-square pixels.
The approach is the same as that used for DSM-creation from highly redundant photography. The workflow has been described by Irschara
et al. [
54], but is very similar to workflows at many computer vision laboratories, for example Gösele
et al. [
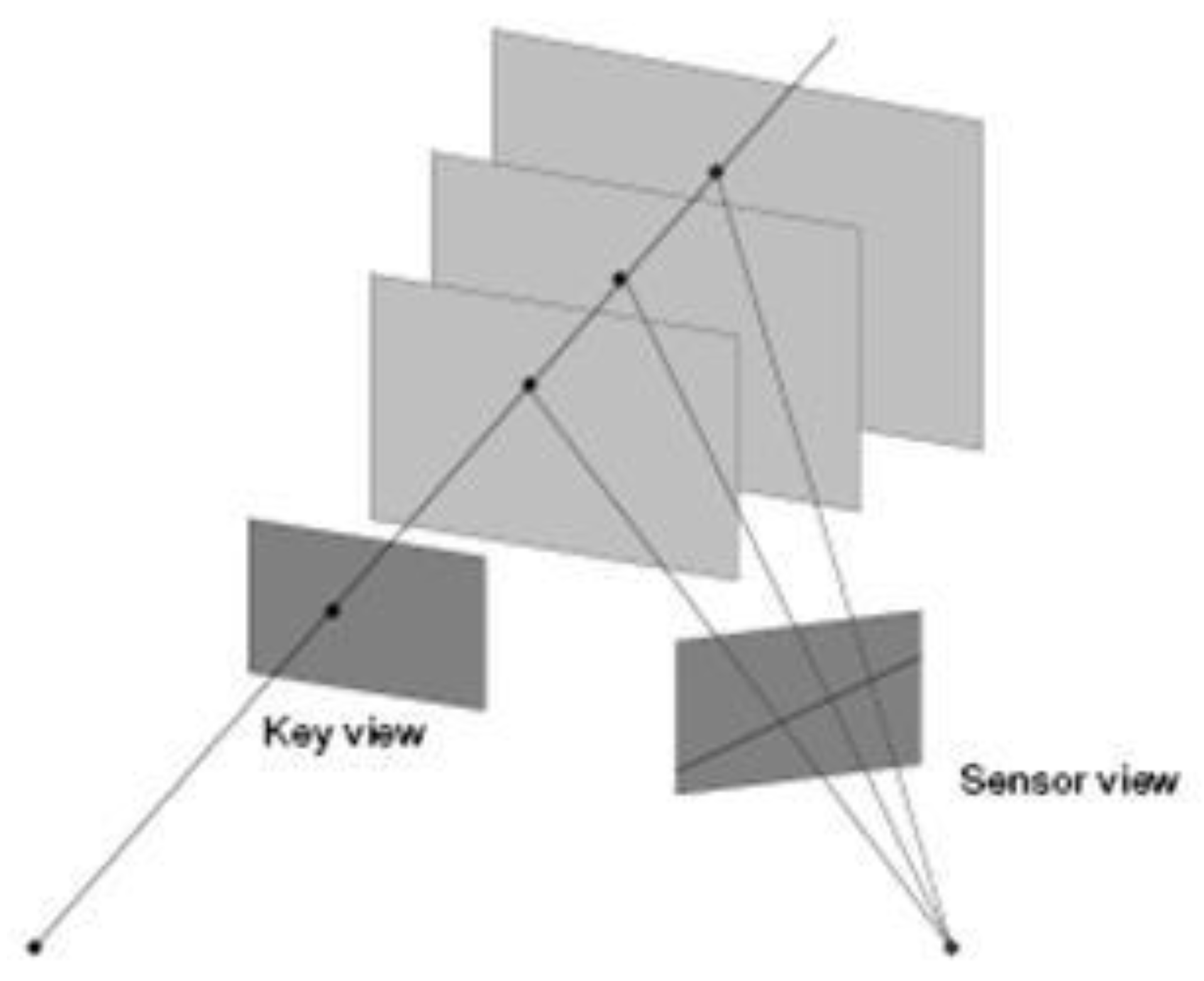
44]. At its core is a so-called plane sweep. We set up a grid in object space consisting of parallel planes at an interval of the pixel size, and intersect these planes with the projection rays of a “key image”.
Figure 17 illustrates the concept.
Conceptually, each sensor image helps one to assign to each point in the 3D grid a likelihood that this grid point is on the surface. To this end, the object points get projected into the sensor image, and a correlation figure-of-merit gets computed at that image location. Since one has multiple overlapping images sensor views, one will get multiple estimates at each grid point. The surface is then defined by an optimization process using both the computed likelihoods at each grid point from image matches, as well as constraints about the surface’s smoothness, thus information about the object. The mathematical formulation of the point cloud generation is found in Zach [
55], Irschara
et al. [
54] and Pock
et al. [
56].
Figure 17.
Our “plane sweep” defines a set of parallel planes in the object space and intersects these planes with the projection rays from a key image, producing an (irregular) 3D grid. All overlapping images are sensor views and help find surface points.
Figure 17.
Our “plane sweep” defines a set of parallel planes in the object space and intersects these planes with the projection rays from a key image, producing an (irregular) 3D grid. All overlapping images are sensor views and help find surface points.
This method has been applied to the four best vertical aerial photographs of the facade of the building in
Figure 16. The 3D point cloud of that facade is shown in
Figure 18. We can recognize the extruded building parts for the staircases. Remarkably, this point cloud comes from vertical aerial photography. The point density is one per pixel, and these are spaced at 10 cm in the horizontal direction and 17 cm in the vertical direction within the facade.
Figure 18.
3D point cloud of the facade shown in
Figure 16. Data extracted from four overlapping vertical aerial photographs. Density of points is (10 × 17 cm) 43,180 points.
Figure 18.
3D point cloud of the facade shown in
Figure 16. Data extracted from four overlapping vertical aerial photographs. Density of points is (10 × 17 cm) 43,180 points.
8.3. Analysis of the 3D Facade Point Clouds
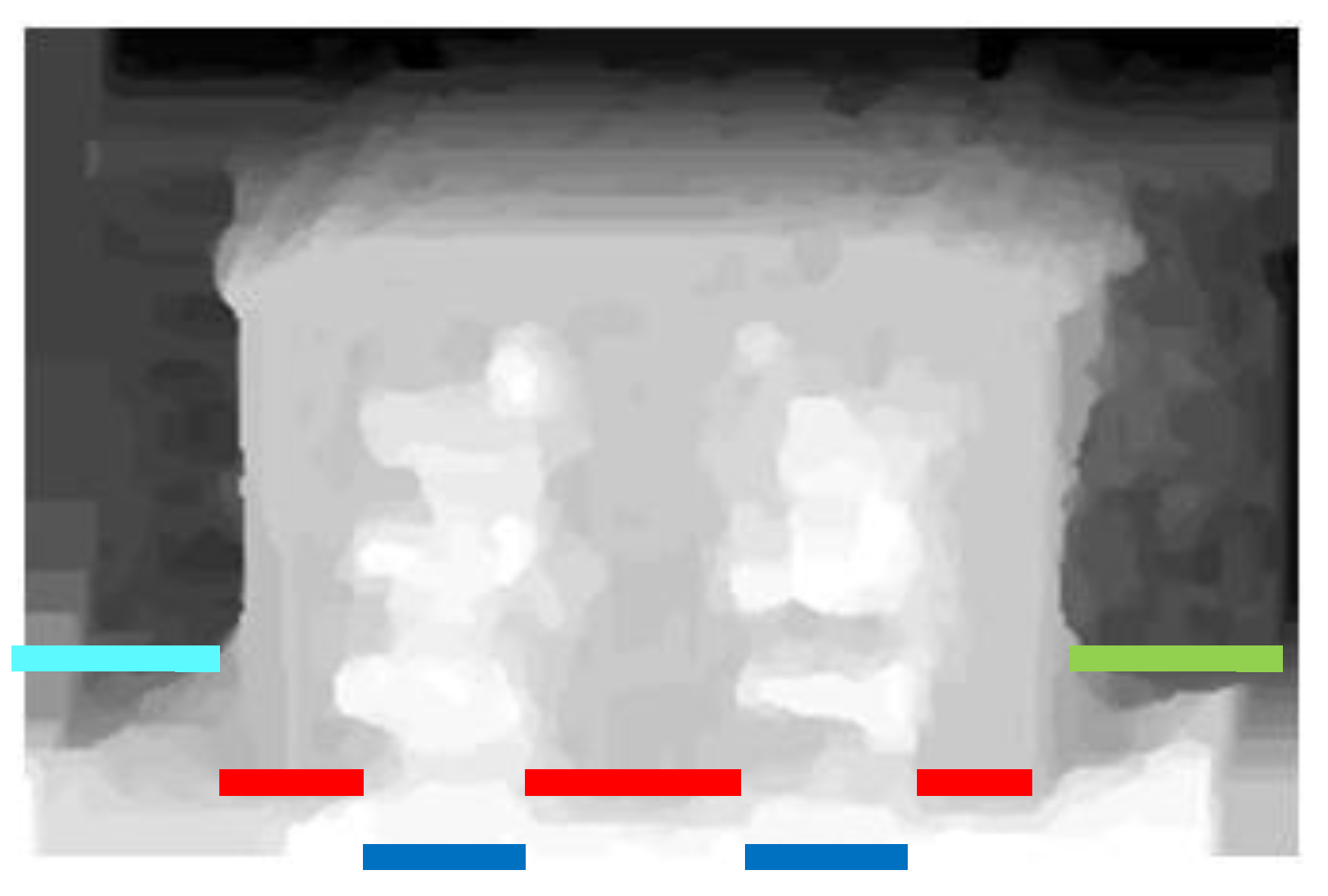
One now has to analyze the 3D points with the goal of segmenting the facade into its planar sub-facades. An initial method to accomplish this moves through the vertical columns of the facade and adds up the point counts. A facade row is found if the point count is high. The color line segments along the foot of the building in
Figure 18 illustrate the result of such an approach.
Figure 19 adds to each sub-facade the photo-texture and visually confirms that the building facade has successfully been segmented for a floor and window count within each plane. We find the existence of four floors and 19 windows, a result that was not possible using the previous 2D method.
Figure 19.
The facade of the building in
Figure 16 has been segmented into plane sub-facades. Each sub-facade is available for a separate floor and window count.
Figure 19.
The facade of the building in
Figure 16 has been segmented into plane sub-facades. Each sub-facade is available for a separate floor and window count.
8.4. Further Developments
There are several avenues for improvements in detail extraction from complex facades, and improvements of our understanding of how well this works. First of course are data experiments in the form of a study with many buildings, thus applying the work flows to many images and many buildings, as well as to a variety of look angles in vertical aerial photographs. Second, is the refinement of the 3D point cloud segmentation by well-thought-out methods of finding planes in point clouds. Third, is the ability of automatically recognizing occlusions and then responding to occluded facades by taking advantage of the overlapping images and their multitude of look angles. Innovations in window recognition will then become relevant, as will be site-dependent approaches to architectural styles.
9. Conclusions
We could demonstrate that vertical aerial photography holds considerable promise as a source of descriptive information about individual properties. Such information is expected to be useful in Internet-based mapping systems. Measures of surface areas covered by a parcel, its buildings and other land use categories, are obvious results from vertical aerial mapping, and are available at an accuracy of about 90% of the surface area. The 10% errors result from uncertainties of a parcel’s definition in an aerial image, given a cadastral record. Uncertainties also exist in the automated classification of the contents of the image and the areas covered by buildings, vegetation, and various land use categories.
While one can expect that 2D measurements of surface areas could be obtained from vertical aerial photography, one might be uncertain about the value of such vertical imagery when analyzing facades. However, our work shows that vertical aerial photography is a valuable source of facade-related information, both in terms of planar facades as well as in the event that facades are complex and require a 3D approach.
Initial work focused on planar facades and resulted in a correct floor count at a rate of 93% and a correct window count of 86%. A study of the dependence of these counts on the angle off-nadir in the images reveals that best results are achieved in the range of 20° to 27° off nadir. At greater angles, such as those used in oblique aerial photography, occlusions start to become distinctive so that floor and window counts fail. Such counts will also fail if a facade is complex, yet the analysis method is unaware of that complexity. One needs then to consider the 3D shape of building facades, for example with extruding stair cases, balconies, awnings. We explain in this paper an approach based on 3D clouds of facade surface points, all extracted from overlapping vertical images. We have explained the approach by example and will have to embark on a systematic study of its performance with many buildings and imaging configurations. It seems not only important to test the work flow on many buildings, but also that the buildings represent a variety of sizes and styles and come from different regions (cities and rural areas) and parts of the world.
The complexity of describing buildings is immense and much work remains to be done. One needs to obtain a good understanding of the accuracy and reliability of a building’s key numbers in all cases. One needs to solve the problems faced when: parts of a building are occluded; the geometric resolution of the source data varies; buildings deviate from expected shapes in the event of add-ons and of complex footprints and roof shapes; the building’s use is mixed and an industrial use leads to windowless facades; cadastral detail contradicts image detail, etc.
At issue in this paper is of course also the motivation for the development of descriptive data about real properties (or real estate). An initial driver to embark on this research has been the disappointment when faced with the lack of detailed information about objects shown in Internet-maps on Google Earth or BingMaps, and the expectation that such information could be available at very little extra cost from image sources in existence for other purposes. Were such detailed information to exist, it could be useful in location-based decisions of both commercial and public interest, and in a better administration of municipal resources. The more thorough use of vertical aerial photography is globally expected to be augmented by significant efforts to conflate various 2D Geodata sources, to be added to business and private address data bases and parcel data, and by the start of massive collections of GNSS and cellular traces. This is separate from an increasing interest in human scale details of urban data that is reflected initially in the form of street-side imagery taken by moving vehicles, but in the long run is expected to come from Community-Photo-Collections (CPC), such as those in FLICKR. This in turn will be part of a broader concept of user-generated content (UGC).
Much of Internet-mapping is currently a result of the search application. However, one may be able to see on the horizon an advent of spatial information as an integral part of the evolution of the Internet-of-Things (“IoT”) and of Ambient Intelligence (“AmI”), as projected by Weiser [
19] or O’Reilly and Batelle [
18].