Environmental Drivers of NDVI-Based Vegetation Phenology in Central Asia
Abstract
:1. Introduction
| Resilience | |||
|---|---|---|---|
| Low | High | ||
| Resistance | Low | Difficult to restore the system Easy to degrade the system | Easy to restore the system Easy to degrade the system |
| High | Difficult to restore the system Difficult to degrade the system | Easy to restore the system Difficult to degrade the system | |
2. Methods and Analysis
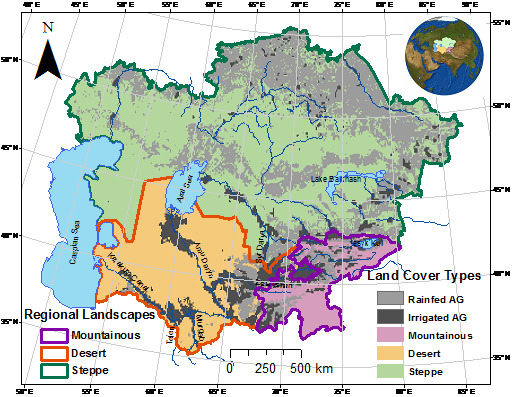
2.1. Study Area
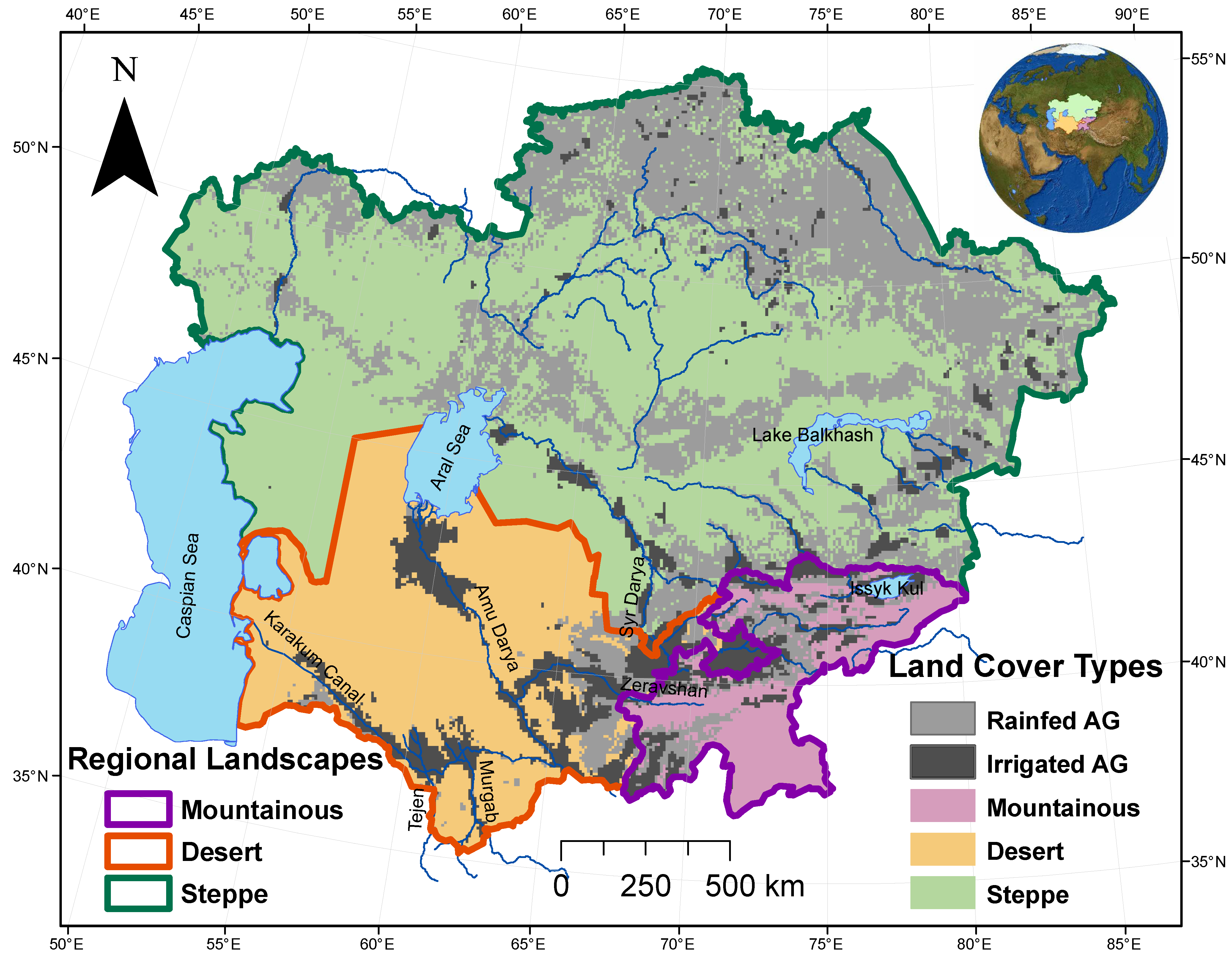
2.2. Datasets
Response Variables: Deriving Metrics of NDVI-Based Vegetation Dynamics
Explanatory Variables: Obtaining Key Environmental Drivers
| Pheno-metrics as response variables | Explanatory factors | |
| Used | Unused | |
| Start of growing season | Antecedent fall T° (d) | *EVPT (d) |
| Length of growing season | Winter T° (d) | *Total canopy water storage (d) |
| Integrated NDVI value | Spring T° (d) | *Surface runoff (d) |
| Summer T° (d) | *Subsurface runoff (d) | |
| Antecedent fall precipitation (d) | *Sensible heat flux (d) | |
| Winter precipitation (d) | *Latent heat flux (d) | |
| Spring precipitation (d) | *Near surface specific humidity (d) | |
| Summer precipitation (d) | *Surface pressure (d) | |
| Topography: Elevation (s) | Topography: Slope (s) | |
| Soil carbon content (s) | Topography: Aspect (s) | |
| Soil nitrogen content (s) | ||
| Soil field capacity (s) | ||
| Soil wilting point (s) | ||
| Soil available water capacity (s) | ||
| Soil thermal capacity (s) | ||
| Soil bulk capacity (s) | ||
2.3. Phenological Modeling Methods: Analyses and Testing Hypothesis
What Environmental Factors Drive Spatial and Temporal Variation in Vegetation Dynamics?
What Environmental Drivers Explain Phenological Variability (COV) across Time (28 yrs)?
3. Results and Discussion
3.1. Yearly Models of Yearly Spatial Variation in Vegetation Dynamics as a Function of Climate, Soil, and Elevation Factors
Steppe Regional Landscape
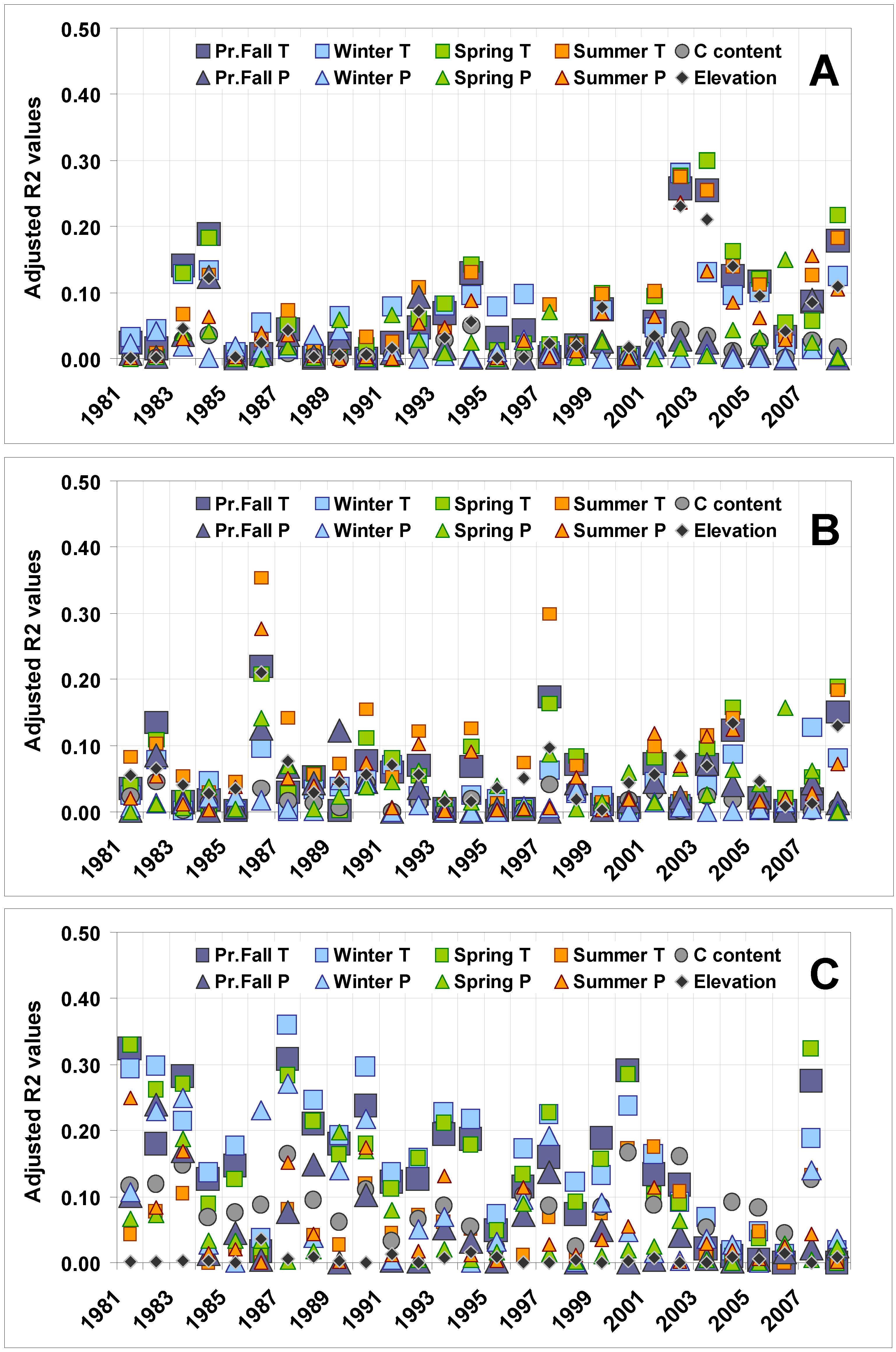
Mountainous Regional Landscape
Desert Regional Landscape

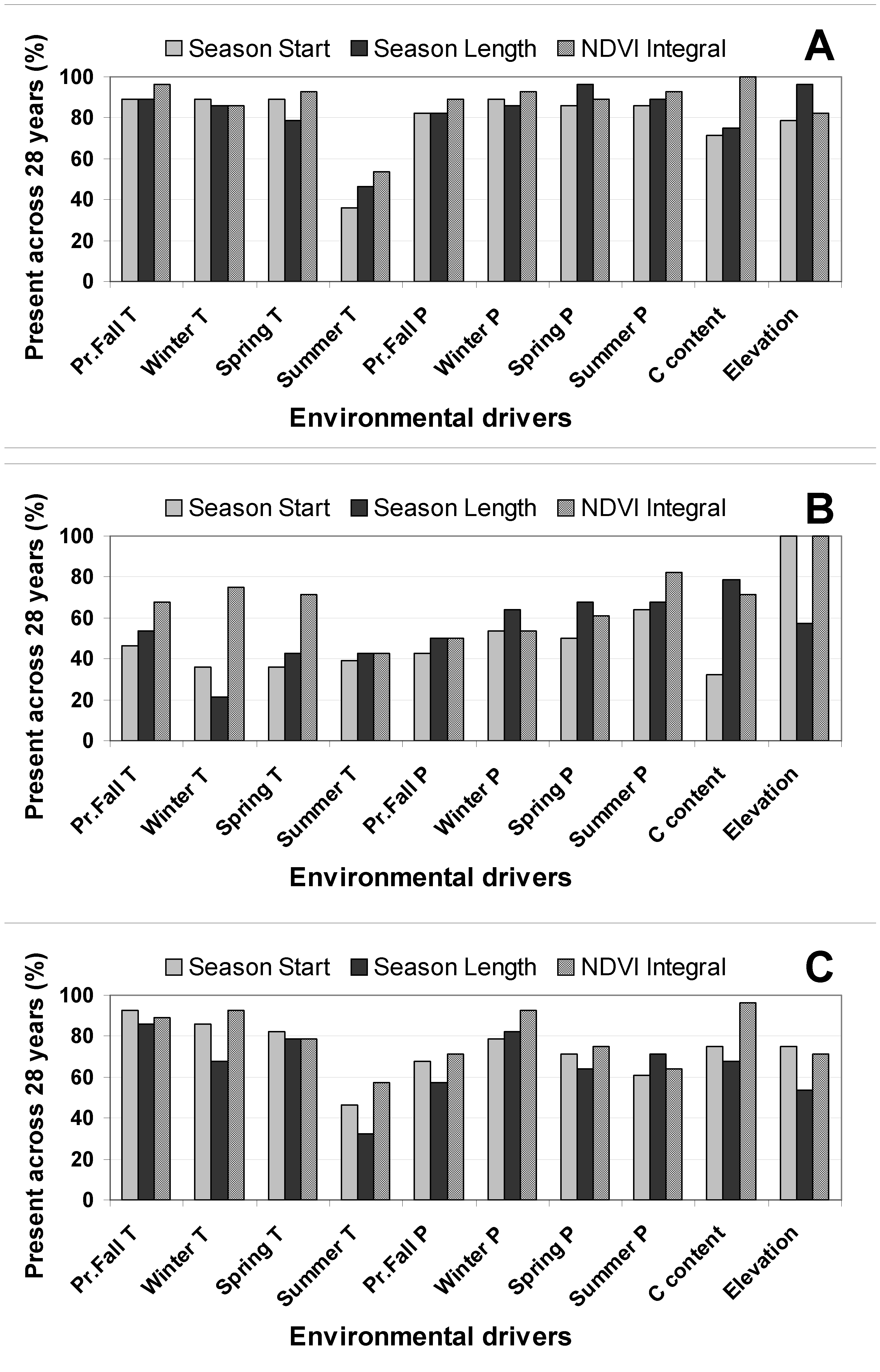
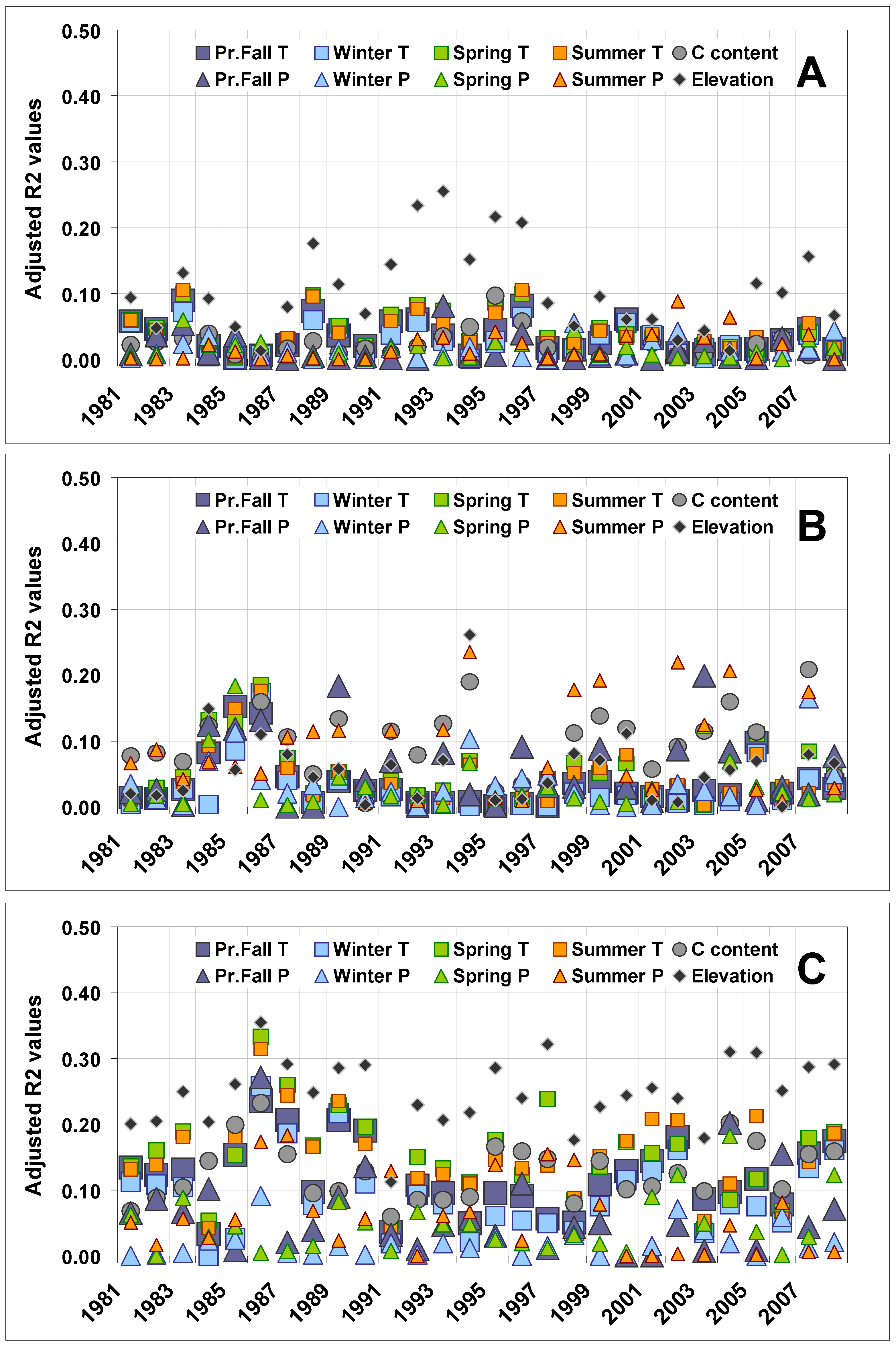
3.2. Drivers of Variability in Vegetation Dynamics over Time
Patterns of Variability in Vegetation Dynamics across Landscapes

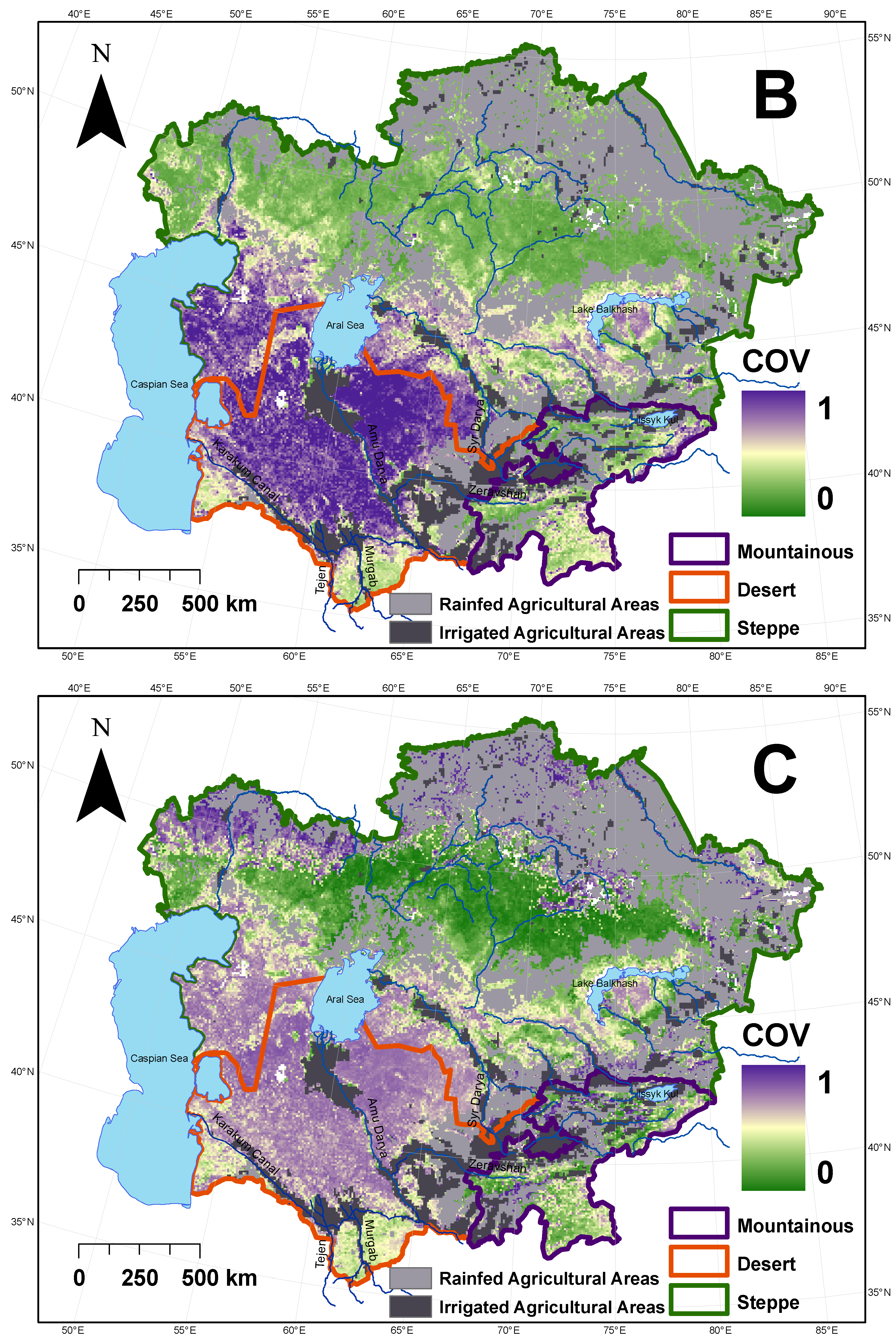
Drivers of Variability in Vegetation Dynamics for Each Regional Landscape
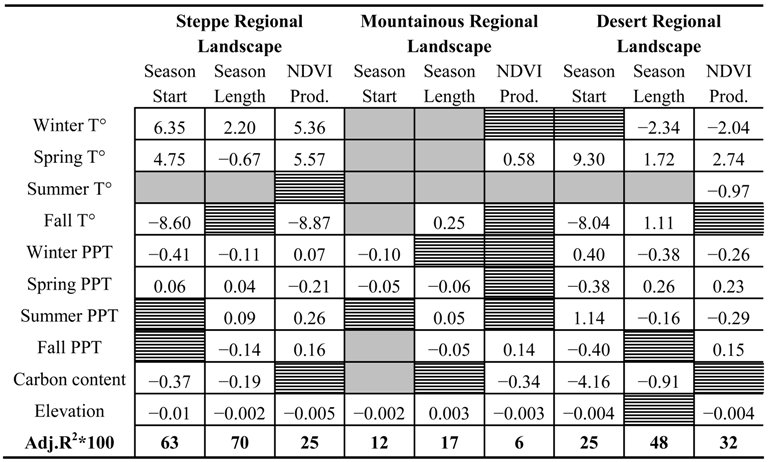

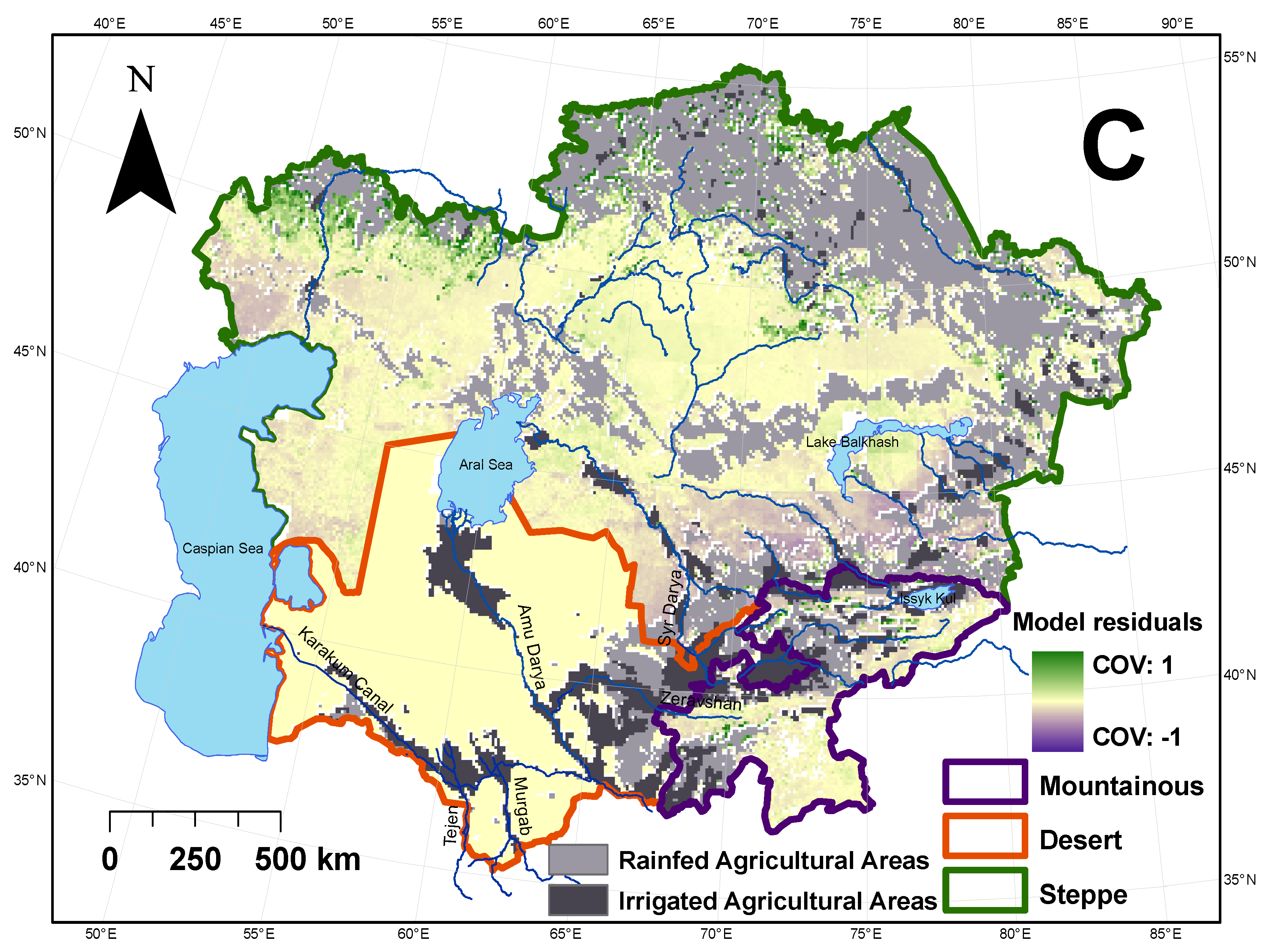
Modeling Interannual Variability of Vegetation Dynamics as a Function of Environmental Drivers for the Steppe Regional Landscape
Modeling Interannual Variability of Vegetation Dynamics as a Function of Environmental Drivers for the Mountainous Regional Landscape
Modeling Interannual Variability of Vegetation Dynamics as a Function of Environmental Drivers for the Desert Regional Landscape
4. Conclusions
Acknowledgements
References and Notes
- Justice, C.O.; Townshend, J.R.G.; Holben, B.N.; Tucker, C.J. Analysis of the phenology of global vegetation using meteorological satellite data. Int. J. Remote Sens. 1985, 6, 1271–1318. [Google Scholar] [CrossRef]
- Karnieli, A. Natural vegetation phenology assessment by ground spectral measurements in two semi−arid environments. Int. J. Biometeorol. 2003, 47, 179–187. [Google Scholar] [CrossRef] [PubMed]
- White, M.A.; Nemani, R.R. Real-time monitoring and short-term forecasting of land surface phenology. Remote Sens. Environ. 2006, 104, 43–49. [Google Scholar] [CrossRef]
- Reed, B.C.; Brown, J.F.; Vanderzee, D.; Loveland, T.R.; Merchant, J.W.; Ohlen, D.O. Measuring phenological variability from satellite imagery. J. Veg. Sci. 1994, 5, 703–714. [Google Scholar] [CrossRef]
- Schwartz, M.D.; Reed, B.C. Surface phenology and satellite sensor-derived onset of greenness: an initial comparison. Int. J. Remote Sens. 1999, 20, 3451–3457. [Google Scholar] [CrossRef]
- Lioubimtseva, E.; Cole, R.; Adams, J.M.; Kapustin, G. Impacts of climate and land-cover changes in arid lands of Central Asia. J. Arid Environ. 2005, 62, 285–308. [Google Scholar] [CrossRef]
- Köppen, W. Grundriss der Klimakunde; Walter D. Gruyter: Berlin, Germany, 1931; p. 388. [Google Scholar] [Green Version]
- Mather, J.R.; Yoshioka, G.A. The role of climate in the distribution of vegetation. Ann. Assoc. Amer. Geogr. 1968, 58, 29–41. [Google Scholar] [CrossRef]
- White, M.A.; Hoffman, F.; Hargrove, W.W.; Nemani, R.R. A global framework for monitoring phenological responses to climate change. Geophys. Res. Lett. 2005, 32, L04705. [Google Scholar] [CrossRef]
- White, M.A.; Thornton, P.E.; Running, S.W. A continental phenology model for monitoring vegetation responses to interannual climatic variability. Global Biogeochem. Cycle. 1997, 11, 217–234. [Google Scholar] [CrossRef]
- Harrison, G.W. Stability under environmental stress: Resistance, resilience, persistence, and variability. Amer. Naturalist 1979, 113, 659–669. [Google Scholar] [CrossRef]
- Elmqvist, T.; Folke, C.; Nystrom, M.; Peterson, G.; Bengtsson, J.; Walker, B.; Jon, N. Response diversity, ecosystem change, and resilience. Front. Ecol. Environ. 2003, 1, 488–494. [Google Scholar] [CrossRef]
- Turner, B.L.; Kasperson, R.E.; Matson, P.A.; McCarthy, J.J.; Corell, R.W.; Christensen, L.; Eckley, N.; Kasperson, J.X.; Luers, A.; Martello, M.L.; Polsky, C.; Pulsipher, A.; Schiller, A. A framework for vulnerability analysis in sustainability science. Proc. Nat. Acad. Sci. USA 2003, 100, 8074–8079. [Google Scholar] [CrossRef] [PubMed]
- White, P. Pattern, process, and natural disturbance in vegetation. Bot. Rev. 1979, 45, 229–299. [Google Scholar] [CrossRef]
- Dalziell, E.P.; McManus, S.T. Resilience, Vulnerability, and Adaptive Capacity: Implications for System Performance. In The First International Forum for Engineering Decision Making (IFED), Stoos, Switzerland, 5–8 December 2004. [Green Version]
- Pfisterer, A.B.; Schmid, B. Diversity−dependent production can decrease the stability of ecosystem functioning. Nature 2002, 416, 84–86. [Google Scholar] [CrossRef] [PubMed]
- Rüger, N.; Schlüter, M.; Matthies, M. A fuzzy habitat suitability index for Populus euphratica in the Northern Amudarya delta (Uzbekistan). Ecol. Model. 2005, 184, 313–328. [Google Scholar] [CrossRef]
- Schlüter, M.; Rüger, N.; Savitsky, A.; Novikova, N.; Matthies, M.; Lieth, H. TUGAI: An integrated simulation tool for ecological assessment of alternative water management strategies in a degraded river delta. Environ. Manage. 2006, 38, 638–653. [Google Scholar] [CrossRef] [PubMed]
- Odum, E.P. The strategy of ecosystem development. Science 1969, 164, 262–270. [Google Scholar] [CrossRef] [PubMed]
- Lewis, T.; Reid, N.; Clarke, P.J.; Whalley, R.D.B. Resilience of a high-conservation-value, semi-arid grassland on fertile clay soils to burning, mowing and ploughing. Austral Ecol. 2010, 35, 464–481. [Google Scholar] [CrossRef]
- Smith, R.L.; Smith, T.M. Elements of Ecology, 5th ed.; Pearson Education, Inc.: San Francisco, CA, USA, 2002; p. 682. [Google Scholar] [Green Version]
- Chibilyov, A. Steppe and forest-steppe. In The Physical Geography of Northern Eurasia; Shahgedanova, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 248–266. [Google Scholar] [Green Version]
- Small, E.E.; Giorgi, F.; Sloan, L.C. Regional climate model simulation of precipitation in central Asia: Mean and interannual variability. J. Geophys. Res.: Atmos. 1999, 104, 6563–6582. [Google Scholar] [CrossRef]
- Nemani, R.; Keeling, C.; Hashimoto, H.; Jolly, W.; Piper, S.; Tucker, C.; Myneni, R.; Running, S. Climate driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1562–1563. [Google Scholar] [CrossRef] [PubMed]
- IPCC. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; p. 996. [Google Scholar] [Green Version]
- Lioubimtseva, E.; Henebry, G.M. Climate and environmental change in arid Central Asia: Impacts, vulnerability, and adaptations. J. Arid Environ. 2009, 73, 963–977. [Google Scholar] [CrossRef]
- Alamanov, S.K.; Lelevkin, V.M.; Podrezov, O.A.; Podrezov, A.O. Climate Change and Water Resources in Central Asia; United Nations Environment Program (UNEP) and World Wildlife Fund (WWF): Bishkek, Kyrgyzstan; Moscow, Russian, 2006; p. 190. (In Russian) [Google Scholar] [Green Version]
- Rahmatulina, G.G. Current state of intergovernmental relationships with regards to water resources in Central Asia. In Current State and Perspective of Use of Water Resources in Central Asia; Chufrin, G.I., Ed.; Asia Strategy Foundation for Strategic Studies of the Central Asian Region: Almaty-Bishkek-Tashkent, 2008. (In Russian) [Google Scholar] [Green Version]
- Orlovsky, N.S. Climatic conditions of world ranges and their agrometeorological support. In Rangeland Ecology, Management and Productivity: Collection of Instructional Materials of the International Training Course; Nechaeva, N.T., Ed.; United Nations Environment Program (UNEP) USSR Commission for Help Publications and Information Support Project: Moscow, Russian, 1981; Volume I. [Google Scholar] [Green Version]
- Jolly, W.M.; Nemani, R.; Running, S.W. A generalized, bioclimatic index to predict foliar phenology in response to climate. Glob. Change Biol. 2005, 11, 619–632. [Google Scholar] [CrossRef]
- White, T.L.; Adams, W.T.; Neale, D.B. Forest Genetics; CAB International: Wallingford, UK, 2007; p. 704. [Google Scholar] [Green Version]
- Lomolino, M.V. Elevation gradients of species−density: historical and prospective views. Global Ecol. Biogeogr. 2001, 10, 3–13. [Google Scholar] [CrossRef]
- Lioubimtseva, E. Arid environments. In The Physical Geography of Northern Eurasia; Shahgedanova, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 267–283. [Google Scholar] [Green Version]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.A.; Pak, E.W.; Mahoney, R.; Vermote, E.F.; Saleous, N.E. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens. 2005, 26, 4485–4498. [Google Scholar] [CrossRef]
- Pinzon, J.; Brown, M.E.; Tucker, C.J. Satellite time series correction of orbital drift artifacts using empirical mode decomposition. In Hilbert−Huang Transform: Introduction and Applications; Huang, N., Shen, S., Eds.; World Scientific Publishing Co. Ltd.: Singapore, 2005; pp. 167–186. [Google Scholar] [Green Version]
- White, M.A.; de Beurs, K.M.; Didan, K.; Inouye, D.W.; Richardson, A.D.; Jensen, O.P.; O’Keefe, J.; Zhang, G.; Nemani, R.R.; van Leeuwen, W.J.D.; Brown, J.F.; de Wit, A.; Schaepman, M.; Lin, X.M.; Dettinger, M.; Bailey, A.S.; Kimball, J.; Schwartz, M.D.; Baldocchi, D.D.; Lee, J.T.; Lauenroth, W.K. Intercomparison, interpretation, and assessment of spring phenology in North America estimated from remote sensing for 1982–2006. Glob. Change Biol. 2009, 15, 2335–2359. [Google Scholar] [CrossRef]
- Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar] [CrossRef]
- Jönsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
- van Leeuwen, W.J.D. Monitoring the effects of forest restoration treatments on post-fire vegetation recovery with MODIS multitemporal data. Sensors 2008, 8, 2017–2042. [Google Scholar] [CrossRef]
- Jönsson, P.; Eklundh, L. Users Guide for TIMESAT 2.3; TIMESAT—A program for analysing time-series of satellite sensor data; Lund University: Lund, Sweden, 2006. [Google Scholar] [Green Version]
- White, M.A.; Running, S.W.; Thornton, P.E. The impact of growing−season length variability on carbon assimilation and evapotranspiration over 88 years in the eastern US deciduous forest. Int. J. Biometeorol. 1999, 42, 139–145. [Google Scholar] [CrossRef] [PubMed]
- Cleland, E.E.; Chuine, I.; Menzel, A.; Mooney, H.A.; Schwartz, M.D. Shifting plant phenology in response to global change. Trend. Ecol. Evolut. 2007, 22, 357–365. [Google Scholar] [CrossRef] [PubMed]
- Prince, S.D.; Goetz, S.J.; Goward, S.N. Monitoring primary production from earth observing satellites. Water Air Soil Pollut. 1995, 82, 509–522. [Google Scholar] [CrossRef]
- Farrar, D.; Glauber, R. Multicollinearity in regression analysis: The problem revisited. Rev. Econ. Statist. 1967, 49, 92–107. [Google Scholar] [CrossRef]
- Davison, J.E.; Breshears, D.D.; van Leeuwen, W.J.D.; Casady, G.M. Remotely sensed vegetation phenology and productivity along a climatic gradient: On the value of incorporating the dimension of woody plant cover. Global Ecol. Biogeogr. 2010, 20, 101–113. [Google Scholar] [CrossRef]
- GLDAS Noah Land Surface Model L4 3 Hourly 1.0 × 1.0 Degree Subsetted; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2009. [Green Version]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; Entin, J.K.; Walker, J.P.; Lohmann, D.; Toll, D. The Global Land Data Assimilation System. Bull. Amer. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Global Gridded Surfaces of Selected Soil Characteristics; International Geosphere−Biosphere Programme—Data and Information System; Oak Ridge National Laboratory Distributed Active Archive Center: Oak Ridge, TN, USA, 2000. [Green Version]
- Thenkabail, P.S.; Biradar, C.M.; Noojipady, P.; Dheeravath, V.; Li, Y.J.; Velpuri, M.; Gumma, M.; Reddy, G.P.O.; Turral, H.; Cai, X.L.; Vithanage, J.; Schull, M.A.; Dutta, R. Global Irrigated Area Map (GIAM) for the end of the last millennium derived from remote sensing. Int. J. Remote Sens. 2009, 30, 3679–3733. [Google Scholar] [CrossRef]
- Biradar, C.M.; Thenkabail, P.S.; Noojipady, P.; Li, Y.J.; Dheeravath, V.; Turral, H.; Velpuri, M.; Gumma, M.K.; Ganguntla, O.R.; Cai, X.L.; Xiao, X.; Schull, M.A.; Alankara, R.D.; Gunasinghe, S.; Mohideen, S. A global map of rainfed cropland areas (GMRCA) at the end of last millennium using remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 114–129. [Google Scholar] [CrossRef]
- IWMI. The Global Irrigated Area Map (GIAM) and Global map of Rainfed Cropland (GMRCA) Web Portals; International Water Management Institute: Colombo, Sri Lanka, 2010. [Google Scholar] [Green Version]
- Barbosa, H.A.; Huete, A.R.; Baethgen, W.E. A 20-year study of NDVI variability over the Northeast Region of Brazil. J. Arid Environ. 2006, 67, 288–307. [Google Scholar] [CrossRef]
- Culbert, P.D.; Pidgeon, A.M.; St−Louis, V.; Bash, D.; Radeloff, V.C. The impact of phenological variation on texture measures of remotely sensed imagery. IEEE J. Sel. Topics Appl. Earth Obs. Remote Sens. 2009, 2, 299–309. [Google Scholar] [CrossRef]
- Antle, J.M.; Capalbo, S.M.; Elliott, E.T.; Paustian, K.H. Adaptation, spatial heterogeneity, and the vulnerability of agricultural systems to climate change and CO2 fertilization: An integrated assessment approach. Climatic Change 2004, 64, 289–315. [Google Scholar] [CrossRef]
- Hurd, B.; Leary, N.; Jones, R.; Smith, B. Relative regional vulnerability of water resources to climate change. J. Amer. Water Resour. Assoc. 1999, 35, 1399–1409. [Google Scholar] [CrossRef]
- Kalluri, S. Monitoring Ecosystems Vulnerable to Climate Change. In Proceedings of 2002 IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; Volume 5, pp. 2802–2804. [Green Version]
- Luers, A.L. The surface of vulnerability: An analytical framework for examining environmental change. Global Environ. Change 2005, 15, 214–223. [Google Scholar] [CrossRef]
- Bowers, J.E.; Webb, R.H.; Rondeau, R.J. Longevity, recruitment and mortality of desert plants in Grand Canyon, Arizona, USA. J. Veg. Sci. 1995, 6, 551–564. [Google Scholar] [CrossRef]
- White, A.B.; Kumar, P.; Tcheng, D. A data mining approach for understanding topographic control on climate-induced inter-annual vegetation variability over the United States. Remote Sens. Environ. 2005, 98, 1–20. [Google Scholar] [CrossRef]
- Stohlgren, T.J.; Bachand, R.R.; Onami, Y.; Binkley, D. Species–environment relationships and vegetation patterns: Effects of spatial scale and tree life-stage. Plant Ecol. 1998, 135, 215–228. [Google Scholar] [CrossRef]
- Bai, Y.; Han, X.; Wu, J.; Chen, Z.; Li, L. Ecosystem stability and compensatory effects in the Inner Mongolia grassland. Nature 2004, 431, 181–184. [Google Scholar] [CrossRef] [PubMed]
- Whittaker, R.H.; Niering, W.A. Vegetation of Santa Catalina Mountains, Arizona. 5. Biomass, production, and diversity along the elevation gradient. Ecology 1975, 56, 771–790. [Google Scholar] [CrossRef]
- Suttle, K.B.; Thomsen, M.A.; Power, M.E. Species interactions reverse grassland responses to changing climate. Science 2007, 315, 640–642. [Google Scholar] [CrossRef] [PubMed]
- Parmesan, C. Ecological and evolutionary responses to recent climate change. Ann. Rev. Ecol. Evol. Syst. 2006, 37, 637–669. [Google Scholar] [CrossRef]
- Bolch, T. Climate change and glacier retreat in northern Tien Shan (Kazakhstan/Kyrgyzstan) using remote sensing data. Global Planet. Change 2007, 56, 1–12. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2007: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2007; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; p. 996. [Google Scholar] [Green Version]
- Kharlamova, N.F.; Revyakin, V.S. Regional climate and environmental change in Central Asia. In Environmental Security and Sustainable Land Use—With Special Reference to Central Asia; Vogtmann, H., Dobretsov, N., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 19–26. [Google Scholar] [Green Version]
- Kutuzov, S.; Shahgedanova, M. Glacier retreat and climatic variability in the eastern Terskey−Alatoo, inner Tien Shan between the middle of the 19th century and beginning of the 21st century. Global Planet. Change 2009, 69, 59–70. [Google Scholar] [CrossRef]
- Podrezov, O.A.; Dikih, N.A.; Bakirov, K.B. Climate change and glaciers of the Tien−Shan for the last 100 years. Вестник КРСУ 2001, 1, 3. (In Russian) [Google Scholar]
- Lomolino, M.V.; Riddle, B.R.; Brown, J.H. Biogeography, 3rd ed.; Sinauer Associates: Sunderland, MA, USA, 2006. [Google Scholar] [Green Version]
- Lal, R. Carbon sequestration in soils of central Asia. Land Degrad. Dev. 2004, 15, 563–572. [Google Scholar] [CrossRef]
- Kharin, N.G. Vegetation Degradation in Central Asia under the Impact of Human Activities; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002; p. 182. [Google Scholar] [Green Version]
- Hijmans, R.; Cameron, S.; Parra, J.; Jones, P.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Chuine, I.; Cour, P.; Rousseau, D.D. Selecting models to predict the timing of flowering of temperate trees: Implications for tree phenology modelling. Plant Cell Environ. 1999, 22, 1–13. [Google Scholar] [CrossRef]
- Morin, X.; Chuine, I. Sensitivity analysis of the tree distribution model PHENOFIT to climatic input characteristics: implications for climate impact assessment. Glob. Change Biol. 2005, 11, 1493–1503. [Google Scholar] [CrossRef]
Appendix A
| Year | X−var./year | Ant.Fall T° | Winter T° | Spring T° | Winter PPT | Spring PPT | Summer PPT | Ant.Fall PPT | Elevation | Carbon content | Summer T° | AdjR2* 100(%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1981 | 9 | 1.471 | 0.081 | −1.332 | −0.002 | −0.009 | 0.009 | −0.004 | −−− | 0.015 | −0.287 | 17 |
| 1982 | 8 | 0.591 | 0.348 | −0.867 | −0.003 | −0.014 | 0.008 | 0.003 | 0.085 | −−− | −−− | 15 |
| 1983 | 7 | −−− | −0.069 | −0.089 | 0.005 | −0.005 | 0.001 | −0.002 | 0.044 | −−− | −−− | 17 |
| 1984 | 10 | −0.086 | 0.102 | −0.285 | −0.006 | −0.003 | 0.007 | 0.013 | 0.111 | 0.015 | 0.243 | 30 |
| 1985 | 6 | −−− | 0.267 | −−− | −0.014 | −0.018 | 0.026 | −−− | 0.065 | −−− | 0.087 | 8 |
| 1986 | 10 | 1.308 | 0.228 | −0.955 | −0.001 | −0.006 | 0.011 | −0.003 | −0.025 | 0.017 | −0.649 | 44 |
| 1987 | 7 | −0.064 | 0.294 | −0.397 | 0.004 | −0.009 | −−− | 0.010 | 0.053 | −−− | −−− | 11 |
| 1988 | 7 | 0.165 | 0.297 | −0.449 | −0.022 | −0.015 | −−− | 0.023 | −−− | 0.028 | −−− | 19 |
| 1989 | 10 | 0.254 | 0.475 | −0.604 | 0.003 | −0.013 | −0.016 | 0.017 | −0.048 | 0.014 | −0.403 | 26 |
| 1990 | 8 | 0.908 | −0.162 | −0.410 | 0.007 | 0.007 | −0.003 | −0.015 | −−− | −−− | −0.588 | 14 |
| 1991 | 8 | 0.145 | 0.825 | −1.176 | −0.007 | −0.004 | −0.019 | 0.017 | −−− | −0.015 | −−− | 33 |
| 1992 | 8 | 0.279 | −−− | −0.275 | −0.003 | 0.004 | −0.003 | 0.016 | 0.086 | 0.016 | −−− | 19 |
| 1993 | 8 | 0.427 | −0.219 | −0.245 | −0.004 | −−− | 0.006 | −0.004 | 0.077 | 0.023 | −−− | 13 |
| 1994 | 8 | −−− | 0.018 | −0.156 | −0.006 | −0.002 | 0.006 | 0.003 | 0.035 | 0.032 | −−− | 17 |
| 1995 | 6 | 0.752 | 0.321 | −1.145 | 0.008 | −−− | −0.008 | −−− | −0.019 | −−− | −−− | 14 |
| 1996 | 7 | 1.960 | 0.853 | −2.426 | −0.006 | 0.007 | −−− | −−− | 0.110 | −0.024 | −−− | 28 |
| 1997 | 8 | 0.246 | 0.452 | −1.006 | 0.016 | −0.022 | 0.006 | −0.007 | −−− | 0.026 | −−− | 29 |
| 1998 | 6 | 0.195 | 0.092 | −0.257 | −−− | −0.010 | −−− | 0.015 | 0.078 | −−− | −−− | 9 |
| 1999 | 8 | 0.272 | 0.266 | −0.677 | −0.013 | −−− | −0.002 | 0.013 | 0.038 | 0.011 | −−− | 20 |
| 2000 | 9 | 0.216 | 0.575 | −0.749 | −0.027 | 0.014 | −0.014 | −0.003 | 0.138 | 0.044 | −−− | 8 |
| 2001 | 7 | 0.852 | −0.110 | −0.405 | 0.010 | −0.023 | 0.005 | −−− | −−− | −−− | −0.384 | 19 |
| 2002 | 8 | −0.076 | −0.081 | −−− | −0.017 | 0.004 | 0.008 | −0.003 | 0.066 | 0.019 | −−− | 35 |
| 2003 | 9 | −0.146 | 0.266 | −0.639 | −0.015 | −−− | 0.005 | 0.008 | 0.064 | 0.022 | 0.378 | 38 |
| 2004 | 7 | 0.742 | −−− | −0.886 | −0.009 | −0.004 | −0.003 | −−− | 0.055 | 0.010 | −−− | 28 |
| 2005 | 8 | 0.102 | −−− | −0.272 | −−− | −0.005 | 0.004 | −0.005 | 0.075 | 0.043 | 0.093 | 15 |
| 2006 | 9 | 0.203 | −0.155 | −0.163 | −0.008 | 0.018 | −0.002 | −0.007 | 0.055 | 0.025 | −−− | 30 |
| 2007 | 8 | −0.204 | 0.253 | −−− | −−− | −0.007 | 0.008 | 0.003 | 0.054 | 0.034 | −0.063 | 21 |
| 2008 | 9 | 0.466 | −0.112 | −0.419 | −0.008 | 0.001 | 0.007 | 0.003 | 0.038 | 0.006 | −−− | 27 |
| Total # from 1981 to 2008 | 25 | 25 | 25 | 25 | 24 | 24 | 23 | 22 | 20 | 10 | ||
| Year | X−var./year | Spring PPT | Elevation | Ant.Fall T° | Summer PPT | Winter T° | Winter PPT | Ant.Fall PPT | Spring T° | Carbon content | Summer T° | AdjR2* 100(%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1981 | 9 | −0.005 | −0.139 | 0.130 | −0.006 | 0.045 | −0.005 | −−− | 0.161 | −0.066 | 0.306 | 11 |
| 1982 | 7 | −−− | −0.173 | 0.341 | −−− | −−− | −0.017 | −0.020 | 0.295 | −0.111 | 0.409 | 16 |
| 1983 | 9 | −0.001 | −0.120 | −−− | −0.008 | −0.050 | 0.002 | −0.006 | 0.055 | 0.001 | 0.196 | 9 |
| 1984 | 10 | −0.020 | −0.098 | −0.331 | −0.003 | −0.254 | 0.015 | −0.004 | −0.200 | 0.112 | 0.147 | 19 |
| 1985 | 8 | 0.002 | −0.135 | −0.054 | −0.015 | −0.090 | 0.010 | −0.006 | 0.013 | −−− | −−− | 16 |
| 1986 | 9 | −0.016 | −0.197 | 0.320 | −0.028 | 0.149 | −0.006 | −0.021 | −−− | −0.078 | 0.479 | 42 |
| 1987 | 8 | −0.019 | −0.180 | 0.063 | −0.013 | −0.040 | −−− | −0.026 | 0.116 | −0.058 | −−− | 22 |
| 1988 | 8 | −0.002 | −0.159 | 0.264 | −0.017 | 0.138 | 0.003 | −0.017 | −−− | −0.081 | −−− | 8 |
| 1989 | 8 | 0.011 | −0.108 | −−− | −0.013 | −0.195 | 0.011 | −0.035 | −−− | −0.023 | 0.230 | 30 |
| 1990 | 9 | −0.015 | −0.132 | 0.209 | −0.012 | 0.107 | −0.012 | −0.014 | 0.306 | −0.101 | −−− | 16 |
| 1991 | 9 | 0.022 | −0.156 | 0.139 | 0.001 | 0.141 | 0.001 | 0.005 | 0.202 | 0.012 | −−− | 15 |
| 1992 | 7 | −0.022 | −0.132 | 0.222 | −0.018 | 0.077 | −0.017 | −−− | 0.167 | −−− | −−− | 15 |
| 1993 | 7 | −0.014 | −0.085 | 0.006 | 0.001 | −−− | 0.001 | −−− | 0.049 | −0.021 | −−− | 5 |
| 1994 | 8 | −0.013 | −0.110 | 0.353 | −0.028 | 0.148 | −0.007 | 0.006 | 0.498 | −−− | −−− | 20 |
| 1995 | 10 | −0.009 | −0.056 | −0.111 | 0.001 | −0.079 | −0.005 | −0.001 | −0.112 | 0.008 | −0.019 | 20 |
| 1996 | 8 | −0.001 | −0.116 | −0.051 | −0.001 | −0.074 | 0.001 | −0.012 | 0.003 | −−− | −−− | 18 |
| 1997 | 8 | 0.013 | −0.211 | 0.392 | −0.010 | 0.168 | −0.011 | −0.006 | −−− | −0.109 | −−− | 35 |
| 1998 | 6 | 0.016 | −−− | 0.301 | −0.021 | 0.099 | −−− | −0.021 | 0.250 | −−− | −−− | 22 |
| 1999 | 9 | 0.021 | −0.022 | −0.095 | 0.007 | −0.116 | 0.010 | −0.004 | −0.098 | −−− | −0.229 | 19 |
| 2000 | 9 | −0.016 | −0.134 | −0.007 | −0.004 | −0.099 | 0.005 | −0.009 | −0.026 | −0.082 | −−− | 19 |
| 2001 | 5 | −0.004 | −0.120 | −−− | −0.018 | 0.106 | −−− | −−− | −−− | −0.086 | −−− | 15 |
| 2002 | 7 | −0.016 | −0.160 | −0.159 | −0.011 | −−− | −0.004 | −−− | −−− | 0.093 | −0.104 | 15 |
| 2003 | 9 | −0.014 | −0.142 | 0.168 | −−− | 0.143 | 0.020 | −0.028 | 0.224 | −0.077 | 0.259 | 23 |
| 2004 | 8 | −0.004 | −0.147 | 0.121 | −0.014 | −−− | 0.003 | −0.008 | 0.174 | −0.042 | −−− | 25 |
| 2005 | 10 | −0.013 | −0.113 | −0.036 | −0.003 | −0.179 | −0.008 | −0.012 | −0.084 | 0.016 | −0.095 | 15 |
| 2006 | 9 | −0.030 | −0.038 | −0.044 | −−− | −0.057 | −0.012 | 0.001 | 0.114 | 0.016 | 0.004 | 23 |
| 2007 | 9 | −0.025 | −0.087 | −0.350 | −0.013 | −0.622 | −−− | −0.027 | −0.353 | 0.016 | −0.168 | 35 |
| 2008 | 8 | 0.001 | −0.185 | 0.360 | −0.020 | 0.221 | 0.020 | −0.010 | 0.377 | −−− | −−− | 27 |
| Total # from 1981 to 2008 | 27 | 27 | 25 | 25 | 24 | 24 | 23 | 22 | 21 | 13 | ||
| Year | X−var./year | Carbon content | Ant.Fall T° | Spring T° | Winter PPT | Summer PPT | Ant.Fall PPT | Spring PPT | Winter T° | Elevation | Summer T° | AdjR2* 100(%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1981 | 10 | 0.037 | 0.075 | −0.302 | 0.009 | 0.007 | −0.005 | 0.003 | −0.059 | −0.010 | 0.146 | 46 |
| 1982 | 9 | 0.036 | 0.155 | −0.104 | 0.011 | 0.006 | 0.007 | −0.004 | −0.118 | 0.014 | −−− | 44 |
| 1983 | 7 | 0.033 | −−− | −0.288 | 0.011 | −0.003 | −−− | 0.002 | 0.016 | −−− | 0.079 | 48 |
| 1984 | 10 | 0.054 | −0.276 | 0.110 | 0.006 | −0.010 | 0.010 | −0.011 | −0.081 | −0.013 | 0.075 | 28 |
| 1985 | 8 | 0.038 | −0.404 | −−− | 0.007 | −0.011 | 0.001 | −0.005 | −−− | −0.020 | 0.111 | 29 |
| 1986 | 8 | 0.051 | −0.290 | 0.214 | 0.016 | −0.008 | −0.004 | −−− | −−− | −0.012 | −0.066 | 32 |
| 1987 | 8 | 0.062 | −0.291 | 0.174 | 0.012 | −−− | −0.015 | −0.003 | −0.083 | −0.014 | −−− | 45 |
| 1988 | 7 | 0.041 | 0.287 | −0.215 | 0.006 | −0.009 | 0.004 | −−− | −0.209 | −−− | −−− | 29 |
| 1989 | 9 | 0.038 | −0.373 | 0.322 | −−− | −0.007 | −0.009 | 0.018 | −0.074 | −0.010 | −0.087 | 28 |
| 1990 | 10 | 0.043 | 0.122 | 0.191 | 0.003 | 0.002 | −0.003 | 0.005 | −0.278 | −0.032 | −0.171 | 38 |
| 1991 | 8 | 0.028 | −0.312 | −0.129 | −0.004 | −0.016 | −0.003 | 0.015 | −−− | −−− | 0.168 | 19 |
| 1992 | 8 | 0.038 | −0.217 | −0.168 | 0.005 | −0.005 | −0.007 | −−− | 0.060 | −0.046 | −−− | 23 |
| 1993 | 9 | 0.038 | 0.246 | −0.185 | 0.007 | 0.004 | −0.003 | −0.003 | −0.216 | −0.015 | −−− | 27 |
| 1994 | 9 | 0.034 | 0.160 | −0.317 | 0.001 | −0.012 | −0.014 | 0.013 | −0.163 | −0.032 | −−− | 28 |
| 1995 | 10 | 0.024 | −0.870 | −1.248 | −0.007 | −0.006 | 0.003 | −0.011 | 0.676 | 0.028 | 1.315 | 23 |
| 1996 | 8 | 0.058 | 0.094 | −0.078 | 0.005 | 0.002 | −−− | −0.003 | −0.115 | 0.013 | −−− | 24 |
| 1997 | 8 | 0.033 | 0.128 | −0.272 | 0.006 | −0.007 | 0.001 | 0.001 | −0.086 | −−− | −−− | 32 |
| 1998 | 10 | 0.018 | −0.423 | −0.788 | −0.005 | 0.007 | −0.013 | 0.012 | 0.377 | 0.060 | 0.961 | 20 |
| 1999 | 10 | 0.033 | −0.380 | 0.081 | 0.015 | −0.003 | −0.002 | 0.004 | 0.045 | −0.014 | 0.074 | 32 |
| 2000 | 10 | 0.066 | −0.166 | −0.154 | 0.011 | 0.006 | −0.015 | −0.012 | 0.087 | −0.078 | −0.093 | 42 |
| 2001 | 10 | 0.048 | 0.552 | 0.031 | −0.003 | 0.005 | −0.005 | −0.006 | −0.282 | −0.025 | −0.488 | 33 |
| 2002 | 8 | 0.087 | −0.163 | −0.047 | 0.005 | −0.009 | 0.018 | −0.013 | −−− | −0.026 | −−− | 36 |
| 2003 | 9 | 0.048 | 0.172 | 0.325 | 0.003 | 0.008 | −0.029 | −0.009 | −0.297 | −−− | −0.306 | 16 |
| 2004 | 9 | 0.075 | 0.471 | −0.250 | 0.024 | 0.004 | 0.002 | −0.014 | −0.331 | −0.042 | −−− | 19 |
| 2005 | 9 | 0.047 | 0.667 | −0.228 | −−− | −0.006 | 0.004 | 0.003 | −0.240 | −0.013 | −0.298 | 30 |
| 2006 | 8 | 0.080 | −0.314 | 0.281 | 0.012 | −0.009 | −−− | 0.002 | −0.107 | −0.021 | −−− | 13 |
| 2007 | 9 | 0.036 | −0.173 | −0.086 | 0.019 | −0.004 | −0.006 | −0.004 | −0.033 | −0.024 | −−− | 44 |
| 2008 | 7 | 0.066 | 0.171 | −−− | −0.012 | −−− | 0.003 | −0.003 | −0.199 | −0.015 | −−− | 8 |
| Total # from 1981−2008 | 28 | 27 | 26 | 26 | 26 | 25 | 25 | 24 | 23 | 15 | ||
| Year | X−var./year | Elevation | Summer PPT | Winter PPT | Spring PPT | Ant.Fall T° | Ant.Fall PPT | Summer T° | Winter T° | Spring T° | Carbon content | AdjR2* 100(%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1981 | 5 | 0.069 | −−− | −−− | 0.003 | 0.159 | −−− | −−− | −0.169 | −−− | −0.020 | 11 |
| 1982 | 7 | 0.040 | 0.011 | −−− | −−− | −0.244 | −0.017 | 0.483 | −−− | −0.268 | −0.031 | 9 |
| 1983 | 5 | 0.078 | 0.012 | −−− | −0.012 | −−− | −−− | −0.212 | 0.213 | −−− | −−− | 18 |
| 1984 | 1 | 0.082 | −−− | −−− | −−− | −−− | −−− | −−− | −−− | −−− | −−− | 9 |
| 1985 | 3 | 0.079 | 0.015 | 0.010 | −−− | −−− | −−− | −−− | −−− | −−− | −−− | 14 |
| 1986 | 4 | 0.081 | −−− | −0.018 | 0.011 | −−− | −−− | −−− | −−− | 0.093 | −−− | 7 |
| 1987 | 4 | 0.078 | 0.006 | 0.007 | −−− | −−− | −0.017 | −−− | −−− | −−− | −−− | 10 |
| 1988 | 6 | 0.102 | 0.005 | −0.004 | −−− | 0.178 | 0.010 | −−− | −−− | −0.198 | −−− | 20 |
| 1989 | 5 | 0.080 | −−− | −−− | 0.012 | −−− | 0.012 | 0.107 | −0.179 | −−− | −−− | 18 |
| 1990 | 3 | 0.069 | −−− | −0.005 | 0.007 | −−− | −−− | −−− | −−− | −−− | −−− | 8 |
| 1991 | 4 | 0.062 | −−− | −−− | −−− | −0.035 | 0.008 | −−− | −−− | −−− | 0.023 | 16 |
| 1992 | 8 | 0.109 | 0.002 | 0.005 | −−− | 0.800 | −0.011 | 1.041 | −0.155 | 0.443 | −−− | 29 |
| 1993 | 6 | 0.107 | 0.002 | −−− | 0.003 | 0.276 | −−− | −−− | −0.117 | −0.140 | −−− | 28 |
| 1994 | 5 | 0.104 | 0.017 | −−− | −0.006 | −−− | −−− | −−− | 0.159 | −0.126 | −−− | 18 |
| 1995 | 2 | 0.079 | −−− | −−− | −−− | −−− | −−− | −−− | −−− | −−− | −0.022 | 22 |
| 1996 | 3 | 0.115 | −−− | −−− | −0.012 | −−− | 0.006 | −−− | −−− | −−− | −−− | 23 |
| 1997 | 3 | 0.086 | 0.004 | −0.005 | −−− | −−− | −−− | −−− | −−− | −−− | −−− | 10 |
| 1998 | 4 | 0.108 | 0.009 | −0.016 | 0.009 | −−− | −−− | −−− | −−− | −−− | −−− | 13 |
| 1999 | 7 | 0.100 | 0.007 | 0.014 | −−− | 0.232 | −−− | 0.096 | −0.346 | −−− | 0.031 | 20 |
| 2000 | 9 | 0.100 | 0.001 | 0.006 | −−− | 0.240 | 0.013 | −0.123 | −0.748 | 0.533 | 0.026 | 16 |
| 2001 | 9 | 0.085 | 0.014 | −−− | −0.012 | 0.568 | 0.003 | −0.334 | −0.774 | 0.613 | −0.082 | 17 |
| 2002 | 6 | 0.091 | 0.003 | −0.015 | 0.007 | −0.250 | −−− | −−− | −−− | 0.296 | −−− | 19 |
| 2003 | 6 | 0.094 | −−− | −0.013 | 0.006 | 0.169 | 0.015 | −0.145 | −−− | −−− | −−− | 14 |
| 2004 | 9 | 0.079 | 0.005 | −0.005 | 0.018 | 1.071 | −0.013 | −0.434 | −0.706 | −−− | 0.026 | 17 |
| 2005 | 3 | 0.083 | −−− | −−− | −−− | −0.209 | −−− | −−− | −−− | 0.228 | −−− | 13 |
| 2006 | 2 | 0.080 | 0.003 | −−− | −−− | −−− | −−− | −−− | −−− | −−− | −−− | 11 |
| 2007 | 6 | 0.139 | 0.007 | −0.006 | 0.003 | −−− | −−− | 0.037 | −−− | −−− | 0.030 | 25 |
| 2008 | 5 | 0.129 | −0.009 | −0.017 | −−− | −−− | 0.022 | −0.047 | −−− | −−− | −−− | 18 |
| Total # from 1981−2008 | 28 | 18 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 9 | ||
| Year | X−var./year | Carbon content | Spring PPT | Summer PPT | Winter PPT | Elevation | Ant.Fall T° | Ant.Fall PPT | Spring T° | Summer T° | Winter T° | AdjR2* 100(%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1981 | 7 | −0.170 | 0.008 | −0.007 | 0.009 | −−− | −1.169 | −0.019 | −−− | 1.069 | −−− | 13 |
| 1982 | 6 | −0.189 | 0.012 | −0.032 | −−− | −0.037 | −0.905 | −−− | −−− | 0.744 | −−− | 14 |
| 1983 | 5 | −0.147 | −−− | −0.022 | 0.016 | −−− | --- | --- | --- | 0.132 | −0.256 | 11 |
| 1984 | 4 | −0.120 | --- | --- | --- | 0.087 | --- | --- | −0.475 | --- | 0.323 | 21 |
| 1985 | 7 | −0.119 | −0.020 | −0.023 | --- | −0.062 | −0.349 | --- | 1.140 | −1.005 | --- | 33 |
| 1986 | 3 | −0.172 | --- | --- | --- | --- | 0.365 | --- | −0.611 | --- | --- | 22 |
| 1987 | 3 | −0.136 | --- | −0.015 | --- | --- | --- | --- | −0.098 | --- | --- | 15 |
| 1988 | 5 | −0.088 | −0.010 | −0.021 | 0.014 | 0.044 | --- | --- | --- | --- | --- | 14 |
| 1989 | 5 | −0.100 | −0.033 | −0.035 | --- | --- | 1.409 | --- | --- | −1.207 | --- | 27 |
| 1990 | 4 | --- | −0.010 | −0.010 | --- | --- | 0.257 | --- | --- | −0.324 | --- | 5 |
| 1991 | 5 | −0.193 | 0.032 | −0.031 | 0.032 | --- | --- | −0.043 | --- | --- | --- | 24 |
| 1992 | 5 | −0.159 | −0.015 | --- | 0.011 | −0.027 | --- | 0.021 | --- | --- | --- | 11 |
| 1993 | 3 | −0.158 | --- | −0.018 | --- | --- | --- | 0.031 | --- | --- | --- | 21 |
| 1994 | 7 | −0.127 | −0.016 | −0.021 | 0.031 | 0.089 | −0.083 | −0.033 | --- | --- | --- | 38 |
| 1995 | 5 | −0.050 | −0.010 | 0.011 | 0.038 | --- | --- | −0.022 | --- | --- | --- | 5 |
| 1996 | 9 | −0.069 | 0.047 | --- | 0.047 | −0.057 | 0.972 | −0.058 | 1.479 | −1.510 | −1.083 | 19 |
| 1997 | 5 | --- | --- | −0.006 | 0.038 | −0.099 | 1.198 | --- | --- | −1.271 | --- | 16 |
| 1998 | 4 | --- | −0.025 | −0.033 | 0.036 | −0.060 | --- | --- | --- | --- | --- | 25 |
| 1999 | 9 | −0.147 | 0.022 | −0.022 | 0.022 | −0.031 | −0.304 | --- | 0.744 | −0.951 | 0.393 | 25 |
| 2000 | 5 | −0.140 | --- | --- | 0.021 | --- | --- | 0.016 | −0.835 | --- | 1.023 | 24 |
| 2001 | 7 | −0.106 | −0.006 | --- | 0.011 | −0.051 | 0.349 | −0.009 | --- | −0.477 | --- | 11 |
| 2002 | 7 | --- | −0.010 | −0.013 | 0.019 | −0.156 | 0.955 | --- | −0.256 | −0.757 | --- | 36 |
| 2003 | 6 | −0.207 | −0.011 | --- | 0.035 | --- | −0.829 | −0.045 | 0.704 | --- | --- | 37 |
| 2004 | 6 | −0.198 | −0.032 | −0.016 | 0.014 | −0.050 | --- | 0.021 | --- | --- | --- | 28 |
| 2005 | 6 | −0.113 | −0.011 | 0.006 | --- | --- | 1.312 | 0.015 | −1.403 | --- | --- | 19 |
| 2006 | 5 | --- | 0.011 | --- | --- | −0.095 | --- | --- | −1.748 | 0.684 | 1.155 | 8 |
| 2007 | 7 | −0.155 | --- | −0.008 | 0.015 | −0.050 | 0.737 | −0.013 | −0.754 | --- | --- | 36 |
| 2008 | 3 | --- | --- | --- | 0.020 | 0.059 | --- | −0.029 | --- | --- | --- | 13 |
| Total # from 1981−2008 | 22 | 19 | 19 | 18 | 16 | 15 | 14 | 12 | 12 | 6 | ||
| Year | X−var./year | Elevation | Summer PPT | Winter T° | Spring T° | Carbon content | Ant.Fall T° | Spring PPT | Winter PPT | Ant.Fall PPT | Summer T° | AdjR2* 100(%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1981 | 5 | −0.061 | 0.002 | --- | --- | 0.025 | 0.030 | 0.004 | --- | --- | --- | 23 |
| 1982 | 10 | −0.059 | −0.007 | −0.058 | 0.118 | 0.028 | 0.165 | 0.011 | −0.014 | 0.017 | −0.194 | 27 |
| 1983 | 7 | −0.062 | −0.008 | −0.165 | 0.319 | --- | −0.176 | 0.015 | −0.008 | --- | --- | 35 |
| 1984 | 4 | −0.060 | −0.011 | --- | --- | 0.041 | --- | --- | --- | 0.017 | --- | 25 |
| 1985 | 7 | −0.035 | 0.003 | −0.271 | --- | 0.035 | --- | 0.003 | 0.004 | --- | 0.275 | 40 |
| 1986 | 7 | −0.052 | 0.003 | −0.115 | 0.478 | 0.043 | −0.306 | --- | 0.010 | --- | --- | 44 |
| 1987 | 8 | −0.052 | 0.005 | −0.178 | −0.200 | --- | --- | 0.008 | −0.011 | 0.015 | 0.453 | 40 |
| 1988 | 7 | −0.061 | 0.004 | −0.216 | 0.376 | --- | −0.163 | 0.004 | 0.006 | --- | --- | 36 |
| 1989 | 5 | −0.066 | --- | --- | 0.204 | --- | −0.442 | 0.012 | --- | --- | 0.236 | 34 |
| 1990 | 9 | −0.062 | 0.006 | −0.475 | 0.283 | --- | 0.619 | 0.003 | 0.012 | 0.003 | −0.394 | 41 |
| 1991 | 7 | −0.040 | 0.021 | 0.138 | −0.119 | 0.040 | --- | −0.010 | 0.014 | --- | --- | 22 |
| 1992 | 6 | −0.063 | 0.006 | −0.203 | 0.216 | --- | --- | 0.010 | −0.003 | --- | --- | 31 |
| 1993 | 7 | −0.046 | 0.006 | −0.288 | 0.151 | 0.015 | 0.164 | 0.008 | --- | --- | --- | 29 |
| 1994 | 5 | −0.059 | --- | −0.250 | 0.119 | --- | 0.153 | --- | --- | 0.012 | --- | 28 |
| 1995 | 8 | −0.067 | 0.014 | −0.079 | 0.469 | 0.033 | −0.354 | --- | 0.024 | −0.015 | --- | 36 |
| 1996 | 9 | −0.055 | −0.008 | −0.591 | 0.737 | 0.056 | 0.546 | 0.039 | --- | 0.018 | −0.690 | 33 |
| 1997 | 9 | −0.057 | --- | −0.726 | 0.805 | 0.027 | 0.519 | 0.013 | −0.020 | 0.043 | −0.530 | 41 |
| 1998 | 6 | −0.035 | 0.003 | −0.459 | --- | --- | --- | 0.011 | --- | −0.029 | 0.322 | 25 |
| 1999 | 9 | −0.043 | −0.006 | −0.336 | −0.804 | 0.045 | 0.214 | --- | −0.003 | 0.011 | 0.965 | 31 |
| 2000 | 3 | −0.077 | --- | --- | 0.050 | 0.034 | --- | --- | --- | --- | --- | 27 |
| 2001 | 10 | −0.078 | −0.007 | 0.236 | −0.243 | 0.043 | −0.235 | 0.009 | −0.005 | 0.002 | 0.298 | 33 |
| 2002 | 9 | −0.064 | --- | 0.588 | −0.569 | 0.056 | −0.399 | 0.011 | −0.012 | −0.013 | 0.423 | 33 |
| 2003 | 5 | −0.085 | −0.003 | −0.090 | --- | 0.055 | 0.140 | --- | --- | --- | --- | 25 |
| 2004 | 8 | −0.086 | −0.005 | 0.259 | −0.576 | 0.059 | --- | --- | −0.007 | 0.009 | 0.303 | 39 |
| 2005 | 5 | −0.093 | −0.003 | −0.236 | --- | 0.048 | 0.228 | --- | --- | --- | --- | 37 |
| 2006 | 5 | −0.082 | −0.003 | --- | --- | 0.029 | --- | 0.007 | --- | −0.011 | --- | 32 |
| 2007 | 5 | −0.094 | −0.006 | --- | 0.194 | 0.052 | −0.188 | --- | --- | --- | --- | 34 |
| 2008 | 4 | −0.098 | −0.006 | --- | --- | 0.037 | 0.049 | --- | --- | --- | --- | 35 |
| Total # from 1981−2008 | 28 | 23 | 21 | 20 | 20 | 19 | 17 | 15 | 14 | 12 | ||
| Year | X−var./year | Ant.Fall T° | Winter T° | Spring T° | Winter PPT | Carbon content | Elevat. | Spring PPT | Ant.Fall PPT | Summer PPT | Summer T° | AdjR2* 100(%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1981 | 8 | 5.882 | 4.493 | 1.882 | --- | 0.439 | −0.196 | 0.023 | 0.060 | −0.051 | --- | 21 |
| 1982 | 7 | 3.112 | 2.641 | --- | −0.011 | 0.450 | −0.718 | --- | --- | 0.042 | −0.503 | 20 |
| 1983 | 7 | 1.134 | 2.484 | --- | 0.143 | 0.657 | −0.147 | --- | 0.031 | --- | 0.298 | 44 |
| 1984 | 5 | --- | 0.738 | −0.387 | --- | −0.397 | −0.063 | 0.036 | --- | --- | --- | 7 |
| 1985 | 7 | 1.004 | 0.280 | −2.191 | −0.034 | --- | −0.279 | 0.026 | --- | 0.098 | --- | 25 |
| 1986 | 7 | 0.556 | 1.208 | −1.792 | --- | 1.148 | −0.448 | 0.080 | --- | −0.126 | --- | 30 |
| 1987 | 7 | −1.540 | 2.458 | −1.611 | 0.069 | 1.017 | −0.400 | --- | --- | −0.123 | --- | 31 |
| 1988 | 9 | 0.885 | −0.849 | 1.632 | --- | 0.170 | −0.292 | −0.026 | 0.106 | −0.030 | −1.952 | 18 |
| 1989 | 6 | 1.432 | −0.364 | −0.652 | −0.069 | 0.306 | --- | --- | 0.060 | --- | --- | 13 |
| 1990 | 6 | 1.753 | −0.416 | --- | −0.028 | --- | --- | 0.032 | 0.084 | −0.034 | --- | 17 |
| 1991 | 7 | 3.607 | 1.765 | 2.660 | −0.015 | --- | −0.141 | −0.034 | --- | --- | −4.165 | 15 |
| 1992 | 6 | 3.284 | 2.888 | 8.185 | --- | --- | −0.243 | --- | −0.023 | --- | −8.532 | 21 |
| 1993 | 8 | 0.886 | 0.380 | −1.025 | --- | 0.599 | −0.359 | 0.058 | −0.094 | 0.053 | --- | 15 |
| 1994 | 9 | −2.006 | 1.774 | 0.860 | 0.023 | 0.927 | −0.211 | 0.085 | −0.017 | 0.109 | --- | 27 |
| 1995 | 8 | 0.882 | 1.138 | −0.796 | 0.020 | 0.426 | −0.240 | 0.112 | 0.013 | --- | --- | 34 |
| 1996 | 9 | −1.834 | 1.347 | 0.952 | 0.183 | −0.168 | −0.110 | −0.138 | 0.028 | −0.079 | --- | 29 |
| 1997 | 6 | 1.422 | −0.619 | −0.962 | −0.061 | --- | --- | −0.033 | 0.044 | --- | --- | 19 |
| 1998 | 7 | 3.110 | 0.329 | −3.747 | −0.019 | 0.199 | --- | −0.041 | --- | −0.100 | --- | 21 |
| 1999 | 6 | 2.957 | --- | −2.930 | −0.126 | --- | −0.133 | 0.111 | 0.070 | --- | --- | 37 |
| 2000 | 5 | 2.037 | 2.063 | --- | 0.047 | --- | --- | --- | --- | 0.053 | 0.951 | 19 |
| 2001 | 9 | 3.960 | 2.445 | −0.926 | 0.125 | 0.282 | 0.251 | −0.061 | −0.175 | 0.201 | --- | 41 |
| 2002 | 7 | 1.759 | --- | −1.390 | 0.077 | 0.781 | --- | 0.025 | −0.089 | --- | 1.807 | 38 |
| 2003 | 6 | --- | 0.488 | −1.541 | 0.023 | 0.886 | −0.167 | --- | --- | --- | −1.712 | 40 |
| 2004 | 9 | 0.725 | --- | −1.819 | 0.037 | 1.090 | −0.269 | −0.024 | 0.105 | −0.155 | −2.422 | 23 |
| 2005 | 9 | 3.884 | 3.217 | --- | 0.050 | 0.184 | −0.258 | −0.045 | 0.046 | −0.060 | 1.442 | 25 |
| 2006 | 8 | −2.224 | 2.160 | −1.448 | 0.050 | 0.359 | --- | −0.063 | 0.025 | --- | 2.768 | 35 |
| 2007 | 8 | 2.648 | --- | −2.672 | 0.058 | 0.296 | −0.197 | --- | −0.089 | 0.157 | 0.686 | 29 |
| 2008 | 10 | 0.501 | 0.613 | −2.466 | 0.025 | 0.527 | −0.091 | −0.046 | 0.053 | −0.174 | 1.829 | 18 |
| Total # from 1981−2008 | 26 | 24 | 23 | 22 | 21 | 21 | 20 | 19 | 17 | 13 | ||
| Year | X−var./year | Ant.Fall T° | Winter PPT | Spring T° | Summer PPT | Winter T° | Carbon content | Spring PPT | Ant.Fall PPT | Elevation | Summer T° | AdjR2* 100(%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1981 | 6 | 0.690 | --- | 0.198 | 0.022 | −0.718 | −0.150 | --- | 0.020 | --- | --- | 7 |
| 1982 | 5 | --- | −0.014 | 0.195 | --- | −0.379 | --- | −0.044 | 0.076 | --- | --- | 12 |
| 1983 | 6 | 1.957 | 0.011 | −0.701 | --- | −1.069 | −0.109 | 0.017 | --- | --- | --- | 8 |
| 1984 | 2 | --- | --- | --- | --- | --- | −0.558 | 0.022 | --- | --- | --- | 4 |
| 1985 | 6 | 2.141 | --- | 1.548 | −0.143 | −2.038 | --- | --- | --- | 0.072 | −1.612 | 15 |
| 1986 | 7 | 1.687 | −0.030 | −1.936 | −0.081 | −0.384 | --- | --- | −0.110 | −0.118 | --- | 34 |
| 1987 | 7 | 1.479 | −0.034 | −2.082 | 0.060 | 0.315 | 0.134 | --- | −0.041 | --- | --- | 17 |
| 1988 | 7 | 0.880 | −0.020 | −1.999 | −0.056 | --- | 0.384 | −0.054 | --- | −0.204 | --- | 22 |
| 1989 | 5 | −1.096 | −0.019 | 0.415 | --- | --- | --- | −0.042 | 0.057 | --- | --- | 27 |
| 1990 | 6 | 0.637 | −0.042 | −0.563 | −0.020 | −0.708 | --- | --- | 0.040 | --- | --- | 22 |
| 1991 | 8 | 1.677 | −0.007 | --- | 0.012 | −0.952 | −0.104 | −0.027 | --- | 0.058 | −0.476 | 8 |
| 1992 | 4 | --- | −0.046 | −1.072 | −0.017 | --- | --- | −0.037 | --- | --- | --- | 21 |
| 1993 | 2 | --- | --- | --- | 0.017 | --- | −0.265 | --- | --- | --- | --- | 2 |
| 1994 | 8 | 0.655 | 0.020 | --- | 0.047 | −0.567 | −0.164 | −0.061 | −0.021 | --- | −0.799 | 15 |
| 1995 | 6 | 0.619 | −0.043 | −0.552 | 0.082 | −0.260 | 0.077 | --- | --- | --- | --- | 7 |
| 1996 | 8 | −2.473 | −0.054 | −3.230 | --- | 2.667 | −0.357 | --- | 0.048 | 0.201 | 3.856 | 23 |
| 1997 | 8 | 3.126 | −0.087 | −0.681 | −0.034 | −2.306 | −0.444 | 0.059 | 0.029 | --- | --- | 28 |
| 1998 | 8 | 3.371 | −0.035 | −2.964 | --- | −0.388 | −0.242 | −0.021 | −0.078 | 0.122 | --- | 13 |
| 1999 | 6 | −0.401 | −0.076 | --- | −0.073 | --- | −0.145 | 0.063 | 0.053 | --- | --- | 11 |
| 2000 | 5 | 0.569 | --- | −0.676 | 0.039 | --- | --- | --- | --- | 0.074 | 0.727 | 12 |
| 2001 | 7 | 2.514 | −0.022 | −0.305 | --- | −1.774 | --- | --- | 0.037 | −0.159 | −0.554 | 14 |
| 2002 | 9 | 3.318 | 0.035 | −1.117 | 0.063 | −2.485 | 0.078 | −0.019 | −0.017 | −0.210 | --- | 16 |
| 2003 | 9 | −0.716 | −0.049 | −0.311 | −0.036 | 0.502 | 0.203 | 0.021 | 0.080 | −0.104 | --- | 12 |
| 2004 | 8 | 0.258 | −0.033 | −0.461 | −0.030 | --- | 0.315 | −0.019 | 0.075 | −0.094 | --- | 12 |
| 2005 | 7 | −3.206 | −0.080 | --- | −0.098 | 2.329 | --- | 0.075 | --- | −0.107 | 0.651 | 26 |
| 2006 | 8 | −3.336 | 0.064 | −1.131 | --- | 2.050 | 0.208 | −0.097 | --- | 0.120 | 3.065 | 31 |
| 2007 | 9 | 0.621 | −0.017 | −1.929 | 0.062 | --- | 0.134 | 0.012 | −0.035 | 0.053 | 1.410 | 20 |
| 2008 | 8 | 1.899 | 0.034 | −2.096 | −0.257 | −1.087 | 0.527 | −0.192 | --- | −0.284 | --- | 20 |
| Total # from 1981−2008 | 24 | 23 | 22 | 20 | 19 | 19 | 18 | 16 | 15 | 9 | ||
| Year | X−var./year | Carbon content | Winter T° | Winter PPT | Ant.Fall T° | Spring T° | Spring PPT | Ant.Fall PPT | Elevation | Summer PPT | Summer T° | AdjR2* 100(%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1981 | 10 | 0.093 | 0.208 | 0.009 | −0.452 | 0.469 | −0.005 | 0.010 | 0.024 | 0.004 | −0.148 | 48 |
| 1982 | 9 | 0.087 | −0.299 | 0.014 | 0.428 | 0.678 | 0.004 | 0.007 | --- | −0.004 | −0.821 | 39 |
| 1983 | 8 | 0.115 | 0.363 | 0.026 | −0.297 | --- | 0.004 | −0.003 | 0.015 | --- | 0.095 | 63 |
| 1984 | 7 | −0.025 | 0.117 | 0.012 | −0.228 | 0.112 | −0.004 | --- | 0.041 | --- | --- | 31 |
| 1985 | 9 | 0.031 | 0.117 | 0.008 | −0.262 | 0.154 | −0.003 | 0.002 | 0.029 | −0.012 | --- | 24 |
| 1986 | 7 | 0.066 | 0.051 | 0.018 | −0.092 | −0.028 | 0.004 | --- | --- | −0.028 | --- | 52 |
| 1987 | 7 | 0.130 | 0.380 | 0.015 | −0.220 | −0.377 | --- | −0.014 | --- | --- | 0.155 | 33 |
| 1988 | 10 | 0.078 | −0.311 | 0.012 | 0.255 | 0.507 | 0.003 | −0.006 | −0.030 | 0.002 | −0.680 | 32 |
| 1989 | 10 | 0.029 | 0.109 | 0.010 | −0.309 | 0.400 | 0.002 | 0.006 | 0.023 | 0.010 | −0.192 | 38 |
| 1990 | 7 | 0.070 | −0.280 | 0.007 | 0.376 | 0.298 | --- | --- | --- | 0.001 | −0.496 | 22 |
| 1991 | 6 | 0.030 | 0.136 | 0.011 | −0.123 | --- | --- | --- | 0.027 | --- | 0.046 | 38 |
| 1992 | 8 | 0.073 | 0.177 | 0.002 | −0.170 | −0.082 | 0.005 | −0.002 | --- | −0.007 | --- | 27 |
| 1993 | 9 | 0.065 | 0.131 | 0.010 | −0.062 | −0.055 | 0.008 | −0.008 | −0.017 | −0.007 | --- | 57 |
| 1994 | 8 | 0.106 | −0.042 | −0.003 | 0.200 | --- | 0.016 | −0.002 | 0.042 | 0.020 | --- | 34 |
| 1995 | 8 | 0.105 | 0.058 | 0.005 | 0.167 | −0.099 | 0.016 | −0.005 | 0.022 | --- | --- | 39 |
| 1996 | 6 | 0.015 | 0.079 | 0.030 | --- | --- | −0.011 | --- | 0.040 | −0.012 | --- | 54 |
| 1997 | 9 | 0.031 | −0.174 | 0.007 | 0.312 | −0.120 | 0.007 | −0.007 | 0.013 | −0.004 | --- | 22 |
| 1998 | 7 | 0.073 | −0.025 | 0.003 | 0.401 | −0.286 | 0.005 | --- | 0.015 | --- | --- | 14 |
| 1999 | 8 | 0.082 | --- | --- | −0.095 | 0.388 | 0.007 | 0.003 | 0.016 | −0.009 | −0.346 | 44 |
| 2000 | 6 | --- | 0.195 | 0.004 | --- | −0.118 | --- | 0.008 | 0.036 | −0.004 | --- | 39 |
| 2001 | 7 | 0.109 | --- | --- | 0.187 | 0.218 | 0.014 | −0.005 | 0.042 | --- | −0.341 | 73 |
| 2002 | 6 | 0.076 | −0.159 | 0.018 | 0.295 | 0.097 | --- | --- | --- | --- | −0.195 | 56 |
| 2003 | 8 | 0.140 | 0.058 | −0.003 | −0.069 | 0.332 | --- | 0.019 | --- | −0.008 | −0.418 | 52 |
| 2004 | 7 | 0.120 | 0.326 | 0.014 | −0.246 | --- | −0.007 | 0.004 | --- | --- | −0.066 | 47 |
| 2005 | 9 | 0.066 | 0.162 | 0.011 | --- | −0.167 | −0.006 | −0.006 | 0.011 | −0.006 | 0.064 | 52 |
| 2006 | 6 | 0.038 | 0.127 | 0.005 | 0.046 | −0.080 | --- | --- | 0.037 | --- | --- | 42 |
| 2007 | 9 | 0.067 | −0.109 | 0.016 | 0.249 | --- | −0.003 | −0.004 | 0.017 | 0.015 | −0.100 | 46 |
| 2008 | 10 | 0.084 | −0.189 | 0.013 | 0.357 | 0.072 | −0.014 | 0.007 | −0.018 | −0.016 | −0.328 | 23 |
| Total # from 1981−2008 | 27 | 26 | 26 | 25 | 22 | 21 | 20 | 20 | 18 | 16 | ||
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kariyeva, J.; Van Leeuwen, W.J.D. Environmental Drivers of NDVI-Based Vegetation Phenology in Central Asia. Remote Sens. 2011, 3, 203-246. https://doi.org/10.3390/rs3020203
Kariyeva J, Van Leeuwen WJD. Environmental Drivers of NDVI-Based Vegetation Phenology in Central Asia. Remote Sensing. 2011; 3(2):203-246. https://doi.org/10.3390/rs3020203
Chicago/Turabian StyleKariyeva, Jahan, and Willem J. D. Van Leeuwen. 2011. "Environmental Drivers of NDVI-Based Vegetation Phenology in Central Asia" Remote Sensing 3, no. 2: 203-246. https://doi.org/10.3390/rs3020203
APA StyleKariyeva, J., & Van Leeuwen, W. J. D. (2011). Environmental Drivers of NDVI-Based Vegetation Phenology in Central Asia. Remote Sensing, 3(2), 203-246. https://doi.org/10.3390/rs3020203