1. Introduction
Forest attribute inventory information and measurements are critical to forest management [
1]. Historically, forest inventories have focused on timber production [
2] but recent inventories have concentrated on fuel biomass and carbon stores due to interest in bioenergy and carbon sequestration and concerns over global climate change [
3,
4,
5]. A significant problem in monitoring carbon stores in vegetation biomass is the persistent deficiency of accurate biomass estimates [
6].
Biomass is the measurement of plant material mass per unit area. Biomass measurement is sometimes limited to living plant material, but based on the slow deterioration of woody vegetation; the measurement sometimes includes dead material. Above ground biomass is the “mass of live or dead organic matter” [
6]. The unit of measure is commonly g/m
2 or kg/ha. Biomass is measured via four primary means: (a)
in situ destructive measurement; (b)
in situ non-destructive using equations or conversion; (c) derived from remote sensing; and (d) modeling [
4,
6]. Allometric equations are used to statistically infer biomass based on
in situ field data or remotely sensed data for extrapolation to larger land areas. Allometry assumes that a relationship exists by species based on structural measurements, usually height and stem or base diameter [
6].
Light Detection and Ranging (LiDAR) has recently emerged as significant technology for forest measurement applications. Forest measurements derived from LiDAR include ground and vegetation surfaces, which are used to assess tree height, volume, and biomass measurements [
7]. Many forest attributes can be measured by LiDAR over large areas including canopy height, subcanopy topography, vertical canopy distribution [
8], and individual tree heights [
9]. Tree height measurement is a critical component of forest inventory measurements [
9,
10]. When measuring tree heights using LiDAR, accuracy is impacted by several factors including size and reflectivity of the tree, shape of the tree crown, and LiDAR pulse density and footprint (pulse diameter). A primary source of error in LiDAR tree height measurement associated with conifer species occurs when laser pulses miss the sharp apex of the tree resulting in an underestimation of tree height [
11,
12]. Discrete returns from LiDAR pulses that strike the canopy may be used to estimate tree heights, or canopy elevations may be derived from a canopy height model (CHM) [
13]. A CHM is raster surface model, similar to a digital elevation model (DEM), interpolated from points acquired on the upper surface of the canopy. Based on the tree structure, errors in LiDAR tree height measurement are also dependent on the algorithm used to create the CHM [
2]. LiDAR tree height estimates are calculated by subtracting the terrain surface as represented by DEM from the highest point associated with an individual tree [
8,
14].
Several key measurements are required to accurately estimate stand height, stem and forest volume, basal area, stem density, biomass [
15], carbon sequestration, growth and site productivity [
9]. Husch
et al. [
10] describe the most common forest measurements of stem diameter, crown diameter and height. The standard US diameter measurement is diameter at breast height (DBH), which is measured at 1.3 m above the ground on the uphill side and 1.4 m when trees are located on level ground. Crown diameter may be used as a predictor variable for determining DBH and therefore used to estimate tree volume. Tree height may also be used to estimate DBH based on allometric equations [
4]. The crown is defined as “the part of the tree or woody plant bearing live branches and foliage”. Crown cover (
synonym canopy cover) is defined as “the ground area covered by the crowns of trees or woody vegetation as delimited by the vertical projection of crown perimeters and commonly expressed as a percent of total ground area” [
16]. One of the critical measurements in forest mensuration for determining volume or mass is tree height [
9]. Stem volume estimation has traditionally been based exclusively on DBH, but estimates combining height and DBH have proven more accurate if the heights are measured with little or no bias [
13,
17]. Husch [
10] defines three different tree heights that are important to consider in forest measurements including total height, bole height, and merchantable height. These are especially important in considering tree heights measured by LiDAR. Total height is “the distance along the axis of the tree stem between the ground and the tip of the tree”; bole height is “the distance along the axis of the tree stem between the ground and the crown point (crown point is the position of the first crown-forming branch)”; merchantable height is the “distance along the axis of the tree stem between the ground and the terminal position of the last usable portion of the tree stem”. These measurements are often summarized and presented as stand level averages.
Much of the focus on LiDAR research has been on trees occupying a dominant and co-dominant portion of the canopy. Some may consider the necessity of a young-tree inventory as not important or less important than established stands, especially considering a priori knowledge resulting from near term management operations. However, monitoring the status of young stands with trees of under 10 m in height is important for growth projections. In addition, stem density is important in planning thinning or planting treatments [
18]. Understory vegetation including shrubs and young trees can amount to large amounts of biomass, which is important for estimating carbon stores and monitoring fuels for fire risk mitigation. Thus, this research not only focuses on LiDAR forest mensuration capabilities in dominant and co-dominant canopies, but also in the suppressed sub-canopy. In other words, what vegetation can discrete return LiDAR detect, and what does it miss? Previous research suggests that LiDAR pulses do not strike as much of the suppressed sub-canopy vegetation compared to the dominant and co-dominant canopy and that these suppressed points are not used in generating the CHM [
2,
3,
4,
19,
20,
21]. We are not only interested in the accuracy of LiDAR in measuring detected trees, but we also seek to quantify the woody vegetation that is missed by LiDAR on an individual tree and area volume basis. Our study has four primary objectives related to measuring forest tree and shrub features.
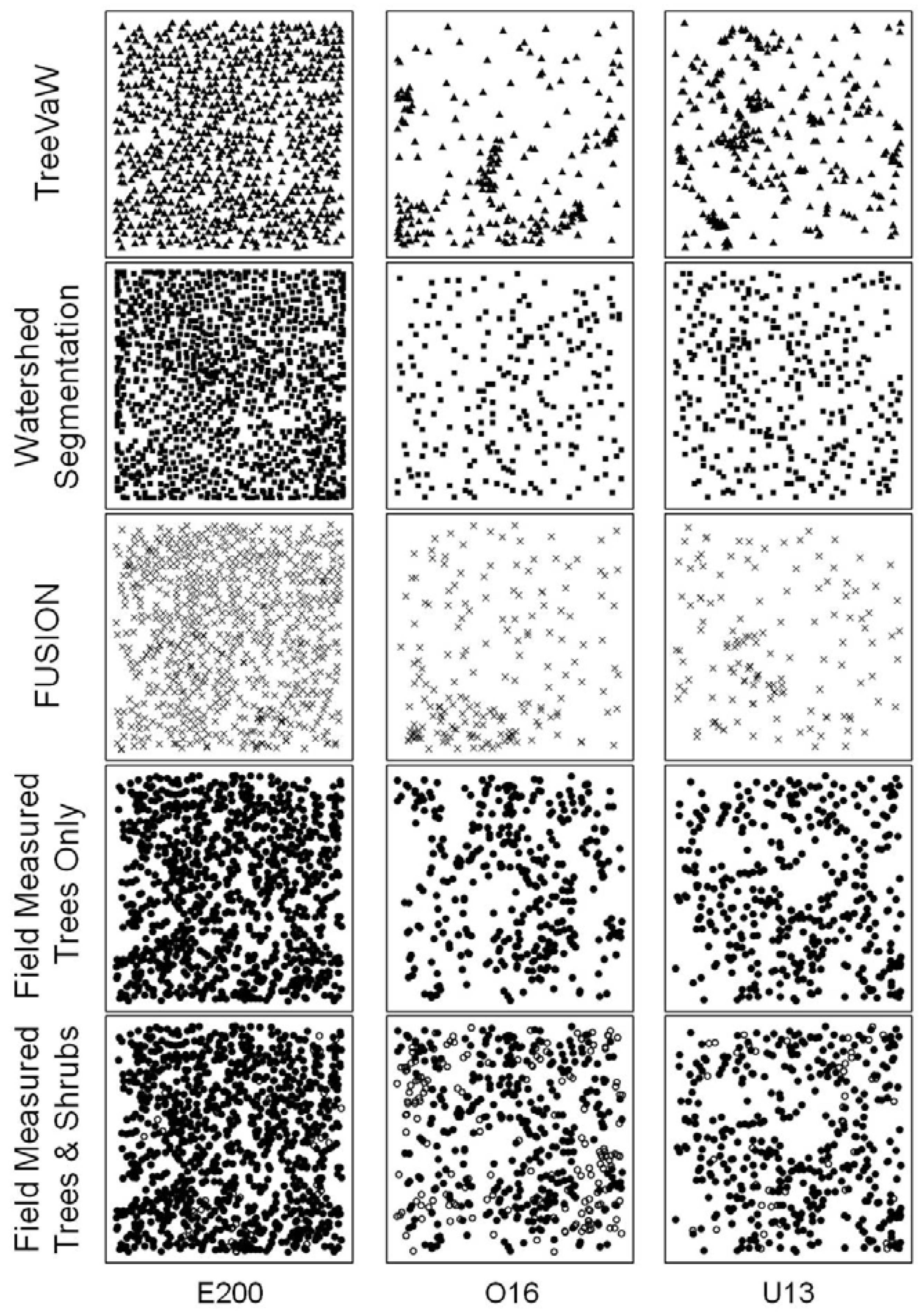
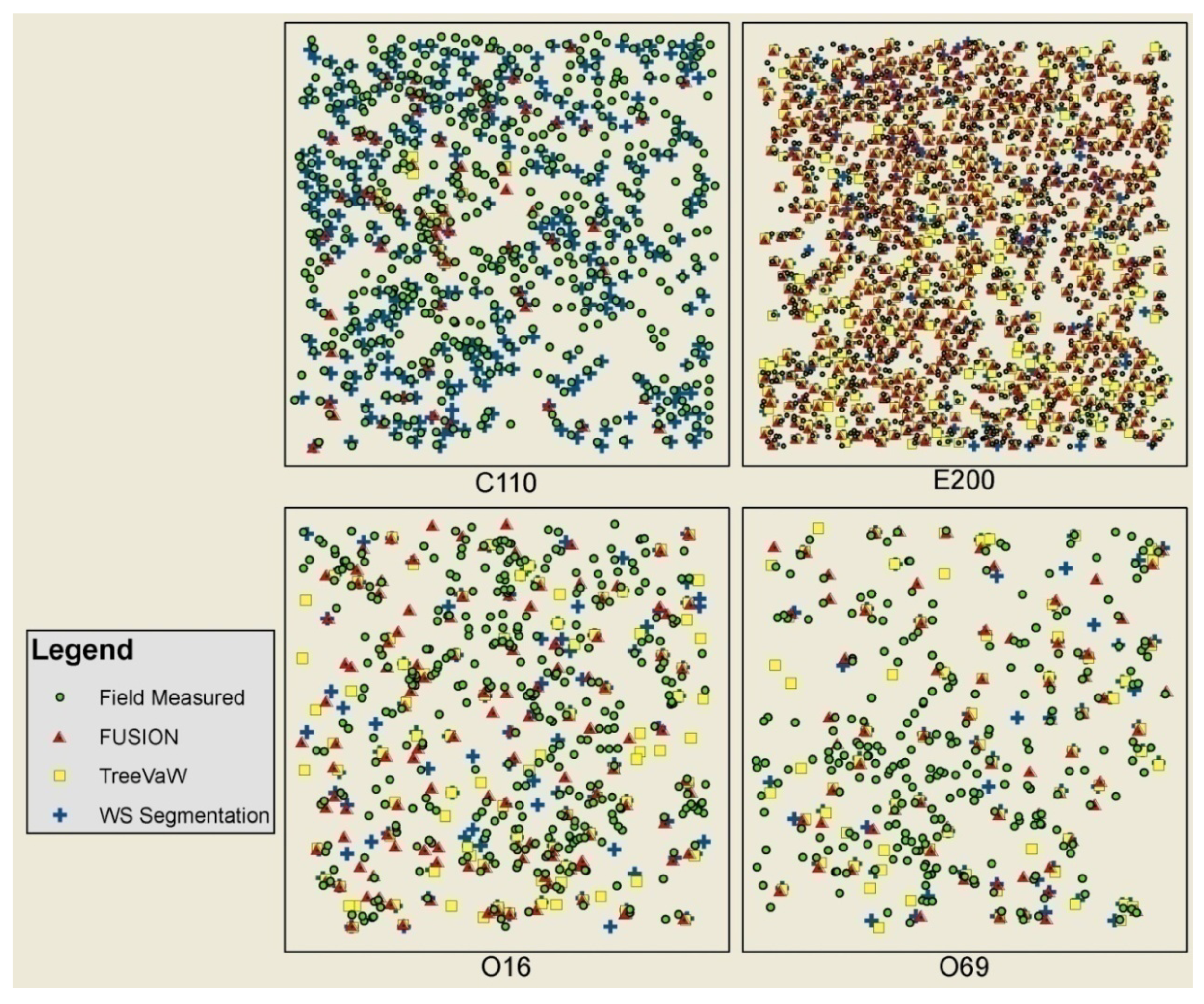
Our first objective was to determine the characteristics of individual trees and shrubs that LiDAR detects and misses within a range of forest settings. We believe this is not only a function of tree and shrub size, but is also influenced by the horizontal and vertical density of vegetation and tree species (deciduous or coniferous). The second objective was to determine the accuracy of LiDAR tree and shrub height measurements of detected features compared to ground measured heights. The third objective was to determine the horizontal x and y location accuracy of LiDAR measured trees and shrubs. The fourth objective was to compare hectare volume estimates derived from LiDAR data to ground measured estimates. We evaluated our study objectives with three different techniques for delineating individual tree and shrub measurements: inverse watershed segmentation, TreeVaW, and FUSION.
Inverse watershed segmentation, henceforth referred to as watershed segmentation, is the most common method applied to determining locations of individual tree crowns using a CHM by segmenting the inverted raster canopy surface into the equivalent of individual hydrologic drainage basins [
22,
23]. Following inversion, a watershed segmentation algorithm separates the CHM into distinct tree polygons with raster crown diameter and height values [
24].
TreeVaW operates on a CHM using a variable window filter (VWF) that varies its search window size [
1,
25], otherwise known as a convolution kernel [
26], by passing a local maxima (LM) filter over the CHM and determines a tree location based on elevation data contained in individual pixels [
1]. Surrounding pixels are assumed to represent laser hits of the same tree crown, and the highest elevation value is taken to indicate the tree apex [
27]. When the filter determines a LM value, a tree x and y coordinate location is identified and then the crown diameter is determined based on the allometric relationship to height [
25,
27].
The Silviculture and Forest Models Team of the United States Department of Agriculture (USDA) Forest Service, Pacific Northwest Research Station in conjunction with the University of Washington Precision Forestry Cooperative has developed a data management and visualization software tool named “FUSION” that is designed specifically for analyzing forest vegetation characteristics using LiDAR data. The program is capable of generating both DEM and CHM surface models, intensity images from the raw LiDAR point files, and analyzing XYZ point data clouds on a plot basis. After identifying a tree, the user manually measures its dimensions using a three-dimensional cylinder measurement marker. The cylindrical measurement marker is capable of measuring a feature’s horizontal coordinate location, height, crown width, and crown height [
28].
2. Materials and Methods
2.1. Study Site
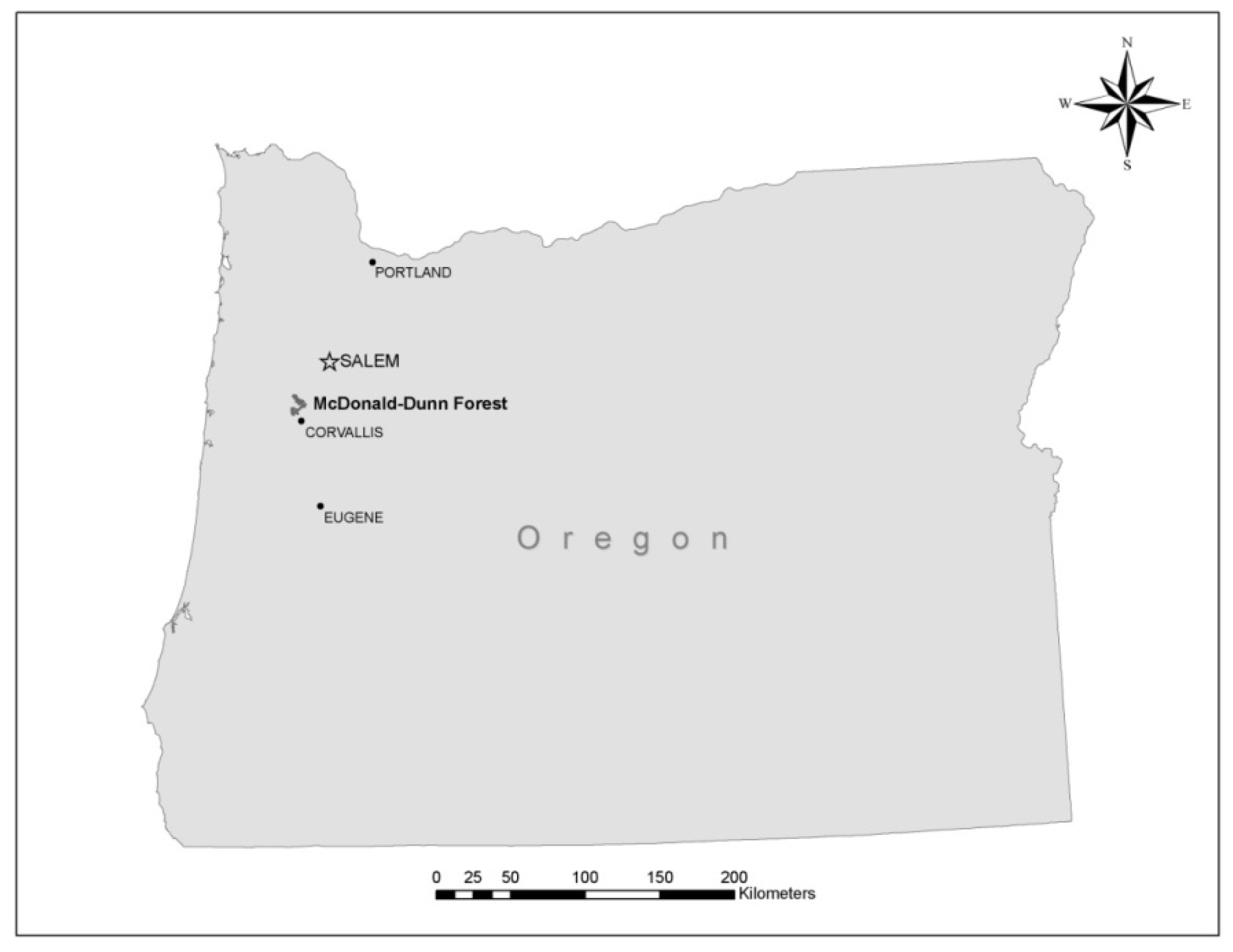
The study was conducted in Oregon State University’s (OSU) 5,475 ha McDonald-Dunn research forest ranging in elevation from approximately 75–660 m above sea level in the eastern foothills of the Oregon Coast Range in the USA (
Figure 1). Conifers dominate the forest with Douglas-fir (
Pseudotsuga menziesii) and grand fir (
Abies grandis) being the apex species. The primary deciduous tree species is bigleaf maple (
Acer macrophyllum) and shrub species California hazel (
Corylus cornuta var. california).
Figure 1.
McDonald-Dunn Forest and surrounding communities within Oregon, USA.
Figure 1.
McDonald-Dunn Forest and surrounding communities within Oregon, USA.
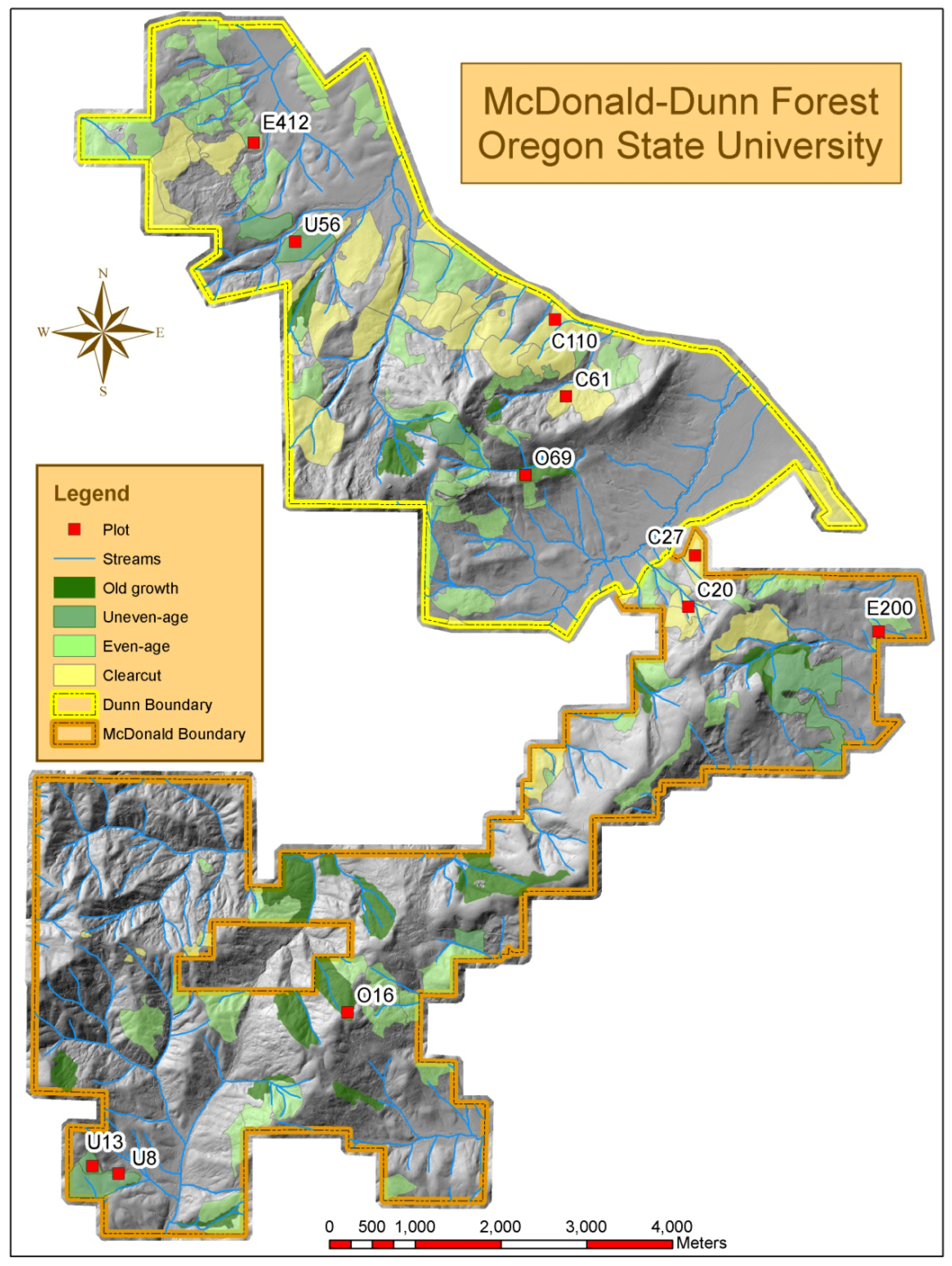
Eleven total plots, one ha (10,000 m
2) in size, were sampled with plot strata consisting of either old growth/mature (referred to as old growth in this study) (two plots), even-aged (two plots), uneven-aged (three plots), or clearcut (four plots) treatments. Plots were selected by stratified random sampling (
Table 1). Plot naming corresponds to the silviculture treatment (C = clearcut; E = even-age; O = old growth; and U = uneven-age) and GIS grid number used for random selection.
Table 1.
Plot statistics for tree and shrub measurement comparison. Total station measurements collected on five plots and GPS measurements collected on all plots.
Table 1.
Plot statistics for tree and shrub measurement comparison. Total station measurements collected on five plots and GPS measurements collected on all plots.
| Plot | C20 | C27 | C61 | C110 | E200 | E412 | O16 | O69 | U8 | U13 | U56 |
|---|
| Slope Aspect | NW | NW | NE | NE | E | NE | NE | N | E | SE | NE |
| Slope Degree | 24 | 18 | 13 | 9 | 7 | 14 | 17 | 28 | 17 | 14 | 8 |
| Slope Percent | 45 | 32 | 22 | 16 | 13 | 25 | 31 | 55 | 32 | 25 | 14 |
| GPS | | | | | | | | | | | |
| Tree Count | 691 | 565 | 534 | 575 | 946 | 929 | 363 | 238 | 192 | 498 | 1255 |
| Shrub Count | 8 | 15 | 0 | 118 | 56 | 57 | 140 | - | - | 47 | 72 |
| Total Station | | | | | | | | | | | |
| Tree Count | | 910 | | 355 | 257 | 367 | 385 | |
| N/A | N/A | N/A |
| Shrub Count | 78 | 173 | 45 | 153 | 48 |
LiDAR
Feature Count | 825 | 647 | 632 | 619 | 1067 | 957 | 210 | 222 | 191 | 311 | 824 |
Percent
Crown Cover | 11 | 9 | 10 | 9 | 65 | 27 | 47 | 46 | 43 | 38 | 70 |
| * Stand Age yrs. | 6 | 6 | 6 | 6 | 21 | 13 | 156 | 138 | 85 | 94 | 57 |
The most represented conifer species within the study plots was Douglas-fir (
Pseudotsuga menziesii) (
Table 2) with a large contingent of grand fir (
Abies grandis) in the uneven-aged and old growth plots (
Figure 2). Ponderosa pine (
Pinus ponderosa) and Pacific yew (
Taxus brevifolia) were found in limited circumstances in addition to several other isolated individuals such as silver fir (
Abies alba) and western hemlock (
Tsuga heterophylla). Although the forest is dominated by conifers, the primary deciduous tree species occupying the subcanopy is bigleaf maple (
Acer macrophyllum). Many other broadleaf tree species were inventoried including cascara buckthorn (
Rhamnus purshiana), cherry (
Prunus sp.), and ocean spray (
Holodiscus discolor) (33 in plot O69) and many others typical of the region in far fewer numbers. California hazel (
Corylus cornuta) is prolific in this region and dominated the understory species of all plots except clearcut where it had obviously been managed. Besides bigleaf maple, many other isolated shrubs typical of the region were inventoried, and ocean spray was conspicuous in two plots. The densest ground cover was found on C110, which had portions covered in Oregon grape (
Berberis nervosa) and poison oak (
Rhus diversiloba) (not inventoried). The discrepancy between GPS and total station in tree counts for Plots U8 and U13 (
Table 1) may be explained by two reasons. In Plot U8, the GPS measurements were made for a separate project where only trees 3 m tall and larger were measured. In Plot U13, several small trees on the cusp of the measurement criteria appear to have been overlooked by the total station survey crew.
Figure 2.
Plot locations in McDonald-Dunn Forest.
Figure 2.
Plot locations in McDonald-Dunn Forest.
2.2. Tree and Shrub Measurements
The field data collected for trees were species, height, crown width, DBH for stem diameters 13 cm and larger, diameter at ground level (DBA) for stem diameters under 13 cm for all trees one meter and taller (0.61 m and taller in clearcut plots) (
Table 2). Heights for tall trees were measured using an Impulse 200LR laser range finder. Height poles were used to measure trees shorter than three meters and all shrubs. A diameter tape was used for DBH and a caliper for DBA. Crown radii for large trees were measured using a range finder and measuring the distance between the projection of the crown vertically to the ground and the tree stem. Small trees and shrub crown measurements were made using a tape measure. In all cases two crown measurements were made per feature. The first length was measured at the longest stem in the crown, and the second was taken at 90° around the stem in a clockwise direction. The crown diameter was then estimated by averaging the two crown measurements, multiplying by two, and adding the DBH. Canopy base height was measured using the FUSION software program as it was not measured by field crews.
Table 2.
Study total tree and shrub counts by species common name.
Table 2.
Study total tree and shrub counts by species common name.
| All Trees | Count | Conifers Only | Count | All Shrubs | Count |
|---|
| SPECIES | | SPECIES | | SPECIES | |
| bigleaf maple | 371 | Douglas-fir | 5,245 | Bigleaf maple | 110 |
| California hazel | 8 | grand fir | 876 | California hazel | 381 |
| cascara buckthorn | 76 | pacific yew | 20 | Cascara buckthorn | 2 |
| cherry | 247 | Pacific silver fir | 8 | cherry | 17 |
| cottonwood | 1 | ponderosa pine | 49 | Douglas-fir | 1 |
| Douglas-fir | 5,245 | Total | 6,198 | holly | 9 |
| grand fir | 876 | | | madrone | 1 |
| hawthorne | 6 | Conifers Minus Snags | | mountain mahogany | 1 |
| holly | 6 | SPECIES | | oceanspray | 73 |
| madrone | 10 | Douglas-fir | 5,156 | Oregon white oak | 5 |
| oceanspray | 3 | grand fir | 866 | Oregongrape | 64 |
| Oregon white oak | 9 | Pacific yew | 20 | Pacific dogwood | 6 |
| Oregongrape | 9 | Pacific silver fir | 8 | red elderberry | 12 |
| Pacific yew | 20 | Ponderosa pine | 48 | Scoular’s willow | 2 |
| Pacific dogwood | 2 | | | snowberry | 1 |
| Pacific silver fir | 8 | Total | 6,098 | vine maple | 12 |
| ponderosa pine | 49 | | | other | 14 |
| red elderberry | 6 | | | | |
| vine maple | 10 | | | Total | 711 |
| other | 18 | | | | |
| Total | 6,980 | | | | |
2.3. Total Station Survey
A Nikon DTM 310 total station with a rated angular accuracy of five-seconds was used to collect the coordinate locations for trees and shrubs in five of the eleven plots. All trees at 1 m and greater in height and all shrubs with a crown diameter of 1 m and greater were measured. Tree sweep was measured for conifer trees that had a noticeable lean angle, thus indicating a different tree apex location compared to its base. Tree coordinate data collected using the total station involved sighting on a rod-person who was positioned directly at the tree stem for small trees or using a two meter rod-measured offset for large trees. The offset distance error was periodically verified using a metric tape and resulted in a mean error of 0.07 m (SD = 0.07). Coordinates, species, health, dbh, and height of all trees and shrubs were determined and recorded.
Survey control was established to transform the local total station coordinates into a Universal Transverse Mercator (UTM), zone 10 North NAD 1983 horizontal map coordinate system. A North American Vertical Datum 1988 (NAVD88) using Geoid Model 2003 (GEOID03) was applied for elevations. Two TOPCON Hiper Lite Plus survey grade GPS receivers were used to establish static control for each plot. The National Geodetic Survey (NGS) Online Position User Service was used for postprocessing control station coordinates.
2.4. GPS Survey
Three different Trimble mapping grade GPS receivers were used for GPS data collection in all eleven plots. These included the GeoXT, GeoXH, and ProXH receivers which all have similar accuracy specifications. We collected GPS data in all plots so that comparisons could be made to total station measurements, the subject of additional research. Based on funding and procurement time lag of the higher accuracy rated ProXH and GeoXH receivers, we chose to begin the project using the GeoXT receiver for data collection in the clearcut and younger even-aged (E412) plots. All but one of the remaining plots was measured using the ProXH, and the final plot data (U8) was collected using the GeoXH based on project time constraints. The GeoXT was configured using the Trimble Hurricane model external antenna while the GeoXH and ProXH were both configured with the Trimble Zephyr external antenna. We used a 15 degree horizon mask, a standard PDOP mask of 6 [
29]), and a default signal-to-noise ratio (SNR) value of 39 dB Hz [
30].
Similar to the total station survey, each tree, shrub, and tree sweep (where applicable) was measured using a GPS. The GPS receiver and antenna were attached to a pole with the antenna mounted 2.2 m above ground. Large tree locations were measured using a two meter offset and hand compass to maintain a consistent azimuth. All others were measured at the feature location. A minimum of thirty and usually not more than sixty points were collected per position. GPS receiver files were downloaded and differentially corrected using Trimble Pathfinder Office version 4.10. Each file collected using the GeoXT was differentially corrected using course acquisition (C/A) code processing using multiple base station providers selected through proximity to the plot and an integrity index. The original intent was to collect data using dual frequency carrier phase ranging. However, when differentially correcting the data, no carrier phase data corrections were possible. The closest available base providers were chosen, unless the integrity index was below eighty. We selected 80 because a priori knowledge indicated that integrity index values above 80 were consistently achievable. Each file collected using the ProXH or GeoXH receiver was differentially corrected with automatic carrier and C/A code processing using multiple base station providers. When using the multiple base provider option, Pathfinder Office averages the coordinate data from each base station provider in the group, weighting the closer base provider higher to determine a single position solution.
2.5. LiDAR Collection
LiDAR data were collected on 2 April 2008 under clear, sunny weather conditions by Watershed Sciences based in Corvallis, Oregon. A Leica ALS50 Phase II laser system was used with a ±14° scan angle from nadir and pulse rate designed to achieve a point density of ≥8 points per square meter. To reduce laser shadows and increase laser coverage, each flight line had ≥50% side-lap, which equates to ≥100% overlap throughout the study area. The system is capable of a maximum number of four returns per pulse. The onboard differential GPS unit measured aircraft position twice per second (2 Hz) and the inertial measurement unit (IMU) measured aircraft attitude 200 times per second (200 Hz) [
31]. Ground control was conducted simultaneously with the airborne LiDAR survey using a static GPS located over ground stations with known locations at a rate of one point collected per second (1 Hz) with indexed time.
The LiDAR data accuracy was described by the vendor as the mean error and standard deviation of the LiDAR point coordinates compared to RTK surveyed ground point coordinates. The vendor provided laser point density and accuracy (
Table 3). Although a 1 meter resolution DEM of the ground surface was provided, no methodology or accuracy statistics were made available by the vendor.
Table 3.
Laser point density and accuracy reported by vendor.
Table 3.
Laser point density and accuracy reported by vendor.
| | Target | Reported |
|---|
| Average First Return Point Density | ≥8 points/m2 | 10 points/m2 |
| Average Ground Point Density | | 1.12 points/m2 |
| Vertical Accuracy (1σ) | <0.13 m | 0.020 m |
| Average Relative Accuracy | | 0.053 m |
| Absolute Accuracy | | 0.026 RMSE |
| Absolute Z Accuracy | | 0.007 ME, 0.026 SD |
2.6. LiDAR Processing
Several different algorithms have been developed to delineate individual tree crowns and measure tree heights. We compared three extraction algorithms (methods) including WS segmentation, TreeVaW, and FUSION. The WS segmentation and TreeVaW methods automatically delineate and measure features determined to be trees from the CHM (
Figure 3), whereas FUSION requires manual location and measurement of each tree feature from the LiDAR point cloud and, if needed to aid in extraction, a CHM. We used FUSION to create CHM rasters at spatial resolutions of 0.1, 0.3, and 1 m in order to examine resolution influence on tree determination processes. Additionally, FUSION uses mean and median convolution smoothing filters in creating a CHM. The program preserves the local maxima (peaks) while smoothing the surrounding pixels based on the mean or median value of the pixel values within the filter kernel, forcing the surface to adhere to the tree tops. Besides the value of the local maxima, which maintains the value as the highest point in each tree neighborhood, the values of the surrounding crown are stepwise smoothed [
28]. We experimented with both filter approaches and found that the mean filter when compared to the field measured data appeared to have increased errors of omission, thus we used the median filter. Filter options tested were: none, 3 × 3, and 5 × 5. We also applied these filter options in examining WS segmentation and TreeVaW output. After running WS segmentation and TreeVaW iteratively using each CHM resolution, two factors were used to select the model that best matched the field survey data. The first factor was the number of trees and the second was spatial variation. The closest matched sum of trees was selected first, and then the spatial variation of the tree points were observed in a GIS. Spatial variation included two subparts: location and pattern. In many cases the LiDAR generated tree count by plot matched the field survey count, however, when viewing the spatial location of the points in a GIS map, it became obvious that errors of commission occurred, e.g., many points were clustered in a location where only one tree was field measured; or many single trees were located in locations that trees did not exist and were well outside a reasonable distance from a field measured tree, thus creating a spatial pattern that did not match the field measured pattern.
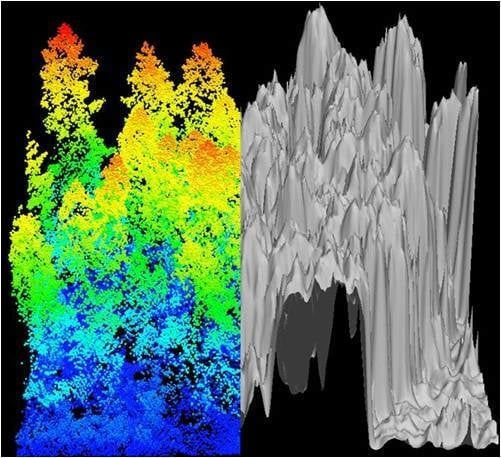
Figure 3.
Canopy Height Model (CHM) representing (a) CHM-Plot C20 Clearcut and (b) CHM-Plot O69 old growth plots. Each CHM image represents 100 m2.
Figure 3.
Canopy Height Model (CHM) representing (a) CHM-Plot C20 Clearcut and (b) CHM-Plot O69 old growth plots. Each CHM image represents 100 m2.
ArcGIS software was used to conduct watershed segmentation. Watershed segmentation determines tree locations and heights by inverting the CHM so that when the model is turned upside down the peaks become depressions. When the raster surface is configured as a depression model, watershed segmentation can then be performed to delineate basins (canopy basins). The canopy basin raster model is converted to canopy polygons which delineate a polygon canopy vector file. The model then uses zonal statistics to overlay the canopy basin file on the CHM and assign the highest pixel value per individual tree canopy basin while replacing all other pixels with a no-data value leaving one pixel remaining with a height value per designated canopy. This value becomes the tree height (Z) and tree bole location (X and Y). Two shapefiles are created in the process, one with only a tree X and Y location and another with a tree X and Y location that includes tree height (Z).
We used TreeVaW software version 1.0 [
32]. TreeVaW implements the CHM processing software in Interface Definition Language (IDL) to locate and measure trees. TreeVaW uses the CHM in ENVI image format and produces output consisting of tree positions in x and y coordinates, tree heights, and crown radii [
32]. The “VaW” in TreeVaW is an acronym for variable window. The program delineates trees by deriving an appropriate size circular search window to find tree tops from the CHM based on the relationship between the height of trees and their crown size. As found in nature, the taller the tree, the larger the crown size [
12]. The program is designed for conifer forest applications and uses a search window based on a default regression relationship of crown diameter as a function of height developed in the southeastern United States, thus the crown diameter relationship was edited using the field collected data for this project. The program’s default regression formula is CW = 2.51503 + 0.012000 H
2 where CW is crown width and H is height. Initial attempts at TreeVaW tree delineation met with poor results in clearcut plots when the regression equation from all field collected trees was used, thus a separate equation was used for the clearcut plots based only on the field database of clearcut plot conifer species. Three attempts were made to determine which regression equation to use for delineating trees in clearcut plots and are further discussed in the results section. For all other plots, the field collected database of all trees except snags having no crown was used for the regression. Dead trees with discernable crowns were included. The input of minimum and maximum crown width and maximum expected tree height parameters are also required before running TreeVaW. We input these values based on our field data.
We applied FUSION software version 2.70 [
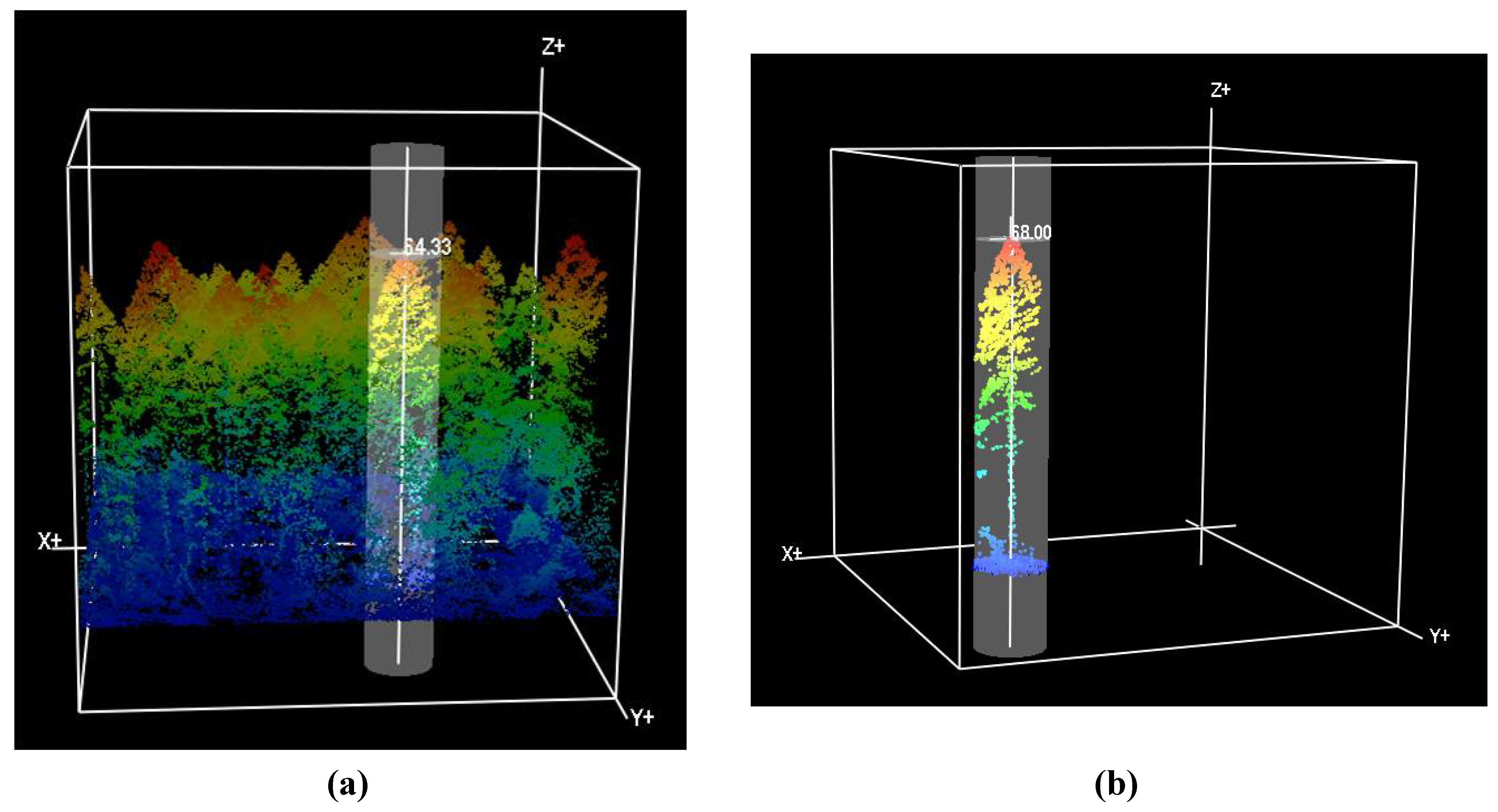
33] for tree delineation. The FUSION software consists of two main programs, FUSION and the LiDAR data viewer (LDV). Many component command line programs also come with the FUSION package for preparing and processing raw LiDAR data for analysis in FUSION and LDV. Once pre-processing steps are completed and the LiDAR data are prepared for plot level analysis, trees are manually selected and measured in LDV using the LiDAR point cloud (
Figure 4(a)) and measurement marker (
Figure 4(b)). Although canopy base height was not measured by field crews in our study, of the three LiDAR software programs used in the study, FUSION is the only one capable of this measurement. In the FUSION generated plots, we measured heights of the upper portion of the point cloud, which in most cases is likely the top of the crown and not the apex of the tree, and measured the lowest discernible portion of the point cloud coincident with what appeared to be the lowest whorl of branches. This was only possible in larger trees in primary canopy where sufficient returns were available to identify the minimum and maximum crown heights. Crown diameter was measured using the measurement marker in either a circular form for a generally round-shaped crown, or elliptically where the crown was more oval-shaped from an orthogonal perspective. Spatial x and y location was measured based on where the analyst determines the apex and center of the tree to be located. Each set of measurements is added to a Comma Separated Value (CSV) file database of individual trees.
Once the LiDAR was prepared for each software program used in this study, there were significant differences in time required to delineate trees. Both TreeVaW and watershed segmentation were automated tree delineation programs that processed each hectare sized plot in this study rapidly within seconds. FUSION on the other hand requires the operator to manually measure and save each tree. This process is relatively quick (30–60 seconds per tree) for large trees in the primary canopy, but becomes progressively more difficult to differentiate smaller trees in the sub-canopy. Based on the time required to delineate individual trees using FUSION, and that this project involved thousands of trees, we limited tree delineation using FUSION to six plots (C110, E200, O16, O69, U8, U13). The advantage to using TreeVaW and watershed segmentation is the speed of processing. The disadvantage to these two programs is that they are limited by the CHM, which inherently due to interpolation loses tree information below the upper canopy. The advantage of FUSION is that it uses the LiDAR point cloud, where all points are available to the user.
Field measured tree X and Y locations and tree heights were compared to those determined by each LiDAR extraction method. For this study, the main purpose of comparing the accuracy of each tree’s spatial location was to establish confidence that tree height comparisons between ground and LiDAR were based on the same tree. The only confirmation of this was similar spatial location and height. The most accurate method used for determining tree spatial location in this study was by total station survey instrument.
Figure 4.
(a) FUSION LiDAR Data Viewer (LDV) measurement window displaying tree height measurement capability. Tree X and Y location, height, crown width, crown base height, and elevation at tree base may be measured and saved to file; (b) FUSION measurement marker surrounding a single LiDAR tree.
Figure 4.
(a) FUSION LiDAR Data Viewer (LDV) measurement window displaying tree height measurement capability. Tree X and Y location, height, crown width, crown base height, and elevation at tree base may be measured and saved to file; (b) FUSION measurement marker surrounding a single LiDAR tree.
2.7. Geographic Information System (GIS) Processing
Tree and shrub locations were measured by total station on five of the eleven plots as discussed above. Height and species was nominally noted, i.e., tree heights were noted as small, average, large, or extra large for the respective plot. Species was noted as conifer or broadleaf. GPS measurements were made in all 11 plots. In addition to absolute spatial location, tree height, crown radius, and species were determined and recorded. In the total station surveyed plots, the specific tree data collected in the GPS survey was used to match total station surveyed trees such that the most accurate horizontal coordinates were combined with specific species and height measurements. Total station feature points were matched to those determined by GPS using ArcGIS software. Each tree feature was matched manually, based on proximity, height (absolute to nominal), and species (specific to nominal) and assigned the same unique identification number. Trees were only matched if relative confidence existed that the two represented the same tree. Where there was doubt, features were not matched. The least amount of confidence in matching occurred in the even-aged plot (E200), where most of the trees were a similar height and species (Douglas-fir). Proximity was the only matching metric, thus some bias may exist in horizontal error between tree locations determined by GPS and total station.
2.8. Biomass
Total above ground biomass (TAGB) was calculated using allometric equations from the biomass computation package BIOPAK [
34] (
Table 4). Because we measured only height and crown diameters for shrubs, and did not measure stem or basal diameters we chose to use percent crown cover for shrub TAGB estimates. We used GIS software to calculate crown cover by creating a polygon layer using the field measured crown diameter measurements for all shrubs in the plot, clipping the shrub crown polygon layer using the plot perimeter data, and then calculating percent crown cover for the 1 ha plot. The majority of the shrubs in the study area were California hazel (
Corylus cornuta), thus we used this species to calculate a general shrub TAGB estimate on a by-plot basis. The closest allometric equations using crown cover we could find for our study area were based on destructive sampling of California hazel collected in riparian zones and meadows in the Sierra Nevada, California. The equation used was BAT = (5.01 × COV) × m
2. BAT is TAGB including foliage, COV is the cover percentage, and m
2 is the plot dimension in square meters [
34]. Crown (canopy) cover is the proportion of vertically projected tree or shrub crown (above ground vegetation) that covers the forest floor measured as the presence or absence of canopy vertically above sample points across an area of forest. The height of the tree or shrub has no impact on this measurement as it is the vertical projection of the crown that is measured. Crown cover may be used to predict volume by species because crown area to trunk (stem) basal area has a near linear relationship (biomass) [
35]. All tree TAGB estimates were based on allometric equations related to DBH or DBA, with some equations including height. For trees smaller than 0.13 m DBH, the DBA equations were used. Where weights were calculated in cm
3, weights were converted to kg. All LiDAR TAGB estimates were based on Douglas-fir TAGB estimates. Two Douglas-fir equations were used, one for trees ≥0.13 m DBH and trees <0.13 m (
Table 4) based on BIOPAK values [
34]. BIOPAK provides a Coast Range region equation for small trees whose stem diameter is measured at the base and another based on DBH of larger trees). We used a cutoff of 0.13 m DBH for large and small trees. If a tree was smaller than 0.13 m DBH, then the stem diameter was measured at ground level (DBA). LiDAR DBH estimates were based on regression analysis from trees measured in this study.
4. Discussion
We presented a comparison of FUSION, TreeVaW, and watershed segmentation tree extraction methods in clearcut, even-age, uneven-age, and old growth forest plots using an extensive tree inventory. Our examination and comparison of metrics from the extraction methods included tree height and spatial position. In addition, we compared resulting TAGB estimates from the tree extraction methods.
We reported LiDAR tree height errors using FUSION, TreeVaW, and watershed segmentation extraction methods in our study plots. These errors are generally consistent with those reported in other studies of LiDAR height measurements in various forest conditions compared to field measurements, albeit somewhat higher than some in old growth plot O69 and uneven-aged plot U8 [
10,
38,
39,
40]. To illustrate the complexity in measuring individual trees with LiDAR, many factors influencing the accuracy of LiDAR forest measurement are reviewed below. Some of the key factors that impact LiDAR tree height measurement include survey control, location the LiDAR pulse(s) strike the tree, base measurement datum, differentiating individual trees, position of the tree within the canopy, and use of a raster CHM versus the LiDAR point cloud.
The vendor provided resolution and accuracy summary for this study stated a point resolution specification of ≥8 points/m2 and an achieved resolution of 10 points/m2, and a vertical accuracy of better than 0.13 m. This accuracy is based on measurements made in perfect LiDAR ground conditions, such as those found on paved road surfaces with no vertical obstruction. The resolution and accuracy deteriorates markedly with variation in natural terrain conditions including forest canopy, understory vegetation, small scale topography, and other environmental conditions.
Field measurements are subject to systematic and random error propagation. The field survey crew was trained in proper procedures and the design of proper protocols prevented many potential errors. However due to the scope of this study, it is wrought with a myriad of potential accidental errors. The field survey measured thousands of features, thus error is likely to have occurred periodically in tree height measurement with a laser range finder (both systematic and accidental). Laser range finders are known to introduce height error, however we used one that has been shown to have the highest accuracy in comparison to other commonly used models [
36].
Where and how many LiDAR pulses strike and reflect off the tree impacts tree identification and measurement. In conifer species the odds of a pulse striking a single, very thin apex are low. These odds decrease further when the tree occurs below the primary canopy where pulses that might strike the tree are intercepted by the upper canopy. In every method of tree extraction used in this study the number of pulses hitting the tree impacts identification and canopy dimension measurements. Without an adequate number of pulses striking a tree in FUSION, tree identification was difficult in both dense and clearcut forest plots. In dense plots, upper tree identification was relatively easy based on the unique shape and canopy of each tree, however, as smaller trees were shrouded by larger ones, tree identification was difficult at best. Manually identifying a three dimensional array of dots (the LiDAR point cloud) that belong to a single tree is a tedious process. Differentiating small trees in a clearcut where overstory trees are not a factor was also very difficult. This is strictly a result of LiDAR resolution. Theoretically one would think that a pulse rate of 8–10 pulses per m2 would be enough to enable the identification of small conifers whose crown is approximately 1 m2. However, due to the sparseness of young conifer foliage, often only one or two LiDAR points struck a tree, which made identification difficult to impossible.
TreeVaW and watershed segmentation both rely on a CHM for tree identification and measurement. If points are generated from trees existing below the primary canopy, these points will be eliminated in rendering the CHM surface, thus the tree that exists in the field will be removed from the model. In creating the CHM, we also experimented with raster interpolation resolution. In both models, the 0.1 m resolution CHMs resulted in extreme commission errors (
Table 7 and
Table 8). This is likely due to false canopy peaks introduced where branch height variation caused algorithm calculation error. The software determined a separate tree location based on a LiDAR branch peak returns surrounded by lower height LiDAR pulse returns, when in fact many returns were associated with a single tree. This consistently occurred in commission errors caused by returns from broadleaf trees where upward facing branches along outward extending large branches caused the algorithm to falsely delineate individual trees. Watershed segmentation results found that in 8 of 11 plots the 1m resolution CHM best matched the field measured results. Since the algorithm relies on an inverted CHM to find sills/pits in the raster elevations and in many cases tree tops are 1m apart, it stands to reason that 1m resolution raster cells would avoid errors of commission caused by branch peaks associated within the same tree. TreeVaW’s algorithm appeared to have difficulty finding small trees, even in the clearcut plots where only small trees existed. Excluding the 0.1 m resolution CHM issues addressed above, the differences in resolution appears to be mostly related errors of omission associated with small trees.
All LiDAR tree height measurement methods rely on some form of ground surface elevation model. In this study, all utilized methods relied on a vendor provided DEM. We chose to use this DEM instead of creating our own based on the vendor having the expertise and software necessary to separate ground points from non-ground points such as understory vegetation, stumps, and slash. In certain circumstances, when conducting the ground survey, it was obvious that a LiDAR pulse would not reach the ground surface. Examples of this are dense blackberry, poison oak, and Oregon grape thickets. It is questionable if computer software or an analyst could always identify these features. Even if positively identified, many thickets in this study occupied 100 m2 or more. Interpolation of the ground surface under this vegetation likely introduced error in the DEM.
What level of vertical accuracy is good enough for a tree height measurement? What is the impact if LiDAR height estimation is off by 1 m? If the estimate is under or over from a timber management perspective, then tree volume estimates will be wrong. On the other hand, a loss of some of the tree top is expected in felling operations. For illustrative purposes and from a biomass estimation perspective, we calculated the impact of height errors based on Douglas-fir TAGB in small trees of the same height used in this study (
Table 17). These calculations are based on small Douglas-fir TAGB equations for a single tree and multiplied by the number of trees. This small tree equation was used to represent the approximate size of the top of a tree. Volume estimates are highly variable based on the height of the tree used in allometric equations, and the allometric equation itself, thus the calculations are conservative. Ground truth confirmation would likely be prudent in economic decisions involving LiDAR volume/biomass estimation.
Table 17.
TAGB error estimate based on LiDAR height error.
Table 17.
TAGB error estimate based on LiDAR height error.
| | 1.0 m error (kg) | 1.5 m error (kg) | 2.0 m error (kg) |
|---|
| Single Tree | 0.68 | 1.07 | 1.62 |
| 100 Trees | 67.85 | 106.58 | 161.67 |
| 500 Trees | 339.25 | 532.91 | 808.35 |
| 1,000 Trees | 678.50 | 1,065.83 | 1,616.71 |
We found that there are three main factors that influence the accuracy of LiDAR forest TAGB estimates: feature (tree/shrub) count, feature height, and species identification. In this study, the factor that contributed the most to biomass calculation differences was the tree count. All three algorithms did well at detecting large trees however watershed segmentation appears to detect small trees better than TreeVaW or FUSION. This study illustrates that the effectiveness of using LiDAR with the protocols we used for forest measurement has its limitations. Based on this research and previous studies, further investigation is warranted and development of regional protocols could result in LiDAR becoming a very effective forest measurement tool for volume and biomass estimates. Clearly, this and previous studies have demonstrated that large trees or even-age stands with consistent species and size can be measured using LiDAR with relatively accurate results. However, measuring all trees and shrubs at the stand or forest level for purposes of estimating TAGB is not necessarily accurate compared to field-based estimates. Detecting and measuring small and understory vegetation would likely improve with increased LiDAR resolution (greater pulse density) and warrants further investigation. We also found that the cell resolution of the CHM impacted tree extraction results in TreeVaW and watershed segmentation. Further research is recommended to determine one ideal CHM resolution for stand level tree extraction and biomass estimation, or a potential solution is to use different resolutions per stand treatment. The use of the LiDAR point clouds enable the measurement of all features vertically throughout the canopy structure, however the manual method of feature extraction in FUSION is tedious and slow relative to automated methods, but automated methods used in this study were limited by the CHM. An automated method of feature extraction using point clouds may be a solution to improved measurement accuracy. This study was also limited in estimating TAGB because we did not differentiate species in LiDAR estimations. One method to identify species is to use other imagery, e.g., multispectral aerial photographs or satellite imagery in conjunction with LiDAR. One recommendation is that, if budgets permit, aerial photographs should be taken simultaneously with the LiDAR. The LiDAR system used in this study also acquired return intensity values, which we feel can be used to differentiate conifer from deciduous species, and will be further investigated to improve biomass estimates. Finally, biomass estimates vary widely in their accuracy when relying on allometric equations. Based on many site specific factors and age classes, predicting TAGB developed from different sites and ages can raise debate [
37]. A great deal more variation in biomass equation prediction exists than many realize. Variation in equations is likely by at least ±25–50% (Harmon, M. Personal communication, 30 November 2010).