Meteorological Influence on Predicting Air Pollution from MODIS-Derived Aerosol Optical Thickness: A Case Study in Nanjing, China
Abstract
:1. Introduction
2. Methodology
2.1. PM and Meteorological Data
2.2. MODIS AOT Data
2.3. Data Analysis
3. Results
3.1. Relationship between PM10 and AOT and Its Seasonal Variability

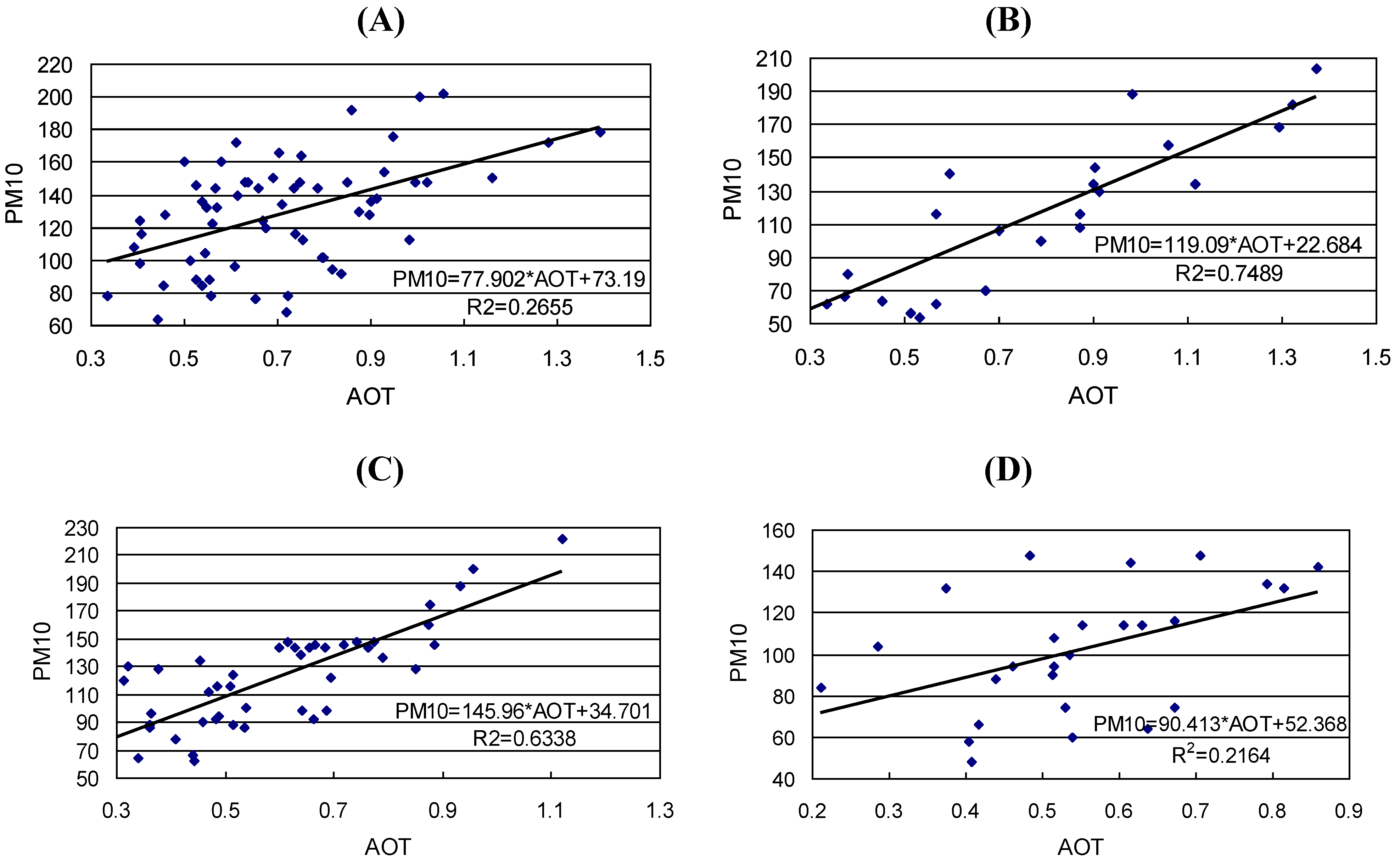
| Season (coefficient) | Statistical parameter | P (hPa) | T (0C) | RH (%) | WV (m s-1) |
|---|---|---|---|---|---|
| Spring (0.52) | AVE | 1,015.47 | 16.27 | 53.24 | 2.23 |
| SD | 7.41 | 6.18 | 9.78 | 0.77 | |
| Summer (0.87) | AVE | 1,004.81 | 29.49 | 59.17 | 2.55 |
| SD | 3.74 | 2.36 | 9.09 | 1.04 | |
| Autumn (0.80) | AVE | 1,020.24 | 16.76 | 67.49 | 1.43 |
| SD | 4.58 | 5.23 | 6.84 | 0.76 | |
| Winter (0.47) | AVE | 1,027.15 | 3.03 | 52.31 | 2.07 |
| SD | 5.46 | 4.01 | 14.53 | 1.07 |
3.2. Meteorological Influence on Residuals of PM10 Estimates
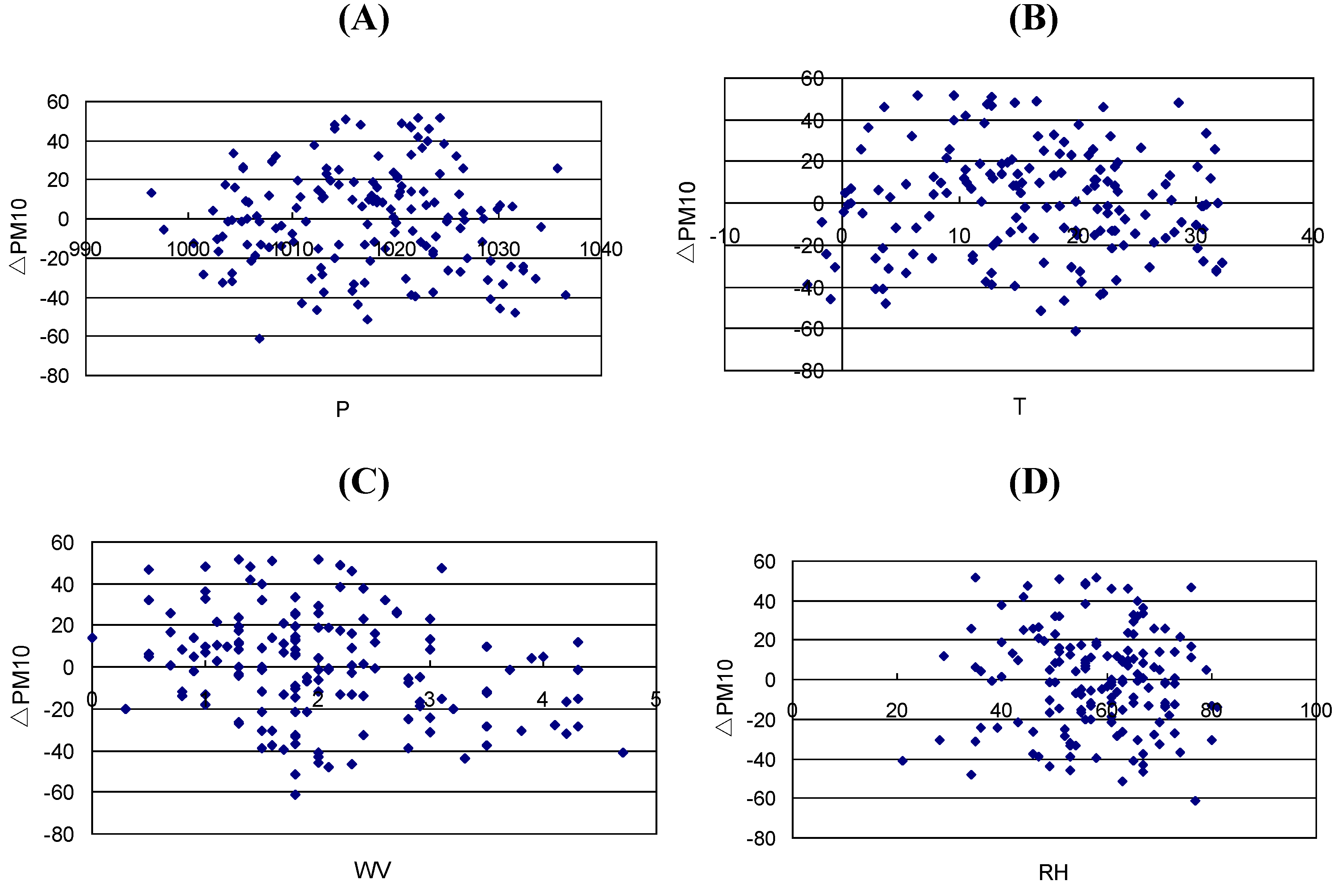
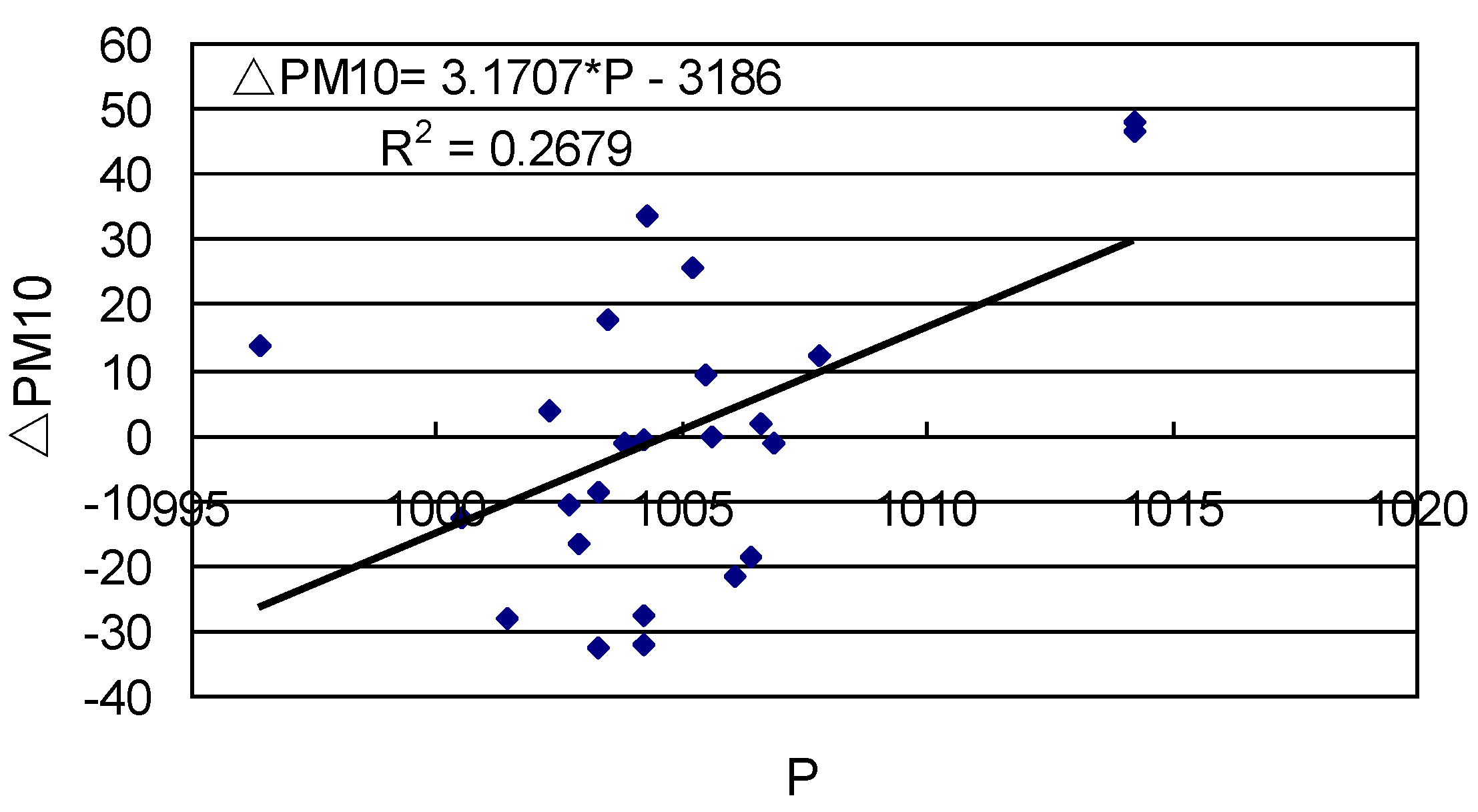
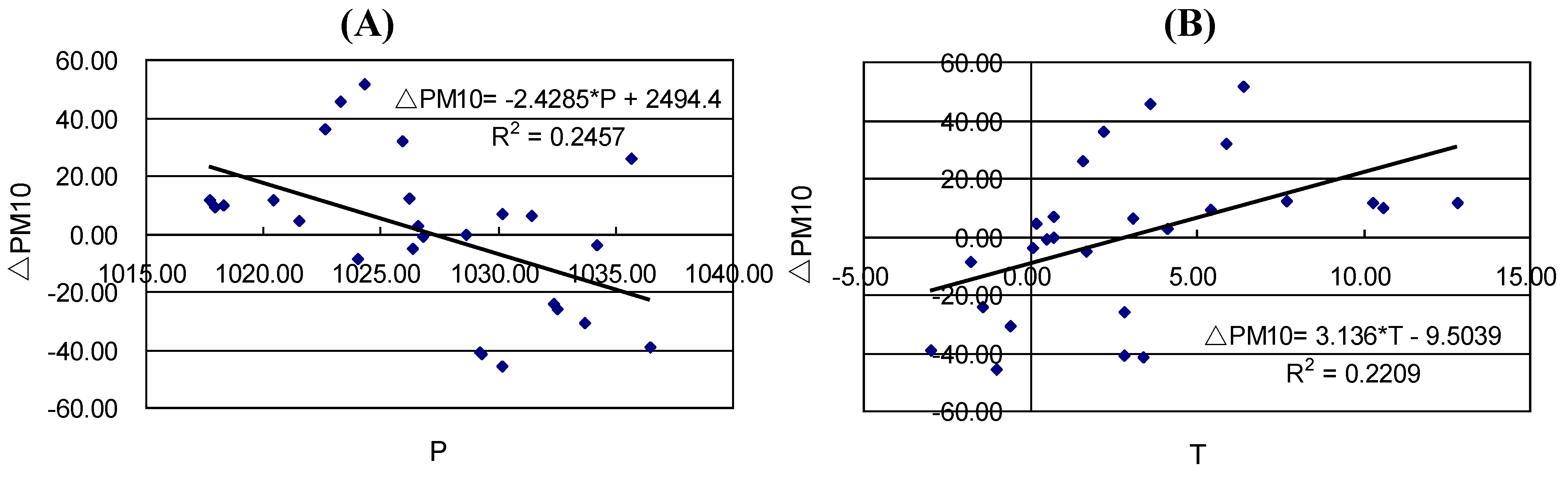
4. Discussion
4.1. Selection of Meteorological Parameters
4.2. Differential Scales of Measurement of Air Pollutants
5. Conclusions
Acknowledgments
References
- Wang, H.; Zha, Y. MODIS-derived aerosol optical thickness as an indicator of urban air quality. Urban Environ. Urban Eco. 2006, 193, 21–24. [Google Scholar]
- Mao, J.T.; Li, C.C.; Zhang, J.H.; Liu, X.Y.; Lau, A.K.H. The comparison of remote sensing aerosol optical depth from MODIS data and ground sun2photometer observations. J. Appl. Meteorol. Sci. 2002, 13, 127–135. [Google Scholar]
- Engel-Cox, J.A.; Hoff, R.M.; Haymet, A.D.J. Recommendations on the use of satellite remote-sensing data for urban air quality. J. Air Waste Manag.t Assoc. 2004a, 54, 1360–1371. [Google Scholar] [CrossRef]
- Chu, D.A.; Kaufman, Y.J.; Zibordi, G.; Chern, J.D.; Mao, J.; Li, C.C.; Holben, B.N. Global monitoring of air pollution over land from the Earth Observing System-Terra Moderate Resolution Imaging Spectroradiometer (MODIS). J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Engel-Cox, J.A.; Holloman, C.H.; Coutant, B.W.; Hoff, R.M. Qualitative and quantitative evaluation of MODIS satellite sensor data for regional and urban scale air quality. Atmos. Environ. 2004, 38, 2495–2509. [Google Scholar] [CrossRef]
- Hutchison, K.D. Applications of MODIS satellite data and products for monitoring air quality in the state of Texas. Atmos. Environ. 2003, 37, 2403–2412. [Google Scholar] [CrossRef]
- Li, C.C.; Lau, A.K.H.; Mao, J.; Chen, A. An aerosol pollution episode in Hong Kong with remote sensing products of MODIS and LIDAR. J. Appl. Meteorol. Sci. 2004, 15, 641–651. [Google Scholar]
- Liu, G.Q.; Li, C.C.; Zhu, A.H.; Mao, J.T. Optical depth research of atmospheric aerosol in the Yangtze River Delta region. Environ. Protection 2003, 8, 50–54. [Google Scholar]
- Wang, J.; Christopher, S.A. Intercomparison between satellite-derived aerosol optical thickness and PM2.5 mass: Implications for air quality studies. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Li, C.C.; Mao, J.T.; Lau, A.K.H.; Liu, X.Y.; Liu, G.Q.; Zhu, A.H. Research on the air pollution in Beijing and its surroundings with MODIS AOD products. Chin. J. Atmos. Sci. 2003a, 27, 869–880. [Google Scholar]
- Li, C.C.; Mao, J.T.; Lau, A.K.H.; Yuan, Z.B.; Wang, M.H.; Liu, X.Y. Application of MODIS satellite products to the air pollution research in Beijing. Sci. China Series D-Earth Sci. 2005, 48 (Suppl), 209–219. [Google Scholar]
- Beran, D.W.; Hall, F.F. Remote-sensing for air-pollution meteorology. Bull. Amer. Meteorol. Soc. 1974, 55, 1097–1105. [Google Scholar] [CrossRef]
- King, M.D.; Kaufman, Y.J.; Menzel, W.P.; Tanré, D. Remote sensing of cloud, aerosol, and water vapor properties from the Moderate Resolution Imaging Spectrometer (MODIS). IEEE Trans. Geosci. Remote Sens. 1992, 30, 2–27. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanr, D.; Remer, L.A.; Vermote, E.F.; Chu, A.; Holben, B.N. Operational remote sensing of tropospheric aerosol over the land from EOS-MODIS. J. Geophys. Res. 1997, 102, (D14). 17051–17068. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Wald, A.E.; Remer, L.A.; Gao, B.-C.; Li, R.-R.; Flynn, L. The MODIS 2.1 μm channel—Correlation with visible reflectance for use in remote sensing of aerosol. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1286–1298. [Google Scholar] [CrossRef]
- Zha, Y.; Gao, J.; Jiang, J.; Lu, H.; Huang, J. Monitoring of urban air pollution from MODIS aerosol data: Effect of meteorological parameters. Tellus 2010, 62B, 109–116. [Google Scholar] [CrossRef]
- Li, C.C.; Mao, J.T.; Lau, A.K.H. Characteristics of aerosol optical depth distributions over Sichuan basin derived from MODIS data. J. Appl. Meteorol. Sci. 2003b, 14, 1–7. [Google Scholar]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gao, J.; Zha, Y. Meteorological Influence on Predicting Air Pollution from MODIS-Derived Aerosol Optical Thickness: A Case Study in Nanjing, China. Remote Sens. 2010, 2, 2136-2147. https://doi.org/10.3390/rs2092136
Gao J, Zha Y. Meteorological Influence on Predicting Air Pollution from MODIS-Derived Aerosol Optical Thickness: A Case Study in Nanjing, China. Remote Sensing. 2010; 2(9):2136-2147. https://doi.org/10.3390/rs2092136
Chicago/Turabian StyleGao, Jay, and Yong Zha. 2010. "Meteorological Influence on Predicting Air Pollution from MODIS-Derived Aerosol Optical Thickness: A Case Study in Nanjing, China" Remote Sensing 2, no. 9: 2136-2147. https://doi.org/10.3390/rs2092136
APA StyleGao, J., & Zha, Y. (2010). Meteorological Influence on Predicting Air Pollution from MODIS-Derived Aerosol Optical Thickness: A Case Study in Nanjing, China. Remote Sensing, 2(9), 2136-2147. https://doi.org/10.3390/rs2092136




