Flood Risk Mapping Using LiDAR for Annapolis Royal, Nova Scotia, Canada
Abstract
:1. Introduction
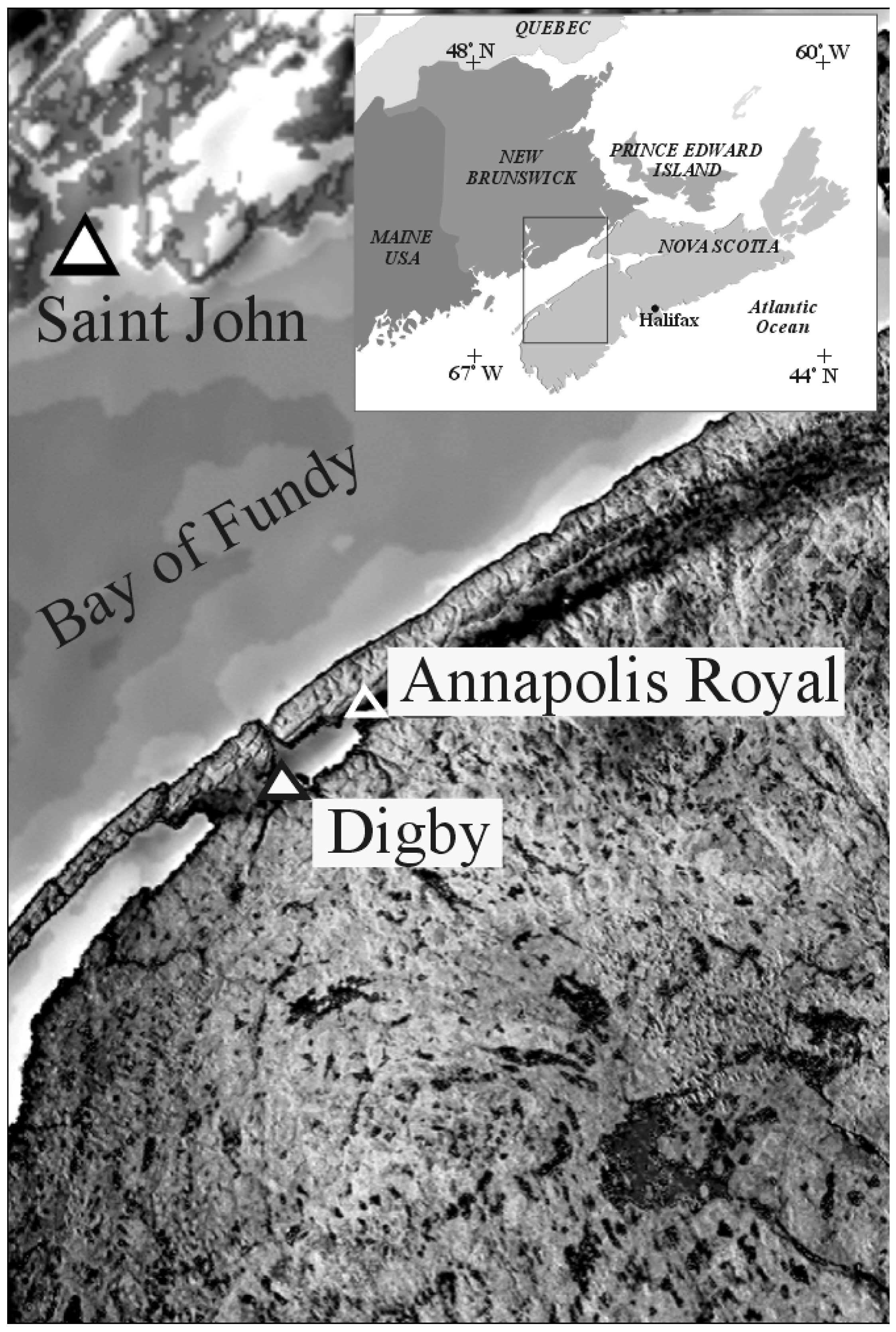
2. Methods
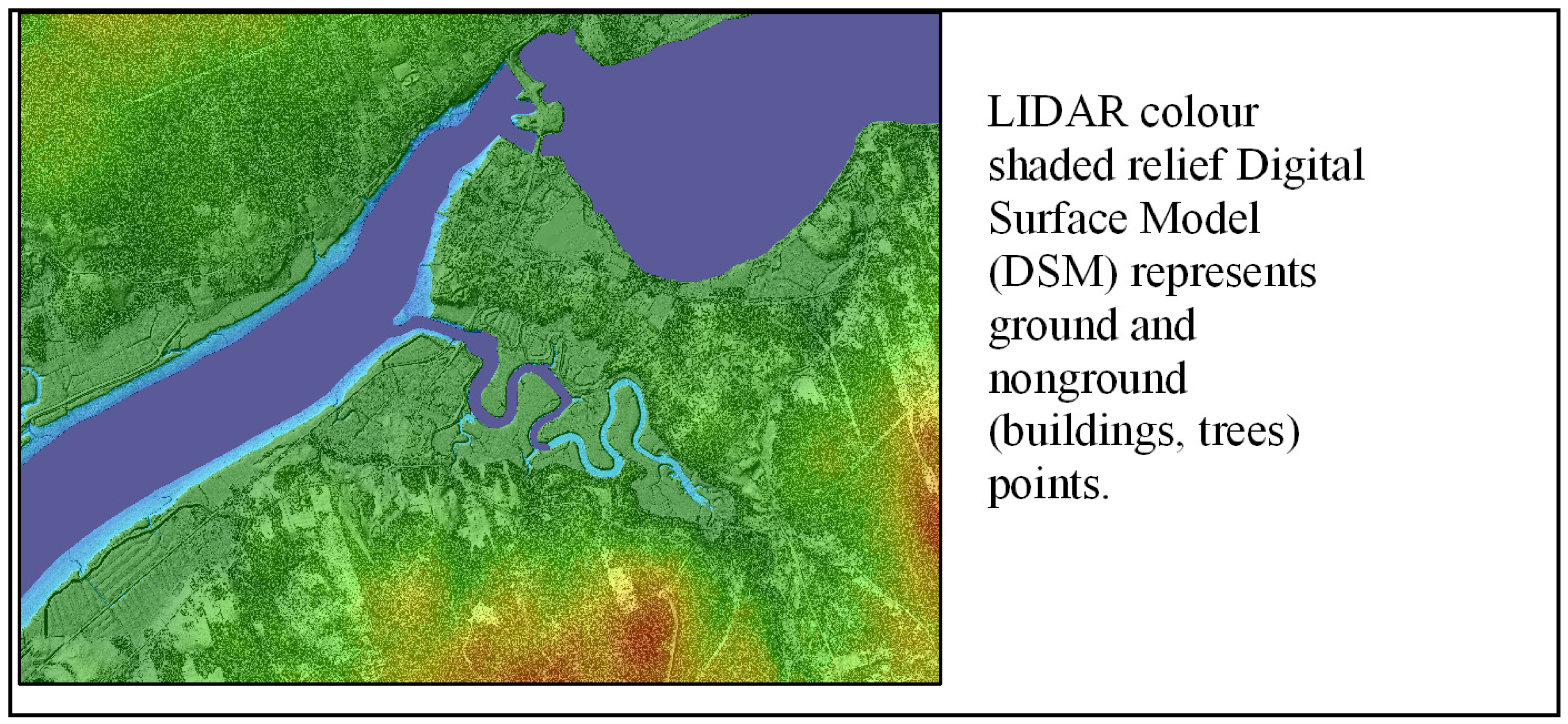
2.1. Airborne LiDAR

2.2. LiDAR Validation
2.3. Seamless DEM Construction & Wave Modeling
2.4. Observed and Predicted Sea-Levels
2.5. Sea-Level Rise from Climate Change Estimates
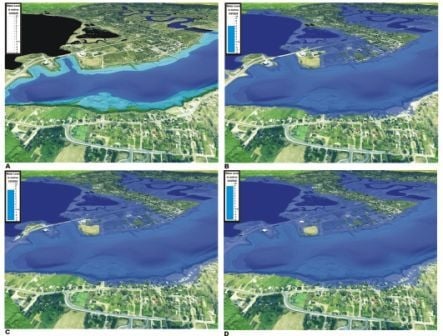
2.6. Flood Inundation Mapping
3. Results
3.1. LiDAR Validation and Surface Construction
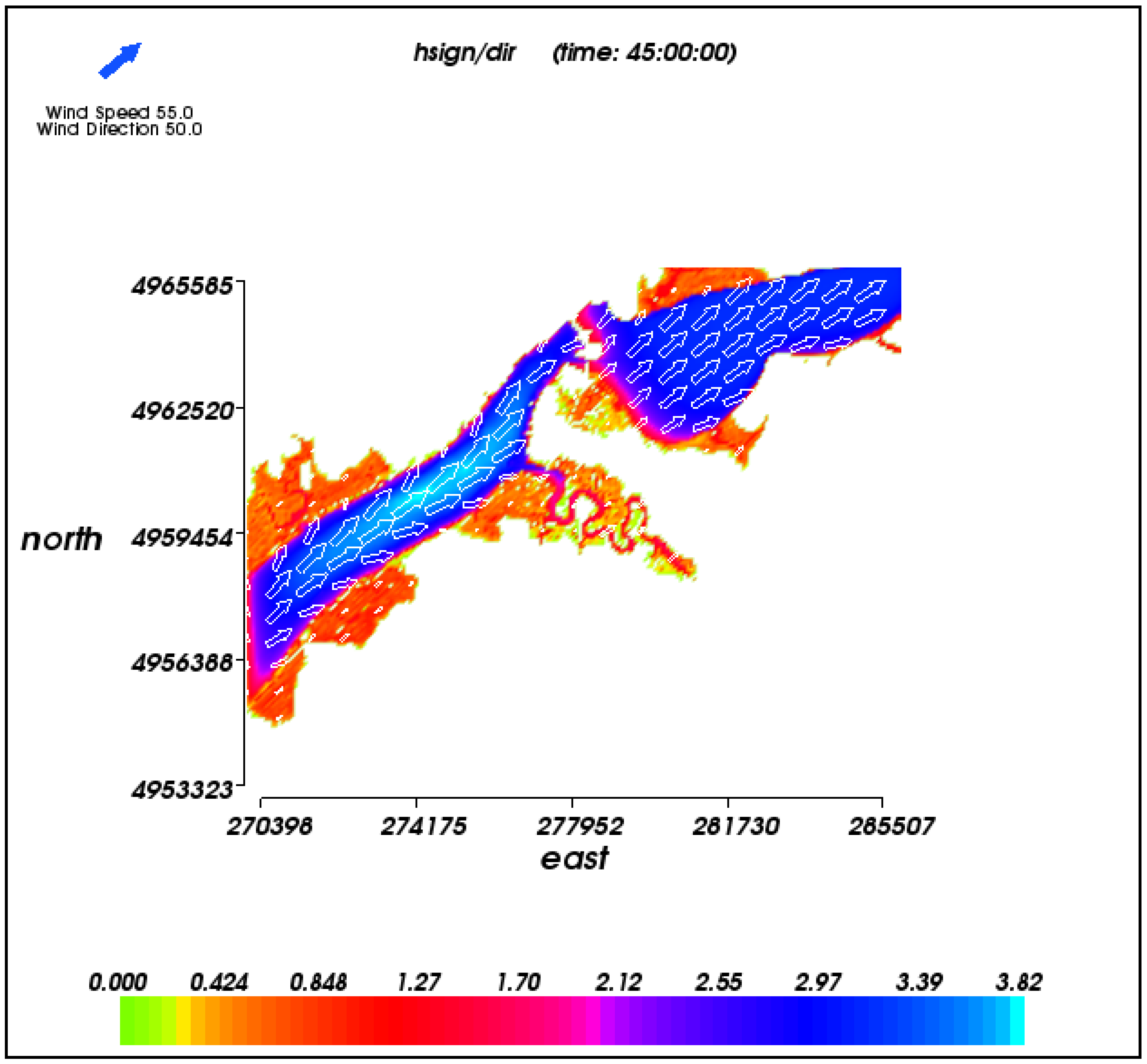
3.2. Wave Modeling of the Benchmark Storm
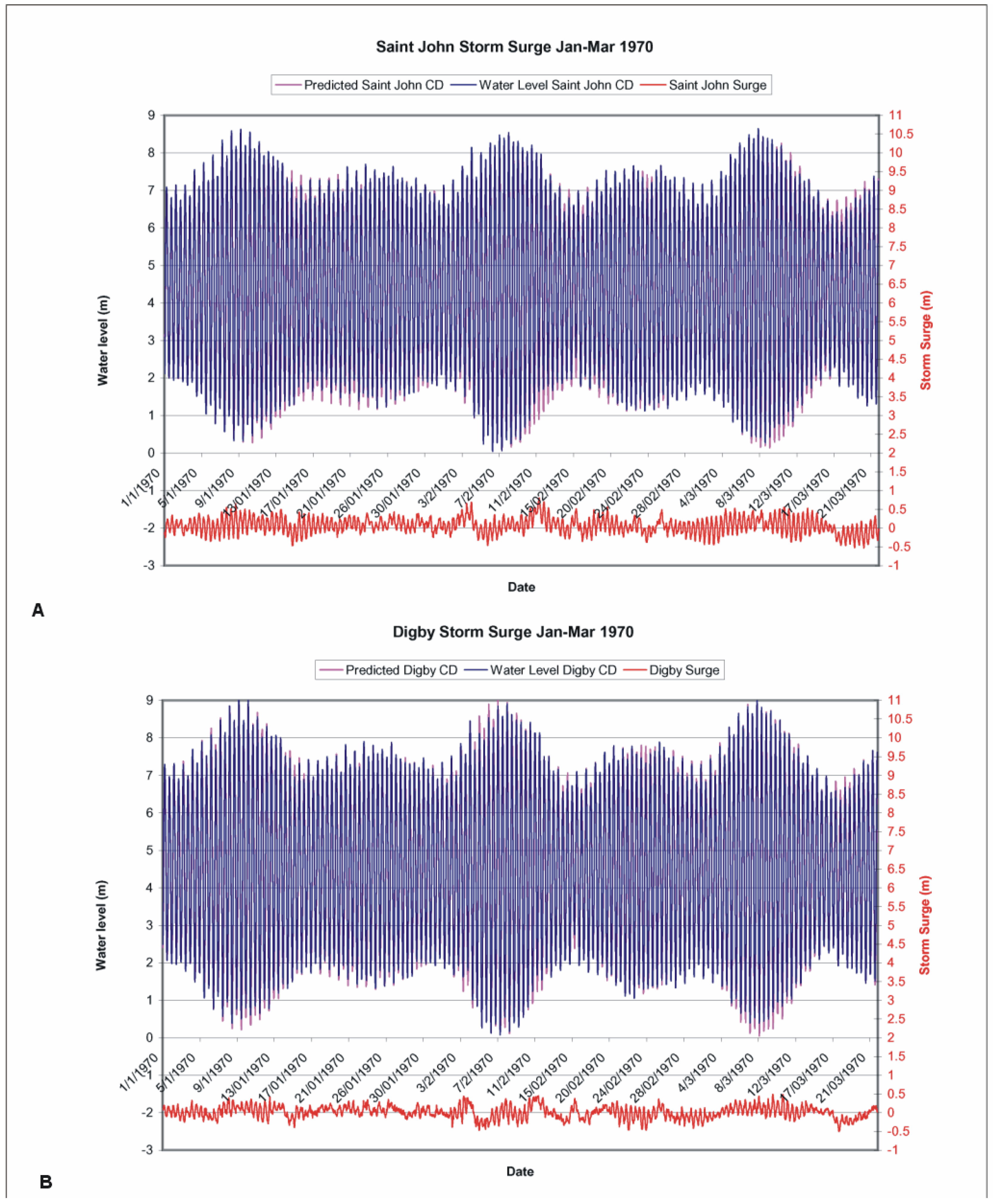
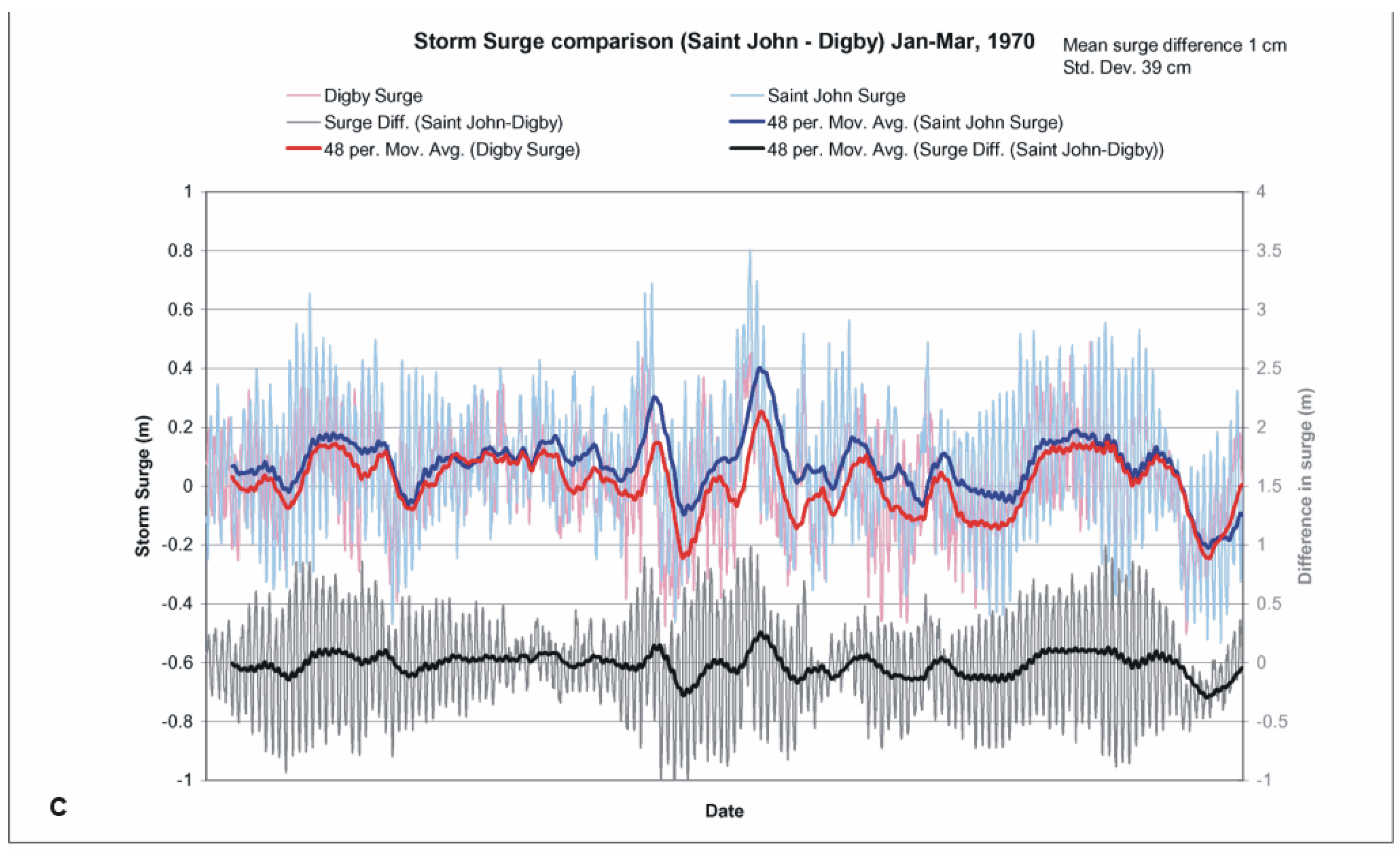
3.3. Observed Water Level Residuals (Storm Surges) between Sites
3.4. Flood Inundation Mapping, Sea-Level Rise and Return Periods

| Probability | Return period (years) RSL = 0.36 cm/year (current) | Return period (years) RSL = 0.80 cm/year (climate change) | Return period (years) RSL = 2.20 cm/year (climate change) |
|---|---|---|---|
| Average (~65–75 %) | 30 | 23 | 14 |
| 100 % | 66 | 44 | 22 |
| Return Period (Years) | Water level (m) with RSL = 0.36 cm/year (current) | Water level (m) with RSL = 0.80 cm/year (climate change) | Water level (m) with RSL = 2.20 cm/year (climate change) |
|---|---|---|---|
| 50 | 4.8 | 4.9 | 5.6 |
| 100 | 5.1 | 5.5 | 6.8 |
4. Discussion and Conclusions
Acknowledgements
References
- Flood, M.; Gutelius, B. Commercial implications of topographic terrain mapping using scanning airborne laser radar. Photogramm. Eng. Remote Sensing 1997, 4, 327–366. [Google Scholar]
- Wehr, A.; Lohr, U. Airborne laser scanning—An introduction and overview. ISPRS J. Photogramm. Remote Sens. 1999, 54, 68–82. [Google Scholar] [CrossRef]
- Meng, X.; Currit, N.; Zhao, K. Ground filtering algorithms for airborne LiDAR data: A review of critical issues. Remote Sensing 2010, 2, 833–860. [Google Scholar] [CrossRef]
- Kraus, K.; Pfeifer, N. A new method for surface reconstruction from laser scanning data. In International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences; ISPRS: Vienna, Austria, 1997; Volume 32, Part 3-2W3; pp. 80–86. [Google Scholar]
- Kraus, K.; Pfeifer, N. Determination of terrain models in wooded areas with airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- Vosselman, G. Slope based filtering of laser altimetry data. In Proceedings of Technical Commission III, Amsterdam, The Netherlands, July 2000. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences; ISPRS: Vienna, Austria, 2000; Volume 33, Part B4; pp. 958–064.
- Axelsson, P. DEM generation from laser scanner data using adaptive tin methods. In Proceedings of Technical Commission III, Amsterdam, The Netherlands, July 2000. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences; ISPRS: Vienna, Austria, 2000; Volume 33, Part B3; pp. 85–92.
- Zhang, K.; Chen, S.; Whitman, D.; Shyu, M.; Yan, J.; Zhang, C. A progressive morphological filter for removing nonground measurments from airborne LIDAR data. IEEE Trans. GeoSci. Remote Sens. 2003, 4, 872–882. [Google Scholar] [CrossRef]
- Raber, G.; Jensen, J.R.; Schill, S.R.; Schuckman, K. Creation of digital terrain models using an adaptive LiDAR vegetation point removal process. Photogramm. Eng. Remote Sensing 2002, 68, 1307–1315. [Google Scholar]
- Hodgson, M.E.; Bresnahan, P. Accuracy of airborne LiDAR-derived elevation: Empirical assessment and error budget. Photogramm. Eng. Remote Sensing 2004, 3, 331–339. [Google Scholar] [CrossRef]
- Lane, S.; James, T.D.; Pritchard, H. Photogrammetric and laser altimetric reconstruction of water levels for extreme flood event analysis. Photgramm. Record 2003, 18, 293–307. [Google Scholar] [CrossRef]
- Bates, P.D.; Marks, K.J.; Horritt, M.S. Optimal use of high-resolution topographic data in flood inundation models. Hydrol. Process. 2003, 17, 537–557. [Google Scholar] [CrossRef]
- Cobby, D.M.; Mason, D.C.; Horritt, M.S.; Bates, P.D. Two-dimensional hydraulic flood modeling using a finite-element mesh decomposed according to vegetation and topographic features derived from airborne scanning laser altimetry. Hydrol. Process. 2003, 17, 1979–2000. [Google Scholar] [CrossRef]
- Haile, A.T.; Rientjes, T.H.M. Effect of LiDAR DEM resolution in flood modeling: A model sensitivity study for the city of Tegucigalpa, Honduras. In Proceedings of ISPRS WG III/3, III/4, V/3 Workshop “Laser scanning 2005”, Enschede, The Netherlands, September 12–14, 2005; pp. 168–173.
- Mason, D.C.; Horritt, M.S.; Hunter, N.M.; Bates, P.D. Use of fused airborne scanning laser altimetry and digital map data for urban flood modeling. Hydrol. Process. 2007, 21, 1436–1447. [Google Scholar] [CrossRef]
- Raber, G.; Jensen, J.R.; Hodgson, M.E.; Tullis, J.A.; Davis, B.A.; Berglund, J. Impact of LiDAR nominal post-spacing on DEM accuracy and flood zone delineation. Photogramm. Eng. Remote Sensing 2007, 73, 793–804. [Google Scholar] [CrossRef]
- Gutierrez, R.; Gibeaut, J.C.; Smyth, R.C.; Hepner, T.L.; Andrews, J.R. Precise airborne LiDAR surveying for coastal research and geohazards applications. In Proceedings of the ISPRS Workshop “Land Surface Mapping and Characterization Using Laser Altimetry”, Annapolis, MD, USA, October 22–24, 2001. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences; ISPRS: Vienna, Austria, 2001; Volume 34-3/W4, pp. 22–24.
- Webster, T.L.; Forbes, D.L.; Dickie, S.; Shreenan, R. Using topographic LiDAR to map flood risk from storm surge events for Charlottetown, Prince Edward Island, Canada. Canad. J. Remote Sens. 2004, 30, 54–76. [Google Scholar] [CrossRef]
- Webster, T.L.; Christian, M.; Sangster, C.; Kingston, D. High-resolution elevation and image data within the Bay of Fundy Coastal Zone, Nova Scotia, Canada. In GIS for Coastal Zone Management; Bartllet, D., Smith, J., Eds.; CRC Press: Boca Raton, FL, USA, 2005; pp. 195–218. [Google Scholar]
- Webster, T.L.; Forbes, D.L.; MacKinnon, E.; Roberts, D. Floodrisk mapping for storm surge events and sea-level rise in Southeast New Brunswick. Canad. J. Remote Sens. 2006, 32, 194–211. [Google Scholar] [CrossRef]
- Webster, T.L.; Forbes, D.L. Airborne laser altimetry for predictive modelling of coastal storm surge flooding. In Remote Sensing of Aquatic Ecosystem Processes, Science and Management Applications; LeDrew, E., Richardson, L., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 157–180. [Google Scholar]
- Webster, T.; Stiff, D. The prediction and mapping of coastal flood risk associated with storm surge events and long-term sea level changes. In Risk Analysis VI Simulations and Hazard Mitigation; Brebbia, C.A., Beriatos, E., Eds.; WIT Press: Wessex, UK, 2008; pp. 129–139. [Google Scholar]
- Webster, T.L.; Mosher, R.; Pearson, M. A coastal zone decision support system to generate flood risk maps from storm surge events and sea level rise. Geomatica 2008, 62, 393–406. [Google Scholar]
- Poulter, B.; Halpin, P.N. Raster modeling of coastal flooding from sea-level rise. Int. J. Geogr. Inf. Sci. 2008, 22, 167–182. [Google Scholar] [CrossRef]
- Klemas, V. The role of remote sensing in predicting and determining coastal storm impacts. J. Coast. Res. 2009, 6, 1264–1275. [Google Scholar] [CrossRef]
- Krabill, W.B.; Wright, C.; Swift, R.; Frederick, E.; Manizade, S.; Yungel, J.; Martin, C.; Sonntag, J.; Duffy, M.; Brock, J. Airborne laser mapping of assateague national seashore beach. Photogramm. Eng. Remote Sensing 1999, 66, 65–71. [Google Scholar]
- Brock, J.C.; Wright, C.W.; Sallenger, A.H.; Krabill, W.B.; Swift, R.N. Basis and methods of NASA airborne topographic mapper LIDAR surveys for coastal studies. J. Coast. Res. 2002, 18, 1–13. [Google Scholar]
- Stockdon, H.F.; Sallenger, A.H.; List, J.H.; Holman, R.A. Estimation of shoreline position and change using airborne topographic LIDAR data. J. Coast. Res. 2002, 18, 502–513. [Google Scholar]
- Sallenger, A.H., Jr.; Krabill, W.B.; Swift, R.N.; Brock, J. Evaluation of airborne topographic LiDAR for quantifying beach changes. J. Coast. Res. 2003, 19, 125–133. [Google Scholar]
- Robertson, W.V.; Whitman, D.; Zhang, K.; Leatherman, S.P. Mapping shoreline position using airborne laser altimetry. J. Coast. Res. 2004, 20, 884–892. [Google Scholar] [CrossRef]
- Morton, R.A.; Miller, T.L.; Moore, L.J. Historical shoreline changes along the US Gulf of Mexico: A summary of recent shoreline comparisons and analysis. J. Coast. Res. 2004, 4, 704–709. [Google Scholar] [CrossRef]
- Zhou, G.; Xie, M. Coastal 3-D morphological change analysis using LiDAR series data: A case study of Assateague Island National Seashore. J. Coast. Res. 2009, 2, 435–447. [Google Scholar] [CrossRef]
- Shaw, J.; Taylor, R.B.; Forbes, D.L.; Ruz, M.-H.; Solomon, S. Sensitivity of the Canadian Coast to Sea-Level Rise; Geological Survey of Canada, Bulletin 505; Natural Resources Canada: Ottawa, ON, Canada, 1994; p. 114. [Google Scholar]
- McCulloch, M.M.; Forbes, D.L.; Shaw, R.W.; the CCAF A041 Scientific Team. Coastal Impacts of Climate Change and Sea-Level Rise on Prince Edward Island; Open File 4261; Geological Survey of Canada, Natural Resources Canada: Ottawa, ON, Canada, 2002. [Google Scholar]
- Church, J.A.; Gregory, J.M.; Huybrechts, P.; Kuhn, M.; Lambeck, K.; Nhuan, M.T.; Qin, D.; Woodworth, P.L. Changes in sea level. In Climate Change 2001: The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2001; pp. 639–693. [Google Scholar]
- Meehl, G.A.; Stocker, T.F.; Collins, W.D.; Friedlingstein, P.; Gaye, A.T.; Gregory, J.M.; Kitoh, A.; Knutti, R.; Murphy, J.M.; Noda, A.; Raper, S.C.B.; Watterson, I.G.; Weaver, A.J.; Zhao, Z.-C. Global climate projections. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK and New York, NY, USA, 2007; pp. 1–844. [Google Scholar]
- Bindoff, N.L.; Willebrand, J.; Artale, V.; Cazenave, A.; Gregory, J.; Gulev, S.; Hanawa, K.; Le Quéré, C.; Levitus, S.; Nojiri, Y.; Shum, C.K.; Talley, L.D.; Unnikrishnan, A. Observations: Oceanic climate change and sea level. In Climate Change 2007: The Physical ScienceBasis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK and New York, NY, USA, 2007; pp. 1–429. [Google Scholar]
- Forbes, D.L.; Manson, G.K.; Charles, J.; Thompson, K.R.; Taylor, R.B. Halifax Harbour Extreme Water levels in the Context of Climate Change: Scenarios for a 100-Year Planning Haorizon; Open File 6346; Geological Survey of Canada, Natural Resources Canada: Ottawa, ON, Canada, 2009; pp. 1–21. [Google Scholar]
- Rhamstorf, S.; Cazenave, A.; Chruch, J.A.; Hansen, J.E.; Keeling, R.F.; Parker, D.E.; Somerville, R.C.J. Recent climate observations compared to projections. Science 2007, 316, 709. [Google Scholar] [CrossRef] [PubMed]
- Levermann, A.; Griesel, A.; Hofmann, M.; Montoya, M.; Rahmstorf, S. Dynamic sea level changes following changes in the thermohaline circulation. Clim. Dynam. 2005, 24, 347–354. [Google Scholar] [CrossRef]
- Vermeer, M.; Rahmstorf, S. Global sea level linked to global temperature. Proc. Nat. Acad. Sci. USA 2009. [Google Scholar] [CrossRef] [PubMed]
- Rahmstorf, S. A semiempirical approach to projecting future sea-level rise. Science 2007, 315, 368–370. [Google Scholar] [CrossRef] [PubMed]
- Bernier, N.B.; Thompson, K.R. Predicting the frequency of storm surges and extreme sea levels in the Northwest Atlantic. J. Geophys. Res. 2006. [Google Scholar] [CrossRef]
- Belbin, J.; Clyburn, D. Tidal Surge Project: The Coastal Flooding Component of the Annapolis Climate Change Outreach Project. Unpublished Report for the Clean Annapolis River Project. 1998. Available online: http://c-ciarn.dal.ca/workshops/3/presentations/Belbin.pdf (accessed on 20 August 2010).
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions 1. Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Abraham, J.; Parkes, G.; Bowyer, P. The transition of the “Saxby Gale” into an extratropical storm. In Proceedings of the 23rd Conference on Hurricanes and Tropical Meteorology, American Meteorological Society, Dallas, TX, USA; 1999; pp. 795–798. [Google Scholar]
- Desplanque, C.; Mossman, D. Tides and their seminal impact on the geology, geography, history, and socio-economics of the Bay of Fundy, eastern Canada. Atlantic Geol. 2004, 40, 1–130. [Google Scholar] [CrossRef]
- MacDonald, A. Winds of Change Severe Weather in The Annapolis Valley. Unpublished Thesis, Bachelor of Arts with Honours in History, Acadia University, Wolfville, NS, Canada, 2006. [Google Scholar]
- Parkes, G.; Ketch, L.; O’Reilly, C. Storm surge events in the Maritimes. In Procedures of the Canadian Coastal Conference, Guelph, ON, Canada; 1997; pp. 115–129. [Google Scholar]
- Desplanque, C.; Mossman, D. Storm tides of the fundy. The Geogr. Rev. 1999, 89, 23–33. [Google Scholar] [CrossRef]
- Brennen, R.; Webster, T.L. Object oriented land cover classification of LiDAR derived surfaces. Canad. J. Remote Sens. 2006, 32, 167–172. [Google Scholar] [CrossRef]
- Webster, T.L.; Dias, G. An automated GIS produce for comparing GPS and proximal LIDAR elevations. Comput.Geosci. 2006, 32, 713–726. [Google Scholar] [CrossRef]
- Webster, T.L. LIDAR validation using GIS: A case study comparison between two LIDAR collection methods. GeoCarto Int. 2005, 20, 11–19. [Google Scholar] [CrossRef]
- Peltier, W.R. Global glacial isostasy and the surface of the ice-age earth: The ice-5G (VM2) model and Grace. Ann. Rev. Earth Planetary Sci. 2004, 32, 111–149. [Google Scholar] [CrossRef]
- Godin, G. Possibility of rapid changes in the tide of the Bay of Fundy, based on a scrutiny of the records from Saint John. Continental Shelf Res. 1992, 12, 327–338. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Webster, T.L. Flood Risk Mapping Using LiDAR for Annapolis Royal, Nova Scotia, Canada. Remote Sens. 2010, 2, 2060-2082. https://doi.org/10.3390/rs2092060
Webster TL. Flood Risk Mapping Using LiDAR for Annapolis Royal, Nova Scotia, Canada. Remote Sensing. 2010; 2(9):2060-2082. https://doi.org/10.3390/rs2092060
Chicago/Turabian StyleWebster, Tim L. 2010. "Flood Risk Mapping Using LiDAR for Annapolis Royal, Nova Scotia, Canada" Remote Sensing 2, no. 9: 2060-2082. https://doi.org/10.3390/rs2092060
APA StyleWebster, T. L. (2010). Flood Risk Mapping Using LiDAR for Annapolis Royal, Nova Scotia, Canada. Remote Sensing, 2(9), 2060-2082. https://doi.org/10.3390/rs2092060