MTFM: Multi-Teacher Feature Matching for Cross-Dataset and Cross-Architecture Adversarial Robustness Transfer in Remote Sensing Applications

Highlights

What are the main findings?

• Adversarial robustness can be transferred across datasets and across architectures without sacrificing clean accuracy.
• The proposed Multi-Teacher Feature Matching (MTFM) framework consistently outperforms standard models and surpasses most existing defense strategies, while requiring less training time.

What is the implication of the main finding?

• Robustness-aware knowledge transfer can serve as a scalable and efficient defense strategy in remote sensing.
• MTFM enables resilient geospatial AI systems without the computational burden of full adversarial training on every new domain.

Abstract

Remote sensing plays a critical role in environmental monitoring, land use analysis, and disaster response by enabling large-scale, data-driven observation of Earth’s surface. Image classification models are central to interpreting remote sensing data, yet they remain vulnerable to adversarial attacks that can mislead predictions and compromise reliability. While adversarial training improves robustness, the challenge of transferring this robustness across models and domains remains underexplored. This study investigates robustness transfer as a defense strategy, aiming to enhance the resilience of remote sensing classifiers against adversarial patch attacks. We propose a novel Multi-Teacher Feature Matching (MTFM) framework to align feature spaces between clean and adversarially robust teacher models and the student model, aiming to achieve an optimal trade-off between accuracy and robustness against adversarial patch attacks. The proposed method consistently outperforms traditional standard models and matches—or in some cases, surpasses—conventional defense strategies across diverse datasets and architectures. The MTFM approach also supersedes the self-attention module-based adversarial robustness transfer. Importantly, it achieves these gains with less training effort compared to traditional adversarial defenses. These results highlight the potential of robustness-aware knowledge transfer as a scalable and efficient solution for building resilient geospatial AI systems.

1. Introduction

Convolutional Neural Networks (CNNs) have become essential tools in remote sensing, enabling automated interpretation of satellite and aerial imagery for land cover classification [1], environmental monitoring [2], disaster response [3], and seagrass detection [4]. However, despite their success, CNNs are highly vulnerable to adversarial attacks—carefully crafted perturbations that can mislead models with minimal or physically realizable changes. Among these, adversarial patch attacks pose a particularly serious threat due to their robustness and deployability in real-world settings. A single printed sticker or patch [5], strategically placed in a scene, can consistently fool a classifier across varying contexts and lighting conditions as shown in Figure 1. This makes patch attacks especially relevant for remote sensing systems, which often operate autonomously over large-scale, high-resolution imagery.

To defend against such threats, adversarial training methods like Projected Gradient Descent Adversarial Training (PGD-AT) have been widely adopted. This approach improves robustness by exposing models to adversarial examples during training, but it is computationally expensive and often degrades clean accuracy. Moreover, it is typically tied to specific datasets and architectures, limiting their scalability across the diverse landscape of remote sensing. In practice, remote sensing models must generalize across different sensors, resolutions, and geographic regions—making cross-dataset and cross-architecture robustness transfer a critical challenge.

Recent research has explored robustness transfer, where adversarial robustness is distilled from robust models into new architectures or datasets. Most existing work [6] focuses on logit-level distillation and often targets pixel-level attacks. In many cases, the source and target models are trained and evaluated on the same dataset, limiting the generalization scope. In contrast, this study implements cross-dataset transfer and cross-architecture distillation within the remote sensing domain—for example, transferring robustness from a ResNet-152 [7] model trained on the EuroSAT [8] remote sensing dataset to a ResNet-50 model on the AID [9] aerial imagery dataset. This setup reflects real-world deployment scenarios where models must adapt to new imagery sources without retraining from scratch.

To tackle this challenge, this study introduces a novel methodology: an enhanced multi-teacher distillation framework tailored for adversarial patch defense in remote sensing. Unlike conventional approaches that rely primarily on logit-level supervision, this framework emphasizes feature-level guidance. It leverages both clean and adversarial robust teachers to supervise the student model’s feature representations, promoting richer semantic alignment and improved spatial robustness. A dynamic loss formulation is employed to weight each teacher’s contribution during training, enabling the student to balance clean accuracy and adversarial resilience adaptively. This multi-teacher feature alignment strategy provides a more expressive and flexible alternative to traditional logit-only distillation methods.

The core contributions of this study are summarized as follows:

• Developed a new methodology to improve adversarial robustness in remote sensing: a feature-level multi-teacher distillation framework (MTFM) that guides the student using both clean and adversarial supervision, offering a better trade-off between clean accuracy and robustness under patch-based attacks.
• Demonstrated effective robustness transfer across datasets (e.g., EuroSAT to AID) and architectures (e.g., ResNet-152 to ResNet-50), addressing a gap in existing literature where most robustness transfer is limited to same-dataset setups.
• Compared the proposed MTFM framework with existing robustness transfer strategies, showing favorable trade-offs between clean accuracy and robustness in diverse settings.
• Validated the proposed methods using adversarial test accuracy and explainable AI techniques to interpret feature alignment under patch-based attacks.

2. Related Work

This section presents the foundational background for the study.

2.1. Remote Sensing

Remote sensing is the science of acquiring information about Earth’s surface without direct contact, typically through satellite or aerial imagery. To interpret these images effectively, image classification plays a central role [10]. Traditional machine learning algorithms have shown limited performance on complex classification tasks [11], particularly in high-dimensional visual domains. Applications of image classification in remote sensing include traffic sign recognition [12], disaster monitoring [3], and urban planning [13].

The advent of convolutional neural networks (CNNs) significantly improved performance across image classification benchmarks. Researchers began investigating the vulnerabilities of CNNs [14], particularly their sensitivity to small, imperceptible perturbations in input images [15]. This phenomenon led to the emergence of adversarial attacks—techniques that intentionally perturb inputs to induce misclassification.

2.2. Adversarial Attacks

One of the earliest and most widely studied attacks is the Fast Gradient Sign Method (FGSM) [15], which perturbs an image x in the direction of the gradient of the loss function with respect to the input:

$$x_{\mathrm{adv}}=x+ϵ·\mathrm{sign}\left({\nabla }_{x}J(\theta ,x,y)\right),$$

(1)

where $ϵ$ controls the perturbation magnitude, J is the loss function, and $\theta$ denotes model parameters.

Building on this, researchers proposed a more physically realizable form of attack known as adversarial patch attacks [5]. Unlike pixel-level perturbations, adversarial patches are localized regions—often printable stickers—generated using model and dataset knowledge. These patches can be placed on real-world objects to induce misclassification, simulating realistic attack scenarios [16]. To generate the adversarial patch $\widehat{p}$, we use a variant of the Expectation over Transformation (EOT) formulation:

$$\widehat{p}=arg\underset{p}{max}{\mathbb{E}}_{x\sim X,t\sim T,l\sim L}\left[logPr(y_b\mid A(p,x,l,t))\mid \right]$$

(2)

where X is a training set of images, $Y_b$ is the target class, T is a distribution over transformations of the patch, and L is a distribution over locations in the image [5]. The patch operator $A(p,x,l,t)$ applies random scaling, transformation t, and location l on the patch $\widehat{p}$ to attach image x. Then, it is trained by gradient descent to create a universal patch for the target class.

Adversarial attacks are typically categorized based on the attacker’s knowledge [17]: - White-box attacks assume full access to model parameters and training data. - Black-box attacks operate without any internal model knowledge. - Gray-box attacks, which are more realistic, assume partial knowledge—such as access to the dataset and a standard model architecture, but no information about the defense mechanism.

This study adopts a gray-box adversarial patch attack framework to evaluate the robustness of defense models under practical constraints.

2.3. Defense Strategy

Adversarial training is a widely adopted defense mechanism aimed at improving model robustness against adversarial attacks. In this approach, the model is trained not only on clean inputs but also on adversarially perturbed examples. By exposing the model to adversarial inputs during training, it learns to generalize better under worst-case perturbations and reduce susceptibility to misclassification.

Formally, adversarial training seeks to minimize the expected loss over both clean and adversarial examples. The adversarial examples can be generated using various attack methods, such as FGSM, PGD, or more advanced techniques. The general training objective can be expressed as:

$$\underset{\theta }{min}{\mathbb{E}}_{(x,y)\sim \mathcal{D}}\left[\mathcal{L}(f_{\theta }\left(x\right),y)+\mathcal{L}(f_{\theta }\left(x_{\mathrm{adv}}\right),y)\right],$$

(3)

where $x_{\mathrm{adv}}$ is the adversarial version of input x, and $f_{\theta }$ is the model with parameters $\theta$.

A more rigorous and effective variant of adversarial training is Projected Gradient Descent adversarial training (PGD-AT) [18], as shown in Figure 2. PGD generates adversarial examples by iteratively applying small perturbations in the direction of the gradient and projecting the result back into an $ϵ$-bounded ball around the original input. This multi-step attack is considered one of the strongest first-order adversaries and serves as a benchmark for evaluating robustness in most recent defense strategies.

The PGD adversarial training objective adopts a min-max formulation, where the inner maximization generates the worst-case adversarial example and the outer minimization updates the model to defend against it:

$$\underset{\theta }{min}{\mathbb{E}}_{(x,y)\sim \mathcal{D}}\left[\underset{\delta \in \mathcal{S}}{max}\mathcal{L}(f_{\theta }(x+\delta ),y)\right],$$

(4)

where $\delta$ is the adversarial perturbation constrained by set $\mathcal{S}$, typically defined as an ${\ell }_{\infty }$-norm ball of radius $ϵ$.

This min-max framework ensures that the model is trained to minimize the worst-case loss over all allowable perturbations, thereby enhancing its robustness against strong adversarial attacks.

Several defense strategies have been proposed to mitigate adversarial patch attacks. One such method is Local Gradient Smoothing (LGS) [19], which suppresses adversarial gradients by smoothing the loss landscape around the input image. LGS modifies the input such that the gradient signal becomes less informative for crafting perturbations. While this technique can reduce the effectiveness of certain attacks, it may cause adversarial images to resemble clean ones without truly enhancing model robustness. In other words, the defense may mask the attack rather than strengthen the model’s decision boundaries. The goal of this study is to develop models that are genuinely robust so that robustness can be transferred across tasks and domains.

PGD adversarial training remains the most widely accepted and empirically validated defense against adversarial patch attacks. Most recent works [20] build upon PGD training as a foundation, coupling it with additional mechanisms to improve spatial awareness or generalization. For example, PatchZero [21] introduces a two-stage adversarial training scheme to defend against stronger adaptive attacks by “zeroing out” the patch—multiplying the input image X with a binary mask M and replacing the patch region with mean pixel values. The preprocessed image $X^{\prime }$ is then passed to the downstream model for final prediction.

Another line of work focuses on physically realizable occlusion-based attacks [22], where adversaries insert small, adversarially crafted rectangles into the image. These attacks simulate real-world scenarios such as sticker-based perturbations on traffic signs or printed patches on objects. Defense strategies in this space include training with synthetic occlusions (e.g., gray patches) and designing attention mechanisms that ignore irrelevant regions.

Adversarial patches, though localized in the input space, often introduce abnormal activations and inflated feature norms in deep networks, leading to distorted intermediate representations [23]. Recent defenses therefore focus on extracting more robust global features—such as semantic context, boundary structures, and long-range correlations—which are less sensitive to localized corruption and can effectively suppress the influence of patch attacks [24].

Self-attention [25] module allows the model to dynamically focus on different parts of the input when making predictions. Unlike traditional convolutional layers, which extract local features using fixed-size kernels, self-attention captures global dependencies by computing interactions between all spatial positions in the input feature map.

In this study, a self-attention block is introduced before the penultimate layer of the model architecture to enhance intermediate feature representations and aimed at improving adversarial robustness by enabling the model to focus on the most informative regions of the image.

Let the input feature map be denoted as $X\in {\mathbb{R}}^{C\times H\times W}$, where C is the number of channels and $H\times W$ are the spatial dimensions. The self-attention mechanism projects the input into three representations: query Q, key K, and value V, computed via learnable $1\times 1$ convolutions:

$$Q=W_{Q}X,K=W_{K}X,V=W_{V}X$$

(5)

where $W_Q,W_K\in {\mathbb{R}}^{C^{\prime }\times C}$, $W_V\in {\mathbb{R}}^{C\times C}$, and $C^{\prime }=C/8$ (as in our implementation).

We then reshape and flatten the spatial dimensions such that:

$$Q\in {\mathbb{R}}^{N\times C^{\prime }},K\in {\mathbb{R}}^{C^{\prime }\times N},V\in {\mathbb{R}}^{C\times N},\mathrm{where}N=H\times W$$

(6)

The attention map $A\in {\mathbb{R}}^{N\times N}$ is computed using a dot product between the query and key followed by a softmax operation:

$$A=\mathrm{softmax}\left(QK\right)$$

(7)

This attention matrix reflects the pairwise similarities between all spatial positions in the feature map. The output of the attention layer is then calculated by:

$$O=V{A}^{\top }$$

(8)

which is reshaped back to ${\mathbb{R}}^{C\times H\times W}$. To preserve the original features and enable residual learning, the final output is:

$$Y=\gamma O+X$$

(9)

where $\gamma \in \mathbb{R}$ is a learnable scalar initialized to zero.

The query–key interaction measures similarity between all spatial locations, enabling the model to capture long-range dependencies. The attention map A controls where the model focuses by weighting spatial features based on these similarities. The value V provides the information to be aggregated according to the attention weights, forming the refined representation. A residual connection is added to ensure stable training and preserve the original spatial context.

This non-local attention mechanism is inspired by [26], and enhances the model’s ability to attend to semantically important regions in the image, improving both classification performance and adversarial robustness.

While these methods introduce novel components, they often come with substantial training overhead—sometimes exceeding that of PGD adversarial training itself—and the transferability of the resulting robustness across datasets and architectures remains uncertain. In this study, PGD adversarial training serves as the base defense strategy. We combine it with transfer learning to address two key challenges: robustness transferability and training efficiency. Our approach aims to retain PGD-level robustness while improving generalization and reducing computational cost.

2.4. Transferring Robustness

Having established the severity of adversarial patch attacks and reviewed traditional defense mechanisms, we now explore the concept of transferring robustness [27]. This idea is inspired by transfer learning, a paradigm in which knowledge gained from one task or domain is leveraged to improve performance on another. In transfer learning, a model trained on a large source dataset (e.g., ImageNet) is fine-tuned on a smaller target dataset, allowing it to retain generalizable features while adapting to new tasks.

Transferring robustness extends this idea by aiming to preserve adversarial resilience across domains. Instead of training a robust model from scratch for every new dataset, we seek to transfer robustness from a source model—typically trained with adversarial defenses—to a target model via fine-tuning or feature alignment. This approach is particularly valuable when computational resources are limited or when the target domain lacks sufficient adversarial examples for training.

Recent research [28] has established the benefits of robustness transfer, demonstrating that adversarially trained models can retain and propagate resilience when adapted to new domains. Studies [29] show that fine-tuning robust source models often leads to improved adversarial accuracy on target tasks, even without direct exposure to adversarial examples during transfer.

Knowledge distillation [30] framework is used for transferring knowledge [31] and robustness from a high-capacity model (teacher) to a smaller or less complex model (student). In this setup, the teacher model is typically pre-trained and exhibits strong performance, often including resilience to adversarial attacks. The student model is trained to mimic the behavior of the teacher by minimizing the divergence between their output distributions, rather than relying solely on ground-truth labels.

In the context of adversarial robustness, the teacher is a robust model trained using techniques such as PGD adversarial training. The student learns not only the classification task but also inherits the robustness characteristics of the teacher through distillation. This enables the student to generalize better under adversarial conditions, even when trained with fewer resources or on smaller datasets.

The training objective combines the standard cross-entropy loss with a distillation loss based on the Kullback–Leibler divergence between temperature-scaled soft logits of the teacher and student, as introduced by Hinton et al. [30] and further detailed in the review by Stanton et al. [32].

$${\mathcal{L}}_{\mathrm{total}}=\alpha ·{\mathcal{L}}_{\mathrm{CE}}(z_s,y)+(1-\alpha )·{\mathcal{L}}_{\mathrm{KD}}(z_s,z_t)$$

(10)

where $z_s$ and $z_t$ are the student and teacher logits respectively, y is the one-hot ground-truth label, and $\alpha \in [0,1]$ balances the two objectives.

The cross-entropy loss is defined as:

$${\mathcal{L}}_{\mathrm{CE}}(z_s,y)=-\sum _{j=1}^C{y}_{j}log{\sigma }_j\left(z_s\right)$$

(11)

The distillation loss uses temperature-scaled softmax distributions:

$${\mathcal{L}}_{\mathrm{KD}}(z_s,z_t)=-{\tau }^2\sum _{j=1}^C{\sigma }_j\left({\displaystyle \frac{z_t}{\tau }}\right)log{\sigma }_j\left({\displaystyle \frac{z_s}{\tau }}\right)$$

(12)

where $\tau$ is the temperature parameter and ${\sigma }_j(·)$ denotes the softmax probability for class j. The factor ${\tau }^2$ ensures proper gradient scaling during backpropagation.

This architecture allows robustness to be transferred in a scalable and modular fashion, making it suitable for deployment in resource-constrained environments. In this study, we use robust teacher models trained on source datasets and distill their robustness into student models trained on target datasets, evaluating their performance under adversarial patch attacks.

3. Methodology

This section outlines the methodology adopted in this study to evaluate robustness transfer under adversarial patch attacks. The process involves training standard models and developing robust models using transfer learning strategies.

3.1. Standard Models

The first step is to train standard models on all source datasets (EuroSAT, PatternNet) and target datasets (UCM, AID), following the architectures and training parameters outlined in the Experimental Setup section. These models serve as baseline classifiers and are denoted as $STD$. These models are later used to generate adversarial patches specific to each dataset.

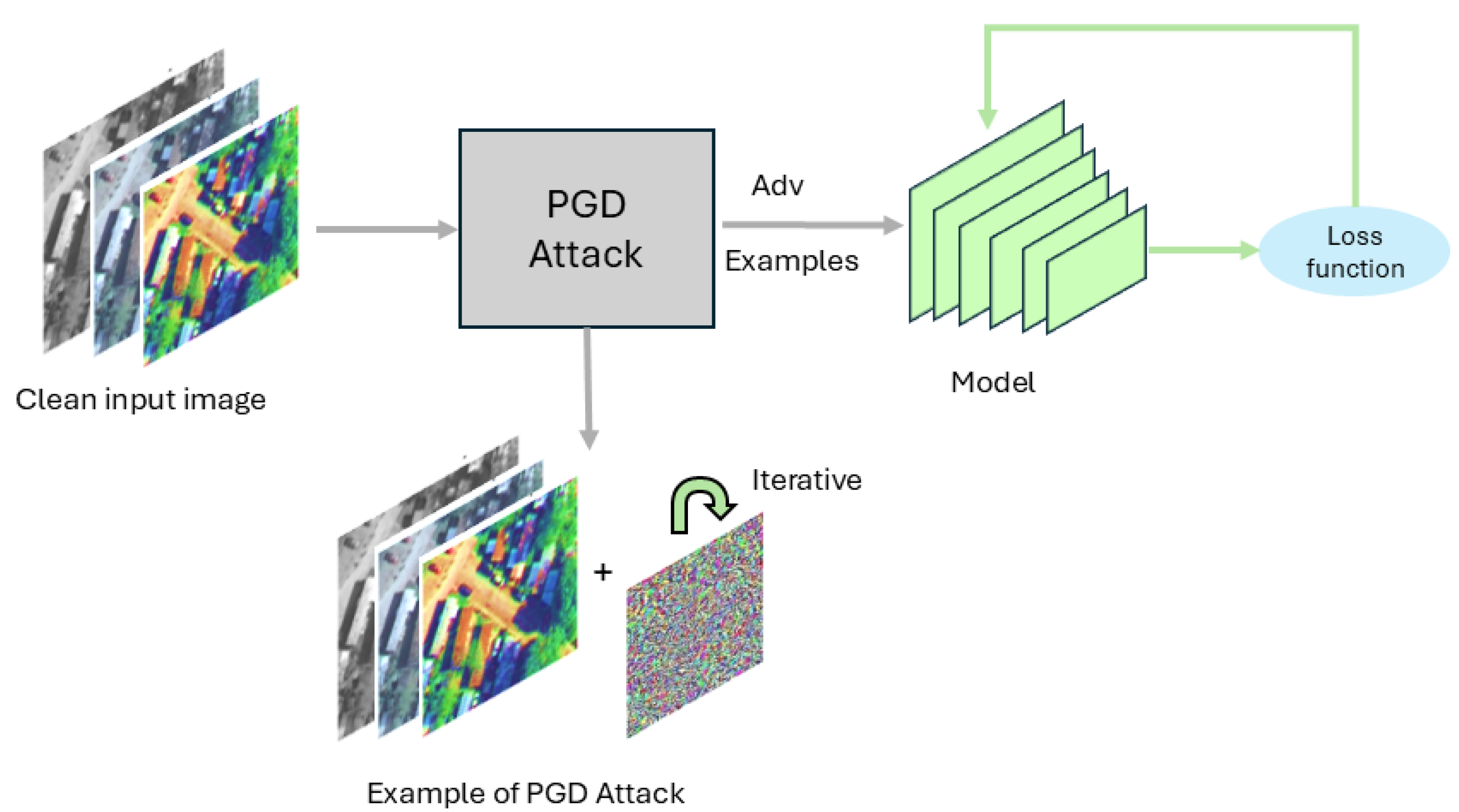
3.2. Projected Gradient Descent Adversarial Training

As discussed, the PGD-AT algorithm [18] is used to develop robust models against adversarial patch attacks. It generates adversarial examples by iteratively perturbing the input image to maximize the model’s loss, thereby encouraging robustness during training. Throughout this work, models trained using the PGD-AT algorithm are referred to as $PGD$, representing the adversarially robust baseline.

3.3. Self-Attention Module-Based Adversarial Robustness Transfer

Transfer learning (TL) enables the reuse of robustness learned from a source model to a target model through selective retraining of network layers. Three TL strategies were employed in this study: (1) Full Network Fine-Tuning (Fullnet), where all layers of the robust source model are transferred and retrained on the target dataset to enable complete adaptation to the new domain; (2) Fixed Feature Fine-Tuning (Fixedfeat), where all layers except the final fully connected (FC) layer are frozen, allowing the model to retain its learned feature representations while adapting its output space; and (3) Freeze 25 Layer Transfer (F25), in which the first 25 layers are frozen while the remaining layers are retrained, balancing feature reuse and domain-specific learning.

A self-attention module is integrated before the penultimate layer of the ResNet architecture to enhance feature representations and is aimed at improving robustness against adversarial patch attacks. This module enables the model to focus on salient spatial regions and suppress less relevant features, thereby improving resistance to localized perturbations. A ResNet-50 model augmented with this self-attention module was first trained on the source dataset using PGD adversarial training and then transferred to the target dataset using the aforementioned TL strategies. The best-performing variant is denoted as SA-TL for comparison.

For example, a PGD-trained ResNet-50 with a self-attention module trained on EuroSAT was transferred to UCM, enabling the model to retain adversarial robustness while adapting to the target domain. To ensure consistency, the same architectural modification was applied to models used for patch generation. While this approach improved robustness, it also introduced additional parameters and deviated from standard model configurations, which may affect its efficiency in lightweight deployment settings. Moreover, it does not support cross-architecture robustness transfer, limiting its flexibility when adapting to models with different backbone structures.

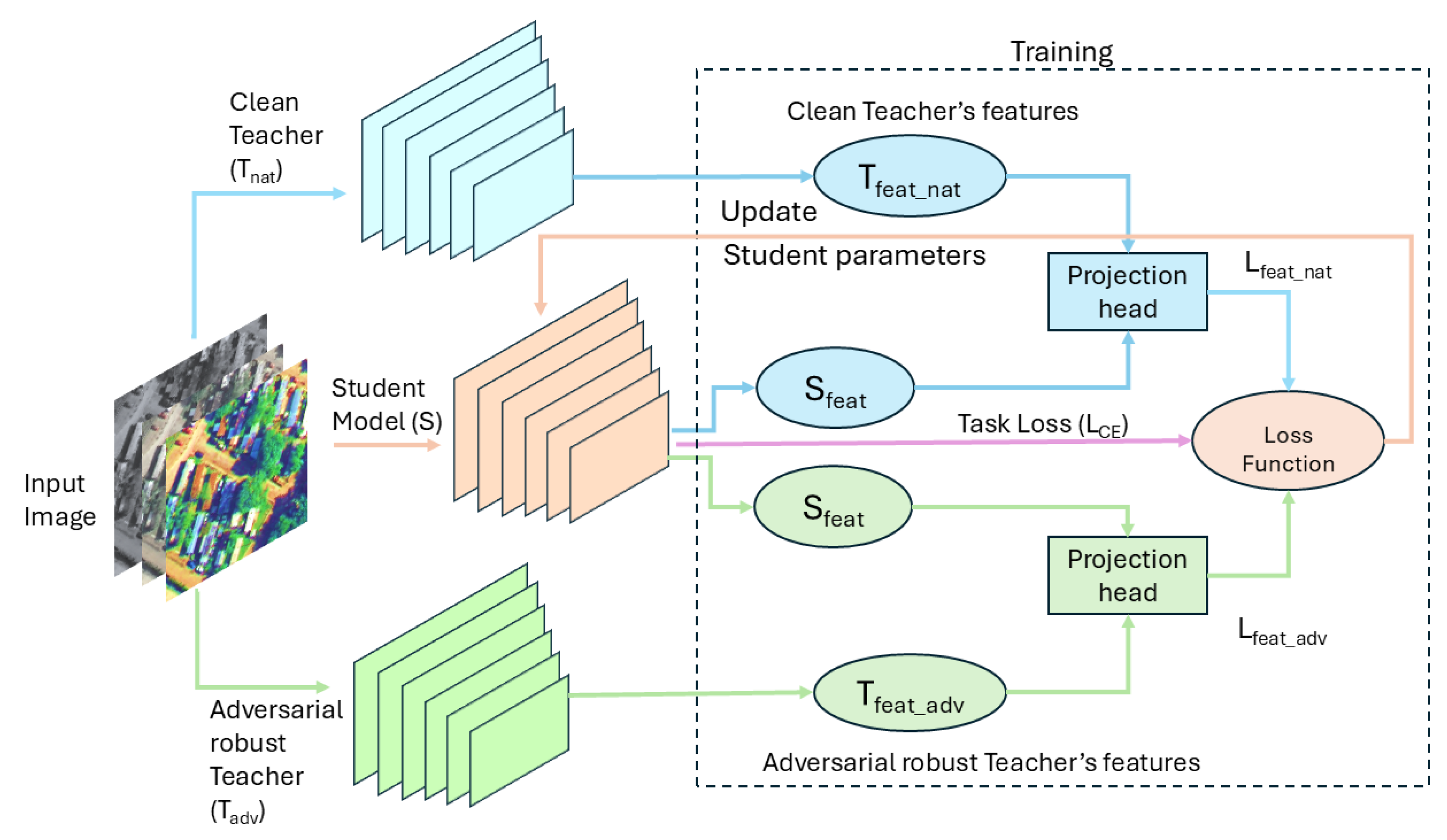
3.4. Proposed Multi-Teacher Feature Matching (MTFM) Approach

Multi-Teacher Feature Matching (MTFM) is a teacher–student framework [31] for knowledge distillation that leverages both adversarial and natural supervision. In this setup (shown in Figure 3), two distinct teacher models are employed: one adversarially robust ($T_{\mathrm{adv}}$) teacher trained via PGD-based adversarial training, and one naturally trained ($T_{\mathrm{nat}}$) teacher using standard clean examples. The previous dual-teacher method MTARD (Multi-Teacher Adversarially Robust Distillation) framework [6], facilitates robust knowledge transfer within the same dataset. The proposed Multi-Teacher Feature Matching (MTFM) explores a more challenging cross-dataset and cross-architecture transfer setting.

The MTFM approach utilizes two types of teachers: adversarially robust and natural teachers. Specifically, the adversarially robust ($T_{\mathrm{adv}}$) and natural teachers ($T_{\mathrm{nat}}$) are trained on a large source dataset (e.g., PatternNet), and their knowledge is distilled into a student model (S) trained on a smaller, unrelated target dataset (e.g., UCM). Due to the mismatch in class semantics between source and target datasets, logit-based distillation becomes ineffective. Instead, feature-level matching is performed, allowing the student ($S_{\mathrm{feat}}$) to learn from the internal representations of both teachers (T_{feat_nat}, T_{feat_adv}), using cosine similarity to compute the feature loss and encourage directional alignment in representation space.

This architecture introduces projection heads to enable effective feature-level distillation across architectures, as illustrated in Figure 3. A projection head is a small neural network that maps features into a shared embedding space for comparison or alignment. For example, the student projection head maps the 512-dimensional penultimate features from ResNet-18 ($S_{\mathrm{feat}}$) into a common 512-dimensional embedding space, while each teacher’s 2048-dimensional features (T_{feat_nat}, T_{feat_adv}) are projected into the same space using their own projection head. This design resolves the dimensional mismatch between models, enabling direct comparison of internal representations. By aligning features in a common embedding space, the student learns directional similarity to the teacher’s representations—even across architectural gaps. This setup supports semantic and spatial robustness transfer from both clean and adversarially robust teachers, without relying on logits or class alignment, and offers flexibility to incorporate diverse teacher architectures across domains.

To accommodate the differing influence of each teacher during training, we use a dynamically weighted loss function. The individual components are defined as follows.

The standard cross-entropy loss between the student predictions and ground-truth labels is:

$${\mathcal{L}}_{\mathrm{CE}}=-\sum _{i=1}^C{y}_{i}log\left(p_i\right)$$

(13)

where C is the number of classes, $y_i$ is the one-hot encoded ground-truth label, and $p_i$ is the predicted probability for class i.

The feature matching losses between the student and the natural/adversarial robust teachers are computed using cosine similarity:

$${\mathcal{L}}_{\mathrm{feat}\_\mathrm{nat}}=1-cos\left({\mathcal{S}}_{\mathrm{feat}},{\mathcal{T}}_{\mathrm{feat}\_\mathrm{nat}}\right),{\mathcal{L}}_{\mathrm{feat}\_\mathrm{adv}}=1-cos\left({\mathcal{S}}_{\mathrm{feat}},{\mathcal{T}}_{\mathrm{feat}\_\mathrm{adv}}\right)$$

(14)

where ${\mathcal{S}}_{\mathrm{feat}}$ is the student feature representation, and ${\mathcal{T}}_{\mathrm{feat}\_\mathrm{nat}}$, ${\mathcal{T}}_{\mathrm{feat}\_\mathrm{adv}}$ are the corresponding features from the natural and adversarial robust teachers.

Cosine similarity is defined as:

$$cos(a,b)={\displaystyle \frac{a·b}{\parallel a\parallel \parallel b\parallel }}$$

(15)

The cross-entropy loss is assigned a constant weight of ${\lambda }_{\mathrm{CE}}=0.2$, while the feature matching weights ${\lambda }_{\mathrm{nat}}$ and ${\lambda }_{\mathrm{adv}}$ are initialized to 0.4 and updated dynamically during training based on the relative magnitude of feature losses from each teacher.

The dynamic weights are computed as:

$${\mathcal{L}}_{\mathrm{feat}\_\mathrm{total}}={\mathcal{L}}_{\mathrm{feat}\_\mathrm{nat}}+{\mathcal{L}}_{\mathrm{feat}\_\mathrm{adv}}+ϵ$$

(16)

$${\lambda }_{\mathrm{nat}}={\displaystyle \frac{{\mathcal{L}}_{\mathrm{feat}\_\mathrm{nat}}}{{\mathcal{L}}_{\mathrm{feat}\_\mathrm{total}}}},{\lambda }_{\mathrm{adv}}={\displaystyle \frac{{\mathcal{L}}_{\mathrm{feat}\_\mathrm{adv}}}{{\mathcal{L}}_{\mathrm{feat}\_\mathrm{total}}}}$$

(17)

where $ϵ={10}^{-6}$ is a small constant added to prevent division by zero.

Finally, the total loss is computed as:

$${\mathcal{L}}_{\mathrm{total}}={\lambda }_{\mathrm{CE}}·{\mathcal{L}}_{\mathrm{CE}}+{\lambda }_{\mathrm{nat}}·{\mathcal{L}}_{\mathrm{feat}\_\mathrm{nat}}+{\lambda }_{\mathrm{adv}}·{\mathcal{L}}_{\mathrm{feat}\_\mathrm{adv}}$$

(18)

This weighting mechanism reflects the student’s learning progress from each teacher. A lower feature loss indicates that the student is already aligned with that teacher’s representation, so its weight is reduced. Conversely, a higher feature loss suggests the student has more to learn from that teacher, increasing its influence. This adaptive balance ensures that the student benefits from both teachers in proportion to their current impact, enabling effective cross-domain robustness transfer even when class labels and architectures differ. For clarity, we denote each multi-teacher feature matching model using the notation $MTFM$.

Before discussing the experimental outcomes, we define a few key terms and evaluation metrics to aid interpretation.

4. Experimental Setup

This section outlines the experimental setup used to evaluate the proposed methodology.

4.1. Threat Model

The threat model considered in this study involves a victim application that relies on an image classification model for remote sensing tasks. An adversary aims to compromise this model by deploying adversarial patches—localized, physically realizable perturbations designed to induce misclassification. These patches are crafted using publicly available remote sensing datasets such as UCM [33] or PatternNet [34], along with standard models trained on those datasets. Unlike imperceptible pixel-level perturbations, adversarial patches can be printed and physically placed on objects within the scene, making them highly relevant for real-world attack scenarios. The attacker’s capabilities are defined by their knowledge of the victim system: in a white-box setting, the attacker has full access to the model architecture and parameters; in a black-box setting, the attacker has no internal knowledge; and in a gray-box setting, the attacker has partial knowledge—typically access to the dataset and a standard model architecture, but no information about the defense mechanism. This study adopts a gray-box attack setup, reflecting a practical and moderately informed adversary. The adversarial patch is generated using a standard model trained on the same dataset as the victim model, without access to the defense strategy. The primary objective of this study is to develop robust models that can withstand adversarial patch attacks while minimizing computational overhead. To achieve this, we explore the concept of transferring robustness—leveraging pre-trained robust models to enhance resilience in new domains without retraining from scratch.

4.2. Datasets

The datasets used in this study are divided into two categories: source datasets, which are used to train robust source models, and target datasets, to which robustness is transferred. This setup mimics a downstream transfer learning scenario, where the goal is to evaluate how well robustness generalizes across domains. The primary source datasets include EuroSAT (E) [8], which contains 27,000 RGB satellite images across 10 land use and land cover classes at a resolution of 64 × 64 pixels. Derived from Sentinel-2 satellite data, EuroSAT is widely used for remote sensing classification tasks. Another source dataset is PatternNet (P) [34], comprising over 30,000 high-resolution aerial images spanning 38 scene categories, each sized at 256 × 256 pixels, making it suitable for fine-grained scene understanding.

The target datasets include the UC Merced Land Use Dataset (UCM) [33], which consists of 2100 aerial images across 21 classes, each image sized at 256 × 256 pixels. It is commonly used for evaluating scene classification performance. The Aerial Image Dataset (AID) [9] contains 10,000 images across 30 scene categories, with varying resolutions and geographic diversity, making it a challenging benchmark for generalization. Robustness transfer is performed from EuroSAT to AID and UCM, and from PatternNet to AID and UCM, to evaluate cross-dataset generalization under adversarial patch attacks.

4.3. Model Architectures

This study employs three variants of the ResNet architecture [7]. ResNet-152 (R152) is a deep residual network with 152 layers, known for its strong representational capacity and robustness in large-scale classification tasks. ResNet-50 (R50) is a 50-layer variant that balances depth and computational efficiency, and is commonly used in transfer learning pipelines. ResNet-18 (R18) is a lightweight 18-layer model suitable for low-resource settings and fast inference. Robustness is transferred from ResNet-152 to both ResNet-50 and ResNet-18, and additionally from ResNet-50 to ResNet-18. This hierarchical transfer setup allows us to evaluate whether robustness learned by deeper models can be effectively inherited by shallower architectures. By experimenting with multiple datasets and model configurations, we demonstrate the generalizability of the proposed robustness transfer framework across both domain and architectural shifts.

4.4. Hyperparameters

Dataset split: All datasets are divided into training, validation, and test sets using a 70%–20%–10% ratio.

Standard models: Trained using a learning rate of $1\times {10}^{-3}$, with categorical cross-entropy as the loss function and stochastic gradient descent as the optimization algorithm. Training is conducted for 10 epochs unless otherwise specified. All models are initialized with ImageNet pre-trained weights to accelerate convergence and enable effective fine-tuning.

Adversarial training: We apply Projected Gradient Descent (PGD) with 10 iterations and an ${\ell }_{\infty }$ perturbation budget of $ϵ=0.2$. This setup is used to train robust models across all source datasets and architectures.

Self attention: Models used in self-attention experiments follow the same learning rate and loss function, and are trained for 10 epochs. These models are evaluated for robustness transfer under adversarial patch attacks.

MTARD: The training procedure follows the setup described in the MTARD paper [6]. All models are initialized with ImageNet-pretrained weights and trained for 10 epochs, consistent with the setup used across other approaches. Teacher models are trained using the adversarial training parameters outlined above, and to maintain consistency, the student model is also trained with the same adversarial parameters as specified in the adversarial training setup.

MTFM: For multi-teacher feature distillation experiments, the training configuration remains consistent: learning rate of $1\times {10}^{-3}$, a custom distillation loss function, and stochastic gradient descent optimizer, with training conducted for 10 epochs. This uniform setup ensures comparability across all robustness transfer strategies. All the models are trained on GPU device: NVIDIA RTX A5000.

4.5. Evaluation Metrics

In this study, we use the following terminology to describe the robustness transfer setup. The Source refers to the dataset used to train the robust teacher models, while the Target denotes the dataset to which robustness is transferred and evaluated. The term Model identifies the specific robustness strategy or training configuration being assessed, and Arch indicates the architecture of the model (e.g., ResNet-18, ResNet-50, ResNet-152).

To evaluate model performance, we report three key metrics. Clean Accuracy (Clean) measures the model’s performance on unperturbed test images. It represents the percentage of clean (non-adversarial) samples correctly classified by the model, indicating generalization and baseline discriminative capability under normal conditions. It is computed as:

$$\mathrm{Clean}\mathrm{Accuracy}=\sum _{i=1}^N{\displaystyle \frac{1\left[{\widehat{y}}_i=y_i\right]}{N}}\times 100\%$$

(19)

where $y_i$ is the ground-truth label for image i, and ${\widehat{y}}_i$ is the model’s prediction on the clean image.

Adversarial Test Accuracy (ATA) quantifies the percentage of adversarially patched images for which the model correctly predicts the ground-truth label despite the presence of an adversarial patch. It is computed as:

$$\mathrm{ATA}=\sum _{i=1}^N{\displaystyle \frac{1\left[{\widehat{y}}_i=y_i\right]}{N}}\times 100\%$$

(20)

where $y_i$ is the ground-truth label for image i, and ${\widehat{y}}_i$ is the model’s prediction on the adversarially patched image.

Attack Success Rate (ASR) measures the percentage of adversarially patched images for which the model’s prediction matches the attacker’s target label. It is defined as:

$$\mathrm{ASR}=\sum _{i=1}^N{\displaystyle \frac{1\left[{\widehat{y}}_i=y_{\mathrm{target}}\right]}{N}}\times 100\%$$

(21)

where ${\widehat{y}}_i$ is the model’s prediction for adversarial image i, $y_{\mathrm{target}}$ is the attacker’s target label, and N is the total number of adversarial samples. The indicator function $1[·]$ returns 1 if the condition is true and 0 otherwise.

5. Results

This section presents the results of the proposed Multi-Teacher Feature Matching (MTFM) framework.

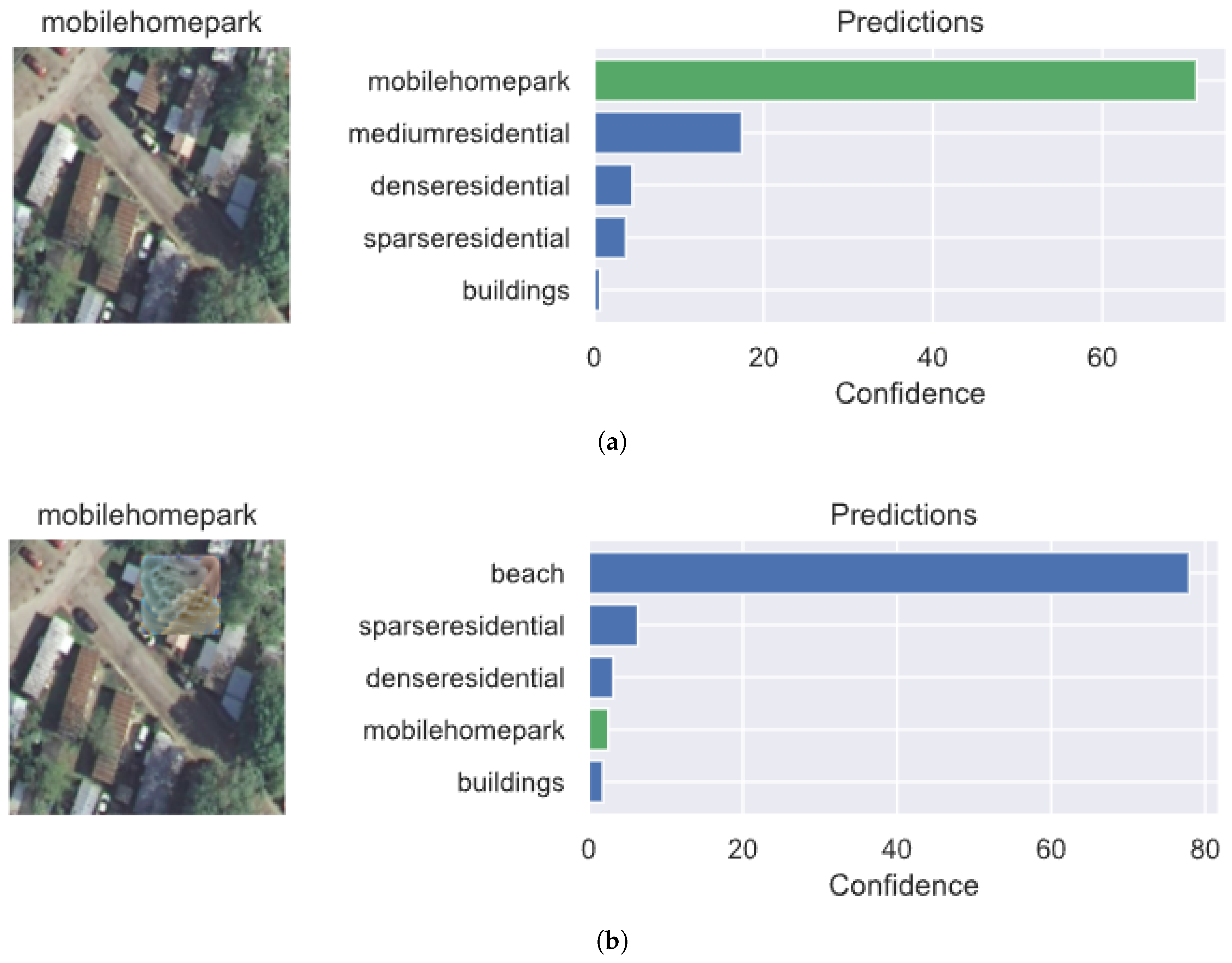
5.1. Generating Adversarial Patches

Adversarial patches [5] represent a stronger class of adversarial attacks that are physically realizable and can be placed directly on input images. To generate these patches, we use the standard model trained on a given dataset along with the dataset itself, following the Expectation Over Transformation (EOT) framework as defined in Equation (2). This approach ensures that the generated patch remains effective under various transformations such as scaling, rotation, and translation. For instance, adversarial patches for EuroSAT are generated using EuroSAT $STD$ model and the EuroSAT dataset as shown in Figure 4.

In this study, we develop adversarial patches of three standard sizes: $32\times 32$, $48\times 48$, and $64\times 64$. These patch sizes correspond to approximately $2.04\%$, $4.59\%$, and $8.16\%$ of the total area of the input image, respectively, assuming a fixed input resolution of $224\times 224$ pixels. This range allows us to evaluate robustness under varying degrees of localized perturbation, from subtle to visually dominant attacks.

5.2. Multi Teacher Feature Matching (MTFM) Result

In this subsection, we compare the results of the proposed Multi-Teacher Feature Matching (MTFM) approach against standard and traditional defense models. The evaluation spans multiple source datasets, target datasets, and model architectures to assess the generalizability of MTFM. All models are attacked using adversarial patches of varying sizes—32 × 32, 48 × 48, and 64 × 64—to test robustness under increasingly localized perturbations.

Table 1. Clean and adversarial accuracies of models trained on source datasets (PatternNet and EuroSAT).

Dataset	Model	Arch	Clean	64 × 64		Time
				ATA	ASR	secs
PatternNet	$STD$	R152	98.23	15.63	84.11	241.78
	$PGD$	R152	96.57	83.26	1.5	2600.42
	$STD$	R50	97.94	11.19	88.74	109.34
	$PGD$	R50	95.56	83.26	8.37	907.23
	$STD$	R18	97.73	31.29	67.86	58.15
	$PGD$	R18	94.31	79.21	9.70	429.19
EuroSAT	$STD$	R152	95.12	5.06	94.43	171.35
	$PGD$	R152	88.80	73.38	6.17	1880.26
	$STD$	R50	93.53	2.59	97.4	90.95
	$PGD$	R50	80.86	60.52	17.31	777.19
	$STD$	R18	93.78	1.81	98.14	65.96
	$PGD$	R18	88.0	78.46	9.31	390.86

Time is calculated as average per epoch (total time/number of epochs).

presents the performance of standard and PGD-trained models. All standard models exhibit a significant drop in Adversarial Test Accuracy (ATA) when attacked with a 64 × 64 adversarial patch. In contrast, models trained with PGD adversarial training show a noticeable decrease in clean accuracy but achieve substantial gains in ATA, albeit with increased training time. These PGD-trained models will be used as robustness sources for transferring to target models.

5.3. PatternNet → UCM and AID

Table 2. Clean and adversarial accuracies of target models developed by transferring robustness from PatternNet.

Dataset	Model	Arch	Clean	32 × 32		48 × 48		64 × 64		Time
				ATA	ASR	ATA	ASR	ATA	ASR	secs
UCM	$STD$	R50	88.09	82.0	3.83	45.0	47.83	15.83	82.17	31.82
	$PGD$	R50	85.56	83.33	1.0	75.67	4.83	70.0	8.33	92.77
	$TL$	R50->R50	92.85	89.50	0.17	85.0	0.17	82.83	0.33	32.74
	SA-TL	R50	91.11	85.83	0.5	83.33	1.83	79.5	8.33	34.99
	$MTARD$	R152->R50	86.82	82.5	0.17	81.17	0.01	77.17	0.05	109.86
	$MTFM$	R152->R50	90.95	85.83	0.33	81.16	0.17	81.83	0.67	38.21
AID	$STD$	R50	91.73	24.78	74.3	10.44	84.49	3.97	96.03	49.83
	$PGD$	R50	84.87	69.2	12.53	58.5	29.33	45.93	49.31	314.18
	$TL$	R50->R50	78.07	73.05	0.89	72.56	0.82	69.33	1.68	39.19
	SA-TL	R50	77.9	71.90	1.64	66.36	1.13	63.52	2.36	39.86
	$MTARD$	R152->R50	76.43	71.63	0.68	67.63	0.51	67.45	0.93	368.52
	$MTFM$	R152->R50	88.23	82.06	1.96	77.17	6.84	76.97	9.68	81.44
UCM	$STD$	R18	85.08	71.33	11.33	48.33	42.67	22.83	73.33	29.99
	$PGD$	R18	79.68	74	2.0	71.66	4.66	63.66	15.33	64.08
	$TL$	R18->R18	84.6	83.0	0.67	80.83	1.67	77.5	2.0	36.52
	SA-TL	R18	86.98	84.33	1.17	82.17	1.33	79.83	1.67	32.12
	$MTARD$	R152->R18	86.51	84.0	0.1	78.83	0.05	78.17	0.01	64.95
	$MTARD$	R50->R18	84.13	82.83	0.01	75.67	0.03	73.5	0.5	61.99
	$MTFM$	R152->R18	89.68	78.5	0.5	77.16	2.5	61.33	21.0	37.03
	$MTFM$	R50->R18	86.99	76.5	0.5	71.83	0.16	71.83	2.83	33.95
AID	$STD$	R18	88.87	32.41	65.16	8.04	91.75	1.53	97.71	44.44
	$PGD$	R18	83.87	58.93	1.3	50.41	10.27	61.34	8.27	148.11
	$TL$	R18->R18	89.2	81.75	0.86	74.28	1.61	68.0	16.46	47.76
	SA-TL	R18	85.37	65.36	0.27	52.70	0.35	69.63	1.44	43.23
	$MTARD$	R152->R18	73.8	66.01	2.46	62.8	2.15	62.22	2.49	208.31
	$MTARD$	R50->R18	70.17	66.87	0.27	63.45	0.58	61.43	0.31	170.81
	$MTFM$	R152->R18	85.37	72.92	1.16	73.02	1.81	69.9	3.63	69.73
	$MTFM$	R50->R18	88.27	79.22	1.02	70.39	1.61	64.50	7.08	55.38

Time is calculated as average per epoch (total time/number of epochs).

summarizes the clean accuracy, adversarial test accuracy (ATA), and attack success rate (ASR) across standard training and various defense strategies, including the proposed Multi-Teacher Feature Matching (MTFM) framework. The source domain is PatternNet, and robustness is transferred to target datasets—UCM and AID—using different architectural configurations: ResNet-152→ResNet-50, ResNet-152→ResNet-18, and ResNet-50→ResNet-18.

The $STD$ model refers to the standard baseline trained directly on the target dataset without any adversarial defense. The $PGD$ model is trained using Projected Gradient Descent adversarial training on the same target dataset, generating perturbations across the entire image to improve robustness. The $TL$ model applies transfer learning, where robustness is inherited from a source dataset and fine-tuned on the target dataset using the same architecture. Similarly, the SA-TL model transfers robustness from a source dataset and fine-tunes it on the target dataset, maintaining the same architecture. The $MTARD$ model uses the same dataset for both source and target domains—for example, teachers are trained on the UCM dataset and transferred to a different architecture on the same UCM dataset. In contrast, the $MTFM$ model performs cross-architecture and cross-dataset robustness transfer, where robustness learned from a source dataset is transferred to a different target dataset to enhance generalization and reduce training overhead.

5.3.1. Results on ResNet-50 (UCM and AID)

For the UCM dataset, all models employ ResNet-50 as the backbone architecture. The standard model ($STD$) achieves a clean accuracy of 88.09%, while the PGD-trained model (PGD) reaches 85.56%. The transfer learning model ($TL$), which inherits robustness from a PGD-trained ResNet-50 on PatternNet, achieves the highest clean accuracy of 92.85%. The self-attention transfer learning variant (SA-TL) achieves a clean accuracy of 91.11%. The ($MTARD$) model achieves a clean accuracy of 86.62%. The proposed Multi-Teacher Feature Matching model ($MTFM$) achieves a clean accuracy of 90.95%, outperforming ($STD$), ($PGD$), and ($MTARD$), while closely approaching the performance of (SA-TL) and ($TL$) models. Under a $32\times 32$ patch, the proposed $MTFM$ model achieves an ATA of 85.83%, outperforming the $STD$, $PGD$, and $MTARD$ models by 3.83%, 2.5%, and 3.33%, respectively, while matching the performance of the SA-TL model. For a larger patch size of $48\times 48$, the $MTFM$ model achieves an ATA of 81.16%, surpassing the $STD$, $PGD$, and matching the performance of both $TL$, SA-TL, and $MTARD$ models. Under the largest patch size of $64\times 64$, the ATA of the $STD$ model drops to 15.83%, while the $PGD$, SA-TL, and $MTARD$ models achieve 70.00%, 79.50%, and 77.17%, respectively. The $MTFM$ model achieves an ATA of 81.83%, outperforming all baseline models and matching the performance of the $TL$ model. In terms of training efficiency, the $MTFM$ model achieves this robustness with 38.21 s per epoch, which is comparatively less training time compared to the $PGD$ and $MTARD$ models.

Switching to the AID dataset as the target domain, the $STD$ model achieves the highest clean accuracy of 91.73%, followed by the $MTFM$ model (88.23%), $PGD$ model (84.87%), $TL$ model (78.07%), SA-TL model (77.90%), and $MTARD$ with a clean accuracy of 76.43%. Under the $32\times 32$ adversarial patch attack, the $MTFM$ model achieves 82.06% ATA—improvements of 57.28% over the $STD$ model, 12.86% over the $PGD$ model, 9.01% over the $TL$ model, 10.16% over the SA-TL model (71.90%), and 10.43% over the $MTARD$ model. When attacked with a $48\times 48$ adversarial patch, the $MTFM$ model again leads with 77.17% ATA, outperforming the $STD$ model (10.44%), $PGD$ model (58.50%), $TL$ model (72.56%), SA-TL model (66.36%), and the $MTARD$ model (67.63%). Under the most challenging $64\times 64$ patch attack, the $MTFM$ model sustains robustness with 76.97% ATA, surpassing the $STD$ model (3.97%), $PGD$ model (45.93%), $TL$ model (69.33%), SA-TL model (63.52%), and $MTARD$ model (67.45%). Notably, the $MTFM$ model achieves these improvements while maintaining substantially lower training times than the $PGD$ model, and performs better than SA-TL and $MTARD$, while matching the performance of the $TL$ model—demonstrating better trade-offs between robustness, accuracy, and computational cost.

5.3.2. Results on ResNet-18 (UCM and AID)

To further assess cross-architecture robustness transfer, the $MTFM$ framework is evaluated with ResNet-18 as the target model, as shown in Table 2. On UCM, $MTFM$ variants (R152→R18 and R50→R18) achieve clean accuracies of 89.68% and 86.99%, respectively, outperforming $STD$ (85.08%), $PGD$ (79.68%), $TL$ (84.60%), SA-TL (86.98%), and $MTARD$. Under $32\times 32$, $48\times 48$, and $64\times 64$ adversarial patch attacks, the $MTFM$ models perform better than $STD$ and $PGD$ in terms of ATA. The defense models $TL$, SA-TL, and $MTARD$ also achieve competitive ATA scores.

For AID with ResNet-18, $STD$ achieves 88.7% clean accuracy, $PGD$ reaches 83.87%, and $TL$ slightly improves to 89.2%. $MTARD$ achieves 73.8% (R152→R18) and 70.17% (R50→R18). The SA-TL model achieves a clean accuracy of 85.37%. $MTFM$ attains 85.37% (R152→R18) and 88.27% (R50→R18). Under the $32\times 32$ adversarial patch attack, the $MTFM$ model (R152→R18) achieves a notable improvement over all baselines and matches the performance of the $TL$ model. A similar trend is observed under the $48\times 48$ adversarial patch attack, where the MTFM model shows similar performance to TL. Under the most severe $64\times 64$ adversarial patch attack, $MTFM$ (R50→R18) achieves the highest ATA of 69.9%, representing improvements of 68.37% over $STD$, 8.56% over $PGD$, 1.9% over $TL$, and 7.68% over the best-performing $MTARD$ variant. Importantly, $MTFM$ achieves these accuracies with less than half the training time compared to $PGD$ and $MTARD$, highlighting its cost-effective nature.

5.4. EuroSAT → UCM and AID

To further validate the robustness transfer hypothesis, we repeat the same experimental setup using EuroSAT as the source dataset (

Table 3. Clean and adversarial accuracies of target models developed by transferring robustness from EuroSAT.

Dataset	Model	Arch	Clean	32 × 32		48 × 48		64 × 64		Time
				ATA	ASR	ATA	ASR	ATA	ASR
UCM	$STD$	R50	88.09	82.0	3.83	45.0	47.83	15.83	82.17	31.82
	$PGD$	R50	85.56	83.33	1.0	75.67	4.83	70.0	8.33	92.77
	$TL$	R50->R50	82.7	80.5	0.17	79.01	0.5	77.0	0.17	33.04
	SA-TL	R50	83.33	81.5	0.5	77.5	0.33	76.83	0.67	34.17
	$MTARD$	R152->R50	86.82	82.5	0.17	81.17	0.01	77.17	0.05	109.86
	$MTFM$	R152->R50	90.95	84.33	1.17	81.83	0.33	79.0	0.67	38.02
AID	$STD$	R50	91.73	24.78	74.3	10.44	84.49	3.97	96.03	49.83
	$PGD$	R50	84.87	69.2	12.53	58.5	29.33	45.93	49.31	314.18
	$TL$	R50->R50	88.0	85.31	0.89	83.77	1.32	81.52	2.32	52.74
	SA-TL	R50	87.3	78.03	1.54	71.42	1.33	73.44	1.88	51.28
	$MTARD$	R152->R50	76.43	71.63	0.68	67.63	0.51	67.45	0.93	368.52
	$MTFM$	R152->R50	90.01	83.81	0.37	78.44	0.72	76.66	2.14	79.04
UCM	$STD$	R18	85.08	71.33	11.33	48.33	42.67	22.83	73.33	29.99
	$PGD$	R18	79.68	74	2.0	71.66	4.66	63.66	15.33	64.08
	$TL$	R18->R18	79.05	75.33	1.17	72.33	0.83	72.17	1.5	29.09
	SA-TL	R18	80.32	76.83	1.5	72.33	1.5	71.0	0.83	32.08
	$MTARD$	R152->R18	86.51	84.0	0.1	78.83	0.05	78.17	0.01	64.96
	$MTARD$	R50->R18	84.13	82.83	0.01	75.67	0.03	73.5	0.5	61.99
	$MTFM$	R152->R18	86.83	78.67	0.67	76.3	0.87	70.17	3.16	30.86
	$MTFM$	R50->R18	85.87	81.67	0.17	76.5	0.5	67.83	0.33	31.02
AID	$STD$	R18	88.87	32.41	65.16	8.04	91.75	1.53	97.71	44.44
	$PGD$	R18	83.87	58.93	1.3	50.41	10.27	61.34	8.27	148.11
	$TL$	R18->R18	83.23	76.18	0.82	68.21	1.16	75.69	0.92	47.76
	SA-TL	R18	82.33	64.22	0.31	51.81	0.43	66.39	0.45	43.23
	$MTARD$	R152->R18	73.8	66.01	2.46	62.8	2.15	62.22	2.49	208.31
	$MTARD$	R50->R18	70.17	66.87	0.27	63.45	0.58	61.43	0.31	170.81
	$MTFM$	R152->R18	84.63	74.19	0.38	67.72	0.27	67.63	2.77	65.25
	$MTFM$	R50->R18	87.3	71.3	0.82	58.11	1.19	58.11	7.43	58.60

Time is calculated as average per epoch (total time/number of epochs).

), replacing PatternNet from the previous experiments.

5.4.1. Results on ResNet-50 (UCM and AID)

On the UCM dataset with ResNet-50 as the target architecture, the $STD$ model achieves a clean accuracy of 88.09%, while the $PGD$-trained model reaches 85.56%. The transfer learning model $TL$, which inherits robustness from EuroSAT, achieves 82.7%. The SA-TL model achieves a clean accuracy of 83.33%, and the $MTARD$ model achieves 86.82%. The proposed $MTFM$ model outperforms all baselines with a clean accuracy of 90.95%. Under a $32\times 32$ adversarial patch attack, all models maintain ATA above or close to 80%, with $MTFM$ achieving the highest at 84.33%. At the $48\times 48$ adversarial patch level, the $STD$ model’s ATA drops to 45.0%, while $PGD$ reaches 75.67%, $TL$ achieves 79.01%, SA-TL achieves 77.5%, $MTARD$ achieves 81.17%, and $MTFM$ leads with 81.83% ATA. Against the strongest $64\times 64$ patch attack, the $STD$ model collapses to 15.83% ATA, $PGD$ reaches 70.0%, $TL$ achieves 77.0%, SA-TL reaches 76.83%, $MTARD$ achieves 77.17%, and $MTFM$ tops the performance with 79.0% ATA—showing strong resilience across patch sizes.

On the AID dataset with ResNet-50, $STD$ achieves a clean accuracy of 91.73%, $PGD$ reaches 84.87%, $TL$ achieves 88.0%, SA-TL achieves 87.3%, $MTARD$ achieves 76.43%, and $MTFM$ attains 90.01%. Under a $32\times 32$ adversarial patch attack, ATA values are 24.78% ($STD$), 69.2% ($PGD$), 85.31% ($TL$), 78.03% (SA-TL), 71.63% ($MTARD$), and 83.81% ($MTFM$). $MTFM$ outperforms $STD$, $PGD$, SA-TL, and $MTARD$, and closely matches $TL$. Attacked with a $48\times 48$ adversarial patch, the models exhibit varying levels of robustness, with $TL$ outperforming most baselines across ATA. Against the strongest $64\times 64$ adversarial patch attack, $STD$ drops to 3.97%, $PGD$ reaches 45.93%, $TL$ achieves 81.52%, SA-TL reaches 73.44%, $MTARD$ achieves 67.45%, and $MTFM$ attains 76.66%—which is within 5% of $TL$ and represents improvements of 72.69% over $STD$ and 30.73% over $PGD$.

5.4.2. Results on ResNet-18 (UCM and AID)

With ResNet-18 as the target architecture on UCM, the $STD$ model achieves 85.08% clean accuracy, with ATA values of 71.33%, 48.33%, and 22.83% under $32\times 32$, $48\times 48$, and $64\times 64$ adversarial patches, respectively. The $PGD$ model achieves 79.68% clean accuracy and ATA values of 74.0%, 71.66%, and 63.66%. $TL$ maintains 79.05% clean accuracy and achieves 75.33%, 72.33%, and 72.17% ATA across the three patch sizes. The SA-TL model achieves 80.32% clean accuracy and ATA values of 76.83%, 72.33%, and 71.0%. The $MTARD$ model (R152→R18) achieves 86.51% clean accuracy and ATA values of 84.0%, 78.83%, and 78.17%. The proposed $MTFM$ model (R152→R18) outperforms all baselines with 86.83% clean accuracy. The $MTFM$ model (R152→R18) achieves ATA values of 78.67%, 76.30%, and 70.17%, respectively—surpassing $STD$ and $PGD$ across all metrics and closely matching $TL$ and $MTARD$.

On AID with ResNet-18, the $STD$ model achieves 88.87% clean accuracy, with ATA values of 32.41%, 8.04%, and 1.53% under increasing patch sizes. The $PGD$ model achieves 83.87% clean accuracy and ATA values of 58.93%, 50.41%, and 61.34%. The $TL$ model achieves 83.23% clean accuracy and ATA values of 76.18%, 68.21%, and 75.69%. The SA-TL model achieves 82.33% clean accuracy and ATA values of 64.22%, 51.81%, and 66.39%, respectively—outperforming $PGD$ and closely matching $TL$. The $MTARD$ model (R152→R18) attains a clean accuracy of 73.8% and ATA values of 66.01%, 62.8%, and 62.22%. The $MTFM$ model (R152→R18) achieves the clean accuracy of 84.63% and ATA values of 74.19%, 67.72%, and 67.73%, respectively—outperforming $STD$, $PGD$, SA-TL, and $MTARD$, while closely matching the $TL$ model.

Overall, the proposed $MTFM$ framework consistently outperforms both $STD$ and $PGD$-trained models in terms of clean accuracy, Adversarial Test Accuracy (ATA), and Attack Success Rate (ASR) under patch-based adversarial attacks. All reported accuracies were averaged over three independent runs to ensure stability and fairness in comparison. In many cases, $MTFM$ also matches or exceeds the performance of transfer learning ($TL$) models. $MTFM$ requires less training time. This demonstrates its effectiveness and efficiency as a robust defense strategy.

5.5. Evaluating Performance Using Grad-CAM Visualizations

While model performance has traditionally been evaluated using accuracy metrics, this study also employs Grad-CAM [35] to assess interpretability and decision focus. Grad-CAM is an explainable AI technique that visualizes the regions of an input image that most influence the model’s predictions. In this context, it highlights where the model attends when making classification decisions.

In Figure 5, the first column shows the clean image, followed by its adversarially patched counterpart. The third column displays the standard model (STD), which tends to focus heavily on the adversarial patch—often leading to misclassification by predicting the patch class instead of the true label. In contrast, the (MTFM) model in the sixth column attends more to the rest of the image, which supports correct classification. The first two rows represent ResNet-50 models trained on UCM and AID datasets with PatternNet as the source, while the next two rows show results when the source is EuroSAT.

A similar trend is observed in Figure 6, which shows Grad-CAM results for ResNet-18 models. The standard model (STD) in the third column again focuses primarily on the patch, whereas the (MTFM) model in the sixth column attends to the broader image context, improving classification accuracy. Although the patch size is $64\times 64$ and the image size is $224\times 224$, some attention leakage toward the patch is still observed. Nevertheless, the (MTFM) models correctly classify the image in most cases, demonstrating both robustness and improved interpretability.

Across all experiments, the proposed MTFM approach consistently demonstrates superior robustness transfer across datasets and architectures. Whether using ResNet-50 or ResNet-18 as the student model, MTFM outperforms baseline defense models in terms of adversarial test accuracy while maintaining competitive or superior clean accuracy.

6. Discussion

The proposed Multi-Teacher Feature Matching (MTFM) approach is evaluated against adversarial patch attacks and compared with traditional defense strategies across benchmark datasets and architectures. Robustness is assessed using adversarial test accuracy (ATA), training efficiency, and interpretability via Grad-CAM visualizations.

Projected Gradient Descent adversarial training (PGD-AT) is used as the baseline defense technique. PGD generates adversarial examples by perturbing all regions of the image. This broader perturbation strategy makes PGD effective against patch attacks, positioning it as a strong baseline. However, PGD suffers from a notable trade-off between clean accuracy and robustness, as shown in Table 1. For example, the EuroSAT ResNet-152 $STD$ model achieves a clean accuracy of 95.12%, but its ATA drops to 5.06% under a $64\times 64$ adversarial patch attack. The $PGD$ defense model improves ATA to 73.38%, but this comes at the cost of nearly a 7% reduction in clean accuracy and a substantial training time of 1880.26 s per epoch. Similarly, in Table 2, the AID dataset’s $PGD$ robust model (R50) shows an ATA improvement of 41.96% but suffers a 6.86% loss in clean accuracy compared to the $STD$ model. In contrast, the proposed MTFM approach achieves a 73% improvement in ATA with only a 3.5% sacrifice in clean accuracy, outperforming PGD in both ATA and clean accuracy.

In most scenarios, PGD-AT develops robust models at the cost of clean accuracy and high computational expense. The larger the dataset, the more training time is required to train the $PGD$ model. In contrast, the proposed $MTFM$ framework achieves superior clean accuracy and better ATA than PGD in most cases. One contributing factor is its two-teacher setup, where both teachers are trained on larger datasets that retain rich semantic features. Since the target datasets are also remote sensing satellite image datasets with similar class types, the teacher feature representations are highly transferable—enabling the development of robust models with lower training overhead. For example, on the UCM dataset, the training time difference between $PGD$ and $MTFM$ is approximately 54.56 s per epoch. On the larger AID dataset, $MTFM$ reduces training time by nearly 232.74 s per epoch compared to $PGD$.

The proposed MTFM approach is also compared against other defense strategies such as $TL$ and $MTARD$. In most cases, $MTFM$ models match or surpass the performance of $TL$ models. The $TL$ training setup employs a single adversarially robust teacher, whereas the $MTFM$ setup leverages two teachers, which helps maintain both clean accuracy and ATA. Furthermore, $MTFM$ match or outperforms $MTARD$ models in most scenarios. The $MTARD$ training setup focuses primarily on logit matching, while $MTFM$ emphasizes feature matching, leading to better overall performance.

7. Conclusions

This study demonstrated that adversarial robustness can be significantly enhanced through the proposed Multi-Teacher Feature Matching (MTFM) framework, achieving a favorable trade-off between clean accuracy and adversarial robustness. We evaluated this method across diverse scenarios, including varying source and target datasets, different architectures, and transfer settings. Our proposed MTFM approach outperformed traditional robustness transfer approaches by achieving a better trade-off between clean accuracy and adversarial robustness. Notably, the training time for MTFM remained consistently low, outperforming many traditional defenses in both robustness and efficiency.

For future work, we aim to extend this robustness to datasets with limited labeled samples by exploring semi-supervised and weakly supervised regimes. Additionally, while this study employed cosine similarity to measure feature alignment, we plan to investigate alternative metrics that may better capture semantic consistency. Overall, this work highlights a promising direction for developing robust models with reduced computational overhead.

8. Supplementary Results

Self Attention Evaluation

This subsection presents additional results for ResNet-50 and ResNet-18 models integrated with self-attention modules, tested against 32 × 32, 48 × 48, and 64 × 64 adversarial patch attacks. Robustness is transferred from source datasets (PatternNet and EuroSAT) to target datasets (UCM and AID) using four previously defined transfer learning strategies: Fullnet, Fixedfeat, F25, and F9 (for ResNet-18).

Table 4. Clean and adversarial accuracies of models trained on source datasets (PatternNet and EuroSAT).

Target	Source	Model	Arch	Clean	32 × 32		48 × 48		64 × 64		Time
					ATA	ASR	ATA	ASR	ATA	ASR
UCM	UCM	$STD$	R50	89.20	73.33	13.33	36.0	60.83	14.17	85.5	33.73
	UCM	$PGD$	R50	83.49	76.67	5.0	69.5	11.67	61.67	23.0	101.13
	UCM	$STD$	R18	84.13	77.83	1.67	56.67	26.83	27.5	67.33	30.53
	UCM	$PGD$	R18	78.57	73.67	0.1	73.5	0.17	68.5	0.01	67.83
	PatterNet	$Fullnet$	R50	91.11	85.83	0.5	82.67	1.83	74.83	8.33	34.99
	PatterNet	$FixedFeat$	R50	84.44	80.17	0.67	77.33	2.83	72.83	4.17	32.43
	PatterNet	$F25$	R50	91.75	85.17	0.67	82.83	3.33	74.17	8.83	34.94
	PatterNet	$Fullnet$	R18	86.98	83.83	1.17	81.0	1.33	78.5	1.67	32.12
	PatterNet	$FixedFeat$	R18	78.10	75.17	0.83	72.33	2.5	71.17	1.83	29.87
	PatterNet	$F9$	R18	86.83	80.33	0.67	78.17	0.5	75.23	0.5	32.72
	EuroSAT	$Fullnet$	R50	83.33	82.0	0.5	77.67	0.33	76.83	0.67	34.17
	EuroSAT	$FixedFeat$	R50	67.61	66.67	2.5	63.0	3.0	62.0	2.5	31.32
	EuroSAT	$F25$	R50	82.70	81.0	0.17	78.0	0.33	76.17	0.67	33.27
	EuroSAT	$Fullnet$	R18	80.32	74.5	1.5	75.5	1.5	73.83	0.83	32.07
	EuroSAT	$FixedFeat$	R18	63.97	61.0	0.83	61.67	0.67	59.67	0.17	30.09
	EuroSAT	$F9$	R18	80.48	75.17	1.33	75.33	1.83	73.5	0.83	30.80
AID	AID	$STD$	R50	90.13	35.49	59.86	11.29	88.4	3.28	96.71	54.36
	AID	$PGD$	R50	86.06	54.65	5.79	52.49	11.57	52.64	34.53	352.73
	AID	$STD$	R18	89.53	38.26	52.74	8.49	91.27	2.46	97.54	48.99
	AID	$PGD$	R18	82.77	48.60	3.87	36.93	31.21	42.10	37.99	158.28
	PatterNet	$Fullnet$	R50	89.73	64.58	2.05	58.59	6.23	50.65	26.52	53.75
	PatterNet	$FixedFeat$	R50	77.9	67.25	1.64	66.91	1.13	64.30	1.16	39.86
	PatterNet	$F25$	R50	89.30	63.59	1.37	63.55	1.13	61.6	7.97	49.81
	PatterNet	$Fullnet$	R18	86.53	68.45	0.58	49.39	0.58	66.05	0.38	40.17
	PatterNet	$FixedFeat$	R18	74.3	69.61	0.48	69.27	0.31	69.95	0.24	37.46
	PatterNet	$F9$	R18	85.37	71.83	0.27	52.64	0.35	67.72	0.14	43.23
	EuroSAT	$Fullnet$	R50	88.33	69.78	2.40	65.57	2.81	64.41	9.21	54.69
	EuroSAT	$FixedFeat$	R50	65.7	64.72	1.3	63.96	0.99	62.59	1.40	40.85
	EuroSAT	$F25$	R50	87.3	74.97	1.54	70.74	1.33	73.54	1.88	51.28
	EuroSAT	$Fullnet$	R18	83.63	74.23	0.21	61.77	0.48	67.13	0.41	40.02
	EuroSAT	$FixedFeat$	R18	64.87	62.01	0.58	62.01	1.13	62.04	0.82	36.18
	EuroSAT	$F9$	R18	82.33	74.18	0.17	62.73	0.55	67.39	0.45	43.23

Time is calculated as average per epoch (total time/number of epochs).

summarizes the performance of self-attention-based defense models under varying adversarial patch sizes. Across both UC_Merced and AID datasets, these models consistently outperform standard and PGD-trained baselines, demonstrating stronger robustness and reduced training time. Robustness is transferred from PatternNet and EuroSAT using strategies such as textitFullnet, Fixedfeat, F25, and F9. The best-performing self-attention model is used as a reference for comparison against the MTFM framework.