CAGFNet: A Cross-Attention Image-Guided Fusion Network for Disparity Estimation of High-Resolution Satellite Stereo Images
Abstract
1. Introduction
- We propose CAGFNet, an end-to-end deep learning network for disparity estimation. It integrates multi-scale convolution and cross-attention for feature extraction, along with 3D convolution and multi-scale cost volume processing to learn depth relationships across scales, improving precision and robustness;
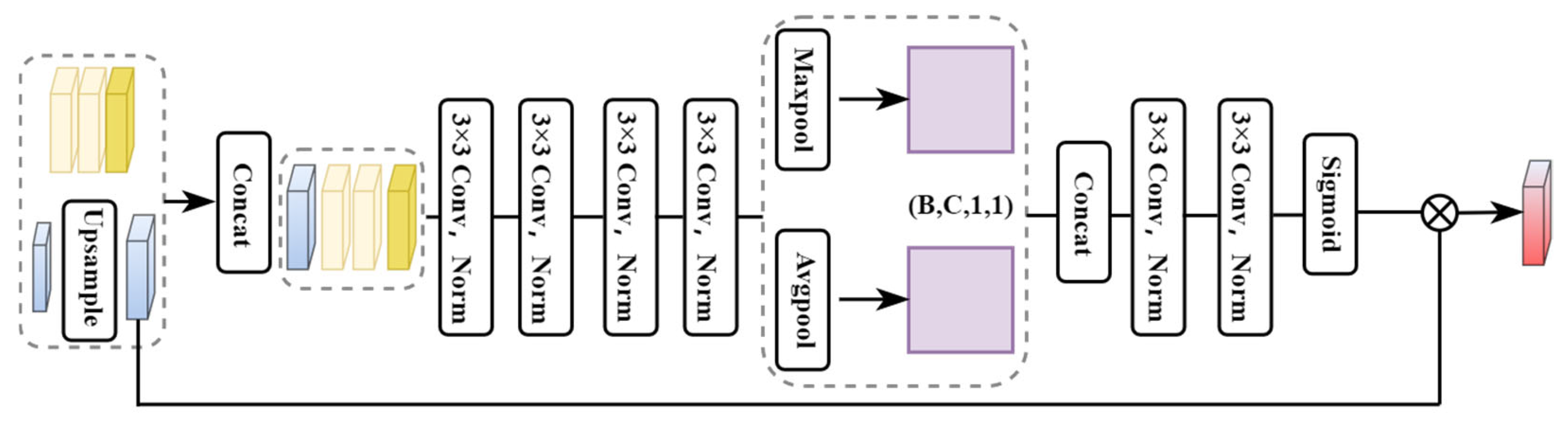
- The IMGD and 3D EMA modules restore and fuse multi-scale features, while the guide attention module refines disparity results, enhancing accuracy in complex scenes;
- Extensive experiments on the US3D and WHU Aerial Stereo datasets validate the functionality of each module and demonstrate the model’s effectiveness and generalization capability.
2. Related Work
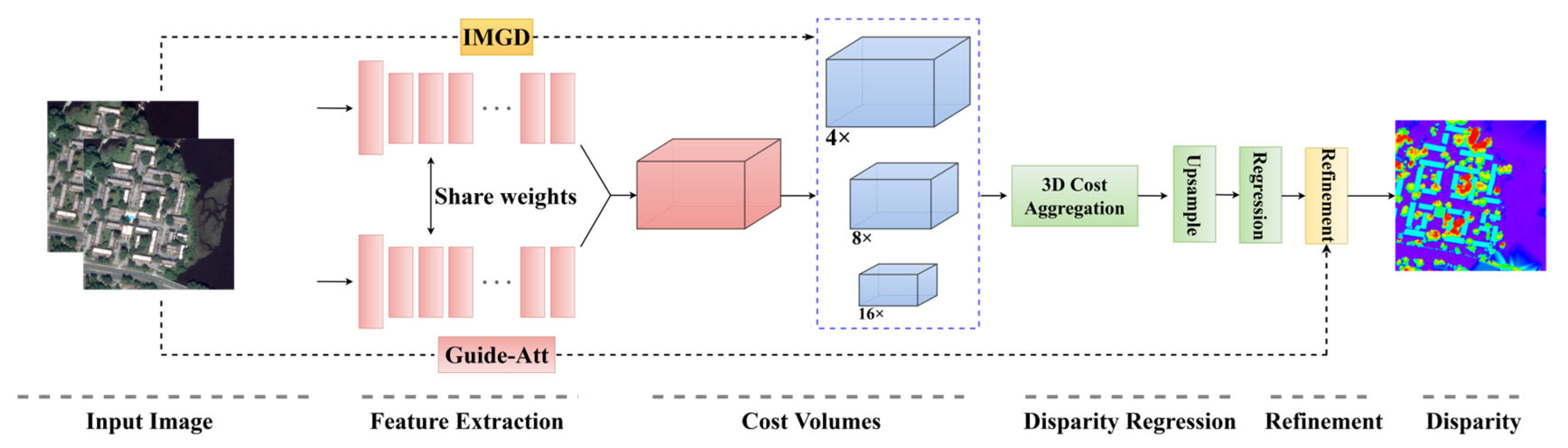
3. Materials and Methods
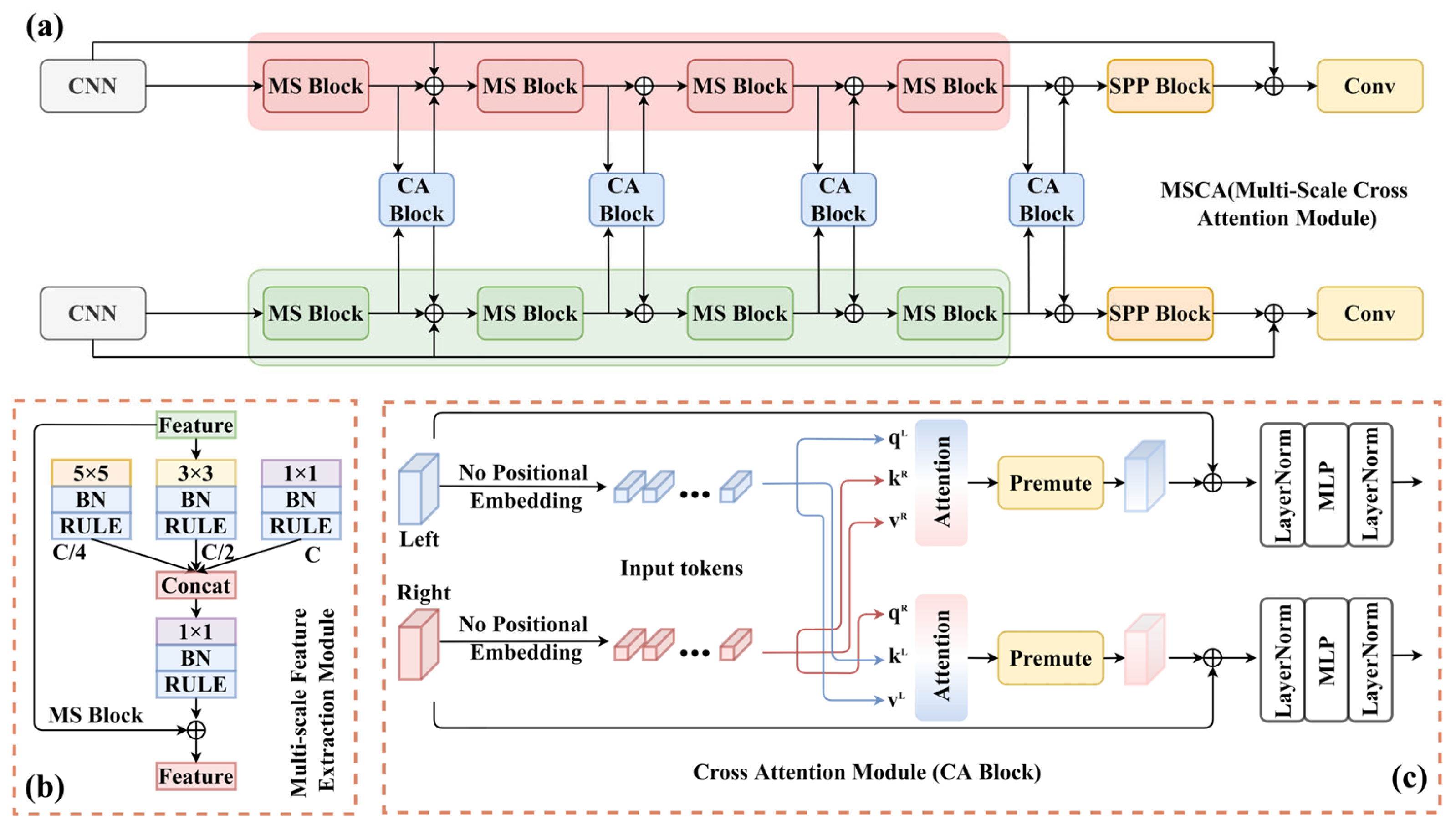
3.1. Feature Extraction Module
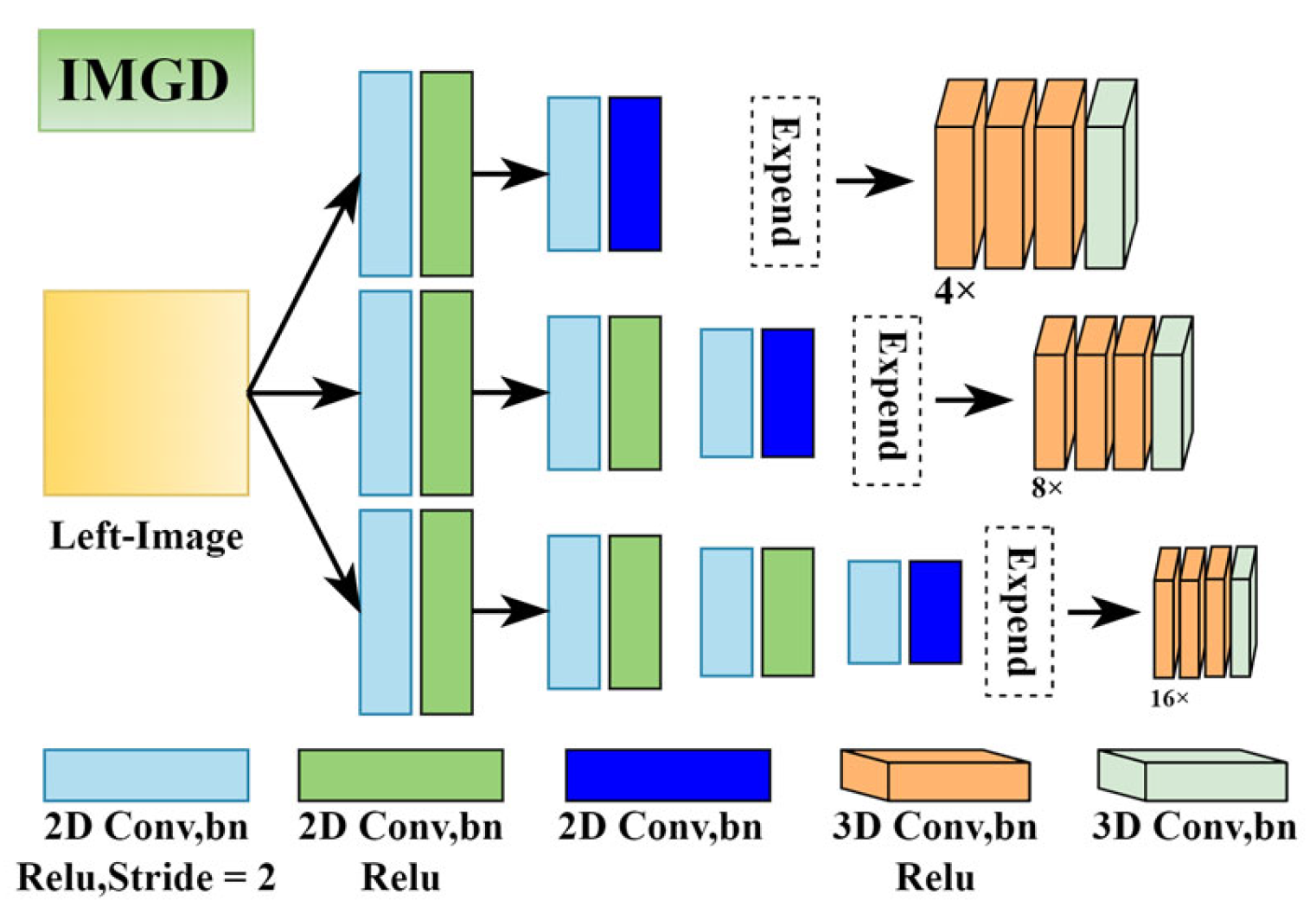
3.2. Cost Volume Construction
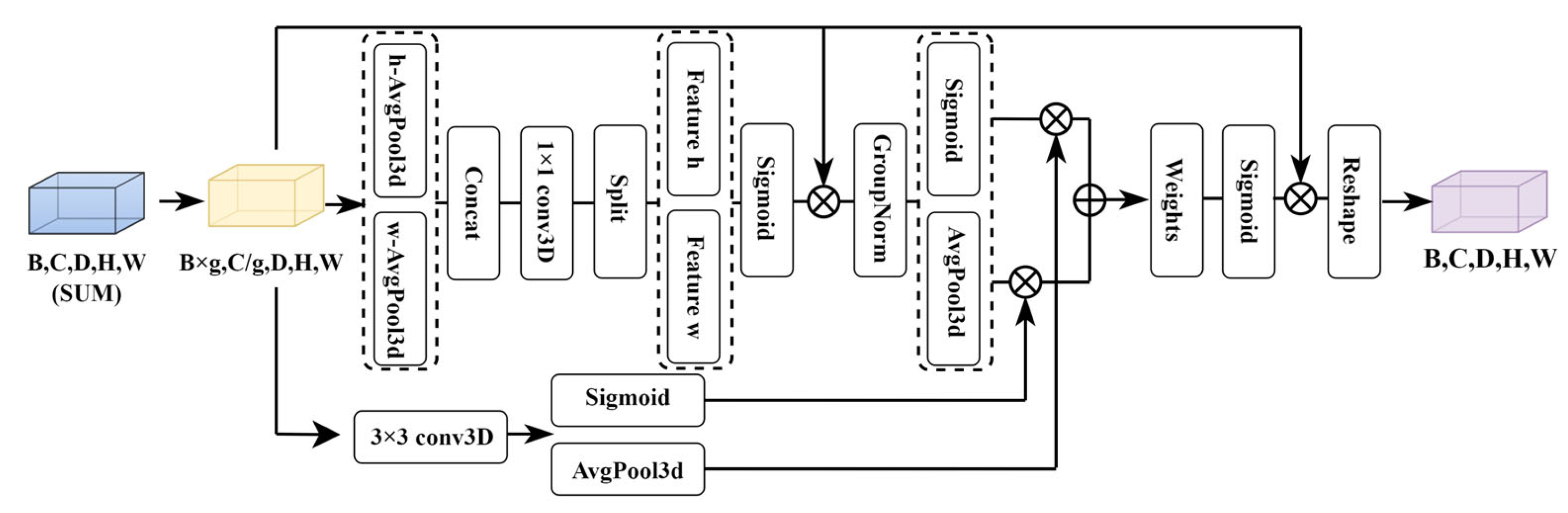
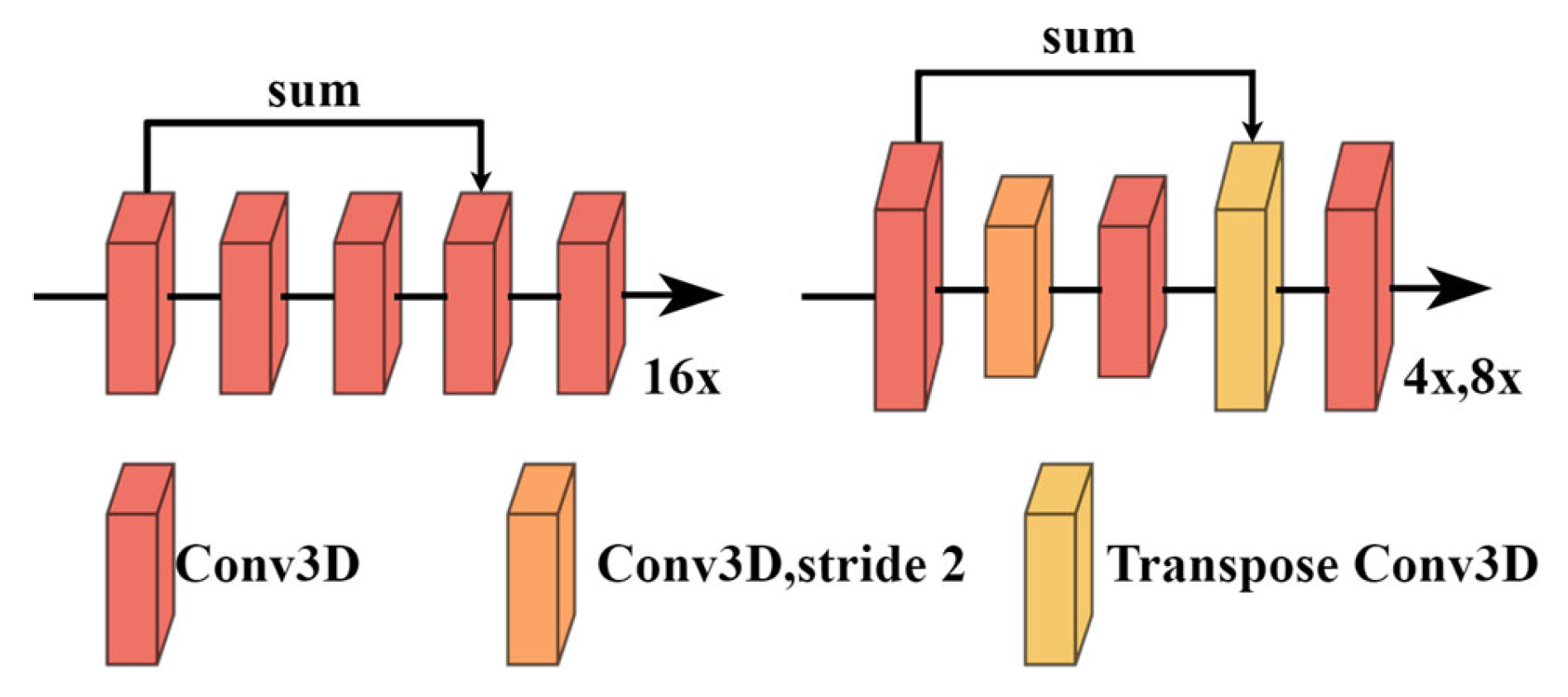
3.3. Three-Dimensional Cost Aggregation
3.4. Disparity Regression
3.5. Loss Function
4. Results
4.1. Experiment Setting
4.1.1. Datasets
4.1.2. Evaluation Metrics
4.1.3. Training Strategies
- Train and test separately on the Jacksonville and Omaha subsets to assess the model’s performance;
- Train on one subset and test on the other to evaluate the model’s generalization ability.
4.1.4. Implementation Details
4.2. Results and Comparisons
Results on the US3D Dataset
5. Discussion
5.1. Generalization Experiments
5.2. Ablation Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Laga, H.; Jospin, L.V.; Boussaid, F.; Bennamoun, M. A survey on deep learning techniques for stereo-based depth estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 1738–1764. [Google Scholar] [CrossRef] [PubMed]
- Tulyakov, S.; Ivanov, A.; Fleuret, F. Practical deep stereo (pds): Toward applications-friendly deep stereo matching. Adv. Neural Inf. Process. Syst. 2018, 31, 5875–5885. [Google Scholar]
- Mayer, N.; Ilg, E.; Hausser, P.; Fischer, P.; Cremers, D.; Dosovitskiy, A.; Brox, T. A large dataset to train convolutional networks for disparity, optical flow, and scene flow estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4040–4048. [Google Scholar]
- He, S.; Zhou, R.; Li, S.; Jiang, S.; Jiang, W. Disparity estimation of high-resolution remote sensing images with dual-scale matching network. Remote Sens. 2021, 13, 5050. [Google Scholar] [CrossRef]
- Horn, B.K.; Schunck, B.G. Determining optical flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef]
- Kolmogorov, V.; Zabih, R. Computing visual correspondence with occlusions using graph cuts. In Proceedings of the Eighth IEEE International Conference on Computer Vision, Vancouver, BC, Canada, 7–14 July 2001; pp. 508–515. [Google Scholar]
- Sun, J.; Zheng, N.-N.; Shum, H.-Y. Stereo matching using belief propagation. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 787–800. [Google Scholar]
- Veksler, O. Stereo correspondence by dynamic programming on a tree. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; pp. 384–390. [Google Scholar]
- Hirschmuller, H. Accurate and efficient stereo processing by semi-global matching and mutual information. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; pp. 807–814. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef]
- Eigen, D.; Fergus, R. Predicting depth, surface normals and semantic labels with a common multi-scale convolutional architecture. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2650–2658. [Google Scholar]
- Luo, W.; Schwing, A.G.; Urtasun, R. Efficient deep learning for stereo matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5695–5703. [Google Scholar]
- Žbontar, J.; LeCun, Y. Stereo matching by training a convolutional neural network to compare image patches. J. Mach. Learn. Res. 2016, 17, 1–32. [Google Scholar]
- Yang, G.; Manela, J.; Happold, M.; Ramanan, D. Hierarchical deep stereo matching on high-resolution images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5515–5524. [Google Scholar]
- Cheng, X.; Wang, P.; Yang, R. Learning depth with convolutional spatial propagation network. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 2361–2379. [Google Scholar] [CrossRef]
- Kendall, A.; Martirosyan, H.; Dasgupta, S.; Henry, P.; Kennedy, R.; Bachrach, A.; Bry, A. End-to-end learning of geometry and context for deep stereo regression. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 66–75. [Google Scholar]
- He, S.; Li, S.; Jiang, S.; Jiang, W. HMSM-Net: Hierarchical multi-scale matching network for disparity estimation of high-resolution satellite stereo images. ISPRS J. Photogramm. Remote Sens. 2022, 188, 314–330. [Google Scholar] [CrossRef]
- He, X.; Jiang, S.; He, S.; Li, Q.; Jiang, W.; Wang, L. Deep learning-based stereo matching for high-resolution satellite images: A comparative evaluation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, 48, 1635–1642. [Google Scholar] [CrossRef]
- Li, S.; He, S.; Jiang, S.; Jiang, W.; Zhang, L. WHU-stereo: A challenging benchmark for stereo matching of high-resolution satellite images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Hirschmuller, H. Stereo processing by semiglobal matching and mutual information. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 30, 328–341. [Google Scholar] [CrossRef] [PubMed]
- Pang, J.; Sun, W.; Ren, J.S.; Yang, C.; Yan, Q. Cascade residual learning: A two-stage convolutional neural network for stereo matching. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 887–895. [Google Scholar]
- Kar, A.; Häne, C.; Malik, J. Learning a multi-view stereo machine. Adv. Neural Inf. Process. Syst. 2017, 30, 365–376. [Google Scholar]
- Liang, Z.; Feng, Y.; Guo, Y.; Liu, H.; Chen, W.; Qiao, L.; Zhou, L.; Zhang, J. Learning for disparity estimation through feature constancy. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2811–2820. [Google Scholar]
- Khamis, S.; Fanello, S.; Rhemann, C.; Kowdle, A.; Valentin, J.; Izadi, S. Stereonet: Guided hierarchical refinement for real-time edge-aware depth prediction. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 573–590. [Google Scholar]
- Chang, J.-R.; Chen, Y.-S. Pyramid stereo matching network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5410–5418. [Google Scholar]
- Nie, G.-Y.; Cheng, M.-M.; Liu, Y.; Liang, Z.; Fan, D.-P.; Liu, Y.; Wang, Y. Multi-level context ultra-aggregation for stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3283–3291. [Google Scholar]
- Zhang, F.; Prisacariu, V.; Yang, R.; Torr, P.H. Ga-net: Guided aggregation net for end-to-end stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 185–194. [Google Scholar]
- Guo, X.; Yang, K.; Yang, W.; Wang, X.; Li, H. Group-wise correlation stereo network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3273–3282. [Google Scholar]
- Cheng, X.; Zhong, Y.; Harandi, M.; Dai, Y.; Chang, X.; Li, H.; Drummond, T.; Ge, Z. Hierarchical neural architecture search for deep stereo matching. Adv. Neural Inf. Process. Syst. 2020, 33, 22158–22169. [Google Scholar]
- Li, Z.; Liu, X.; Drenkow, N.; Ding, A.; Creighton, F.X.; Taylor, R.H.; Unberath, M. Revisiting stereo depth estimation from a sequence-to-sequence perspective with transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 6197–6206. [Google Scholar]
- Xu, G.; Cheng, J.; Guo, P.; Yang, X. Attention concatenation volume for accurate and efficient stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12981–12990. [Google Scholar]
- Xu, G.; Zhou, H.; Yang, X. Cgi-stereo: Accurate and real-time stereo matching via context and geometry interaction. arXiv 2023, arXiv:2301.02789. [Google Scholar]
- Lou, J.; Liu, W.; Chen, Z.; Liu, F.; Cheng, J. Elfnet: Evidential local-global fusion for stereo matching. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 17784–17793. [Google Scholar]
- Chebbi, M.A.; Rupnik, E.; Pierrot-Deseilligny, M.; Lopes, P. Deepsim-nets: Deep similarity networks for stereo image matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 2097–2105. [Google Scholar]
- Guo, X.; Zhang, C.; Nie, D.; Zheng, W.; Zhang, Y.; Chen, L. Lightstereo: Channel boost is all your need for efficient 2d cost aggregation. arXiv 2024, arXiv:2406.19833. [Google Scholar]
- Guan, T.; Wang, C.; Liu, Y.-H. Neural markov random field for stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 5459–5469. [Google Scholar]
- Feng, M.; Cheng, J.; Jia, H.; Liu, L.; Xu, G.; Yang, X. Mc-stereo: Multi-peak lookup and cascade search range for stereo matching. In Proceedings of the 2024 International Conference on 3D Vision (3DV), Davos, Switzerland, 18–21 March 2024; pp. 344–353. [Google Scholar]
- Jiang, X.; Bian, X.; Guo, C. Ghost-Stereo: GhostNet-based Cost Volume Enhancement and Aggregation for Stereo Matching Networks. arXiv 2024, arXiv:2405.14520. [Google Scholar]
- Chen, Z.; Long, W.; Yao, H.; Zhang, Y.; Wang, B.; Qin, Y.; Wu, J. Mocha-stereo: Motif channel attention network for stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 27768–27777. [Google Scholar]
- Tahmasebi, M.; Huq, S.; Meehan, K.; McAfee, M. DCVSMNet: Double cost volume stereo matching network. Neurocomputing 2025, 618, 129002. [Google Scholar] [CrossRef]
- Tao, R.; Xiang, Y.; You, H. An edge-sense bidirectional pyramid network for stereo matching of vhr remote sensing images. Remote Sens. 2020, 12, 4025. [Google Scholar] [CrossRef]
- Rao, Z.; He, M.; Zhu, Z.; Dai, Y.; He, R. Bidirectional guided attention network for 3-D semantic detection of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2020, 59, 6138–6153. [Google Scholar] [CrossRef]
- Liao, P.; Zhang, X.; Chen, G.; Wang, T.; Li, X.; Yang, H.; Zhou, W.; He, C.; Wang, Q. S2Net: A Multi-task Learning Network for Semantic Stereo of Satellite Image Pairs. IEEE Trans. Geosci. Remote Sens. 2023, 62, 5601313. [Google Scholar] [CrossRef]
- Zheng, Z.; Wan, Y.; Zhang, Y.; Hu, Z.; Wei, D.; Yao, Y.; Zhu, C.; Yang, K.; Xiao, R. Digital surface model generation from high-resolution satellite stereos based on hybrid feature fusion network. Photogramm. Rec. 2024, 39, 36–66. [Google Scholar] [CrossRef]
- Cao, X.; Zhang, X.; Yu, A.; Yu, W.; Bu, S. CSStereo: A UAV scenarios stereo matching network enhanced with contrastive learning and feature selection. Int. J. Appl. Earth Obs. Geoinf. 2024, 134, 104189. [Google Scholar] [CrossRef]
- Wei, K.; Huang, X.; Li, H. Stereo matching method for remote sensing images based on attention and scale fusion. Remote Sens. 2024, 16, 387. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, G.; Tan, X.; Wang, T.; Wang, J.; Zhang, X. S3Net: Innovating Stereo Matching and Semantic Segmentation with a Single-Branch Semantic Stereo Network in Satellite Epipolar Imagery. In Proceedings of the IGARSS 2024—2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; pp. 8737–8740. [Google Scholar]
- Chen, C.; Zhao, L.; He, Y.; Long, Y.; Chen, K.; Wang, Z.; Hu, Y.; Sun, X. SemStereo: Semantic-Constrained Stereo Matching Network for Remote Sensing. arXiv 2024, arXiv:2412.12685. [Google Scholar] [CrossRef]
- Xu, Z.; Jiang, Y.; Wang, J.; Wang, Y. A Dual Branch Multi-scale Stereo Matching Network for High-resolution Satellite Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 18, 949–964. [Google Scholar] [CrossRef]
- Yin, A.; Ren, C.; Yan, Z.; Xue, X.; Yue, W.; Wei, Z.; Liang, J.; Zhang, X.; Lin, X. HRU-Net: High-Resolution Remote Sensing Image Road Extraction Based on Multi-Scale Fusion. Appl. Sci. 2023, 13, 8237. [Google Scholar] [CrossRef]
- Zhou, X.; Wei, X. Feature Aggregation Network for Building Extraction from High-Resolution Remote Sensing Images. In Proceedings of the Pacific Rim International Conference on Artificial Intelligence, Jakarta, Indonesia, 15–19 November 2023; pp. 105–116. [Google Scholar]
- Chu, X.; Yao, X.; Duan, H.; Chen, C.; Li, J.; Pang, W. Glacier extraction based on high-spatial-resolution remote-sensing images using a deep-learning approach with attention mechanism. Cryosphere 2022, 16, 4273–4289. [Google Scholar] [CrossRef]
- Wu, P.; Fu, J.; Yi, X.; Wang, G.; Mo, L.; Maponde, B.T.; Liang, H.; Tao, C.; Ge, W.; Jiang, T. Research on water extraction from high resolution remote sensing images based on deep learning. Front. Remote Sens. 2023, 4, 1283615. [Google Scholar] [CrossRef]
- Li, Z.; He, W.; Li, J.; Lu, F.; Zhang, H. Learning without Exact Guidance: Updating Large-scale High-resolution Land Cover Maps from Low-resolution Historical Labels. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 27717–27727. [Google Scholar]
- Wang, Y.; Dong, M.; Ye, W.; Liu, D.; Gan, G. A contrastive learning-based iterative network for remote sensing image super-resolution. Multimed. Tools Appl. 2024, 83, 8331–8357. [Google Scholar] [CrossRef]
- Wu, Z.; Wu, X.; Zhang, X.; Wang, S.; Ju, L. Semantic stereo matching with pyramid cost volumes. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 7484–7493. [Google Scholar]
- Ouyang, D.; He, S.; Zhang, G.; Luo, M.; Guo, H.; Zhan, J.; Huang, Z. Efficient multi-scale attention module with cross-spatial learning. In Proceedings of the ICASSP 2023—2023 IEEE International Conference on Acoustics, Speech and Signal Processing, Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Bosch, M.; Foster, K.; Christie, G.; Wang, S.; Hager, G.D.; Brown, M. Semantic stereo for incidental satellite images. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 7–11 January 2019; pp. 1524–1532. [Google Scholar]
- Le Saux, B.; Yokoya, N.; Hansch, R.; Brown, M.; Hager, G. 2019 data fusion contest [technical committees]. IEEE Geosci. Remote Sens. Mag. 2019, 7, 103–105. [Google Scholar] [CrossRef]
- De Franchis, C.; Meinhardt-Llopis, E.; Michel, J.; Morel, J.-M.; Facciolo, G. On stereo-rectification of pushbroom images. In Proceedings of the 2014 IEEE International Conference on Image Processing, Paris, France, 27–30 October 2014; pp. 5447–5451. [Google Scholar]
- Liu, J.; Ji, S. A novel recurrent encoder-decoder structure for large-scale multi-view stereo reconstruction from an open aerial dataset. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 6050–6059. [Google Scholar]
- Atienza, R. Fast disparity estimation using dense networks. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation, Brisbane, QLD, Australia, 21–25 May 2018; pp. 3207–3212. [Google Scholar]
- Xu, H.; Zhang, J. Aanet: Adaptive aggregation network for efficient stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1959–1968. [Google Scholar]






| Name | Layer Setting | Output Dimension |
|---|---|---|
| CNN | ||
| Input | H × W × 3 | |
| initial_conv | [3 × 3, 132] × 3 | H × W × 32 |
| res_block1 | [3 × 3, 132] × 3 | H × W × 32 |
| res_block2 | [3 × 3, 164] × 3 | H × W × 64 |
| res_block3 | [3 × 3, 128] × 3 | H × W × 128 |
| Stereo Pair | Mode | Size | Data Splitting | Usage |
|---|---|---|---|---|
| Jacksonville | RGB | 1024 × 1024 | 1739/200/200 | Training/Validation/Test |
| Omaha | RGB | 1024 × 1024 | 1753/200/200 | Training/Validation/Test |
| WHU | RGB | 768 × 384 | 240 | Test |
| Method | Jacksonville | Omaha | ||
|---|---|---|---|---|
| EPE (Pixel) | D1 (%) | EPE (Pixel) | D1 (%) | |
| DenseMapNet | 2.857 | 33.60 | 1.306 | 14.40 |
| StereoNet | 1.791 | 19.01 | 1.282 | 14.03 |
| PSMNet | 1.711 | 16.00 | 1.422 | 12.92 |
| ACVnet | 1.838 | 17.70 | 1.632 | 15.58 |
| HMSMNet | 1.529 | 15.25 | 1.082 | 11.53 |
| DCVSMNet | 2.034 | 20.29 | 1.759 | 18.59 |
| CAGFNet | 1.466 | 14.71 | 0.996 | 10.53 |
| EPE (Pixel) | |||||||
|---|---|---|---|---|---|---|---|
| DenseMapNet | StereoNet | PSMNet | ACVNet | HMSMNet | DCVSMNet | CAGFNet | |
| JAX_204_004_011 | 1.606 | 2.755 | 1.195 | 1.194 | 1.092 | 1.541 | 0.975 |
| JAX_156_007_022 | 2.058 | 5.463 | 0.797 | 0.753 | 0.71 | 0.787 | 0.632 |
| OMA134_003_002 | 1.369 | 3.168 | 1.367 | 1.319 | 1.258 | 1.338 | 1.095 |
| D1 (%) | |||||||
|---|---|---|---|---|---|---|---|
| DenseMapNet | StereoNet | PSMNet | ACVNet | HMSMNet | DCVSMNet | CAGFNet | |
| JAX_204_004_011 | 18.76 | 31.92 | 10.32 | 10.44 | 10.23 | 18.46 | 10.1 |
| JAX_156_007_022 | 24.66 | 46.75 | 4.47 | 3.81 | 3.92 | 5.38 | 3.31 |
| OMA134_003_002 | 15.58 | 33.49 | 12.51 | 11.56 | 12.5 | 14.13 | 11.35 |
| EPE (Pixel) | |||||||
|---|---|---|---|---|---|---|---|
| DenseMapNet | StereoNet | PSMNet | ACVNet | HMSMNet | DCVSMNet | CAGFNet | |
| JAX_280_023_003 | 2.709 | 3.191 | 1.869 | 1.753 | 1.827 | 2.005 | 1.711 |
| JAX_427_016_013 | 2.785 | 4.211 | 2.028 | 2.012 | 1.907 | 2.228 | 1.815 |
| OMA132_003_039 | 1.155 | 3.229 | 1.198 | 1.074 | 0.966 | 1.001 | 0.875 |
| D1 (%) | |||||||
|---|---|---|---|---|---|---|---|
| DenseMapNet | StereoNet | PSMNet | ACVNet | HMSMNet | DCVSMNet | CAGFNet | |
| JAX_280_023_003 | 31.35 | 35.01 | 19.23 | 17.93 | 18.58 | 21.79 | 17.71 |
| JAX_427_016_013 | 29.22 | 40.76 | 20.73 | 20.58 | 19.21 | 23.21 | 18.85 |
| OMA132_003_039 | 13.79 | 31.63 | 10.45 | 7.93 | 8.72 | 8.78 | 8.14 |
| EPE (Pixel) | |||||||
|---|---|---|---|---|---|---|---|
| DenseMapNet | StereoNet | PSMNet | ACVNet | HMSMNet | DCVSMNet | CAGFNet | |
| JAX_072_011_006 | 1.658 | 2.217 | 1.296 | 1.251 | 1.133 | 1.261 | 1.054 |
| JAX_264_003_011 | 2.608 | 4.821 | 1.485 | 1.126 | 1.578 | 1.316 | 0.996 |
| OMA212_008_030 | 0.48 | 2.022 | 0.753 | 0.753 | 0.488 | 0.632 | 0.305 |
| D1 (%) | |||||||
|---|---|---|---|---|---|---|---|
| DenseMapNet | StereoNet | PSMNet | ACVNet | HMSMNet | DCVSMNet | CAGFNet | |
| JAX_072_011_006 | 21.66 | 24.81 | 12.13 | 11.17 | 10.86 | 14.03 | 10.86 |
| JAX_264_003_011 | 33.02 | 35.92 | 12.18 | 9.55 | 20 | 13.94 | 9.03 |
| OMA212_008_030 | 5.43 | 22.24 | 3.97 | 3.48 | 3.18 | 4.95 | 2.71 |
| Training Set | Testing Set | ||||
|---|---|---|---|---|---|
| Jacksonville | Omaha | ||||
| EPE (Pixel) | D1 (%) | EPE (Pixel) | D1 (%) | ||
| DenseMapNet | Jacksonville | 29.41 | 2.512 | 28.86 | |
| Omaha | 2.612 | ||||
| StereoNet | Jacksonville | 4.269 | 35.02 | ||
| Omaha | 5.041 | 45.99 | |||
| PSMNet | Jacksonville | 2.118 | 19.33 | ||
| Omaha | 2.666 | 27.48 | |||
| ACVNet | Jacksonville | 2.164 | 19.87 | ||
| Omaha | 2.463 | 25.35 | |||
| HMSMNet | Jacksonville | 1.885 | 18.44 | ||
| Omaha | 2.417 | 26.3 | |||
| DCVSMNet | Jacksonville | 2.064 | 19.20 | ||
| Omaha | 2.411 | 26.4 | |||
| CAGFNet | Jacksonville | 1.87 | 19.79 | ||
| Omaha | 2.349 | 25.77 | |||
| Method | EPE (Pixel) | D1 (%) | Total Params (MB) | FLOPS (G) |
|---|---|---|---|---|
| DenseMapNet | 38.998 | 33.44 | 0.19 | 7.37 |
| StereoNet | 38.943 | 32.74 | 0.65 | 45.99 |
| PSMNet | 39.278 | 33.75 | 5.22 | 381.53 |
| ACVnet | 37.349 | 30.28 | 7.12 | 436.55 |
| HMSMNet | 38.801 | 33.08 | 4.51 | 324.41 |
| DCVSMNet | 38.758 | 32.99 | 4.29 | 70.6 |
| CAGFNet | 38.573 | 32.42 | 5.7 | 497.71 |
| Model | Jacksonville | Omaha | Total Params (MB) | FLOPS (G) | ||
|---|---|---|---|---|---|---|
| EPE (Pixel) | D1 (%) | EPE (Pixel) | D1 (%) | |||
| Model Ⅰ (Feature Change) | 1.643 | 14.90 | 1.270 | 10.60 | 5.44 | 410.53 |
| Model Ⅱ (Cost Change) | 1.561 | 15.70 | 1.158 | 10.90 | 5.48 | 468.72 |
| Model Ⅲ (Drop 3DEMA) | 1.516 | 15.20 | 1.063 | 11.41 | 5.69 | 489.11 |
| Model Ⅳ (Drop Image Guide) | 1.532 | 15.32 | 1.062 | 11.01 | 5.22 | 423.82 |
| Model V(Drop Refinement) | 1.581 | 14.52 | 1.246 | 10.71 | 5.65 | 489.34 |
| PSMNet | 1.711 | 16.02 | 1.422 | 12.91 | 5.22 | 381.53 |
| CAGFNet | 1.466 | 14.72 | 0.996 | 10.51 | 5.70 | 497.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Ge, J.; Tian, S.; Xi, L. CAGFNet: A Cross-Attention Image-Guided Fusion Network for Disparity Estimation of High-Resolution Satellite Stereo Images. Remote Sens. 2025, 17, 1572. https://doi.org/10.3390/rs17091572
Zhang Q, Ge J, Tian S, Xi L. CAGFNet: A Cross-Attention Image-Guided Fusion Network for Disparity Estimation of High-Resolution Satellite Stereo Images. Remote Sensing. 2025; 17(9):1572. https://doi.org/10.3390/rs17091572
Chicago/Turabian StyleZhang, Qian, Jia Ge, Shufang Tian, and Laidian Xi. 2025. "CAGFNet: A Cross-Attention Image-Guided Fusion Network for Disparity Estimation of High-Resolution Satellite Stereo Images" Remote Sensing 17, no. 9: 1572. https://doi.org/10.3390/rs17091572
APA StyleZhang, Q., Ge, J., Tian, S., & Xi, L. (2025). CAGFNet: A Cross-Attention Image-Guided Fusion Network for Disparity Estimation of High-Resolution Satellite Stereo Images. Remote Sensing, 17(9), 1572. https://doi.org/10.3390/rs17091572







