Lossless Hyperspectral Image Compression in Comet Interceptor and Hera Missions with Restricted Bandwith
Abstract
1. Introduction
1.1. Comet Interceptor and Hera Missions
1.2. Legacy Image Compression Techniques
1.3. CCSDS 122.0
1.4. JPEG 2000
- Reversible Component Transform (RCT), used for both lossy and lossless compression modes. Implemented with the Le Gall–Tabatabai (LGT) 5/3 wavelet transform utilizing only integer coefficients, mitigating the effect of quantization noise (rounding).
- Irreversible Component Transform (ICT), used for the lossy compression mode. Implemented with the CDF 9–7 wavelet transform with quantization noise depending on the precision of the decoder.
2. Materials and Methods
2.1. Simulated Hyperspectral Test Data
2.2. CCSDS Implementation on EnVisS/OPIC DHU
2.3. JPEG 2000 Implementation on ASPECT DPU
2.4. Differential Encoding
2.5. Noise Filtering
2.6. Test Procedure
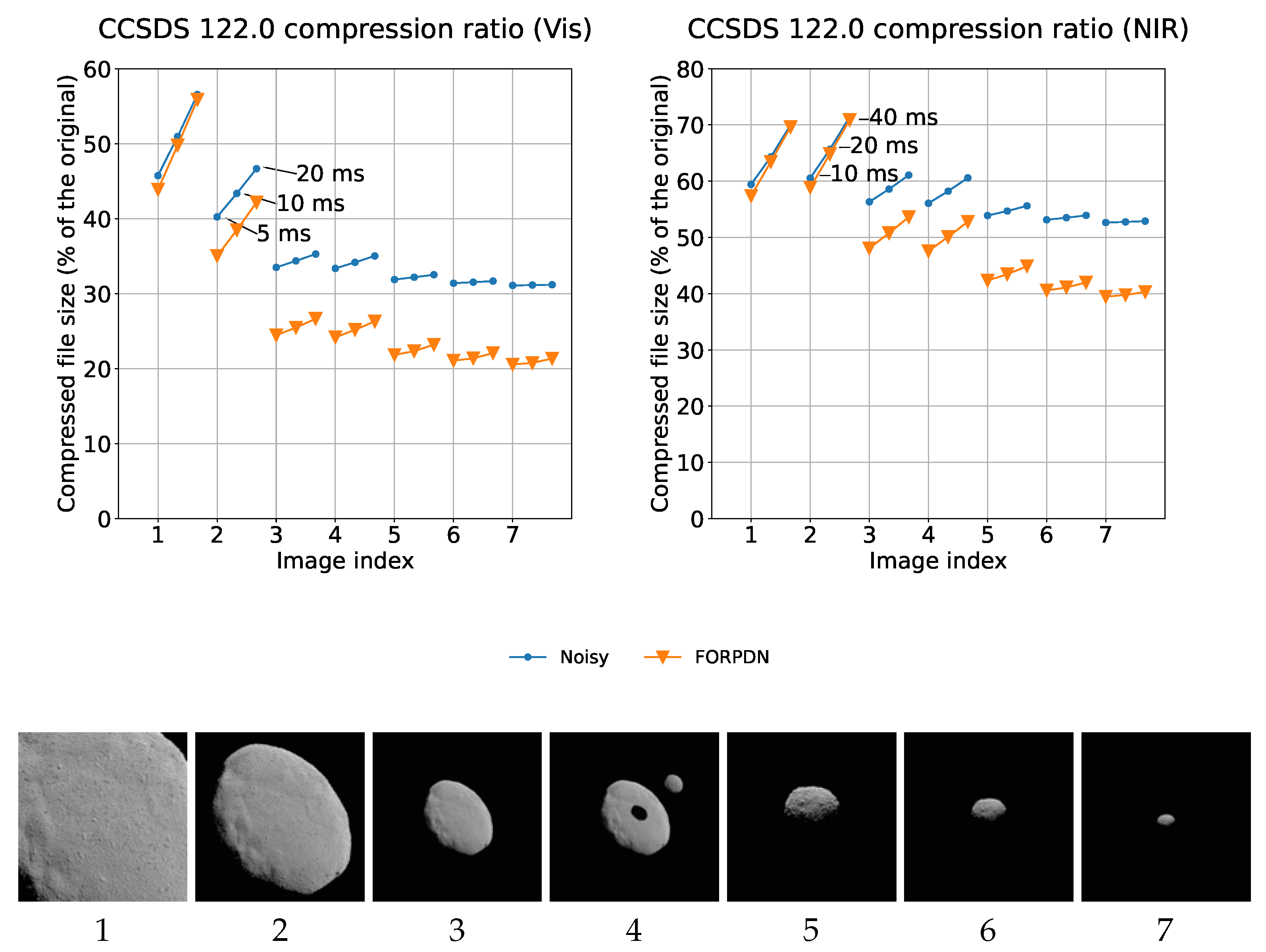
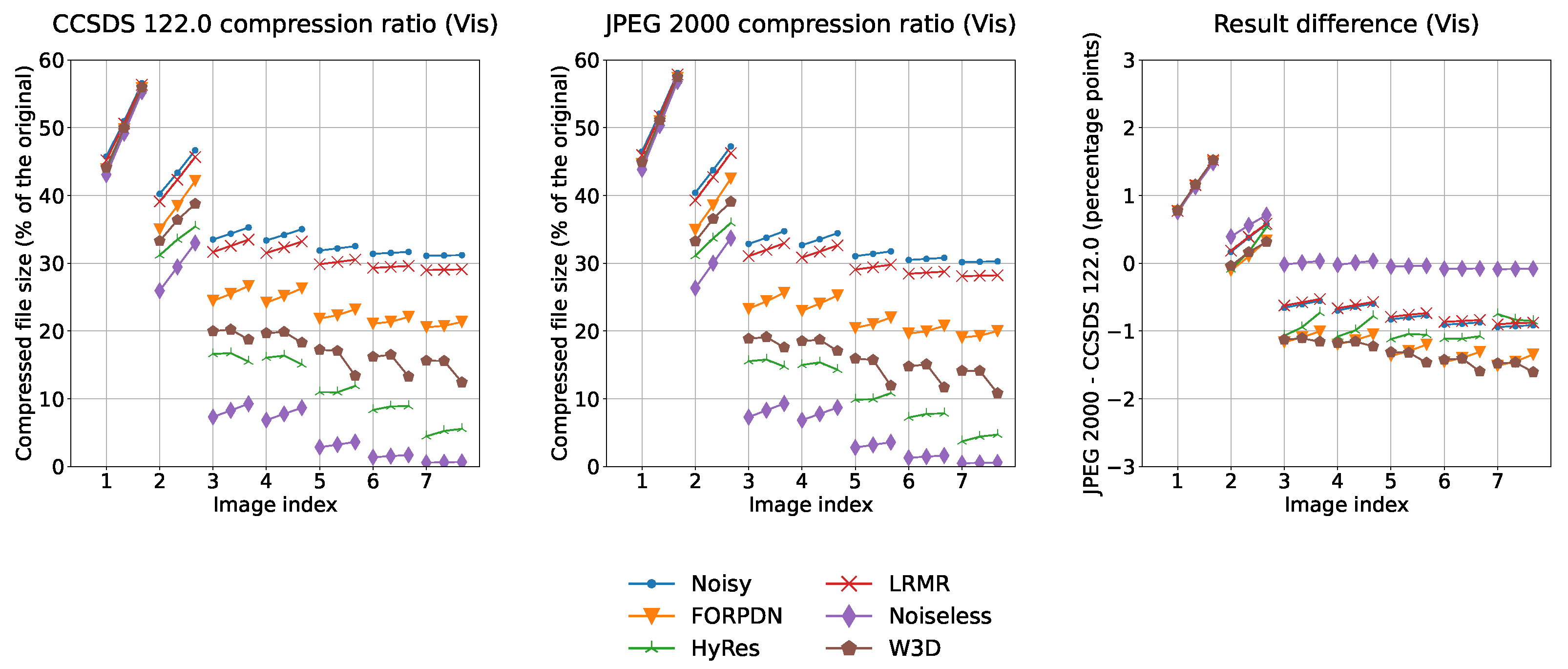
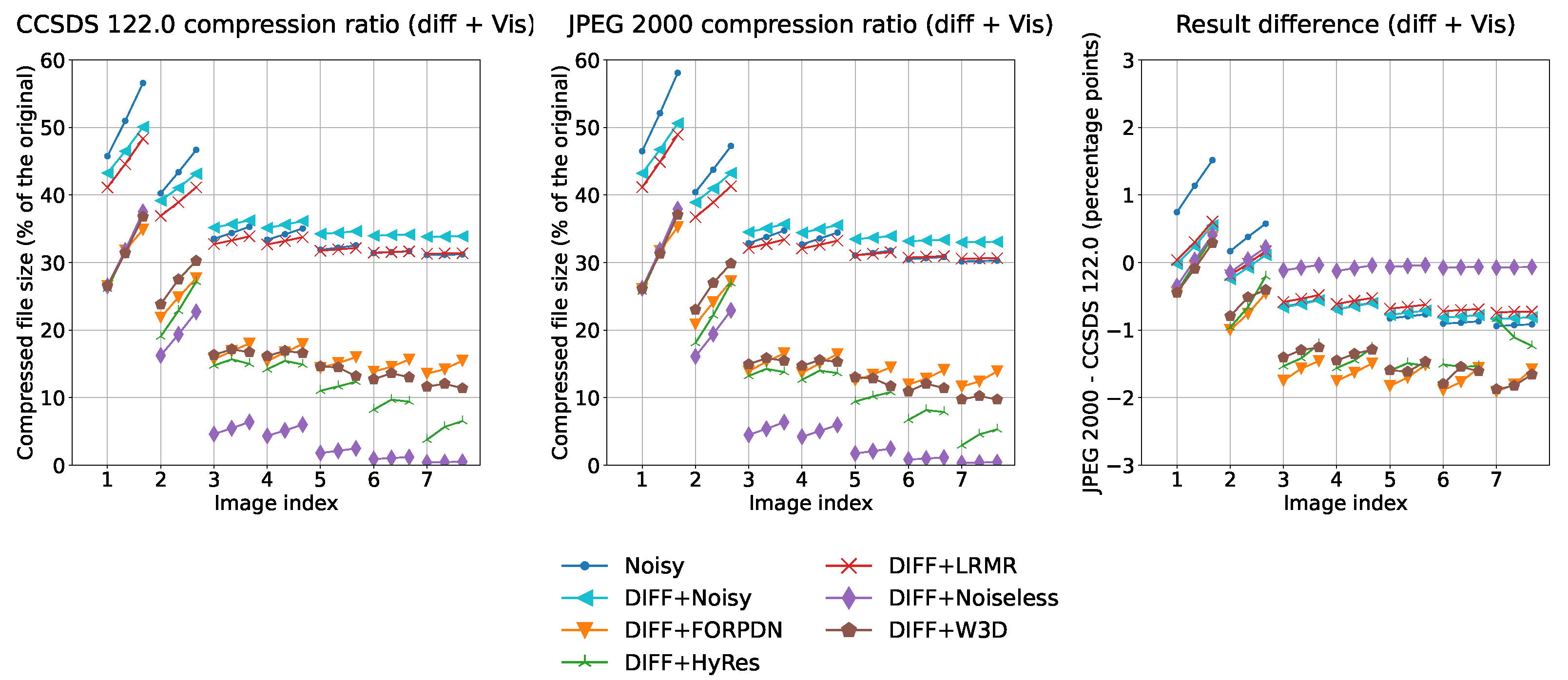
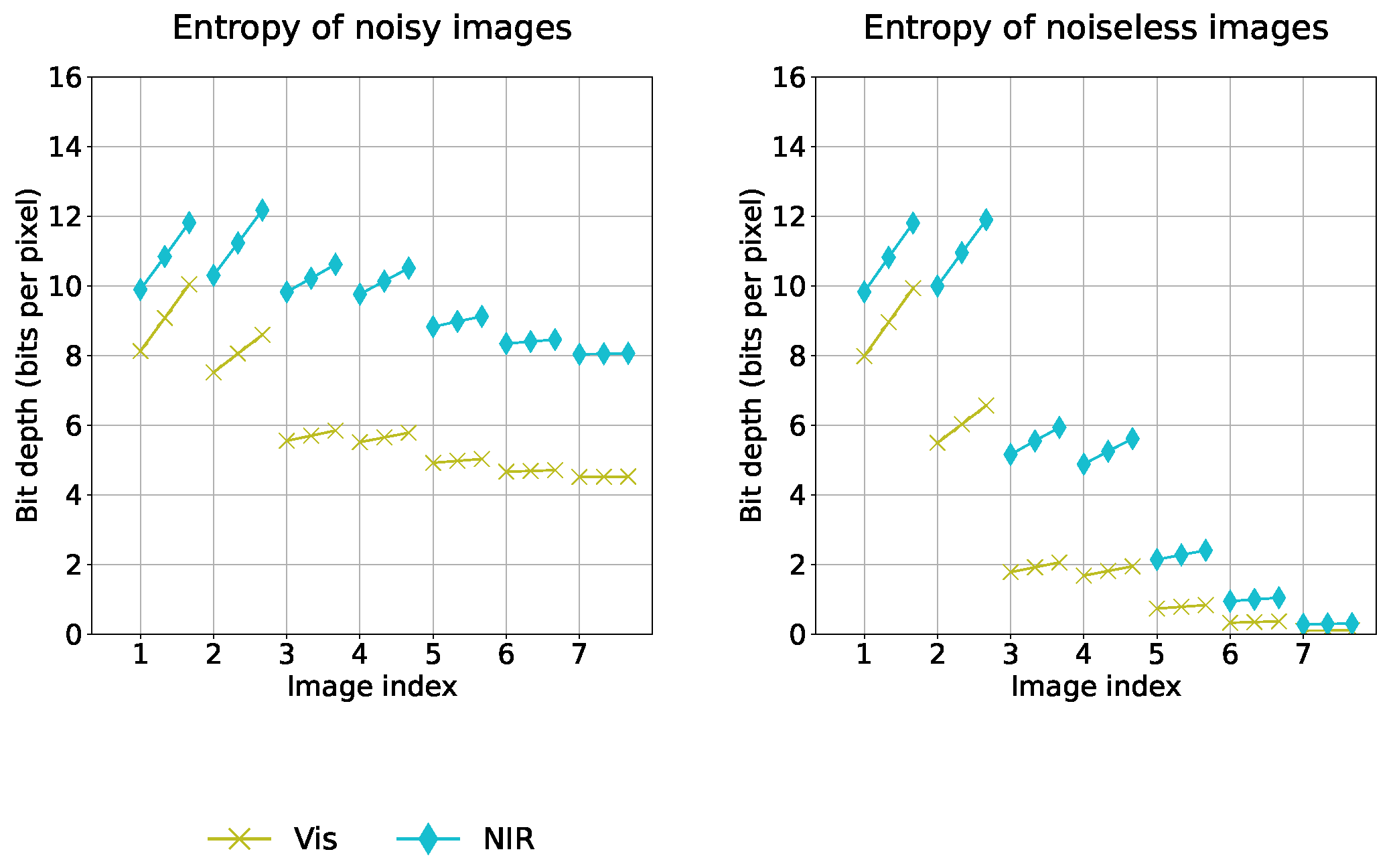
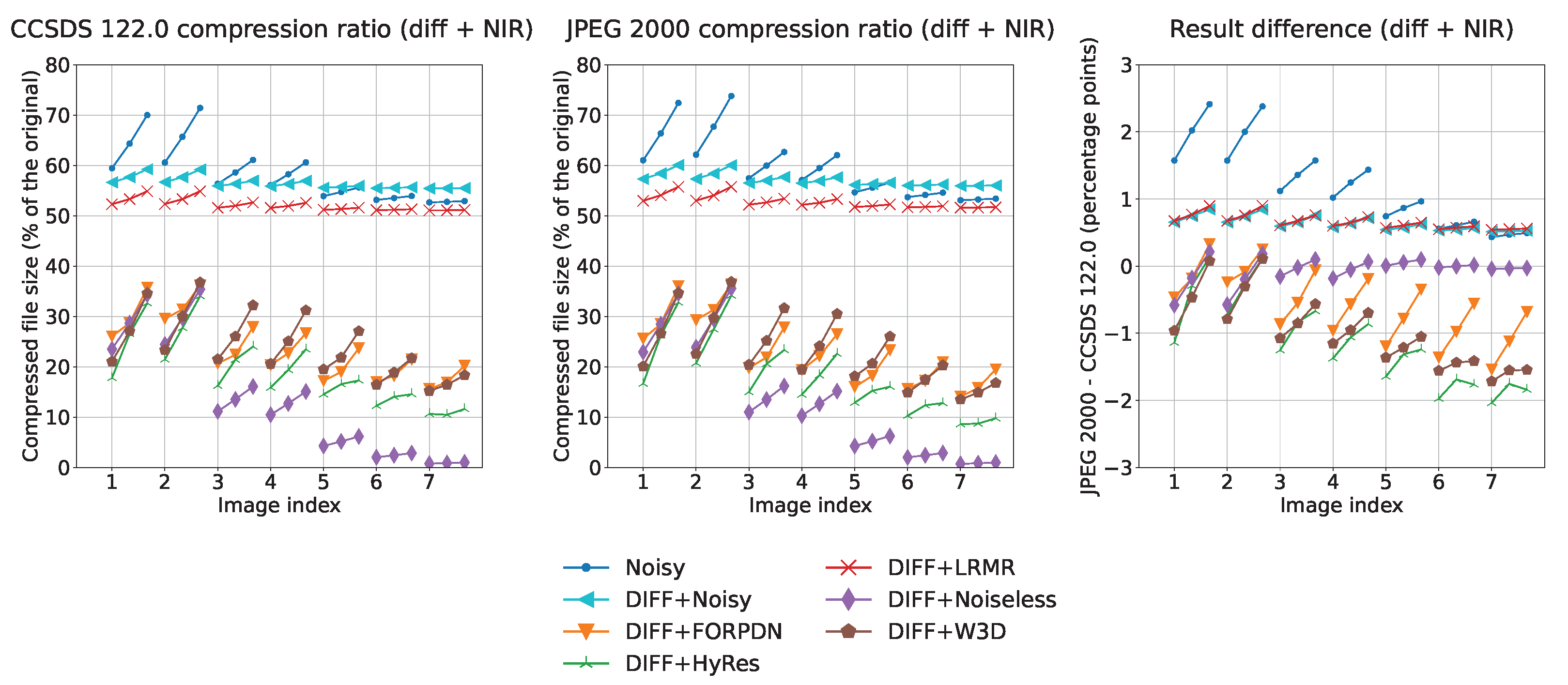
3. Results
4. Discussion
4.1. Interpretation of Results
4.2. Limitations and Future Prospects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ESA | European Space Agency |
| CI | Comet Interceptor |
| OPIC | Optical Periscopic Imager for Comets |
| EnVisS | Entire Visible Sky |
| ASPECT | Asteroid Spectral Imager |
| SP | Science Programme |
| FoV | Field of View |
| DHU | Data Handling Unit |
| MCU | Microcontroller Unit |
| S2P | Space Safety and Security Programme |
| DART | Double Asteroid Redirect Test |
| Vis | Visible |
| SWIR | Short-Wave Infrared |
| DPU | Data Processing Unit |
| DPCM | Differential Pulse-Code Modulation |
| SPOT | Satellite Pour l’Observation de la Terre |
| DCT | Discrete Cosine Transform |
| JPEG | Joint Photographic Experts Group |
| DWT | Discrete Wavelet Transform |
| CCSDS | Consultative Committee for Space Data Systems |
| CDF | Cohen–Daubechies–Feauveau |
| RCT | Reversible Component Transform |
| LGT | Le Gall–Tabatabai |
| ICT | Irreversible Component transform |
| EBCOT | Embedded Block Coding with Optimal Truncation Points |
| AIS | Asteroid Image Simulator |
| DN | Digital numbers |
| RAM | Random Access Memory |
| FORPDN | First Order Spectral Roughness Penalty Denoising |
| HyRes | Hyperspectral Restoration |
| LRMR | Low-Rank Matrix Recovery |
| SURE | Stein’s Unbiased Risk Estimator |
References
- Jones, G.H.; Snodgrass, C.; Tubiana, C.; Küppers, M.; Kawakita, H.; Lara, L.M.; Agarwal, J.; André, N.; Attree, N.; Auster, U.; et al. The Comet Interceptor mission. Space Sci. Rev. 2024, 220, 9. [Google Scholar] [CrossRef] [PubMed]
- Michel, P.; Küppers, M.; Bagatin, A.C.; Carry, B.; Charnoz, S.; De Leon, J.; Fitzsimmons, A.; Gordo, P.; Green, S.F.; Hérique, A.; et al. The ESA Hera mission: Detailed characterization of the DART impact outcome and of the binary asteroid (65803) Didymos. Planet. Sci. J. 2022, 3, 160. [Google Scholar] [CrossRef]
- Daly, R.; Ernst, C.; Barnouin, O.; Chabot, N.; Rivkin, A.; Cheng, A.; Adams, E.; Agrusa, H.; Abel, E.; Alford, A.; et al. Successful kinetic impact into an asteroid for planetary defence. Nature 2023, 616, 443–447. [Google Scholar] [CrossRef]
- Kohout, T.; Näsilä, A.; Tikka, T.; Granvik, M.; Kestilä, A.; Penttilä, A.; Kuhno, J.; Muinonen, K.; Viherkanto, K.; Kallio, E. Feasibility of asteroid exploration using CubeSats—ASPECT case study. Adv. Space Res. 2018, 62, 2239–2244. [Google Scholar] [CrossRef]
- Kumar, A.; Kumaran, R.; Paul, S.; Mehta, S. ADPCM Image Compression Techniques for Remote Sensing Applications. Int. J. Inf. Eng. Electron. Bus. 2015, 7, 26. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Lier, P.; Moury, G.A.; Latry, C.; Cabot, F. Selection of the SPOT5 image compression algorithm. In Earth Observing Systems III; SPIE: Bellingham, WA, USA, 1998; Volume 3439, pp. 541–552. [Google Scholar]
- Wallace, G.K. The JPEG still picture compression standard. IEEE Trans. Consum. Electron. 1992, 38, xviii–xxxiv. [Google Scholar] [CrossRef]
- McEwen, A.; Robinson, M. Mapping of the Moon by Clementine. Adv. Space Res. 1997, 19, 1523–1533. [Google Scholar] [CrossRef]
- Berghmans, D.; Hochedez, J.; Defise, J.; Lecat, J.; Nicula, B.; Slemzin, V.; Lawrence, G.; Katsyiannis, A.; Van der Linden, R.; Zhukov, A.; et al. SWAP onboard PROBA 2, a new EUV imager for solar monitoring. Adv. Space Res. 2006, 38, 1807–1811. [Google Scholar] [CrossRef]
- Kumar, G.; Brar, E.S.S.; Kumar, R.; Kumar, A. A review: DWT-DCT technique and arithmetic-Huffman coding based image compression. Int. J. Eng. Manuf. 2015, 5, 20. [Google Scholar] [CrossRef][Green Version]
- Zhang, D.; Zhang, D. Wavelet transform. In Fundamentals of Image Data Mining: Analysis, Features, Classification and Retrieval; Springer Nature: Berlin/Heidelberg, Germany, 2019; pp. 35–44. [Google Scholar]
- Boliek, M. JPEG2000 Part I Final Draft International Standard; (ISO/IEC FDIS15444-1), ISO/IEC JTC1/SC29/WG1 N1855; International Organization for Standardization: Geneva, Switzerland, 2000. [Google Scholar]
- Image Data Compression; Image Data Compression Blue Book; CCSDS Secretariat National Aeronautics and Space Administration: Washington, DC, USA, 2005.
- Vonesch, C.; Blu, T.; Unser, M. Generalized Daubechies wavelet families. IEEE Trans. Signal Process. 2007, 55, 4415–4429. [Google Scholar] [CrossRef]
- Perfetto, S.; Wilder, J.; Walther, D.B. Effects of spatial frequency filtering choices on the perception of filtered images. Vision 2020, 4, 29. [Google Scholar] [CrossRef] [PubMed]
- Adams, M.D.; Ward, R.K. JasPer: A portable flexible open-source software tool kit for image coding/processing. In Proceedings of the 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP 2004, Montreal, QC, Canada, 17–21 May 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 241–244. [Google Scholar] [CrossRef]
- ISO/IEC 15444-5:2003; Information Technology — JPEG 2000 Image Coding System: Reference Software Part 5. International Organization for Standardization: Geneva, Switzerland, 2003.
- Unser, M.; Blu, T. Mathematical properties of the JPEG2000 wavelet filters. IEEE Trans. Image Process. 2003, 12, 1080–1090. [Google Scholar] [CrossRef] [PubMed]
- Delaunay, X.; Chabert, M.; Charvillat, V.; Morin, G. Satellite image compression by post-transforms in the wavelet domain. Signal Process. 2010, 90, 599–610. [Google Scholar] [CrossRef]
- Daly, R.; Ernst, C.; Barnouin, O.; Gaskell, R.; Nair, H.; Agrusa, H.; Chabot, N.; Cheng, A.; Dotto, E.; Mazzotta Epifani, E.; et al. An Updated Shape Model of Dimorphos from DART Data. Planet. Sci. J. 2024, 5, 24. [Google Scholar] [CrossRef]
- de León, J.; Licandro, J.; Serra-Ricart, M.; Pinilla-Alonso, N.; Campins, H. Observations, compositional, and physical characterization of near-Earth and Mars-crosser asteroids from a spectroscopic survey. Astron. Astrophys. 2010, 517, A23. [Google Scholar] [CrossRef]
- Rasti, B.; Scheunders, P.; Ghamisi, P.; Licciardi, G.; Chanussot, J. Noise reduction in hyperspectral imagery: Overview and application. Remote. Sens. 2018, 10, 482. [Google Scholar] [CrossRef]
- Basuhail, A.A.; Kozaitis, S.P. Wavelet-based noise reduction in multispectral imagery. In Algorithms for Multispectral and Hyperspectral Imagery IV; SPIE: Bellingham, WA, USA, 1998; Volume 3372, pp. 234–240. [Google Scholar]
- Rasti, B.; Sveinsson, J.R.; Ulfarsson, M.O.; Benediktsson, J.A. Hyperspectral image denoising using first order spectral roughness penalty in wavelet domain. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2013, 7, 2458–2467. [Google Scholar] [CrossRef]
- Rasti, B.; Sveinsson, J.R.; Ulfarsson, M.O.; Sigurdsson, J. First order roughness penalty for hyperspectral image denoising. In Proceedings of the 2013 5th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Gainesville, FL, USA, 26–28 June 2013; pp. 1–4. [Google Scholar]
- Rasti, B.; Ulfarsson, M.O.; Ghamisi, P. Automatic Hyperspectral Image Restoration Using Sparse and Low-Rank Modeling. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 2335–2339. [Google Scholar] [CrossRef]
- Zhang, H.; He, W.; Zhang, L.; Shen, H.; Yuan, Q. Hyperspectral image restoration using low-rank matrix recovery. IEEE Trans. Geosci. Remote. Sens. 2013, 52, 4729–4743. [Google Scholar] [CrossRef]
- Rasti, B.; Koirala, B.; Scheunders, P.; Ghamisi, P. How hyperspectral image unmixing and denoising can boost each other. Remote. Sens. 2020, 12, 1728. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Ulfarsson, M.O.; Sveinsson, J.R. Sure based convolutional neural networks for hyperspectral image denoising. In Proceedings of the IGARSS 2020–2020 IEEE International Geoscience and Remote Sensing Symposium, IEEE, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 1784–1787. [Google Scholar]
- Coquelin, D.; Rasti, B.; Götz, M.; Ghamisi, P.; Gloaguen, R.; Streit, A. Hyde: The first open-source, python-based, gpu-accelerated hyperspectral denoising package. In Proceedings of the 2022 12th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), IEEE, Rome, Italy, 13–16 September 2022; pp. 1–5. [Google Scholar]
- Zabala, A.; Vitulli, R.; Pons, X. Impact of CCSDS-IDC and JPEG 2000 Compression on Image Quality and Classification. J. Electr. Comput. Eng. 2012, 2012, 761067. [Google Scholar] [CrossRef]
- Indradjad, A.; Nasution, A.S.; Gunawan, H.; Widipaminto, A. A comparison of Satellite Image Compression methods in the Wavelet Domain. IOP Conf. Ser. Earth Environ. Sci. 2019, 280, 012031. [Google Scholar] [CrossRef]
- Palsson, B.; Sigurdsson, J.; Sveinsson, J.R.; Ulfarsson, M.O. Hyperspectral Unmixing Using a Neural Network Autoencoder. IEEE Access 2018, 6, 25646–25656. [Google Scholar] [CrossRef]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Sparse Unmixing of Hyperspectral Data. IEEE Trans. Geosci. Remote. Sens. 2011, 49, 2014–2039. [Google Scholar] [CrossRef]
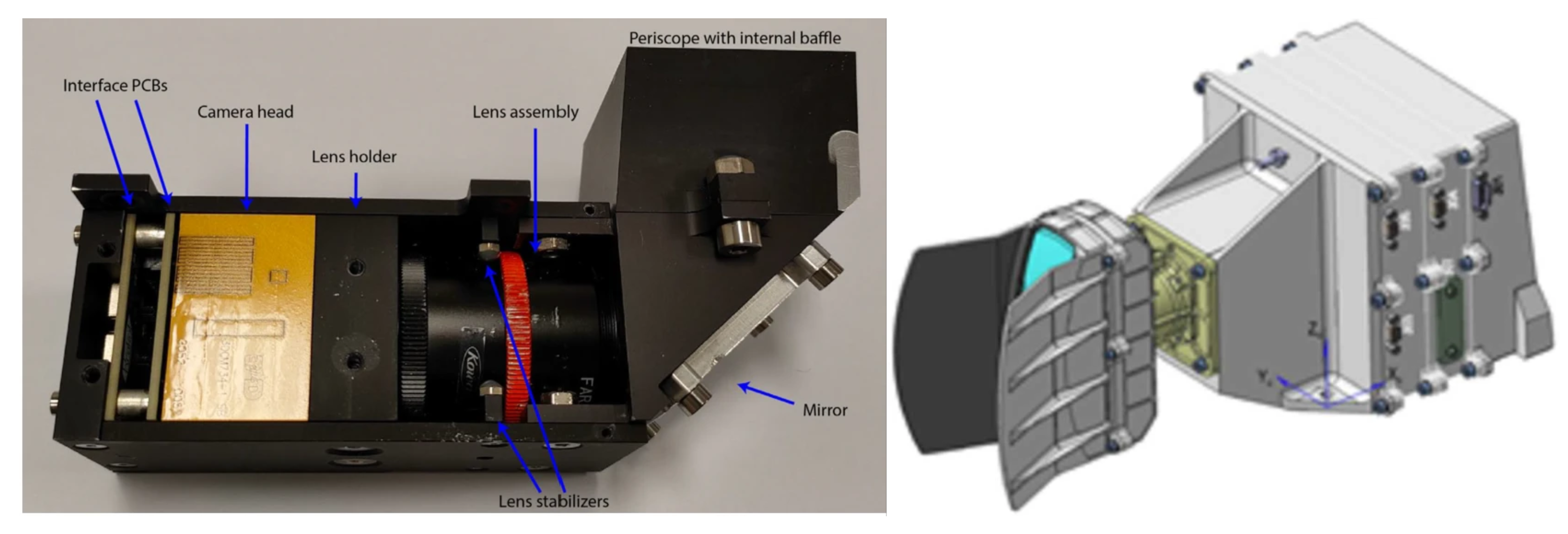







| Parameter | VIS Channel | NIR1 Channel | NIR2 Channel | SWIR Channel |
|---|---|---|---|---|
| Field of view (deg) | 10° × 10° | 6.7° × 5.4° | 6.7° × 5.6° | 5.85° circular |
| Spectral range (nm) | 650–900 | 850–1250 | 1200–1600 | 1650–2500 |
| Image size (px) | 1 pixel | |||
| No. spectral bands | 14 | 14 | 14 | 30 |
| Spectral resolution (nm) | <30 | <40 | <40 | <45 |
| Algorithm | Image Set | Min (ms) | Max (ms) | Mean (ms) |
|---|---|---|---|---|
| CCSDS 122.0 | Vis | 20 | 327 | 159 |
| Vis+diff | 18 | 314 | 143 | |
| NIR | 7 | 130 | 74 | |
| NIR+diff | 6 | 124 | 54 | |
| JPEG 2000 | Vis | 66 | 442 | 203 |
| Vis+diff | 64 | 382 | 182 | |
| NIR | 24 | 159 | 97 | |
| NIR+diff | 21 | 136 | 72 |
| Algorithm | Image Set | Min (KB) | Max (KB) | Mean (KB) |
|---|---|---|---|---|
| CCSDS 122.0 | Vis | 6765 | 6765 | 6765 |
| Vis+diff | 6765 | 6765 | 6765 | |
| NIR | 2124 | 2124 | 2124 | |
| NIR+diff | 2124 | 2124 | 2124 | |
| JPEG 2000 | Vis | 3426 | 3695 | 3570 |
| Vis+diff | 3409 | 3695 | 3521 | |
| NIR | 2001 | 2264 | 2214 | |
| NIR+diff | 1966 | 2263 | 2116 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skog, K.; Kohout, T.; Kašpárek, T.; Penttilä, A.; Wolfmayr, M.; Praks, J. Lossless Hyperspectral Image Compression in Comet Interceptor and Hera Missions with Restricted Bandwith. Remote Sens. 2025, 17, 899. https://doi.org/10.3390/rs17050899
Skog K, Kohout T, Kašpárek T, Penttilä A, Wolfmayr M, Praks J. Lossless Hyperspectral Image Compression in Comet Interceptor and Hera Missions with Restricted Bandwith. Remote Sensing. 2025; 17(5):899. https://doi.org/10.3390/rs17050899
Chicago/Turabian StyleSkog, Kasper, Tomáš Kohout, Tomáš Kašpárek, Antti Penttilä, Monika Wolfmayr, and Jaan Praks. 2025. "Lossless Hyperspectral Image Compression in Comet Interceptor and Hera Missions with Restricted Bandwith" Remote Sensing 17, no. 5: 899. https://doi.org/10.3390/rs17050899
APA StyleSkog, K., Kohout, T., Kašpárek, T., Penttilä, A., Wolfmayr, M., & Praks, J. (2025). Lossless Hyperspectral Image Compression in Comet Interceptor and Hera Missions with Restricted Bandwith. Remote Sensing, 17(5), 899. https://doi.org/10.3390/rs17050899







