Sparse Regularization Least-Squares Reverse Time Migration Based on the Krylov Subspace Method

Abstract

Least-squares reverse time migration (LSRTM) is an advanced seismic imaging technique that reconstructs subsurface models by minimizing the residuals between simulated and observed data. Mathematically, the LSRTM inversion of the sub-surface reflectivity is a large-scale, highly ill-posed sparse inverse problem, where conventional inversion methods typically lead to poor imaging quality. In this study, we propose a regularized LSRTM method based on the flexible Krylov subspace inversion framework. Through the strategy of the Krylov subspace projection, a basis set for the projection solution is generated, and then the inversion of a large ill-posed problem is expressed as the small matrix optimization problem. With flexible preconditioning, the proposed method could solve the sparse regularization LSRTM, like with the Tikhonov regularization style. Sparse penalization solution is implemented by decomposing it into a set of Tikhonov penalization problems with iterative reweighted norm, and then the flexible Golub–Kahan process is employed to solve the regularization problem in a low-dimensional subspace, thereby finally obtaining a sparse projection solution. Numerical tests on the Valley model and the Salt model validate that the LSRTM based on Krylov subspace method can effectively address the sparse inversion problem of subsurface reflectivity and produce higher-quality imaging results.

1. Introduction

Seismic migration is a crucial technology for subsurface imaging. It generates subsurface reflectivity images by repositioning recorded seismic reflections to their original locations. In recent years, with the continuous advancement in computational power, migration methods have also been continuously developing. Traditional migration methods often have difficulty achieving precise subsurface imaging, particularly in complex geological settings. Reverse time migration (RTM), utilizing the two-way wave equation for wavefield propagation, is initially proposed and studied in the early 1980s [1,2,3]. Compared to ray-based or single-wave equation methods, RTM method is an advanced seismic imaging technique. By utilizing the full wavefield information, RTM is capable of handling complex subsurface velocity models as well as intricate wave phenomena such as multiple reflections, diffractions, and refractions, thereby producing high resolution images of subsurface structures. However, RTM imaging results commonly encounter several issues, including artifacts, incomplete illumination, and low-frequency noise. Traditional RTM algorithms use the adjoint of the linearized wave equation rather than its inverse. To overcome some of the limitations of RTM, several methods have been proposed, such as two-dimensional Laplacian filters, wavefield separation methods, inverse scattering imaging conditions, artifact-removal techniques, and wavefield compensation techniques [4,5,6,7,8]. Guo et al. proposed a hybrid wave separation workflow based on the wave equation (data-domain and model-domain) [9], which effectively generates seismic images with improved resolution and fewer artifacts. Lyu and Nakata utilized a geometric mean RTM to further optimize passive seismic imaging problems [10]. And, various compensation methods during the computational process have also been proposed to further optimize RTM [11,12]. Furthermore, least-squares reverse time migration (LSRTM) is another effective technique for improving the quality of RTM imaging. LSRTM builds upon RTM by incorporating least-squares migration (LSM) [13]. Through iterative resolution of the least-squares optimization problem, LSRTM progressively reduces errors in the imaging process [14] and continuously approximates the inverse modeling operator. This enables higher resolution, artifact suppression, mitigation of cross-talk noise, and improved amplitude recovery, ultimately producing more accurate imaging results.

Commonly, LSRTM includes the image-domain methods and the data-domain methods. Imaging-domain LSRTM is generally considered to calculate the Hessian matrix explicitly, and deblurring the imaging space by inverting the Hessian matrix. Another method is the data-domain approach. Data-domain LSRTM utilizes reflection data and employs least-squares migration (LSM) as the inversion framework to construct the physical model, where the LSM framework can also be used in full-waveform inversion (FWI) [15]. Instead of migrating the seismic gather once in the conventional migration, data-domain LSRTM migrates the data multiple to improve the fidelity of the reconstruction. By reducing the misfit between the observation and modeling data, the means of inversion, the LSRTM could improve the seismic imaging result greatly when the subsurface becomes more complex [13]. Therefore, LSRTM is one of the technical issues that the industry is concentrating its efforts the most [16]. Not only on primary waves, LSRTM also has good effects on multiple wave imaging. In addition to the acoustic wave equation-based LSRTM for marine seismic exploration, the elastic wave equation-based LSRTM has also developed, especially for land seismic exploration [14,17,18,19]. Furthermore, the attenuation-medium-based LSRTM advances its application in reservoir evaluation and AVO analysis [17,20]. As geological exploration moves towards more complex underground media, there are also more studies on LSRTM in the anisotropic media [21,22,23].

However, the high computational cost of LSRTM is a constraining factor. As each iteration of LSRTM requires a migration operator and its adjoint operator, which means that it needs to numerically solve the partial differential equation twice, its calculation burden is cumbersome. Therefore, improving computational efficiency is a problem for the broader applications of LSRTM. An effective method is to perform source encoding and combine multiple shot gathers into a super shot gather according to its time shift, phase, and polarity [24]. However, in this case, direct imaging will bring migration artifacts due to crosstalk noise caused by mutual interference between different shot gathers. Additionally, LSRTM inversion often encounters difficulties with convergence and inversion instability. So, introducing regularized term into the inversion, or inversion with prior information constraints, is one of the ways to improve the LSRTM inversion results [15,25]. Dai et al. introduce regularization terms into LSRTM [26], demonstrating that appropriate regularization effectively improves the convergence of LSRTM and enhances imaging quality within the same iterations [27]. Traditional Tikhonov regularization imposes an L2 norm constraint, which effectively suppresses high-frequency noise and enhances inversion stability. However, it tends to smooth the imaging results, reducing the resolution of fine structures. In contrast, sparse regularization employs an L1 norm constraint, which maintains imaging stability while enhancing the sparse representation of subsurface structures [28,29], thereby improving imaging clarity and resolution [30]. Dutta et al. impose a sparsity constraint on the local Radon domain reflectivity, which mitigates artifacts and noise, thereby improving the imaging quality [31]. Additionally, a sparse LSRTM method using seislets as the basis for the reflectivity distribution is proposed to solve the reflectivity coefficient problem [14]. Zand et al. introduce a sparse LSRTM inversion based on a Bregmanized operator splitting algorithm, which enhanced image resolution [32]. Then, a combined regularization method for LSRTM inversion is employed, enabling high-quality estimation of the reflectivity model [33]. In addition, methods for determining the regularization parameter include empirical selection, the L-curve method [34], and the generalized cross-validation (GCV) criterion [35], which is considered an adaptive selection method.

The LSRTM inversion of subsurface reflectivity is a large scale ill-posed inverse problem, and conventional LSRTM methods typically struggle to achieve high-quality imaging results. Krylov subspace method can be used to solve such large scale ill-posed inverse problems. The core idea of Krylov subspace method is to generate a subspace of increasing dimension and search for an approximate solution within that subspace. By iteratively constructing lower-dimensional problems and solving them within lower-dimensional subspaces. Key features of Krylov subspace method include avoiding the explicit solution of large matrix equations, making them suitable for sparse problems, and typically achieving convergence in a small number of iterations. Morikuni et al. propose a fixed inner iteration method combined with Krylov subspace method to solve least-squares problems [36]. Gazzola et al. introduce the use of flexible Krylov methods for image reconstruction problems, resulting in improved reconstruction performance [37]. Recently, there has been considerable research on improving Krylov subspace theory and related imaging applications for solving large-scale inverse problems from 2019 to 2024 [38,39,40,41,42]. In this study, we propose a novel LSRTM inversion method, which is based on the flexible Krylov subspace approach for regularized projection. By leveraging Krylov subspace strategies, a basis set for the solution is generated, thereby transforming a large ill-posed problem into a small matrix optimization problem. Then, we combine this with a hybrid strategy and the flexible Golub–Kahan bidiagonalization algorithm (FGK) and achieve Krylov inversion with Tikhonov regularization. The method, through flexible preconditioning, effectively handles sparse regularization in LSRTM. Finally, the efficacy of the LSRTM based on Krylov subspace method is validated through numerical tests on Valley and Salt models.

In Section 2 we discuss the setup and background of the LSRTM problem, including the theory and regularization concepts, as well as the flexible Krylov subspace method used for LSRTM inversion. In Section 3, we apply the proposed sparse LSRTM based on Krylov subspace method for imaging tests. Finally, in Section 4 and Section 5, we present a discussion of the application of the LSRTM based on Krylov subspace method and summarize our research findings.

2. Methods

2.1. Least-Squares Reverse Time Migration

In general, LSM updates imaging results by fitting observation data d_obs and modeling data. For the unconstrained LSM, the inversion problem could be expressed as

$$\underset{\mathbf{m}}{\mathrm{arg\; min}}{‖{\mathbf{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}-\mathbf{L}\mathbf{m}‖}_2^2,$$

(1)

where L denotes the Born approximation modeling operator, m denotes the imaging space, the subscript 2 refers to the norm L2, and the superscript 2 refers to the square of the norm. The relationship between the imaging space m and the data d can be written as

$$\mathbf{m}={\mathbf{L}}^{\ast }\mathbf{d},$$

(2)

$$\mathbf{d}=\mathbf{L}\mathbf{m},$$

(3)

where ${\mathbf{L}}^{\ast }$ is the adjoint migration operator of $\mathbf{L}$. When the RTM and RTM-based demigration operators are implemented in the LSM, the problem turns to the LSRTM.

The least-squares solution of Equation (1) is ${\mathbf{m}}_{\mathrm{l}\mathrm{s}}={\left(\mathbf{H}\right)}^{-1}{\mathbf{L}}^{\ast }{\mathbf{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}$, where $\mathbf{H}={\mathbf{L}}^{\ast }\mathbf{L}$ is named as Hessian matrix with the function of blurring [43]. Thus, ${\left(\mathbf{H}\right)}^{-1}$ has the function of deblurring which eliminates the influence of wavelets [44,45]. However, the condition number of the Hessian matrix $\mathbf{H}$ generated by solving the imaging space with least-squares solution is quite large, and the ill-posedness of ${\left(\mathbf{H}\right)}^{-1}$ is more serious compared to L. Meanwhile, solving the inverse of the large-scale matrix ${\left(\mathbf{H}\right)}^{-1}$ is difficult. In practice, the inverse of H is not directly found, but the gradient of the model to the data is calculated indirectly to solve Equation (1).

Usually, Equation (1) is solved by a gradient algorithm, such as the steepest descent algorithm. The direction of the inversion iteration accords with the minus of the gradient model to data, and the updated amount of the iteration is controlled by the step of the inversion. When the maximum number of iterations is reached or the data error is less than a certain small value, the update is terminated, since the observation data d_obs will inevitably have small errors, such as instrumentation errors, data processing, and interpretation errors, etc. These small errors may be amplified by the fact that the matrix decomposition results contain very small singular values, which may affect the accuracy of the imaging results or even cause the iteration not to converge after a certain number of iterations. So, in order to enhance the imaging accuracy, improve the convergence, and obtain a robust solution for the LSRTM, the additional regularization terms are introduced into the Equation (1) to constrain the model space. The regularization term can convert the non-well-posed attributes of the Equation (1) into a relatively well-posed problem, avoid the amplification of such small errors described above during the iteration process, and improve the stability of the model solution, which can be written as

$$\underset{\mathbf{m}}{\mathrm{arg\; min}} \lambda {‖{\mathbf{W}}_{\mathbf{m}}\left(\mathbf{m}-{\mathbf{m}}_0\right)‖}_p^p+{‖{\mathbf{W}}_{\mathbf{d}}\left({\mathbf{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}-\mathbf{L}\mathbf{m}\right)‖}_2^2,$$

(4)

where W_d and W_m are the weighted matrices for the data and model space, respectively. m₀ denotes the prior information of the model, λ is the tradeoff parameter that balances the penalization of the model and misfit of the data domain, and p is the norm order for the model space. For p = 2, Equation (4) turns to the standard Tikhonov regularization problem, and the solution towards a smooth result, avoids the overfitting, and becomes more stable. For p = 1, Equation (4) turns into the sparse regularization problem. The subsurface reflectivity model is commonly considered the sparse space; thus, the sparse regularization could work well in the LSRTM. L1-norm LSRTM could obtain a sparse imaging model otherwise the smooth imaging model. Also, by reducing the size of the imaging space, the L1-norm constraints can guide the solution of the inverse problem to converge to the desired result. If there is no weight on the data and the model space, this means that W_d = I and W_m = I, and, if the initial imaging result is not available, the problem turns to

$$\underset{\mathbf{m}}{\mathrm{arg\; min}} \lambda {\left|\left|\mathbf{m}\right|\right|}_1+{‖{\mathbf{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}-\mathbf{L}\mathbf{m}‖}_2^2,$$

(5)

Equation (5) is a typical mixed model-constraint L1 and data-fitting L2 norm optimization problem, which leads to a sparse model space resolution. The sparse regularization of Equation (5) will alleviate the non-convexity of optimization problems in the process of solving LSRTM or full waveform inversion (FWI) problems [27]. The FISTA algorithm [46] is a method for solving optimization Equation (5) with sparse solution. In each iteration, the FISTA method computes a gradient and performs a linear update with momentum acceleration, followed by a soft-thresholding operation to ensure the sparsity of the solution.

2.2. Krylov Subspace Inversion Method for LSRTM

The Krylov subspace iteration method is a mathematical algorithm used in linear algebra to solve large systems of linear equations. Based on the idea of Krylov subspace, the large-scale inverse problem could be solved by an iterative style in a reasonable subspace, especially if the matrix is indefinite and ill-posed.

For the optimization Equation (1), the order-r Krylov subspace ${\mathcal{K}}_r$ could be expressed as

$${\mathbf{d}}_0={\mathbf{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}-\mathbf{L}\mathbf{m},$$

(6)

$${\mathcal{K}}_r\left({\mathbf{L}}^{\mathit{*}}\mathbf{L},{{\mathbf{L}}^{\mathit{*}}\mathbf{d}}_0\right)=span\left\{{\mathbf{L}}^{\mathit{*}}{\mathbf{d}}_0,\left({\mathbf{L}}^{\mathit{*}}\mathbf{L}\right){\mathbf{L}}^{\mathit{*}}{\mathbf{d}}_0,{{(\mathbf{L}}^{\mathit{*}}{\mathbf{L})}^2\mathbf{L}}^{\mathrm{*}}{\mathbf{d}}_0,\dots ,{{(\mathbf{L}}^{\mathit{*}}\mathbf{L})}^{r-1}{\mathbf{L}}^{\mathit{*}}{\mathbf{d}}_0\right\},$$

(7)

where span denotes the set of vectors that are combined into a Krylov space.

For the Krylov subspace, a set of unit orthogonal vectors ${\mathbf{V}}_r=\left[{\mathbf{v}}_1\dots {\mathbf{v}}_r\right]$ and a Hessenberg matrix H_r can be constructed by the Arnoldi approach [42,47]. The Arnoldi process constructs an orthonormal basis for the Krylov subspace by iteratively processing the current basis vectors and enforcing orthogonality using the Gram–Schmidt process (Appendix A,

Table A1. Decomposition process of the Arnoldi method.

(1) Choose a vector ${\mathbf{v}}_1$ (2) For $j=1,\dots ,r$ do: (3)   Compute $h_{ij}=({\mathbf{L}}^{\ast }{\mathbf{v}}_j,{\mathbf{v}}_i)$ for $i=\mathrm{1,2},\dots ,j$ (4)   Compute ${\mathbf{w}}_j={\mathbf{L}}^{\mathit{*}}{\mathbf{v}}_j-\sum _{i=1}^j h_{ij}{\mathbf{v}}_i$ (5)   $h_{j+1,j}=\parallel {\mathbf{w}}_{j }{\parallel }_2$ (6)   If $h_{j+1,j}=0$ then Stop (7)   ${\mathbf{v}}_{j+1}={\mathbf{w}}_j/h_{j+1,j}$ (8) End do Through the above loop calculation, the orthogonal vector ${\mathbf{V}}_r=\left[{\mathbf{v}}_1\dots {\mathbf{v}}_r\right]$ can be obtained.

), so that the following equation holds:

$$\mathbf{L}{\mathbf{V}}_r={\mathbf{V}}_{r+1}{\mathbf{H}}_r,$$

(8)

Let $\beta ={\left|\left|{\mathbf{d}}_0\right|\right|}_2$, ${\mathbf{v}}_1={\displaystyle \frac{{\mathbf{d}}_0}{\beta }}$, and ${\mathbf{e}}_1={\left[\mathrm{1,0},\dots ,0\right]}^T$, based on the orthogonality of the vectors ${\mathbf{V}}_r$, the Equation (1) converts into

$${\mathbf{y}}_r=\mathrm{a}\mathrm{r}\mathrm{g}\underset{\mathbf{y}}{ \min }{ ‖{\mathbf{H}}_r\mathbf{y}-\beta {\mathbf{e}}_1‖}_2^2,$$

(9)

Here, the transformation process above solves the optimization problem by projecting it to a smaller subspace via the Krylov method, replacing the original forward modeling operator L with the more regular Hessenberg matrix H_r. To improve the accuracy of the Krylov subspace method in solving inversion problems, we only need to increase order-r. Theoretically when order-r is infinite, this method can be infinitely close to the real solution, but of course, the amount of calculation will also increase as order-r increases.

For sparse regularization optimization problem, it is difficult to solve it directly in the Krylov subspace. Therefore, we decompose the L1-norm constrained problem into the series of L2-norm constrained problems through the adaptive regularization matrix. Then, the Equation (5) is transformed into an iteratively preconditioned weighted Tikhonov regularization problem as follows [48]

$$\underset{\mathbf{m}}{\mathrm{arg\; min}}\lambda {‖{\mathbf{W}}_r\mathbf{m}‖}_2^2+{‖{\mathbf{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}-\mathbf{L}\mathbf{m}‖}_2^2,$$

(10)

where ${\mathbf{W}}_r=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\right(f_{\tau }\left(\right[\left|\mathbf{m}\right|{]}_i{)}^{\frac{p-2}{2}}{)}_{i=1,\dots ,n})$, $p$ is the order of the norm in the L$p$—regularization term, and $f_{\tau }([|\mathbf{m}|{]}_i)=\left\{\begin{array}{l}\left[\right|\mathbf{m}|{]}_i \mathrm{if} [\left|\mathbf{m}\right|{]}_i\ge {\tau }_1\\ {\tau }_2 \mathrm{if} \left[\right|\mathbf{m}|{]}_i<{\tau }_1 \end{array}\right., {\tau }_1$ and ${\tau }_2$ are small thresholds. The operator ${\mathbf{W}}_r$ is updated with the iterative calculation of the model space. For the Krylov-Tikhonov inversion process, the iteration number k can be used as a regularization parameter to participate in smooth regularization, which makes the solution avoid overfitting.

If ${\mathbf{W}}_r=\mathbf{I}$, Equation (10) turns to the standard Tikhonov–Krylov optimization problem as

$$\underset{\mathbf{m}}{\mathrm{arg\; min}} \lambda {‖\mathbf{m}‖}_2^2+{‖{\mathbf{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}-\mathbf{L}\mathbf{m}‖}_2^2.$$

(11)

In the same manner as the derivation of Equation (9), the Equation (11) can be solved by the following equation according to the orthogonal characteristic of ${\mathbf{V}}_r$. For the Equation (11), it is equivalent to solving the following problem:

$${\mathbf{y}}_r=\mathrm{a}\mathrm{r}\mathrm{g}\underset{\mathbf{y}}{ \min } \left\{{\lambda {‖\mathbf{y}‖}_2^2+‖{\mathbf{H}}_r\mathbf{y}-\beta {\mathbf{e}}_1‖}_2^2\right\}.$$

(12)

Equation (12) is the standard Tikhonov inversion in the Krylov subspace. The r-th iteration solution of Equation (12) is ${{\mathbf{m}}_r=\mathbf{V}}_r{\mathbf{y}}_r$.

For ${\mathbf{W}}_r\ne \mathbf{I}$, the Equation (10) with the variable-preconditioned Tikhonov problem could be solved by hybrid approaches based on the Golub–Kahan bidiagonalization algorithm [49]. This method requires operator L and its adjoint operator L* to design the iterative process. For LSRTM, the L denotes the modeling operator that reconstructs data from the reflectivity model, and the L* denotes the adjoint operator that images the subsurface space. Here, solving the objective function with L1-norm constraints is transformed from n-dimensional to an r-dimensional problem, and the sparse effects of the L1-norm is transferred to the weighted L2-norm. By projecting to the Krylov subspace, the implicit modeling operator L maps approximately to a low-dimensional Hessenberg matrix M_r. To better regularize the inversion, the flexible Golub–Kahan (FGK) method is proposed to solve sparse regularization by incorporating the weighted matrix, which makes the expensive regularization parameter selection techniques be avoided [42]. Its algorithm process is described as follows:

For the Krylov subspace about the seismic modeling operator $\mathbf{L}$, let ${\mathbf{u}}_1={\displaystyle \frac{{\mathbf{d}}_0}{\beta }}$, where $\beta =\parallel {\mathbf{d}}_0{\parallel }_2,{\mathbf{d}}_0={\mathbf{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}-\mathbf{L}\mathbf{m}$, and ${\mathbf{e}}_1=[\mathrm{1,0},\dots ,0{]}^T$. Then, the upper Hessenberg matrix ${\mathbf{M}}_r$ and upper triangle matrix ${\mathbf{T}}_{r+1}$ can be constructed by Algorithm 1. So that the following equation holds:

$$\mathbf{L}{\mathbf{Z}}_r={\mathbf{U}}_{r+1}{\mathbf{M}}_r,$$

(13)

$${\mathbf{L}}^{\ast }{\mathbf{U}}_{r+1}={\mathbf{V}}_{r+1}{\mathbf{T}}_{r+1},$$

(14)

where ${\mathbf{U}}_{r+1}=\left[{\mathbf{u}}_1\dots {\mathbf{u}}_{r+1}\right]$ and ${\mathbf{V}}_{r+1}=\left[{\mathbf{v}}_1\dots {\mathbf{v}}_{r+1}\right]$ are both the orthonormal vectors. ${\mathbf{M}}_r$ and ${\mathbf{T}}_{r+1}$ are introduced as the upper Hessenberg matrix and upper triangle matrix. And ${\mathbf{Z}}_r=\left[{\mathbf{W}}_1^{-1}{\mathbf{v}}_1,\dots ,{{\mathbf{W}}_r^{-1}\mathbf{v}}_r\right]$ provides the basis for the solution. Based on the orthogonality of the vectors ${\mathbf{U}}_{r+1}$, combining Equations (13) and (14), then we derive

$$\begin{array}{c}{\mathbf{L}\mathbf{Z}}_{r}y-d=-\beta {\mathbf{U}}_1+{\mathbf{U}}_{\mathbf{r}+1}{\mathbf{M}}_{\mathbf{r}}y,\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=-\beta {\mathbf{U}}_{\mathbf{r}+1}{\mathbf{e}}_1+{\mathbf{U}}_{\mathbf{r}+1}{\mathbf{M}}_{\mathbf{r}}y,\\ ={\mathbf{U}}_{\mathbf{r}+1}\left[{\mathbf{M}}_{\mathbf{r}}\mathbf{y}-\beta {\mathbf{e}}_1\right],\end{array}$$

(15)

From the point of view of minimizing data error, the projected residual of Krylov subspace can be achieved. Then ${\mathbf{y}}_r$ is calculated by the reduced-dimension damped least squares approach, which is written as

$${\mathbf{y}}_r=\mathrm{a}\mathrm{r}\mathrm{g}\underset{\mathbf{y}}{ \min }{‖\left(\sqrt{\lambda }\mathbf{I}{\mathbf{M}}_r\right)\mathbf{y}-\left(\begin{array}{c}0\\ \beta {\mathbf{e}}_1\end{array}\right)‖}_2^2.$$

(16)

Equation (16) can be solved by damped least-squares inversion [49]. Thus, the r-th iteration solution of Equation (5) is ${{\mathbf{m}}_r=\mathbf{Z}}_r{\mathbf{y}}_r$. For sparse regularization of LSRTM, the choice of trade-off λ is very critical. We determine the regularization parameter in Equation (16) by the GCV method [35, 48]. The core idea of the GCV criterion is to identify the regularization parameter by minimizing the generalized cross-validation function [35], thereby balancing data fitting and model complexity. Therefore, the inversion does not require any pre-determined regularization parameter at the initialization stage of the iteration. On the other hand, the Krylov subspace method is also considered to possess intrinsic iterative regularization properties [38]. During each iteration, the Krylov subspace method achieves regularization effect through iterative control and the expansion of the solution space, with the number of iterations can also play a regularization role. As the number of iterations increases, the solution progressively stabilizes and becomes more accurate. Krylov subspace methods can solve the projected least-squares problem by extending the approximate subspace of the solution and solving it at each iteration. In such an iterative process, an FGK method is used. The key of FGK is the introduction of an upper Hessenberg matrix and an upper triangular matrix, which can reduce the size of the original large-scale regularization problem. The Hessenberg matrix M constructed through flexible Krylov subspace method, compared to our forward modeling operator L, has a smaller dimension. And we use the efficient projection methods with variable preconditioners instead of inner-outer schemes. Thus, such advantages of flexible Krylov subspace methods are obvious when compared to traditional methods of objective function solving.

Algorithm 1: FGK projection process

(1) Input: observed data ${\mathbf{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}$, modeling operator $\mathbf{L}$, migration operator ${\mathbf{L}}^{\ast }$, initial image ${\mathbf{m}}_0$  (2) Initialize: ${\mathbf{u}}_1={\mathbf{d}}_0/\beta$, where ${\mathbf{d}}_0={\mathbf{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}-\mathbf{L}{\mathbf{m}}_0,\beta =$ $\parallel {\mathbf{d}}_0{\parallel }_2,{\mathbf{V}}_r=\left[{\mathbf{v}}_1,\dots ,{\mathbf{v}}_r\right]$  (3) For $i=1,\dots ,r$ do:    (a) Compute $\mathbf{q}={\mathbf{L}}^{\ast }{\mathbf{u}}_i,t_{j,i}={\mathbf{q}}^T{\mathbf{v}}_j$ for $j=$ $1,\dots ,i-1$    (b) Set $\mathbf{q}=\mathbf{q}-\sum _{j=1}^{i-1}{t}_{j,i}{\mathbf{v}}_j$, compute $t_{i, i }=\parallel \mathbf{q} \parallel$ and take ${\mathbf{v}}_i=\mathbf{q}/t_{i,i}$    (c) Compute ${\mathbf{z}}_i={\mathbf{W}}_i^{-1}{\mathbf{v}}_i$ and $\mathbf{q}=\mathbf{L}{\mathbf{z}}_i$    (d) $m_{j,i}={\mathbf{q}}^T{\mathbf{u}}_j$ for $j=1,\dots ,i$ and set $\mathbf{q}=\mathbf{q}-\sum _{j=1}^i{m}_{j,i}{\mathbf{u}}_j$    (e) Compute $m_{i+1,i}=\parallel \mathbf{q} \parallel$, and take ${\mathbf{u}}_{i+1}=\mathbf{q}/m_{i+1,i}$  (4) End do  $\mathrm{Through} \mathrm{the} \mathrm{above} \mathrm{loop} \mathrm{calculation}, \mathrm{the} \mathrm{upper} \mathrm{Hessenberg} {\mathbf{M}}_r$ $(\mathrm{elements} \mathrm{are} m_{ij})$$\mathrm{and} \mathrm{an} \mathrm{upper} \mathrm{triangular} \mathrm{matrix} { \mathbf{T}}_{r+1}\left[i,j\right]$ $\mathrm{can} \mathrm{be} \mathrm{obtained}, \mathrm{where} {\mathbf{T}}_{r+1}\left[i,j\right]=\{0, \mathrm{if} i>j; t_{ij}, \mathrm{e}\mathrm{l}\mathrm{s}\mathrm{e}\}$.

3. Results

The Valley velocity model is established to verify the effectiveness of flexible Krylov subspace method for solving LSRTM problems. In Figure 1, the velocities from the upper layer to the lower layer are 1800 m/s, 2400 m/s, and 3000 m/s, respectively. The grid number in both the horizontal direction and the depth direction is 400, the grid spacing is 8 m, and the physical dimension of horizon and depth is 3200 m. The first-order velocity stress acoustic wave equation is involved in modeling the shot gathers, and the staggered grid finite difference method is used for numeral calculations for the forward waveform and backpropagation. Twenty shot gathers are synthetic and calculated as the observation data. The total shot record is 3 s, the time sampling step is 1 ms, and the main frequency of the Ricker wavelet as the source wavelet is 10 Hz. The specific parameters are detailed in

Table 1. Parameters for Valley model.

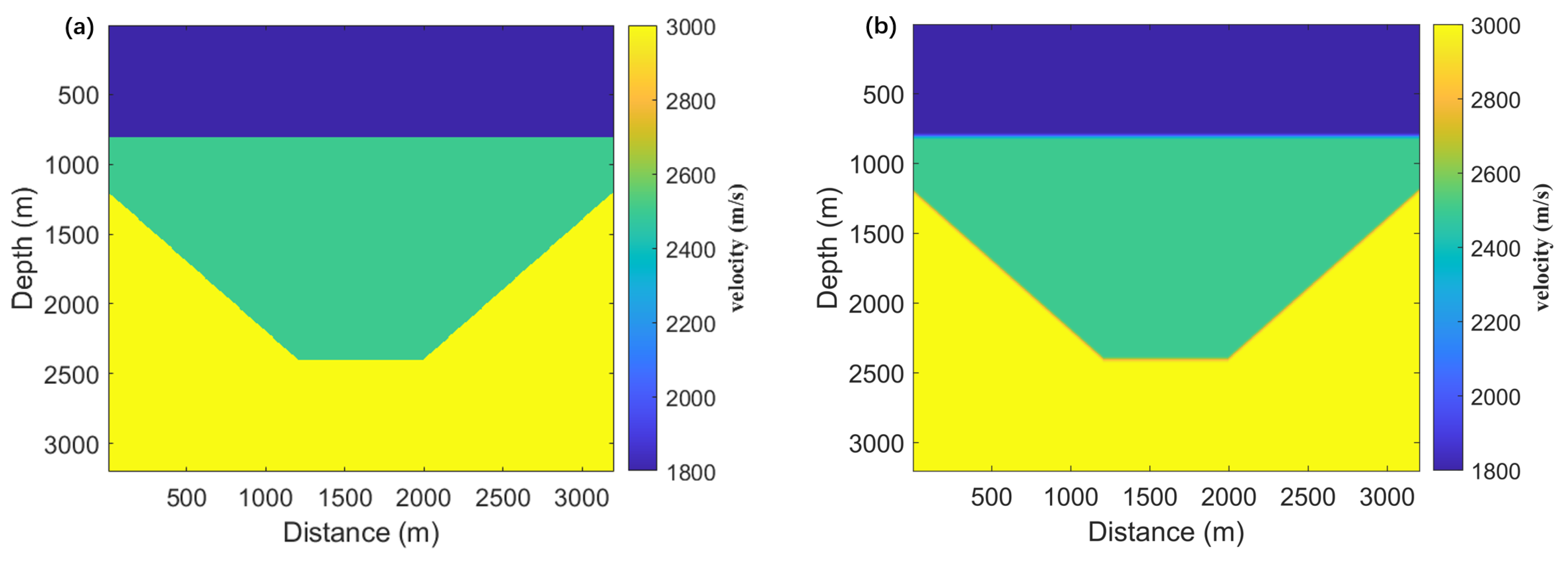
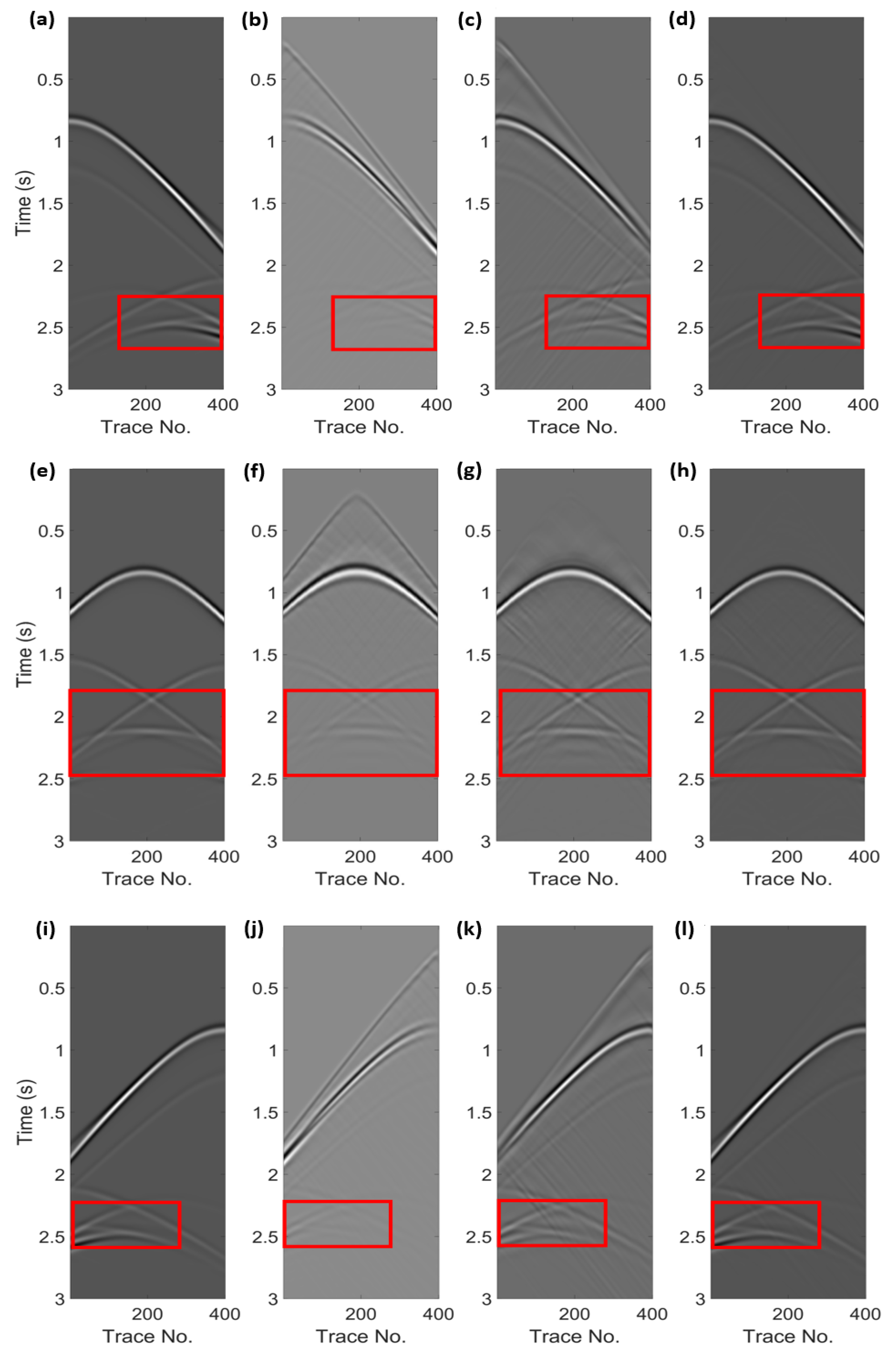
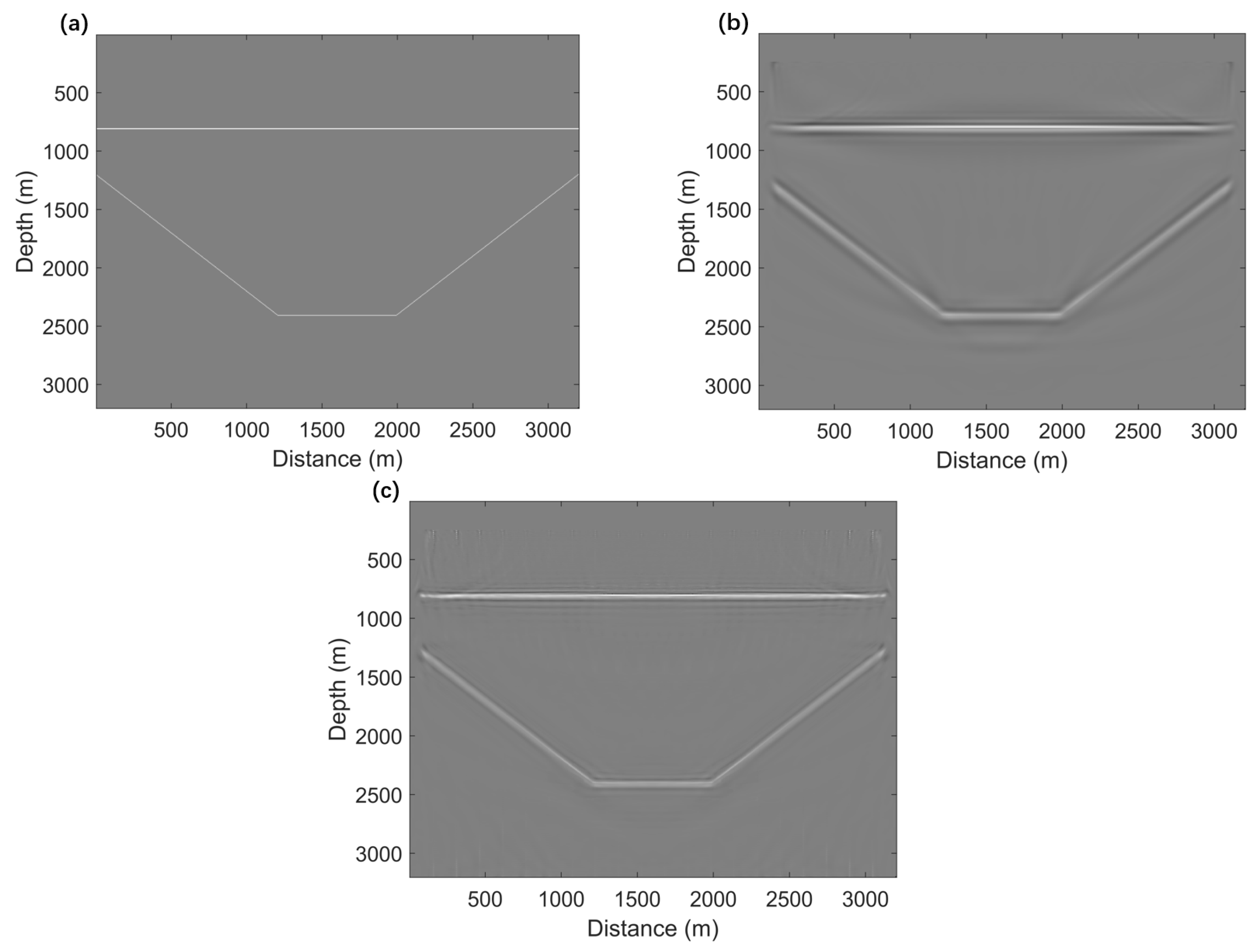
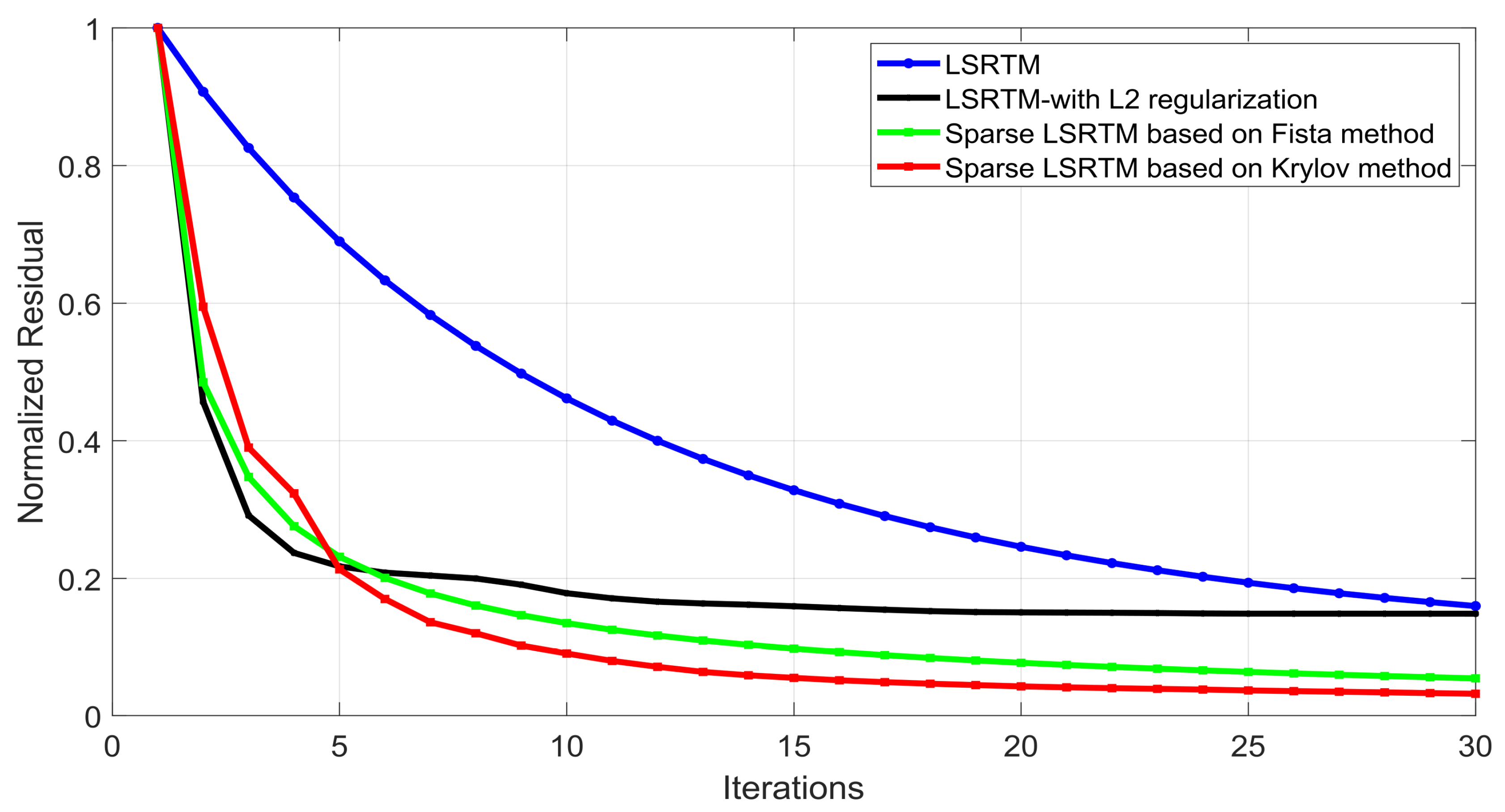
Model parameter	Mesh	Rectangular grid with a grid size of 400 × 400 and a grid spacing of 8 m
	Velocity distribution	From 1800 m/s to 3000 m/s, refer to Figure 1 for detail
Observation system	Position	At the shallow surface
	Source	The Ricker wavelet with a main frequency of 10 Hz excited a total of 20 shots
Seismic forward modeling parameters	Wave field continuation	Finite Difference
	Propagation time	Propagation time Recorded duration of 3000 ms, sampling interval of 1 ms
	Wave equation	Acoustic wave Wave equation, assuming the density is constant
	Boundary	Sponge boundary condition

.

The imaging result of RTM is shown in Figure 2a. The cross-correlation imaging condition with 2D Laplace filtering is used to suppress low-wavenumber artificial noise. Horizontal and large-angle dip reflections can be imaged, but the amplitudes on both sides of the horizontal layer are somewhat distorted, as are the amplitudes at large-angle dip position close to the horizontal layer. Figure 2b–d illustrates the results of LSRTM, LSRTM with L2 regularization (LSRTM-L2), and LSRTM with sparse regularization based on Krylov method (LSRTM-Krylov), respectively. In comparison, the LSRTM-L2 and LSRTM-Krylov methods demonstrate a more extensive imaging scope, and the amplitude of reflection layer is more uniform. The artificial noise generated by RTM near the source and receiver is well suppressed by LSRTM-Krylov method. Meanwhile, the imaging structural resolution of our proposed LSRTM-Krylov method has been further improved compared to other methods, as shown in Figure 2d.

To further evaluate the accuracy of imaging results, Born approximate-based forward simulations are conducted using the imaging results presented in Figure 2. After de-migration, seismic data, specifically the first, tenth, and twentieth shot gathers, are compared with the observation data, as illustrated in Figure 3. When comparing Figure 3a and Figure 3b (Figure 3e and Figure 3f; Figure 3i and Figure 3j), it is clear that the RTM imaging results in deep regions exhibiting insufficient energy and significant event loss. And, in the shallow region, RTM imaging events also display noticeable noise interference, indicating that RTM-derived simulated data substantially deviate from the actual seismic observation. Furthermore, shallow disturbances within the depth range of 250 to 750 m, as depicted in Figure 2, can also lead to interfering reflection waves in de-migration results (see Figure 3b,c,f,g,j,k). However, the single-shot records of the LSRTM-Krylov method, as shown in Figure 3d,h,i, demonstrate that the reflection waves caused by low-frequency disturbances are effectively suppressed. Finally, comparing Figure 3a and Figure 3d (Figure 3e and Figure 3h; Figure 3i and Figure 3l), the sparse LSRTM-Krylov method effectively recovers the model in spite of some low energy manifestation of some of its components in the data.

In addition, we conduct sparse LSRTM inversion based on the Fista method (LSRTM-Fista) and compare the imaging result with that of LSRTM-Krylov as shown in Figure 4. Compared to the inversion results obtained using the LSRTM-Fista method (Figure 4b), the inversion results from LSRTM-Krylov method (Figure 4c) are closer to the true subsurface reflection coefficients (Figure 4a). Additionally, the LSRTM-Krylov method produces a more balanced energy distribution in the subsurface structure, with higher resolution and imaging quality. Then, the residual decline curves of the imaging inversion for these methods are presented in Figure 5. Here, the horizontal axis denotes the number of iterations, ranging from 0 to 30, while the vertical axis is the normalized residual, spanning from 0 to 1. The blue, black, green, and red curves represent the residual variation across 30 iterations of the LSRTM, LSRTM-L2, LSRTM-Fista, and LSRTM-Krylov method, respectively. In the initial iterations (1–5 iterations), the LSRTM-L2, LSRTM-Fista, and LSRTM-Krylov methods show faster convergence and a more significant decrease in residuals as iterations increase. In comparison, LSRTM without regularization, while also exhibiting a decrease in residuals, has a slower decrease rate and maintains higher residuals overall. These comparisons indicate that the regularization technology can enhance the convergence speed of LSRTM, especially in the early iteration phase when it significantly reduces the residuals quickly. During the later stages (5–30 iterations), the LSRTM-Krylov method consistently maintains lower residual levels, continually outperforming other methods. This indicates that sparse regularization not only benefits the initial iteration phases of LSRTM but also positively impacts its long-term efficacy. Above all, it appears that regularization techniques, particularly sparse regularization based on Krylov subspace method, can substantially accelerate the convergence of LSRTM and achieve lower residual errors after fewer iterations.

The comparison of single trace results of different shot gathered from true observation, RTM, LSRTM, and LSRTM-Krylov methods is shown in Figure 6. The amplitude variations of single trace from models above are represented by red, blue, green, and black curves. The horizontal axis denotes the time, extending from 0 to 3 s, and the vertical axis indicates the amplitude, reflecting the strength of the reflected signals. Comparing the reflectivity profiles results of true model, RTM, LSRTM, and LSRTM-Krylov, RTM exhibits the strongest reflection signal at the subsurface interface in shallow region. And, it has the greatest discrepancy from the true model. The reason for this is that the use of cross-correlation imaging condition in RTM generates a large low-frequency noise near the seismic source, resulting in an exaggerated and false amplitude response. Such noise can be removed through a specific number of iterations. Excluding this, the LSRTM-Krylov result exhibits the best amplitude preservation at the shallow subsurface interface, which aligns best with the true model. In areas without interfaces, both RTM and LSRTM without regularization exhibit low-frequency noise, while LSRTM with regularization offers a smoother background, which may help distinguish real geological reflections from noise. Furthermore, it is noteworthy that RTM exhibits significant sidelobe effects at the first interface, attributed to the preservation of seismic source signal characteristics during RTM process. After iterations, the sidelobe effect in LSRTM tends to decrease, leading to improved vertical resolution. More notably, after sufficient iterations, the sidelobe effects in the LSRTM-Krylov result almost entirely vanish, indicating that the LSRTM-Krylov method is effective in suppressing sidelobe effects and noise.

We have also conducted numerical tests using the salt model for these methods, aiming to analyze the imaging accuracy of salt-bottomed interface and subsalt structures. The true velocity of salt model is depicted in Figure 7, where it extends laterally for 19.2 km and has a vertical depth of 4.56 km. The model in Figure 7 presents strong scattering salt structures, which poses a challenge for seismic energy to penetrate and carry information back to the surface. Therefore, many methods are difficult to image clearly. The specific parameters are detailed in

Table 2. Parameters for salt model.

Model parameter	Mesh	Rectangular grid with a grid size of 190 × 800 and a grid spacing of 24 m
	Velocity distribution	From 1500 m/s to 4500 m/s, refer to Figure 6 for detail
Observation system	Position	At the shallow surface
	Source	The Ricker wavelet with a main frequency of 10 Hz excited a total of 48 shots
Seismic forward modeling parameters	Wave field continuation	Finite Difference
	Propagation time	Propagation time Recorded duration of 8800 ms, sampling interval of 1 ms
	Wave equation	Acoustic wave Wave equation, assuming the density is constant
	Boundary	Sponge boundary condition

.

The imaging results of salt model using different methods are shown in Figure 8, where Figure 8a–d represent the results of RTM, LSRTM-without regularization, LSRTM-L2, and LSRTM-Krylov, respectively. In Figure 8a, a significant loss of subsalt structural features and apparent imaging deficiencies are observed. This is mainly due to the rapid attenuation of seismic wave energy in such strong scattering structures, resulting in weaker signals from deep reflections. After some iterations, the subsalt structure boundaries become relatively clear in Figure 8b. Furthermore, comparing the imaging results of Figure 8b–d, it is apparent that the LSRTM-Krylov method has successfully restored the deep structural information of salt model, maintaining balanced amplitude from shallow to deep layers, and the resolution of the salt structure is relatively high. We select a region within the red rectangle in Figure 8 for magnified comparison, as shown in Figure 9. The close-up to a smaller region in Figure 9a–d also confirms that the imaging result of the LSRTM-Krylov method exhibits the clearest and most complete structure. This indicates that our proposed LSRTM method based on the Krylov subspace also has advantages in imaging subsalt structures through strong scattering geological bodies.

4. Discussion

Our research incorporates the flexible Krylov subspace methodology. The dimensions of such Krylov subspace typically expand as the number of iterations grow. In practical applications, approximating a smaller subspace is often sufficient to effectively address the problem. Consequently, this inversion approach can be regarded as a projection inversion method. It involves projecting the objective function of the original problem into a finite-dimensional Krylov subspace. Following this projection, the inversion problem is solved through iterative procedures. This methodological choice is particularly advantageous as it allows for a more focused and efficient inversion process. Targeting key elements within a manageable subspace, thereby more precise and computationally efficient solutions are facilitated. Regularization inversion is a crucial strategy to improve the stability of LSRTM. Typically, conventional LSRTM inversion is a large-scale sparse ill-posed inverse problem. To mitigate these challenges, regularized inversion overcomes the instability inherent in traditional LSRTM by introducing additional constraints or prior information, which may encompass geological knowledge, characteristics of subsurface structures, sparsity and smoothness of the model. By incorporating these priors into the objective function during the inversion process, we can achieve better solving the solution of the inversion. In our approach, we incorporate the sparse regularization term into the objective function. By reducing the size of the model space, imaging results demonstrate that the sparse inversion within the Krylov subspace framework can achieve high quality imaging results. Additionally, we employ an adaptive regularization matrix to approximate the sparse penalty term as a set of weighted L2-norm penalty terms, which are suitable to solve through the Krylov subspace method. Flexible preconditioning techniques are applied to effectively integrate weight updates for solving within the Krylov subspace. Overall, the Krylov subspace inversion method can provide a valuable reference for seismic exploration, thereby offering another powerful tool for high-resolution imaging inversion of subsurface structures.

5. Conclusions

LSRTM inversion is a typical large-scale ill-posed inverse problem. We use the Krylov subspace method to solve this problem by projection into small matrix optimization. For the sparse regularization problem in the model space, an iterative reweighted norm is used to convert it into a set of Krylov–Tikhonov problems to solve. Subsequently, the flexible Golub–Kahan process is employed to solve the regularization problem in a low-dimensional subspace. Each time the solution space is increased, the projection process can add sparse preconditioner to the iterative reweight calculation. Numerical tests have been carried out through Valley model and SEG salt model, which demonstrate that our proposed LSRTM based on Krylov subspace method can further enhance imaging quality.