Multi-Function Working Mode Recognition Based on Multi-Feature Joint Learning
Abstract
1. Introduction
- Difficulty in modeling and characterization: Advanced MFR systems have the ability to freely allocate multi-domain resources, such as in the time domain, space domain, frequency domain, and energy domain. Their antenna beams and working waveforms are complex and diverse, and beam scheduling and transmission waveform combinations are flexible and changeable. In addition, the software customization feature allows new working states of MFR to appear at any time. Its flexible and convenient dynamic characteristics bring challenges to radar behavior modeling and characterization.
- Difficulty in sorting and identification: Advanced MFR systems have a hierarchical signal generation mechanism, characterized by complex signal forms and joint variations in multi-dimensional parameters. The working state sequence is influenced by scheduling strategies and environmental target states. Reconnaissance pulse sequences often include complex pulse sequences from multiple radiation sources, and sparse observations frequently occur due to incomplete detection signals caused by reconnaissance equipment limitations and radar beam scheduling.
- Difficulty in accurate pattern identification in complex environments: In complex electromagnetic environments, where different radar systems exhibit similar parameters in multiple modes, the model may mistakenly identify the radar in the wrong mode. This misclassification may lead to incorrect threat assessment and tactical decisions.
- We developed the MFR-PDWS dataset based on the Mercury MFR, integrating it with MFR syntax modeling research. This dataset includes multi-level semantic information reflecting MFR behavior and simulates various disturbance factors, such as signal loss, stray pulses, and noise, which may occur in real adversarial environments. The dataset enables the trained model to better address real-world challenges, providing valuable support for related MFR research.
- We proposed a lightweight hybrid model based on CNN and Transformer architectures for RWMR. The model extracts both intra-pulse and inter-pulse characters from reconnaissance signals using convolution modules and multi-head attention mechanisms. By jointly learning local characters and long-term dependencies at different levels from the reconnaissance pulses, the model achieves efficient and accurate MFR working mode recognition.
- A series of extensive experiments were conducted to demonstrate the effectiveness and robustness of the proposed method in complex electromagnetic environments.
2. Related Work
3. Radar Signal Model
3.1. RWMR Characteristic Parameters
- (1)
- Time of Arrival (TOA)
- (2)
- Pulse repetition interval (PRI)
- (3)
- Pulse Width (PW)
- (4)
- Carrier frequency (RF)
- (5)
- Pulse Amplitude (PA)
- (6)
- Bandwidth (BW)
MFR Multi-Level Signal Model
4. Model Architecture
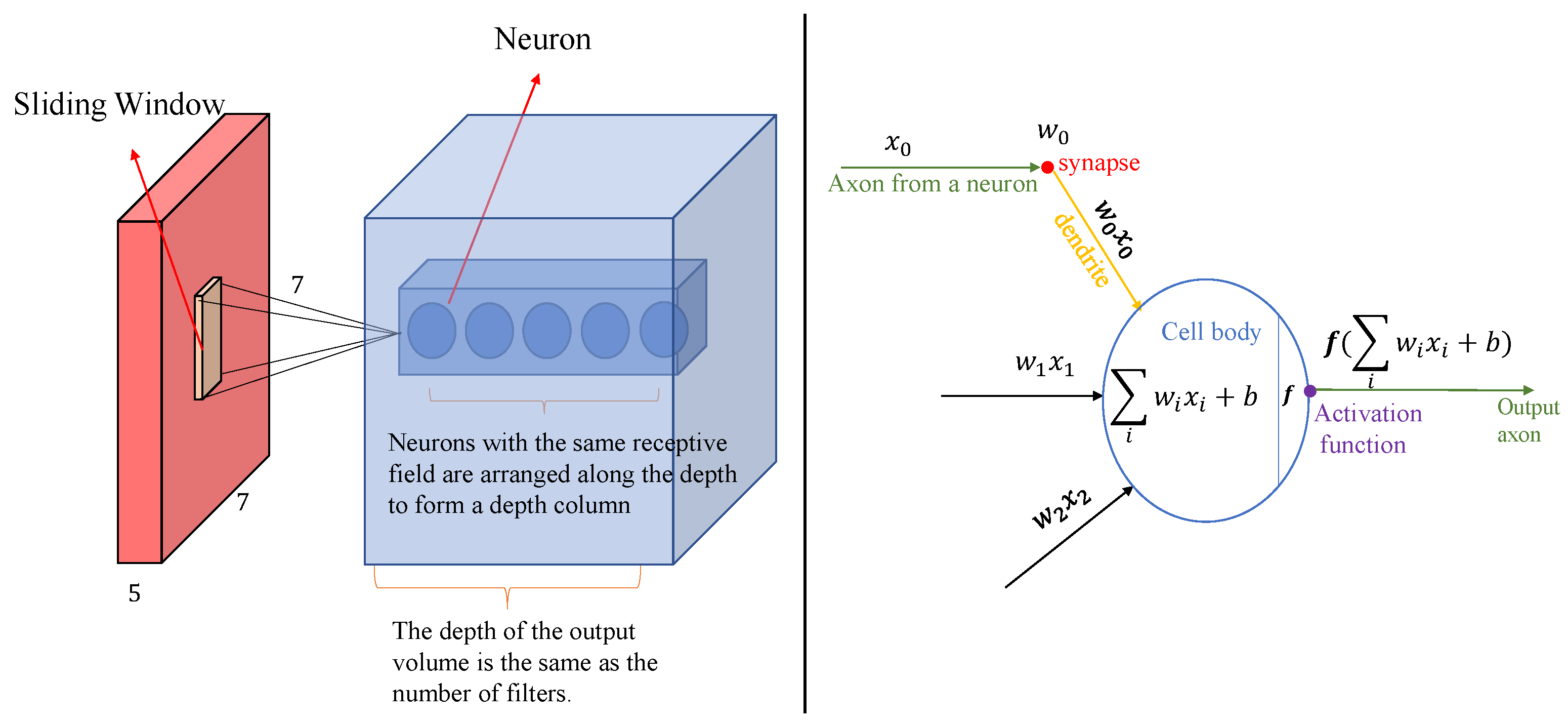
4.1. CNN Modules
- In radar signal processing, many key characters (such as frequency, pulse width, bandwidth, etc.) are manifested as local patterns of the signal. Through convolution operations, CNN can adaptively extract these local characters from radar signals, especially the frequency domain characters of the signal, which is crucial for the recognition of radar working modes. For example, for broadband radar signals, CNN can effectively identify the local high-frequency components in the signal to help distinguish different working modes.
- CNN has a natural filtering capability and can learn appropriate filters based on the characteristics of the input signal. It is highly robust to noise and interference. This is particularly important for the common noise problem in radar signal processing. CNN can automatically learn and remove irrelevant signal interference, extract cleaner and more useful pattern characters, and thus improve recognition accuracy.
4.1.1. Receptive Field
4.1.2. Spatial Arrangement of Neurons
4.2. Transformer Modules
- The working mode of radar signals is usually manifested as time-series data with long-term dependencies. These dependencies may span a long time window and have complex interactions with other parts of the signal. Transformer can effectively capture these global dependencies through the self-attention mechanism, which is particularly suitable for processing long time series data.
- Unlike CNN, Transformer can directly perform weighted calculations on the input signal and adaptively adjust the weights of different signal parts, especially when the importance of information in different time periods in the signal is different. This makes Transformer highly adaptable and able to flexibly respond to dynamic changes in radar signals.
- The temporal changes in radar working modes usually have complex dependencies, and the various modes in the signal may have nonlinear interactions. Traditional neural networks may find it difficult to effectively model these complex relationships, while Transformer can comprehensively examine the relationship of the entire input sequence through the self-attention mechanism, not only focusing on local spatial information, but also understanding global temporal changes, providing richer contextual information for radar signal processing.
4.2.1. Input Block
4.2.2. Encode Decode Block
4.2.3. Output Block
4.3. Hybrid Model Architecture
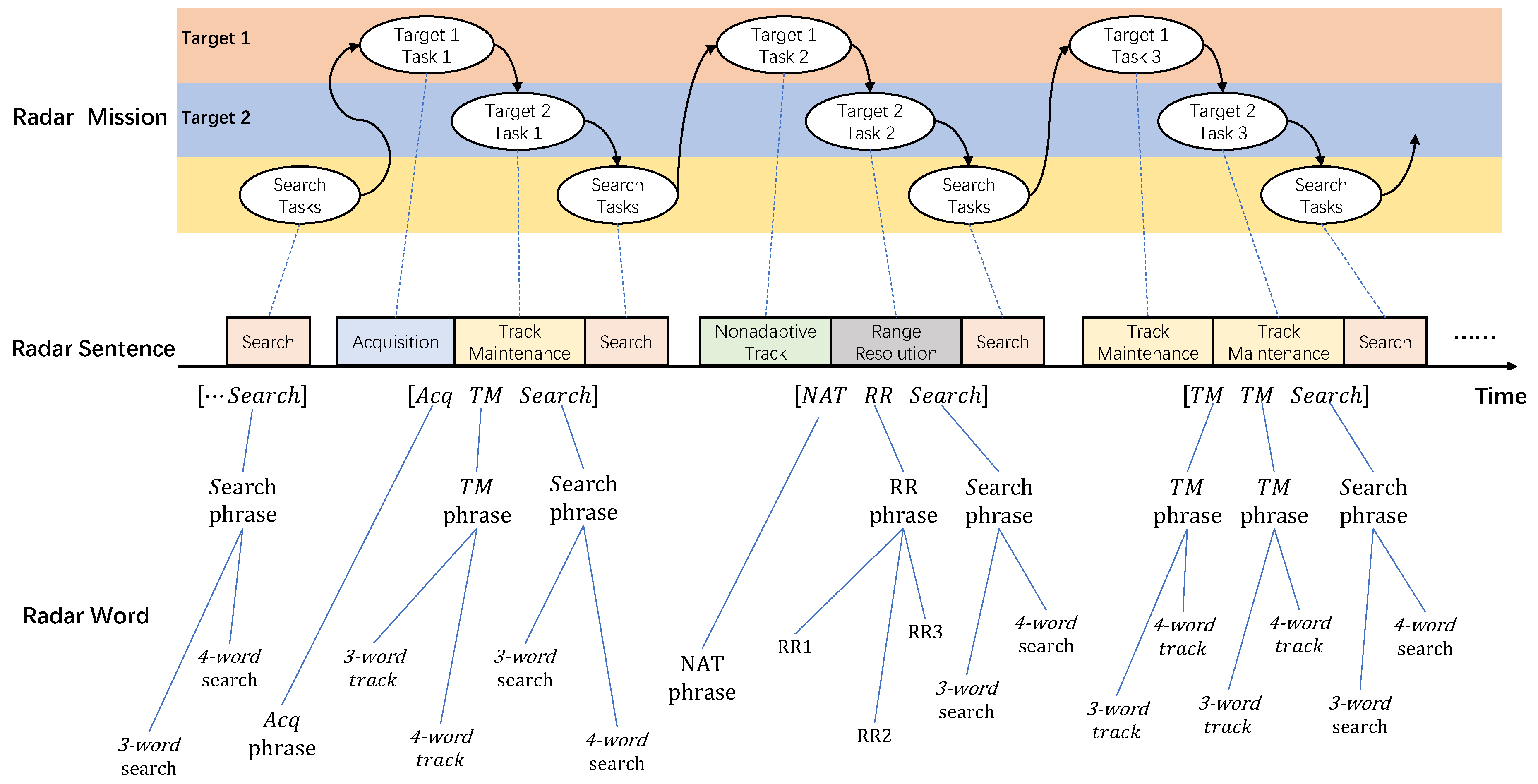
5. Creation of Radar Dataset
5.1. Mercury MFR
- Search: This is one of the most basic working modes of MFR. The beam scans in a certain order in a specific airspace to detect unknown targets in a timely manner.
- Acquisition (Acq): When a target is detected in search mode, the same radar word as the search signal is used to continuously illuminate the same direction at a higher data rate to confirm the detection result and complete the acquisition of the target.
- Non-Adaptive Track (NAT): NAT is used for targets with a lower threat level. Search is dominant, and tracking does not occupy additional radar resources, that is, no special tracking beam is arranged. Instead, the search beam and data rate are used to detect the target to achieve a monitoring effect.
- Range Resolution (RR): Alternately transmits multiple different PRF signals (radar words) to resolve range ambiguity and determine target location.
- Track Maintenance (TM): When a target poses a high threat level, a dedicated beam is used to illuminate the target and keep tracking the target at a higher data rate.
5.2. Radar Word Settings
Creation of MFR-PDWS
6. Experiment and Result Analysis
6.1. Model Training Process
6.2. Model Testing Results
6.3. Comparison of the Model with Other Models
6.4. Ablation Experiment
6.5. Model Robustness Testing
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuxin, F.; Jie, H.; Jiantao, W.; Tongxin, D.; Yiming, L.; Zhenyu, S. A review of multifunctional phased array radar behavior identification. Telecommun. Eng. 2024, 64, 643–654. [Google Scholar]
- Shafei, W.; Mengtao, Z.; Yunjie, L.; Jian, Y.; Yan, L. Identification, reasoning and prediction of advanced multifunctional radar system behavior: Review and prospect. Signal Process. 2024, 40, 17–55. [Google Scholar] [CrossRef]
- Yaoliu, Y.; Weigang, Z.; Shouye, L.; Hongyu, Z.; Yaoyan, H. A review of multifunctional radar working mode recognition methods. Telecommun. Eng. 2020, 60, 1384–1390. [Google Scholar]
- Shuaiying, Y.; Peng, P.; Yuan, R. Development Status and Trend of Shipborne Multifunctional Phased Array Radar. Ship Sci. Technol. 2023, 45, 141–147. [Google Scholar]
- Jian, O. Research on Multifunctional Radar Behavior Identification and Prediction Technology. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2017. [Google Scholar]
- Visnevski, N.; Dilkes, F.; Haykin, S.; Krishnamurthy, V. Non-self-embedding context-free grammars for multi-function radar modeling–electronic warfare application. In Proceedings of the IEEE International Radar Conference, Arlington, VA, USA, 9–12 May 2005; pp. 669–674. [Google Scholar] [CrossRef]
- Ya, S.; Wenbo, Z.; Mingzhe, Z.; Lei, W.; Shengjun, X. A review of radar emitter individual identification. J. Electron. Inf. Technol. 2022, 44, 2216–2229. [Google Scholar]
- Wang, J.; Zheng, T.; Lei, P.; Wei, S. A review of deep learning in radar. J. Radar 2018, 7, 395–411. [Google Scholar]
- Yu, K.; Qi, Y.; Shen, L.; Wang, X.; Quan, D.; Zhang, D. Radar Signal Recognition Based on Bagging SVM. Electronics 2023, 12, 4981. [Google Scholar] [CrossRef]
- Zhou, Z.; Fei, W.; Zheng, F.; Luo, J. A Radar Working Mode Recognition Algorithm with Approximate Coherent Metric and Multi-Agent PSR Model. In Proceedings of the 12th International Conference on Computer Engineering and Networks, Haikou, China, 4–7 November 2022; Liu, Q., Liu, X., Cheng, J., Shen, T., Tian, Y., Eds.; Springer: Singapore, 2022; pp. 456–465. [Google Scholar] [CrossRef]
- Lang, P.; Fu, X.; Martorella, M.; Dong, J.; Qin, R.; Meng, X.; Xie, M. A Comprehensive Survey of Machine Learning Applied to Radar Signal Processing. arXiv 2020, arXiv:2009.13702. [Google Scholar]
- Ou, J.; Chen, Y.; Zhao, F.; Liu, J.; Xiao, S. Novel Approach for the Recognition and Prediction of Multi-Function Radar Behaviours Based on Predictive State Representations. Sensors 2017, 17, 632. [Google Scholar] [CrossRef] [PubMed]
- Ou, J.; Chen, Y.; Zhao, F.; Liu, J.; Xiao, S. Method for operating mode identification of multi-function radars based on predictive state representations. IET Radar Sonar Navig. 2017, 11, 426–433. [Google Scholar] [CrossRef]
- Chi, K.; Shen, J.; Li, Y.; Wang, L.; Wang, S. A novel segmentation approach for work mode boundary detection in MFR pulse sequence. Digit. Signal Process. 2022, 126, 103462. [Google Scholar] [CrossRef]
- Geng, Z.; Yan, H.; Zhang, J.; Zhu, D. Deep-Learning for Radar: A Survey. IEEE Access 2021, 9, 141800–141818. [Google Scholar] [CrossRef]
- Liu, L.; Li, X. Radar signal recognition based on triplet convolutional neural network. EURASIP J. Adv. Signal Process. 2021, 2021, 112. [Google Scholar] [CrossRef]
- Shao, G.; Chen, Y.; Wei, Y. Convolutional neural network-based radar jamming signal classification with sufficient and limited samples. IEEE Access 2020, 8, 80588–80598. [Google Scholar] [CrossRef]
- Gao, J.; Shen, L.; Gao, L. Modulation recognition for radar emitter signals based on convolutional neural network and fusion features. Trans. Emerg. Telecommun. Technol. 2019, 30, e3612. [Google Scholar] [CrossRef]
- Wang, L.; Yang, X.; Tan, H.; Bai, X.; Zhou, F. Few-shot class-incremental SAR target recognition based on hierarchical embedding and incremental evolutionary network. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–11. [Google Scholar] [CrossRef]
- Geng, J.; Wang, H.; Fan, J.; Ma, X. SAR Image Classification via Deep Recurrent Encoding Neural Networks. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2255–2269. [Google Scholar] [CrossRef]
- Li, X.; Liu, Z.; Huang, Z.; Liu, W. Radar Emitter Classification With Attention-Based Multi-RNNs. IEEE Commun. Lett. 2020, 24, 2000–2004. [Google Scholar] [CrossRef]
- Xu, X.; Bi, D.; Pan, J. Method for functional state recognition of multifunction radars based on recurrent neural networks. IET Radar Sonar Navig. 2021, 15, 724–732. [Google Scholar] [CrossRef]
- Chen, H.; Feng, K.; Kong, Y.; Zhang, L.; Yu, X.; Yi, W. Multi-Function Radar Work Mode Recognition Based on Encoder-Decoder Model. In Proceedings of the IGARSS 2022–2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 1189–1192. [Google Scholar] [CrossRef]
- Chen, H.; Feng, K.; Kong, Y.; Zhang, L.; Yu, X.; Yi, W. Function Recognition Of Multi-function Radar Via CNN-GRU Neural Network. In Proceedings of the 2022 23rd International Radar Symposium (IRS), Gdansk, Poland, 12–14 September 2022; pp. 71–76. [Google Scholar] [CrossRef]
- Apfeld, S.; Charlish, A. Recognition of Unknown Radar Emitters With Machine Learning. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 4433–4447. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, M.; Ma, Y.; Yang, J. Work modes recognition and boundary identification of MFR pulse sequences with a hierarchical seq2seq LSTM. IET Radar Sonar Navig. 2020, 14, 1343–1353. [Google Scholar] [CrossRef]
- Liu, Z.M. Recognition of Multifunction Radars Via Hierarchically Mining and Exploiting Pulse Group Patterns. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4659–4672. [Google Scholar] [CrossRef]
- Li, X.; Liu, Z.; Huang, Z. Attention-Based Radar PRI Modulation Recognition With Recurrent Neural Networks. IEEE Access 2020, 8, 57426–57436. [Google Scholar] [CrossRef]
- Tian, T.; Zhang, Q.; Zhang, Z.; Niu, F.; Guo, X.; Zhou, F. Shipborne Multi-Function Radar Working Mode Recognition Based on DP-ATCN. Remote Sens. 2023, 15, 3415. [Google Scholar] [CrossRef]
- Li, X.; Cai, Z. Deep Learning and Time-Frequency Analysis Based Automatic Low Probability of Intercept Radar Waveform Recognition Method. In Proceedings of the 2023 IEEE 23rd International Conference on Communication Technology (ICCT), Wuxi, China, 20–22 October 2023; pp. 291–296. [Google Scholar] [CrossRef]
- Wang, C.; Wang, J.; Zhang, X. Automatic radar waveform recognition based on time-frequency analysis and convolutional neural network. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 2437–2441. [Google Scholar] [CrossRef]
- Wei, C.; Wang, Z.; Xiong, S.; Zhang, Y. ISAR Target Recognition Method Based on Time-Frequency Two-Dimensional Joint Domain Adversarial Learning Network. In Proceedings of the 2023 Cross Strait Radio Science and Wireless Technology Conference (CSRSWTC), Guilin, China, 10–13 November 2023; pp. 1–3. [Google Scholar] [CrossRef]
- Feng, K.; Chen, H.; Kong, Y.; Zhang, L.; Yu, X.; Yi, W. Prediction of Multi-Function Radar Signal Sequence Using Encoder-Decoder Structure. In Proceedings of the 2022 7th International Conference on Signal and Image Processing (ICSIP), Suzhou, China, 20–22 July 2022; pp. 152–156. [Google Scholar] [CrossRef]
- Zhai, Q.; Li, Y.; Zhang, Z.; Li, Y.; Wang, S. Few-Shot Recognition of Multifunction Radar Modes via Refined Prototypical Random Walk Network. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2376–2387. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; Zhai, Q.; Li, Y.; Gao, M. Few-Shot Learning for Fine-Grained Signal Modulation Recognition Based on Foreground Segmentation. IEEE Trans. Veh. Technol. 2022, 71, 2281–2292. [Google Scholar] [CrossRef]
- Juyuan, Z. Research and Application of Radar Working Mode Recognition Based on Machine Learning. Master’s Thesis, Beijing University of Posts and Telecommunications, Beijing, China, 2021. [Google Scholar]
- Shuang, Z. Research on key technologies of multi-function radar electronic intelligence signal processing. Electron. Qual. 2019, 1, 2–23. [Google Scholar]
- Visnevski, N.; Krishnamurthy, V.; Wang, A.; Haykin, S. Syntactic Modeling and Signal Processing of Multifunction Radars: A Stochastic Context-Free Grammar Approach. Proc. IEEE 2007, 95, 1000–1025. [Google Scholar] [CrossRef]
- Gallego, J.A.; Osorio, J.F.; Gonzalez, F.A. Fast kernel density estimation with density matrices and random fourier features. In Proceedings of the Ibero-American Conference on Artificial Intelligence; Springer: Cham, Switzerland, 2022; pp. 160–172. [Google Scholar] [CrossRef]
- Longjun, Z.; Bo, D.; Weijian, S.; Shan, G. Multi-function radar working mode recognition based on cluster analysis method. Ship Electron. Eng. 2022, 42, 86–88. [Google Scholar]
- Su, X.; Xue, S.; Liu, F.; Wu, J.; Yang, J.; Zhou, C.; Hu, W.; Paris, C.; Nepal, S.; Jin, D.; et al. A Comprehensive Survey on Community Detection With Deep Learning. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 4682–4702. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Han, Y.; Fan, J. Laplacian-based Cluster-Contractive t-SNE for High-Dimensional Data Visualization. ACM Trans. Knowl. Discov. Data 2023, 18, 22. [Google Scholar] [CrossRef]















| Working Mode | Phase | Working Mode | Phase | ||
|---|---|---|---|---|---|
| Search | 4-Word Serrch (FS) | Track Maintenance (TM) | 4-Word Track (FT) | ||
| 3-Word Track (ST) | |||||
| 3-Word Serrch (TS) | |||||
| Nonadaptive Track (ANT) | |||||
| Acquisition (Acq) | |||||
| Range Resolution (RR) | RR1 | ||||
| RR2 | |||||
| RR3 | |||||
| RF | PW | BW | PRI | PA | |
|---|---|---|---|---|---|
| 3000–3600 | 15–30 | 5–10 | 300–500 | −10–7 | |
| 3400–4000 | 0.5–20 | 1–7 | 100–400 | −5–0 | |
| 4000–4600 | 2–10 | 12–16 | 50–150 | 0–3 | |
| 4400–5000 | 0.5–10 | 6–15 | 50–250 | −3–0 | |
| 9900–11,000 | 15–30 | 10–18 | 4000–6000 | −5–5 | |
| 9200–9600 | 10–22 | 15–27 | 800–2000 | 0–3 | |
| 9600–9900 | 0.5–2 | 4–12 | 400–1000 | −1–7 | |
| 9600–11,000 | 12.5–20 | 2–20 | 50–500 | 2–10 | |
| 3000–4500 | 15–20 | 9–18 | 3000–4500 | −5–0 |
| ARI | SS | |
|---|---|---|
| K-means | 0.580322 | 0.389653 |
| Agglomerative | 0.480269 | 0.38024 |
| DBSCAN | 0.123411 | N/A |
| Modules | Parameter | Value | Modules | Parameter | Value |
|---|---|---|---|---|---|
| Hardware Resources | Processor | Inter CORE i7-12700F,.1G | Tramsformer | 0.1 | |
| Memory | 16384MB(RAM) | 4 | |||
| Graphics | NVIDIA GeForce GT 730 | 128 | |||
| Hyperparameter | 5 | VGGnet | 1 | ||
| 80 | 3 | ||||
| 0.001 | 1 | ||||
| 64 | 15 | ||||
| 300 | Restnet | 0.1 | |||
| 7 | 3 | ||||
| CNN-Bclock | 3 | 1 | |||
| 1 | 1 | ||||
| 1 | GRUED | 3 | |||
| LSTM | 64 | 64 | |||
| RNN | 64 | 3 |
| Model | RNN | LSTM | GRUED | Hybrid | VGGnet | ResNet |
|---|---|---|---|---|---|---|
| Train-accuracy | ||||||
| Test-accuracy |
| CNN-Block | Transformer-Block | Accuracy | |
|---|---|---|---|
| CNN Model | ✓ | × | |
| Transformer Model | × | ✓ | |
| Hybri Model | ✓ | ✓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Wu, M.; Cheng, D.; Wang, W. Multi-Function Working Mode Recognition Based on Multi-Feature Joint Learning. Remote Sens. 2025, 17, 521. https://doi.org/10.3390/rs17030521
Liu L, Wu M, Cheng D, Wang W. Multi-Function Working Mode Recognition Based on Multi-Feature Joint Learning. Remote Sensing. 2025; 17(3):521. https://doi.org/10.3390/rs17030521
Chicago/Turabian StyleLiu, Lei, Minghua Wu, Dongyang Cheng, and Wei Wang. 2025. "Multi-Function Working Mode Recognition Based on Multi-Feature Joint Learning" Remote Sensing 17, no. 3: 521. https://doi.org/10.3390/rs17030521
APA StyleLiu, L., Wu, M., Cheng, D., & Wang, W. (2025). Multi-Function Working Mode Recognition Based on Multi-Feature Joint Learning. Remote Sensing, 17(3), 521. https://doi.org/10.3390/rs17030521





