Cross-Domain Land Surface Temperature Retrieval via Strategic Fine-Tuning-Based Transfer Learning: Application to GF5-02 VIMI Imagery
Highlights
- A three-stage SFTL framework enhances GF5-02/VIMI LST retrieval by combining large simulated datasets with limited in situ measurements and shows that in situ sample size and statistical variability determine the optimal neural network and fine-tuning strategy.
- The framework achieves strong cross-site generalization (≈2.9–3.4 K RMSE), outperforming both Split-Window and direct-training machine-learning models.
- The approach enables reliable LST mapping in regions with sparse ground observations, reducing dependence on large labeled in situ datasets.
- The method offers a scalable route for operational GF5-02/VIMI LST retrieval across heterogeneous surface types and atmospheric conditions.
Abstract
1. Introduction
2. Study Area and Data
2.1. Study Regions and Ground-Measured Data
- -
- Heihe Region in Gansu Province: The Heihe region (Figure 1a), located in Gansu Province, was chosen for its access to well-distributed radiation measurement stations, ensuring high-quality data for validation purposes. Three ground sites were established across this region and equipped with CNR1 net radiometers, covering diverse landforms such as the cropland, wetland and desert steppe (Table 1). Owing to these varied landforms, the environmental characteristics of Heihe differ significantly from those of Huailai, enabling cross-validation of LST algorithms across distinct climatic and geographic contexts.
- -
- Huailai Remote Sensing Comprehensive Experiment Station: The Huailai station, affiliated with the Chinese Academy of Sciences (CAS), is situated at the boundary between Hebei and Beijing Provinces (Figure 1b). This area is surrounded by diverse land use and cover types—including water bodies, farmland, wetlands, mountains, and grasslands—making it ideal for evaluating LST retrieval under heterogeneous surface conditions. Fifteen radiation stations were strategically deployed throughout the region, each equipped with a Kipp and Zonen CGR3 net radiometer (spectral range: 4.5–42 µm; field of view: 150°; accuracy: 1 W/m2 after blackbody calibration). The stations collectively monitor a wide spectrum of land covers, such as shrub, forest, and crop (Table 1), thereby supporting comprehensive validation across different surface types.
2.2. Satellite Data
2.3. Simulation Dataset
2.4. Auxiliary Meteorological and Reanalysis Data
3. Methods
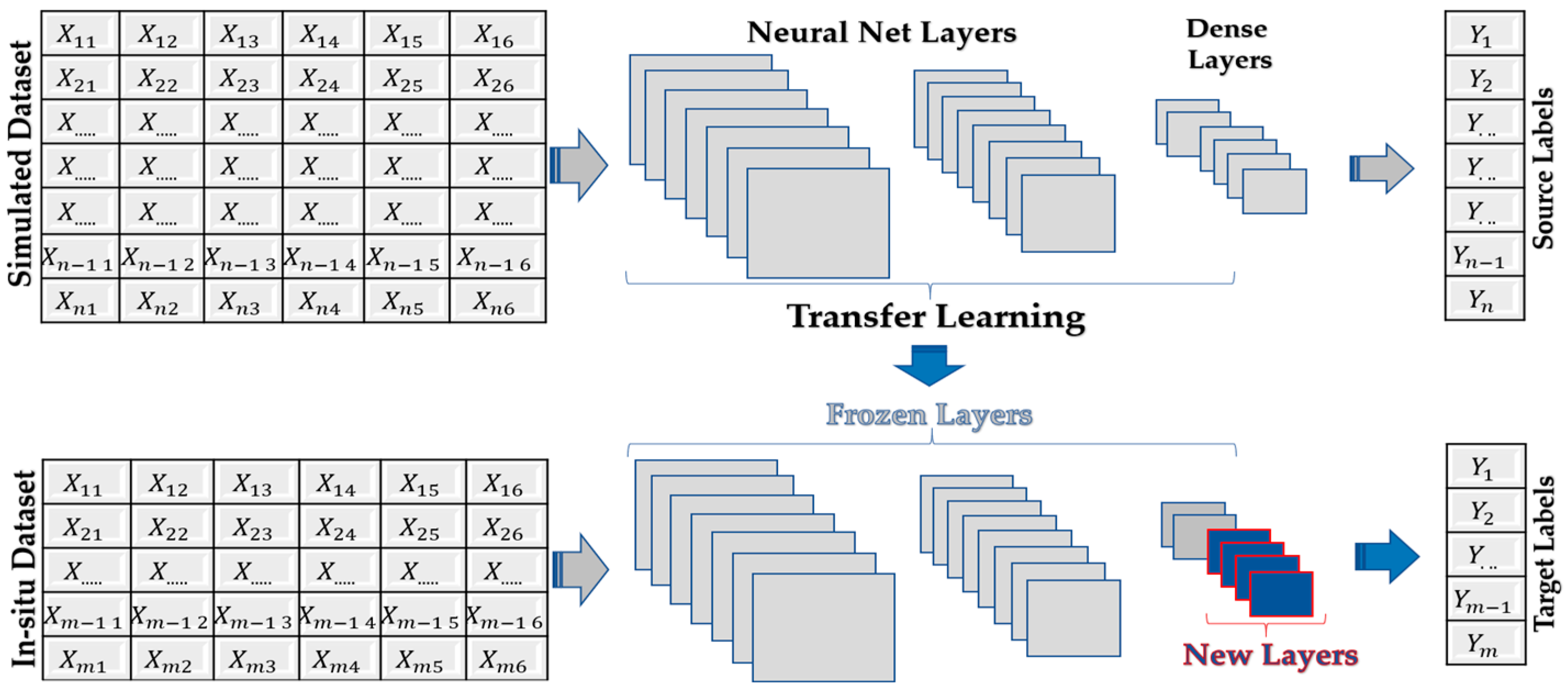
3.1. Transfer-Learning and SFTL Framework
3.1.1. Pre-Training Process
3.1.2. Fine-Tunning
- -
- -
- Head fine-tuning: It preserves the pre-trained feature extraction layers by freezing all weights except those in the final prediction head. This strategy initializes the prediction head with random weights while keeping other layers fixed [70].
- -
- -
- Adapter fine-tuning: It freezes all pre-trained weights and updates only lightweight adapter modules inserted between layers. Each adapter consists of a down-projection layer (typically reducing dimensionality by a specified factor), a nonlinear activation function, and an up-projection layer [72,73].
- -
3.2. Operational SW Algorithm
LSE Estimation
3.3. Accuracy Metrics and Sensitivity Analysis
4. Results
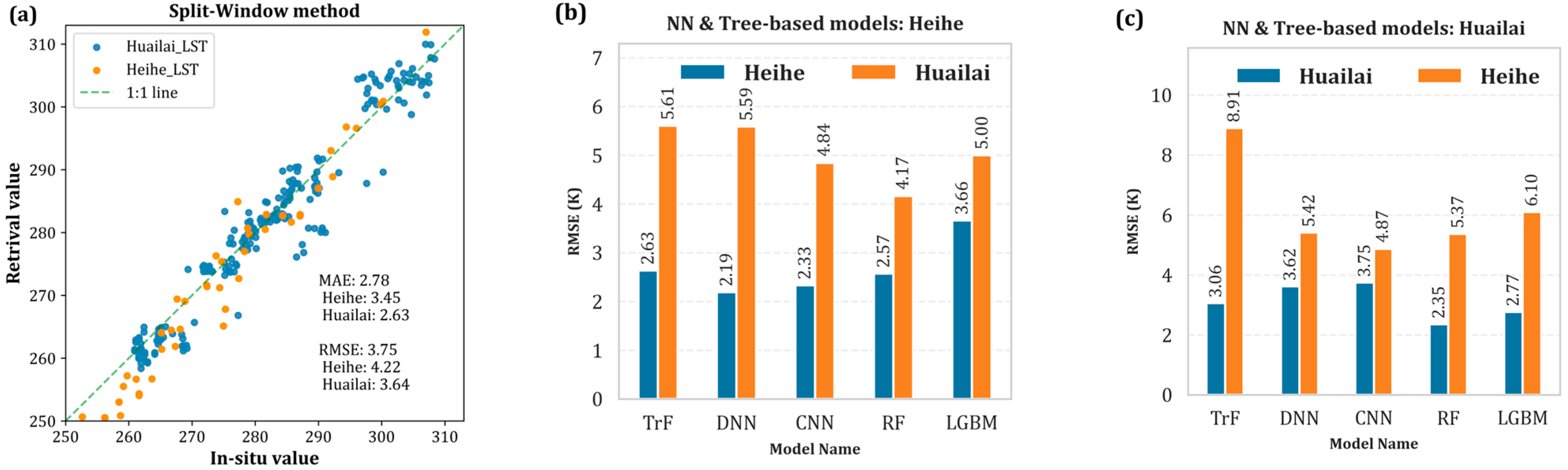
4.1. The SW Algorithm and ML Models LST Retrieval
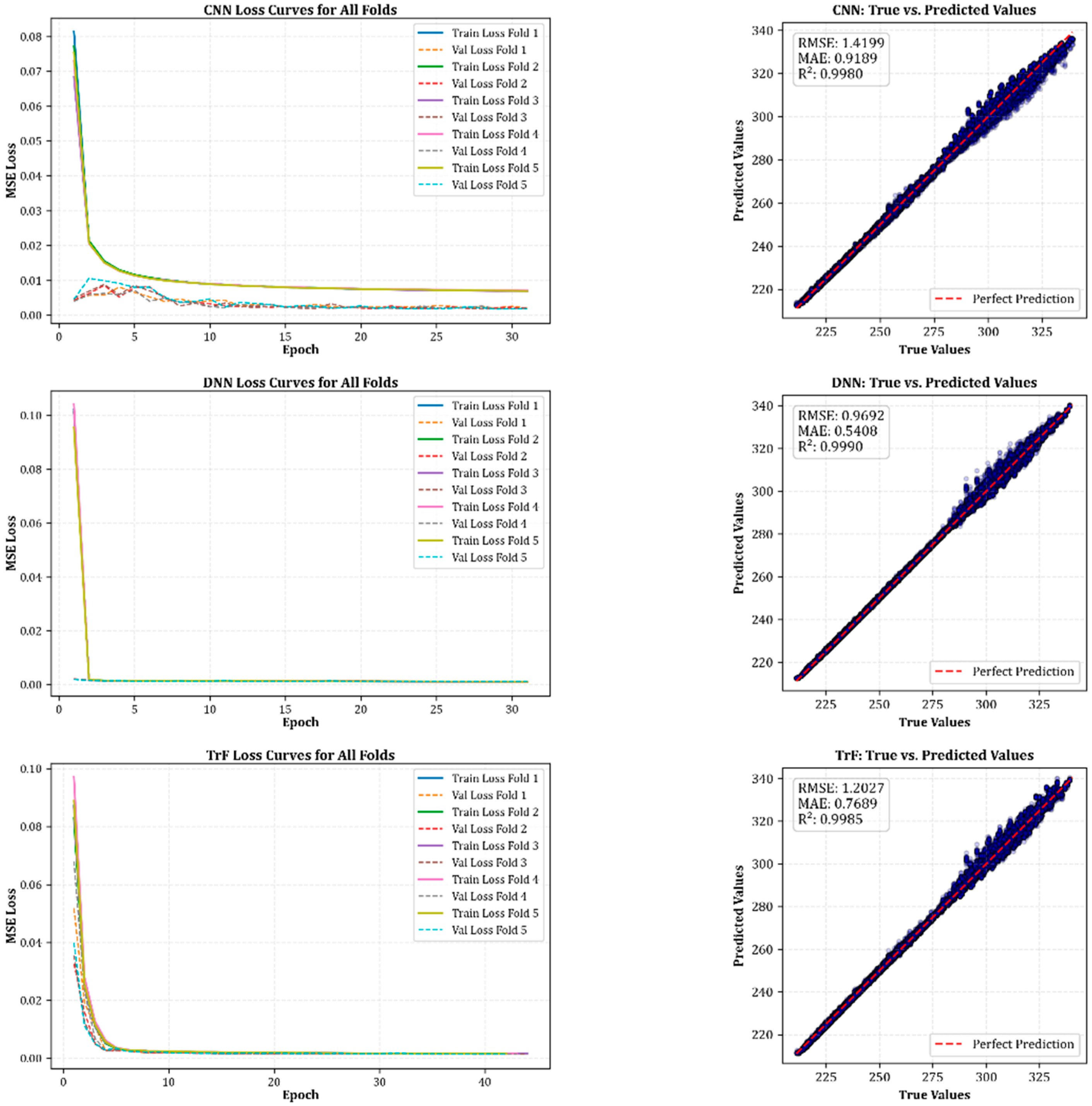
4.2. Pre-Training on the Simulated Dataset
4.3. Fine-Tuning and Cross-Domain Generalization
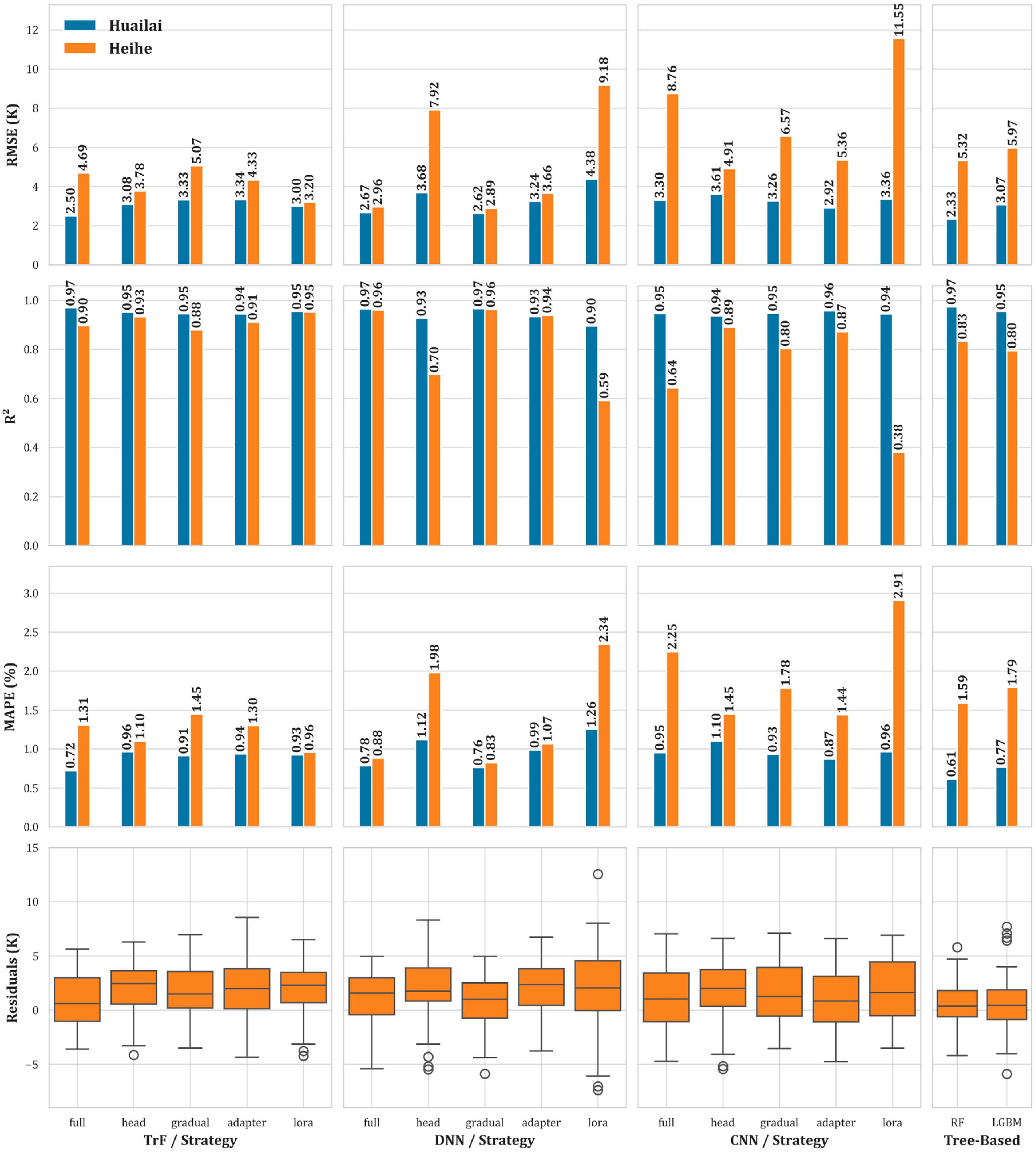
4.3.1. Fine-Tuning on Huailai → Generalization to Heihe
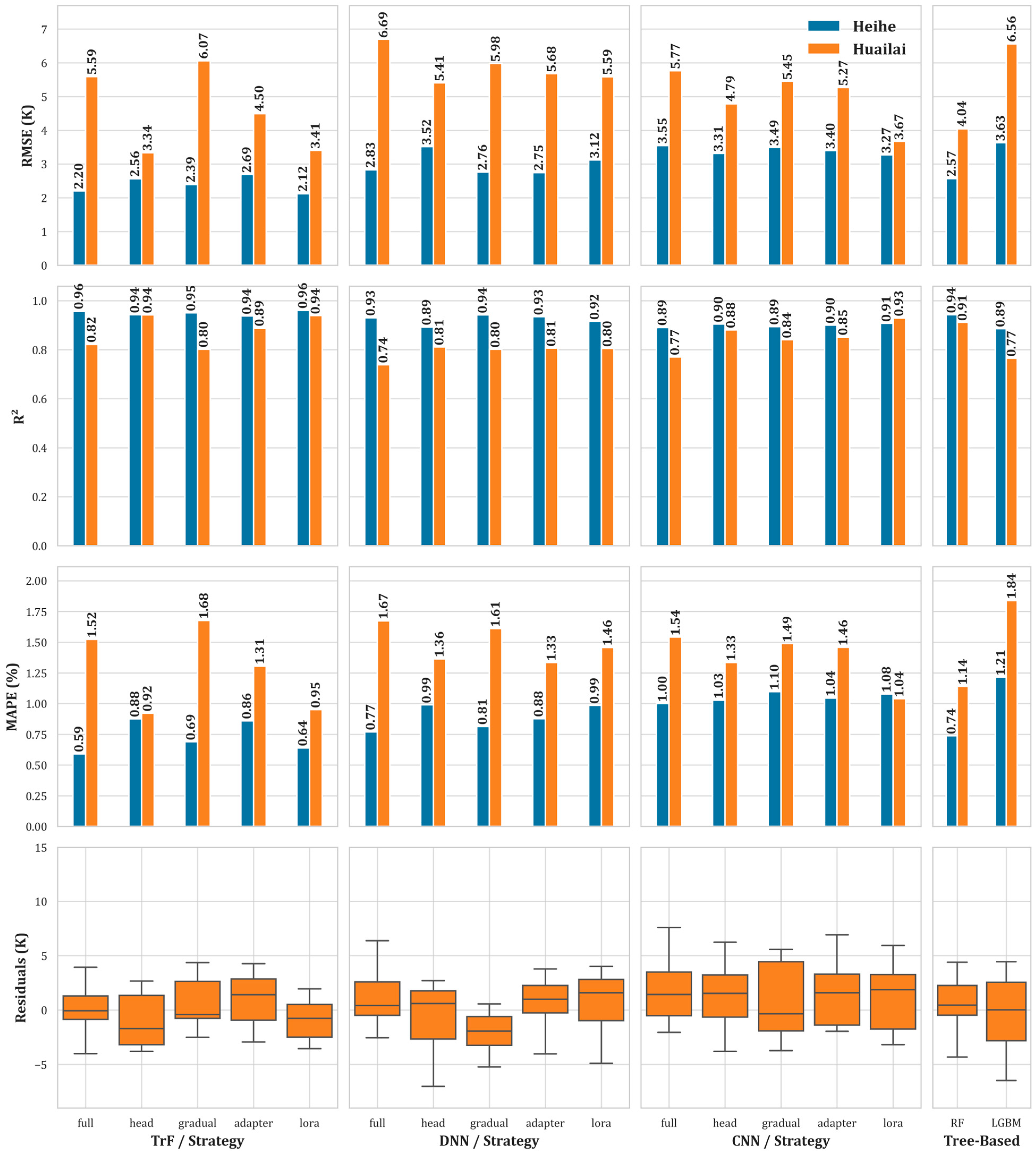
4.3.2. Fine-Tuning on Heihe → Generalization to Huailai
5. Validation
- (I)
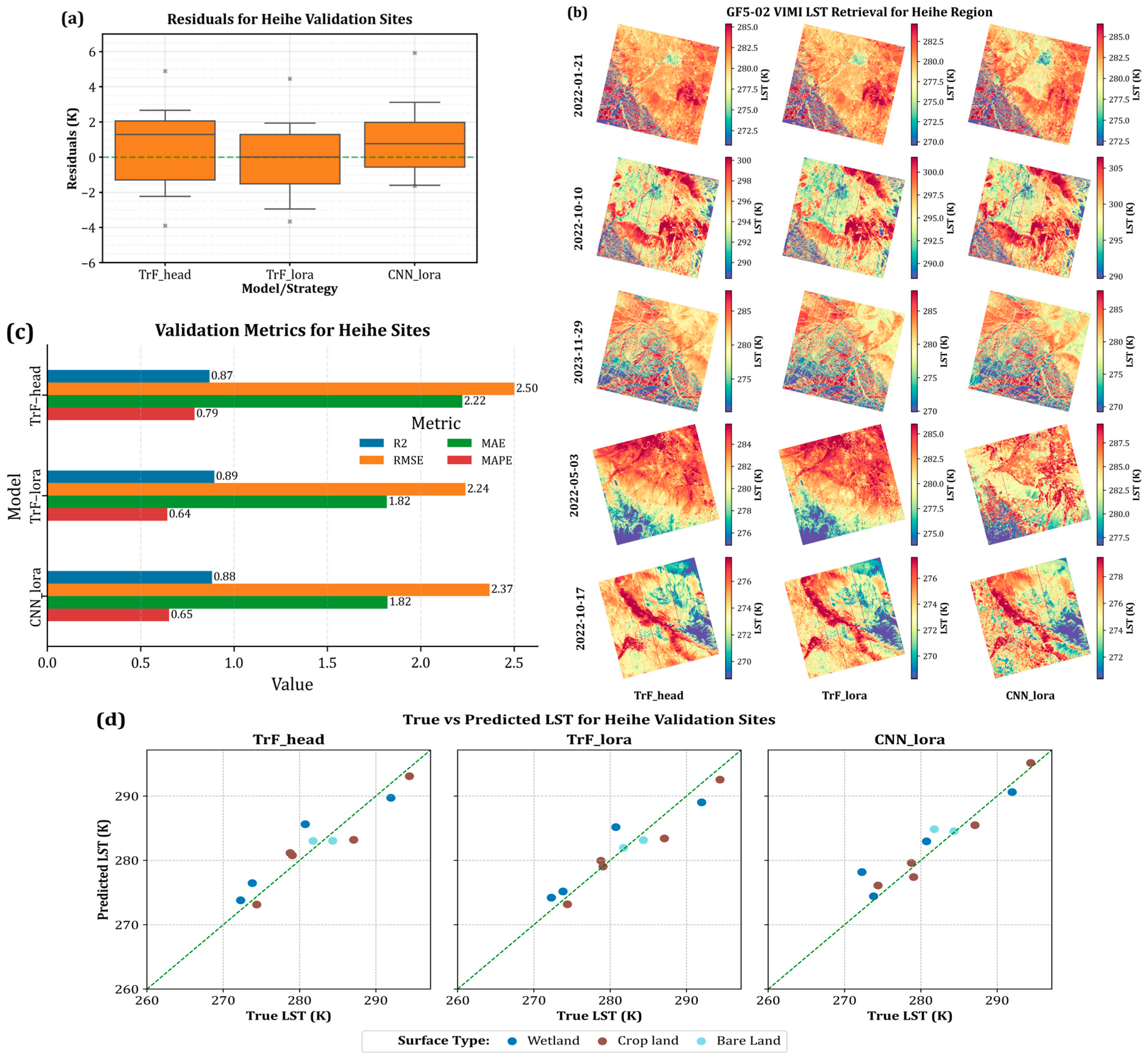
- Real image LST retrieval: The GF5-02/VIMI thermal images at the Huailai and Heihe sites were used for validating real image LST retrieval, focusing on the strongest model–strategy configurations per site and their agreement with co-located, time-matched in situ observations (Figure 9 and Figure 10 describe residual distributions, five date-specific LST maps, aggregated site-level metrics, and pointwise true–predicted agreement by surface type). For Huailai, the DNN with gradual unfreezing and full fine-tuning emerged as the leading strategies, followed by TrF-LoRA and head-only fine-tuning. Gradual unfreezing DNN achieves RMSE = 2.66 K, R2 = 0.96, MAE = 2.24 K, and MAPE = 0.80%, with a bias of +1.76 K over 71 validation samples; the fully fine-tuned DNN is slightly lower on RMSE (2.91 K) and R2 (0.95) with the close MAE (2.45) and MAPE (0.88%), and a comparable bias of +2.13 K across 71 samples. These two configurations therefore deliver sub-3 K errors with >0.95 explained variance in operational imagery while maintaining near-zero median residuals, which is consistent with the tight, symmetric residual boxplots and the near-1:1 scatter evident in Figure 9d. Other strong baselines—TrF-LoRA (RMSE = 3.27 K; R2 = 0.93) and TrF-head (3.5 K; 0.92)—remain competitive. However, gradual unfreezing and full fine-tuning for sufficiently large target domains are defensible and indicate that excessively lightweight adaptation can underfit the radiative variability present in real scenes (Table 7).
- (II)
- Within-site fidelity and cross-site generalization: Fine-tuning on the larger Huailai dataset (≈235 valid samples after physically screening LST ranges) yields consistently low errors on its hold-out set and, crucially, transfers well to Heihe. Among neural strategies, DNN with gradual unfreezing provides the most balanced performance: RMSE ≈ 2.62 K (Huailai hold-out) and ≈2.89 K on Heihe, with R2 around 0.95 and ≈0.93, respectively. TrF-LoRA and head-tuning variants perform similarly on the Huailai holdout (RMSE ≈ 3.00–3.08 K) but are less stable on Heihe (RMSE ≈ 3.20–3.78 K). Tree-based transfer (RF/LGBM) trails the neural approaches in this direction (RMSE ≈ 5.32–5.97 K on Heihe), underscoring the benefit of a pre-trained representation that can be lightly adapted. When the direction is reversed—fine-tuning on the much smaller Heihe dataset (≈54 samples)—the models achieve excellent in-domain accuracy (e.g., TrF-LoRA ≈ 2.12 K and TrF-head ≈ 2.50 K). However, cross-site performance on Huailai is less favorable, with the best results being TrF-head at ≈3.34 K, TrF-LoRA at ≈3.41 K, and CNN-LoRA at ≈3.67 K. Tree models again degrade strongly under distribution shift (RF ≈ 4.13 K; LGBM ≈ 6.57 K). This asymmetry is consistent with sample size and distributional effects: the smaller Heihe set constrains the diversity of radiative and land-cover conditions seen during adaptation, while the richer Huailai set better regularizes the model and improves transfer. Together, the two directions reveal that (a) the pre-trained backbone retains broadly useful thermal structure and (b) the depth of adaptation matters—exposing a modest set of parameters (head-tuning, gradual unfreezing, or compact LoRA) is generally preferable to either freezing too much (adapter-only underfits) or over-specializing.
- (III)
- Sensitivity to outlier filtering (IQR multiplier): To ensure robustness of the reported statistics to the outlier definition, the IQR multiplier used to mask residuals was swept from 0.5 to 4.0. Two stability properties emerge. First, for the reference range of 1.0–1.5, model rankings are unchanged and RMSE variability is typically <1%, confirming that headline conclusions are not artifacts of the threshold. Second, the “stable multiplier”—the smallest multiplier ≥1.0 that keeps RMSE within ±1% of the value at 1.5—lies at 1.0 or 1.5 for almost all model/strategy/site combinations. For example, DNN-full/gradual and TrF-LoRA-head remain stable at 1.5 in Huailai, while CNN/LoRA and TrF-LoRA/head are stable at 1.5 in Heihe. This analysis provides a quantitative guardrail: performance claims persist under reasonable, defensible choices of the residual-masking threshold and are therefore not the result of aggressive outlier trimming.
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, H.; Li, R.; Tu, H.; Cao, B.; Liu, F.; Bian, Z.; Hu, T.; Du, Y.; Sun, L.; Liu, Q. An operational split-window algorithm for generating long-term Land Surface Temperature products from Chinese Fengyun-3 series satellite data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5004514. [Google Scholar] [CrossRef]
- Wang, X.; Yaojun, Z.; Yu, D. Exploring the Relationships between Land Surface Temperature and Its Influencing Factors Using Multisource Spatial Big Data: A Case Study in Beijing, China. Remote Sens. 2023, 15, 1783. [Google Scholar] [CrossRef]
- Adeyeri, O.E.; Folorunsho, A.H.; Ayegbusi, K.I.; Bobde, V.; Adeliyi, T.E.; Ndehedehe, C.E.; Akinsanola, A.A. Land surface dynamics and meteorological forcings modulate land surface temperature characteristics. Sustain. Cities Soc. 2024, 101, 105072. [Google Scholar] [CrossRef]
- Ru, C.; Duan, S.B.; Jiang, X.G.; Li, Z.L.; Huang, C.; Liu, M. An extended SW-TES algorithm for land surface temperature and emissivity retrieval from ECOSTRESS thermal infrared data over urban areas. Remote Sens. Environ. 2023, 290, 113544. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Li, Z.L.; Wu, H.; Duan, S.B.; Zhao, W.; Ren, H.; Liu, X.; Leng, P.; Tang, R.; Ye, X.; Zhu, J.; et al. Satellite remote sensing of global land surface temperature: Definition, methods, products, and applications. Rev. Geophys. 2023, 61, e2022RG000777. [Google Scholar] [CrossRef]
- Bright, R.M.; Davin, E.; O’Halloran, T.; Pongratz, J.; Zhao, K.; Cescatti, A. Local temperature response to land cover and management change driven by non-radiative processes. Nat. Clim. Change 2017, 7, 296–302. [Google Scholar] [CrossRef]
- Xu, S.; Wang, D.; Liang, S.; Jia, A.; Li, R.; Wang, Z.; Liu, Y. A novel approach to estimate land surface temperature from Landsat top-of-atmosphere reflective and emissive data using transfer-learning neural network. Sci. Total Environ. 2024, 955, 176783. [Google Scholar] [CrossRef]
- Luyssaert, S.; Jammet, M.; Stoy, P.C.; Estel, S.; Pongratz, J.; Ceschia, E.; Churkina, G.; Don, A.; Erb, K.; Ferlicoq, M.; et al. Land management and land-cover change have impacts of similar magnitude on surface temperature. Nat. Clim. Change 2014, 4, 389–393. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, M.; Motesharrei, S.; Mu, Q.; Kalnay, E.; Li, S. Local cooling and warming effects of forests based on satellite observations. Nat. Commun. 2015, 6, 6603. [Google Scholar] [CrossRef]
- Wang, W.; Brönnimann, S.; Zhou, J.; Li, S.; Wang, Z. Near-surface air temperature estimation for areas with sparse observations based on transfer learning. ISPRS J. Photogramm. Remote Sens. 2025, 220, 712–727. [Google Scholar] [CrossRef]
- Song, L.; Ding, Z.; Kustas, W.P.; Xu, Y.; Zhao, G.; Liu, S.; Ma, M.; Xue, K.; Bai, Y.; Xu, Z. Applications of a thermal-based two-source energy balance model coupled to surface soil moisture. Remote Sens. Environ. 2022, 271, 112923. [Google Scholar] [CrossRef]
- Chen, J.M.; Liu, J. Evolution of evapotranspiration models using thermal and shortwave remote sensing data. Remote Sens. Environ. 2020, 237, 111594. [Google Scholar] [CrossRef]
- Gallego-Elvira, B.; Taylor, H.M.; Harris, P.P.; Ghent, D. Evaluation of regional-scale soil moisture-surface flux dynamics in Earth system models based on satellite observations of land surface temperature. Geophys. Res. Lett. 2019, 46, 5480–5488. [Google Scholar] [CrossRef]
- Alexander, C. Normalized difference spectral indices and urban land cover as indicators of land surface temperature (LST). Int. J. Appl. Earth Obs. Geoinf. 2020, 86, 102013. [Google Scholar]
- Masoudi, M.; Tan, P.Y. Multi-year comparison of the effects of spatial pattern of urban green spaces on urban land surface temperature. Landsc. Urban Plan. 2019, 184, 44–58. [Google Scholar] [CrossRef]
- Wu, C.; Li, J.; Wang, C.; Song, C.; Chen, Y.; Finka, M.; La Rosa, D. Understanding the relationship between urban blue infrastructure and land surface temperature. Sci. Total Environ. 2019, 694, 133742. [Google Scholar] [CrossRef] [PubMed]
- Zhou, D.C.; Xiao, J.F.; Bonafoni, S.; Berger, C.; Deilami, K.; Zhou, Y.Y.; Frolking, S.; Yao, R.; Qiao, Z.; Sobrino, J.A. Satellite remote sensing of surface urban heat islands: Progress, challenges, and perspectives. Remote Sens. 2019, 11, 48. [Google Scholar] [CrossRef]
- Zink, M.; Mai, J.; Cuntz, M.; Samaniego, L. Conditioning a hydrologic model using patterns of remotely sensed land surface temperature. Water Resour. Res. 2018, 54, 2976–2998. [Google Scholar] [CrossRef]
- Parinussa, R.M.; Lakshmi, V.; Johnson, F.; Sharma, A. Comparing and combining remotely sensed land surface temperature products for improved hydrological applications. Remote Sens. 2016, 8, 162. [Google Scholar] [CrossRef]
- Reyes, B.; Hogue, T.; Maxwell, R. Urban irrigation suppresses land surface temperature and changes the hydrologic regime in semi-arid regions. Water 2018, 10, 1563. [Google Scholar] [CrossRef]
- Bojinski, S.; Verstraete, M.; Peterson, T.C.; Richter, C.; Simmons, A.; Zemp, M. The concept of essential climate variables in support of climate research, applications, and policy. Bull. Am. Meteorol. Soc. 2014, 95, 1431–1443. [Google Scholar] [CrossRef]
- Dolman, A.J.; Belward, A.; Briggs, S.; Dowell, M.; Eggleston, S.; Hill, K.; Richter, C.; Simmons, A. A post-Paris look at climate observations. Nat. Geosci. 2016, 9, 646. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, B.H.; Li, Z.L. A practical two-step framework for all-sky land surface temperature estimation. Remote Sens. Environ. 2024, 303, 113991. [Google Scholar] [CrossRef]
- Li, R.; Li, H.; Hu, T.; Bian, Z.; Liu, F.; Cao, B.; Du, Y.; Sun, L.; Liu, Q. Land surface temperature retrieval from sentinel-3A SLSTR data: Comparison among split-window, dual-window, three-channel, and dual-angle algorithms. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5003114. [Google Scholar] [CrossRef]
- Mo, Y.; Xu, Y.; Chen, H.; Zhu, S. A review of reconstructing remotely sensed land surface temperature under cloudy conditions. Remote Sens. 2021, 13, 2838. [Google Scholar] [CrossRef]
- Duan, S.B.; Li, Z.L.; Tang, B.H.; Wu, H.; Tang, R.; Bi, Y.; Zhou, G. Estimation of diurnal cycle of land surface temperature at high temporal and spatial resolution from clear-sky MODIS data. Remote Sens. 2014, 6, 3247–3262. [Google Scholar] [CrossRef]
- Chen, Y.; Duan, S.B.; Ren, H.; Labed, J.; Li, Z.L. Algorithm development for land surface temperature retrieval: Application to Chinese Gaofen-5 data. Remote Sens. 2017, 9, 161. [Google Scholar] [CrossRef]
- Meng, X.; Cheng, J. Estimating land and sea surface temperature from cross-calibrated Chinese Gaofen-5 thermal infrared data using split-window algorithm. IEEE Geosci. Remote Sens. Lett. 2019, 17, 509–513. [Google Scholar] [CrossRef]
- Ye, X.; Ren, H.; Liu, R.; Qin, Q.; Liu, Y.; Dong, J. Land surface temperature estimate from Chinese Gaofen-5 satellite data using split-window algorithm. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5877–5888. [Google Scholar] [CrossRef]
- Ye, X.; Ren, H.; Liang, Y.; Zhu, J.; Guo, J.; Nie, J.; Zeng, H.; Zhao, Y.; Qian, Y. Cross-calibration of Chinese Gaofen-5 thermal infrared images and its improvement on land surface temperature retrieval. Int. J. Appl. Earth Obs. Geoinf. 2021, 101, 102357. [Google Scholar] [CrossRef]
- Chen, Y.; Duan, S.B.; Labed, J.; Li, Z.L. Development of a split-window algorithm for estimating sea surface temperature from the Chinese Gaofen-5 data. Int. J. Remote Sens. 2018, 40, 1621–1639. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H.; Du, Y.; Cao, B.; Liu, Q.; Sun, L.; Zhu, J.; Mo, F. A temperature and emissivity separation algorithm for Chinese gaofen-5 satellite data. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Zhao, E.; Han, Q.; Gao, C. Surface temperature retrieval from Gaofen-5 observation and its validation. IEEE Access 2020, 9, 9403–9410. [Google Scholar] [CrossRef]
- Tang, B.H. Nonlinear split-window algorithms for estimating land and sea surface temperatures from simulated Chinese Gaofen-5 satellite data. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6280–6289. [Google Scholar] [CrossRef]
- Wang, H.; Mao, K.; Yuan, Z.; Shi, J.; Cao, M.; Qin, Z.; Duan, S.; Tang, B. A method for land surface temperature retrieval based on model-data-knowledge-driven and deep learning. Remote Sens. Environ. 2021, 265, 112665. [Google Scholar] [CrossRef]
- Ren, H.; Ye, X.; Liu, R.; Dong, J.; Qin, Q. Improving land surface temperature and emissivity retrieval from the Chinese Gaofen-5 satellite using a hybrid algorithm. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1080–1090. [Google Scholar] [CrossRef]
- Zheng, X.; Li, Z.L.; Nerry, F.; Zhang, X. A new thermal infrared channel configuration for accurate land surface temperature retrieval from satellite data. Remote Sens. Environ. 2019, 231, 111216. [Google Scholar] [CrossRef]
- Gillespie, A.R.; Abbott, E.A.; Gilson, L.; Hulley, G.; Jiménez-Muñoz, J.C.; Sobrino, J.A. Residual errors in ASTER temperature and emissivity standard products AST08 and AST05. Remote Sens. Environ. 2011, 115, 3681–3694. [Google Scholar] [CrossRef]
- Ye, X.; Ren, H.; Nie, J.; Hui, J.; Jiang, C.; Zhu, J.; Fan, W.; Qian, Y.; Liang, Y. Simultaneous estimation of land surface and atmospheric parameters from thermal hyperspectral data using a LSTM–CNN combined deep neural network. IEEE Geosci. Remote Sens. Lett. 2021, 19, 5508705. [Google Scholar] [CrossRef]
- Ye, X.; Hui, J.; Wang, P.; Zhu, J.; Yang, B. A Modified Transfer-Learning-Based Approach for Retrieving Land Surface Temperature from Landsat-8 TIRS Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4411511. [Google Scholar] [CrossRef]
- Iman, M.; Arabnia, H.R.; Rasheed, K. A review of deep transfer learning and recent advancements. Technologies 2023, 11, 40. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, S.; Ermon, S.; Lobell, D.B. Transfer learning in environmental remote sensing. Remote Sens. Environ. 2024, 301, 113924. [Google Scholar] [CrossRef]
- Tan, J.; NourEldeen, N.; Mao, K.; Shi, J.; Li, Z.; Xu, T.; Yuan, Z. Deep learning convolutional neural network for the retrieval of land surface temperature from AMSR2 data in China. Sensors 2019, 19, 2987. [Google Scholar] [CrossRef]
- Mao, K.; Wang, H.; Shi, J.; Heggy, E.; Wu, S.; Bateni, S.M.; Du, G. A general paradigm for retrieving soil moisture and surface temperature from passive microwave remote sensing data based on artificial intelligence. Remote Sens. 2023, 15, 1793. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proc. IEEE 2021, 109, 43–76. [Google Scholar] [CrossRef]
- Niu, S.; Liu, Y.; Wang, J.; Song, H. A decade survey of transfer learning (2010–2020). IEEE Trans. Artif. Intell. 2020, 1, 151–166. [Google Scholar] [CrossRef]
- Fathi, M.; Arefi, H.; Shah-Hosseini, R.; Moghimi, A. Super-Resolution of Landsat-8 Land Surface Temperature Using Kolmogorov–Arnold Networks with PlanetScope Imagery and UAV Thermal Data. Remote Sens. 2025, 17, 1410. [Google Scholar] [CrossRef]
- Zheng, L.; Cao, B.; Na, Q.; Qin, B.; Bai, J.; Du, Y.; Li, H.; Bian, Z.; Xiao, Q.; Liu, Q. Estimation and Evaluation of 15 Minute, 40 Meter Surface Upward Longwave Radiation Downscaled from the Geostationary FY-4B AGRI. Remote Sens. 2024, 16, 1158. [Google Scholar] [CrossRef]
- Heidarian, P.; Li, H.; Zhang, Z.; Li, R.; Liu, Q.; Yumin, T. High-Resolution Land Surface Temperature Retrieval from GF5-02 VIMI Data using an Operational Split-Window Algorithm. In Proceedings of the IGARSS 2024-2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024. [Google Scholar]
- Li, H.; Li, R.; Yang, Y.; Cao, B.; Bian, Z.; Hu, T.; Du, Y.; Sun, L.; Liu, Q. Temperature-based and radiance-based validation of the collection 6 MYD11 and MYD21 land surface temperature products over barren surfaces in northwestern China. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1794–1807. [Google Scholar] [CrossRef]
- Li, H.; Sun, D.; Yu, Y.; Wang, H.; Liu, Y.; Liu, Q.; Du, Y.; Wang, H.; Cao, B. Evaluation of the VIIRS and MODIS LST products in an arid area of Northwest China. Remote Sens. Environ. 2014, 142, 111–121. [Google Scholar] [CrossRef]
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Ball, J.E.; Anderson, D.T.; Chan, C.S. Comprehensive survey of deep learning in remote sensing: Theories, tools, and challenges for the community. J. Appl. Remote Sens. 2017, 11, 042609. [Google Scholar] [CrossRef]
- Torrey, L.; Shavlik, J. Transfer learning. In Handbook of Research on Machine Learning Applications and Trends: Algorithms, Methods, and Techniques; IGI Global Scientific Publishing: Hershey, PA, USA, 2010; pp. 242–264. [Google Scholar]
- Chevallier, F.; Chéruy, F.; Scott, N.A.; Chédin, A. A neural network approach for a fast and accurate computation of a longwave radiative budget. J. Appl. Meteorol. Climatol. 1998, 37, 1385–1397. [Google Scholar] [CrossRef]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How transferable are features in deep neural networks? Adv. Neural Inf. Process. Syst. 2014, 27, 3320–3328. [Google Scholar]
- Marmanis, D.; Datcu, M.; Esch, T.; Stilla, U. Deep learning earth observation classification using ImageNet pre-trained networks. IEEE Geosci. Remote Sens. Lett. 2016, 13, 105–109. [Google Scholar] [CrossRef]
- Li, J.; Yang, H.; Chen, W.; Li, C.; Yang, G. Generating Spatiotemporal Seamless Data of Clear-Sky Land Surface Temperature Using Synthetic Aperture Radar, Digital Elevation Mode, and Machine Learning over Vegetation Areas. J. Remote Sens. 2024, 4, 0071. [Google Scholar] [CrossRef]
- Heidarian, P.; Antezana Lopez, F.P.; Tan, Y.; Fathtabar Firozjaee, S.; Yousefi, T.; Salehi, H.; Osman Pour, A.; Elena Oscori Marca, M.; Zhou, G.; Azhdari, A.; et al. Deep Learning and Transformer Models for Groundwater Level Prediction in the Marvdasht Plain: Protecting UNESCO Heritage Sites—Persepolis and Naqsh-e Rustam. Remote Sens. 2025, 17, 2532. [Google Scholar] [CrossRef]
- Bragilovski, M.; Kapri, Z.; Rokach, L.; Levy-Tzedek, S. TLTD: Transfer learning for tabular data. Appl. Soft Comput. 2023, 147, 110748. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random Forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Segev, N.; Harel, M.; Mannor, S.; Crammer, K.; El-Yaniv, R. Learn on source, refine on target: A model transfer learning framework with random forests. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1811–1824. [Google Scholar] [CrossRef]
- Massaoudi, M.; Refaat, S.S.; Chihi, I.; Trabelsi, M.; Oueslati, F.S.; Abu-Rub, H. A novel stacked generalization ensemble-based hybrid LGBM-XGB-MLP model for Short-Term Load Forecasting. Energy 2021, 214, 118874. [Google Scholar] [CrossRef]
- Yao, S.; Kang, Q.; Zhou, M.; Rawa, M.J.; Abusorrah, A. A survey of transfer learning for machinery diagnostics and prognostics. Artif. Intell. Rev. 2023, 56, 2871–2922. [Google Scholar] [CrossRef]
- Chen, W.; Qiu, Y.; Feng, Y.; Li, Y.; Kusiak, A. Diagnosis of wind turbine faults with transfer learning algorithms. Renew. Energy 2021, 163, 2053–2067. [Google Scholar] [CrossRef]
- Vrbancic, G.; Podgorelec, V. Transfer learning with adaptive fine-tuning. IEEE Access 2020, 8, 196197–196211. [Google Scholar] [CrossRef]
- Davila, A.; Colan, J.; Hasegawa, Y. Comparison of fine-tuning strategies for transfer learning in medical image classification. Image Vis. Comput. 2024, 146, 105012. [Google Scholar] [CrossRef]
- Kumar, A.; Raghunathan, A.; Jones, R.; Ma, T.; Liang, P. Fine-tuning can distort pre-trained features and underperform out-of-distribution. arXiv 2022, arXiv:2202.10054. [Google Scholar]
- Howard, J.; Ruder, S. Universal language model fine-tuning for text classification. arXiv 2018, arXiv:1801.06146. [Google Scholar] [CrossRef]
- Yin, D.; Hu, L.; Li, B.; Zhang, Y. Adapter is all you need for tuning visual tasks. arXiv 2023, arXiv:2311.15010. [Google Scholar] [CrossRef]
- Yin, D.; Yang, Y.; Wang, Z.; Yu, H.; Wei, K.; Sun, X. 1% vs. 100%: Parameter-efficient low rank adapter for dense predictions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 20116–20126. [Google Scholar]
- Li, X.; Kim, A. A Study to Evaluate the Impact of LoRA Fine-tuning on the Performance of Non-functional Requirements Classification. arXiv 2025, arXiv:2503.07927. [Google Scholar]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Becker, F.; Li, Z.L. Surface temperature and emissivity at various scales: Definition, measurement and related problems. Remote Sens. Rev. 1995, 12, 225–253. [Google Scholar] [CrossRef]
- Li, Z.L.; Wu, H.; Wang, N.; Qiu, S.; Sobrino, J.A.; Wan, Z.; Tang, B.H.; Yan, G. Land surface emissivity retrieval from satellite data. Int. J. Remote Sens. 2013, 34, 3084–3127. [Google Scholar] [CrossRef]
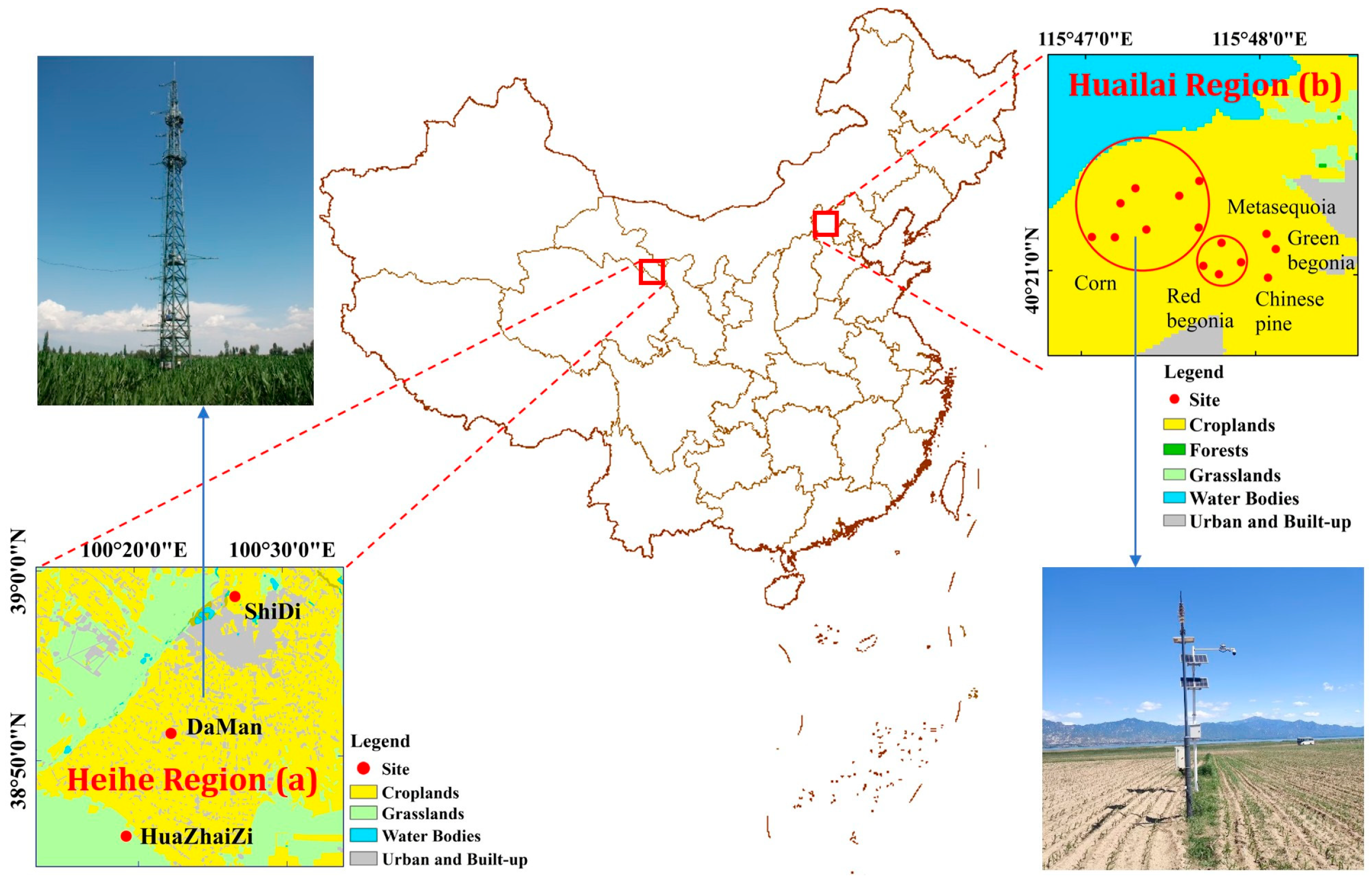


| Network | Site | Longitude | Latitude | Surface Type |
|---|---|---|---|---|
| Heihe | DaMan | 100.3722 | 38.8556 | Corn |
| HuaZhaizi | 100.3201 | 38.7659 | Desert Steppe | |
| ShiDi | 100.4464 | 38.9751 | Weed | |
| Huailai | Red begonia1 | 115.7966 | 40.3522 | Shrub |
| Red begonia2 | 115.7985 | 40.3508 | ||
| Red begonia3 | 115.7949 | 40.3505 | ||
| Red begonia4 | 115.7964 | 40.3499 | ||
| Green begonia | 115.8018 | 40.3518 | ||
| Metasequoia | 115.8009 | 40.3529 | Forest | |
| Chinese pine | 115.8011 | 40.3497 | ||
| Corn1 | 115.7842 | 40.3525 | Crop | |
| Corn2 | 115.7864 | 40.3525 | ||
| Corn3 | 115.7869 | 40.3550 | ||
| Corn4 | 115.7883 | 40.3561 | ||
| Corn5 | 115.7944 | 40.3567 | ||
| Corn6 | 115.7925 | 40.3556 | ||
| Corn7 | 115.7944 | 40.3533 | ||
| Corn8 | 115.7894 | 40.3531 |
| Band | Spectral Range | Band | Spectral Range |
|---|---|---|---|
| B1 B2 B3 B4 B5 B6 | 0.45–0.52 μm 0.52–0.60 μm 0.62–0.68 μm 0.76–0.86 μm 1.6–1.8 μm 2.1–2.4 μm | B7 B8 B9 B10 B11 B12 | 3.5–3.9 μm 4.8–5.0 μm 8.0–8.4 μm 8.4–8.9 μm 10.4–11.3 μm 11.4–12.5 μm |
| Model | Hyperparameters | Variables | Top Features (Permutation Importance) |
|---|---|---|---|
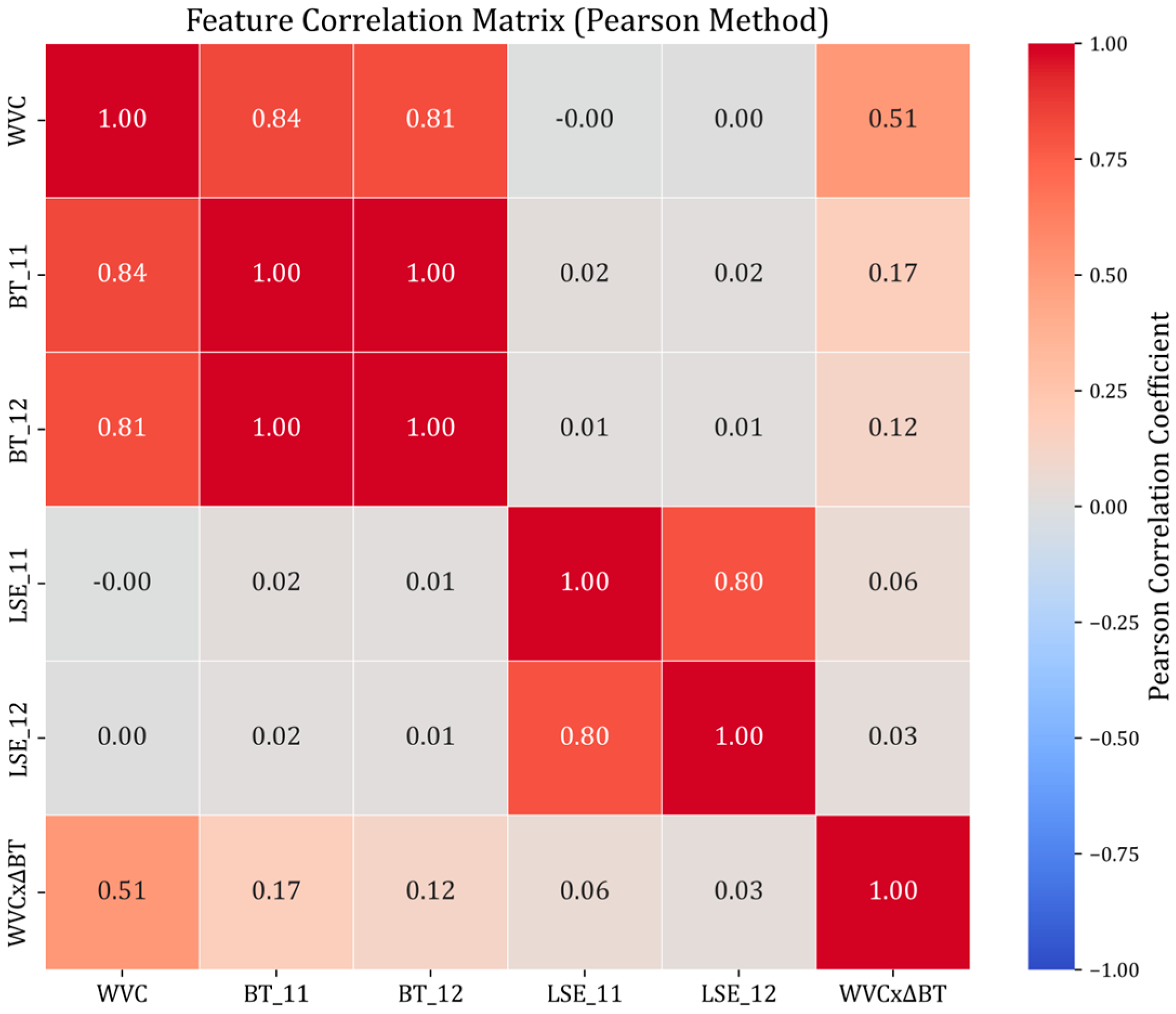
| TrF | hidden_dim = 128, num_layers = 6, dropout = 0.3, num_head = 8 | water vapor content (WVC), brightness temperature (BT) for channel-11&12, land surface emissivity (LSE) for channel-11&12, and WVC × ΔBT | BT_11, BT_12, WVC × ΔBT |
| DNN | hidden_dim = 128, num_layers = 6, dropout = 0.3 | BT_11, BT_12, WVC × ΔBT | |
| CNN | hidden_dim = 128, dropout = 0.3 | BT_11, BT_12, WVC | |
| RF | n_estimators = 300, max_depth = 30, max_features = ‘sqrt’, min_samples_split = 2, min_samples_leaf = 1 | BT_11, BT_12, WVC | |
| LGBM | n_estimators = 300, max_depth = 30, num_leaves = 70, learning_rate = 0.1, feature_fraction = 0.8, bagging_fraction = 0.7, lambda_l1 = 0, lambda_l2 = 1.0 | BT_11, WVC, BT_12 |
| Model | Avg CV RSME (K) | Avg CV R2 | Test RMSE (K) | Test MAE (K) | Test R2 | Top Features (Permutation Importance) |
|---|---|---|---|---|---|---|
| TrF | 1.21 | 0.9980 | 0.999 | 0.6000 | 0.9990 | BT_11, BT_12, WVC × ΔBT |
| DNN | 0.96 | 0.9990 | 0.936 | 0.5182 | 0.9991 | BT_11, BT_12, WVC × ΔBT |
| CNN | 1.42 | 0.9980 | 1.280 | 0.8109 | 0.9983 | BT_11, BT_12, WVC |
| RF | 0.29 | 0.9999 | 0.296 | 0.1600 | 0.9999 | BT_11, BT_12, WVC |
| LGBM | 0.416 | 0.9998 | 0.410 | 0.2920 | 0.9998 | BT_11, WVC, BT_12 |
| Model | Strategy | Huailai RMSE(K) | Huailai R2 | Huailai MAPE (%) | Heihe RMSE (K) | Heihe R2 | Heihe MAPE (%) |
|---|---|---|---|---|---|---|---|
| TrF | full | 2.50 | 0.97 | 0.72 | 4.69 | 0.90 | 1.31 |
| head | 3.08 | 0.95 | 0.96 | 3.78 | 0.93 | 1.10 | |
| gradual | 3.33 | 0.95 | 0.91 | 5.07 | 0.88 | 1.45 | |
| adapter | 3.34 | 0.94 | 0.94 | 4.33 | 0.91 | 1.30 | |
| lora | 3.00 | 0.95 | 0.93 | 3.20 | 0.95 | 0.96 | |
| DNN | full | 2.67 | 0.97 | 0.78 | 2.96 | 0.96 | 0.88 |
| head | 3.68 | 0.93 | 1.12 | 7.92 | 0.70 | 1.98 | |
| gradual | 2.62 | 0.97 | 0.76 | 2.89 | 0.96 | 0.83 | |
| adapter | 3.24 | 0.93 | 0.99 | 3.66 | 0.94 | 1.07 | |
| lora | 4.38 | 0.90 | 1.26 | 9.18 | 0.59 | 2.34 | |
| CNN | full | 3.30 | 0.95 | 0.95 | 8.76 | 0.64 | 2.25 |
| head | 3.61 | 0.94 | 1.10 | 4.91 | 0.89 | 1.45 | |
| gradual | 3.26 | 0.95 | 0.93 | 6.57 | 0.80 | 1.78 | |
| adapter | 2.92 | 0.96 | 0.87 | 5.36 | 0.87 | 1.44 | |
| lora | 3.36 | 0.94 | 0.96 | 11.55 | 0.38 | 2.91 | |
| RF | default | 2.33 | 0.97 | 0.61 | 5.32 | 0.83 | 1.59 |
| LGBM | default | 3.07 | 0.95 | 0.77 | 5.97 | 0.80 | 1.79 |
| Model | Strategy | Heihe RMSE (K) | Heihe R2 | Heihe MAPE (%) | Huailai RMSE (K) | Huailai R2 | Huailai MAPE (%) |
|---|---|---|---|---|---|---|---|
| TrF | full | 2.20 | 0.96 | 0.59 | 5.59 | 0.82 | 1.52 |
| head | 2.56 | 0.94 | 0.88 | 3.34 | 0.94 | 0.92 | |
| gradual | 2.39 | 0.95 | 0.69 | 6.07 | 0.80 | 1.68 | |
| adapter | 2.69 | 0.94 | 0.86 | 4.50 | 0.89 | 1.31 | |
| lora | 2.12 | 0.96 | 0.64 | 3.41 | 0.94 | 0.59 | |
| DNN | full | 2.83 | 0.93 | 0.77 | 6.69 | 0.74 | 1.67 |
| head | 3.53 | 0.89 | 0.99 | 5.41 | 0.81 | 1.36 | |
| gradual | 2.76 | 0.94 | 0.81 | 5.98 | 0.80 | 1.61 | |
| adapter | 2.75 | 0.93 | 0.88 | 5.68 | 0.81 | 1.33 | |
| lora | 3.12 | 0.92 | 0.99 | 5.59 | 0.80 | 1.46 | |
| CNN | full | 3.55 | 0.89 | 1.00 | 5.77 | 0.77 | 1.54 |
| head | 3.31 | 0.90 | 1.03 | 4.79 | 0.88 | 1.33 | |
| gradual | 3.49 | 0.89 | 1.10 | 5.45 | 0.84 | 1.49 | |
| adapter | 3.40 | 0.90 | 1.04 | 5.27 | 0.85 | 1.46 | |
| lora | 3.27 | 0.91 | 1.08 | 3.67 | 0.93 | 1.04 | |
| RF | default | 2.57 | 0.94 | 0.74 | 4.04 | 0.91 | 1.14 |
| LGBM | default | 3.63 | 0.89 | 1.21 | 6.56 | 0.77 | 1.84 |
| Region | Best Model/Strategy | RMSE (K) | R2 | MAE (K) | MAPE (%) | Bias (K) | Valid Sample (n) |
|---|---|---|---|---|---|---|---|
| Huailai | TrF/head | 3.50 | 0.92 | 3.26 | 1.17 | 3.03 | 71 |
| TrF/lora | 3.27 | 0.93 | 3.00 | 1.08 | 2.64 | 71 | |
| DNN/full | 2.91 | 0.95 | 2.45 | 0.88 | 2.13 | 71 | |
| DNN/gradual | 2.66 | 0.96 | 2.24 | 0.80 | 1.76 | 71 | |
| Heihe | TrF/head | 2.50 | 0.87 | 2.22 | 0.79 | 0.42 | 11 |
| TrF/lora | 2.24 | 0.90 | 1.81 | 0.64 | −0.14 | 11 | |
| CNN/lora | 2.37 | 0.88 | 1.82 | 0.65 | 0.99 | 11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heidarian, P.; Li, H.; Zhang, Z.; Tan, Y.; Zhao, F.; Cao, B.; Du, Y.; Liu, Q. Cross-Domain Land Surface Temperature Retrieval via Strategic Fine-Tuning-Based Transfer Learning: Application to GF5-02 VIMI Imagery. Remote Sens. 2025, 17, 3803. https://doi.org/10.3390/rs17233803
Heidarian P, Li H, Zhang Z, Tan Y, Zhao F, Cao B, Du Y, Liu Q. Cross-Domain Land Surface Temperature Retrieval via Strategic Fine-Tuning-Based Transfer Learning: Application to GF5-02 VIMI Imagery. Remote Sensing. 2025; 17(23):3803. https://doi.org/10.3390/rs17233803
Chicago/Turabian StyleHeidarian, Peyman, Hua Li, Zelin Zhang, Yumin Tan, Feng Zhao, Biao Cao, Yongming Du, and Qinhuo Liu. 2025. "Cross-Domain Land Surface Temperature Retrieval via Strategic Fine-Tuning-Based Transfer Learning: Application to GF5-02 VIMI Imagery" Remote Sensing 17, no. 23: 3803. https://doi.org/10.3390/rs17233803
APA StyleHeidarian, P., Li, H., Zhang, Z., Tan, Y., Zhao, F., Cao, B., Du, Y., & Liu, Q. (2025). Cross-Domain Land Surface Temperature Retrieval via Strategic Fine-Tuning-Based Transfer Learning: Application to GF5-02 VIMI Imagery. Remote Sensing, 17(23), 3803. https://doi.org/10.3390/rs17233803







