Multi-Scale Long- and Short-Range Structure Aggregation Learning for Low-Illumination Remote Sensing Imagery Enhancement

Abstract

Profiting from the surprising non-linear expressive capacity, deep convolutional neural networks have inspired lots of progress in low illumination (LI) remote sensing image enhancement. The key lies in sufficiently exploiting both the specific long-range (e.g., non-local similarity) and short-range (e.g., local continuity) structures distributed across different scales of each input LI image to build an appropriate deep mapping function from the LI images to their corresponding high-quality counterparts. However, most existing methods can only individually exploit the general long-range or short-range structures shared across most images at a single scale, thus limiting their generalization performance in challenging cases. We propose a multi-scale long–short range structure aggregation learning network for remote sensing imagery enhancement. It features flexible architecture for exploiting features at different scales of the input low illumination (LI) image, with branches including a short-range structure learning module and a long-range structure learning module. These modules extract and combine structural details from the input image at different scales and cast them into pixel-wise scale factors to enhance the image at a finer granularity. The network sufficiently leverages the specific long-range and short-range structures of the input LI image for superior enhancement performance, as demonstrated by extensive experiments on both synthetic and real datasets.

1. Introduction

Optical remote sensing imaging technology offers a powerful tool for wide-area, high-spatial-resolution observation of the ocean, atmosphere, and earth surface, among others [1], through satellites or airborne platforms. It has been widely used in various fields such as environmental monitoring [2], military surveillance [3], and precision agriculture [4]. However, in real-world scenarios, the capture of remote sensing images under low-illumination (LI) conditions—such as at night or in adverse weather—presents a significant challenge. Under these conditions, remote sensing images often suffer from poor visibility, low contrast, and noise, making it difficult for machines to accurately interpret the image content and make correct decisions for downstream tasks. Therefore, enhancing the brightness and contrast of LI images is crucial for improving their quality and enabling reliable analysis.

Considering that inverting high-dimensional LI images into their high-quality counterparts can be highly complex and non-linear, increasing attention has been paid to learning a mapping function from the LI images to their high-quality counterparts using deep convolution neural networks. For example, Eilertsen et al. [5] specifically design a deep convolutional neural network (CNN) to predict the high-dynamic (i.e., high-quality) counterpart of the input images. Liu et al. [6] decompose the problem which recovering a high dynamic range (HDR) image from a single low dynamic range (LDR) input image into specific sub-tasks and use three specialized CNNs to resolve each sub-task. Prarabdh et al. [7] present a novel conditional GAN (cGAN)-based framework trained in an end-to-end fashion to reconstruct a high dynamic range (HDR) image from a single LDR image. These methods establish the deep mapping function using CNNs which mainly focus on exploiting the short-range (i.e., short) structure around each pixel via convolution operations. Recently, inspired by the great success of transformers [8] in both natural language processing (NLP) and computer vision domains, some works introduce vision transformer networks to capture the long-range (e.g., non-local similarity) structure within each image for enhancement [9,10,11,12]. For example, Chen et al. [10] establishes a powerful pre-trained model using transformer network for low-level image restoration tasks, e.g., denoising, super-resolution, deblurring, etc. Zhang et al. [12] proposed a structure-aware lightweight transformer network which utilizes a multi-head attention module to exploit the long-range structures among different local patches and reconstruct high-quality images under the IL imaging conditions.

In general, most existing methods only individually exploit the long-range or short-range structures of input LI images for HDR reconstruction at original image scale. However, many previous studies [13,14] have proven that both long-range and short-range structures in the observed images are crucial for image quality enhancement. Moreover, these structures are often image-specific rather than shared across different images as most existing methods [6,7,15], and often concealed at different scales of the observed images. Therefore, it is necessary to exploit the image-specific long–short range structure across different scales of the images for accurate image enhancement; however, little attention has been paid to this. To fill this gap, we propose a multi-scale long–short range structure aggregation learning network for LI remote sensing imagery enhancement.

Compared with existing methods, we introduce a flexible multi-scale feature aggregation architecture that learns to simultaneously exploit features at different scales of the input LI image for enhancement. Moreover, each branch consists of a short-range structure learning module and a long-range structure learning model. The former adopts a function-mixture architecture which empowers the model to adaptively exploit the short-range structure around each pixel according to its features representation at test phase, while the latter utilizes an image-patch-based transformer architecture to dynamically exploit the long-range correlations between different image patches in a deep feature space. Then, all structures exploited from different scales are aggregated and cast into pixel-wise scale factors for fine-grained image enhancement. By performing these, both the image-specific long-range and short-range structures across different scales of the input LI image can be integrated for enhancement. Extensive experiments on both synthetic and real datasets under different levels of LI conditions demonstrate the superiority of the proposed method over several state-of-the-art competitors in terms of image-quality enhancements.

In summary, this study mainly contributes to the following two aspects:

• We present a novel structure aggregation learning network which is able to simultaneously exploit long-range and short-range structures in the input LI images for quality enhancement. Moreover, different from most existing methods that mainly focus on those general structures shared by different images, the proposed network can exploit the specific structure for each image, thus being flexible to restore images with various contents and illumination conditions.
• We establish the proposed network in a multi-scale manner, which is able to sufficiently exploit the structures concealed across different scales of the input IL image.

The rest of this paper is arranged as follows. A brief review of existing methods related to this study is given in Section 2. Section 3 introduces the proposed multi-scale dynamic long–short range structure aggregation learning network followed by the experimental results in Section 4. Section 5 concludes the paper.

2. Related Work

In this section, we briefly review two lines of existing research that are closely related to this study, including deep learning-based LI image enhancement and dynamic neural networks.

2.1. Deep Learning Based LI Image Enhancement

Due to the low-illumination environment, the captured LI images often lost extensive textures of the target scene, and thus reconstructing a corresponding high-quality counterpart from it is ill-posed [16]. To solve this problem, most recent progress resorts to directly learning a deep mapping function from the LI image and the high-quality counterpart using deep neural networks.

2.1.1. Mapping-Based Method

Learning a model to directly map the features from LDR to HDR is a direct solution. Some methods use single branch networks such as CNN [17,18], and GAN [19], or multi-scale networks [20] to generate HDR images. The direct reconstruction method based on convolutional network is often realized by minimizing the loss. Instead, previous methods that focus on minimizing mean squared-error (MSE) between the target and reconstructed images [18] minimize a hybrid loss that consists of perceptual and adversarial losses in addition to HDR-reconstruction loss. The author thinks that reconstruction loss instead of MSE is more suitable for HDR since it puts more weight on both under-/overexposed regions. The perceptual loss enables the networks to utilize knowledge about objects and image structure for recovering the intensity gradients of saturated and grossly quantized areas. Adversarial loss helps to select the most plausible appearance from multiple solutions. Therefore, the hybrid loss combined with these three losses is more suitable for the current task. Although this method is superior to many methods only using MSE, it is difficult to recover when the saturation area is too large. In [17], an approach with a feature masking mechanism that reduces the contribution of the features from the saturated areas was proposed. This masking approach significantly reduces the artifacts and improves the quality of the final results. Moreover, it adapts the perceptual loss function to the application to be able to reconstruct sharp textures in the saturated regions. Recently, Generative Adversarial Neural Networks (GANs) [21], which consists of a generator and a discriminator, have attracted attention for image generation. The Cycle GAN showed efficient image conversion with a small amount of data compared with other GAN models [22]. Jung et al. [19] propose the enhanced Cycle GAN as a method to increase the exposure of dark images while maintaining the color map of the original image and tone up the image locally while maintaining the bright part. It only uses the luminance channel for training to neglect unnecessary color information and reduce learning time. However, in over saturated areas, the proposed method would have information loss around boundary regions. Also, the proposed method is a little bit darker than the HDR scenes. To avoid the up-sampling of down-sampled features and attempt to reduce blocking and haloing artifacts that may arise from more straight forward approaches, in [20], a novel multi scale CNN architecture, called ExpandNet, is presented. On a local scale, one branch of the network learns how to maintain and expand high-frequency detail, while a dilation branch learns information on larger pixel neighborhoods. A final and third branch provides overall information by learning the global context of the input. Although it does well in certain cases, particularly for content which is heavily under- or overexposed, it cannot completely remove artifacts and needs to require further design to maintain temporal coherence. In [23], Li et al. propose a knowledge distillation approach within a teacher–student framework for end-to-end low-light image enhancement [2]. This approach transfers sophisticated feature representation from a complex teacher network to a more efficient student network, enhancing the student’s performance without increasing computational costs during inference. However, the method faces challenges, especially in its reliance on the teacher’s pre-learned knowledge, which may not be optimally adaptable to the student network’s architecture or the specific characteristics of low-light images. Additionally, the two-stage training process, while effective, adds complexity and requires the careful tuning of the distillation loss for optimal performance.

2.1.2. Generating Exposure Stack-Based Method

A neural network would be an ideal problem solver if it directly extracted the actual scene luminance values from a single LDR image. However, two problems arise when generating an HDR image from a single LDR image. First, there is a lack of mapping information so mapping becomes difficult. Second, if the meta data for the input image does not exist, it is impossible to accurately estimate the HDR luminance. In order to solve these problems, some people put forward that producing a multiple exposure image stack from a single LDR image. In [16], using neural networks with a chain structure to create an LDR image stack by sequentially generating images with different exposure levels from the input LDR image was proposed. In addition, this method solves the gradient vanishing problem by inserting an additional loss function and proposes a new activation function. This method alleviates the dataset quantity problem, but it suffers from severe local inversion artifacts due to the limitations of networks being trained only with the ground truth multi-exposure stack’s supervision. In order to overcome these shortcomings, in [24], an improved method proposed a framework with a different HDR image synthesis method. It incorporates the image decomposition method for reconstructing the HDR image to focus on preserving the image details in exposure transfer tasks. In addition, it proposes a recurrent approach in the multi exposure stack generation to efficiently utilize the recursive process. This approach can remove the severe local inversion artifacts and restore the details regardless of image conditions. In [25], an approach that takes the image filtered by the specific optical filter which can change the transmittance of the channel as the input to generate a logarithmic HDR image and a multi exposure LDR image stack was proposed. By learning the correlation between the filtered LDR image and the HDR image, the merging network successfully realizes the HDR reconstruction of the filtered image. The filtered image contains more dynamic range, but in this paper, the filter is fixed, so it cannot be well adapted to different data. In the realm of low-light image enhancement, the work of Wencheng Wang et al. presents a significant contribution through their adaptive framework leveraging the concept of virtual exposure [26]. The authors propose a method that generates multiple image frames from a single low-light input, employing a virtual exposure enhancer constructed by a quadratic function. This approach adeptly fuses these frames at different exposure levels to produce an enhanced image that improves visual perception. However, despite the method’s effectiveness in revealing details in dark areas and preserving image fidelity, it is not without its shortcomings. One notable limitation is the method’s potential to over-amplify certain local areas with uneven illumination, leading to possible over-enhancement and the introduction of artifacts. Additionally, the reliance on a fixed set of parameters may restrict its adaptability to diverse low-light conditions, suggesting a need for more dynamic parameter adjustment mechanisms.

2.2. Dynamic Neural Networks

Most existing neural network models deal with all pixels equally and learn a general mapping. However, this often fails to achieve satisfactory results. Dynamic networks can adaptively learn image features according to different image characteristics or spatial locations.

2.2.1. Attention Mechanisms

As an important development of deep learning, attention mechanism is widely used in computer vision tasks. The attention mechanism can dynamically generate the attention matrix according to the input image, make the network focus on the information that is more critical to the current task, and filter the irrelevant information, so as to improve the efficiency and accuracy of the model. For example, in [27], it is assumed that all sub functions related to pixels can be accurately approximated by mixing some basic functions with pixel level weights, which can be directly generated through the network. This use of a pixel level mixing weight can be regarded as pixel-level channel attention. In [28], learnable attention modules are proposed to evaluate the importance of different image regions to obtain the required HDR images. They are expected to highlight features complementary to the reference image and exclude regions with motion and severe saturation.

2.2.2. Vision Transformer

Transformer is first proposed to be applied to NLP and achieved remarkable results. After [8,29], transformer is applied to computer vision tasks. In traditional visual tasks, a convolutional neural network is considered as the basic component, but using transformer as an alternative has achieved remarkable results [30]. In visual tasks, patches are used instead of each pixel as input. For example, in [9], the standard transformer is directly applied to the image with as little modification as possible, and an image is divided into multiple patches. These patches are the same as the word processing method in NLP, completely eliminating the dependence on traditional CNNs and obtaining advanced results in image recognition. In [10], the image processing transformer (IPT) proposed by Chen et al. achieves the most advanced performance in super resolution, denoising, and deriving tasks. The IPT consists of multiple different task headers, an encoder, a decoder and multiple different tails. According to different tasks, the features are divided into patches and sent to the encoder. After decoding, it is output through a specific tail. In this way, once the model is trained, the corresponding head and tail modules can be used to complete each task. Building on the success of transformers in computer vision, recent works have further demonstrated their versatility in various imaging tasks. For instance, the Restoration Transformer (Restormer) has been proposed to efficiently handle high-resolution image restoration tasks such as deraining and denoising by capturing long-range interactions, achieving state-of-the-art results with reduced computational complexity [31]. In the realm of remote sensing image change detection, the bitemporal image transformer (BIT) leverages the spatial–temporal context modeling capability of transformers to efficiently detect changes in high-resolution imagery, outperforming convolutional methods with lower computational costs [32]. SpectralFormer introduces a novel approach to hyperspectral image classification by employing transformers to learn spectral sequence information, yielding superior performance over conventional CNN-based methods [33]. Lastly, the integration of Swin Transformer within the UNet architecture (ST-UNet) enhances semantic segmentation of remote sensing images by incorporating global context information, resulting in significant improvements over traditional CNN-based approaches [34].

We have drawn upon the excellent work in deep learning and convolutional neural networks, particularly those focused on low-illumination image enhancement, and proposed a novel approach using multi-scale feature extraction to capture rich features for enhanced performance. This approach effectively overcomes the limitations of traditional deep convolutional neural networks, which rely on fixed receptive fields. Additionally, we have introduced advanced dynamic neural networks into the task of low-illumination remote sensing image enhancement, enabling the model to dynamically and adaptively enhance low-light images across different images or regions. This incorporation of dynamic network principles allows for improved flexibility and performance in handling a variety of low-light conditions.

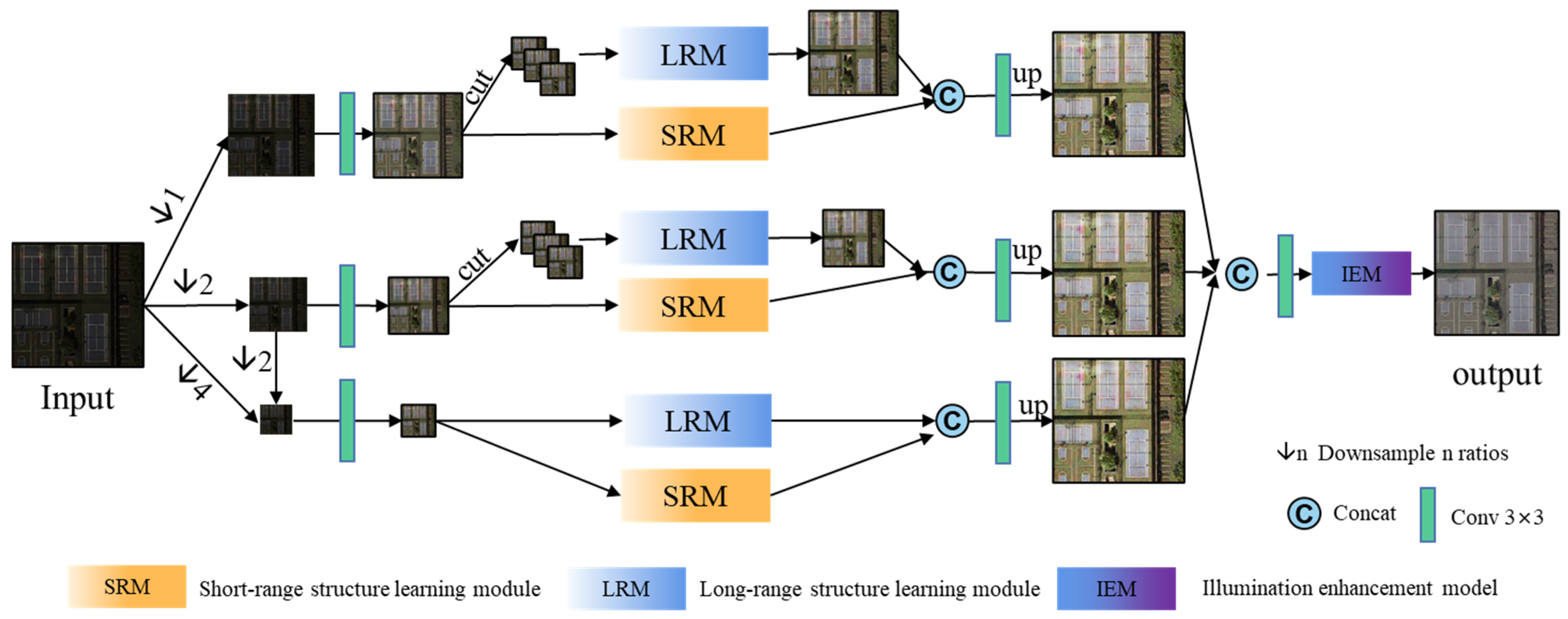
3. The Proposed Method

3.1. Problem Definition and Framwork

Let $I\in {\mathbb{R}}^{H\times W\times C}$ denote a low-illumination (LI) image, where $H$ and $W$ are the image height and width, respectively, and $C$ is the number of color channels. The goal is to transform this low-illumination image III into its corresponding high-quality counterpart $I^{\prime }\in {\mathbb{R}}^{H\times W\times C}$ through a deep learning model, represented as

$$\begin{array}{c}{I}^{\prime }=f\left(I,\theta \right)\end{array}$$

(1)

where $f\left(.,\theta \right)$ represents the mapping function defined by the model, with the form of fff determined by the designed model architecture, and $\theta$ represents the model parameters. The input is the low-illumination image $I$, and the goal is to optimize the parameters $\theta$ such that the model can effectively restore a high-quality image from the low-illumination image. To achieve this, the model must learn from a dataset containing pairs of low-illumination images $I_n$ and their corresponding high-quality counterparts $I_n^{\prime }$, enabling it to handle a variety of lighting conditions and image contents.

The parameters optimization of the model involves adjusting its parameters $\theta$ through training. Given a dataset $\left\{\right(I_n,I_n^{\prime }){\}}_{n=1^{\prime }}^N$, where $I_n$ is a low-illumination image and $I_n^{\prime }$ is its corresponding high-quality image, the model produces an output $f\left(I_n,\theta \right)$, which is the predicted high-quality image.

The optimization objective is to minimize the following loss function with respect to the model parameters $\theta$:

$$\begin{array}{c}\mathcal{L}\left(\theta \right)={\displaystyle \frac{1}{N}}{\displaystyle \sum _{n=1}^N}{\mathcal{L}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\left(f\left(I_n,\theta \right),I_n^{\prime }\right)\end{array}$$

(2)

where ${\mathcal{L}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}$ is the loss function that measures the discrepancy between the model’s predicted output $f\left(I_n,\theta \right)$ and the true high-quality image $I_n^{\prime }$ (e.g., using mean squared error). The loss function is minimized using backpropagation, which adjusts the parameters $\theta$ over the course of training.

This optimization process enables the model to effectively learn image-specific features from low-illumination images, while providing high-quality enhancement across various image contents and illumination conditions. However, the performance ceiling of model optimization is determined by the model architecture.

In this study, we propose a multi-scale long- and short-range structure aggregation learning network for LI remote sensing imagery enhancement. As shown in Figure 1, different from existing single-branch network, we introduce a flexible multi-scale feature aggregation architecture that learns to simultaneously exploit features at different scales of the input LI image for enhancement. Moreover, each branch consists of two dynamic modules, namely a short-range structure learning module that can adaptively exploit the structure around each pixel according to its features representation, and a long-range structure learning module that dynamically exploits the long-range correlations between different image patches in a deep feature space. Then, all structures exploited from different scales are aggregated and branches and convert them cast into pixel-wise scale factors for fine-grained image enhancement. In the following, we will introduce each module in detail.

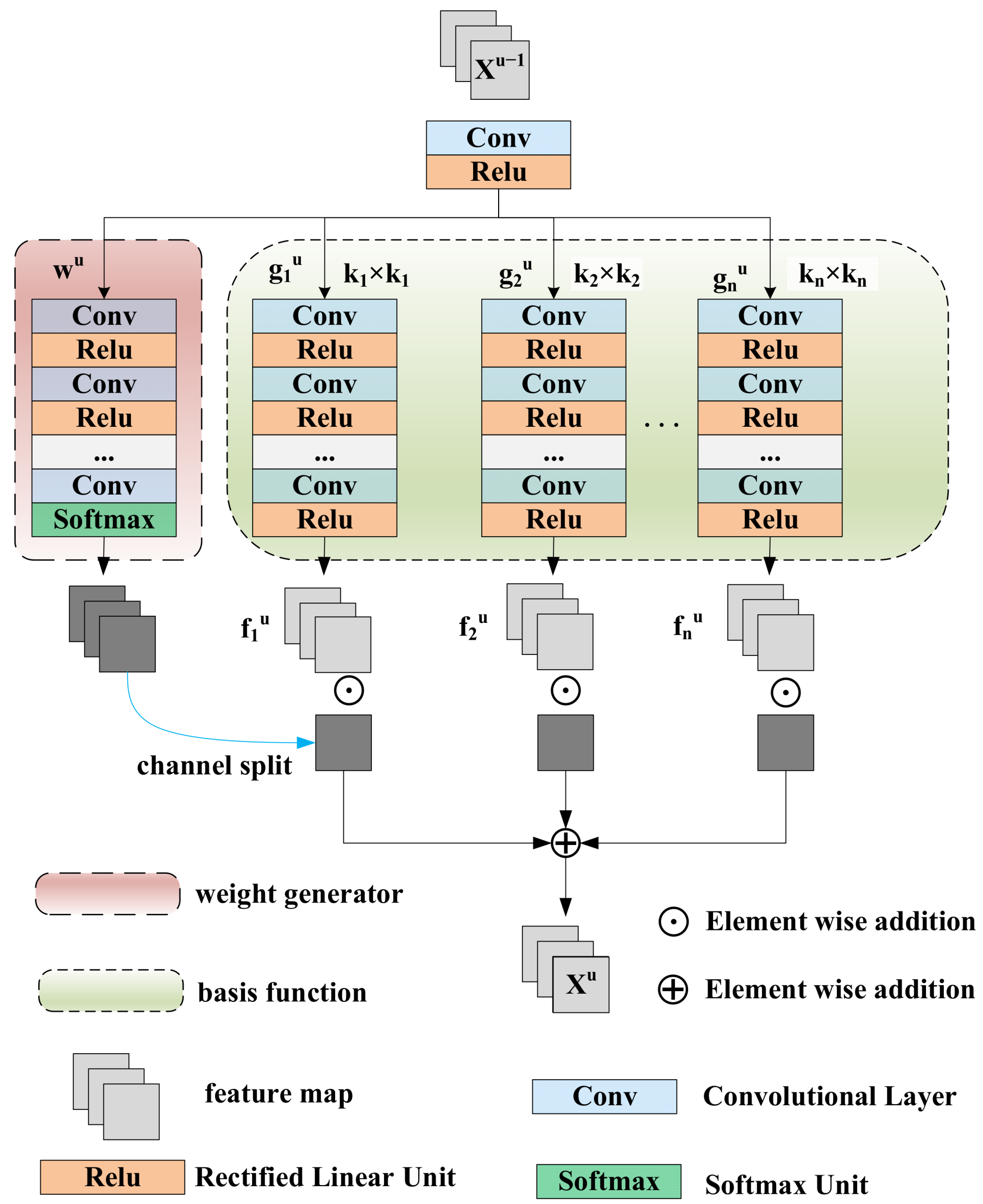
3.2. Short-Range Structure Learning Module

The short-range structure learning module is designed to focus on capturing the local features within the image. In low-illumination images, local details such as edges, textures, and fine-grained variations are often suppressed. This module helps enhance these local features, thereby recovering fine details that are crucial for improving the quality of low-illumination images. By focusing on small regions around each pixel, the short-range module allows the model to perform pixel-level enhancements, which are essential for restoring image sharpness and contrast.

Deep convolutional neural networks (DCNNs) have proven to be effective in exploiting the short-range structures of the images for subsequent regression tasks, e.g., image denoising, image supre-resolution, and LI image enhancement [6,14,35]. Its key lies in establishing a deep mapping function from the low-illumination image to the high-quality counterpart using hierarchical convolution layers. Since the convolution operation is translation invariant across the whole image, the DCNN essentially establishes a unique deep mapping function for each pixel which takes the information located in the receptive fields centered around the pixel as input and finally outputs its reconstruction result.

However, due to the various image contents as well as the non-uniform LI degeneration, each pixel in the LI image often shows different contexts and thus requires a specific deep mapping function for LI enhancement, e.g., pixels in flat areas with slight LI degeneration can be well reconstructed using a rather simple deep mapping function, while pixels in texture area with complex LI degeneration requires a complicated deep mapping function. Following this idea, a direct solution is to establish a deep mapping function for each pixel using an individual DCNN. Due to the infinite unknown pixels in the test phase, such a solution is infeasible. To mitigate this problem, we borrow the idea in [27] and assume that all deep mapping functions related to pixels can be accurately approximated by mixing some basic functions with some pixel-wise mixing weights. More importantly, to make sure each pixel will be assigned a specific mapping function, those pixel-wise mixing weights are dynamically generated using an individual weight generation block which takes the context of each pixel as input. On the other hand, those basic functions are established by individual DCNN branches with different kernel sizes to take different receptive fields for short-range structure learning. The details for this module are given as shown in Figure 2.

First, we employ a convolutional layer and rectified linear unit (ReLu) as a convolutional block to perform initial feature representation on the input image $x_{in}$ to obtain $F_x$. Then, the initial feature map $F_x$ is fed into some parallel sub-networks each of which works as the basic function. At the same time, a weight generation sub-network is utilized to generate pixel-wise mixing weights, and those weights are finally utilized to linearly mix the output of those basic functions as the output for a specific pixel. According to the function mixing rule [27], we further require that each generated weight vector is non-negative and their summation equals to 1. Since the weight vector is generated for a specific pixel according to its context feature representation, such a structure-learning module is able to establish a specific deep mapping function to exploit the corresponding short-range structures for LI enhancement on each pixel. According to the above description, the short-range structure learning module can be formulated as

$$y_s={\sum }_{i=1}^n{g}_i\left(F_x,{\theta }_i\right)\odot w\left(F_x,\vartheta \right)\left[i\right],$$

(3)

$$s.t.,{\displaystyle \sum _{i=1}^n}w\left(F_x,\mathsf{\vartheta }\right)\left[i\right]=\mathbf{1},w\left(F_x,\mathsf{\vartheta }\right)⪰0$$

where $g_i\left(F_{\mathrm{x}},{\mathsf{\theta }}_i\right)$ denotes the $i$-th basic function parameterized by ${\mathrm{\theta }}_{\mathrm{i}}$, $\mathrm{n}$ is the total number of basic functions, and $\mathrm{w}\left(F_x,\mathsf{\vartheta }\right)$ represents the weight generator parameterized by $\mathsf{\vartheta }.$ In addition, a softmax unit is introduced at the end of the mixed function to constrain the generated weights.

3.3. Long-Range Structure Learning Module

In contrast, the long-range structure learning module is focused on capturing global relationships across the entire image. Low-illumination images often suffer from poor global contrast and spatial coherence. This module helps to capture non-local similarity and long-range correlations between different regions of the image, facilitating the restoration of global image structure and consistency. The long-range module is particularly useful for enhancing large-scale patterns and maintaining coherent structures across the image.

Recent progress has shown that long-range structures are also crucial for image restoration tasks. Inspired by the surge of vision transformers in the computer vision domain, we employ vision transformer in [8,9] to capture the long-range structure in the LI image for enhancement. Standard transformers take a sequence of token embeddings as input when dealing with natural language. When processing the image, we tokenize the input image ${\mathrm{F}}_{\mathrm{x}}\in {\mathrm{R}}^{\mathrm{H}\times \mathrm{W}\times \mathrm{C}}$ into a sequence of flattened tokens ${\mathrm{F}}_{\mathrm{t}}\in {\mathrm{R}}^{\mathrm{L}\times {\mathrm{C}}_{\mathrm{t}}}$, where $\left(\mathrm{H},\mathrm{W}\right)$ is the resolution of the original input image. $\mathrm{C}$ is the number of channels and ${\mathrm{C}}_{\mathrm{t}}$ is the number of mapped channels. As shown in Figure 3, the long-range module includes a multi-headed self attention describing the dependencies between patches in the depth feature space, and a feed forward network with skip connections. We use Layernorm [36] before each block. Because the attention calculation in transformer is global, it has less location information than CNNs. Therefore, similar to [20], we add a learnable embedding in the features of each tag for long range structure learning. The learnable self-attention in transformer can dynamically calculate the attention weight of each patch according to the characteristics, so that the module can capture the long-range structure of a specific image in the input image for HDR reconstruction. According to the description above, the long-range module can be formulated as

$${\mathrm{y}}_0={\mathrm{F}}_{\mathrm{t}}+\mathrm{p}$$

(4)

$$\overline{\mathrm{y}}=\mathrm{M}\mathrm{S}\mathrm{A}\left(\mathrm{L}\mathrm{N}\left({\mathrm{y}}_0\right)\right)+{\mathrm{y}}_0$$

(5)

$${\mathrm{y}}_{\mathrm{l}}=\mathrm{F}\mathrm{F}\mathrm{N}\left(\mathrm{L}\mathrm{N}\left(\overline{\mathrm{y}}\right)\right)+\overline{\mathrm{y}}$$

(6)

where $\mathrm{p}$ is a learnable position encoding. MSA denotes the multi-head self-attention module, FFN is the feed-forward neural network, and LN represents the layer normalization.

3.4. Fine-Grained Illumination Enhancement Module

Following [12,37], the illumination enhancement model maps all pixels of the RGB channel of the LI image by estimating a set of enhancement curves to obtain the final reconstructed image. The enhancement curve is required to be monotonic, and the form should be as simple and differentiable as possible. In order to avoid the loss of information caused by data overflow, each pixel value of the enhanced image should be within the normalization range of $\left[\mathrm{0,1}\right]$. In order to meet the above conditions, the basic enhancement curve of the luminance can be formulated as

$$\mathrm{L}\mathrm{E}\left(\mathrm{I}\left(\mathrm{x}\right);\mathsf{\alpha }\right)=\mathrm{I}\left(\mathrm{x}\right)+\mathsf{\alpha }\mathrm{I}\left(\mathrm{x}\right)\left(1-\mathrm{I}\left(\mathrm{x}\right)\right)$$

(7)

where $\mathsf{\alpha }$ is a pixel-wise scaling factor. $\mathrm{L}\mathrm{E}\left(\mathrm{I}\left(\mathrm{x}\right);\mathsf{\alpha }\right)$ denotes the enhanced results and $\mathrm{I}\left(\mathrm{x}\right)$ denotes the input image. In order to deal with more challenging images, Formula (5) is iterated, and the final brightness enhancement curve can be formulated as

$${\mathsf{\alpha }}_{\mathrm{i}}=\mathsf{\tau }\left(\tanh \left(\mathrm{F}\mathrm{C}\left(\left[{\mathrm{y}}_{\mathrm{s}},{\mathrm{y}}_{\mathrm{l}}\right]\right)\right)\right)$$

(8)

$$\mathrm{L}{\mathrm{E}}_{\mathrm{i}}\left(\mathrm{I}\left(\mathrm{x}\right);{\mathsf{\alpha }}_{\mathrm{i}}\right)=\mathrm{L}{\mathrm{E}}_{\mathrm{i}-1}\left(\mathrm{x}\right)+{\mathsf{\alpha }}_{\mathrm{i}}\mathrm{L}{\mathrm{E}}_{\mathrm{i}-1}\left(\mathrm{x}\right)\left(1-\mathrm{L}{\mathrm{E}}_{\mathrm{i}-1}\left(\mathrm{x}\right)\right)$$

(9)

where $\mathrm{F}\mathrm{C}$ denotes full connection layer and ${\mathsf{\alpha }}_{\mathrm{i}}$ is a pixel-wise scaling factor computed by transforming the long–short range features using a fully connected layer, i.e., $\mathrm{F}\mathrm{C}\left(\right[\mathrm{y}\text{\_}\mathrm{s},\mathrm{y}\text{\_}\mathrm{l}]$. $\mathrm{L}{\mathrm{E}}_{\mathrm{i}}$ denotes the enhanced results and $\mathrm{L}{\mathrm{E}}_0\left(\mathrm{x}\right)=\mathrm{x}$, i.e., input image. $\mathsf{\tau }$ represents an interpolation function.

3.5. Multi-Scale Aggregation

Unlike conventional single-branch networks, our method introduces a flexible multi-scale feature aggregation architecture. This approach allows the model to simultaneously learn features at multiple scales, which is crucial for addressing the diverse nature of low-illumination images. Through multi-scale aggregation, the model can effectively capture both fine local details and large-scale global structures. By combining features from these different scales, the model enhances the image at a fine-grained level, accounting for both local variations and global coherence. As a result, this approach significantly improves performance across a variety of illumination conditions.

While the incorporation of the transformer model helps mitigate the issue of limited receptive fields in CNNs, traditional transformer models still rely on fixed-size patches for images. This constraint inevitably limits the ability of each self-attention layer to capture multi-scale features, resulting in the decline of performance in dealing with complex problems. Self-attention leads to great memory consumption, and the computational complexity increases quadratic with the spatial resolution [38]. As a result, it is very difficult to train large-scale images directly, so we have to down-sample before the transformer, which inevitably leads to the decline in performance.

To address this limitation, we introduce a multi-scale structure with different scales to learn the features of different scales in parallel. As shown in Figure 1, each branch contains a local-range dynamic module and a long-range module. The difference is that the input of each branch is different. For an input image, it is adjusted to different sizes in different branches, then mapped to the hidden field through convolution, and then sent to the local-range dynamic module and long-range module. Because the computational complexity of transformer increases rapidly with the resolution of input features, it is divided into several small blocks of equal size for the relatively large feature map after adjustment. These blocks are spliced in the original order after passing through the long-range module, and then concatenated with the output of the local range dynamic module. After the multi scale feature is adjusted to the initial size, contact realizes the reconstruction of LI remote sensing image through the illumination enhancement model.

4. Experiments

In this section, we will conduct extensive comparative experiments and ablation studies to prove the effectiveness of the proposed method in the task of LI remote sensing image reconstruction.

4.1. Experimental Setting

4.1.1. Datasets

We randomly selected 650 images and 550 images as benchmarks in two widely used remote sensing image datasets VHR-10 [39,40,41] and Dior [42]. Following [43], we simulate the camera through the formula

$${\mathrm{Z}}_{\mathrm{i},\mathrm{j}}=\mathrm{f}\left({\mathrm{E}}_{\mathrm{i}}\mathsf{\Delta }{\mathrm{t}}_{\mathrm{j}}\right)$$

(10)

where ${\mathrm{Z}}_{\mathrm{i},\mathrm{j}}$ represents the LI pixel value at position $\mathrm{i}$ and exposure time $\mathrm{j}$, $\mathrm{f}$ represents the non-linear camera response functions (CRFs), and ${\mathrm{E}}_{\mathrm{i}}$ represents the HDRI pixel value at position $\mathrm{i}$ and $\mathsf{\Delta }{\mathrm{t}}_{\mathrm{j}}$ represents exposure durations. We use the method in [44] which chooses the representative CRFs and $\mathsf{\Delta }{\mathrm{t}}_{\mathrm{j}}$ as a power between stops to degenerate each image into three different levels of IL images, denoted as I1 which is the brightest, I2 and I3 which is the darkest.

In addition, we use methods to adjust luminance by using linear relationship. In order to verify the effectiveness of our method, we also degenerate the image to three different levels of IL images, denoted as L1 which is the brightest, L2 and L3 which is the darkest as shown in Figure 4.

In addition, in order to verify the effectiveness of our method in real scenes, we randomly selected real scenes at night from 20 different locations on Google Earth for testing. We adjust the resolution of each picture to 512 × 512.

4.1.2. Comparison Methods

In this study, to demonstrate the effectiveness of the proposed method, we compare it with five state-of-the-art baselines, namely DeepUPE [45], RetineNet [46], FMB [27], STAR [12], and DCE [37]. Among them, DeepUPE [45] can better learn the complex illumination of ground truth by learning the mapping between underexposed images and illumination maps. RetineNet [46] adopts decomposition networks and continuous low brightness enhancement networks for low-light enhancement. DCE uses CNNs to predict the parameters of the proposed enhancement curve, and STAR [12] is a method to estimate the parameters of the enhancement curve by using transformer instead of CNNs. FMB [27] is a dynamic pixel level learning module. We use it to replace the multi branch structure at baseline for comparison.

4.1.3. Evaluation Metrics

We employ two metrics to assess model performance: peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM). PSNR measures the quality of image reconstruction, with higher values indicating greater accuracy in reproducing the original image. SSIM quantifies the structural similarity between the original and generated images, where higher values suggest that the model preserves more structural information from the original image.

4.1.4. Implementation Details

In the proposed method, each image is processed in full resolution when evaluation and resized to 256 × 256 during training. We use three branches with different scales, i.e., 256 × 256, 128 × 128 and 32 × 32. In each branch, following [47], we apply a 7 × 7 convolutions with stride 4 and output channels 16 on the image. In the local range dynamic module, stacking 2 convolutional blocks are implemented in n = 3 basic functions which are equipped with 3 × 3, 7 × 7 and 11 × 11 filters for convolution. The filter size in other convolution blocks is fixed to 3 × 3. In the long-range module, each image is divided into 32 × 32 patches. Because different branches have different input sizes, even patches of the same size in different branches contain different features. In implementation, our model is implemented on the Pytorch platform [48]. We train the network using the following model:

$$\underset{\mathsf{\theta }}{\min }{\displaystyle \frac{1}{\mathrm{N}}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}}{‖{\mathrm{y}}_{\mathrm{i}}-\mathrm{f}\left({\mathrm{x}}_{\mathrm{i}},\mathsf{\theta }\right)‖}_1$$

(11)

where ${(\mathrm{y}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{i}})$ respectively denotes the i-th paired HDR and LI image. $\mathrm{N}$ denotes the number of training pairs. f denotes the ultimate mapping function defined by the proposed network and $\mathsf{\theta }$ represents all involved parameters. ${‖\cdot ‖}_1$ represents the ${\mathrm{l}}_1$ norm-based loss. We perform our experiments on a server equipped with an NVIDIA GeForce RTX 3090 GPU, manufactured by NVIDIA Corporation headquartered in Santa Clara, California, United States of America, which provides the necessary computational power for our deep learning tasks. The model is implemented using PyTorch 1.8.0 a widely utilized deep learning framework. For the training process, we employ the Adam optimizer [49], a method recognized for its adaptive learning rate properties. The learning rate is set to $1\times {10}^{-4}$ and the batch size is 8. The optimization process is halted at the 500th epoch to prevent overfitting and ensure model generalization.

4.2. Performance Evaluation

Under the same experimental setup, we evaluate all these methods on the test sets of the above simulation datasets. Their numerical results are reported in

Table 1. Numerical results of different methods on LI simulation datasets VHR-10 using different methods.

		I1	I2	I3	L1	L2	L3
DeepUpe [45]	PSNR	33.341	31.68	29.75	33.20	32.57	29.84
	SSIM	0.9608	0.9476	0.9300	0.9381	0.9123	0.8532
RetineNet [46]	PSNR	34.47	32.99	31.25	33.99	32.45	30.97
	SSIM	0.9587	0.9467	0.9351	0.9191	0.893	0.8524
FMB [27]	PSNR	32.02	30.30	28.17	34.17	32.61	30.41
	SSIM	0.9536	0.9370	0.9163	0.9202	0.8945	0.8418
DCE [37]	PSNR	35.53	33.23	31.36	34.20	32.65	30.86
	SSIM	0.9633	0.9515	0.9335	0.9116	0.8964	0.8529
STAR [12]	PSNR	35.28	33.14	31.62	33.09	32.41	30.55
	SSIM	0.9622	0.9490	0.9344	0.9178	0.8929	0.8477
ours	PSNR	36.45	34.71	32.04	34.22	32.73	30.99
	SSIM	0.9639	0.9518	0.9354	0.9204	0.8965	0.8529

and

Table 2. Numerical results of different methods on LI simulation datasets DIOR using different methods.

		I1	I2	I3	L1	L2	L3
DeepUpe [45]	PSNR	30.33	29.50	26.89	33.77	32.57	30.43
	SSIM	0.9509	0.9334	0.9080	0.9307	0.9123	0.8801
RetineNet [46]	PSNR	31.41	30.18	28.42	35.40	34.10	32.32
	SSIM	0.9434	0.9310	0.9112	0.9351	0.9161	0.8809
FMB [27]	PSNR	32.19	30.64	28.22	35.71	34.35	32.36
	SSIM	0.9549	0.9397	0.9186	0.9364	0.9186	0.8811
DCE [37]	PSNR	32.02	30.45	28.37	35.46	34.35	32.26
	SSIM	0.9550	0.9398	0.9101	0.936	0.9195	0.8839
STAR [12]	PSNR	31.97	29.85	28.30	34.99	33.66	30.67
	SSIM	0.9553	0.9394	0.9199	0.9342	0.9152	0.8742
ours	PSNR	33.18	31.27	29.07	35.75	34.44	32.48
	SSIM	0.9564	0.9409	0.9186	0.9367	0.9185	0.8820

. As can be seen, the proposed method can produce more accurate results than other methods and achieves the best HDR reconstruction performance on PSNR and SSIM. For example, on the I2 of VHR-10 dataset, compared with the STAR, the proposed method improves the PSNR by 1.77 and improves the SSIM by 0.003. Compared with the DCE, the proposed method improves the PSNR by 1.48. On the I2 of DIOR dataset, compared with the STAR, the improvement on PSNR is up to 1.42 db. This is due to the fact that the proposed method uses multi-scale network to extract the long-range and short-range features of different scales, so as to process each pixel more flexibly and obtain better reconstruction results.

DeepUPE comprises a local module and a global module, allowing it to capture features at both long- and short distances simultaneously. However, due to its relatively simplistic model architecture, it fails to achieve superior performance. In contrast, our proposed method demonstrates a performance improvement of up to 3 dB. RetineNet employs network operations for both reflectance-illumination decomposition and low-light enhancement to improve image brightness. However, this approach unevenly amplifies noise in the reflectance. DCE is an illumination enhancement method that utilizes pure convolution to learn the illumination curve of an image. However, due to the shared nature of the model across all images, it cannot adaptively fit the image-specific features of each individual image. STAR utilizes a transformer structure to learn long-range features. STAR and DCE singularly leverage long-range and short-range features, respectively. They fail to fully exploit image information. In our proposed method, we combine both to achieve optimal performance, further underscoring the rationality of our designed network.

Additionally, we present the results of low-light enhancement and their corresponding error images. We have selected a small section of the image (indicated by a red box) and enlarged it to the upper left corner of the image for easy observation. In these error images, colors closer to blue indicate that the model’s predictions are nearer to the actual values, while colors approaching red signify a greater discrepancy between the predictions and the ground truth.

Figure 5 presents a visual comparison of the reconstruction error for illumination enhancement across different simulated remote sensing images from the VHR-10 dataset, utilizing the setting referenced in [45]. Our proposed network not only achieves a visually pleasing effect but also demonstrates the capability to perform satisfactory image reconstruction even under extreme low-light conditions. The error images predominantly exhibit blue hues, indicating that the model’s predictions closely align with the actual values, with minimal red areas that would indicate larger discrepancies.

Figure 6 offers a similar comparison but with a distinct line setting. The results are consistent with those observed in Figure 5, further validating the robustness of our network across a range of conditions. The visually appealing outcomes and the satisfactory reconstruction quality reaffirm the effectiveness of our approach in addressing challenging low-light scenarios.

Figure 7 extends this analysis to the DIOR dataset, again employing the setting from reference [45]. The error images continue to favor the blue spectrum, suggesting that our method maintains high performance in reconstructing images from this distinct dataset.

Figure 8, which uses the line setting for the DIOR dataset, mirrors the observations from Figure 7. The consistent trend towards blue in the error images across both datasets and settings underscores the reliability and generalizability of our proposed network in enhancing low-light remote sensing images.

The absence of extensive red areas in the error images, particularly in the challenging I3 scenario depicted in Figure 7, highlights our network’s ability to extract rich multi-level features from the input images and perform precise, pixel-wise dynamic enhancement. This analysis corroborates the effectiveness of our methodology in accurately capturing and enhancing the nuances of low-light imagery, as evidenced by the reconstruction results presented in these figures.

4.3. Ablation Study

We evaluated the effectiveness of individual components in our model in VHR-10 dataset, including local range dynamic module and long-range module. In addition, we also discussed the impact of different numbers and scales of branches on the network, as shown in

Table 3. Numerical results of different modules on LI simulation datasets.

		VHR-10
		I1	I2	I3	L1	L2	L3
w/o long-range module	PSNR	35.87	33.2	31.00	34.18	32.67	30.44
	SSIM	0.9637	0.9502	0.9340	0.9201	0.8952	0.8530
w/o short-range dynamic module	PSNR	35.49	34.55	32.04	34.20	32.61	30.80
	SSIM	0.9636	0.9526	0.9375	0.9202	0.8945	0.8503
w/o dynamic	PSNR	36.36	34.56	31.81	34.19	32.59	30.29
	SSIM	0.9643	0.9545	0.9394	0.9207	0.8938	0.8505
two branches (2*)	PSNR	36.30	34.05	31.93	34.14	32.72	30.88
	SSIM	0.9650	0.9518	0.9350	0.9196	0.8965	0.852
two branches (4*)	PSNR	36.03	33.82	31.68	34.11	32.73	30.77
	SSIM	0.9627	0.9506	0.9339	0.9201	0.8964	0.8494
one branch	PSNR	35.94	33.68	31.40	34.06	32.54	30.7
	SSIM	0.9621	0.9496	0.9334	0.9188	0.8932	0.8484
ours	PSNR	36.45	34.71	32.04	34.22	32.73	30.89
	SSIM	0.9639	0.9518	0.9354	0.9204	0.8965	0.8519

.

4.3.1. Short-Range Structure Learning Module

The illumination distribution of each image is distinct. The short-range dynamic feature extraction module establishes a mapping function related to each pixel and employs diverse receptive fields for learning, leading to improved reconstruction results. As depicted in Table 3, this module effectively enhances the model’s reconstruction performance, raising the PSNR by more than 0.45. Additionally, traditional convolution modules were employed in lieu of the short-range dynamic feature extraction module. Experimental results indicate a decline in performance, underscoring the effectiveness of the dynamic structure.

4.3.2. Long-Range Structure Learning Module

In order to better capture long-range features in the images, this paper incorporates a long-range dynamic feature extraction module. As shown in Table 3, this module significantly improves PSNR, with a notable increase of 1.51 in PSNR for I2 illumination intensity on the VHR-10 dataset. The experiments above fully demonstrate that both the short-range dynamic feature extraction module and the long-range dynamic feature extraction module play crucial roles in high dynamic range image reconstruction. However, using either module alone cannot achieve state-of-the-art performance. Only when both modules are combined, the network structure can thoroughly exploit the feature information contained in the images, leading to the best high dynamic range reconstruction results.

4.3.3. Multi-Scale Structure with Different Scales

Due to the fixed receptive field size of convolutional neural networks (CNNs), when the feature map size changes, the network is able to focus on different scales of the image. To investigate the impact of the multi-branch, multi-scale structure on the proposed method, we evaluate the performance using different numbers of branches, namely, M = 1, 2, 3M = 1, 2, 3M = 1, 2, 3, corresponding to one branch, two branches, and Ours in Table 3. As shown in Table 3, when only one branch is used, the reconstruction performance significantly decreases, especially on the underexposed data in non-local simulations (e.g., I1, I2, and I3), where this decrease is even more pronounced. However, as the number of branches increases, the model’s performance gradually improves. To further investigate the impact of different down sampling ratios on the experimental results, we conducted experiments with varying down sampling factors under the two branches configuration. Specifically, we combined the original scale branch with branches down sampled by factors of two and four, corresponding to two branches (2*) and two branches (4*), respectively. The experimental results shown in Table 3 indicate that the combination of the original scale branch and the two-times down sampled branch (two branches (2*)) yields better image detail recovery. In contrast, the combination with the four-times down sampled branch (two branches (4*)) produces slightly worse results, although both configurations outperform the single-branch, single-scale approach. These findings suggest that the multi-branch, multi-scale structure enhances model performance by learning from features at different scales and selecting an appropriate down sampling ratio further improves performance.

4.4. Evaluation on the Real World Data

We randomly crawl a set of real scene datasets at different times on Google Earth and use our proposed model to restore the brightness in the early morning with insufficient sunshine and the afternoon with dim light. The results are shown in Figure 9 and Figure 10. Our method can effectively restore the brightness and obtain a pleasant effect. At the same time, we also crawl the daytime image with sufficient illumination in the same scene as a control to prove the rationality of the reconstructed image obtained by our method. However, since there are no paired real datasets for training, there is no guarantee that the selected LI images in real-world scenes have the same illumination intensity as the simulated images. As shown in Figure 10, when images taken at dusk are used, images with higher light intensity tend to be produced.

4.5. Limitations and Future Directions

Although the proposed method introduces a multi-scale approach to improve the performance of low-illumination enhancement for remote sensing imagery, there are some limitations that need to be addressed in future work. One of the primary challenges is the increased computational load and time resulting from the multi-scale network design. While the multi-scale strategy allows for better extraction of features at various scales, it also demands more resources, which may hinder real-time applications. Future research will explore more efficient multi-scale model architectures and optimization techniques to reduce computation time and improve processing speed without compromising performance.

In addition, moving forward, we aim to construct a larger-scale dataset of real low-light enhanced remote sensing scenes for training and evaluating model performance in authentic settings. This dataset will help in assessing the generalization capability of our model under various real-world conditions and provide more diverse examples for training.

To further enhance the robustness of our model, we will explore the incorporation of adversarial perturbation training methods. These methods are expected to improve the model’s ability to handle potential artifacts and mitigate over-enhancement issues that might arise when enhancing extremely low-light images. Moreover, to address the problem of over-exposure when enhancing normally lit images, we plan to integrate perceptual loss functions. These functions are designed to preserve the natural appearance and visual fidelity of the enhanced images, ensuring that they do not exhibit unnatural overexposure while maintaining high-quality enhancements.

By addressing these limitations and exploring these future directions, we aim to further advance the capabilities of low-illumination remote sensing imagery enhancement and broaden the practical applicability of our model.

5. Conclusions

In this paper, we propose a novel multi-scale dynamic long- and short-range structure learning network for HDR reconstruction of low-illumination remote sensing images. Traditional methods often rely on fixed receptive fields, which limit their ability to capture long-range dependencies and fine image details. Our approach, however, leverages both long-distance and short-distance features, enabling more effective extracting of image characteristics. Specifically, we use a local range dynamic module which can adaptively use pixels to perceive the short-range structure around each pixel according to its features and a long-range module which dynamically exploits the correlation between different image patches in the deep feature space. In addition, we propose multi-scale architecture. Different branches have different scales that can fully capture image features and reduce the amount of computation of parallel computing multiple large-scale images. Through the comprehensive use of multi-scale long-range and short-range structural features for HDR reconstruction, the generalization ability of this method is better improved. The effectiveness of the proposed method was proven on both the synthetic and real datasets, through a comparative study with other prevailing methods.