A High Efficiency Discontinuous Galerkin Method for 3D Ground-Penetrating Radar Simulation
Abstract
1. Introduction
2. Methods
2.1. Governing Equations
2.2. Nodal Basis Functions
2.3. Time Discretization
2.4. Application of UPML Absorbing Boundary
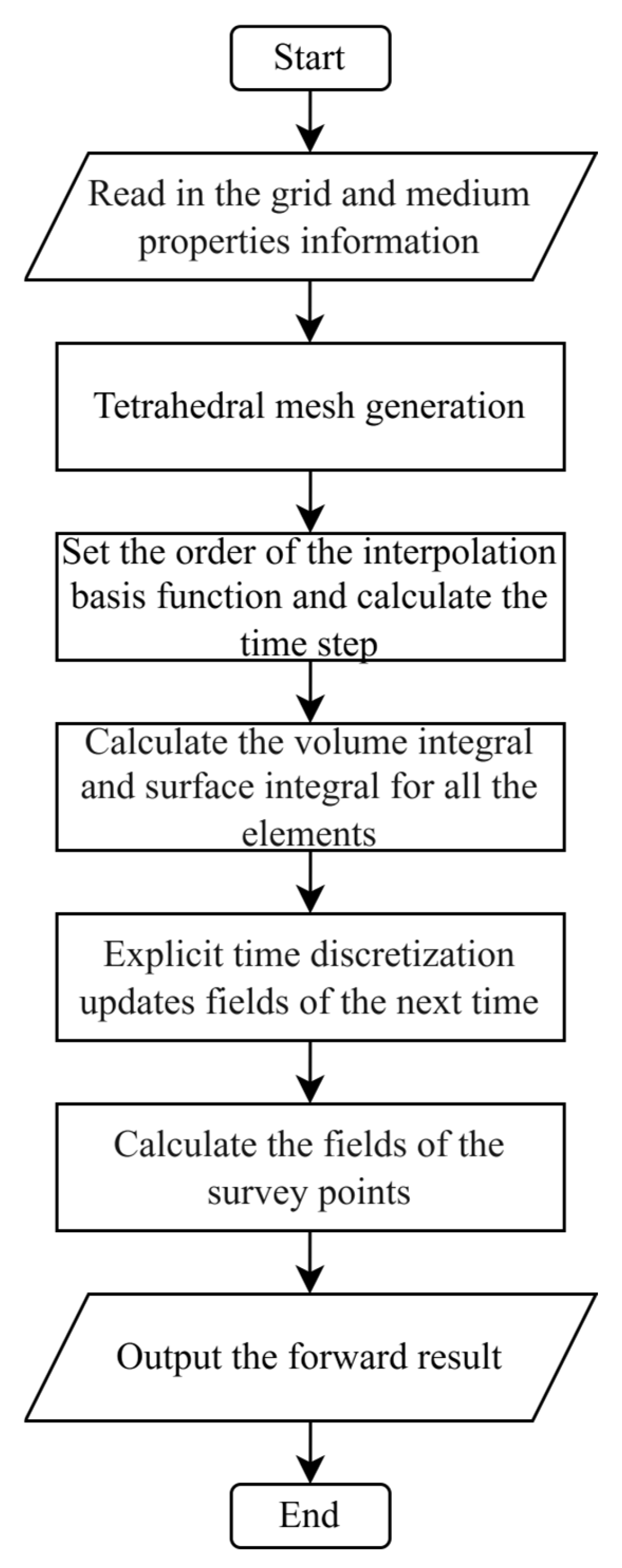
2.5. Calculation Flow of the DG Method
3. Numerical Experiments
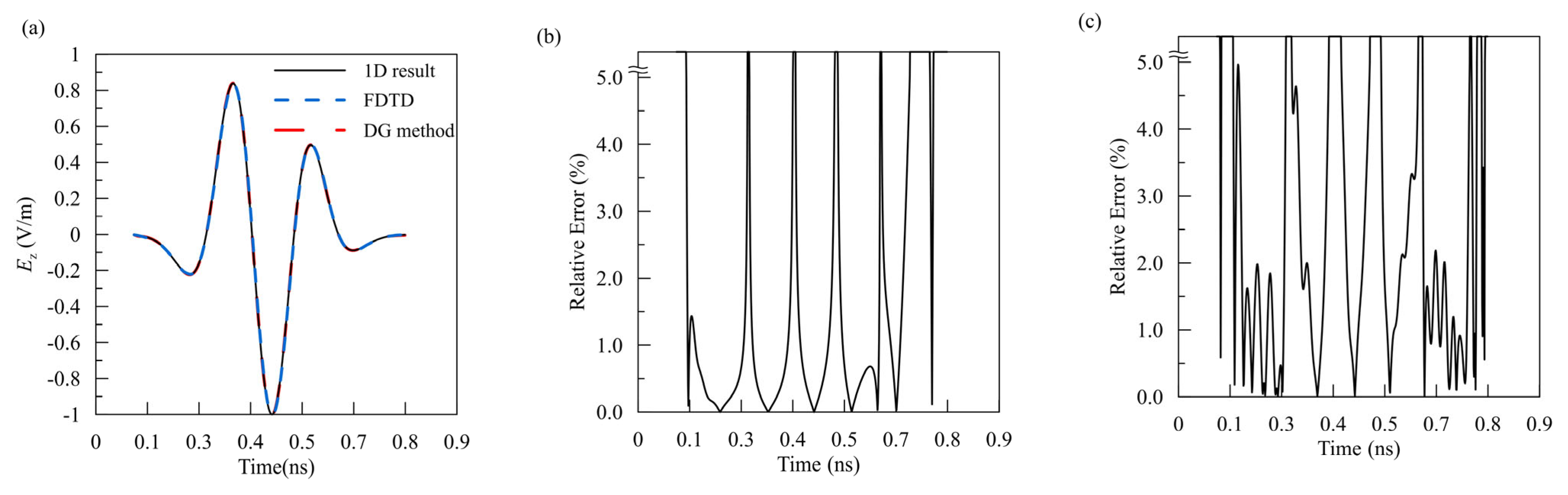
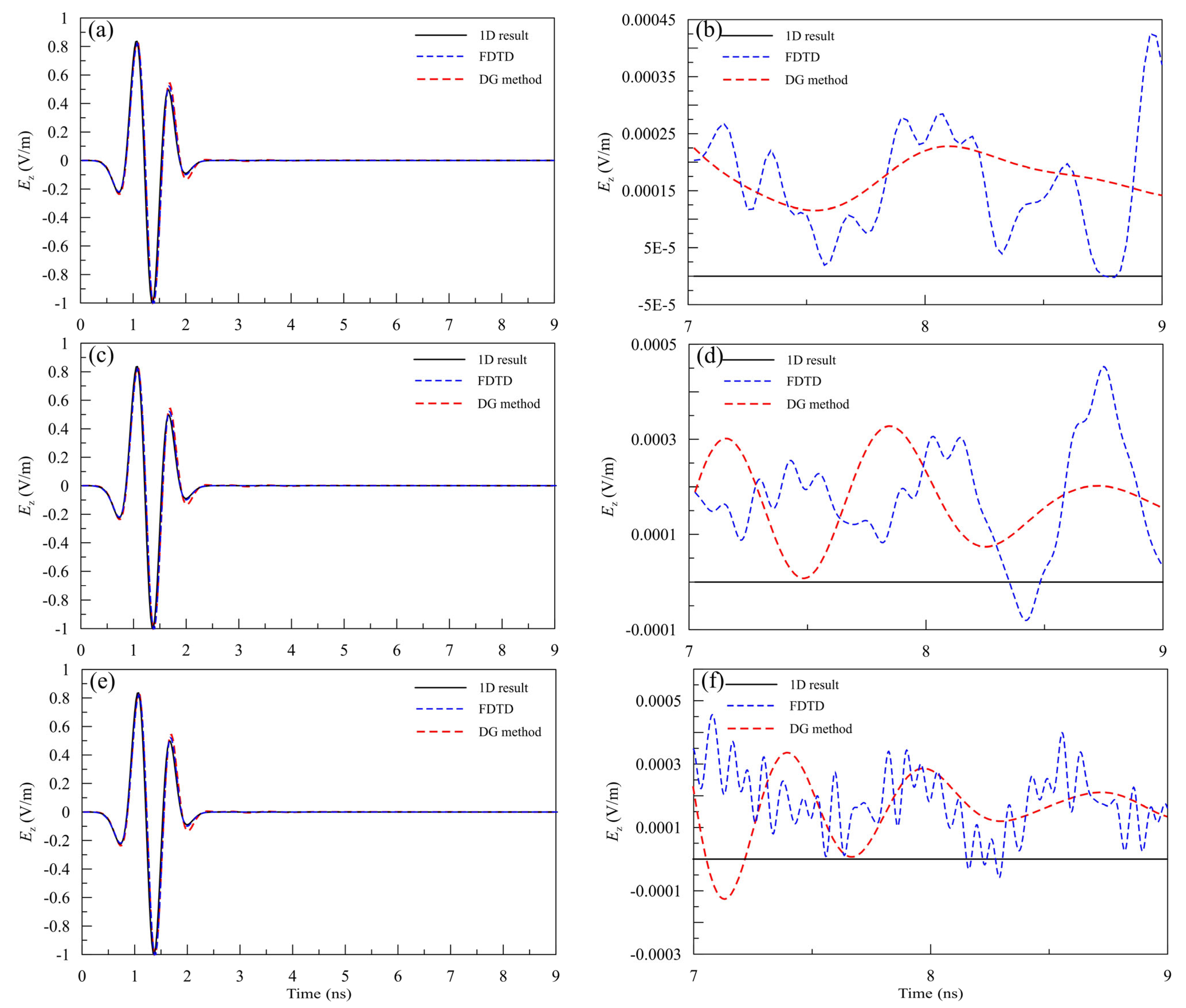
3.1. Accuracy Analysis
3.2. Influence of the Order of Basis Functions on Modeling Accuracy
3.3. Experiments with Anomalous Body Model
3.4. Experiments with Undulating Surface Model

4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gurel, L.; Oguz, U. Three-dimensional FDTD modeling of a ground-penetrating radar. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1513–1521. [Google Scholar] [CrossRef]
- Baradello, L.; Carcione, J.M.; Gei, D. Fast monostatic GPR modeling. Geophysics 2004, 69, 466–471. [Google Scholar] [CrossRef][Green Version]
- Roberts, R.L.; Daniels, J.J. Modeling near-field GPR in three dimensions using the FDTD method. Geophysics 1997, 62, 1114–1126. [Google Scholar] [CrossRef]
- Irving, J.; Knight, R. Numerical modeling of ground-penetrating radar in 2-D using MATLAB. Comput. Geosci. 2006, 32, 1247–1258. [Google Scholar] [CrossRef]
- Shankar, V.; Mohammadian, A.H.; Hall, W.F. A time-domain, finite-volume treatment for the Maxwell equations. Electromagnetics 1990, 10, 127–145. [Google Scholar] [CrossRef]
- Liu, H.; Dai, D.; Zou, L.; He, Q.; Meng, X.; Chen, J. Refined Modeling of Heterogeneous Medium for Ground-Penetrating Radar Simulation. Remote Sens. 2024, 16, 3010. [Google Scholar] [CrossRef]
- Chi, Y.; Pang, S.; Mao, L.; Zhou, Q.; Chi, Y. Research on Airborne Ground-Penetrating Radar Imaging Technology in Complex Terrain. Remote Sens. 2024, 16, 4174. [Google Scholar] [CrossRef]
- Xu, J.; Lai, Q.; Wei, D.; Ji, X.; Shen, G.; Yuan, H. The Ground-Penetrating Radar Image Matching Method Based on Central Dense Structure Context Features. Remote Sens. 2024, 16, 4291. [Google Scholar] [CrossRef]
- Bourgeois, J.M.; Smith, G.S. A fully three-dimensional simulation of a ground-penetrating radar: FDTD theory compared with experiment. IEEE Trans. Geosci. Remote Sens. 1996, 34, 36–44. [Google Scholar] [CrossRef]
- Ge, D.; Yan, Y. Finite-Difference Time-Domain Method for Electromagnetic Waves; Xi’an Electronic and Science University Press: Xi’an, China, 2005. [Google Scholar]
- Zhang, B.; Dai, Q.; Yin, X.; Feng, D. A new approach of rotated staggered grid FD method with unsplit convolutional PML for GPR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 9, 52–59. [Google Scholar] [CrossRef]
- Wang, X.; Yu, T.; Feng, D.; Ding, S.; Li, B.; Liu, Y.; Feng, Z. A high-efficiency spectral element method based on CFS-PML for GPR numerical simulation and reverse time migration. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 1232–1243. [Google Scholar] [CrossRef]
- Teixeira, F.L. FDTD/FETD methods: A review on some recent advances and selected applications. J. Microw. Optoelectron. Electromagn. Appl. (JMOe) 2007, 6, 83–95. [Google Scholar]
- Liu, H.; Xing, B.; Wang, H.; Cui, J.; Spencer, B.F. Simulation of ground penetrating radar on dispersive media by a finite element time domain algorithm. J. Appl. Geophys. 2019, 170, 103821. [Google Scholar] [CrossRef]
- Feng, D.; Wang, X.; Zhang, B. Specific evaluation of tunnel lining multi-defects by all-refined GPR simulation method using hybrid algorithm of FETD and FDTD. Constr. Build. Mater. 2018, 185, 220–229. [Google Scholar] [CrossRef]
- Feng, D.; Zhang, H.; Wang, X. Second-generation wavelet finite element based on the lifting scheme for GPR simulation. Appl. Geophys. 2020, 17, 143–153. [Google Scholar] [CrossRef]
- Li, Z.; Cao, X.; Zhu, Z. 3D forward simulation of ground penetrating radar pseudo-spectral method based on GPU parallel acceleration. J. Eng. Geophys. 2021, 18, 67–74. [Google Scholar] [CrossRef]
- Reed, W.H.; Hill, T.R. Triangular Mesh Methods for the Neutron Transport Equation; Los Alamos Scientific Lab.: Los Alamos, NM, USA, 1973. [Google Scholar]
- Ren, Q.; Sun, Q.; Tobón, L.; Zhan, Q.; Liu, Q.H. EB scheme-based hybrid SE-FE DGTD method for multiscale EM simulations. IEEE Trans. Antennas Propag. 2016, 64, 4088–4091. [Google Scholar] [CrossRef]
- Hesthaven, J.S.; Warburton, T. Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Zhan, Q.; Fang, Y.; Zhuang, M.; Yuan, M.; Liu, Q.H. Stabilized DG-PSTD method with nonconformal meshes for electromagnetic waves. IEEE Trans. Antennas Propag. 2020, 68, 4714–4726. [Google Scholar] [CrossRef]
- Lu, T.; Cai, W.; Zhang, P. Discontinuous Galerkin time-domain method for GPR simulation in dispersive media. IEEE Trans. Geosci. Remote Sens. 2005, 43, 72–80. [Google Scholar] [CrossRef]
- Etienne, V.; Chaljub, E.; Virieux, J.; Glinsky, N. An hp-adaptive discontinuous Galerkin finite-element method for 3-D elastic wave modelling. Geophys. J. Int. 2010, 183, 941–962. [Google Scholar] [CrossRef]
- Mercerat, E.D.; Glinsky, N. A nodal high-order discontinuous Galerkin method for elastic wave propagation in arbitrary heterogeneous media. Geophys. J. Int. 2015, 201, 1101–1118. [Google Scholar] [CrossRef]
- He, X.; Yang, D.; Wu, H. Numerical dispersion and wave-field simulation of the Runge-Kutta discontinuous Galerkin method. Chin. J. Geophys. 2014, 57, 906–917. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, D.; He, X.; Ma, X. Discontinuous Galerkin method for solving wave equations in two-phase and viscoelastic media. Chin. J. Geophys. 2018, 61, 926–937. [Google Scholar] [CrossRef]
- Feng, D.; Liu, S.; Wang, X.; Wang, X.; Li, G. High-order GPU-DGTD method based on unstructured grids for GPR simulation. J. Appl. Geophys. 2022, 202, 104666. [Google Scholar] [CrossRef]
- Zhu, J.; Yin, C.; Ren, X.; Liu, Y.; Hui, Z.; Gu, Y. DC resistivity forward modelling for arbitrarily anisotropic media using the unstructured spectral element method. Chin. J. Geophys. 2021, 64, 4644–4657. [Google Scholar] [CrossRef]
- Warburton, T. An explicit construction of interpolation nodes on the simplex. J. Eng. Math. 2006, 56, 247–262. [Google Scholar] [CrossRef]
- Sun, Q.; Zhan, Q.; Ren, Q.; Liu, Q.H. Wave equation-based implicit subdomain DGTD method for modeling of electrically small problems. IEEE Trans. Microw. Theory Tech. 2017, 65, 1111–1119. [Google Scholar] [CrossRef]
- Zhan, Q.; Ren, Q.; Sun, Q.; Chen, H.; Liu, Q.H. Isotropic Riemann solver for a nonconformal discontinuous Galerkin pseudospectral time-domain algorithm. IEEE Trans. Geosci. Remote Sens. 2016, 55, 1254–1261. [Google Scholar] [CrossRef]
- Sacks, Z.S.; Kingsland, D.M.; Lee, R.; Lee, J.-F. A perfectly matched anisotropic absorber for use as an absorbing boundary condition. IEEE Trans. Antennas Propag. 1995, 43, 1460–1463. [Google Scholar] [CrossRef]
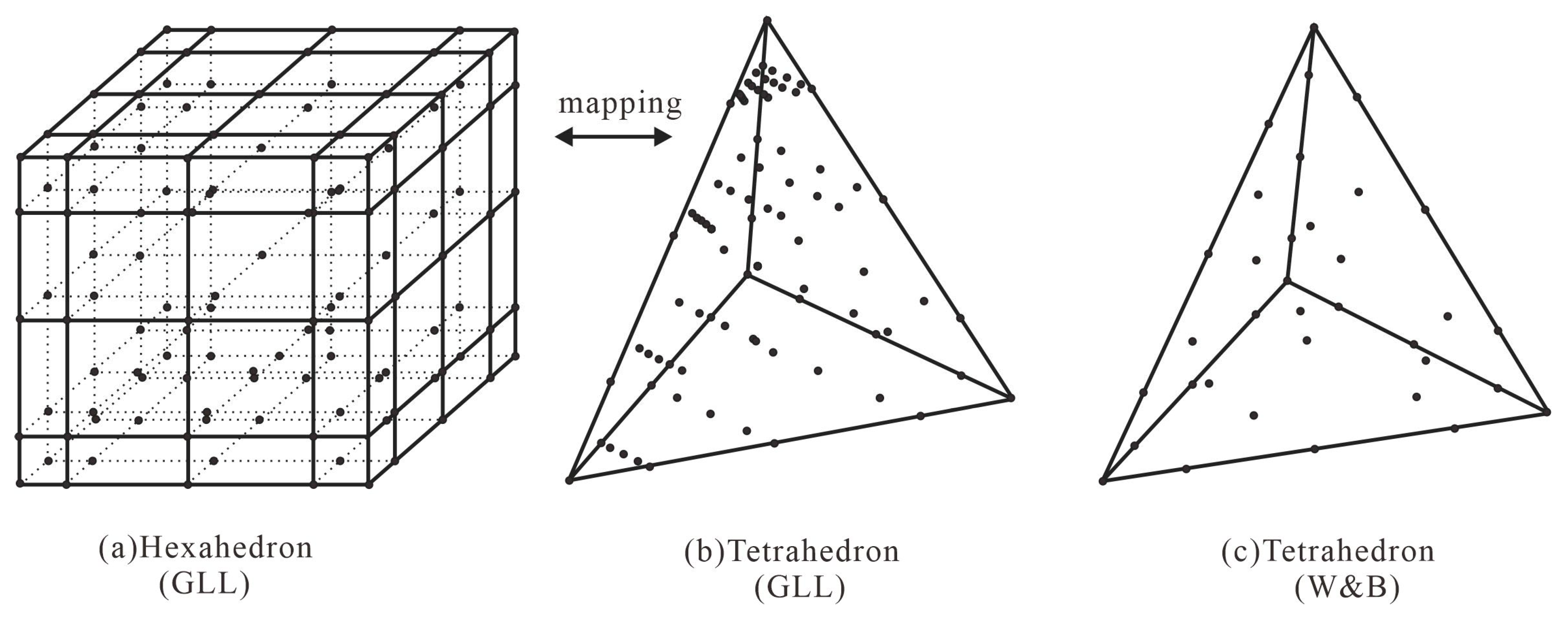
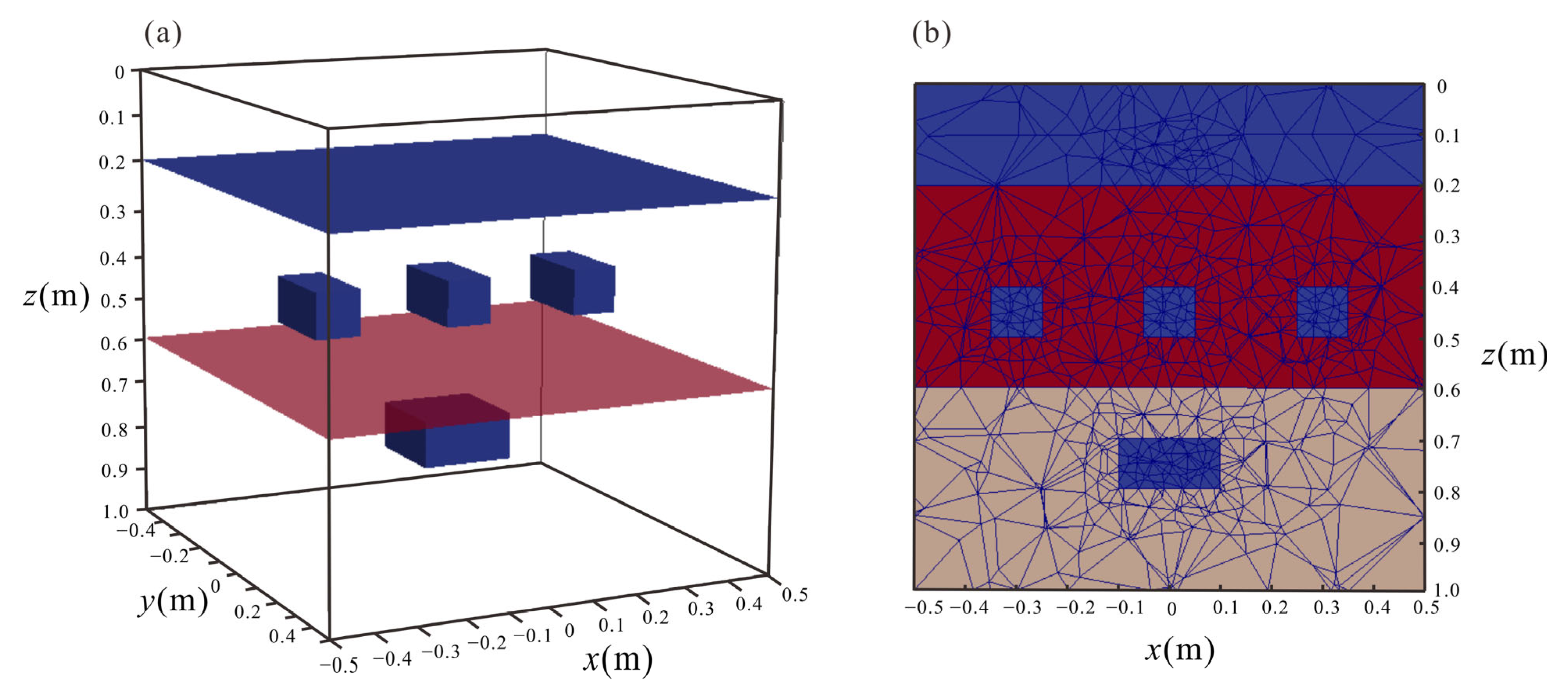
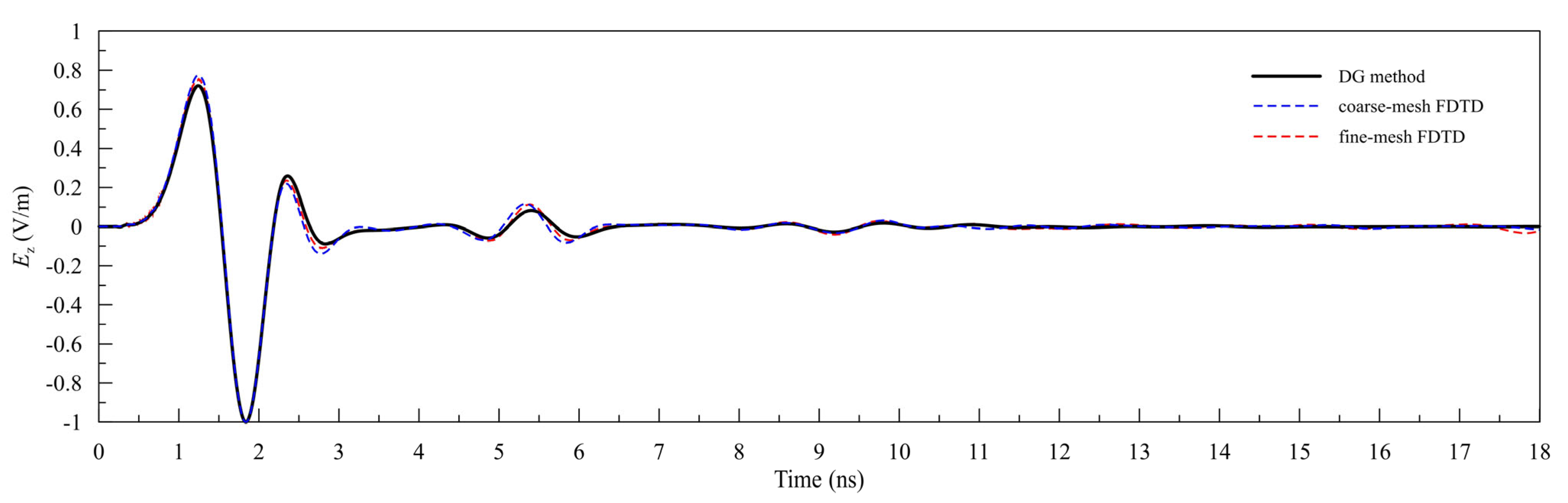

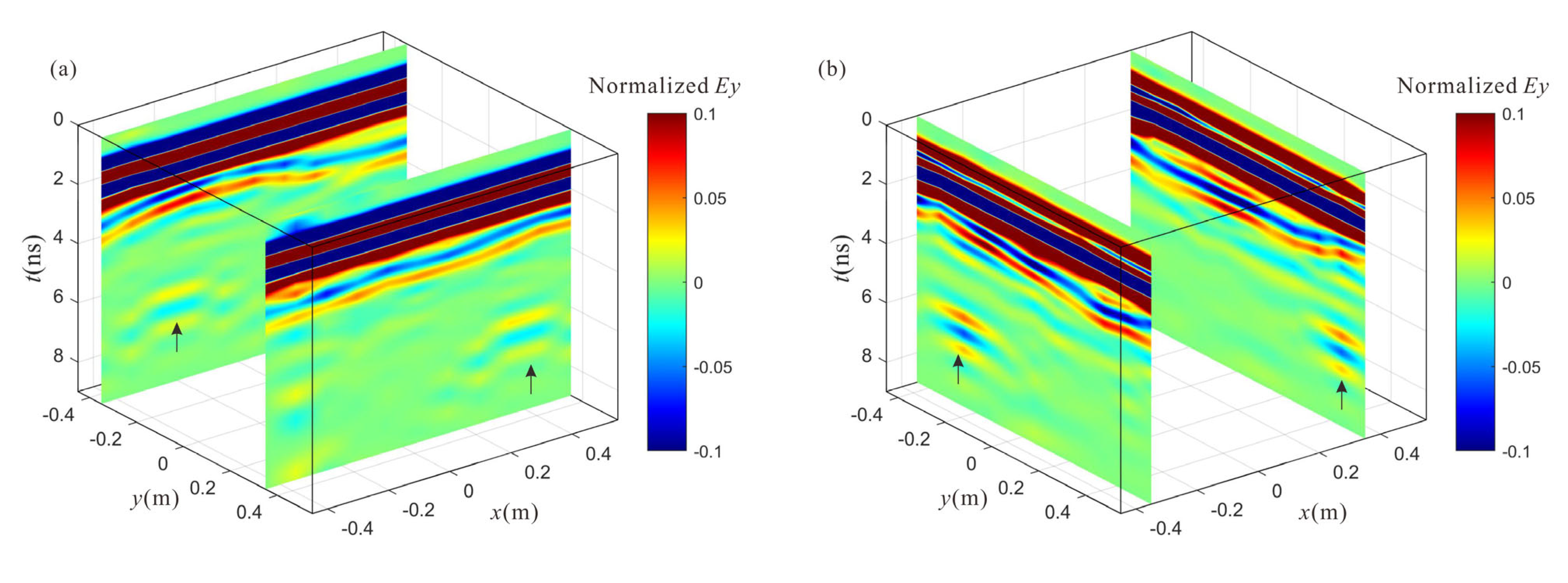
| Methods | Number of Elements | DoFs | Δt (ns) | Calculation Time (s) | Memory Usages (Mb) | Errors |
|---|---|---|---|---|---|---|
| 1st-order DGTD | 6988 | 167,712 | 0.025 | 1.43 | 27 | 0.02796 |
| FDTD-1 | 175,616 | 1,053,696 | 0.025 | 18.85 | 204 | 0.03088 |
| 2nd-order DGTD | 6988 | 419,280 | 0.00625 | 11.55 | 49 | 0.00326 |
| FDTD-2 | 343,000 | 2,058,000 | 0.00625 | 63.46 | 260 | 0.00503 |
| 3rd-order DGTD | 6988 | 2,515,680 | 0.0028 | 59.76 | 84 | 0.00033 |
| FDTD-3 | 2,744,000 | 16,464,000 | 0.0028 | 1070.13 | 678 | 0.00053 |
| Methods | DoFs | Calculation Time (s) | Memory Usages (Mb) |
|---|---|---|---|
| coarse-mesh FDTD | 6,000,000 | 994.45 | 522 |
| fine-mesh FDTD | 384,000,000 | 58,569.41 | 21,042 |
| DGTD | 5,435,280 | 190.45 | 161 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, S.; Yin, C.; Li, J.; Zhu, J.; Liu, W. A High Efficiency Discontinuous Galerkin Method for 3D Ground-Penetrating Radar Simulation. Remote Sens. 2025, 17, 228. https://doi.org/10.3390/rs17020228
Xue S, Yin C, Li J, Zhu J, Liu W. A High Efficiency Discontinuous Galerkin Method for 3D Ground-Penetrating Radar Simulation. Remote Sensing. 2025; 17(2):228. https://doi.org/10.3390/rs17020228
Chicago/Turabian StyleXue, Shuyang, Changchun Yin, Jing Li, Jiao Zhu, and Wuyang Liu. 2025. "A High Efficiency Discontinuous Galerkin Method for 3D Ground-Penetrating Radar Simulation" Remote Sensing 17, no. 2: 228. https://doi.org/10.3390/rs17020228
APA StyleXue, S., Yin, C., Li, J., Zhu, J., & Liu, W. (2025). A High Efficiency Discontinuous Galerkin Method for 3D Ground-Penetrating Radar Simulation. Remote Sensing, 17(2), 228. https://doi.org/10.3390/rs17020228








