Band Selection Algorithm Based on Multi-Feature and Affinity Propagation Clustering
Abstract
1. Introduction
- We propose a novel similarity matrix construction method that integrates band texture features with Euclidean distance to construct the similarity matrix. This approach addresses the limitations of traditional methods, which rely on a single source of information for constructing similarity matrices and face challenges in selecting initial values for clustering algorithms. Notably, it also mitigates the issue of Euclidean distance being relatively insensitive to differences in spectral amplitude.
- A band selection method (GE-AP) combining multi-feature extraction and Affine Propagation Clustering is proposed. This method considers the column and row directions, interval, distribution degree, information content, and spectral relationships of the band images, offering better universality compared to traditional methods based on mutual information and Euclidean distance.
- The feasibility of the above two points is objectively and thoroughly validated. In practical applications, the GE-AP method is compared with three other state-of-the-art methods using the overall classification accuracy (OA) [21] and Kappa coefficient [22] metrics. The experimental results further verify the classification performance after band selection by the GE-AP method, demonstrating its effectiveness and consistency.
2. Related Works
3. Methods
3.1. Grayscale Symbiosis Matrix
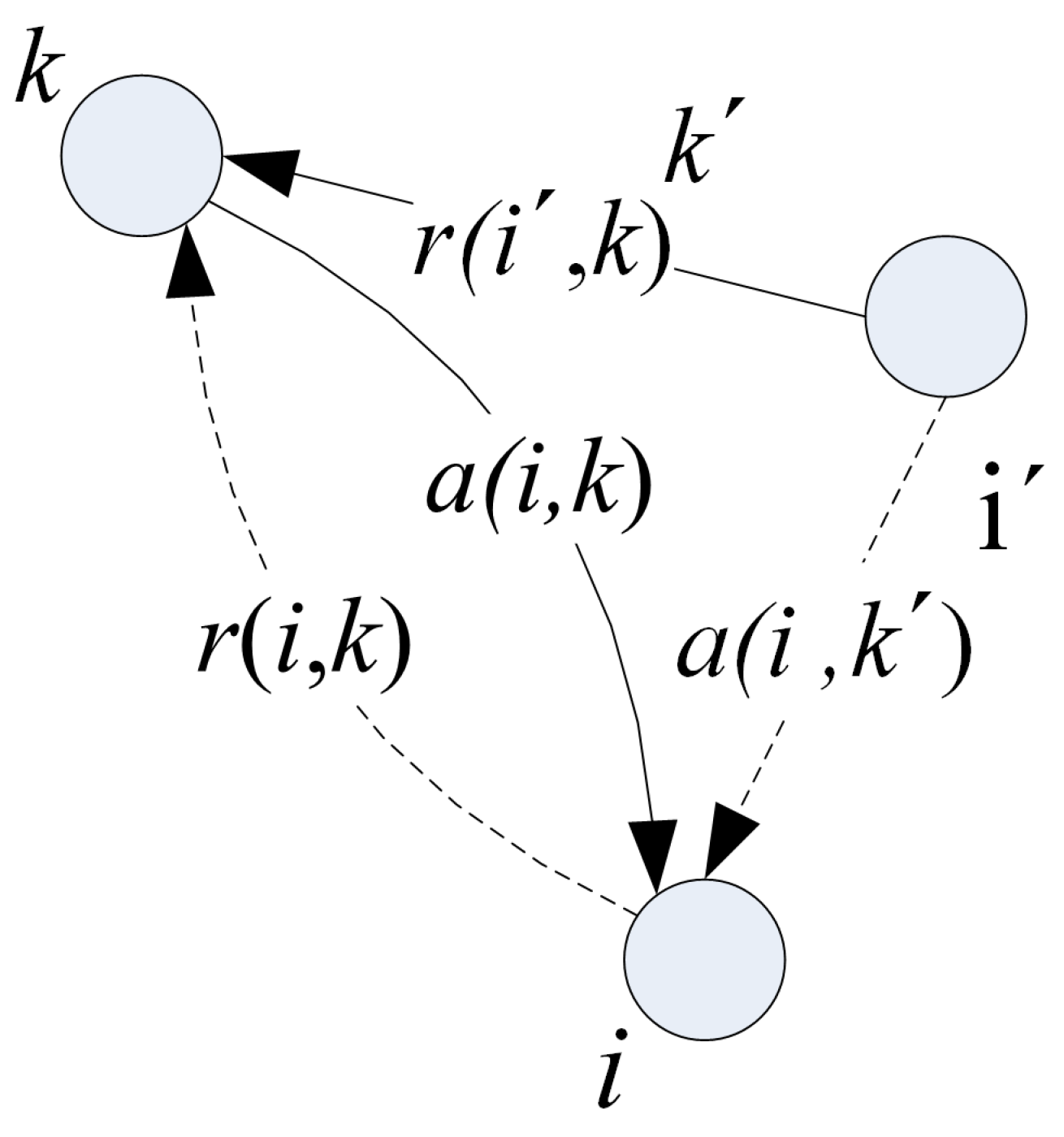
3.2. Affine Propagation Clustering Algorithm (AP)
3.3. Band Selection Based on Multi-Feature and Affine Propagation Clustering Algorithm
3.3.1. Similarity Matrix Construction
3.3.2. Band Selection Process of Affine Propagation Clustering Algorithm
3.3.3. Band Selection Framework Based on GE-AP Algorithm
4. Experiment
4.1. Experimental Setup
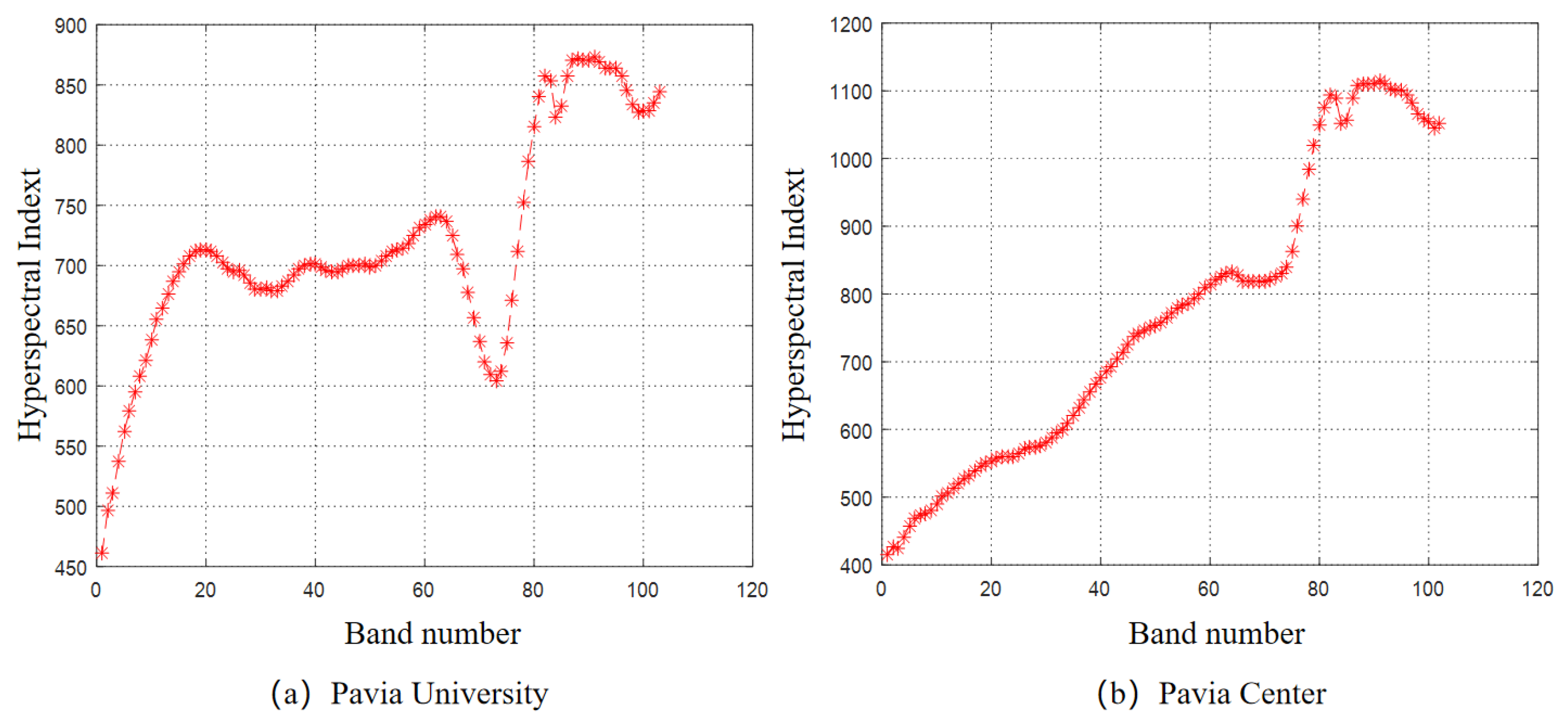
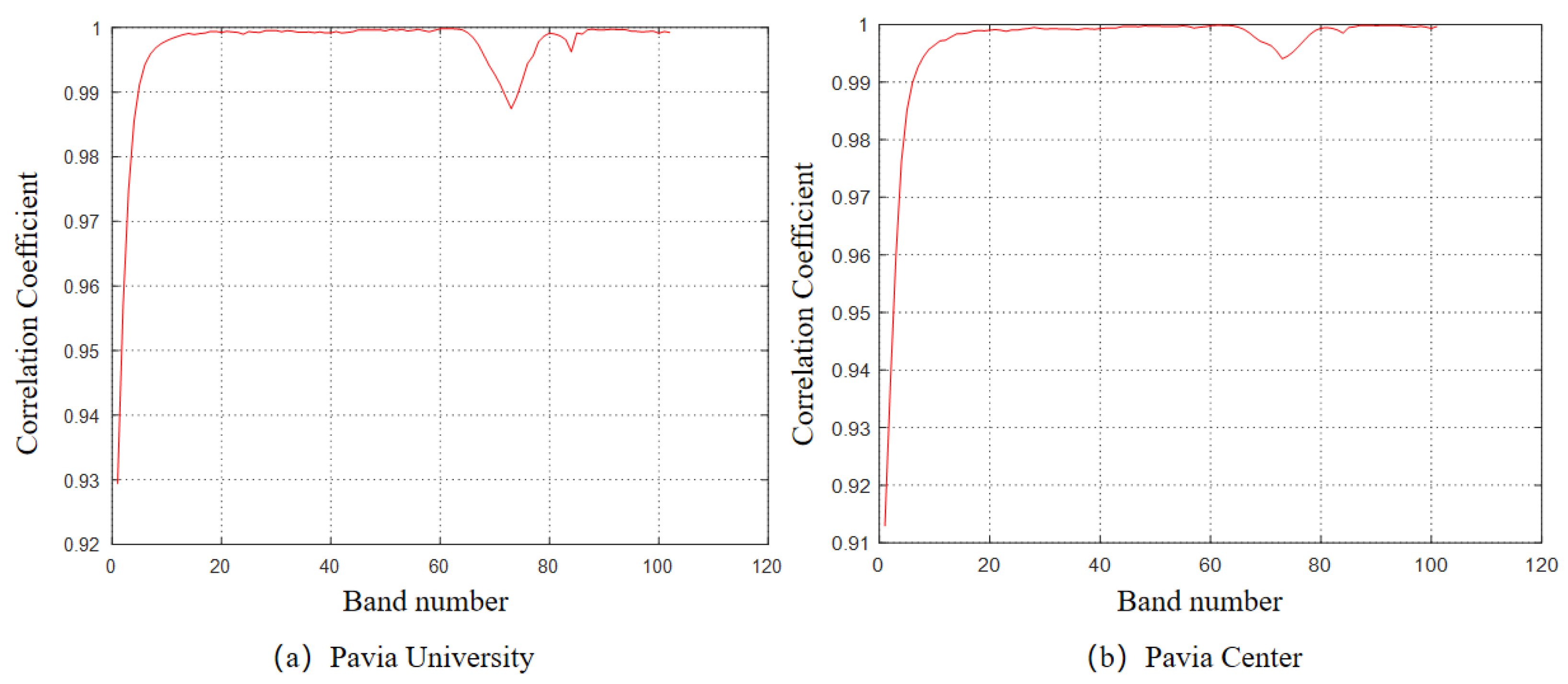
4.2. Compare the Experimental Simulation Results
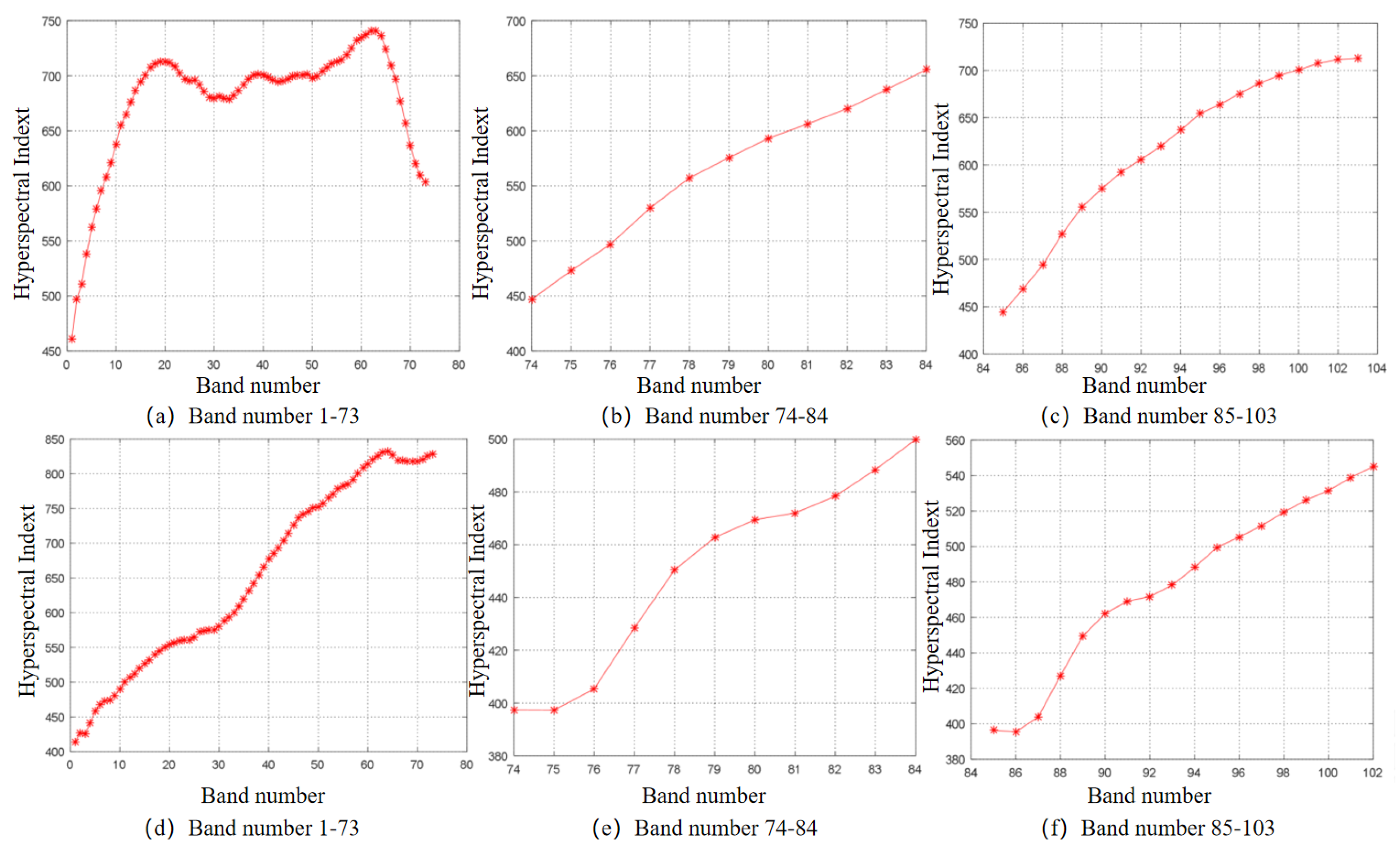
4.3. Experimental Results of Band Selection Based on GE-AP Algorithm
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cozzolino, D.; Williams, P.; Hoffman, L. An overview of pre-processing methods available for hyperspectral imaging applications. Microchem. J. 2023, 193, 109129. [Google Scholar] [CrossRef]
- Cheng, X.; Huo, Y.; Lin, S.; Dong, Y.; Zhao, S.; Zhang, M.; Wang, H. Deep feature aggregation network for hyperspectral anomaly detection. IEEE Trans. Instrum. Meas. 2024, 73, 5033016. [Google Scholar] [CrossRef]
- Shaik, R.U.; Periasamy, S.; Zeng, W. Potential assessment of PRISMA hyperspectral imagery for remote sensing applications. Remote. Sens. 2023, 15, 1378. [Google Scholar] [CrossRef]
- Khan, A.; Vibhute, A.D.; Mali, S.; Patil, C. A systematic review on hyperspectral imaging technology with a machine and deep learning methodology for agricultural applications. Ecol. Inform. 2022, 69, 101678. [Google Scholar] [CrossRef]
- Vivone, G. Multispectral and hyperspectral image fusion in remote sensing: A survey. Inf. Fusion 2023, 89, 405–417. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, M.; Lin, S.; Zhou, K.; Zhao, S.; Wang, H. Two-stream isolation forest based on deep features for hyperspectral anomaly detection. IEEE Geosci. Remote. Sens. Lett. 2023, 20, 5504205. [Google Scholar] [CrossRef]
- Huo, Y.; Cheng, X.; Lin, S.; Zhang, M.; Wang, H. Memory-augmented Autoencoder with Adaptive Reconstruction and Sample Attribution Mining for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote. Sens. 2024, 62, 5518118. [Google Scholar] [CrossRef]
- Mou, L.; Saha, S.; Hua, Y.; Bovolo, F.; Bruzzone, L.; Zhu, X.X. Deep reinforcement learning for band selection in hyperspectral image classification. IEEE Trans. Geosci. Remote. Sens. 2021, 60, 5504414. [Google Scholar] [CrossRef]
- Fu, B.; Sun, X.; Cui, C.; Zhang, J.; Shang, X. Structure-preserved and weakly redundant band selection for hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2024, 17, 12490–12504. [Google Scholar] [CrossRef]
- Zhuang, J.; Zheng, Y.; Guo, B.; Yan, Y. Globally Deformable Information Selection Transformer for Underwater Image Enhancement. IEEE Trans. Circuits Syst. Video Technol. 2024. [Google Scholar] [CrossRef]
- Lever, J.; Krzywinski, M.; Altman, N. Principal Component Analysis. Nat. Methods 2017, 14, 641–642. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, M.; Bian, X.; Tian, L.; Tang, C. Progress of Independent Component Analysis and Its Recent Application in Spectroscopy Quantitative Analysis. Microchem. J. 2024, 202, 110836. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, B.; Yang, J.; Zhou, J.; Xu, Y. Linear Discriminant Analysis. Nat. Rev. Methods Prim. 2024, 4, 70. [Google Scholar] [CrossRef]
- Dash, S.; Chakravarty, S.; Giri, N.C.; Agyekum, E.B.; AboRas, K.M. Minimum Noise Fraction and Long Short-Term Memory Model for Hyperspectral Imaging. Int. J. Comput. Intell. Syst. 2024, 17, 16. [Google Scholar] [CrossRef]
- Chavez, P.S.; Kwarteng, A.Y. Extracting spectral contrast in Landsat thematic mapper image data using selective principal component analysis. Photogramm. Eng. Remote. Sens. 1989, 57, 339–348. [Google Scholar]
- Jia, X.P.; Richards, J.A. Segmented principal components transformation for efficient hyperspectral remote image display and classification. IEEE Trans. Geosci. Remote. Sens. 1999, 37, 538–542. [Google Scholar]
- Mika, S.; Ratsch, G.; Weston, J.; Scholkopf, B.; Mullers, K.R. Fisher discriminant analysis with kernels. In Proceedings of the Neural Networks for Signal Processing IX, Madison, WI, USA, 25 August 1999. [Google Scholar]
- Velasco-Forero, S.; Angulo, J.; Chanussot, J. Morphological image distances for hyperspectral dimensionality exploration using Kernel-PCA and ISOMAP. In Proceedings of the Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; pp. III-109–III-112. [Google Scholar]
- He, X.F.; Niyogi, P. Locality preserving projections. In Proceedings of the Annual Conference on Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023; pp. 153–160. [Google Scholar]
- Ma, L.; Crawford, M.M.; Tian, J. Local manifold learning-based k-nearest neighbor for hyperspectral image classification. IEEE Trans. Geosci. Remote. Sens. 2010, 48, 4099–4109. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, C.; Zhang, L. A New Dimensionality Reduction Method for Hyperspectral Images. J. Image Graph. 2005, 10, 218–222. [Google Scholar]
- Tang, W.; Hu, J.; Zhang, H.; Wu, P.; He, H. Kappa Coefficient: A Popular Measure of Rater Agreement. Shanghai Arch. Psychiatry 2015, 27, 62–67. [Google Scholar]
- Zhang, B.; Wang, X.; Liu, J.; Zheng, L.; Tong, Q. Hyperspectral image processing and analysis system (HIPAS) and its applications. Photogramm. Eng. Remote. Sens. 2000, 66, 605–609. [Google Scholar]
- Chavez, P.S.; Berlin, G.L.; Sowers, L.B. Statistical method for selecting Landsat MSS ratio. J. Appl. Photogr. Eng. 1982, 1, 23–30. [Google Scholar]
- Charles, S. Selecting band combination from multispectral data. Photogramm. Eng. Remote. Sens. 1985, 51, 681–687. [Google Scholar]
- Velez-Reyes, M.; Linares, D.M. Comparison of principal-component-based band selection methods for hyperspectral imagery. In Proceedings of the International Symposium on Remote Sensing, Toulouse, France, 17–21 September 2021; SPIE: St Bellingham, WA, USA, 2002; pp. 361–369. [Google Scholar]
- Nakariyakul, S.; Casasent, D.P. Hyperspectral waveband selection for contaminant detection on poultry carcasses. Opt. Eng. 2008, 47, 1–9. [Google Scholar]
- Diani, M.; Acito, N.; Greco, M.; Corsini, G. A new band selection strategy for target detection in hyperspectral images. Knowl.-Based Intell. Inf. Eng. Syst. 2008, 5159, 424–431. [Google Scholar]
- Omam, M.A.; Torkamani-Azar, F. Band selection of hyperspectral-image based on weighted independent component analysis. Opt. Rev. 2010, 17, 367–370. [Google Scholar] [CrossRef]
- Fisher, K.; Chang, C.I. Progressive band selection for satellite hyperspectral data compression and transmission. J. Appl. Remote. Sens. 2010, 4, 041770. [Google Scholar]
- Gu, Y.; Zhang, Y. Feature extraction of hyperspectral data based on automatic subspace division. Remote. Sens. Technol. Appl. 2003, 18, 801–804. [Google Scholar]
- Ni, G.; Shen, Y. Wavelet-Based Principal Components Analysis Feature Extraction Method for Hyperspectral Images. Trans. Beijing Inst. Technol. 2007, 7, 621–624. [Google Scholar]
- Luo, R.; Pi, Y. Supervised Neighborhood Preserving Embedding Feature Extraction of Hyperspectral Imagery. Acta Geod. Cartogr. Sin. 2014, 43, 508–513. [Google Scholar]
- Ding, L.; Tang, P.; Li, H. Mixed spectral unmixing analysis based on manifold learning. Infrared Laser Eng. 2013, 9, 2421–2425. [Google Scholar]
- Qian, Y.; Yao, F.; Jia, S. Band selection for hyperspectral imagery using affinity propagation. IET Comput. Vis. 2009, 3, 213–222. [Google Scholar] [CrossRef]
- Yin, J.; Wang, Y.; Zhao, Z. Optimal band selection for hyperspectral image classification based on inter-class separability. In Proceedings of the 2010 Symposium on Photonics and Optoelectronics, Chengdu, China, 19–21 June 2010; pp. 1–4. [Google Scholar]
- Jia, S.; Ji, Z.; Qian, Y.; Shen, L. Unsupervised band selection for hyperspectral imagery classification without manual band removal. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2012, 5, 531–543. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, D.; Zhang, L. Feature band selection for online multispectral palmprint recognition. IEEE Trans. Inf. Forensics Secur. 2012, 7, 1094–1099. [Google Scholar] [CrossRef]
- Zhao, H.; Li, M.; Li, N. A band selection method based on improved subspace partition. Infrared Laser Eng. 2015, 44, 3155–3160. [Google Scholar]
- Guo, T.; Hua, W.; Liu, X. Rapid hyperspectral band selection approach based on clustering and optimal index algorithm. Opt. Tech. 2016, 42, 496–500. [Google Scholar]
- Zhang, A.; Du, N.; Kang, X.; Guo, C. Hyperspectral adaptive band selection method through nonlinear transform and information adjacency correlation. Infrared Laser Eng. 2017, 46, 05308001. [Google Scholar]
- Zhai, H.; Zhang, H.; Zhang, L. Spectral-spatial clustering of hyperspectral remote sensing image with sparse subspace clustering model. In Proceedings of the 2015 7th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Tokyo, Japan, 2–5 June 2015; pp. 1–4. [Google Scholar]
- Zhai, H.; Zhang, H.; Zhang, L. Squaring weighted low-rank subspace clustering for hyperspectral image band selection. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 2434–2437. [Google Scholar]
- Haralick, R.M.; Shanmugarm, K.; Dinstein, I. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Kouyate, F.; Brisco, B.; Williams, T.L. Textural information in SAR Images. IEEE Trans. Geosci. Remote Sens. 1986, 24, 235–245. [Google Scholar] [CrossRef]
- Frey, B.J.; Dueck, D. Clustering by passing messages between data points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef]
- Pavia University and Pavia Center Hyperspectral Datasets. Available online: http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes#Pavia_Centre_and_University (accessed on 15 October 2024).
- Chang, C.I.; Du, Q.; Sun, T.L.; Althouse, M.L. A joint band prioritization and band-decorrelation approach to band selection for hyperspectral image classification. IEEE Trans. Geosci. Remote. Sens. 1999, 37, 2631–2641. [Google Scholar] [CrossRef]
- Huang, R.; Li, X. Band selection based on evolution algorithm and sequential search for hyperspectral classification. In Proceedings of the 2008 International Conference on Audio, Language and Image Processing, Shanghai, China, 7–9 July 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1270–1273. [Google Scholar]
- Zhao, H.; Bruzzone, L.; Guan, R.; Zhou, F.; Yang, C. Spectral-spatial genetic algorithm-based unsupervised band selection for hyperspectral image classification. IEEE Trans. Geosci. Remote. Sens. 2021, 59, 9616–9632. [Google Scholar] [CrossRef]





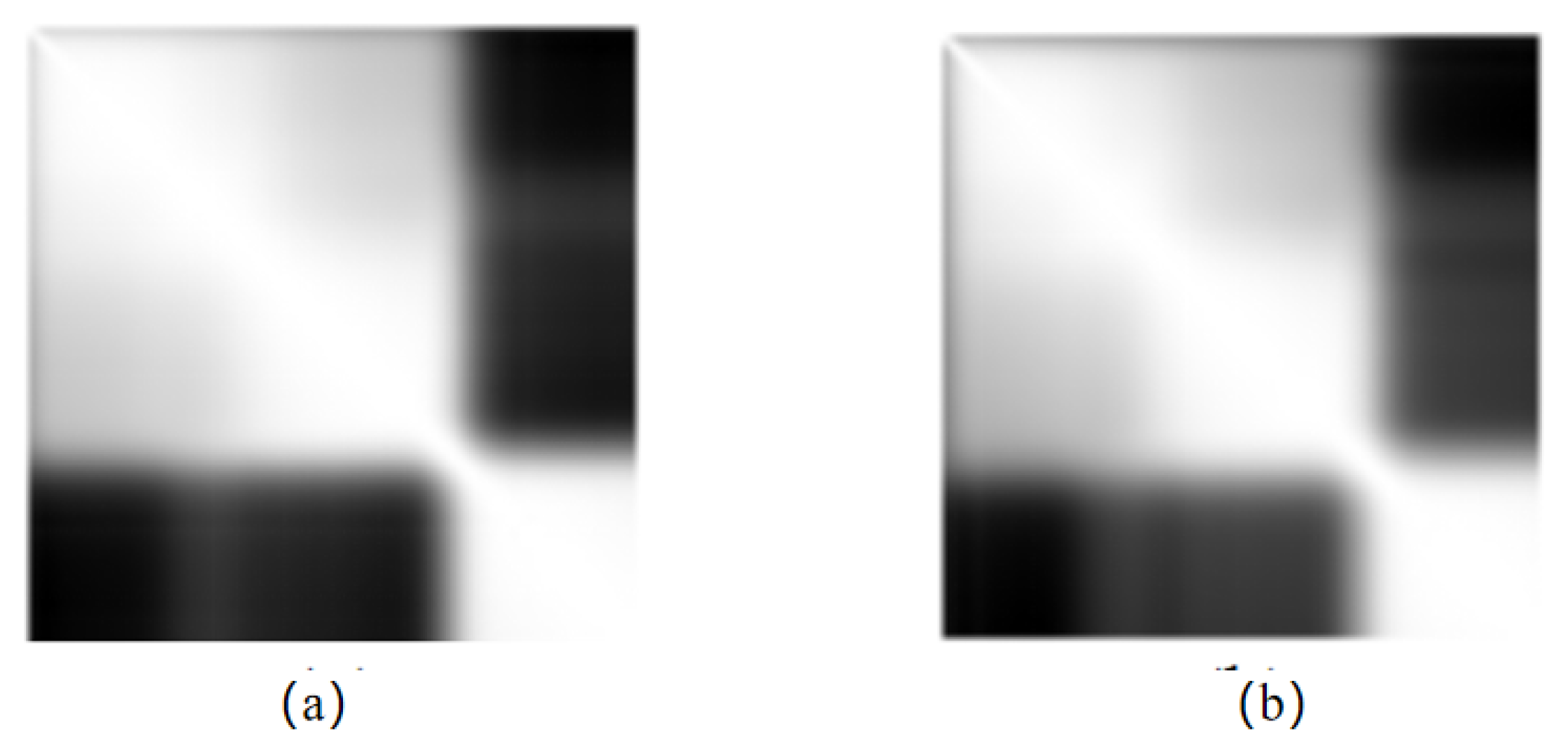


| Ingredient | Extract the Percentage of the Sum of Squares | ||
|---|---|---|---|
| Eigenvalue | Percentage Contribution of Variance% | Cumulative Percentage% | |
| 1 | 66.792 | 64.847 | 64.847 |
| 2 | 29.310 | 28.456 | 93.303 |
| 3 | 5.289 | 5.135 | 98.439 |
| Ingredient | Extract the Percentage of the Sum of Squares | ||
|---|---|---|---|
| Eigenvalue | Percentage Contribution of Variance% | Cumulative Percentage% | |
| 1 | 74.307 | 72.850 | 72.850 |
| 2 | 21.447 | 21.026 | 93.876 |
| 3 | 4.316 | 4.232 | 98.108 |
| Pavia University | Pavia Center | ||
|---|---|---|---|
| Band Number | Band Index | Band Number | Band Index |
| 91 | 872.9048 | 91 | 1114.185 |
| 88 | 871.5208 | 90 | 1111.205 |
| 90 | 870.9870 | 88 | 1110.937 |
| 89 | 870.7075 | 89 | 1110.31 |
| 87 | 870.1934 | 92 | 1109.339 |
| 92 | 869.1692 | 87 | 1107.67 |
| 93 | 863.9795 | 93 | 1102.059 |
| 95 | 863.7521 | 95 | 1101.782 |
| 94 | 863.5711 | 94 | 1101.5 |
| 96 | 857.7908 | 82 | 1095.023 |
| 96 | 1094.566 | ||
| Cluster Center Band Number | Number of Bands per Class | Band Number of Each Class |
|---|---|---|
| 5 | 7 | 3~9 |
| 19 | 9 | 13~21 |
| 23 | 7 | 10~12, 22~25 |
| 33 | 15 | 26~37, 67~69 |
| 42 | 10 | 38~46, 66 |
| 51 | 11 | 47~56, 65 |
| 59 | 8 | 57~64 |
| 71 | 5 | 2, 70~73 |
| 75 | 5 | 1, 74~77 |
| 93 | 26 | 78~103 |
| Cluster Center Band Number | Number of Bands per Class | Band Number of Each Class |
|---|---|---|
| 7 | 10 | 3~12 |
| 14 | 9 | 13~21 |
| 23 | 4 | 2, 22, 23, 24 |
| 30 | 12 | 1, 25~35 |
| 40 | 9 | 36~44 |
| 46 | 3 | 45, 46, 47 |
| 51 | 9 | 48~53, 68, 69, 70 |
| 55 | 5 | 54~56, 66, 67 |
| 64 | 9 | 57~65 |
| 75 | 8 | 71~78 |
| 86 | 24 | 79~102 |
| Dataset | Methods | OA% | Kappa |
|---|---|---|---|
| MVPCA | 82.18 | 0.762 | |
| ABS | 85.95 | 0.811 | |
| Pavia | ASP | 87.95 | 0.836 |
| University | GA | 84.12 | 0.784 |
| SSGA | 88.45 | 0.846 | |
| GE-AP | 88.21 | 0.838 | |
| MVPCA | 97.65 | 0.967 | |
| ABS | 90.58 | 0.865 | |
| Pavia | ASP | 97.12 | 0.959 |
| Center | GA | 84.12 | 0.784 |
| SSGA | 97.28 | 0.962 | |
| GE-AP | 98.63 | 0.979 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, J.; Chen, W.; Huang, X.; Yan, Y. Band Selection Algorithm Based on Multi-Feature and Affinity Propagation Clustering. Remote Sens. 2025, 17, 193. https://doi.org/10.3390/rs17020193
Zhuang J, Chen W, Huang X, Yan Y. Band Selection Algorithm Based on Multi-Feature and Affinity Propagation Clustering. Remote Sensing. 2025; 17(2):193. https://doi.org/10.3390/rs17020193
Chicago/Turabian StyleZhuang, Junbin, Wenying Chen, Xunan Huang, and Yunyi Yan. 2025. "Band Selection Algorithm Based on Multi-Feature and Affinity Propagation Clustering" Remote Sensing 17, no. 2: 193. https://doi.org/10.3390/rs17020193
APA StyleZhuang, J., Chen, W., Huang, X., & Yan, Y. (2025). Band Selection Algorithm Based on Multi-Feature and Affinity Propagation Clustering. Remote Sensing, 17(2), 193. https://doi.org/10.3390/rs17020193






